Azimuth-Variant Signal Processing in High-Altitude Platform Passive SAR with Spaceborne/Airborne Transmitter
Abstract
: High-altitude platforms (HAP) or near-space vehicle offers several advantages over current low earth orbit (LEO) satellite and airplane, because HAP is not constrained by orbital mechanics and fuel consumption. These advantages provide potential for some specific remote sensing applications that require persistent monitoring or fast-revisiting frequency. This paper investigates the azimuth-variant signal processing in HAP-borne bistatic synthetic aperture radar (BiSAR) with spaceborne or airborne transmitter for high-resolution remote sensing. The system configuration, azimuth-variant Doppler characteristics and two-dimensional echo spectrum are analyzed. Conceptual system simulation results are also provided. Since the azimuth-variant BiSAR geometry brings a challenge for developing high precision data processing algorithms, we propose an image formation algorithm using equivalent velocity and nonlinear chirp scaling (NCS) to address the azimuth-variant signal processing problem. The proposed algorithm is verified by numerical simulation results.1. Introduction
Satellite and airplane represent two well established platforms in radar and remote sensing arena for years [1,2]. However, in recent years a new platform has received much attention, which operates at an altitude between 20 km and 100 km above the Earth’s surface and is called high-altitude platform [3–6] or near-space vehicle [7]. Traditionally very few sensors can operate in the altitude between 20 km and 100 km because the atmosphere is too thin to support flying for airplanes and too thick to sustain orbit for satellites. In this region, there are no ionospheric scintillations that may significantly degrade microwave communication and navigation performance. Moreover, not constrained by orbital mechanics like satellites and high fuel consumption like airplanes, HAPs can move at a high speed. More importantly, HAPs can provide a large footprint and a long mission duration that are commonly associated with satellites and fast responsiveness that is commonly associated with unmanned aerial vehicles. These advantages are particularly useful for some specific remote sensing applications that require a fast revisiting frequency [8]. This also explains why HAPs have received so much attention in recent years [9].
By placing a radar transmitter or receiver inside a HAP, many functions that are currently performed by satellites or airplanes could be performed in a more efficient way [10]. In [11], we investigated the application of HAP passive radar for regional remote sensing. In this paper, we present azimuth-variant signal processing for HAP passive bistatic synthetic aperture radar (BiSAR) with spaceborne/airborne transmitter for high-resolution remote sensing. In recent years, BiSAR has received much recognition [12–14]. There is also a resurgence of interest in passive radar [15], partly because bistatic radar requires no expensive transmitter. The BiSARs discussed in literature are mainly azimuth-invariant configurations, for example the “Tandem” configuration where the transmitter and receiver moving one after another with the same trajectory and the “translational invariant” configuration where the transmitter and receiver moving along parallel trajectories with the same velocity. Several representative azimuth-variant configurations are the SARs with forward-looking receivers [16,17] or different experimented configurations with the moving transmitter (receiver) and fixed receiver (transmitter) [18]. Several signal processing algorithms have also been proposed for these configurations [19,20]. The HAP-borne BiSAR described in this paper is an azimuth-variant configuration; when compared with the azimuth-invariant configurations, it has much more complex characteristics in signal models, spatial resolution, and image formation algorithm.
In this paper, we present the azimuth-variant signal processing in HAP-borne passive BiSAR with spaceborne or airborne transmitter for high-resolution remote sensing. First, the system model and azimuth-variant characteristics are introduced. Then, an extended nonlinear chirp scaling (NCS) imaging algorithm is derived to address the azimuth-variant Doppler signal characteristics. The remaining sections are organized as follows. In Section 2, the background of HAP and the motivation of this paper are introduced. In Section 3, the system configuration and geometry model are introduced. Next, the azimuth-variant Doppler chirp rate and two-dimensional (2-D) spectrum model are analyzed in Section 4. Finally, an imaging algorithm using equivalent velocity and NCS is derived in Section 5. This paper is concluded in Section 6.
2. Background and Motivation
It appears that HAP or near-space vehicle can provide an optimal platform for passive BiSAR due to the following reasons [9,10,21]:
HAP includes free-floater and maneuvering vehicle, but this paper considers only the free-floater. Free-floater has extremely small radar cross section (RCS), making it relatively invulnerable to most traditional track and location methods. At this altitude the acquisition and tracking will be a difficulty since few weapons are designed to engage a target with a very low RCS. Even if the acquisition and location problems are resolved, HAP-borne sensors are still difficult to be destroyed. Free-floater can be manufactured in two basic types: super-pressure and zero-pressure. Super-pressure free-floater is inflated and sealed like a child’s helium balloon. Zero-pressure free-floater has a venting system that ensures the pressure inside the balloon is same as the surrounding atmosphere and thus it is less vulnerable to puncture.
HAP operates in the altitude above the troposphere and atmosphere region where most weather occurs. There are no clouds, thunderstorms and precipitation in this altitude. Free-floater can stay at a specific near-space site almost indefinitely to provide a stationary observation. Maneuvering vehicle can station-keep over a specific position and fly at a high speed. Moreover, HAP can use some propulsion scheme to overcome unusual winds.
HAP is much closer to the desired targets than its orbital cousins. Distance is critical to receiving low power signals. Consider a point at nadir, HAPs are 10–20 times closer to the targets than a typical 400 km LEO satellite. This distance differential implies that HAP radar could detect much weaker signals (10 dB to 13 dB weaker). Moreover, the footprint covered by a HAP is also satisfactory for regional remote sensing.
The last advantage is low cost. The inherent simplicity, recoverability, relative lack of requirement for complex infrastructures, and lack of space-hardening requirements all contribute this strong advantage.
3. HAP-borne Passive BiSAR Remote Sensing
The HAP-borne passive BiSAR involves placing a passive receiver inside a HAP and utilizing opportunistic illuminators such as global navigation satellite systems (GNSS) and spaceborne or airborne radars. The use of GNSS as the transmitter has the advantages of entire planet coverage and simple transmitter-receiver synchronization [22], but the received GNSS signals are too weak [23–26]. To overcome this disadvantage, this paper uses spaceborne or airborne radar as the passive BiSAR transmitter, in which the transmitter and receiver may have unequal velocities. Note that, although the passive receiver may be stationary, an aperture synthesis can still be obtained by the motion of the transmitter only.
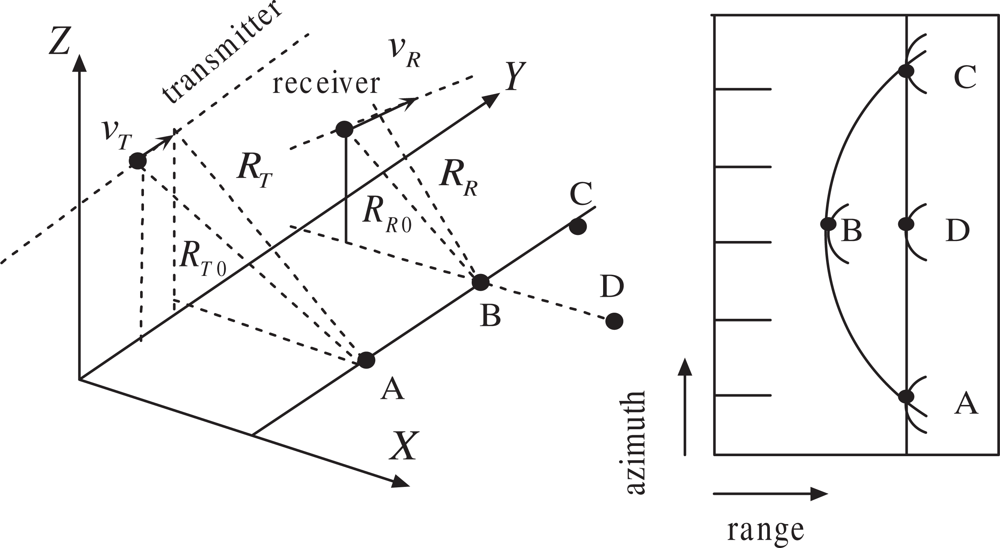
The HAP-borne passive receiver considered in this paper consists of two channels, as shown in Figure 1. One channel is fixed to collect the direct-path signals coming from the transmitter antenna sidelobes, which can be used as the reference signal for subsequent matched filtering or for BiSAR time and phase/frequency synchronization compensation [27]. The second channel is configured to gather the reflected signals with which remote sensing is attempted. Note that another configuration using digital beamforming on the receiver [28] is also implementable. In this case, the receiver antenna is split into multiple sub-apertures, and each sub-aperture signal is separately amplified, down-converted and digitized. The digital signals are then combined in a dedicated processor to form multiple sub-beams.
When compared with spaceborne or airborne BiSARs, this passive BiSAR offers several promising superiorities. Besides possible persistent regional monitoring and low cost, another superiority is the robust survivability in military reconnaissances because detecting its passive receiver is a technical challenge. Moreover, rather than emitting signals, it relies on opportunistic transmitters; hence, it has no impacts on existing communication and navigation systems. This is an advantage for urban area and human settlement remote sensing.
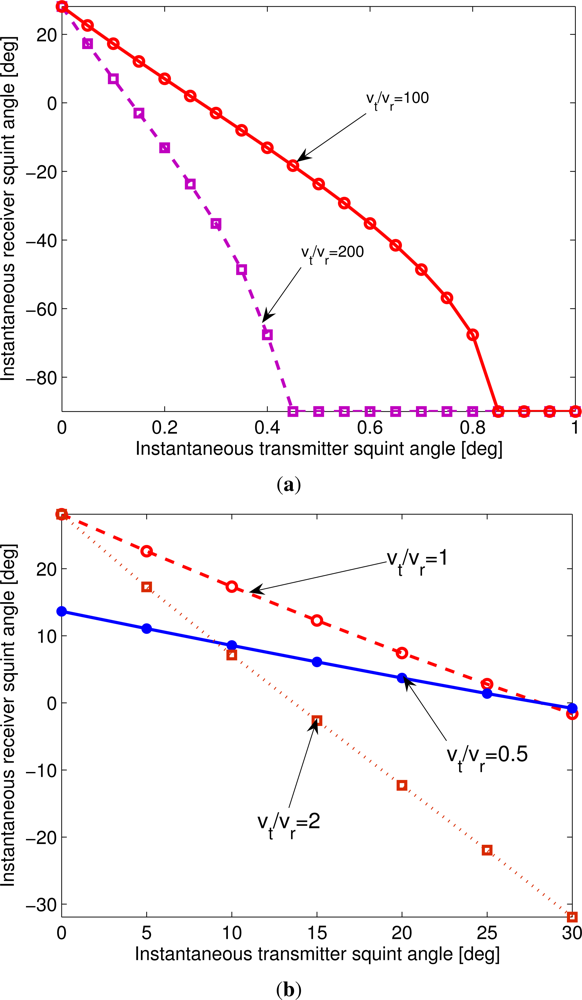
For a given imaging target, the target must be simultaneously within the line-of-sight (LOS) to both the transmitter and the receiver. That is to say, antenna direction synchronization must be ensured for the passive BiSAR system [29]. If airborne transmitter is used, the antenna direction synchronization can be implemented though a cooperative flying plan. However, if spaceborne transmitter is employed, it will be a challenge due to the fact that the transmitter and the receiver have a big difference in the flying velocities. Moreover, the satellite antenna direction is often uncontrollable for us. The pulse chasing technique proposed in [30] cannot be easily implemented for noncooperative passive BiSAR configurations, particularly when spaceborne transmitter is employed. For these reasons, we use a wide antenna beamwidth on receiver due to its advantage of high signal-to-noise ratio (SNR) in this system. This can be easily understood from the bistatic radar equation [31].
To implement successfully BiSAR remote sensing, both of the transmitter and receiver antennas should be steered to obtain an overlapping beam coverage on the ground and the exposure of a target is governed by this composite beam pattern. It is necessary to analyze the imaging time and imaging coverage. A space-time diagram-base method was investigated in [32] by employing a rectangular approximation. Consider a flat Earth model and parallel transmitter and receiver flying tracks without squint angles but with different velocities, the imaging time of the HAP-borne passive BiSAR is determined by
4. Azimuth-Variant Doppler Characteristics Analysis
As azimuth-variant geometry brings a challenge for developing high-precision data processing algorithm, an analysis of the azimuth-variant characteristics, such as Doppler and two-dimensional spectrum, is necessary for developing an efficient image formation algorithm. Note that parallel flying tracks and flat Earth model are assumed in this section.
4.1. Doppler Characteristics
At an azimuth time τ, the range history sum to an arbitrary point target can be expressed as
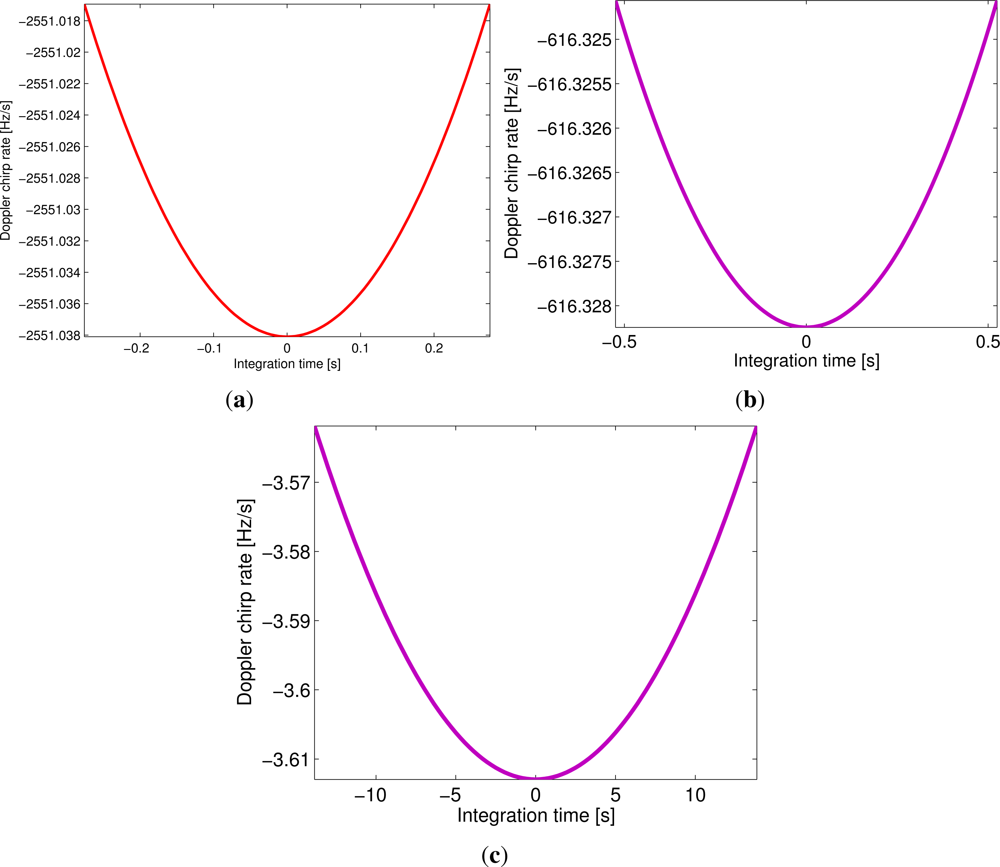
The Doppler chirp rate can be easily derived as
Consequently, the locus of the slant ranges at the beam center crossing times of all targets that are parallel to the azimuth axis follow an approximate hyperbola. As an example, we consider a typical geometry shown in Figure 3(left), where the (x, y) plane is locally tangent to the Earth surface. The targets are assumed to lie on this plane, and the transmitter velocity vector is parallel to the y-axis. Figure 3(right) shows the trajectories of three targets A, B, and C follow a hyperbolic locus. As a consequence, the imaged targets A, B and C will have an equal slant range, i.e., the target B will be shifted to the position D. This is different from general monostatic case, which has a linear locus instead of a hyperbolic one. General range Doppler image formation algorithms cannot handle this problem in a high-precision manner. Consequently, there will be a range ambiguity that does not exist in monostatic SARs. It can be observed from Figure 3 that two and more targets (e.g., A, C and D) locating at different positions with the same range delay at the zero-Doppler but will have different range histories (curvature). Similar phenomena was investigated in [35], where a ground-based stationary receiver is assumed. However, for nonstationary receiver this problem will be much more complex, because the transmitter follows a rectilinear trajectory, while the receiver follows also a rectilinear trajectory and has a different velocity.
The azimuth-variant problem will become more complicated for unflat digital Earth model (DEM) topography. In monostatic or azimuth-invariant BiSAR systems, scene topography can be ignored in developing image formation algorithms because the measured range delay is related with the double target distance and the observed range curvature; hence, topography is only used to project the compressed image from the slant range to the ground range. However, for azimuth-variant BiSAR, it is mandatory to know both the transmitter-to-target distance and the target-to-receiver distance to properly focus the raw data, but they clearly depend also on the target height. In this case, conventional imaging algorithms such as the chirp-scaling and wavenumber-domain may be not suitable to accurately focus the collected data.
It is necessary to develop an image formation algorithm that is usable for azimuth-variant BiSAR configurations. However, most existing BiSAR imaging algorithms are only usable to handle azimuth-invariant BiSAR configurations [36,37] and only a few azimuth-variant BiSAR algorithm can be found [19,20]. Before developing an imaging algorithm for the HAP-borne passive BiSAR system, it is necessary to analyze the two-dimensional spectrum model of the returned signal.
4.2. Two-Dimensional Echo Spectrum Characteristics
Loffeld et al.[38] divided the bistatic phase history into two quasi-monostatic phase histories and expanded them into two Taylor series around the individual points of the stationary phase. In this way, an approximation of the stationary-phase azimuth time is constructed, and a two-dimensional BiSAR spectrum is deduced. Several algorithms have been developed based on this model [39]. Another BiSAR spectrum model using series expansion to express azimuth time as a function of azimuth frequency during azimuth Fourier transform was proposed in [40], and a chirp scaling algorithm was developed based on this model [41]. However, the accuracy is controlled by keeping enough terms in the power series, but only the first several series can be used. Using the Fresnel approximation, a two-dimensional BiSAR spectrum model was derived in [42]. This model can be used only in small a squint angle. Moreover, it has no advantages in approximate error because the Fresnel approximation is used in the algorithm. In summary, most BiSAR spectrum models cannot be used in the BiSAR with a large difference between the transmitter-to-target distance and target-to-receiver distance or a large squint angle.
To evaluate the applicability of the Loffeld’s model for azimuth-variant BiSAR, we suppose the transmitted signal is
After Fourier transforming from range-time domain to range-frequency domain, we then have
Loffeld et al.[38] expanded the phase histories into two Taylor series arond the individual stationary phase points and
However, as noted in [38], the validity of Equation (14) is constrained by
Considering the phase history in Equation (11) and supposing its stationary phase point is τ*, from the principle of stationary phase, we can get
As the instantaneous bistatic range history at the azimuth time, τ can be presented by
For a general monostatic SAR system, a focused SAR image can be obtained from a two-dimensional inverse Fourier transform of Equation (19). However, this method is not effective for the azimuth-variant BiSAR configurations. One reason is that azimuth Doppler frequency is non-uniformly sampled for the azimuth-variant BiSAR configurations, and the other reason is that its precision two-dimensional spectrum is difficult to be obtained in a high-precision manner. This is the reason why azimuth-variant BiSAR imaging algorithm has not been thoroughly researched [39,43,44], while many azimuth-invariant BiSAR imaging algorithms have been proposed [45–48].
5. Azimuth-Variant Bistatic SAR Imaging Algorithm
For the HAP-borne BiSAR with fast-moving transmitter and slow-moving receiver,
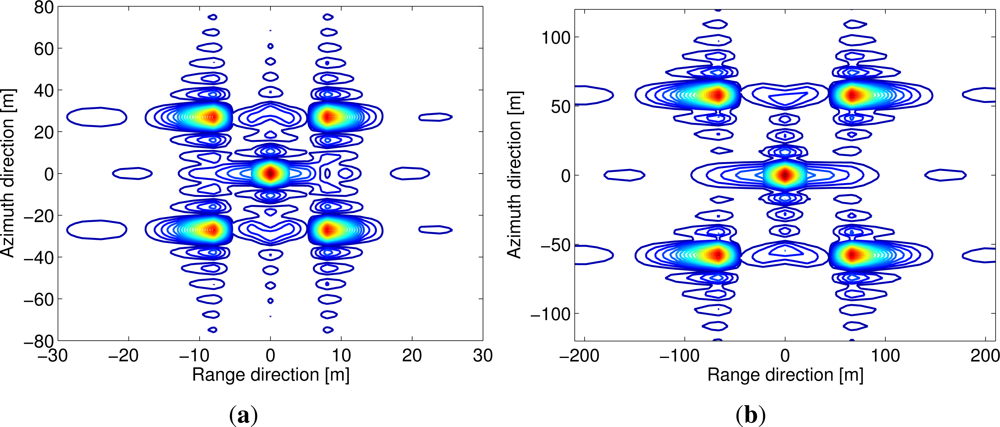
Suppose the transmitter slant range and receiver slant range are fixed to be 800 km and 30 km, Figure 6 gives the range errors caused by the equivalent BiSAR system model. As the relevant phase errors that are smaller than π/4 can be ignored for subsequent imaging algorithms, we can conclude that the equivalent model for small vr is satisfactory for subsequent image formation processing.
The equivalent instantaneous azimuth Doppler frequency fa can then be expressed as
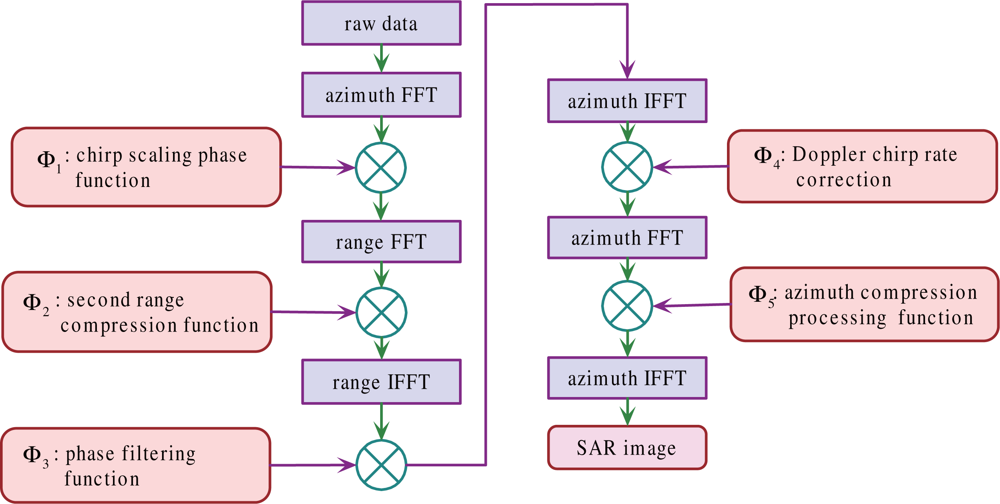
Next, a NCS algorithm, which is similar to the algorithms developed in [35,41], can then be applied. Our algorithm has the processing steps similar to [35,41], but has different compensation phase terms, Φi (i = [1, 2, 3, 4, 5]), because the azimuth-variant Doppler characteristics are considered in deriving the algorithm. Suppose the transmitted signal is
Applying the Fourier transform to the azimuth time τ yields
We perform the Chirp scaling processing with the phase term
Next, the Doppler chirp rate is corrected by
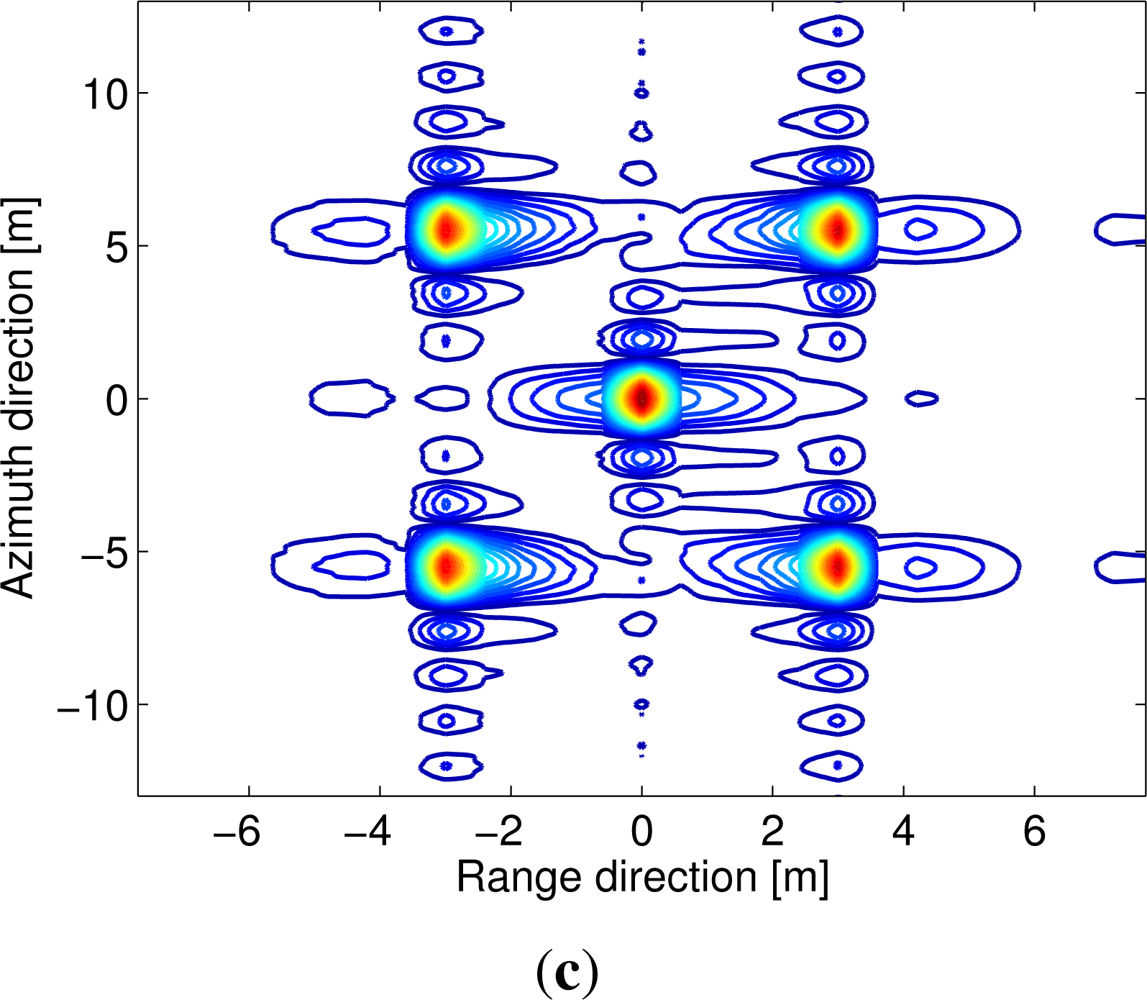
To evaluate the performance of the derived imaging algorithm, four example BiSAR data for five point targets are simulated using the parameters listed in Table 1 and the pulsed repeated frequency (PRF) and pulse duration listed in Table 2. A distance separation of five times of the range/azimuth resolution is assumed in the simulation examples. Additionally, the instantaneous squint angles of the transmitter and receiver at their zero-Doppler frequencies are supposed to be ζt0(τ = 0) = 0 and ζr0(τ = 0) = 0. After being processed by the proposed image formation algorithm, the results are given in Figure 8. Note that there is a small image shift between Cases A and C, but it is difficult to be observed with the unaided eye because they have only a small difference in the receiver’s velocity. As the reference range used in the imaging algorithm is chosen to be the central target range, it can be noticed that the imaging performance of the central target is better than the edge target. From the results we conclude that the five point targets are well focused and the imaging performance is acceptable. For large scenes, we can divide the entire scene into sub-scenes characterized by different reference ranges.
6. Conclusions
HAP can provide a remote sensing platform that is more responsive and more persistent (i.e., longer observation time) than satellite and airplane. In this paper, we present an azimuth-variant signal processing in HAP-borne passive BiSAR with spaceborne/airborne transmitter. The system models, azimuth-variant characteristics and two-dimensional spectrum model are investigated. Conceptual design examples and simulation results are also provided. We show that HAP-borne BiSAR has azimuth-variant resolution and Doppler characteristics, which brings a challenge for developing high precision data processing algorithms. To address the azimuth-variant signal processing problem, we present an imaging algorithm with equivalent velocity and NCS. This imaging algorithm is verified by numerical simulation results. This paper assumes that the HAP is moving at a slow speed. In fact, HAP can also move at a high speed. High-speed HAP can serve as a good platform for wide-swath SAR remote sensing, but there is a technical challenge in suppressing the range ambiguities. This topic will be further investigated in our future work.
Acknowledgments
This work was supported in part by the National Natural Science Foundation of China under grant No. 41101317, the First Grade of 49th Chinese Post-Doctor Research Funds under grant No. 20110490143, and the Fundamental Research Fund for the Central Universities under contract ZYGX2010J001.
References
- Crosetto, M.; Monserrat, O.; Cuevas, M.; Crippa, B. Spaceborne differential SAR interferometry: Data analysis tools for deformation measurement. Remote Sens 2011, 3, 305–318. [Google Scholar]
- Churnside, J.H.; Brown, E.D.; Stetter, S.P.; Horne, J.K.; Hunt, G.L., Jr.; Hillgruber, N.; Sigler, M.F.; Vollenweider, J.J. Airborne remote sensing of a biological hot spot in the southeastern Bering sea. Remote Sens 2011, 3, 621–637. [Google Scholar]
- Mohammed, A.; Mehmood, A.; Pavlidou, F.; Mohorcic, M. The role of high-altitude platforms (HAPs) in the global wireless connectivity. Proc. IEEE 2011, 99, 1939–1493. [Google Scholar]
- Luglio, M.; Theodoridis, G.; Roseti, C.; Pavlidou, N. A TCP driven CAC scheme: Efficient resource utlization in a leaky HAP-satellite integrated scenario. IEEE Trans. Aerosp. Electron. Syst 2009, 45, 885–898. [Google Scholar]
- Jaroslav, H.; David, G.; Pavel, P. Effect of antenna power roll-off on the performance of 3G cellular system for high altitude platforms. IEEE Trans. Aerosp. Electron. Syst 2010, 46, 1468–1477. [Google Scholar]
- Anastaspoulo, M.P.; Cottis, P.G. High altitude platform networks: A feedback suppression algorithm for reliable multicast/broadcast services. IEEE Trans. Wirel. Commun 2009, 8, 1639–1643. [Google Scholar]
- Wang, W.Q. Near-space vehicles: Supply a gap between satellites and airplanes. IEEE Aerosp. Electron. Syst. Mag 2011, 25, 4–9. [Google Scholar]
- Wang, W.Q. Near-space vehicle-borne SAR with reflector antenna for high-resolution and wide-swath remote sensing. IEEE Trans. Geosci. Remote Sens 2012, 50, 338–348. [Google Scholar]
- Grace, D.; Nihael, M. Broadband Communications via High Altitude Platforms; John Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Wang, W.Q.; Cai, J.Y.; Peng, Q.C. Near-space microwave radar remote sensing: Potentials and challenge analysis. Remote Sens 2010, 2, 717–739. [Google Scholar]
- Wang, W.Q. Regional remote sensing by near-space vehicle-borne passive radar system. ISPRS J. Photogramm 2012, 69, 29–36. [Google Scholar]
- Krieger, G.; Moreira, A. Spaceborne bi- and multistatic SAR: Potential and challenges. IEE Proc. Radar Sonar Navig 2006, 153, 184–198. [Google Scholar]
- Cherniakov, M.; Nezlin, D.V. Bistatic Rdar: Principles and Practice; John Wiley: New York, NY, USA, 2007. [Google Scholar]
- Wang, W.Q. GPS-based time & phase synchronization processing for distributed SAR. IEEE Trans. Aerosp. Electron. Syst 2009, 45, 1041–1052. [Google Scholar]
- Colone, F.; O’Hagan, D.W.; Lombardo, P.; Baker, C.J. A multistage processing algorithm for disturbance removal and target detection in passive bistatic radar. IEEE Trans. Aerosp. Electron. Syst 2009, 45, 698–722. [Google Scholar]
- Walterscheid, I.; Espeter, T.; Klare, J.; Brenner, A. Bistatic Spaceborne-Airborne Forward-Looking SAR. Proceedings of the 8th European Conference on Synthetic Aperture Radar, Aachen, Germany, 7–10 June 2010; pp. 986–989.
- Moccia, A.; Renga, A. Spatial resolution of bistatic synthetic aperture radar: Impact of acquisition geometry on imaging performance. IEEE Trans. Geosci. Remote Sens 2011, 49, 3487–3503. [Google Scholar]
- Wang, R.; Loffeld, O.; Neo, Y.L.; Nies, H.; Walterscheid, I.; Espeter, T.; Klare, J.; Ender, J.H.G. Focusing bistatic SAR data in airborne/stationary configuration. IEEE Trans. Geosci. Remote Sens 2010, 48, 452–465. [Google Scholar]
- Wang, R.; Deng, Y.K.; Loffeld, O.; Nies, H.; Walterscheid, I.; Espeter, T.; Klare, J.; Ender, J.H.G. Processing the azimuth-variant bistatic SAR data by using monostatic imaging algorithms based on two-dimensional principle of stationary phase. IEEE Trans. Geosci. Remote Sens 2011, 49, 3504–3520. [Google Scholar]
- Wang, R.; Loffeld, O.; Neo, Y.L.; Nies, H.; Dai, Z. Extending Loffeld’s bistatic formula for the general bistatic SAR configuration. IET Radar Sonar Navig 2010, 4, 74–84. [Google Scholar]
- Wang, W.Q. Near-Space Remote Sensing: Potential and Challenges; Springer: New York, NY, USA, 2011. [Google Scholar]
- Heise, S.; Wickert, J.; Beyerle, G.; Schmidt, T.; Smit, H.; Cammas, J.P.; Rothacher, M. Comparison of water vapor and temperature results from GPS radio occultation aboard CHAMP with MOZAIC aircraft measurements. IEEE Trans. Geosci. Remote Sens 2008, 46, 3406–3411. [Google Scholar]
- Gleason, S. Towards sea ice remote sensing with space detected GPS signal: Demonstration of technical feasibility and initial consistency check using low resolution sea ice information. Remote Sens 2010, 2, 2017–2039. [Google Scholar]
- Soloviev, A.; van Graas, F.; Gunawardena, S. Decoding navigation data messages from weak GPS signals. IEEE Trans. Aerosp. Electron. Syst 2009, 45, 660–666. [Google Scholar]
- Cherniakov, M.; Saini, R.; Antoniou, M.; Zuo, R.; Plakidis, E. Experiences gained during the development of a passive BSAR with GNSS transmitters of opportunity. Int. J. Navig. Obs 2008, 1, 1–12. [Google Scholar]
- Borio, D.; Akos, D. Noncoherent integrations for GNSS detection: Analysis and comparisons. IEEE Trans. Aerosp. Electron. Syst 2009, 45, 360–375. [Google Scholar]
- Wang, W.Q.; Ding, C.B.; Liang, X.D. Time and phase synchronization via direct-path signal for bistatic synthetic aperture radar systems. IET Radar Sonar Navig 2008, 2, 1–11. [Google Scholar]
- Gebert, N.; Krieger, G.; Moreira, A. Digital beamforming on receive: Techniques and optimization strategies for high-resolution wide-swath SAR imaging. IEEE Trans. Aerosp. Electron. Syst 2009, 45, 564–592. [Google Scholar]
- D’Errico, M.; Moccia, A. Altitude and antenna pointing design of bistatic radar formations. IEEE Trans. Aerosp. Electron. Syst 2003, 39, 949–960. [Google Scholar]
- Purdy, D.S. Receiver antenna scan rate requirements needed to implement pulse chasing in a bistatic radar receiver. IEEE Trans. Aerosp. Electron. Syst 2001, 37, 285–288. [Google Scholar]
- Willis, N.J. Bistatic Radar; Artech House: Boston, MA, USA, 1991. [Google Scholar]
- Nico, G.; Tesauro, M. On the existence of coverage and integration time regimes in bistatic SAR configurations. IEEE Geosci. Remote Sens. Lett 2007, 4, 426–430. [Google Scholar]
- Cherniakov, M.; Zeng, T. Passive Bistatic SAR with GNSS Transmitters. In Bistatic Radar: Emerging Technology; Wiley: Chichester, UK, 2008; Chapter 9. [Google Scholar] [CrossRef]
- Renga, A.; Graziano, M.D.; D’Errico, M.; Moccia, A.; Menichino, F.; Vetrella, S.; Accardo, D.; Corraro, F.; Cuciniello, G.; Nebula, F.; Monte, L.D. Galileo-based space-airborne bistatic SAR for UAS navigation. Aerosp. Sci. Technol. 2013. doi.org/10.1016/j.ast.2012.08.009. [Google Scholar]
- Wong, F.; Neo, T. New application of nonlinear chirp scaling in SAR data processing. IEEE Trans. Geosci. Remote Sens 2001, 39, 946–953. [Google Scholar]
- Neo, Y.; Wong, F.; Cumming, I. A comparison of point target spectra derived for bistatic SAR processing. IEEE Trans. Geosci. Remote Sens 2008, 46, 2481–2492. [Google Scholar]
- Zhang, H.; Xing, M.; Ding, J.; Bao, Z. Focusing parallel bistatic SAR data using the analytic transfer function in the wavenumber domain. IEEE Trans. Geosci. Remote Sens 2009, 45, 3633–3645. [Google Scholar]
- Loffeld, O.; Nies, H.; Peters, V.; Knedlik, S. Models and useful relations for bistatic SAR processing. IEEE Trans. Geosci. Remote Sens 2004, 42, 2031–2038. [Google Scholar]
- Natroshvili, K.; Loffeld, O.; Nies, H.; Ortiz, A.; Knedlik, S. Focusing of general bistatic SAR configuration data with a two-dimensional inverse scaled FFT. IEEE Trans. Geosci. Remote Sens 2006, 44, 2718–2727. [Google Scholar]
- Neo, Y.; Wong, F.; Cumming, I. A two-dimensional spectrum for bistatic SAR processing using series reversion. IEEE Geosci. Remote Sens. Lett 2007, 4, 93–96. [Google Scholar]
- Wong, F.; Neo, T.; Cumming, I. Focusing bistatic SAR data using the nonlinear chirp scaling algorithm. IEEE Trans. Geosci. Remote Sens 2008, 46, 2493–2505. [Google Scholar]
- Geng, X.; Yan, H.; Wang, Y. A two-dimensional spectrum model for general bistatic SAR. IEEE Trans. Geosci. Remote Sens 2008, 46, 2216–2223. [Google Scholar]
- Lv, X.; Xing, M.; Deng, Y.; Zhang, S.; Wu, Y. Coherence-improving algorithm for image pairs of bistatic SARs with nonparallel trajectories. IEEE Trans. Geosci. Remote Sens 2009, 47, 2884–2898. [Google Scholar]
- Yarman, C.; Yazc, B.; Cheey, M. Bistatic synthetic aperture radar imaging for arbitrary flight trajectories. IEEE Trans. Image Processing 2008, 17, 84–93. [Google Scholar]
- Liu, B.; Wang, T.; Wu, Q.; Bao, Z. Bistatic SAR data focusing using an omega-K algorithm based on method of series reversion. IEEE Trans. Geosci. Remote Sens 2009, 47, 2899–2912. [Google Scholar]
- Nies, H.; Loffeld, O.; Natroshvili, K. Analysis and focusing of bistatic SAR data. IEEE Trans. Geosci. Remote Sens 2007, 45, 3342–3349. [Google Scholar]
- Shi, J.; Zhang, X.; Yang, J. Principle and methods on bistatic SAR signal processing via image correction. IEEE Trans. Geosci. Remote Sens 2008, 46, 3163–3178. [Google Scholar]
- Zeng, T.; Cherniakov, M.; Long, T. Generalized approach to resolution analysis in BSAR. IEEE Trans. Aerosp. Electron. Syst 2005, 41, 461–474. [Google Scholar]



| Parameters | Configuration A | Configuration B | Configuration C | |||
|---|---|---|---|---|---|---|
| Transmitter | Receiver | Transmitter | Receiver | Transmitter | Receiver | |
| Carry Frequency (GHz) | 9.5 | 5.33 | 1.25 | |||
| Signal bandwidth (MHz) | 150 | 16 | 500 | |||
| Flying altitude (km) | 515 | 20 | 800 | 20 | 10 | 20 |
| Flying velocity (m/s) | 7,600 | 5 | 7,450 | 5 | 100 | 5 |
| Beam incidence angle (°) | 45 | 60 | 30 | 60 | 60 | 60 |
| Beamwidth in range (°) | 2.3 | 10 | 2.3 | 15 | 15 | 15 |
| Beamwidth in azimuth (°) | 0.33 | 10 | 0.28 | 15 | 13.75 | 13.75 |
| Configuration | PRF (Hz) | Puls duration (s) |
|---|---|---|
| Case A | 4,000 | 45 × 10−6 |
| Case C | 2,000 | 25 × 10−6 |
| Case D | 1,000 | 35 × 10−6 |
Share and Cite
Wang, W.-Q.; Shao, H. Azimuth-Variant Signal Processing in High-Altitude Platform Passive SAR with Spaceborne/Airborne Transmitter. Remote Sens. 2013, 5, 1292-1310. https://doi.org/10.3390/rs5031292
Wang W-Q, Shao H. Azimuth-Variant Signal Processing in High-Altitude Platform Passive SAR with Spaceborne/Airborne Transmitter. Remote Sensing. 2013; 5(3):1292-1310. https://doi.org/10.3390/rs5031292
Chicago/Turabian StyleWang, Wen-Qin, and Huaizong Shao. 2013. "Azimuth-Variant Signal Processing in High-Altitude Platform Passive SAR with Spaceborne/Airborne Transmitter" Remote Sensing 5, no. 3: 1292-1310. https://doi.org/10.3390/rs5031292




