Model-Based Biomass Estimation of a Hemi-Boreal Forest from Multitemporal TanDEM-X Acquisitions
Abstract
:1. Introduction
2. Test Site and Datasets
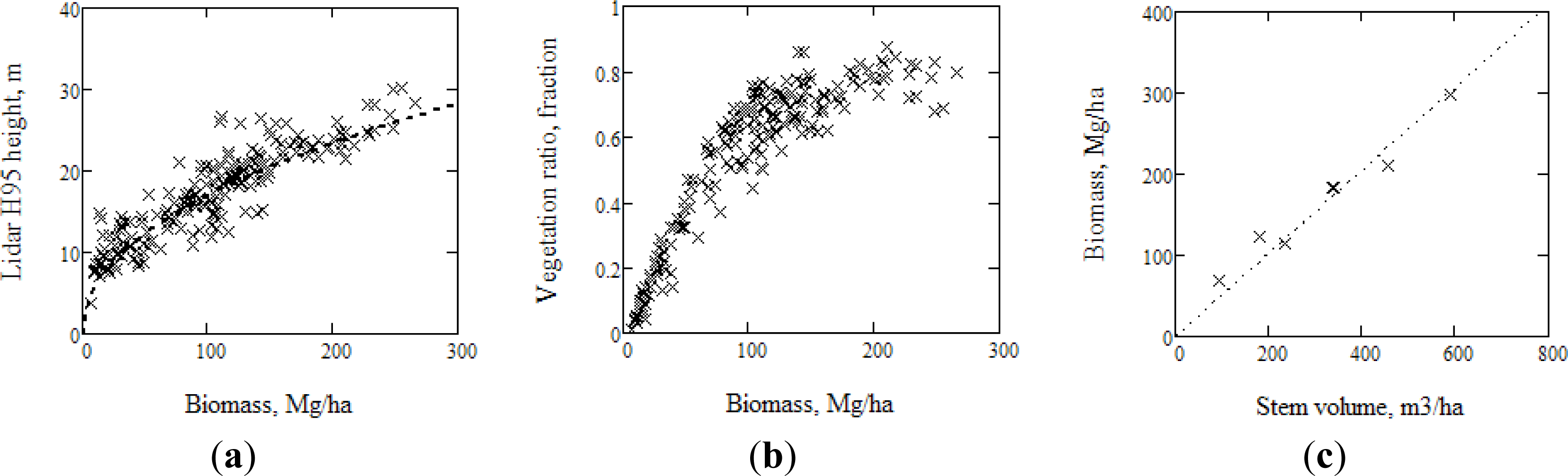
2.1. Field Observations
2.2. TanDEM-X SAR Dataset
2.3. Meteorological Data
3. Interferometric Forest Models
3.1. Interferometric Water Cloud Model
3.2. Random Volume over Ground Model
3.3. Penetration Depth Model
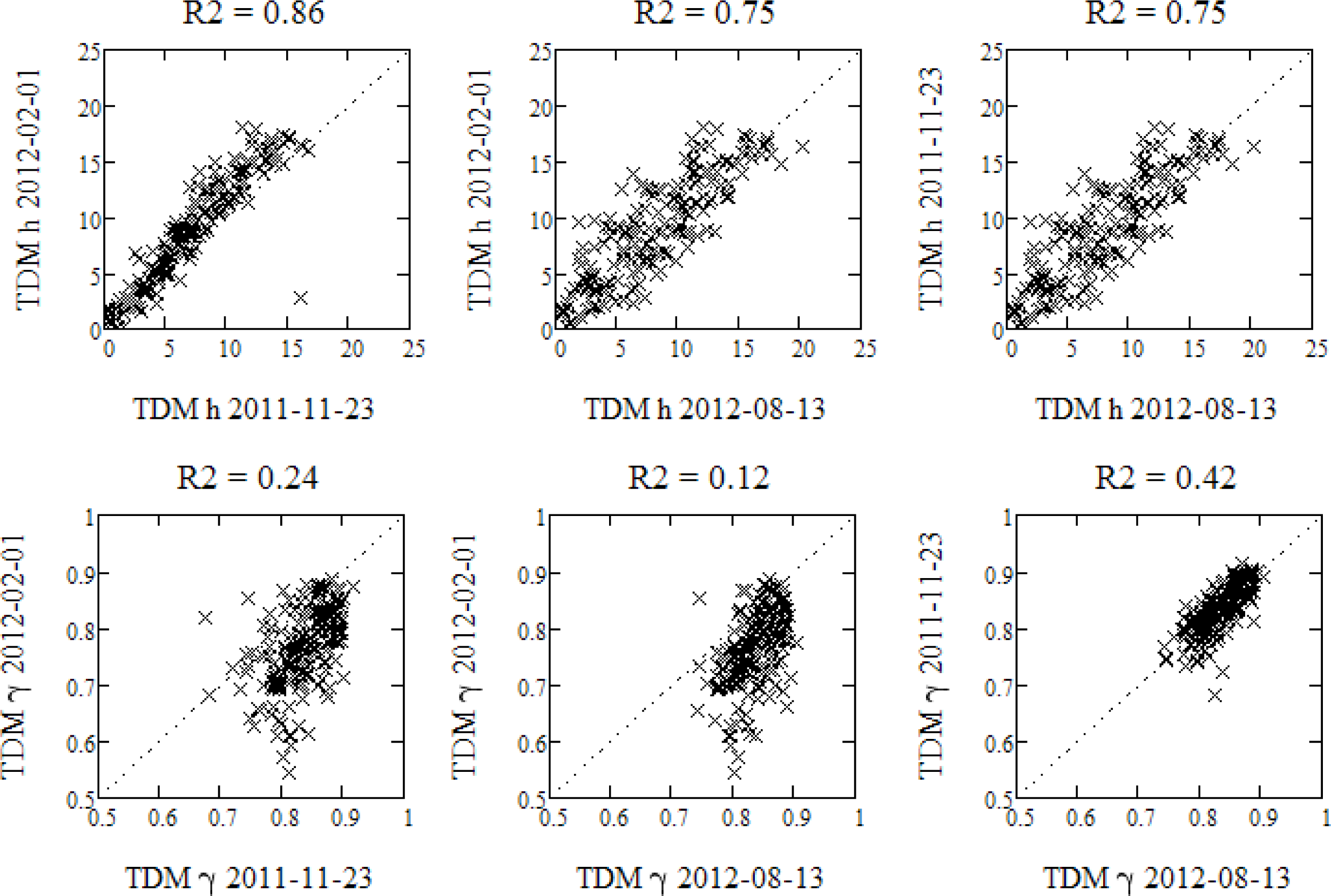
3.4. Estimation of Model Parameters
3.5. Model Training and Inversion Procedure
4. Modeling and Biomass Retrieval Results
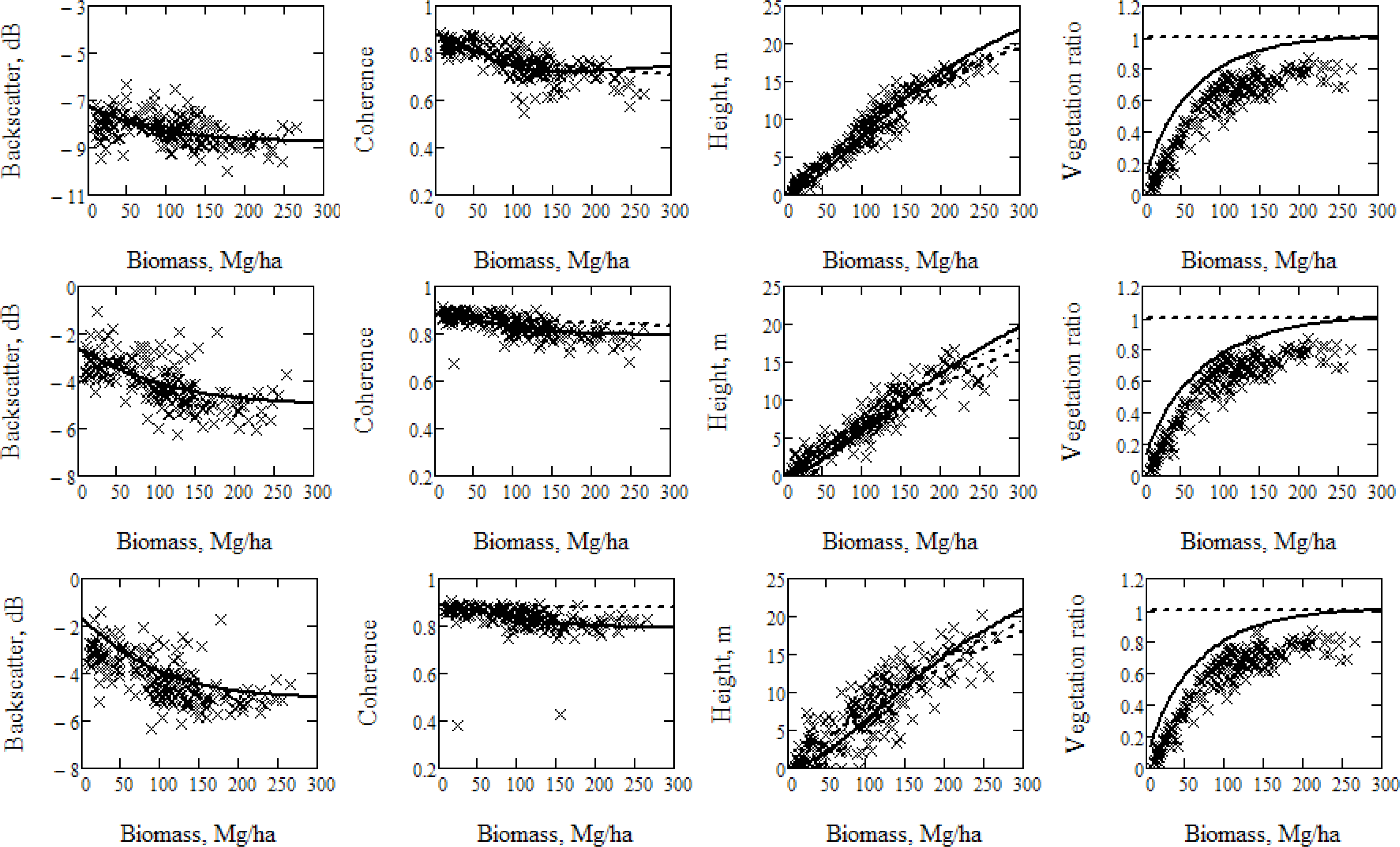
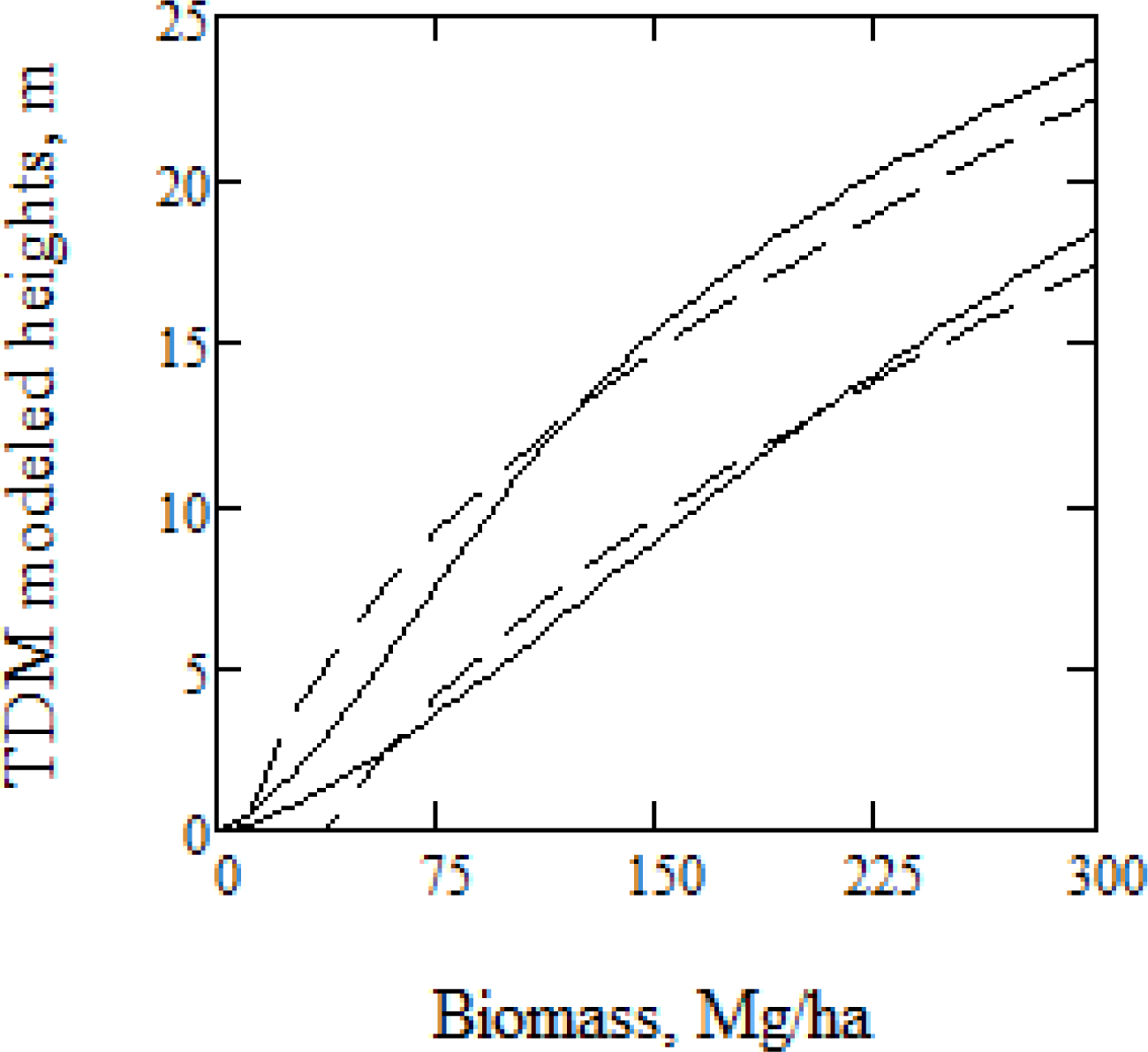
4.1. Model Properties and Parameters Estimates
4.2. Biomass Estimation
5. Discussion
6. Conclusions
Acknowledgments
Conflicts of Interest
References
- Houghton, R.A. Aboveground forest biomass and the global carbon balance. Glob. Change Biol 2005, 11, 945–958. [Google Scholar]
- Houghton, R.A.; Hall, F.; Goetz, S.J. Importance of biomass in the global carbon cycle. J. Geophys. Res.: Biogeosci 2009, 114. [Google Scholar] [CrossRef]
- Ouchi, K. Recent trend and advance of synthetic aperture radar with selected topics. Remote Sens 2013, 5, 716–807. [Google Scholar]
- Balzter, H.; Luckman, A.; Skinner, L.; Rowland, C.; Dawson, T. Observations of forest stand top height and mean height from interferometric SAR and LiDAR over a conifer plantation at Thetford Forest, UK. Int. J. Remote Sens 2007, 28, 1173–1197. [Google Scholar]
- Hajnsek, I.; Kugler, F.; Lee, S.; Papathanassiou, K.P. Tropical-forest-parameter estimation by means of Pol-InSAR: The INDREX-II campaign. IEEE Trans. Geosci. Remote Sens 2009, 47, 481–493. [Google Scholar]
- Praks, J.; Antropov, O.; Hallikainen, M.T. LIDAR-Aided SAR interferometry studies in boreal forest: Scattering phase center and extinction coefficient at X- and L-Band. IEEE Trans. Geosci. Remote Sens 2012, 50, 3831–3843. [Google Scholar]
- Solberg, S.; Astrup, R.; Gobakken, T.; Næsset, E.; Weydahl, D.J. Estimating spruce and pine biomass with interferometric X-band SAR. Remote Sens. Environ 2010, 114, 2353–2360. [Google Scholar]
- Krieger, G.; Moreira, A.; Fiedler, H.; Hajnsek, I.; Werner, M.; Younis, M.; Zink, M. TanDEM-X: A satellite formation for high-resolution SAR interferometry. IEEE Trans. Geosci. Remote Sens 2007, 45, 3317–3341. [Google Scholar]
- Weydahl, D.J.; Sagstuen, J.; Dick, Ø.B.; Rønning, H. SRTM DEM accuracy assessment over vegetated areas in Norway. Int. J. Remote Sens 2007, 28, 3513–3527. [Google Scholar]
- Neeff, T.; Dutra, L.V.; Santos, J.R.; Freitas, C.C.; Araújo, L.S. Tropical forest measurement by interferometric height modeling and P-band backscatter. For. Sci 2005, 51, 585–594. [Google Scholar]
- Askne, J.; Dammert, P.; Ulander, L.M.H.; Smith, G. C-band repeat-pass interferometric SAR observations of forest. IEEE Trans. Geosci. Remote Sens 1997, 35, 25–35. [Google Scholar]
- Askne, J.; Dammert, P.; Ulander, L.M.H.; Smith, G. Multi-temporal repeat pass SAR interferometry of boreal forests. IEEE Trans. Geosci. Remote Sens 2003, 41, 1540–1550. [Google Scholar]
- Askne, J.; Santoro, M. Experiences in Boreal Forest Stem Volume Estimation from Multitemporal C-Band InSAR. In Recent Interferometry Applications in Topography and Astronomy; Padron, I., Ed.; InTech: Morn Hill, Winchester, UK, 2012; pp. 169–194. Available online: http://cdn.intechopen.com/pdfs/33100/InTech-Experiences_in_boreal_forest_stem_volume_estimation_from_multitemporal_c_band_insar.pdf (accessed on 25 October 2013).
- Santoro, M.; Askne, J.; Smith, G.; Fransson, J.E.S. Stem volume retrieval in boreal forests from ERS-1/2 interferometry. Remote Sens. Environ 2002, 81, 19–35. [Google Scholar]
- Cloude, S.R.; Papathanassiou, K.P. Polarimetric SAR interferometry. IEEE Trans. Geosci. Remote Sens 1998, 36, 1551–1565. [Google Scholar]
- Papathanassiou, K.P.; Cloude, S.R. Single-baseline polarimetric SAR interferometry. IEEE Trans. Geosci. Remote Sens 2001, 39, 2352–2363. [Google Scholar]
- Treuhaft, R.N.; Madsen, S.N.; Moghaddam, M.; van Zyl, J.J. Vegetation characteristics and underlaying topography from interferometric data. Radio Sci 1996, 31, 1449–1495. [Google Scholar]
- Ulander, L.M.H.; Gustavsson, A.; Dubois-Fernandez, P.; Dupuis, X.; Fransson, J.E.S.; Holmgren, J.; Wallerman, J.; Eriksson, L.; Sandberg, G.; Soja, M. BIOSAR 2010–A SAR Campaign in Support to the BIOMASS Mission. Proceedings of 2011 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Vancouver, BC, Canada, 24–29 July 2011; pp. 1528–1531.
- Ulander, L.M.H.; Gustavsson, A.; Flood, B.; Murdin, D.; Dubois-Fernandez, P.; Depuis, X.; Sandberg, G.; Soja, M.J.; Eriksson, L.E.B.; Fransson, J.E.S.; et al. BIOSAR 2010 Technical Assistance for the Development of Airborne SAR and Geophysical Measurements during the BioSAR 2010 Experiment; Final Report; ESA contract no. 4000102285/10/NL/JA/ef; ESA: Noordwijk, The Netherlands, 2011; p. 212. Available online: http://earth.esa.int/campaigns/DOC/BioSAR_2010_final_report_v1.0.pdf (accessed on 25 October 2013).
- ESA. Report for Mission Selection: Biomass; European Space Agency: Noordwijk, The Netherlands, 2012. [Google Scholar]
- Ahti, T.; Hämet-Ahti, L.; Jalas, J. Vegetationzones and their sections innorthwestern Europe. Annales Botanici Fennici 1968, 5, 169–211. [Google Scholar]
- Wikström, P.; Edenius, L.; Elfving, B.; Eriksson, L.O.; Lämås, T.; Sonesson, J.; Öhman, K.; Wallerman, J.; Waller, C.; Klintebäck, F. The Heureka forestry decision support system: An overview. Math. Comput. For. Nat.-Resour. Sci 2011, 3, 87–94. [Google Scholar]
- Petersson, H. Biomassafunktioner för Trädfraktioner av Tall, Gran och Björk i Sverige; Department of Forest Resource Management, Swedish University of Agricultural Sciences: Umeå, Sweden, 1999. [Google Scholar]
- Marklund, L.G. Biomassafunktioner för Tall, Gran och Björk i Sverige; Institutionen för Skogstaxering, Sveriges Lantbruksuniversitet: Umeå, Sweden, 1988. [Google Scholar]
- Näslund, M. Funktioner och Tabeller för Kubering av Stående Träd. Tall, Gran och Björk i Södra Sverige samt Hela Landet; Statens Skogsforskningsinstitut: Stockholm, Sweden, 1947. [Google Scholar]
- Næsset, E. Predicting forest stand characteristics with airborne scanning laser using a practical two-stage procedure and field data. Remote Sens. Environ 2002, 80, 88–99. [Google Scholar]
- Sandberg, G.; Ulander, L.M.H.; Fransson, J.E.S.; Holmgren, J.; Toan, T.L. L- and P-band backscatter intensity for biomass retrieval in hemiboreal forest. Remote Sens. Environ 2011, 115, 2874–2886. [Google Scholar]
- Jalkanen, A.; Mäkipää, R.; Ståhl, G.; Lehtonen, A.; Petersson, H. Estimation of the biomass stock of trees in Sweden: comparison of biomass equations and age-dependent biomass expansion factors. Ann. For. Sci 2005, 62, 845–851. [Google Scholar]
- Woodhouse, I.H. Predicting backscatter-biomass and height-biomass trends using a macroecology model. IEEE Trans. Geosci. Remote Sens 2006, 44, 871–877. [Google Scholar]
- Balss, U.; Breit, H.; Duque, S.; Fritz, T.; Rossi, C. TanDEM-X Payload Ground Segment: CoSSC Generation and Interferometric Considerations. Available online: https://tandemx-science.dlr.de/pdfs/TD-PGS-TN-3129_CoSSCGenerationInterferometricConsiderations_1.0.pdf (accessed on 25 October 2013).
- Huber, S.; Fiedler, H.; Krieger, G.; Zink, M. TanDEM-X Performance Optimization. Proceedings of International Radar Symposium, Cologne, Germany, 5–7 September 2007.
- Soja, M.; Ulander, L. Digital Canopy Model Estimation from TanDEM-X Interferometry Using High-resolution Lidar DEM. Proceedings of 2013 IEEE International Geoscience and Remote Sensing Symposium (IGARSS) 2013, Melbourne, VIC, Australia, 22–26 July 2013.
- Attema, E.P.W.; Ulaby, F.T. Vegetation modelled as a water cloud. Radio Sci 1978, 13, 357–364. [Google Scholar]
- De Zan, F.; Krieger, G.; López-Dekker, P. On some spectral properties of TanDEM-X Interferograms over forested areas. IEEE Geosci. Remote Sens. Lett 2013, 10, 71–75. [Google Scholar]
- Pulliainen, J.T.; Heiska, K.; Hyyppä, J.; Hallikainen, M.T. Backscattering properties of boreal forests at the C-and X-band. IEEE Trans. Geosci. Remote Sens 1994, 32, 1041–1050. [Google Scholar]
- Fransson, J.E.S.; Smith, G.; Askne, J.; Olsson, H. Stem volume estimation in boreal forests using ERS-1/2 coherence and SPOT XS optical data. Int. J. Remote Sens 2001, 22, 2777–2791. [Google Scholar]
- Santoro, M.; Shvidenko, A.; McCallum, I.; Askne, J.; Schmullius, C. Properties of ERS-1/2 coherence in the Siberian boreal forest and implications for stem volume retrieval. Remote Sens. Environ 2007, 106, 154–172. [Google Scholar]
- Santoro, M.; Askne, J.; Dammert, P. Tree height retrieval from ERS interferometric phase in boreal forest. IEEE Trans. Geosci. Remote Sens 2005, 43, 207–217. [Google Scholar]
- Mette, T.; Papathanassiou, K.P.; Hajnsek, I.; Zimmermann, R. Forest Biomass Estimation Using Polarimetric SAR Interferometry. Proceedings of Workshop on POLinSAR—Applications of SAR Polarimetry and Polarimetric Interferometry, Frascati, Italy, 14–16 January 2003.
- Caicoya, A.T.; Kugler, F.; Hajnsek, I.; Papathanassiou, K. Boreal Forest Biomass Classification with TanDEM-X. Proceedings of 2012 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Munich, Germany, 22–27 July 2012.
- Santoro, M.; Beer, C.; Cartus, O.; Schmullius, C.; Shvidenko, A.; McCallum, I.; Wegmüller, U.; Wiesmann, A. Retrieval of growing stock volume in boreal forest using hyper-temporal series of Envisat ASAR ScanSAR backscatter measurements. Remote Sens. Environ 2011, 115, 490–507. [Google Scholar]
- Soja, M.J.; Sandberg, G.; Ulander, L.M.H. Regression-based retrieval of boreal forest biomass in sloping terrain using P-band SAR backscatter intensity data. IEEE Trans. Geosci. Remote Sens 2013, 51, 2646–2665. [Google Scholar]
- Folkesson, K.; Smith-Jonforsen, G.; Ulander, L.M.H. Validating backscatter models for CARABAS SAR images of coniferous forests. Can. J. Remote Sens 2008, 34, 480–495. [Google Scholar]
- Solberg, S.; Astrup, R.; Breidenbach, J.; Nilsen, B.; Weydahl, D. Monitoring spruce volume and biomass with InSAR data from TanDEM-X. Remote Sens. Environ 2013, 139, 60–67. [Google Scholar]
- Ulander, L.M.H.; Askne, J.I.H.; Eriksson, L.E.B.; Franssson, J.E.S.; Persson, H.; Soja, M. Effects of Tree Species and Season on Boreal Forest Biomass Estimates from TanDEM-X. Proceedings of 4th TanDEM-X Science Team Meeting, Oberpfaffenhofen, Germany, 12–14 June 2013; p. 15. Available online https://tandemx-science.dlr.de/pdfs/ScienceMeeting2013_OralPresentations/TDX_8_Forest_Applications/3_Ulander.pdf (accessed on 25 October 2013).
- Häme, T.; Salli, A.; Lahti, K. Estimation of Carbon Storage in Boreal Forests Using Remote Sensing Data, Pilot Study. In The Finnish Programme on Climate Change, Progress Report; Kanninen, M., Anttila, P., Eds.; Publications of the Academy of Finland; VAPK Publishing: Helsinki, Finland, 1992; Volume 3/92, pp. 250–255. [Google Scholar]





| Date | HOA (m) | ATB (m) | Incidence Angle | Temperature (°C) | Wind Speed (m/s) | Precipitation (mm) |
|---|---|---|---|---|---|---|
| 2011-06-04 | 49 | 110 | 41° | 24 | 2 | 0 |
| 2011-11-23 | −185 | 4 | 34° | 5 | 3 | 1.2 |
| 2011-12-26 | −178 | 64 | 34° | 6 | 5 | 0 |
| 2012-01-17 | −172 | −1 | 34° | −2 | 1 | 0 |
| 2012-01-28 | −182 | 7 | 34° | −3 | 2 | 0 |
| 2012-02-01 | 80 | 267 | 41° | −4 | 1 | 0.2 |
| 2012-02-08 | −179 | 29 | 34° | −3 | 1 | 0 |
| 2012-02-12 | −79 | −244 | 41° | −3 | 1 | 0.2 |
| 2012-02-19 | −186 | −8 | 34° | 1 | 6 | 3.4 |
| 2012-02-23 | 79 | 232 | 41° | 3 | 3 | 0 |
| 2012-03-01 | −186 | −11 | 34° | 5 | 4 | 0 |
| 2012-03-12 | −187 | −11 | 34° | 4 | 2 | 0 |
| 2012-03-23 | −183 | 14 | 34° | −1 | 0 | 0 |
| 2012-05-28 | 349 | 262 | 34° | 15 | 2 | 1.3 |
| 2012-07-22 | 339 | 262 | 34° | 14 | 3 | 4.1 |
| 2012-08-02 | 315 | 233 | 34° | 15 | 3 | 0.6 |
| 2012-08-13 | 358 | 229 | 34° | 14 | 0 | 0 |
| 2012-08-24 | 301 | 208 | 34° | 13 | 3 | 0.2 |
| Model | Input | Output |
|---|---|---|
| IWCM | Parameters of satellite look geometry, DTM, h(B), BEF, biomass, σ°TDM, γTDM and hTDM of training stands | , , γgr, γveg, α, β, |
| RVoG | Parameters of satellite look geometry, DTM, h(B), BEF, biomass, σ°TDM, γTDM and hTDM of training stands | , , γgr,γveg, α, |
| PD | DTM, h(B), biomass and hTDM of training stands | αeff, |
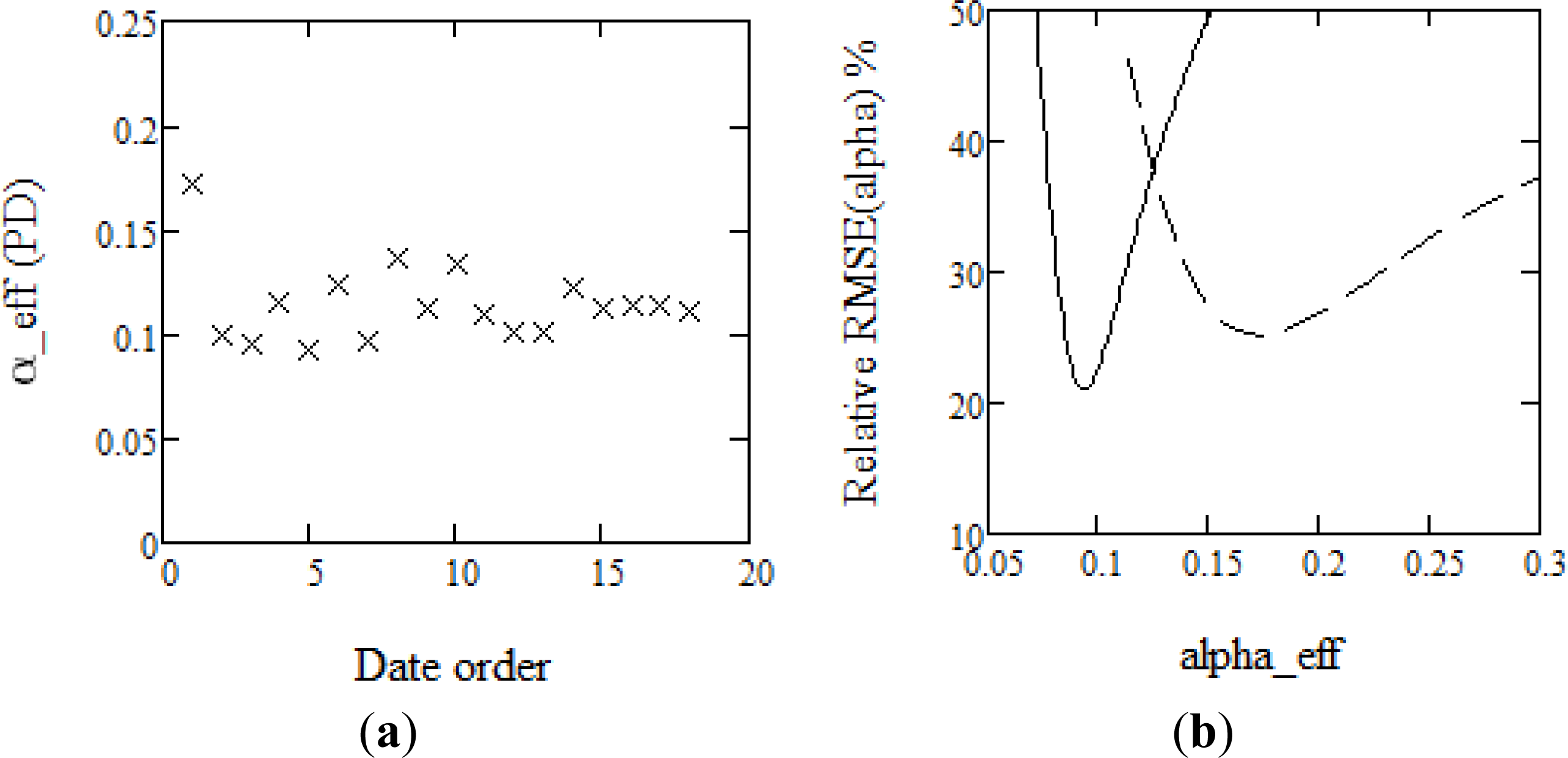
| # | Date | α IWCM | β IWCM | H150 IWCM | α RVoG | αeff PD |
|---|---|---|---|---|---|---|
| 1 | 2011-06-04 | 0.20 | 0.0093 | 15.0 | 0.14 | 0.17 |
| 2 | 2011-11-23 | 0.12 | 0.0056 | 9.4 | 0.09 | 0.10 |
| 3 | 2011-12-26 | 0.11 | 0.0053 | 8.9 | 0.08 | 0.10 |
| 4 | 2012-01-17 | 0.15 | 0.0070 | 11.2 | 0.11 | 0.12 |
| 5 | 2012-01-28 | 0.10 | 0.0049 | 8.5 | 0.07 | 0.09 |
| 6 | 2012-02-01 | 0.15 | 0.0070 | 12.0 | 0.11 | 0.12 |
| 7 | 2012-02-08 | 0.12 | 0.0056 | 9.2 | 0.09 | 0.10 |
| 8 | 2012-02-12 | 0.17 | 0.0080 | 13.1 | 0.12 | 0.14 |
| 9 | 2012-02-19 | 0.14 | 0.0068 | 10.9 | 0.10 | 0.11 |
| 10 | 2012-02-23 | 0.16 | 0.0078 | 12.8 | 0.12 | 0.13 |
| 11 | 2012-03-01 | 0.14 | 0.0066 | 10.4 | 0.10 | 0.11 |
| 12 | 2012-03-12 | 0.12 | 0.0058 | 9.6 | 0.09 | 0.10 |
| 13 | 2012-03-23 | 0.13 | 0.0061 | 9.8 | 0.09 | 0.10 |
| 14 | 2012-05-28 | 0.16 | 0.0076 | 11.8 | 0.12 | 0.12 |
| 15 | 2012-07-22 | 0.14 | 0.0068 | 10.8 | 0.10 | 0.11 |
| 16 | 2012-08-02 | 0.14 | 0.0068 | 10.9 | 0.10 | 0.11 |
| 17 | 2012-08-13 | 0.14 | 0.0066 | 10.3 | 0.10 | 0.11 |
| 18 | 2012-08-24 | 0.14 | 0.0065 | 10.6 | 0.10 | 0.11 |
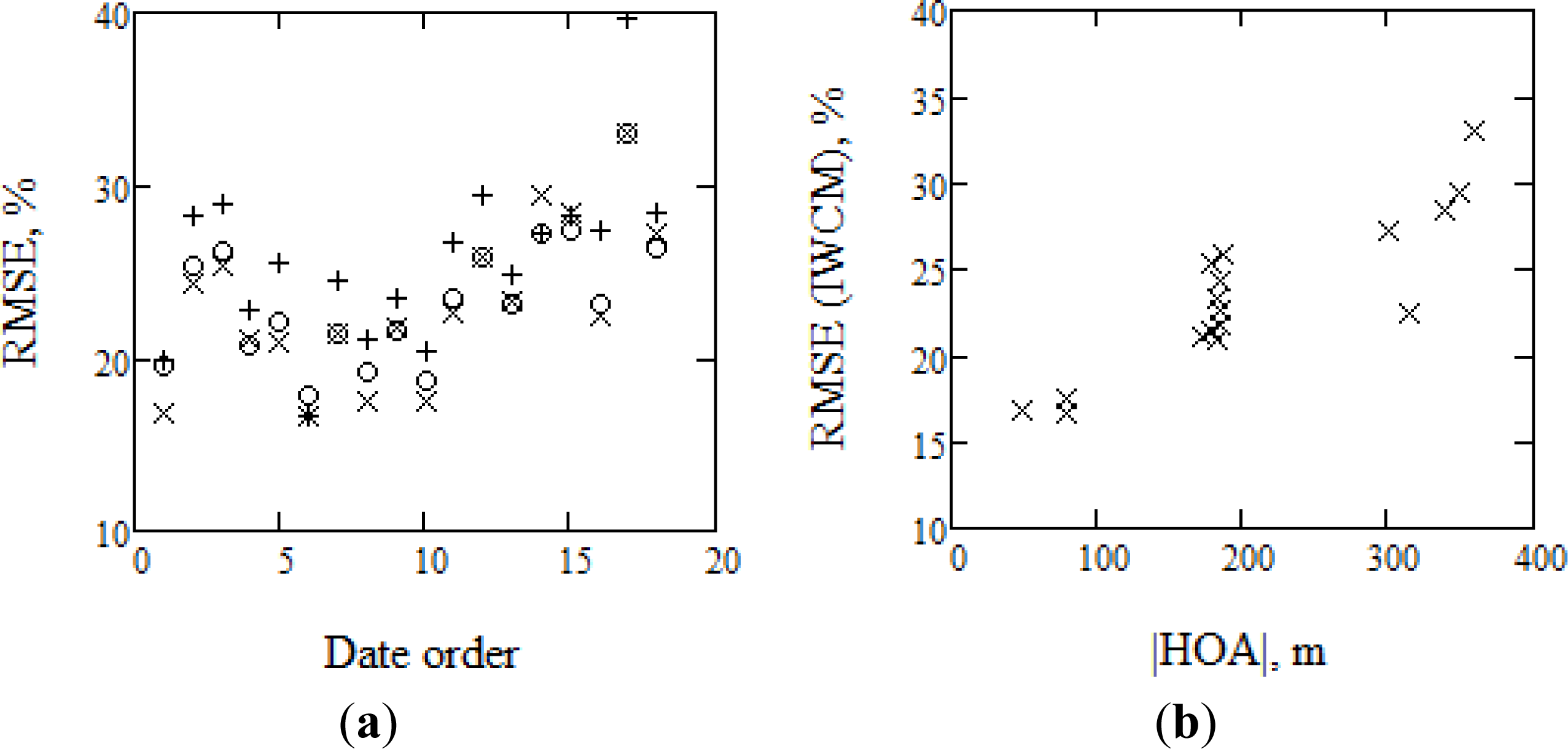
| # | Date | RMSE % IWCM | RMSE % RVoG | RMSE % PD |
|---|---|---|---|---|
| 1 | 2011-06-04 | 16.8 | 19.9 | 19.5 |
| 2 | 2011-11-23 | 24.3 | 28.2 | 25.4 |
| 3 | 2011-12-26 | 25.4 | 28.9 | 26.2 |
| 4 | 2012-01-17 | 21.1 | 22.8 | 20.7 |
| 5 | 2012-01-28 | 20.8 | 25.4 | 22.0 |
| 6 | 2012-02-01 | 16.7 | 16.7 | 17.9 |
| 7 | 2012-02-08 | 21.3 | 24.5 | 21.4 |
| 8 | 2012-02-12 | 17.5 | 21.1 | 19.1 |
| 9 | 2012-02-19 | 21.7 | 23.5 | 21.7 |
| 10 | 2012-02-23 | 17.5 | 20.5 | 18.7 |
| 11 | 2012-03-01 | 22.5 | 26.8 | 23.5 |
| 12 | 2012-03-12 | 25.9 | 29.3 | 25.8 |
| 13 | 2012-03-23 | 23.3 | 24.8 | 23.0 |
| 14 | 2012-05-28 | 29.5 | 27.2 | 27.2 |
| 15 | 2012-07-22 | 28.4 | 28.3 | 27.4 |
| 16 | 2012-08-02 | 22.5 | 27.4 | 23.1 |
| 17 | 2012-08-13 | 33.0 | 39.7 | 33.1 |
| 18 | 2012-08-24 | 27.2 | 28.3 | 26.4 |
| Mean RMSE | 23.1 | 25.7 | 23.4 |
| Date | RMSE % Stands ≥ 1 ha | RMSE % Stands ≥ 0.5 ha | RMSE % Stands ≥ 0.25 ha |
|---|---|---|---|
| 2012-02-01 | 16.7 | 20.2 | 22.6 |
| 2012-08-13 | 33.0 | 35.2 | 38.3 |
© 2013 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Askne, J.I.H.; Fransson, J.E.S.; Santoro, M.; Soja, M.J.; Ulander, L.M.H. Model-Based Biomass Estimation of a Hemi-Boreal Forest from Multitemporal TanDEM-X Acquisitions. Remote Sens. 2013, 5, 5574-5597. https://doi.org/10.3390/rs5115574
Askne JIH, Fransson JES, Santoro M, Soja MJ, Ulander LMH. Model-Based Biomass Estimation of a Hemi-Boreal Forest from Multitemporal TanDEM-X Acquisitions. Remote Sensing. 2013; 5(11):5574-5597. https://doi.org/10.3390/rs5115574
Chicago/Turabian StyleAskne, Jan I.H., Johan E.S. Fransson, Maurizio Santoro, Maciej J. Soja, and Lars M.H. Ulander. 2013. "Model-Based Biomass Estimation of a Hemi-Boreal Forest from Multitemporal TanDEM-X Acquisitions" Remote Sensing 5, no. 11: 5574-5597. https://doi.org/10.3390/rs5115574






