Examining the Satellite-Detected Urban Land Use Spatial Patterns Using Multidimensional Fractal Dimension Indices
Abstract
:1. Introduction
2. Methods
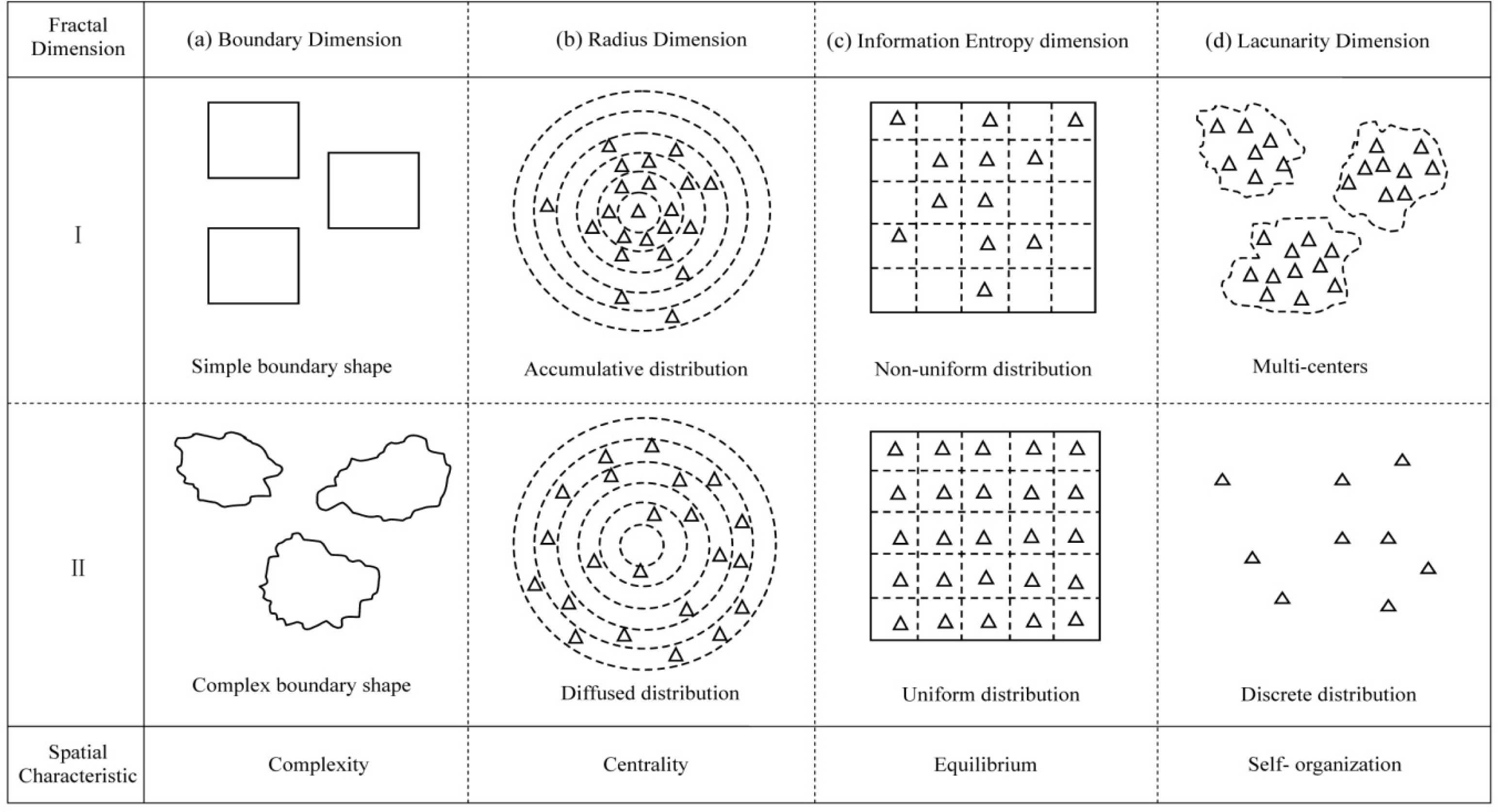
2.1. Three Typical Fractal Dimensions
2.2. A Novel Fractal Dimension—Lacunarity Dimension
3. Study Area and Data Processing
4. Results and Discussion
4.1. Boundary Dimension
4.2. Radius Dimension
4.3. Information Entropy Dimension
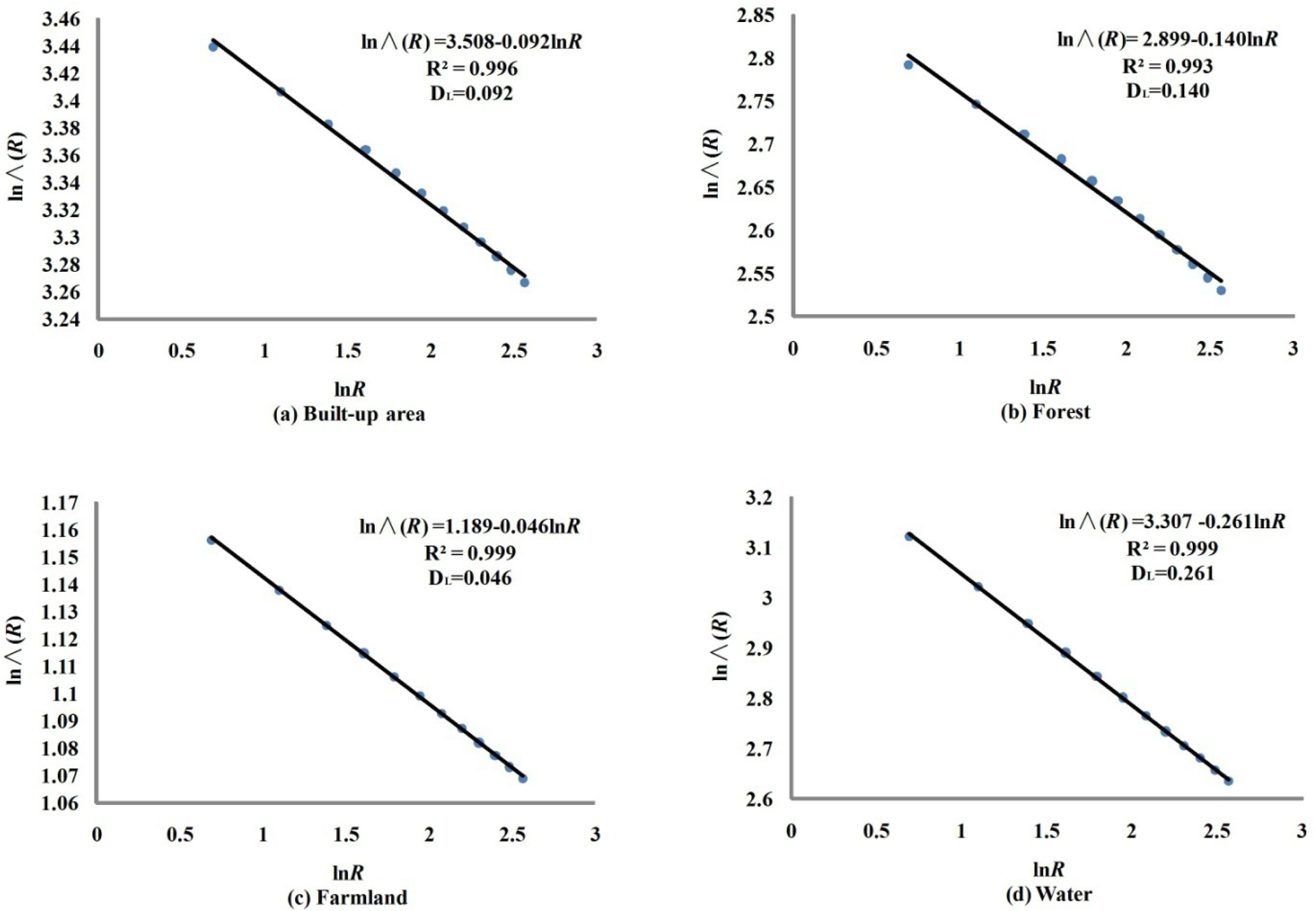
4.4. Lacunarity Dimension
5. Conclusions
- (1)
- The utility of multidimensional fractal indices to analyze the spatial patterns of urban land use proved to be more comprehensive than the utility of any single fractal dimension index. The thorough analysis exhibits accurate spatial pattern detection, including correlation coefficients greater than 0.85 and statistically significant with p < 0.001.
- (2)
- It is feasible to use the proposed lacunarity dimension to solve the typical modifiable areal unit problem associated with the scale effects of lacunarity index. It can effectively distinguish the self-organization feature (multiple centers) from the centrality (only one center) as well as the balance (no center) of land use spatial patterns at macro level.
- (3)
- Although the shape complexity of water was found to be highly similar to that of built-up area at micro level in Wuhan, there is a remarkable difference for their macro spatial patterns: Water patches tend to aggregate around multiple individual centers while built-up area only to the urban commercial center.
- (4)
- It is suggested that we should confirm the goodness of fit and the statistical significance of estimated fractal dimensions before using the multidimensional fractal dimension indices to examine the satellite-detected urban land use spatial patterns.
Acknowledgments
Conflict of Interest
References
- Carlson, T.N.; Arthur, S.T. The impact of land use-land cover changes due to urbanization on surface microclimate and hydrology: A satellite perspective. Glob. Planet. Chang 2000, 25, 49–65. [Google Scholar]
- Thapa, R.B.; Murayama, Y. Examining spatiotemporal urbanization patterns in Kathmandu Valley, Nepal: Remote sensing and spatial metrics approaches. Remote Sens 2009, 1, 534–556. [Google Scholar]
- Vitousek, P.M.; Mooney, H.A.; Lubchenco, J.; Melillo, J.M. Human domination of earth’s ecosystems. Science 1997, 277, 494–499. [Google Scholar]
- Wu, H.; Zhou, L.; Chi, X.; Li, Y.; Sun, Y. Quantifying and analyzing neighborhood configuration characteristics to cellular automata for land use simulation considering data source error. Earth Sci. Inform 2012, 5, 77–86. [Google Scholar]
- Dewan, A.M.; Yamaguchi, Y. Land use and land cover change in Greater Dhaka, Bangladesh: Using remote sensing to promote sustainable urbanization. Appl. Geogr 2009, 29, 390–401. [Google Scholar]
- Dewan, A.M.; Yamaguchi, Y.; Rahman, M.Z. Dynamics of land use/cover changes and the analysis of landscape fragmentation in Dhaka Metropolitan, Bangladesh. GeoJournal 2012, 77, 315–330. [Google Scholar]
- Herold, M.; Goldstein, N.C.; Clarke, K.C. The spatiotemporal form of urban growth: Measurement, analysis and modeling. Remote Sens. Environ 2003, 86, 286–302. [Google Scholar]
- Herold, M.; Mayaux, P.; Woodcock, C.E.; Baccini, A.; Schmullius, C. Some challenges in global land cover mapping: An assessment of agreement and accuracy in existing 1 km datasets. Remote Sens. Environ 2008, 112, 2538–2556. [Google Scholar]
- Xiong, Y.Z.; Huang, S.P.; Chen, F.; Ye, H.; Wang, C.P.; Zhu, C.B. The impacts of rapid urbanization on the thermal environment: A remote sensing study of Guangzhou, South China. Remote Sens 2012, 4, 2033–2056. [Google Scholar]
- Atzberger, C.; Rembold, F. Mapping the spatial distribution of winter crops at sub-pixel level using AVHRR NDVI time series and neural nets. Remote Sens 2013, 5, 1335–1354. [Google Scholar]
- Fritz, S.; McCallum, I.; Schill, C.; Perger, C.; Grillmayer, R.; Achard, F.; Kraxner, F.; Obersteiner, M. Geo-Wiki.Org: The use of crowdsourcing to improve global land cover. Remote Sens 2009, 1, 345–354. [Google Scholar]
- Thenkabail, P.S.; Enclona, E.A.; Ashton, M.S.; Legg, C.; de Dieu, M.J. Hyperion, IKONOS, ALI, and ETM plus sensors in the study of African rainforests. Remote Sens. Environ 2004, 90, 23–43. [Google Scholar]
- Rudorff, B.F.T.; Aguiar, D.A.; Silva, W.F.; Sugawara, L.M.; Adami, M.; Moreira, M.A. Studies on the rapid expansion of sugarcane for ethanol production in Sao Paulo State (Brazil) using landsat data. Remote Sens 2010, 2, 1057–1076. [Google Scholar]
- Mundia, C.N.; Aniya, M. Dynamics of land use/cover changes and degradation of Nairobi City, Kenya. Land Degrad. Dev 2006, 17, 97–108. [Google Scholar]
- Jat, M.K.; Garg, P.K.; Khare, D. Monitoring and modeling of urban sprawl using remote sensing and GIS techniques. Int. J. Appl. Earth Obs. Geoinf 2008, 10, 26–43. [Google Scholar]
- Dewan, A.M.; Yamaguchi, Y. Using remote sensing and GIS to detect and monitor land use and land cover change in Dhaka Metropolitan of Bangladesh during 1960–2005. Environ. Monit. Assess 2009, 150, 237–249. [Google Scholar]
- Braimoh, A.K.; Onishi, T. Spatial determinants of urban land use change in Lagos, Nigeria. Land Use Policy 2007, 24, 502–515. [Google Scholar]
- Foody, G.M. Mapping land cover from remotely sensed data with a softened feedforward neural network classification. J. Intell. Robot. Syst 2000, 29, 433–449. [Google Scholar]
- Kalluri, S.N.V.; Jaja, J.; Bader, D.A.; Zhang, Z.; Townshend, J.R.G.; Fallah-Adl, H. High performance computing algorithms for land cover dynamics using remote sensing data. Int. J. Remote Sens 2000, 21, 1513–1536. [Google Scholar]
- Tadesse, W.; Tsegaye, T.; Coleman, T. Land Use/Cover Change Detection of the City of Addis Ababa, Ethiopia Using Remote Sensing and Geographic Information System Technology. Proceedings of IEEE International Geoscience and Remote Sensing Symposium, Sydney, NSW, Australia, 9–13 July 2001.
- Friedl, M.A.; McIver, D.K.; Hodges, J.C.F.; Zhang, X.Y.; Muchoney, D.; Strahler, A.H.; Woodcock, C.E.; Gopal, S.; Schneider, A.; Cooper, A.; et al. Global land cover mapping from MODIS: Algorithms and early results. Remote Sens. Environ 2002, 83, 287–302. [Google Scholar]
- Huete, A.R.; Miura, T.; Gao, X. Land cover conversion and degradation analyses through coupled soil-plant biophysical parameters derived from hyperspectral EO-1 Hyperion. IEEE Trans. Geosci. Remote Sens 2003, 41, 1268–1276. [Google Scholar]
- Gitas, I.Z.; Mitri, G.H.; Ventura, G. Object-based image classification for burned area mapping of Creus Cape, Spain, using NOAA-AVHRR imagery. Remote Sens. Environ 2004, 92, 409–413. [Google Scholar]
- Thenkabail, P.S.; Schull, M.; Turral, H. Ganges and Indus river basin land use/land cover (LULC) and irrigated area mapping using continuous streams of MODIS data. Remote Sens. Environ 2005, 95, 317–341. [Google Scholar]
- De Almeida, C.M.; Monteiro, A.M.V.; Soares, G.; Cerqueira, G.C.; Pennachin, C.L.; Batty, M. GIS and remote sensing as tools for the simulation of urban land-use change. Int. J. Remote Sens 2005, 26, 759–774. [Google Scholar]
- Duran, Z.; Musaoglu, N.; Seker, D.Z. Evaluating urban land use change in historical peninsula, Istanbul, by using gis and remote sensing. Fresenius Environ. Bull 2006, 15, 806–810. [Google Scholar]
- Chang, L.; Tang, Z.H. Using remote sensing technology to assess land-use changes after the northridge earthquake. Disaster Adv 2010, 3, 5–10. [Google Scholar]
- Zurita-Milla, R.; Gomez-Chova, L.; Guanter, L.; Clevers, J.G.P.W.; Camps-Valls, G. Multitemporal unmixing of medium-spatial-resolution satellite images: A case study using meris images for land-cover mapping. IEEE Trans. Geosci. Remote Sens 2011, 49, 4308–4317. [Google Scholar]
- Myint, S.W.; Gober, P.; Brazel, A.; Grossman-Clarke, S.; Weng, Q. Per-pixel vs. object-based classification of urban land cover extraction using high spatial resolution imagery. Remote Sens. Environ 2011, 115, 1145–1161. [Google Scholar]
- Dymond, J.R.; Shepherd, J.D.; Newsome, P.F.; Gapare, N.; Burgess, D.W.; Watt, P. Remote sensing of land-use change for Kyoto Protocol reporting: The New Zealand case. Environ. Sci. Policy 2012, 16, 1–8. [Google Scholar]
- Lambin, E.F.; Geist, H.J.; Lepers, E. Dynamics of land-use and land-cover change in tropical regions. Annu. Rev. Environ. Resour 2003, 28, 205–241. [Google Scholar]
- Le, Q.B.; Park, S.J.; Vlek, P.L.G.; Cremers, A.B. Land-Use Dynamic Simulator (LUDAS): A multi-agent system model for simulating spatio-temporal dynamics of coupled human-landscape system. I. Structure and theoretical specification. Ecol. Inform 2008, 3, 135–153. [Google Scholar]
- Crews-Meyer, K.A. Agricultural landscape change and stability in northeast Thailand: Historical patch-level analysis. Agric. Ecosyst. Environ 2004, 101, 155–169. [Google Scholar]
- Wickham, J.D.; Riitters, K.H.; Wade, T.G.; Coulston, J.W. Temporal change in forest fragmentation at multiple scales. Landsc. Ecol 2007, 22, 481–489. [Google Scholar]
- Roy, P.S.; Tomar, S. Landscape cover dynamics pattern in Meghalaya. Int. J. Remote Sens 2001, 22, 3813–3825. [Google Scholar]
- Kwan, M.P; Weber, J. Scale and accessibility: Implications for the analysis of land use—Travel interaction. Appl. Geogr 2008, 28, 110–123. [Google Scholar]
- Schmit, C.; Rounsevell, M.D.A.; La, J.I. The limitations of spatial land use data in environmental analysis. Environ. Sci. Policy 2006, 9, 174–188. [Google Scholar]
- Ling, Y.Y. The Study of Urban Land Use Structure and Its Non-Linear Transformation (In Chinese). Ms.C. Thesis, East China Normal University, Shanghai, China,. 2004. [Google Scholar]
- Shi, P.J. Methodology and Practice of Land Use/Cover Change Study; (In Chinese). Science Press: Beijing, China, 2000. [Google Scholar]
- Weng, Q.H. Fractal analysis of satellite-detected urban heat island effect. Photogramm. Eng. Remote Sens 2003, 69, 555–566. [Google Scholar]
- De Cola, L. Fractal analysis of a classified Landsat scene. Photogramm. Eng. Remote Sens 1989, 55, 601–610. [Google Scholar]
- Lam, N.S.N. Description and measurement of landsat TM images using fractals. Photogramm. Eng. Remote Sens 1990, 56, 187–195. [Google Scholar]
- Lam, N.S.N.; Quattrochi, D.A. On the issues of scale, resolution, and fractal analysis in the mapping sciences. Prof. Geogr 1992, 44, 88–98. [Google Scholar]
- Myint, S.W.; Lam, N.S.N.; Tyler, J.M. Wavelets for urban spatial feature discrimination: Comparisons with fractal, spatial autocorrelation, and spatial co-occurrence approaches. Photogramm. Eng. Remote Sens 2004, 70, 803–812. [Google Scholar]
- Emerson, C.W.; Lam, N.S.N.; Quattrochi, D.A. A comparison of local variance, fractal dimension, and Moran’s I as aids to multispectral image classification. Int. J. Remote Sens 2005, 26, 1575–1588. [Google Scholar]
- Myint, S.W.; Lam, N.S.N. Examining lacunarity approaches in comparison with fractal and spatial autocorrelation techniques for urban mapping. Photogramm. Eng. Remote Sens 2005, 71, 927–937. [Google Scholar]
- Zhou, G.Y.; Lam, N.S.N. A comparison of fractal dimension estimators based on multiple surface generation algorithms. Comput. Geosci 2005, 31, 1260–1269. [Google Scholar]
- Myint, S.W.; Mesev, V.; Lam, N.S.N. Urban textural analysis from remote sensor data: Lacunarity measurements based on the differential box counting method. Geogr. Anal 2006, 38, 371–390. [Google Scholar]
- Ju, W.X.; Lam, N.S.N. An improved algorithm for computing local fractal dimension using the triangular prism method. Comput. Geosci 2009, 35, 1224–1233. [Google Scholar]
- Zeng, Y.; Zhang, J.; Li, H. Fractal Characteristics of very High Resolution Satellite Imagery. Proceedings of IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 23–27 July 2007.
- Emerson, C.W.; Lam, N.S.N.; Quattrochi, D.A. A comparison of local variance, fractal dimension, and Moran’s I as aids to multispectral image classification. Int. J. Remote Sens 2005, 26, 1575–1588. [Google Scholar]
- Tang, J.; Bu, K.; Yang, J.; Zhang, S.; Chang, L. Multitemporal analysis of forest fragmentation in the upstream region of the Nenjiang River Basin, Northeast China. Ecol. Indic 2012, 23, 597–607. [Google Scholar]
- Tran, T.D.B.; Puissant, A.; Badariotti, D.; Weber, C. Optimizing spatial resolution of imagery for urban form detection—The cases of France and vietnam. Remote Sens 2011, 3, 2128–2147. [Google Scholar]
- Liang, B.; Weng, Q.; Tong, X. An evaluation of fractal characteristics of urban landscape in Indianapolis, USA, using multi-sensor satellite images. Int. J. Remote Sens 2013, 34, 804–823. [Google Scholar]
- Sun, J.; Southworth, J. Remote sensing-based fractal analysis and scale dependence associated with forest fragmentation in an amazon tri-national frontier. Remote Sens 2013, 5, 454–472. [Google Scholar]
- Sun, W.; Xu, G.; Gong, P.; Liang, S. Fractal analysis of remotely sensed images: A review of methods and applications. Int. J. Remote Sens 2006, 27, 4963–4990. [Google Scholar]
- Batty, M. Fractals - geometry between dimensions. New Sci 1985, 105, 31–35. [Google Scholar]
- Batty, M.; Longley, P.A. Fractal-based description of urban form. Environ. Plann. B 1987, 14, 123–134. [Google Scholar]
- Frankhauser, P.; Sadler, R. Fractal Analysis of Agglomerations. In Natural Structures: Principles, Strategies, and Models in Architecture and Nature; Hilliges, M., Ed.; University of Stuttgart: Stuttgart, Germany, 1991; pp. 57–65. [Google Scholar]
- White, R.; Engelen, G. Cellular automata and fractal urban form: A cellular modelling approach to the evolution of urban land-use patterns. Environ. Plan. A 1993, 25, 1175–1199. [Google Scholar]
- Culling, W.E.H. Dimension and entropy in the soil-covered landscape. Earth Surf. Process. Landf 1988, 13, 619–648. [Google Scholar]
- Martin, M.A.; Rey, J.M.; Taguas, F.J. An entropy-based heterogeneity index for mass-size distributions in Earth science. Ecol. Model 2005, 182, 221–228. [Google Scholar]
- Wang, D.; Fu, B.; Zhao, W.; Hu, H.; Wang, Y. Multifractal characteristics of soil particle size distribution under different land-use types on the Loess Plateau, China. Catena 2008, 72, 29–36. [Google Scholar]
- Fernández, E.; Jelinek, H.F. Use of fractal theory in neuroscience: Methods, advantages, and potential problems. Methods 2001, 24, 309–321. [Google Scholar]
- Dong, P. Lacunarity for spatial heterogeneity measurement in GIS. Geogr. Inf. Sci 2000, 6, 20–26. [Google Scholar]
- Mandelbrot, B.B. The Fractal Geometry of Nature; W.H. Freeman and Company: New York, NY, USA, 1982. [Google Scholar]
- Mandelbrot, B.B.; Vespignani, A.; Kaufman, H. Crosscut analysis of large radial DLA: Departures from self-similarity and lacunarity effects. Europhys. Lett 1995, 32, 199–204. [Google Scholar]
- Plotnick, R.E.; Gardner, R.H.; O’Neill, R.V. Lacunarity indices as measures of landscape texture. Landsc. Ecol 1993, 8, 201–211. [Google Scholar]


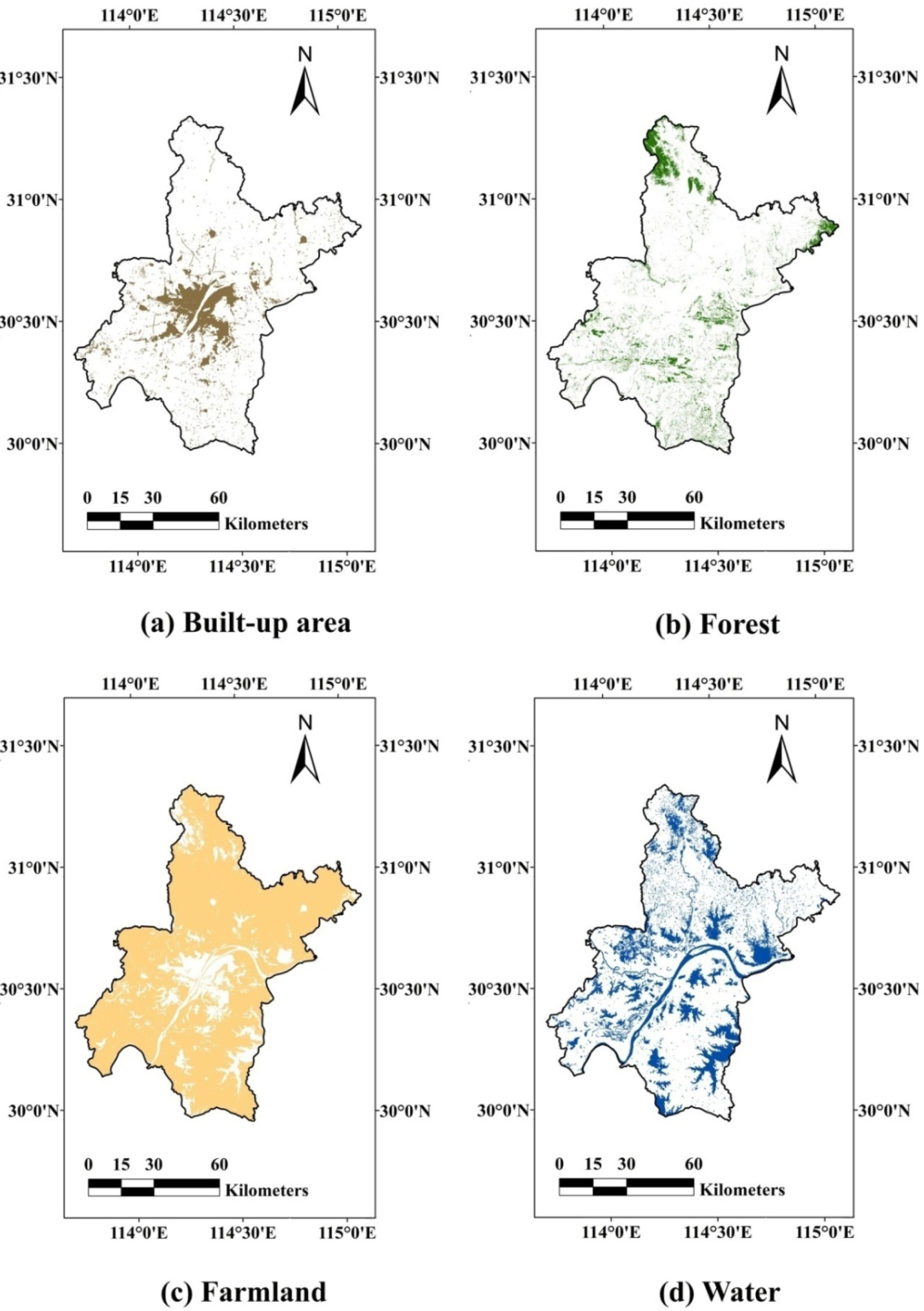




| ID | Land Use Types | Number of Patches | Percentage of Patches (%) | Area (m2) | Percentage of Area (%) |
|---|---|---|---|---|---|
| 1 | Built-up area | 7,274 | 10.089 | 607,801,492 | 7.075 |
| 2 | Forest | 31,849 | 44.174 | 734,558,400 | 8.550 |
| 3 | Farmland | 15,137 | 20.995 | 6,701,792,036 | 71.023 |
| 4 | Water | 16,864 | 23.390 | 1,134,048,588 | 13.200 |
© 2013 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Wu, H.; Sun, Y.; Shi, W.; Chen, X.; Fu, D. Examining the Satellite-Detected Urban Land Use Spatial Patterns Using Multidimensional Fractal Dimension Indices. Remote Sens. 2013, 5, 5152-5172. https://doi.org/10.3390/rs5105152
Wu H, Sun Y, Shi W, Chen X, Fu D. Examining the Satellite-Detected Urban Land Use Spatial Patterns Using Multidimensional Fractal Dimension Indices. Remote Sensing. 2013; 5(10):5152-5172. https://doi.org/10.3390/rs5105152
Chicago/Turabian StyleWu, Hao, Yurong Sun, Wenzhong Shi, Xiaoling Chen, and Dongjie Fu. 2013. "Examining the Satellite-Detected Urban Land Use Spatial Patterns Using Multidimensional Fractal Dimension Indices" Remote Sensing 5, no. 10: 5152-5172. https://doi.org/10.3390/rs5105152





