Evaluation of Clear-Sky Incoming Radiation Estimating Equations Typically Used in Remote Sensing Evapotranspiration Algorithms
Abstract
:1. Introduction
2. Methodology
2.1. Estimating Equations for Incoming Shortwave Radiative Flux ( )
2.1.1. Theoretical Framework
- For sloping surfaces,
- For horizontal surfaces,
2.1.2. Equations for Estimating Clear-Sky
2.1.3. Summary of Clear-Sky Estimating Equations
2.2. Estimating Equations for Incoming Longwave Radiative Flux ( )
2.2.1. Theoretical Framework
2.2.2. Equations for Estimating Clear Sky
- LW2a refers to Equations (19a) and (19b), where air temperature [K] and vapor pressure [kPa] measurements are at the screen level.
- LW2d refers to Equations (19a) and (19e), where air temperature [K] and vapor pressure [kPa] measurements are at the screen level.
2.2.3. Summary of Clear-Sky Estimating Equations
3. Data and Approach
3.1. Data
3.2. Approach
4. Results and Discussions
4.1. Evaluation of Clear-Sky Incoming Shortwave Radiation ( ) Estimating Equations
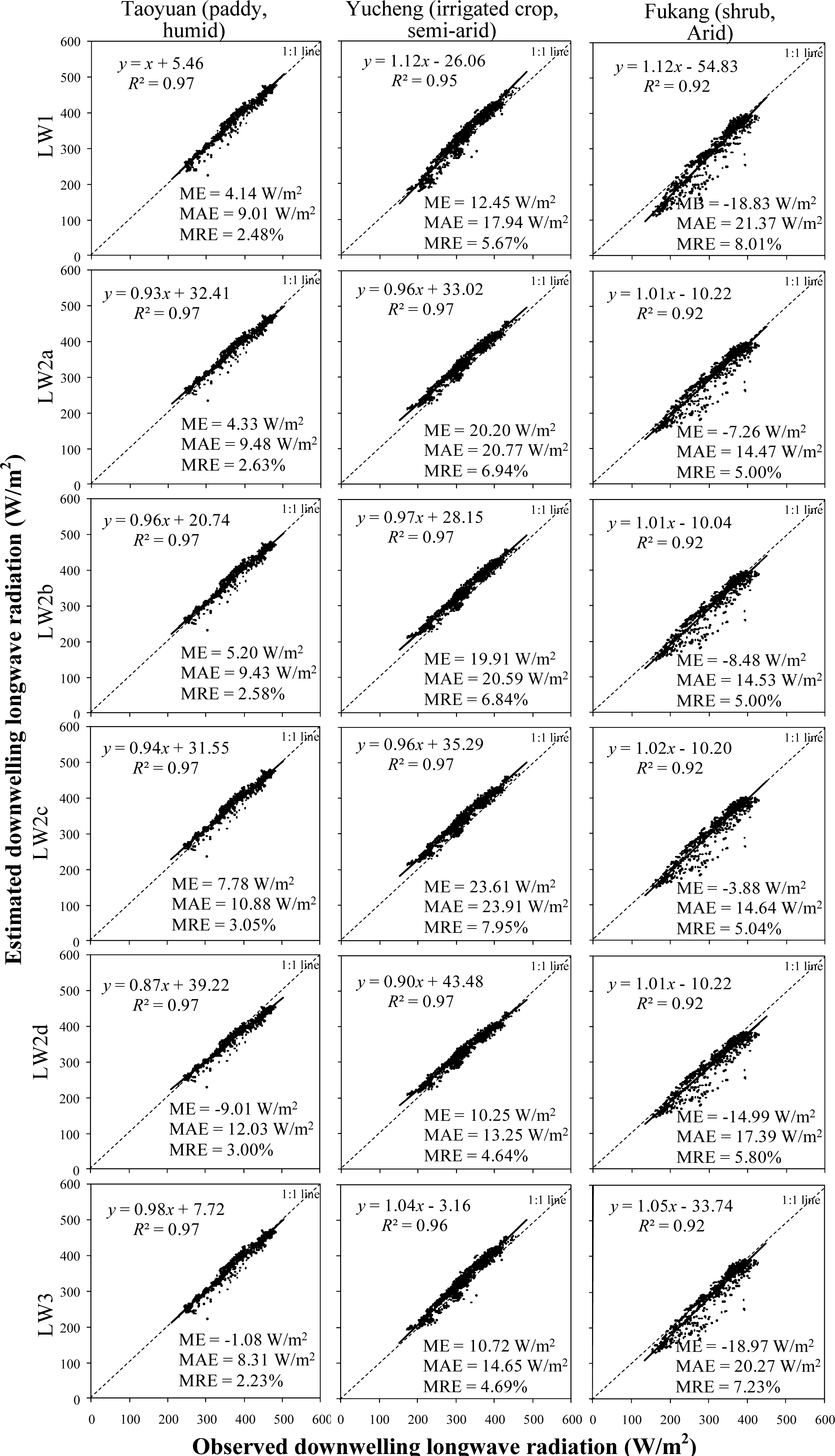
4.2. Evaluation of Clear-sky Incoming Longwave Radiation ( ) Estimating Equations
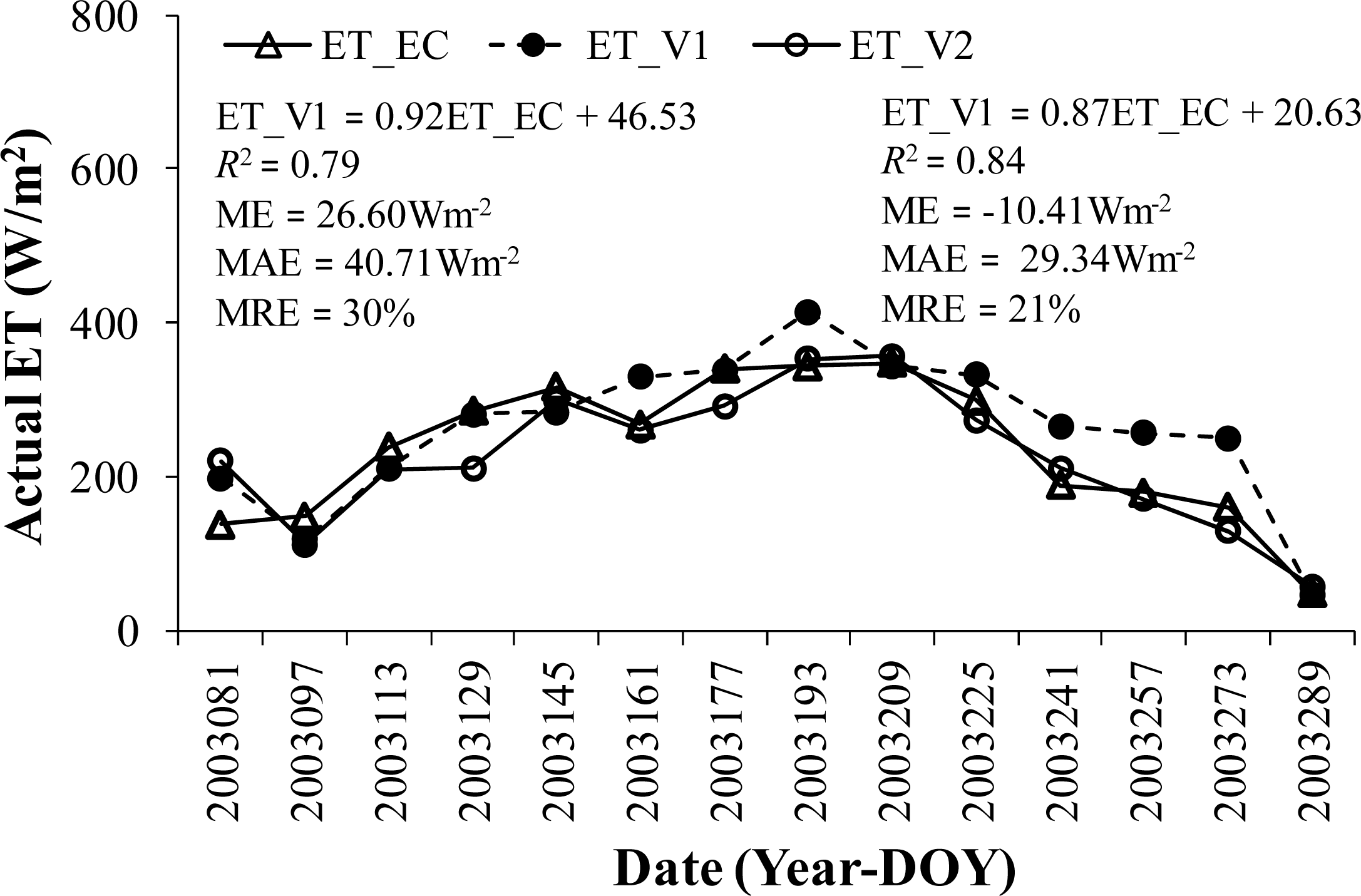
4.3. Evaluation of Clear-Sky Net Radiation (Rn) Estimating Equations
4.4. Suggestions on Incoming Radiation Estimation Equations for Remote Sensing ET Algorithms and Further Studies
5. Conclusions
- Both and estimates from all evaluated equations well correlate with observations (R2 ≥ 0.92).
- The estimating equations tend to overestimate, especially at higher values. The equations give large errors in the morning and late afternoon hours, where diffuse radiation is substantial. Of all the estimating equations, the equation treats the diffusive radiation component using two clearness indices and the equation assumes a linear increase of atmospheric transmissivity with elevation give the best estimates, and the mean relative absolute errors (MRE) are less than 10%. The equations that estimate atmospheric transmissivity from vapor pressure data or involve several complex relations produce worse results, and their MREs tend to be more than 10%.
- The estimating equations produce biased estimates at the arid and semi-arid sites (MRE: >4%) and less-biased estimates at the humid site (MRE: <3%).
- As a whole, the estimating equations tend to perform better than the estimating equations.
- The MRE in the net radiation (Rn) estimates caused by the use and estimating equations varies from 10% to 22%. The equation that gives the best estimate of Rn involves (1) the best estimating equation for estimation, and (2) the estimating equation that gives the largest negative bias or the smallest positive bias for estimation to compensate for the large positive bias in the estimates.
Acknowledgments
Conflicts of Interest
References
- Ruhoff, A.L.; Paz, A.R.; Collischonn, W.; Aragao, L.E.O.C.; Rocha, H.R.; Malhi, Y.S. A MODIS-based energy balance to estimate evapotranspiration for clear-sky days in Brazilian tropical savannas. Remote Sens 2012, 4, 703–725. [Google Scholar]
- Mariotto, I.; Gutschick, V.P. Non-lambertian corrected albedo and vegetation index for estimating land evapotranspiration in a heterogeneous semi-arid landscape. Remote Sens 2010, 2, 926–938. [Google Scholar]
- Cuenca, R.; Ciotti, S.; Hagimoto, Y. Application of Landsat to evaluate effects of irrigation forbearance. Remote Sens 2013, 5, 3776–3802. [Google Scholar]
- Hankerson, B.; Kjaersgaard, J.; Hay, C. Estimation of evapotranspiration from fields with and without cover crops using remote sensing and in situ methods. Remote Sens 2012, 4, 3796–3812. [Google Scholar]
- Llasat, M.C.; Snyder, R.L. Data error effects on net radiation and evapotranspiration estimation. Agric. For. Meteorol 1998, 91, 209–221. [Google Scholar]
- Sun, Z.G.; Wang, Q.X.; Matsushita, B.; Fukushima, T.; Ouyang, Z.; Watanabe, M. Development of a simple remote sensing evapotranspiration model (Sim-ReSET): Algorithm and model test. J. Hydrol 2009, 376, 476–485. [Google Scholar]
- Gueymard, C.A. Clear-sky irradiance predictions for solar resource mapping and large-scale applications: Improved validation methodology and detailed performance analysis of 18 broadband radiative models. Solar Energy 2012, 86, 2145–2169. [Google Scholar]
- Liang, S.L.; Wang, K.C.; Zhang, X.T.; Wild, M. Review on estimation of land surface radiation and energy budgets from ground measurement, remote sensing and model simulations. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens 2010, 3, 225–240. [Google Scholar]
- Wu, H.R.; Zhang, X.T.; Liang, S.L.; Yang, H.; Zhou, G.Q. Estimation of clear-sky land surface longwave radiation from MODIS data products by merging multiple models. J. Geophys. Res.-Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Chen, L.; Yan, G.J.; Wang, T.X.; Ren, H.Z.; Calbo, J.; Zhao, J.; McKenzie, R. Estimation of surface shortwave radiation components under all sky conditions: Modeling and sensitivity analysis. Remote Sens. Environ 2012, 123, 457–469. [Google Scholar]
- Bastiaanssen, W.G.M.; Menenti, M.; Feddes, R.A.; Holtslag, A.A.M. A remote sensing surface energy balance algorithm for land (SEBAL)-1. Formulation. J. Hydrol 1998, 212, 198–212. [Google Scholar]
- Nishida, K.; Nemani, R.R.; Running, S.W.; Glassy, J.M. An operational remote sensing algorithm of land surface evaporation. J. Geophys. Res.-Atmos. 2003. [Google Scholar] [CrossRef]
- Gao, Y.C.; Long, D.; Li, Z.L. Estimation of daily actual evapotranspiration from remotely sensed data under complex terrain over the upper Chao River Basin in North China. Int. J. Remote Sens 2008, 29, 3295–3315. [Google Scholar]
- Gubler, S.; Gruber, S.; Purves, R.S. Uncertainties of parameterized surface downward clear-sky shortwave and all-sky longwave radiation. Atmos. Chem. Phys 2012, 12, 5077–5098. [Google Scholar]
- Trnka, M.; Žalud, Z.; Eitzinger, J.; Dubrovský, M. Global solar radiation in central European lowlands estimated by various empirical formulae. Agric. For. Meteorol 2005, 131, 54–76. [Google Scholar]
- Marthews, T.R.; Malhi, Y.; Iwata, H. Calculating downward longwave radiation under clear and cloudy conditions over a tropical lowland forest site: An evaluation of model schemes for hourly data. Theor. Appl. Climatol 2012, 107, 461–477. [Google Scholar]
- Carmona, F.; Rivas, R.; Caselles, V. Estimation of daytime downward longwave radiation under clear and cloudy skies conditions over a sub-humid region. Theor. Appl. Climatol. 2013. [Google Scholar] [CrossRef]
- Duffie, J.A.; Beckman, W.A. Solar Engineering of Thermal Process, 1st ed.; John Wiley and Sons: New York, NY, USA, 1980. [Google Scholar]
- Garner, B.J.; Ohmura, A. A method for calculating direct shortwave radiation income of slopes. J. Appl. Meteorol 1968, 7, 796–800. [Google Scholar]
- Tasumi, M.; Allen, R.G.; Bastiaanssen, W.G.M. The Theoretical Basis of Sebal; University of Idaho: Moscow, ID, USA, 2000; pp. 46–69. [Google Scholar]
- Zillman, J.W. A Study of Some Aspects of the Radiation and Heat Budgets of the Southern Hemisphere Oceans; Bureau of Meteorology, Department of the Interior: Canberra, ACT, Australia, 1972. [Google Scholar]
- Shine, K.P. Parameterization of the shortwave flux over high albedo surfaces as a function of cloud thickness and surface albedo. Q. J. Roy. Meteor. Soc 1984, 110, 747–764. [Google Scholar]
- Allen, R.G.; Trezza, R.; Tasumi, M. Analytical integrated functions for daily solar radiation on slopes. Agric. For. Meteorol 2006, 139, 55–73. [Google Scholar]
- Kondo, J. Atmospheric Science near the Ground Surface; University of Tokyo Press: Tokyo, Japan, 2000. [Google Scholar]
- Bisht, G.; Venturini, V.; Islam, S.; Jiang, L. Estimation of the net radiation using MODIS (moderate resolution imaging spectroradiometer) data for clear sky days. Remote Sens. Environ 2005, 97, 52–67. [Google Scholar]
- Venturini, V.; Islam, S.; RodrigueZ, L. Estimation of evaporative fraction and evapotranspiration from MODIS products using a complementary based model. Remote Sens. Environ 2008, 112, 132–141. [Google Scholar]
- Jiang, L.; Islam, S.; Guo, W.; Jutla, A.S.; Senarath, S.U.S.; Ramsay, B.H.; Eltahir, E.A.B. A satellite-based daily actual evapotranspiration estimation algorithm over south florida. Glob. Planet. Change 2009, 67, 62–77. [Google Scholar]
- Brutsaert, W. On a derivable formula for longwave radiation from clear skies. Water Resour. Res 1975, 11, 742–744. [Google Scholar]
- Prata, A.J. A new long-wave formula for estimating downward clear-sky radiation at the surface. Q. J. Roy. Meteor. Soc 1996, 122, 1127–1151. [Google Scholar]
- Reitan, C.H. Surface dew point and water vapor aloft. J. Appl. Meteorol 1963, 2, 776–779. [Google Scholar]
- Venäläinen, A. The Spatial Variation of Mean Monthly Global Radiation in Finland; University of Helsinki: Helsinki, Finland, 1994. [Google Scholar]
- Watanabe, M.; Wang, Q.X.; Hayashi, S. Monitoring and simulation of water, heat, and CO2 fluxes in terrestrial ecosystems based on the APEIS-flux system. J. Geogr. Sci 2005, 15, 131–141. [Google Scholar]
- Kutsch, W.L.; Hanan, N.; Scholes, B.; McHugh, I.; Kubheka, W.; Eckhardt, H.; Williams, C. Response of carbon fluxes to water relations in a savanna ecosystem in South Africa. Biogeosciences 2008, 5, 1797–1808. [Google Scholar]
- Wang, J.M.; Miller, D.R.; Sammis, T.W.; Gutschick, V.P.; Simmons, L.J.; Andales, A.A. Energy balance measurements and a simple model for estimating pecan water use efficiency. Agric. Water Manage 2007, 91, 92–101. [Google Scholar]
- Sun, Z.G.; Wang, Q.X.; Matsushita, B.; Fukushima, T.; Ouyang, Z.; Watanabe, M.; Gebremichael, M. Further evaluation of the Sim-ReSET model for et estimation driven by only satellite inputs. Hydrol. Sci. J 2013, 58, 994–1012. [Google Scholar]



| Site | Location | Climate (Annual Average Temperature, Annual Precipitation) | Land Cover | Measurements * | Date Available over the Whole Year of |
|---|---|---|---|---|---|
| Taoyuan (China) | 111.469°E 28.944°N 108 m a.s.l. | Humid (16.5 °C, 1,450 mm) | Paddy | Ta, RH, P, Ts, , , , , Rn | 2003 |
| Yucheng (China) | 116.571°E 36.829°N 28 m a.s.l. | Semi-arid (13.1 °C, 610 mm) | Irrigated crop | Ta, RH, P, Ts, , , , , Rn | 2007 |
| Fukang (China) | 87.937°E 44.292°N 470 m a.s.l. | Arid, (6.6 °C, 164 mm) | Shrub | Ta, RH, P, Ts, , , , , Rn | 2003 |
| Skukuza (South Africa) | 31.497°E 25.020°S 365 m a.s.l. | Semi-arid (21.9 °C, 547 mm) | Savanna | Ta, RH, P, , | 2008 |
| OPEC (New Mexico, USA) | 106.756°W 32.225°N 1177 m a.s.l. | Arid, (17.8 °C, 280 mm) | Pecan orchard | Ta, RH, P, , Rn | 2003 |
| SW1 | SW2 | SW3 | SW4 | SW5 | SW6 | SW7 | ||
|---|---|---|---|---|---|---|---|---|
| LW1 | Taoyuan (paddy, humid) | 12.84 | 15.05 | 14.44 | 13.83 | 13.17 | 12.25 | 13.06 |
| Yucheng (irrigated crop, semi-arid) | 11.07 | 16.69 | 15.21 | 14.36 | 12.88 | 14.80 | 14.43 | |
| Fukang (shrub, arid) | 13.84 | 20.85 | 18.17 | 17.78 | 15.50 | 15.75 | 17.88 | |
| LW2a | Taoyuan (paddy, humid) | 12.86 | 15.01 | 14.51 | 13.91 | 13.36 | 12.18 | 13.15 |
| Yucheng (irrigated crop, semi-arid) | 10.90 | 16.56 | 15.36 | 14.18 | 13.05 | 14.50 | 14.72 | |
| Fukang (shrub, arid) | 13.81 | 21.38 | 18.53 | 18.10 | 15.78 | 15.61 | 18.22 | |
| LW2b | Taoyuan (paddy, humid) | 12.92 | 15.00 | 14.45 | 13.95 | 13.34 | 12.11 | 13.06 |
| Yucheng (irrigated crop, semi-arid) | 10.88 | 16.63 | 15.39 | 14.21 | 13.04 | 14.56 | 14.74 | |
| Fukang (shrub, arid) | 13.81 | 21.28 | 18.45 | 18.03 | 15.70 | 15.63 | 18.13 | |
| LW2c | Taoyuan (paddy, humid) | 13.21 | 15.29 | 14.76 | 14.35 | 13.72 | 12.11 | 13.30 |
| Yucheng (irrigated crop, semi-arid) | 11.05 | 16.73 | 15.55 | 14.39 | 13.28 | 14.45 | 14.88 | |
| Fukang (shrub, arid) | 13.76 | 21.57 | 18.69 | 18.24 | 15.93 | 15.48 | 18.35 | |
| LW2d | Taoyuan (paddy, humid) | 11.14 | 14.18 | 13.78 | 12.53 | 12.21 | 12.40 | 12.67 |
| Yucheng (irrigated crop, semi-arid) | 10.53 | 15.99 | 14.88 | 13.51 | 12.53 | 14.74 | 14.43 | |
| Fukang (shrub, arid) | 13.74 | 20.44 | 17.73 | 17.31 | 15.22 | 15.63 | 17.49 | |
| LW3 | Taoyuan (paddy, humid) | 12.03 | 14.68 | 14.12 | 13.20 | 12.60 | 12.30 | 12.83 |
| Yucheng (irrigated crop, semi-arid) | 10.81 | 16.43 | 15.01 | 14.02 | 12.66 | 14.78 | 14.37 | |
| Fukang (shrub, arid) | 13.65 | 20.39 | 17.82 | 17.36 | 15.23 | 15.51 | 17.56 | |
© 2013 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Sun, Z.; Gebremichael, M.; Wang, Q.; Wang, J.; Sammis, T.W.; Nickless, A. Evaluation of Clear-Sky Incoming Radiation Estimating Equations Typically Used in Remote Sensing Evapotranspiration Algorithms. Remote Sens. 2013, 5, 4735-4752. https://doi.org/10.3390/rs5104735
Sun Z, Gebremichael M, Wang Q, Wang J, Sammis TW, Nickless A. Evaluation of Clear-Sky Incoming Radiation Estimating Equations Typically Used in Remote Sensing Evapotranspiration Algorithms. Remote Sensing. 2013; 5(10):4735-4752. https://doi.org/10.3390/rs5104735
Chicago/Turabian StyleSun, Zhigang, Mekonnen Gebremichael, Qinxue Wang, Junming Wang, Ted W. Sammis, and Alecia Nickless. 2013. "Evaluation of Clear-Sky Incoming Radiation Estimating Equations Typically Used in Remote Sensing Evapotranspiration Algorithms" Remote Sensing 5, no. 10: 4735-4752. https://doi.org/10.3390/rs5104735





