Analysis of Cross-Seasonal Spectral Response from Kettle Holes: Application of Remote Sensing Techniques for Chlorophyll Estimation
Abstract
:1. Introduction
2. Methods
2.1. Study Area
2.2. Kettle Holes’ Hydro-Morphological Characteristics
2.3. Field Sampling
2.4. Measurement of Spectral Reflectance
2.5. Statistical Methods
3. Results
3.1. Typology of Spectral Response
3.2. Spectral Algebra Algorithms and Biomass Concentrations
3.3. Derivative Reflectance Analysis
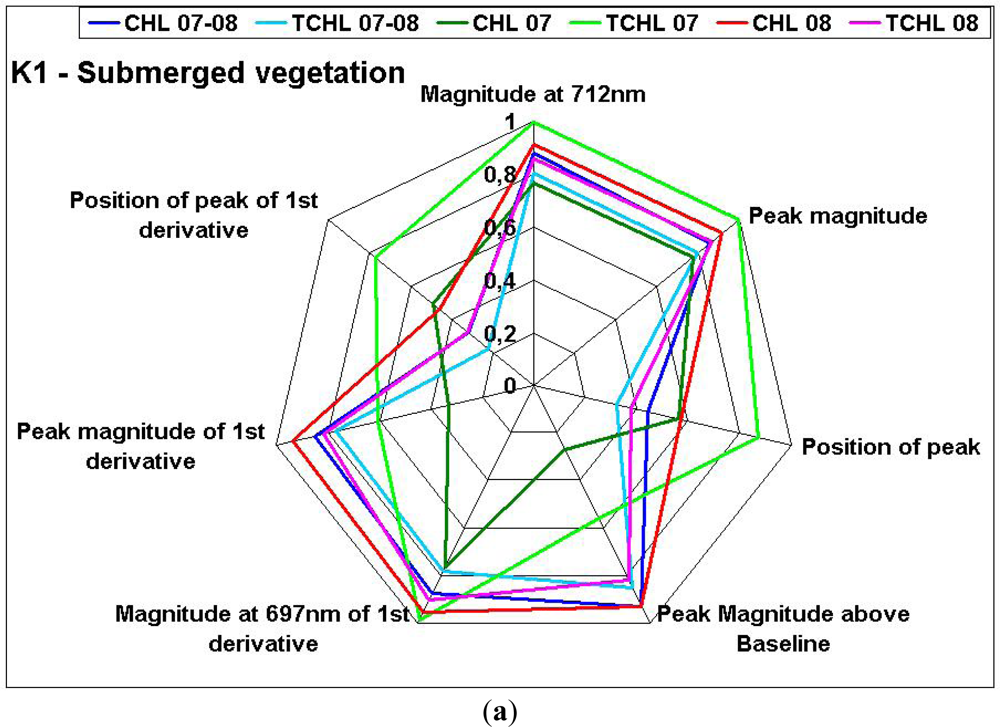
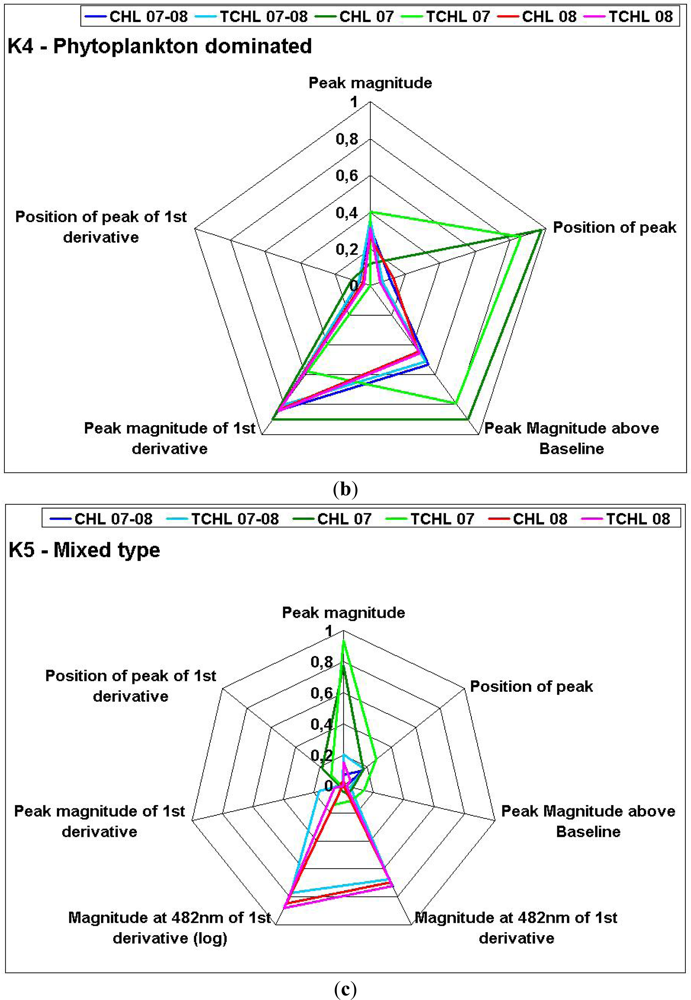
3.4. Application of Remote Sensing Techniques for Chlorophyll Estimation
3.5. Analysis of Biomass Estimation Algorithms Accuracy
4. Conclusions
Acknowledgments
References
- Merbach, W.; Kalettka, T.; Rudat, C.; Augustin, J. Trace Gas Emissions from Riparian Areas of Small Eutrophic Inland Waters in Northeast-Germany. In Wetlands in Central Europe; Broll, G., Merbach, W., Pfeiffer, E.-M., Eds.; Springer Berlin Heidelberg: New York, NY, USA, 2002; pp. 235–244. [Google Scholar]
- Kalettka, T.; Berger, M.; Pfeffer, H.; Rudat, C. Integrated Conservation and Management of Kettle Holes in Young Moraine Agricultural Landscapes of Northeast Germany. Proceedings of 21st European Regional Conference of the International Commission on Irrigation and Drainage, Frankfurt (Oder), Germany and Slubice, Poland, 15–19 May 2005; pp. 1–4.
- Igamberdiev, R.M.; Lennartz, B.; Grenzdoerffer, G.; Bill, R.; Schubert, H. Analysis of spectral signatures of small water bodies (kettle holes) in the agricultural young moraine landscape of North-Eastern Germany. Int. J. Remote Sens 2010, 31, 5495–5511. [Google Scholar]
- Vohland, M.; Bossung, C.; Frund, H.C. A spectroscopic approach to assess trace-heavy metal contents in contaminated flood plain soils via spectrally active soil components. J. Plant Nutr. Soil Sc 2009, 172, 201–209. [Google Scholar]
- Bhatti, A.M.; Rundquist, D.; Schalles, J.; Ramirez, L.; Nasu, S. A comparison between above-water surface and subsurface spectral reflectances collected over inland waters. Geocarto Int 2009, 24, 133–141. [Google Scholar]
- Jensen, J.R. Remote Sensing of the Environment: An Earth Resource Perspective, 2nd ed; Prentice Hall: Upper Saddle River, NJ, USA, 2006; p. 592. [Google Scholar]
- Wiangwang, N. Hyperspectral Data Modelling for Water Quality Studies in Michigan’s Inland Lakes. Michigan State University, East Lansing, MI, USA, 2006. [Google Scholar]
- Salama, M.S.; Dekker, A.; Su, Z.; Mannaerts, C.M.; Verhoef, W. Deriving inherent optical properties and associated inversion-uncertainties in the Dutch Lakes. Hydrol. Earth Syst. Sci 2009, 13, 1113–1121. [Google Scholar]
- Matthews, M.W.; Bernard, S.; Winter, K. Remote sensing of cyanobacteria-dominant algal blooms and water quality parameters in Zeekoevlei, a small hypertrophic lake, using MERIS. Remote Sens. Environ 2010, 114, 2070–2087. [Google Scholar]
- Gomez, J.A.D.; Alonso, C.A.; Garcia, A.A. Remote sensing as a tool for monitoring water quality parameters for Mediterranean Lakes of European Union water framework directive (WFD) and as a system of surveillance of cyanobacterial harmful algae blooms (SCyanoHABs). Environ. Monit. Assess 2011, 181, 317–334. [Google Scholar]
- Lee, B.S.; McGwire, K.C.; Fritsen, C.H. Identification and quantification of aquatic vegetation with hyperspectral remote sensing in western Nevada rivers, USA. Int. J. Remote Sens 2011, 32, 9093–9117. [Google Scholar]
- Dekker, A.G. Detection of Optical Water Quality Parameters for Eutrophic Waters by High Resolution Remote Sensing. Vrije Univecsiteit, Amsterdam, The Netherlands, 1993. [Google Scholar]
- Gege, P.; Albert, A. A Tool for inverse Modelling of Spectral Measurements in Deep and Shallow Water. In Remote Sensing of Aquatic Coastal Ecosystems Processes: Science and Management Applications; Richardson, L.L., LeDrew, E.F., Eds.; Springer: Dordrecht, The Netherlands, 2006; pp. 81–109. [Google Scholar]
- Bukata, R.P.; Jerome, J.H.; Kondratiev, K.Y.; Pozdnyakov, D.V. Optical Properties and Remote Sensing of Inland and Coastal Waters; CRC Press: New York, NY, USA, 1995; p. 362. [Google Scholar]
- Liu, Y.S.; Islam, M.A.; Gao, J. Quantification of shallow water quality parameters by means of remote sensing. Prog. Phys. Geog 2003, 27, 24–43. [Google Scholar]
- Kneubuehler, M.; Gemperli, C.; Schlapfer, D.; Zah, R.; Itten, K. Determination of Water Quality Parameters in Indian Ponds Using Remote Sensing Methods. Proceedings of EARSeL 4th Workshop on Imaging Spectroscopy, Warsaw, Poland, 27–29 April 2005; pp. 301–315.
- Kalettka, T.; Rudat, C. Hydrogeomorphic types of glacially created kettle holes in North-East Germany. Limnologica 2006, 36, 54–64. [Google Scholar]
- Porra, R.J.; Thompson, W.A.; Kriedemann, P.E. Determination of accurate extinction coefficients and simultaneous-equations for assaying chlorophyll-A and chlorophyll-B extracted with 4 different solvents—Verification of the concentration of chlorophyll standards by atomic-absorption spectroscopy. Biochim. Biophys. Acta 1989, 975, 384–394. [Google Scholar]
- Lee, Z.-P. Remote Sensing of Inherent Optical Properties: Fundamentals, Tests of Algorithms, and Applications; The International Ocean-Colour Coordinating Group: Dartmouth, NS, Canada, 2006. [Google Scholar]
- Igamberdiev, R.M.; Lennartz, B. Spectral Response from Various Types of Kettle Holes: Analysis and Application of Remote Sensing Techniques for Chlorophyll Estimation. Proceedings of 4th EPCN (European Pond Conservation Network) Conference, Berlin, Germany, 1–4 June 2010.
- Gitelson, A.A. Nature of the peak near 700-nm on the radiance spectra and its application for remote estimation of phytoplankton pigments in inland waters. Proc. SPIE 1993, 170, 170–179. [Google Scholar]
- Doxaran, D.; Froidefond, J.M.; Castaing, P. A reflectance band ratio used to estimate suspended matter concentrations in sediment-dominated coastal waters. Int. J. Remote Sens 2002, 23, 5079–5085. [Google Scholar]
- Gitelson, A.; Yacobi, Y.; Rundquist, D.C.; Stark, R.; Han, L.; Etzion, D. Remote Estimation of Chlorophyll Concen-Tration in Productive Waters: Principals, Algorithm Development and Validation. Proceedings of NWQMC National Conference, Austin, TX, USA, 25–27 April 2000; pp. 149–160.
- Han, L.H. Spectral reflectance with varying suspended sediment concentrations in clear and algae-laden waters. Photogramm. Eng. Remote Sensing 1997, 63, 701–705. [Google Scholar]
- Thiemann, S.; Kaufmann, H. Lake water quality monitoring using hyperspectral airborne data—A semiempirical multisensor and multitemporal approach for the Mecklenburg Lake District, Germany. Remote Sens. Environ 2002, 81, 228–237. [Google Scholar]
- Han, L.H. Estimating chlorophyll-a concentration using first-derivative spectra in coastal water. Int. J. Remote Sens 2005, 26, 5235–5244. [Google Scholar]
- Dekker, A.G.; Malthus, T.J.; Hoogenboom, H.J. The Remote Sensing of Inland Water Quality. In Advances in Environmental Remote Sensing, 1st ed; Danson, F.M., Plummer, S.E., Eds.; John Wiley and Sons: London, UK, 1995; pp. 123–142. [Google Scholar]
- Thiemann, S.; Kaufmann, H. Determination of chlorophyll content and trophic state of lakes using field spectrometer and IRS-1C satellite data in the Mecklenburg lake district, Germany. Remote Sens. Environ 2000, 73, 227–235. [Google Scholar]
- Scheffer, M. Ecology of Shallow Lakes; Springer: Berlin, Germany, 1998; p. 384. [Google Scholar]
- Gitelson, A. The peak near 700 nm on radiance spectra of algae and water: Relationships of its magnitude and position with chlorophyll concentration. Int. J. Remote Sens 1992, 13, 3367–3373. [Google Scholar]
- Jiao, H.B.; Zha, Y.; Gao, J.; Li, Y.M.; Wei, Y.C.; Huang, J.Z. Estimation of chlorophyll-a concentration in Lake Tai, China using in situ hyperspectral data. Int. J. Remote Sens 2006, 27, 4267–4276. [Google Scholar]
- Murphy, R.J.; Underwood, A.J.; Tolhurst, T.J.; Chapman, M.G. Field-based remote-sensing for experimental intertidal ecology: Case studies using hyperspatial and hyperspectral data for New South Wales (Australia). Remote Sens. Environ 2008, 112, 3353–3365. [Google Scholar]
- Wang, J.J.; Lu, X.X.; Liew, S.C.; Zhou, Y. Remote sensing of suspended sediment concentrations of large rivers using multi-temporal MODIS images: an example in the Middle and Lower Yangtze River, China. Int. J. Remote Sens 2010, 31, 1103–1111. [Google Scholar]
- Han, L.H.; Rundquist, D.C. Comparison of NIR/RED ratio and first derivative of reflectance in estimating algal-chlorophyll concentration: A case study in a turbid reservoir. Remote Sens. Environ 1997, 62, 253–261. [Google Scholar]
- Tsai, F.; Philpot, W. Derivative analysis of hyperspectral data. Remote Sens. Environ 1998, 66, 41–51. [Google Scholar]
- Ma, R.; Tang, J.; Dai, J.; Zhang, Y.; Song, Q. Absorption and scattering properties of water body in Taihu Lake, China: Absorption. Int. J. Remote Sens 2006, 27, 4277–4304. [Google Scholar]
- Scheffer, M.; van Nes, E.H. Shallow lakes theory revisited: Various alternative regimes driven by climate, nutrients, depth and lake size. Hydrobiologia 2007, 584, 455–466. [Google Scholar]
- Igamberdiev, R.M.; Grenzdoerffer, G.; Bill, R.; Schubert, H.; Bachmann, M.; Lennartz, B. Determination of chlorophyll content of small water bodies (kettle holes) using hyperspectral airborne data. Int. J. Appl. Earth Obs. Geoinf 2011, 13, 912–921. [Google Scholar]
- Gilerson, A.A.; Gitelson, A.A.; Zhou, J.; Gurlin, D.; Moses, W.; Ioannou, I.; Ahmed, S.A. Algorithms for remote estimation of chlorophyll-a in coastal and inland waters using red and near infrared bands. Opt. Express 2010, 18, 24109–24125. [Google Scholar]
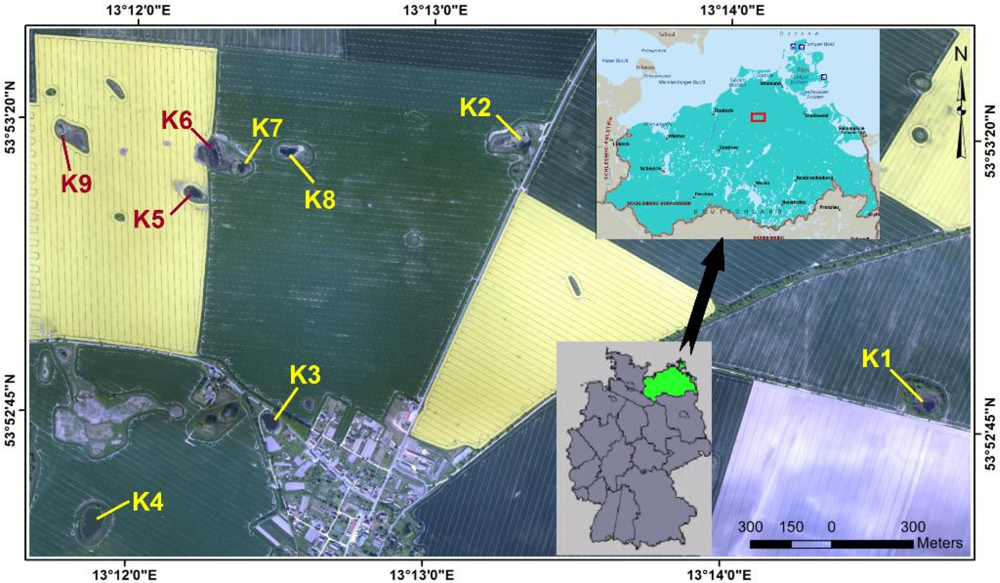
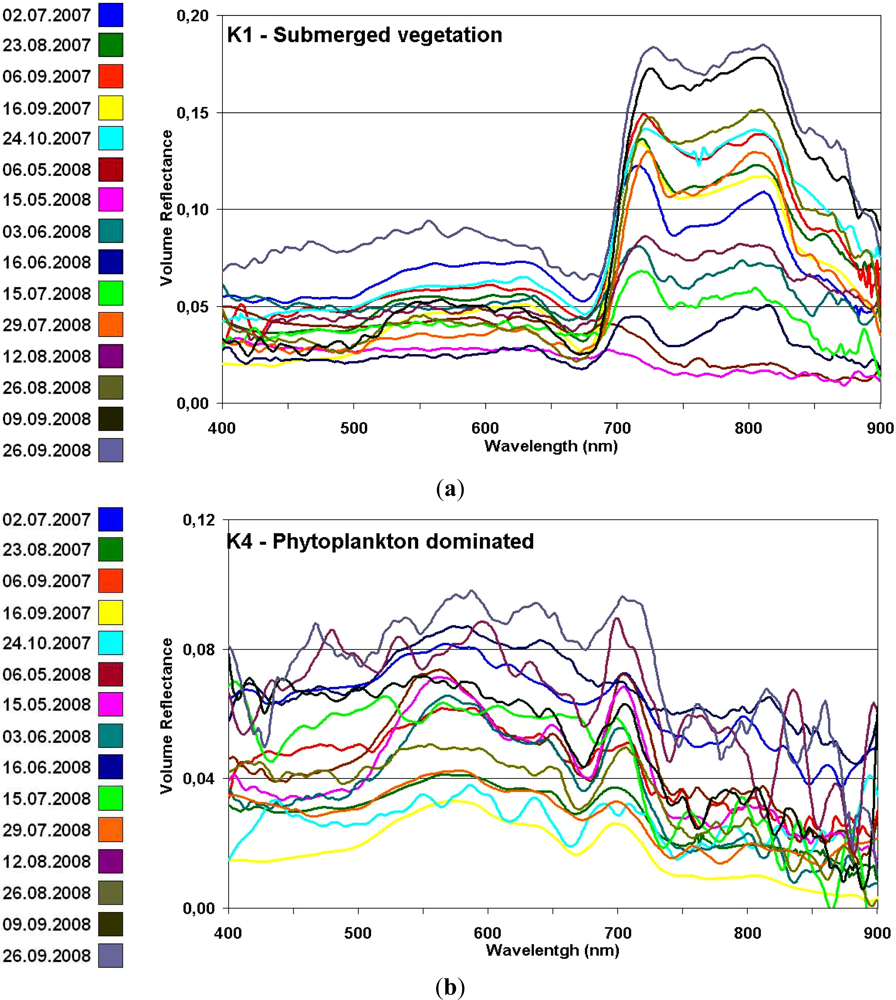
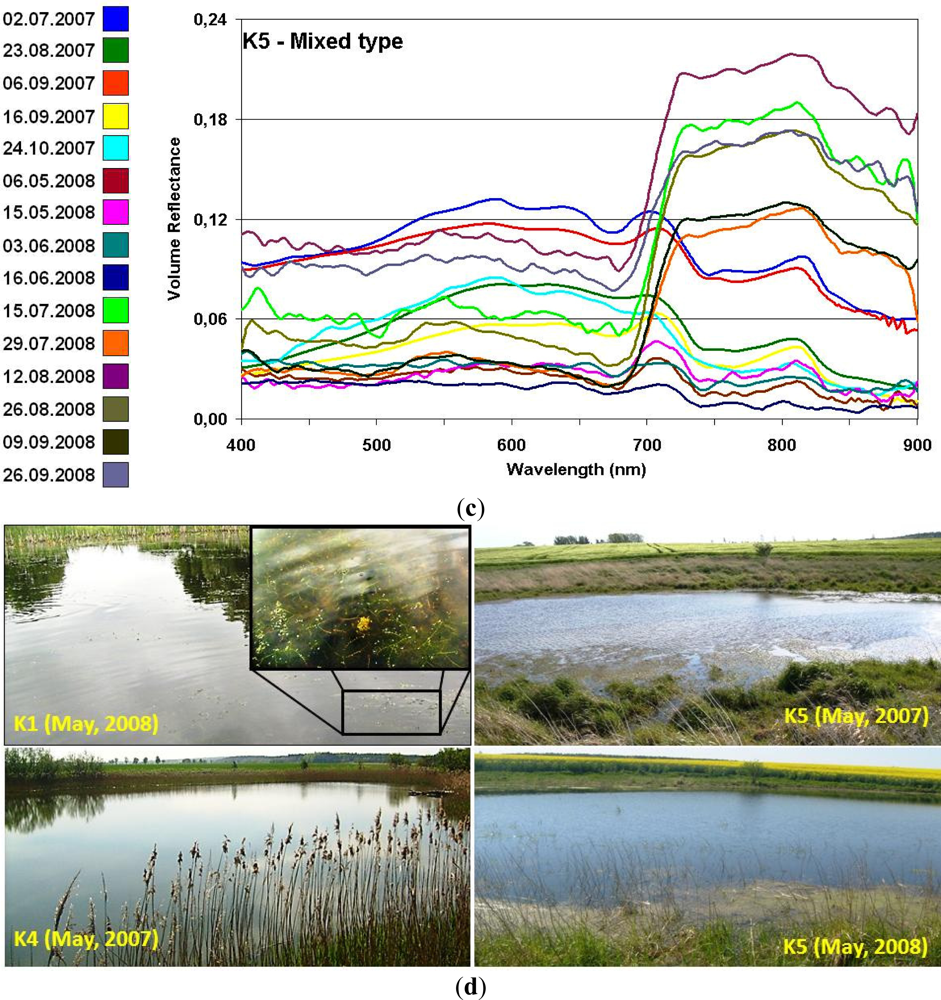
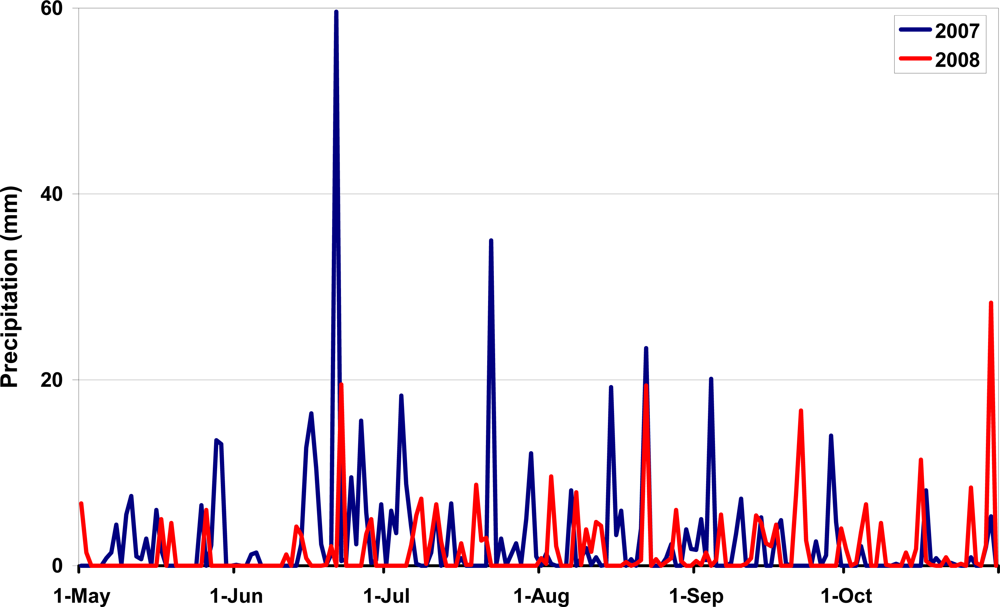
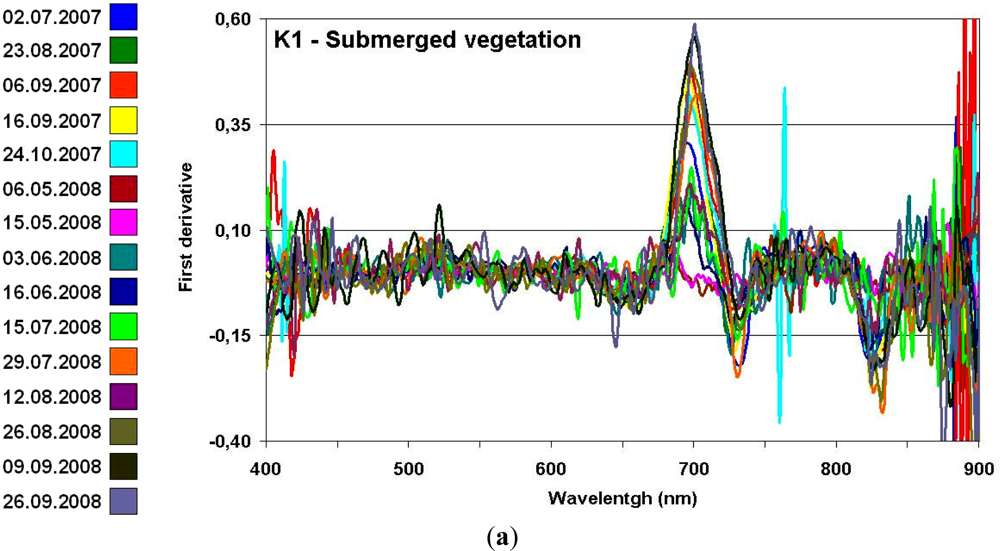
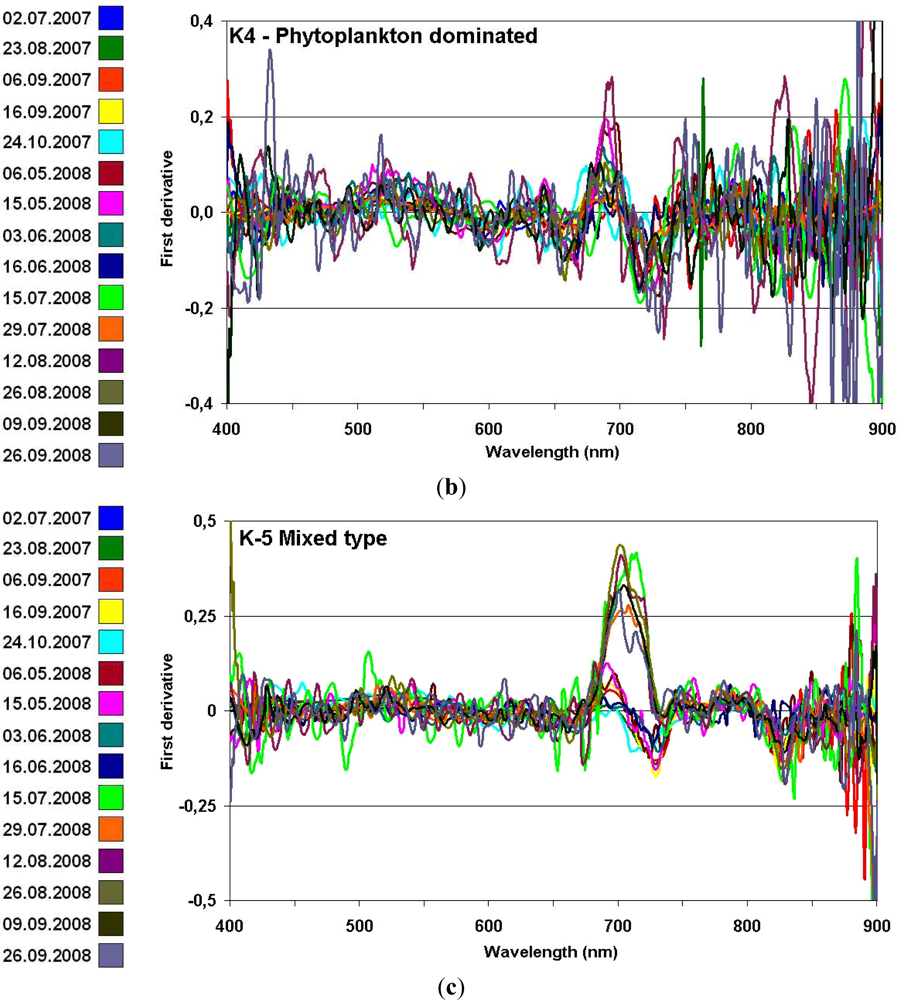
| Name | Area (ha) | Depth (m) | Algae Coverage | Water Color | Subtype | Spectral Response Type |
|---|---|---|---|---|---|---|
| K1 | ≈0.12 | ≈ 1 ÷ 1.5 | Close to the surface | Transparent | Big shallow | Submerged vegetation |
| K2 | ≈0.14 | ≈ 0.5 ÷ 1.0 | Close to the surface | Transparent | Big shallow | Submerged vegetation |
| K4 | ≈0.80 | ≈ 2.5 ÷ 3.5 | Very Low | Dark green | Big deep | Phytoplankton dominated |
| K5 | ≈0.10 | ≈ 0.3 ÷ 0.5 | Close to the surface | 2007-Light brown 2008-Transparent | Small wadeable | Mixed |
| K6 | ≈0.25 | ≈ 0.6 ÷ 1.3 | Only on the banks | Transparent | Big shallow | Phytoplankton dominated |
| K7 | ≈0.23 | ≈ 0.8 ÷ 1.2 | Low | Transparent | Big shallow | Phytoplankton dominated |
| Date | K1 | K4 | K5 | K6 | K7 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P1 | P2 | P3 | P1 | P2 | P3 | P1 | P2 | P3 | P1 | P2 | P3 | P1 | P2 | P3 | |
| 07.06.07 | 15.8 | 20.0 | 5.7 | 33.4 | 41.7 | 2.3 | 94.3 | 111.4 | 21.3 | 17.3 | 19.4 | 9.4 | 1.9 | 3.0 | 2.0 |
| 02.07.07 | 4.6 | 9.5 | 2.0 | 64.6 | 95.3 | 13.8 | 62.0 | 100.6 | 12.3 | 3.2 | 5.5 | 6.0 | 4.6 | 9.5 | 2.0 |
| 23.08.07 | 1.9 | 3.1 | 1.6 | 43.2 | 62.7 | 3.9 | 4.2 | 6.8 | 8.7 | 4.5 | 7.3 | 2.4 | 1.9 | 3.1 | 1.6 |
| 06.09.07 | 2.1 | 2.5 | 1.7 | 80.9 | 109.9 | 6.0 | 5.0 | 11.0 | 7.4 | 54.8 | 55.0 | 5.8 | 2.1 | 2.5 | 1.7 |
| 16.09.07 | 5.1 | 10.6 | 1.7 | 35.0 | 42.3 | 12.0 | 2.3 | 3.5 | 11.8 | 14.9 | 20.9 | 2.4 | 5.1 | 10.6 | 1.7 |
| 24.10.07 | 2.4 | 2.9 | 4.7 | 83.7 | 93.0 | 10.4 | 2.6 | 3.4 | 7.0 | 6.5 | 6.9 | 2.8 | 2.4 | 2.9 | 4.7 |
| 06.05.08 | 1.2 | 1.6 | 2.1 | 108.0 | 110.8 | 5.2 | 7.0 | 7.0 | 3.2 | 2.2 | 3.2 | 1.7 | 1.2 | 1.6 | 2.1 |
| 15.05.08 | 2.5 | 3.2 | 2.5 | 78.6 | 102.9 | 13.9 | 3.4 | 4.6 | 2.6 | 5.9 | 10.2 | 3.1 | 2.5 | 3.2 | 2.5 |
| 03.06.08 | 6.4 | 7.5 | 1.9 | 59.0 | 61.3 | 17.4 | 17.0 | 18.6 | 5.3 | 9.5 | 10.2 | 2.3 | 6.4 | 7.5 | 1.9 |
| 16.06.08 | 6.3 | 6.8 | 4.3 | 30.0 | 34.8 | 5.9 | 8.5 | 9.4 | 2.2 | 4.2 | 6.1 | 1.5 | 6.3 | 6.8 | 4.3 |
| 15.07.08 | 5.2 | 7.1 | 4.4 | 79.2 | 87.1 | 7.2 | 2.5 | 3.3 | 9.2 | 5.3 | 7.1 | 1.4 | 5.2 | 7.1 | 4.4 |
| 29.07.08 | 3.2 | 4.3 | 4.0 | 32.9 | 40.2 | 4.8 | 4.4 | 6.2 | 2.3 | 3.2 | 4.0 | 0.8 | 3.2 | 4.3 | 4.0 |
| 12.08.08 | 3.3 | 4.9 | 3.0 | 156.1 | 224.7 | 11.7 | 18.9 | 33.6 | 6.5 | 5.0 | 7.0 | 1.4 | 3.3 | 4.9 | 3.0 |
| 26.08.08 | 4.4 | 6.6 | 1.1 | 129.2 | 145.3 | 11.6 | 5.4 | 6.1 | 4.9 | 10.3 | 12.2 | 3.9 | 4.4 | 6.6 | 1.1 |
| 09.09.08 | 2.7 | 5.3 | 1.3 | 181.0 | 218.9 | 13.3 | 23.4 | 28.5 | 6.0 | 4.3 | 8.7 | 0.8 | 2.7 | 5.3 | 1.3 |
| 26.09.08 | 3.6 | 6.8 | 1.8 | 143.0 | 171.9 | 8.8 | 15.1 | 24.1 | 8.4 | 3.6 | 5.2 | 0.9 | 3.6 | 6.8 | 1.8 |
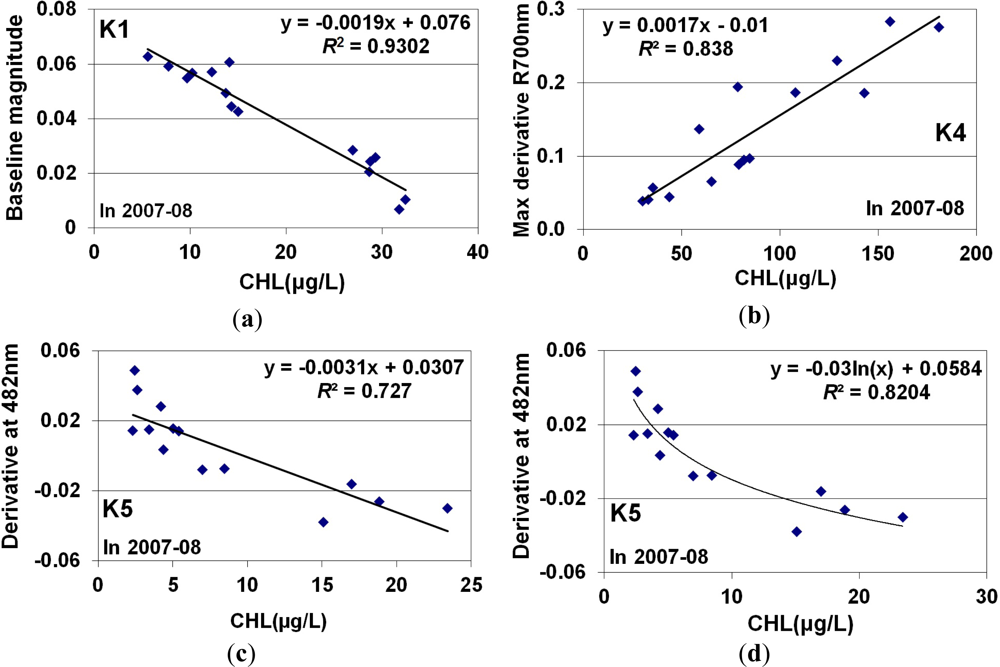
| Kettle Hole | Spectral Response Type | Algorithm | Biomass Type | R2 | RMSE (μg·L−1) | MDa |
|---|---|---|---|---|---|---|
| K1 | Submerged vegetation | Peak Magnitude above a Baseline | CHL | 0.93 | 0.088 | 2.09 |
| Magnitude at 697 nm of 1st derivative | CHL | 0.87 | 0.11 | 3.00 | ||
| K2 | Submerged vegetation | Magnitude at 743 nm | CHL | 0.98 | 0.05 | 0.09 |
| Magnitude at 697 nm of 1st derivative | CHL | 0.82 | 0.14 | 0.31 | ||
| K4 | Phytoplankton dominated | Peak Magnitude of 1st derivative | CHL | 0.84 | 0.11 | 16.65 |
| K5 | Mixed | Magnitude at 482 nm of 1st derivative (linear) | CHL | 0.73 | 0.30 | 3.46 |
| Magnitude at 482 nm of 1st derivative (logarithmic) | CHL | 0.82 | 0.16 | 2.39 | ||
| K6 | Phytoplankton dominated | Peak Magnitude of 1st derivative | TCHL | 0.59 | 0.52 | 8.70 |
| K7 | Phytoplankton dominated | Peak Magnitude above a Baseline | CHL | 0.85 | 0.09 | 0.52 |
| Peak Magnitude of 1st derivative | CHL | 0.76 | 0.13 | 0.81 |
Share and Cite
Igamberdiev, R.M.; Bill, R.; Schubert, H.; Lennartz, B. Analysis of Cross-Seasonal Spectral Response from Kettle Holes: Application of Remote Sensing Techniques for Chlorophyll Estimation. Remote Sens. 2012, 4, 3481-3500. https://doi.org/10.3390/rs4113481
Igamberdiev RM, Bill R, Schubert H, Lennartz B. Analysis of Cross-Seasonal Spectral Response from Kettle Holes: Application of Remote Sensing Techniques for Chlorophyll Estimation. Remote Sensing. 2012; 4(11):3481-3500. https://doi.org/10.3390/rs4113481
Chicago/Turabian StyleIgamberdiev, Rahmatulla M., Ralf Bill, Hendrik Schubert, and Bernd Lennartz. 2012. "Analysis of Cross-Seasonal Spectral Response from Kettle Holes: Application of Remote Sensing Techniques for Chlorophyll Estimation" Remote Sensing 4, no. 11: 3481-3500. https://doi.org/10.3390/rs4113481




