Numerical Simulation of a Dual-Chamber Oscillating Water Column Wave Energy Converter
Abstract
:1. Introduction
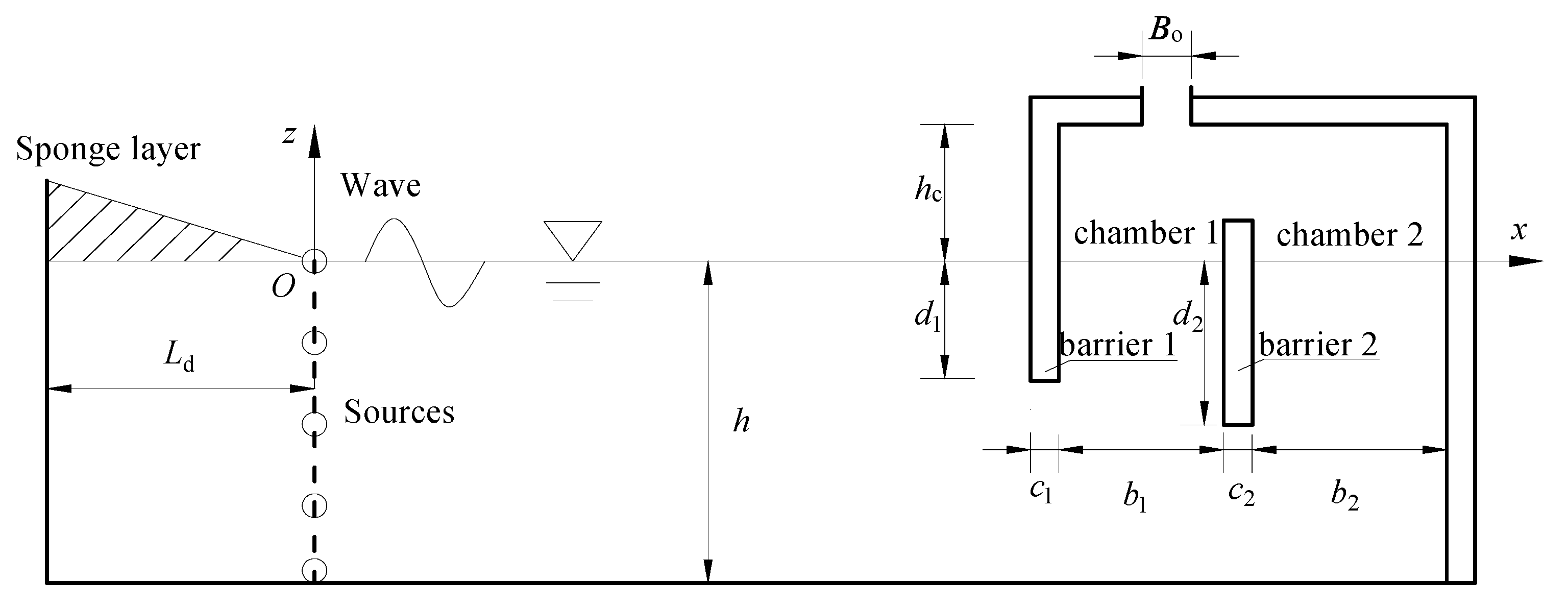
2. Numerical Model
3. Results and Discussions
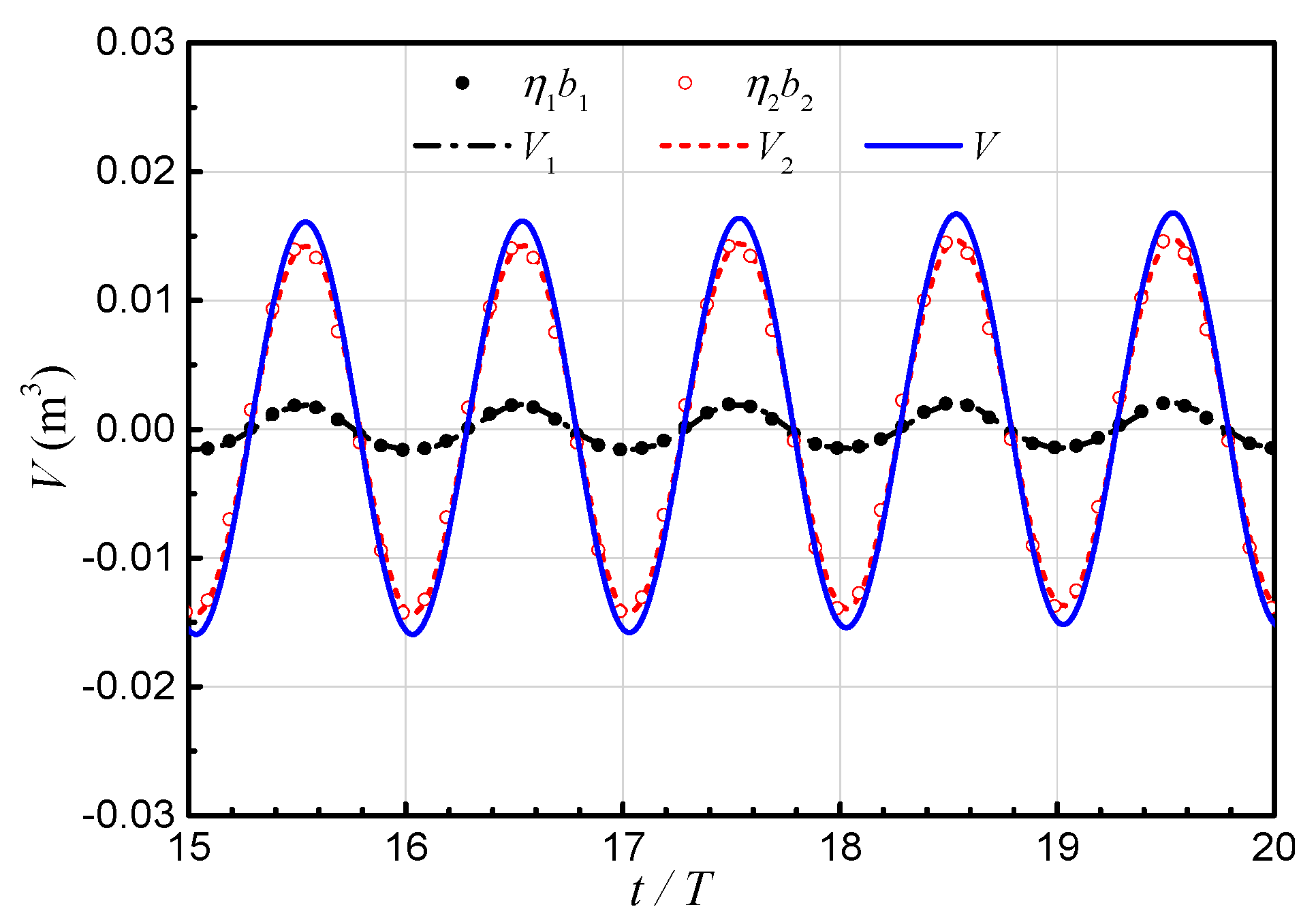
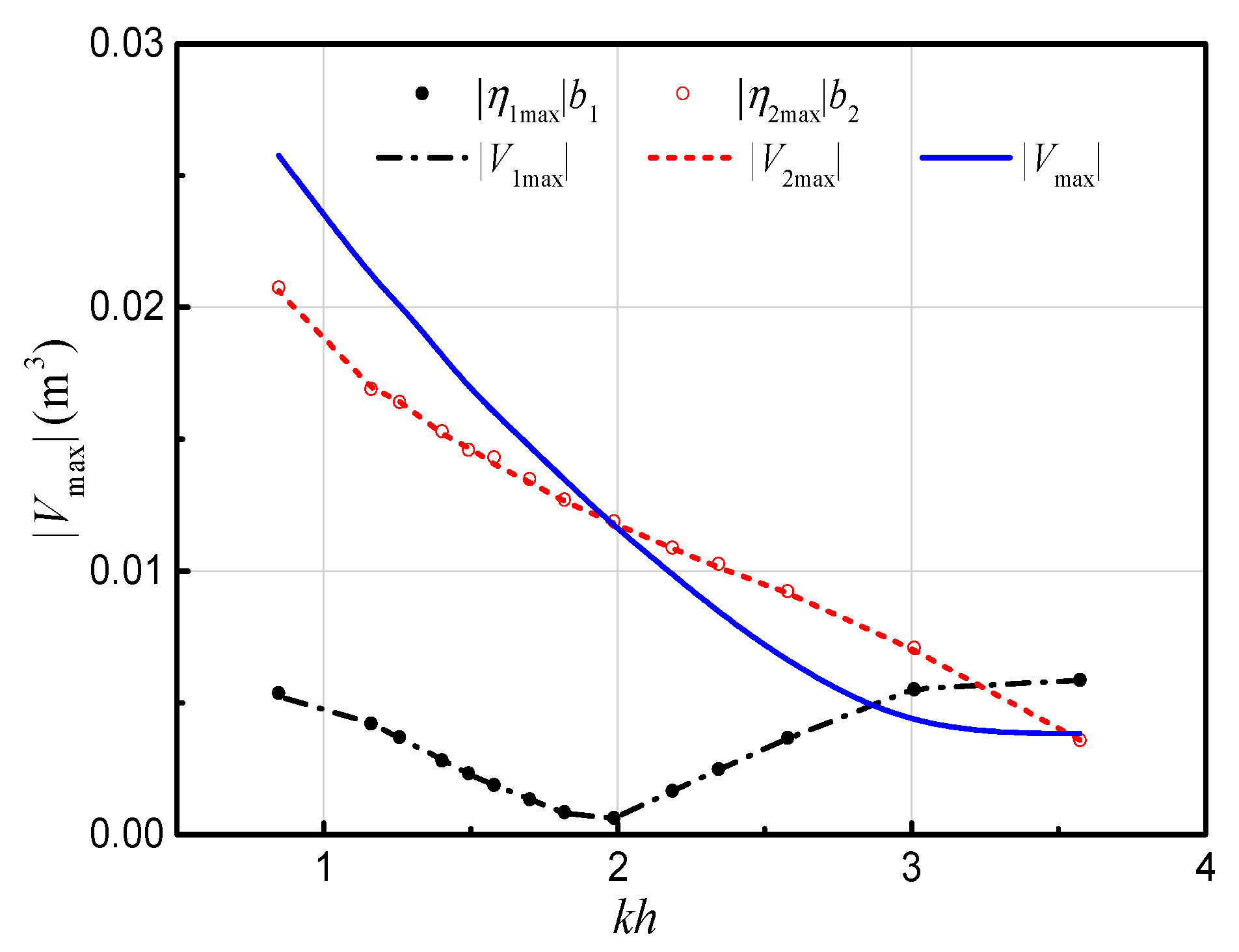
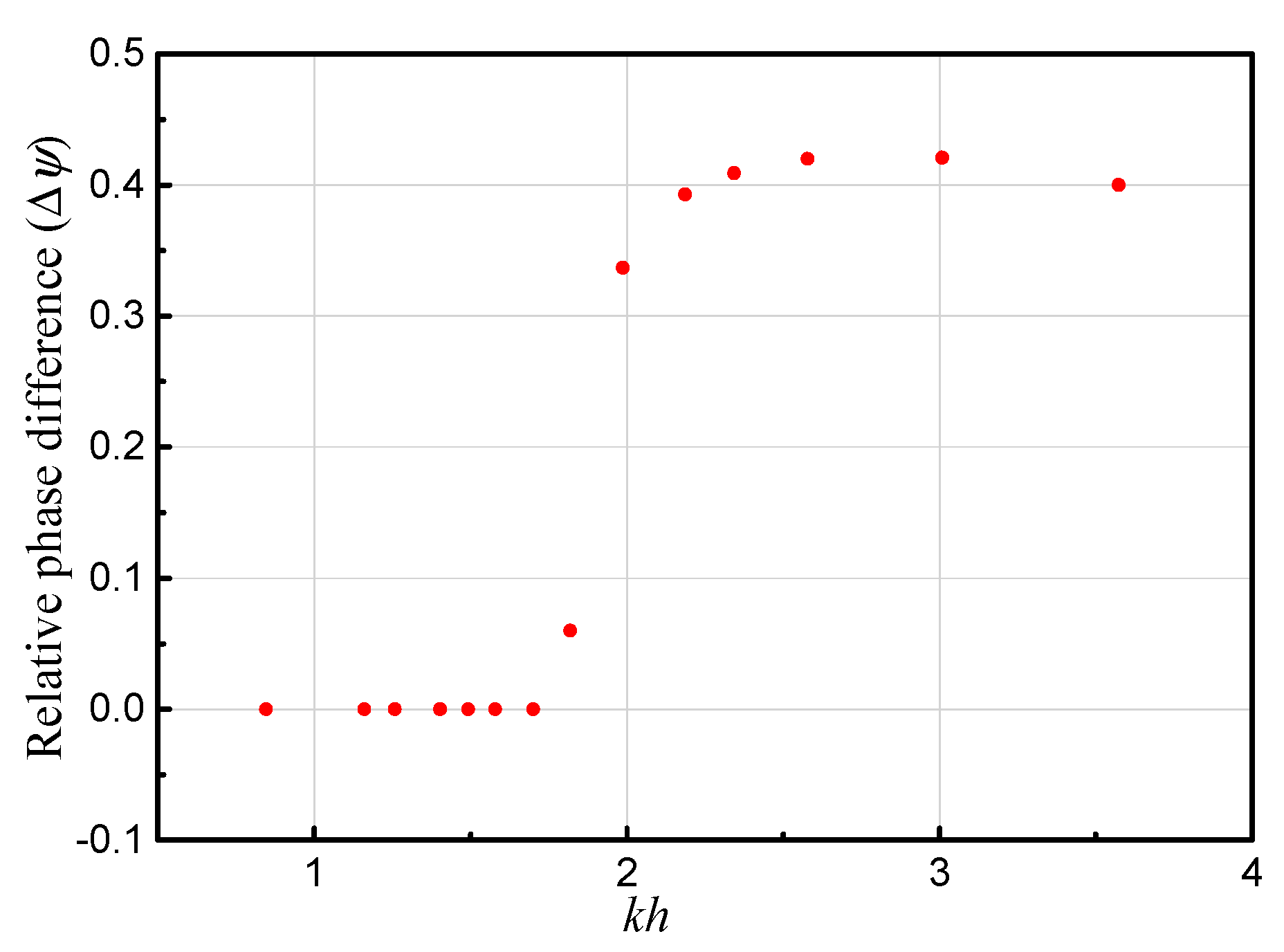
3.1. Water Volume Variation Inside the Chambers
3.2. Surface Elevation in Chambers
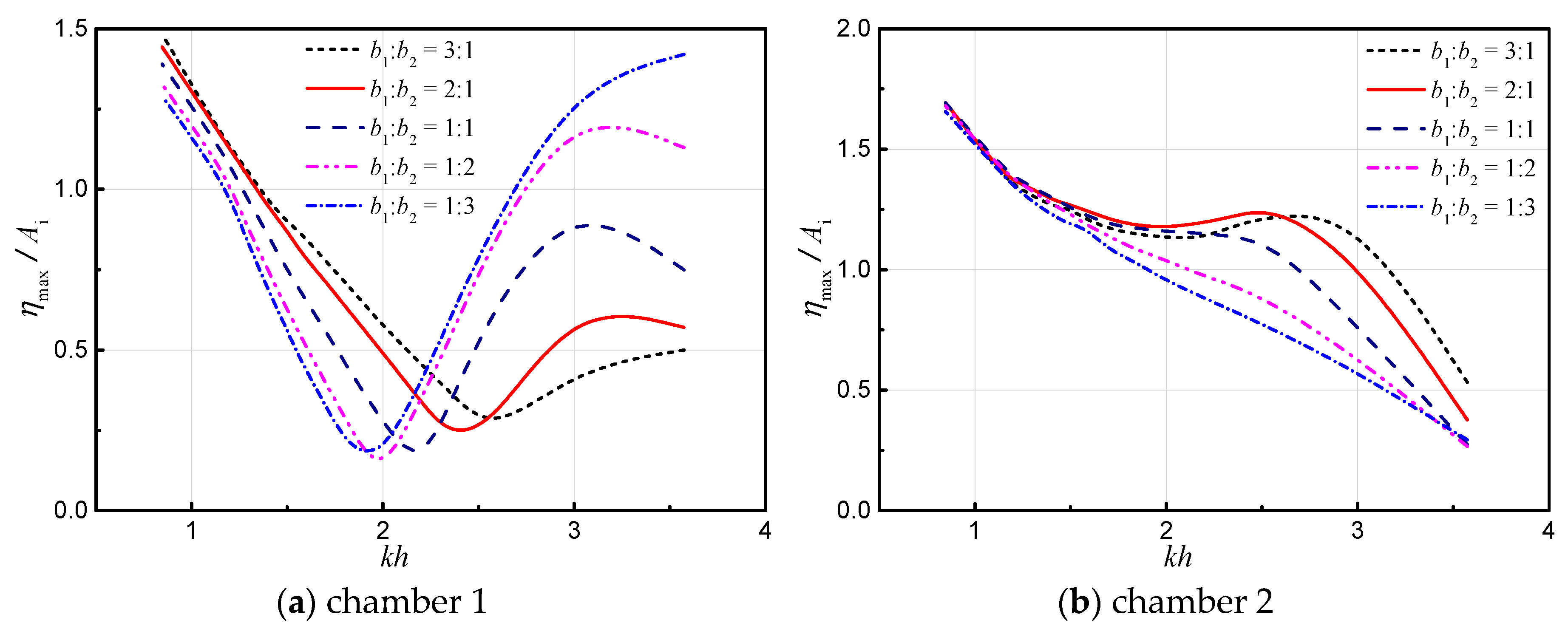
3.2.1. Effects of Chamber Breadths
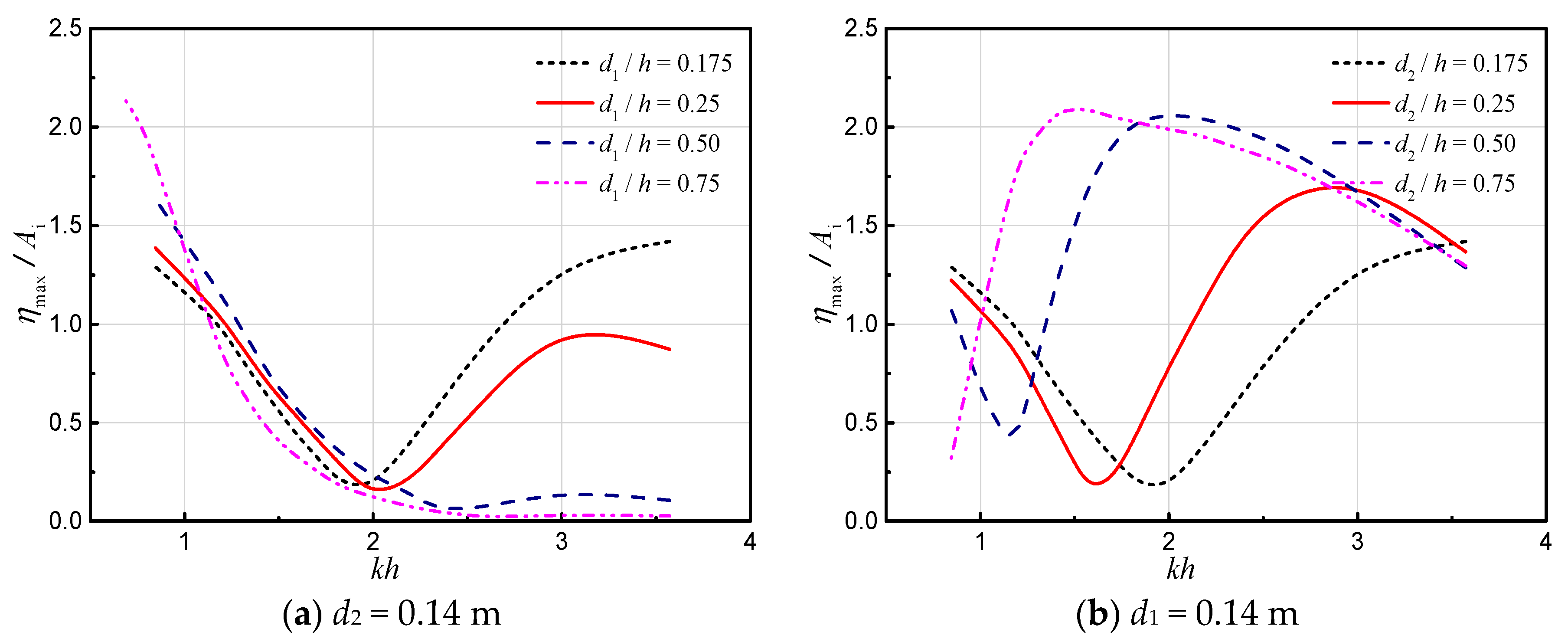
3.2.2. Effects of Barrier Wall Drafts
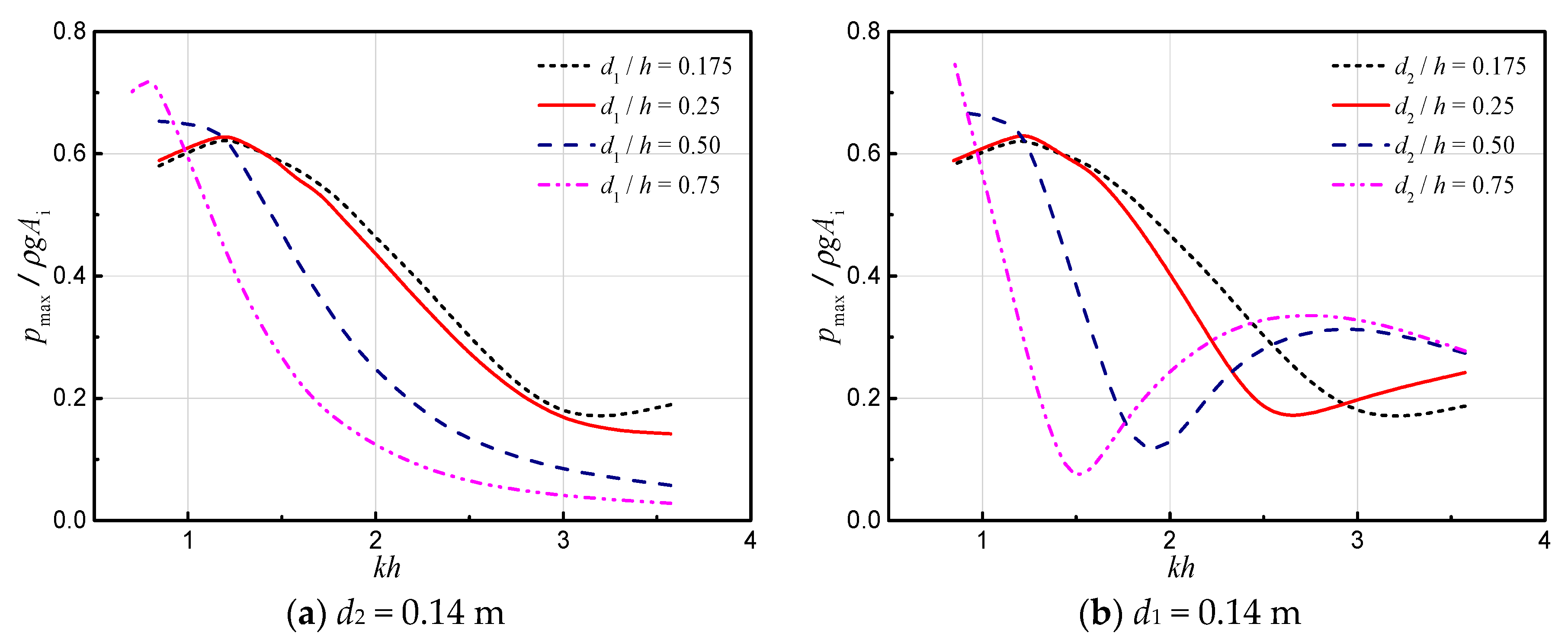
3.3. Air Pressure in Chamber
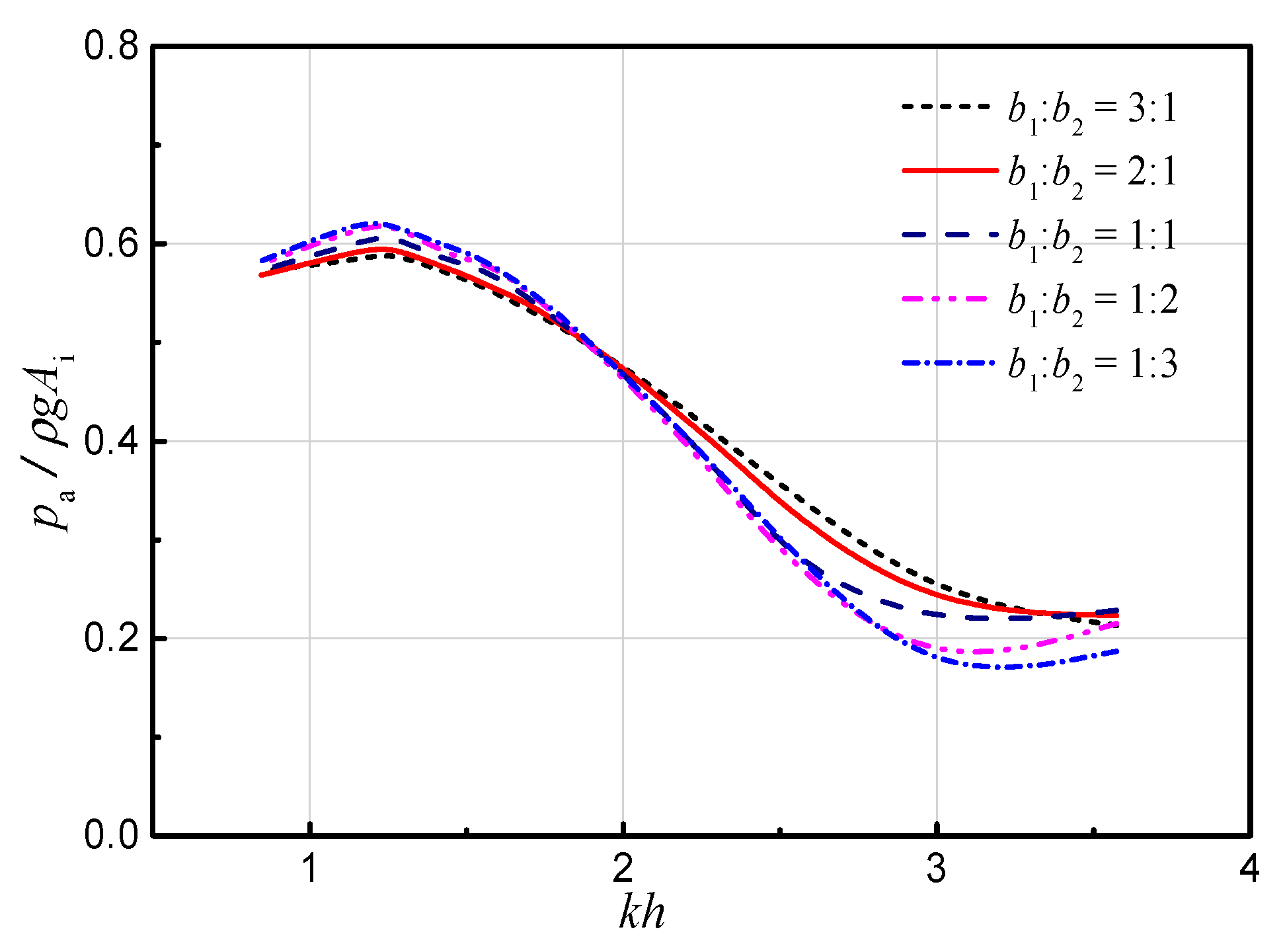
3.3.1. Effects of Chamber Breadths
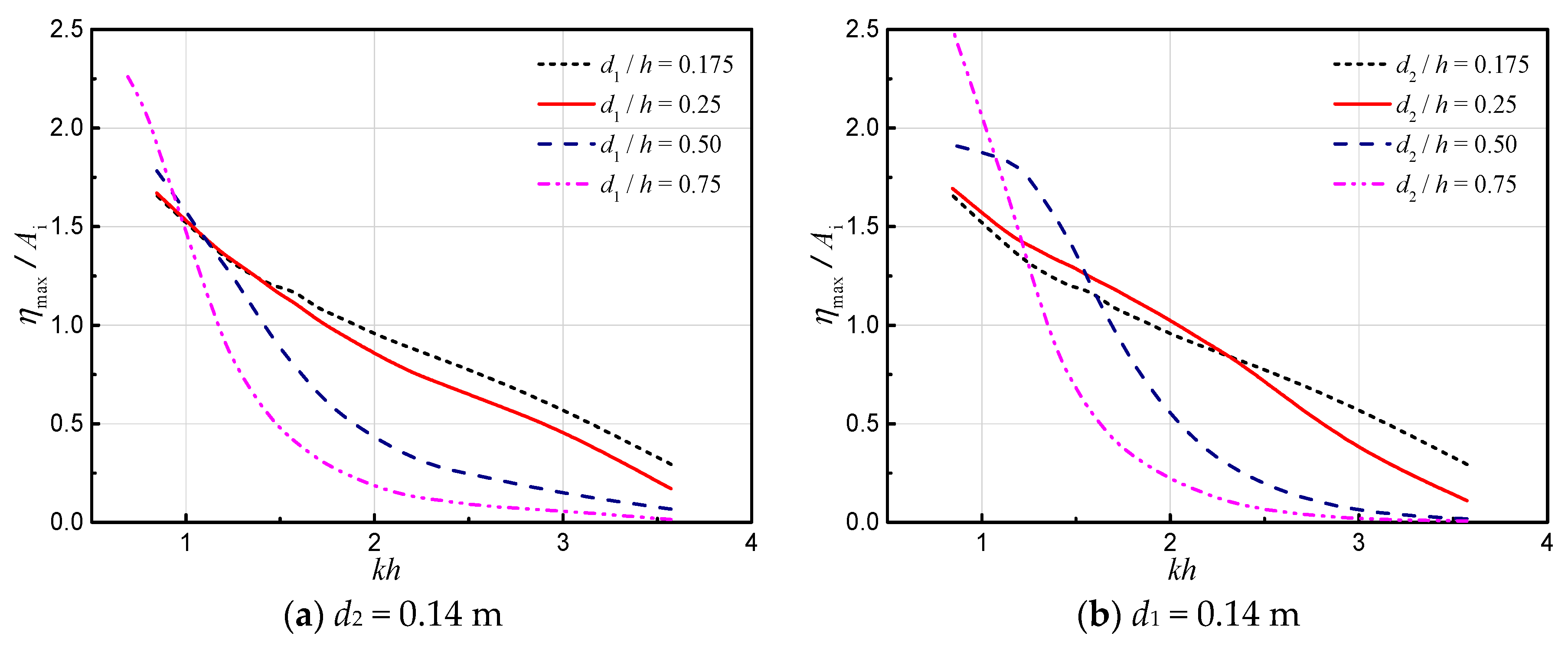
3.3.2. Effects of Barrier Wall Drafts
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Murakami, T.; Imai, Y.; Nagata, S.; Takao, M.; Setoguchi, T. Experimental Research on Primary and Secondary Conversion Efficiencies in an Oscillating Water Column-Type Wave Energy Converter. Sustainability 2016, 8. [Google Scholar] [CrossRef]
- Delaure, Y.M.C.; Lewis, A. 3D hydrodynamic modelling of fixed oscillating water column wave power plant by a boundary element methods. Ocean Eng. 2003, 30, 309–330. [Google Scholar] [CrossRef]
- Naty, S.; Viviano, A.; Foti, E. Wave Energy Exploitation System Integrated in the Coastal Structure of a Mediterranean Port. Sustainability 2016, 8, 1342. [Google Scholar] [CrossRef]
- Mccormick, M.E. Modified Linear-Analysis of a Wave-Energy Conversion Buoy. Ocean Eng. 1976, 3, 133–144. [Google Scholar] [CrossRef]
- Evans, D.V. The Oscillating Water Column Wave-energy Device. IMA J. Appl. Math. 1978, 22, 423–433. [Google Scholar] [CrossRef]
- Falcão, A.F.O.; Sarmento, A. Wave generation by a periodic surface pressure and its application in wave-energy extraction. In Proceedings of the 15th International Congress of Theoritical and Applied Mechanics, Toronto, ON, Canada, 17–23 August 1980. [Google Scholar]
- Evans, D.V. Wave-Power Absorption by Systems of Oscillating Surface Pressure Distributions. J. Fluid Mech. 1982, 114, 481–499. [Google Scholar] [CrossRef]
- Zhang, Y.L.; Zou, Q.P.; Greaves, D. Air–water two-phase flow modelling of hydrodynamic performance of an oscillating water column device. Renew. Energy 2012, 41, 159–170. [Google Scholar] [CrossRef]
- Teixeira, P.R.F.; Davyt, D.P.; Didier, E.; Ramalhais, R. Numerical simulation of an oscillating water column device using a code based on Navier–Stokes equations. Energy 2013, 61, 513–530. [Google Scholar] [CrossRef]
- Luo, Y.Y.; Wang, Z.W.; Peng, G.J.; Xiao, Y.X.; Zhai, L.M.; Liu, X.; Zhang, Q. Numerical simulation of a heave-only floating OWC (oscillating water column) device. Energy 2014, 76, 799–806. [Google Scholar] [CrossRef]
- Ning, D.Z.; Shi, J.; Zou, Q.P.; Teng, B. Investigation of hydrodynamic performance of an OWC (oscillating water column) wave energy device using a fully nonlinear HOBEM (higher-order boundary element method). Energy 2015, 83, 177–188. [Google Scholar] [CrossRef]
- Elhanafi, A.; Fleming, A.; Macfarlane, G.; Leong, Z. Numerical hydrodynamic analysis of an offshore stationary–floating oscillating water column–wave energy converter using CFD. Int. J. Nav. Arch. Ocean 2017, 9, 77–99. [Google Scholar] [CrossRef]
- Morris-Thomas, M.T.; Irvin, R.J.; Thiagarajan, K.P. An investigation into the hydrodynamic efficiency of an oscillating water column. J. Offshore Mech. Arct. Eng. 2007, 129, 273–278. [Google Scholar] [CrossRef]
- Gouaud, F.; Rey, V.; Piazzola, J.; Van Hooff, R. Experimental study of the hydrodynamic performance of an onshore wave power device in the presence of an underwater mound. Coast. Eng. 2010, 57, 996–1005. [Google Scholar] [CrossRef]
- He, F.; Huang, Z.H.; Law, A.W.K. Hydrodynamic performance of a rectangular floating breakwater with and without pneumatic chambers: An experimental study. Ocean Eng. 2012, 51, 16–27. [Google Scholar] [CrossRef]
- He, F.; Huang, Z.H.; Law, A.W.K. An experimental study of a floating breakwater with asymmetric pneumatic chambers for wave energy extraction. Appl. Energy 2013, 106, 222–231. [Google Scholar] [CrossRef]
- Ning, D.Z.; Wang, R.Q.; Zou, Q.P.; Teng, B. An experimental investigation of hydrodynamics of a fixed OWC Wave Energy Converter. Appl. Energy 2016, 168, 636–648. [Google Scholar] [CrossRef]
- Viviano, A.; Naty, S.; Foti, E.; Bruce, T.; Allsop, W.; Vicinanza, D. Large-scale experiments on the behaviour of a generalised Oscillating Water Column under random waves. Renew. Energy 2016, 99, 875–887. [Google Scholar] [CrossRef]
- Vyzikas, T.; Deshoulieres, S.; Barton, M.; Giroux, O.; Greaves, D.; Simmonds, D. Experimental investigation of different geometries of fixed oscillating water column devices. Renew. Energy 2017, 104, 248–258. [Google Scholar] [CrossRef]
- El Marjani, A.; Castro Ruiz, F.; Rodriguez, M.A.; Parra Santos, M.T. Numerical modelling in wave energy conversion systems. Energy 2008, 33, 1246–1253. [Google Scholar] [CrossRef]
- Drew, B.; Plummer, A.R.; Sahinkaya, M.N. A review of wave energy converter technology. Proc. Inst. Mech. Eng. A J. Power Energy 2009, 223, 887–902. [Google Scholar] [CrossRef]
- Falcão, A.F.D. Wave energy utilization: A review of the technologies. Renew. Sustain. Energy Rev. 2010, 14, 899–918. [Google Scholar] [CrossRef]
- Iturrioz, A.; Guanche, R.; Lara, J.L.; Vidal, C.; Losada, I.J. Validation of OpenFOAM® for Oscillating Water Column three-dimensional modeling. Ocean Eng. 2015, 107, 222–236. [Google Scholar] [CrossRef]
- Falcão, A.F.D. Wave-power absorption by a periodic linear array of oscillating water columns. Ocean Eng. 2002, 29, 1163–1186. [Google Scholar] [CrossRef]
- Nader, J.R.; Zhu, S.P.; Cooper, P.; Stappenbelt, B. A finite-element study of the efficiency of arrays of oscillating water column wave energy converters. Ocean Eng. 2012, 43, 72–81. [Google Scholar] [CrossRef]
- Nihous, G.C. Wave power extraction by arbitrary arrays of non-diffracting oscillating water columns. Ocean Eng. 2012, 51, 94–105. [Google Scholar] [CrossRef]
- O’Boyle, L.; Elsäßer, B.; Whittaker, T. Experimental Measurement of Wave Field Variations around Wave Energy Converter Arrays. Sustainability 2017, 9, 70. [Google Scholar] [CrossRef]
- Boccotti, P. Caisson breakwaters embodying an OWC with a small opening—Part I: Theory. Ocean Eng. 2007, 34, 806–819. [Google Scholar] [CrossRef]
- Boccotti, P.; Filianoti, P.; Fiamma, V.; Arena, F. Caisson breakwaters embodying an OWC with a small opening—Part II: A small-scale field experiment. Ocean Eng. 2007, 34, 820–841. [Google Scholar] [CrossRef]
- Wilbert, R.; Sundar, V.; Sannasiraj, S.A. Asymmetry Effect on Hydrodynamic Characteristics of Double Chamber Oscillating Water Column Device. J. Ocean Mech. Aero. 2014, 5, 1–17. [Google Scholar]
- Rezanejad, K.; Bhattacharjee, J.; Soares, C.G. Stepped sea bottom effects on the efficiency of nearshore oscillating water column device. Ocean Eng. 2013, 70, 25–38. [Google Scholar] [CrossRef]
- Rezanejad, K.; Bhattacharjee, J.; Soares, C.G. Analytical and numerical study of dual-chamber oscillating water columns on stepped bottom. Renew. Energy 2015, 75, 272–282. [Google Scholar] [CrossRef]
- He, F.; Leng, J.; Zhao, X. An experimental investigation into the wave power extraction of a floating box-type breakwater with dual pneumatic chambers. Appl. Ocean Res. 2017, 67, 21–30. [Google Scholar] [CrossRef]
- Wang, R.Q.; Ning, D.Z.; Zhang, C.W. Numerical Investigation of the Hydrodynamic Performance of the Dual-Chamber Oscillating Water Columns. In Proceedings of the 27th International Ocean and Polar Engineering Conference, San Francisco, CA, USA, 25–30 June 2017; pp. 66–70. [Google Scholar]
- Mitchell Ferguson, T.; Penesis, I.; Macfarlane, G.; Fleming, A. A PIV investigation of OWC operation in regular, polychromatic and irregular waves. Renew. Energy 2017, 103, 143–155. [Google Scholar] [CrossRef]
- Kuo, Y.S.; Chung, C.Y.; Hsiao, S.C.; Wang, Y.K. Hydrodynamic characteristics of Oscillating Water Column caisson breakwaters. Renew. Energy 2017, 103, 439–447. [Google Scholar] [CrossRef]
- Gato, L.M.C.; de Falcão, A.F.O. Aerodynamics of the wells turbine. Int. J. Mech. Sci. 1988, 30, 383–395. [Google Scholar] [CrossRef]
- Suzuki, M.; Arakawa, C. Guide vanes effect of Wells turbine for wave power generator. Int. J. Offshore Polar 2000, 10, 153–159. [Google Scholar]
- Falcão, A.F.O.; Henriques, J.C.C. Model-prototype similarity of oscillating-water-column wave energy converters. Int. J. Mar. Energy 2014, 6, 18–34. [Google Scholar] [CrossRef]
- Elhanafi, A.; Macfarlane, G.; Fleming, A.; Leong, Z. Scaling and air compressibility effects on a three-dimensional offshore stationary OWC wave energy converter. Appl. Energy 2017, 189, 1–20. [Google Scholar] [CrossRef]
- Elhanafi, A.; Macfarlane, G.; Fleming, A.; Leong, Z. Investigations on 3D effects and correlation between wave height and lip submergence of an offshore stationary OWC wave energy converter. Appl. Ocean Res. 2017, 64, 203–216. [Google Scholar] [CrossRef]
- Rezanejad, K.; Bhattacharjee, J.; Soares, C.G. Analytical and Numerical Study of Nearshore Multiple Oscillating Water Columns. J. Offshore Mech. Arct. Eng. 2016, 138, 021901. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ning, D.; Wang, R.; Zhang, C. Numerical Simulation of a Dual-Chamber Oscillating Water Column Wave Energy Converter. Sustainability 2017, 9, 1599. https://doi.org/10.3390/su9091599
Ning D, Wang R, Zhang C. Numerical Simulation of a Dual-Chamber Oscillating Water Column Wave Energy Converter. Sustainability. 2017; 9(9):1599. https://doi.org/10.3390/su9091599
Chicago/Turabian StyleNing, Dezhi, Rongquan Wang, and Chongwei Zhang. 2017. "Numerical Simulation of a Dual-Chamber Oscillating Water Column Wave Energy Converter" Sustainability 9, no. 9: 1599. https://doi.org/10.3390/su9091599





