Comparison between Inverse Model and Chaos Time Series Inverse Model for Long-Term Prediction
Abstract
:1. Introduction
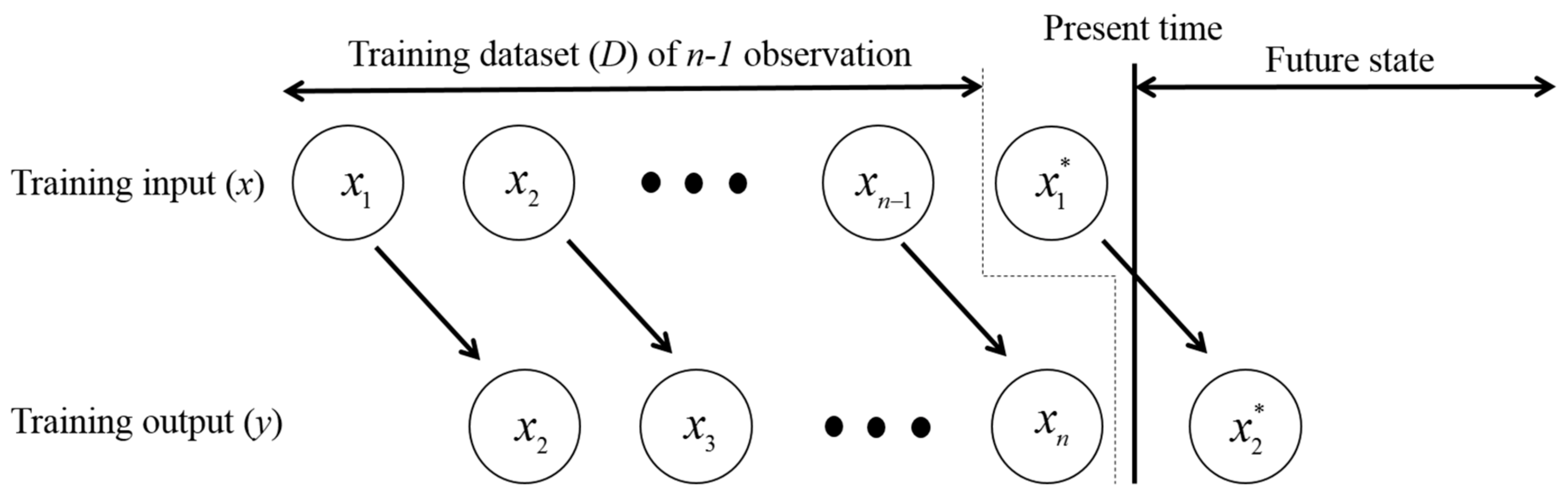
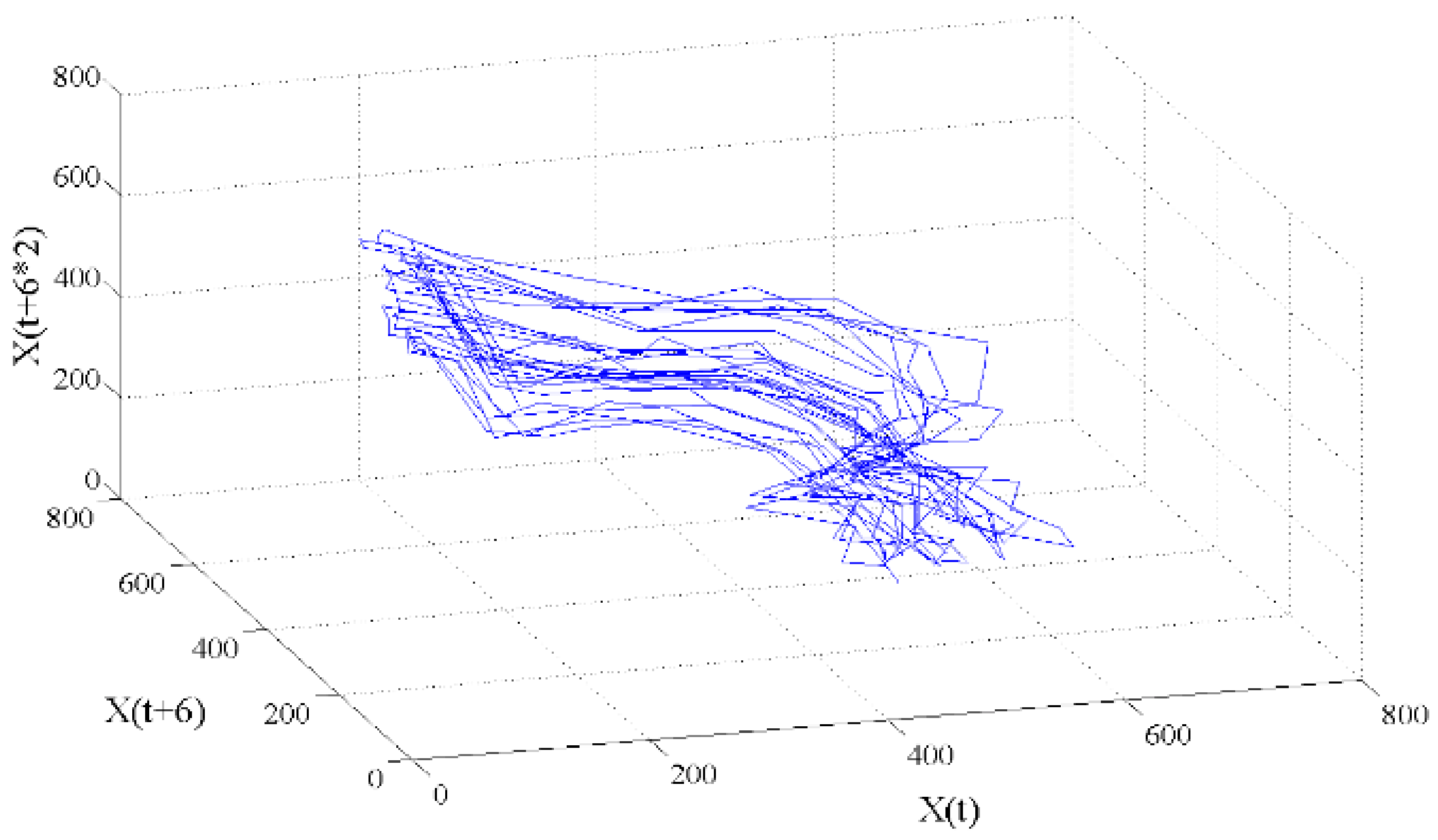
2. Chaos Time Series Inverse Model
3. Support Vector Regression (SVR)
4. SVR vs. Chaos Time Series Inverse Model
4.1. Target Building and Training Data
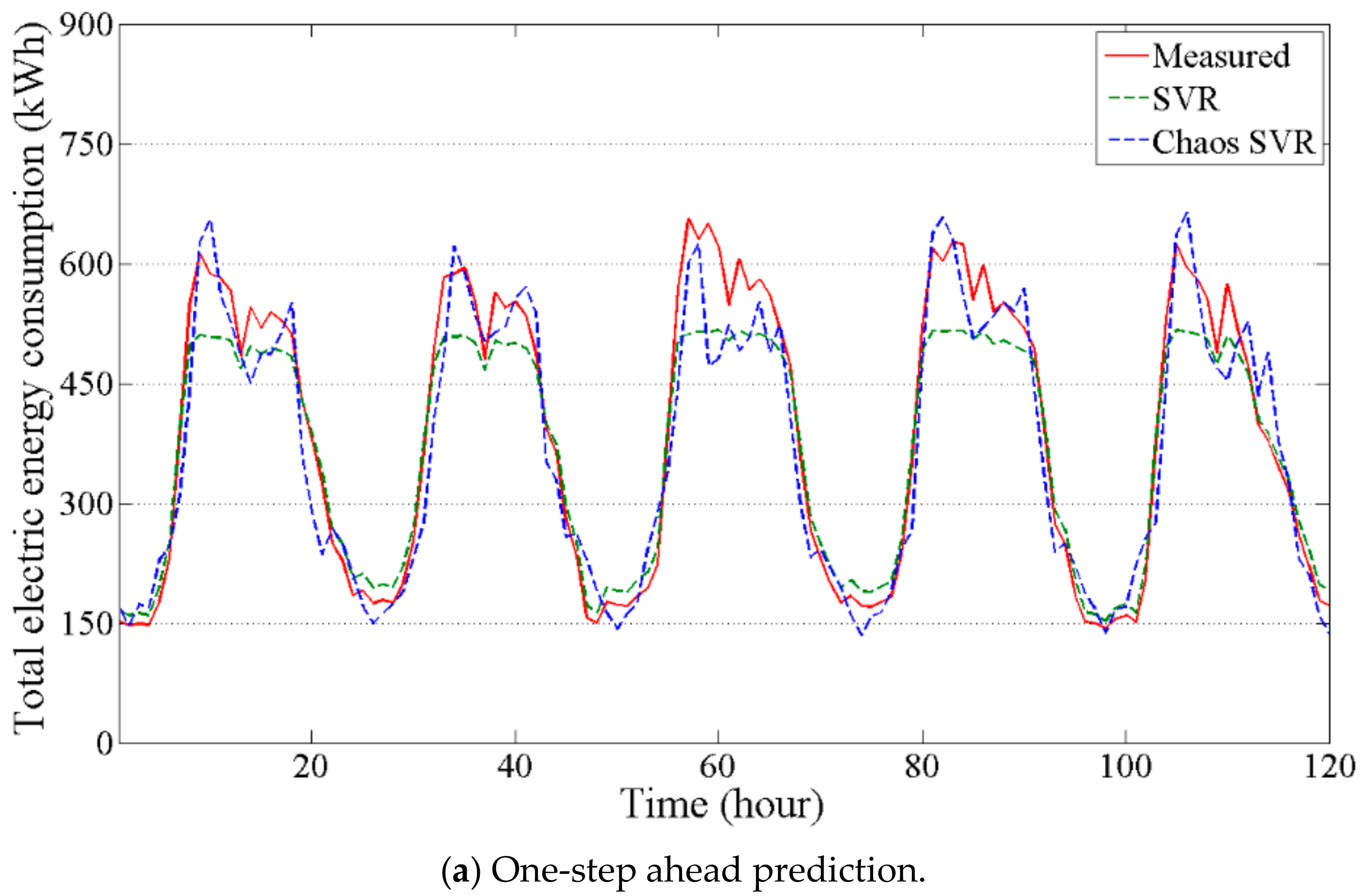
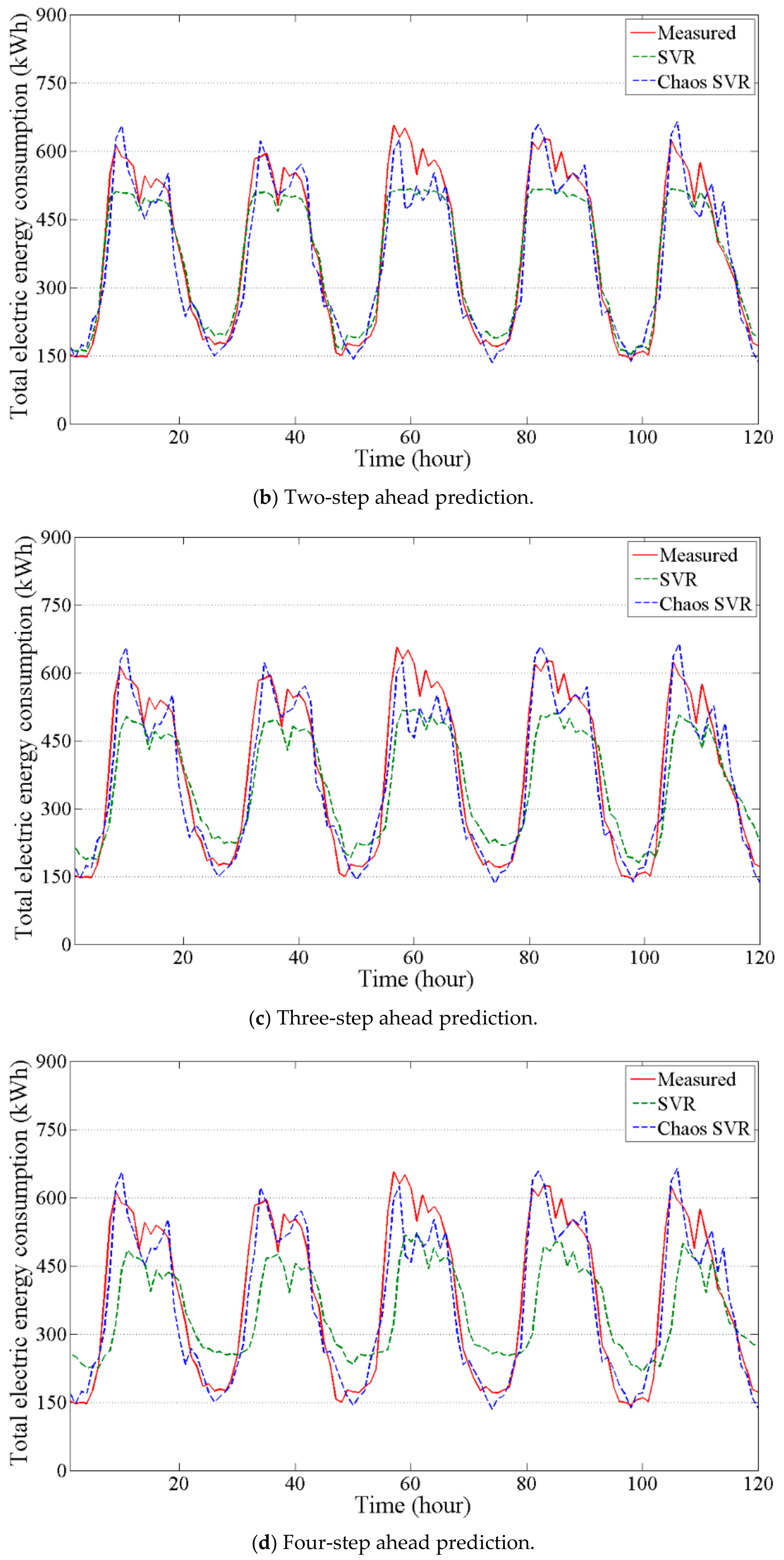
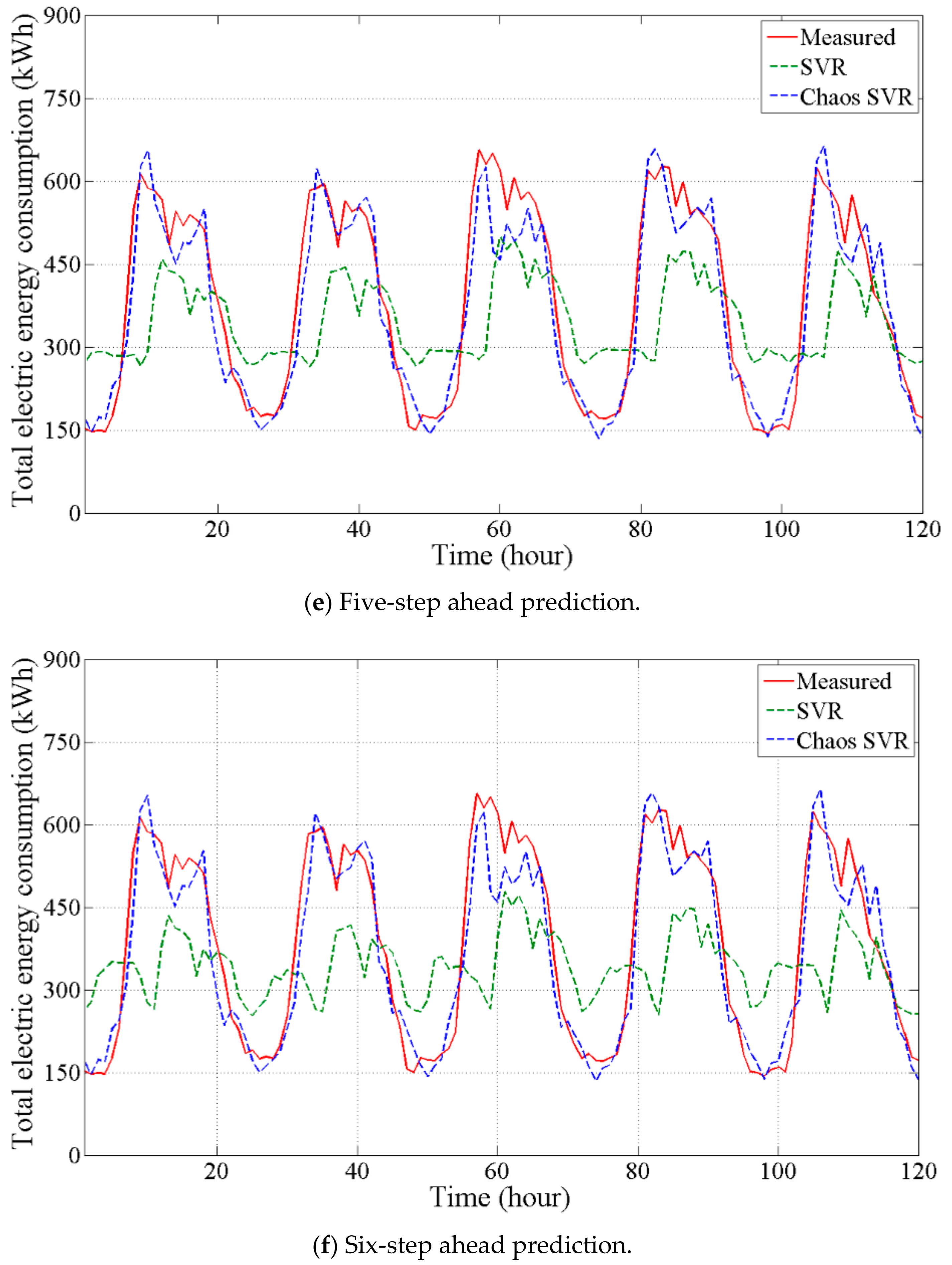
4.2. Comparison between SVR and Chaos Time Series Inverse Model
5. Conclusions and Future Work
- ●
- Application of the chaos time series inverse model to a variety of building systems: the proposed chaos time series inverse model will be applied to various building systems (lights, blinds, HVAC system, plants, etc.).
- ●
- Real-time optimal control: to implement real-time MPC, the validated chaos time series inverse model will be coupled with optimization techniques (e.g., genetic algorithm, particle swarm optimization) and used to find optimal control variables.
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| BEMS | Building Energy Management System |
| MPC | Model Predictive Control |
| BPS | Building Performance Simulation |
| ARIMA | Auto Regressive Integrated Moving Average |
| ANN | Artificial Neural Network |
| SVR | Support Vector Regression |
| GPM | Gaussian Process Model |
| MBE | Mean Bias Error |
| CVRMSE | Coefficient of Variance of the Root Mean Square Error |
| FNN | False Nearest Neighbour |
| AMI | Average Mutual Information |
| GA | Genetic Algorithm |
| PSO | Particle Swarm Optimization |
| Nomenclature | |
| Inputs in training dataset | |
| Outputs in training dataset | |
| Time | |
| State vector in time t | |
| Embedding dimension | |
| Time delay | |
| Euclidean distance for nearest neighbour (nn) of the ith data in the time series | |
| Euclidean distance for false nearest neighbour (fnn) of the ith data in the time series | |
| FNN ratio of the ith data in the time series | |
| Probability density function to find a time series value in the ith interval | |
| Probability density function to find a time series value in the jth interval | |
| Joint probability density function to find a time series value in the ith and jth interval | |
| Linear regression model | |
| Weight factor | |
| Threshold value | |
| Lagrange multiplier | |
| High-dimensional feature space | |
| Kernel matrix | |
| Slack variable | |
| ,, | Free parameter |
References
- Afram, A.; Janabi-Sharifi, F. Theory and applications of HVAC control systems—A review of Model Predictive Control (MPC). Build. Environ. 2014, 72, 343–355. [Google Scholar] [CrossRef]
- American Society of Heating, Refrigerating and Air-Conditioning Engineers, Inc. ASHRAE Handbook Fundamentals; American Society of Heating, Refrigerating and Air-Conditioning Engineers, Inc.: Atlanta, GA, USA, 2013. [Google Scholar]
- Zhao, J.; Lam, K.P.; Ydstie, B.E. Energyplus Model-based Predictive Control (EMPC) by using MATLA/SIMULINK and MLE+. In Proceedings of the 13th IBPSA Conference, Chambery, France, 26–28 August 2013; pp. 2466–2473. [Google Scholar]
- Wetter, M. Co-simulation of building energy and control SYSTEMS with the Building Controls Virtual Test Bed. J. Build. Perform. Simul. 2011, 4, 185–203. [Google Scholar] [CrossRef]
- Nouidui, T.; Wetter, M.; Zuo, W. Functional mock-up unit for co-simulation import in EnergyPlus. J. Build. Perform. Simul. 2014, 7, 192–202. [Google Scholar] [CrossRef]
- Heo, Y.S. Bayesian Calibration of Building Energy Models for Energy Retrofit Decision-Making under Uncertainty. Ph.D. Thesis, Georgia Institute of Technology, Atlanta, GA, USA, 2011. [Google Scholar]
- Niu, D.; Wang, Y.; Wu, D.D. Power load forecasting using support vector machine and ant colony optimization. Expert Syst. Appl. 2010, 37, 2531–2539. [Google Scholar] [CrossRef]
- Kim, Y.J.; Park, C.S. Nonlinear predictive control of chiller system using gaussian process model. In Proceedings of the 2nd Asia Conference of International Building Performance Simulation Association, Nagoya, Japan, 28–29 November 2014; pp. 594–601. [Google Scholar]
- Kiguchi, Y.; Heo, Y.S.; Choudhary, R. Data-driven model for rooftop excess electricity generation. In Proceedings of the 14th IBPSA Conference, Hyderabad, India, 7–9 December 2015; pp. 2631–2638. [Google Scholar]
- Karatasou, S.; Santamouris, M. Detection of low-dimensional chaos in buildings energy consumption time series. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 1603–1612. [Google Scholar] [CrossRef]
- Wang, J.; Chi, D.; Wu, J.; Lu, H. Chaotic time series method combined with particle swarm optimization and trend adjustment for electricity demand forecasting. Expert Syst. Appl. 2011, 38, 8419–8429. [Google Scholar] [CrossRef]
- Cam, M.L.; Zmeureanu, R.; Daoud, A. Comparison of inverse models used for the forecast of the electric demand of chillers. In Proceedings of the 13th IBPSA Conference, Chambery, France, 26–28 August 2013; pp. 2044–2051. [Google Scholar]
- American Society of Heating, Refrigerating, and Air-Conditioning Engineers. Guideline14-Measurement of Energy and Demand Siavings; American Society of Heating, Refrigerating, and Air-Conditioning Engineers: Atlanta, GA, USA, 2004. [Google Scholar]
- Rijal, H.B.; Tuohy, P.; Humphreys, M.A.; Nicol, J.F.; Samuel, A.; Clarke, J. Using results from field surveys to predict the effect of open windows on thermal comfort and energy use in buildings. Energy Build. 2007, 39, 823–836. [Google Scholar] [CrossRef]
- Lam, K.P.; Höynck, M.; Dong, B.; Andrews, B.; Chiou, Y.S.; Zhang, R.; Benitez, D.; Choi, J. Occupancy detection through an extensive environmental sensor network in an open-plan office building. In Proceedings of the 11th IBPSA Conference, Glasgow, UK, 27–30 July 2009; pp. 1452–1459. [Google Scholar]
- Nicol, J.F. Characterising occupant behaviour in buildings: Towards a stochastic model of occupant use of windows, lights, blinds, heaters and fans. In Proceedings of the 9th IBPSA Conference, Rio de Janeiro, Brazil, 13–15 August 2001; pp. 1073–1078. [Google Scholar]
- Andersen, R.K.; Fabi, V.; Corgnati, S.P. Predicted and actual indoor environmental quality: Verification of occupants’ behaviour models in residential buildings. Energy Build. 2016, 127, 105–115. [Google Scholar] [CrossRef]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Phys. D Nonlinear Phenom. 1985, 16, 285–317. [Google Scholar] [CrossRef]
- Harris, C.M.; Todd, R.W.; Bungard, S.J.; Lovitt, R.W.; Morris, J.G.; Kell, D.B. The dielectric permittivity of microbial suspensions at radio-frequencies: A novel method for the estimation of microbial biomass. Enzym. Microb. Technol. 1987, 9, 181–186. [Google Scholar] [CrossRef]
- Kim, D.W.; Kim, K.C.; Park, C.S.; de Wilde, P.; Lee, K.H. ‘Random Walk’ pattern of occupant presence. In Proceedings of the 2nd Asia Conference of International Building Performance Simulation Association, Nagoya, Japan, 28–29 November 2014; pp. 602–609. [Google Scholar]
- Takens, F. Detecting strange attractors in turbulence. In Dynamical Systems and Turbulence; Warwick, Lecture Notes in Mathematics, No. 898; Rand, D.A., Yong, L.-S., Eds.; Spriger: Berlin, Germany, 1981; pp. 366–381. [Google Scholar]
- Kennel, M.; Brown, R.; Abarbanel, H. Determining embedding dimension for phase-space reconstruction using a geometrical construction. Phys. Rev. 1992, 45, 3403–3411. [Google Scholar] [CrossRef]
- Fraser, A.M.; Swinney, H.L. Independent coordinates for strange attractors from mutual information. Phys. Rev. 1986, 33, 1134–1140. [Google Scholar] [CrossRef]
- Vapnik, V.N. The Nature of Statistical Learning Theory; Springer: Berlin, Germany, 1995. [Google Scholar]
- He, W. Forecasting electricity load with optimized local learning models. Int. J. Electr. Power Energy Syst. 2008, 30, 603–608. [Google Scholar] [CrossRef]
- Li, Q.; Meng, Q.; Cai, J.; Yoshino, H.; Mochida, A. Predicting hourly cooling load in the building: A comparison of support vector machine and different artificial neural networs. Energy Convers. Manag. 2009, 50, 90–96. [Google Scholar] [CrossRef]
- Ruelle, D.; Takens, F. On the nature of turbulence. Commun. Math. Phys. 1971, 20, 167–192. [Google Scholar] [CrossRef]
- Sprott, J.C. Chaos and Time-Series Analysis; Oxford University Press: Oxford, UK, 2003. [Google Scholar]




| k-Step | SVR | Chaos SVR | ||
|---|---|---|---|---|
| MBE | CVRMSE | MBE | CVRMSE | |
| 1-step | 4.85 | 12.26 | 4.13 | 13.75 |
| 2-step | 6.43 | 21.39 | 4.19 | 13.95 |
| 3-step | 8.32 | 31.33 | 4.20 | 13.97 |
| 4-step | 10.15 | 38.93 | 4.18 | 13.90 |
| 5-step | 10.87 | 43.08 | 4.18 | 13.90 |
| 6-step | 10.36 | 43.87 | 4.21 | 13.97 |
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, Y.-J. Comparison between Inverse Model and Chaos Time Series Inverse Model for Long-Term Prediction. Sustainability 2017, 9, 982. https://doi.org/10.3390/su9060982
Kim Y-J. Comparison between Inverse Model and Chaos Time Series Inverse Model for Long-Term Prediction. Sustainability. 2017; 9(6):982. https://doi.org/10.3390/su9060982
Chicago/Turabian StyleKim, Young-Jin. 2017. "Comparison between Inverse Model and Chaos Time Series Inverse Model for Long-Term Prediction" Sustainability 9, no. 6: 982. https://doi.org/10.3390/su9060982





