A Hybrid Local Search Algorithm for the Sequence Dependent Setup Times Flowshop Scheduling Problem with Makespan Criterion
Abstract
:1. Introduction
2. The Flowshop Scheduling Problem with Sequence Dependent Setup Times
3. A Hybrid Local Search Algorithm
3.1. Overall Framework
| Algorithm 1 HLS. |
| Input: |
| The population size N. |
| The number of jobs n. |
| The maximum times of further search FSNum. |
| Output: |
The best individual .
|
3.2. Initialization
- (1)
- Select a solution s from randomly, the first two jobs are extracted and two partial possible schedules with these two jobs are evaluated. The better one based on makespan is chosen as the current sequence.
- (2)
- For each unscheduled job j in s, put it into all the possible positions of the current scheduled sequence to generate all the possible partial sequences. The best one is selected as the current sequence for scheduling the next job.
- (3)
- A new individual is formed after scheduling all jobs, if is better than s, then it will replace s.
3.3. Global Search Method
| Algorithm 2 GlobalSearch. |
| Input: |
| The number of jobs n. |
| The current population . |
| The maximal number of GlobalSearch GSNum. |
| The mutation probability . |
| Output: |
The improved population .
|
3.4. Update Method
| Algorithm 3 UpdateInds. |
| Input: |
| The current population . |
| An individual to be used for updating s. |
| Output: |
The current population with updated individuals .
|
| Algorithm 4 UpdateP. |
| Input: |
| The population size N. |
| Each individual in the current population . |
| The maximal update number UpdateNum. |
| Output: |
The updated population .
|
3.5. Perturbation and Local Search Methods
- The heavy perturbation:
- (1)
- Input a solution s. Three different positions of s are randomly selected, where .
- (2)
- Let represent the partial sequence between and and denote the other partial sequence between and (not including ), then exchange and to generate a new solution to be outputted.
- The light perturbation:
- (1)
- Input a solution s. Two different positions of s are randomly selected, where .
- (2)
- Let S represent the partial sequence between and (not including ), then move the job in position behind S to generate a new solution to be outputted.
- (1)
- Input a solution s and a position r.
- (2)
- Let the job j be a job in the position r. Put j into each of the left possible positions of s to generate neighborhood solutions.
- (3)
- Let be the best solution based on the minimal makespan among the neighborhood solutions.
- (4)
- Output .
3.6. How to Balance between Exploitation and Exploration
- (1)
- Regarding the exploitation: It means that a further search in the large and deep search space can be executed. For the purpose of searching better solutions, firstly we have used the single insertion-based local search to begin the evolution of population. Furthermore, if the current individual cannot be replaced with the new one after carrying out the single local search, thus secondly we choose the further search based on the insertion-based local search to search the solutions deeply. After above methods, the rate of convergence can be improved quickly.
- (2)
- Regarding the exploration: In other words, the central idea of it is to maintain the diversity of the population. In the search process, we have applied the heavy perturbation method to the individuals which are trapped in the local optima. This way effectively avoids the current population being trapped into the local optima and urges that population to an anticipant direction for next generation. It is particularly worth mentioning here that the light perturbation in GlobalSearch keeps the diversity of the improved population, which has a high convergence for searching good solutions at the same time.
4. Experimental Results
4.1. Environmental Setup
4.2. Benchmark Problem Instances and Benchmark Algorithms
4.3. Experimental Parameter Settings
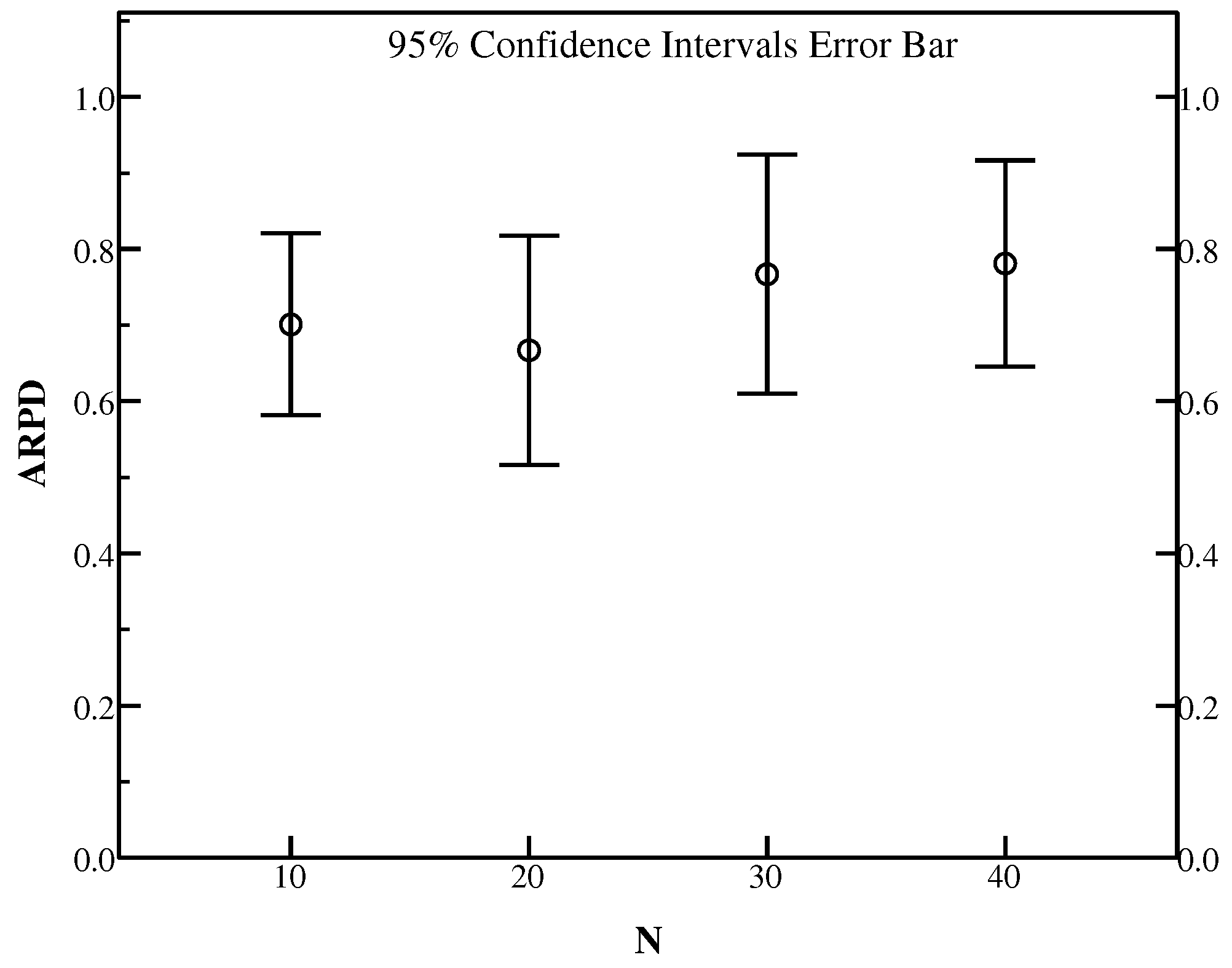
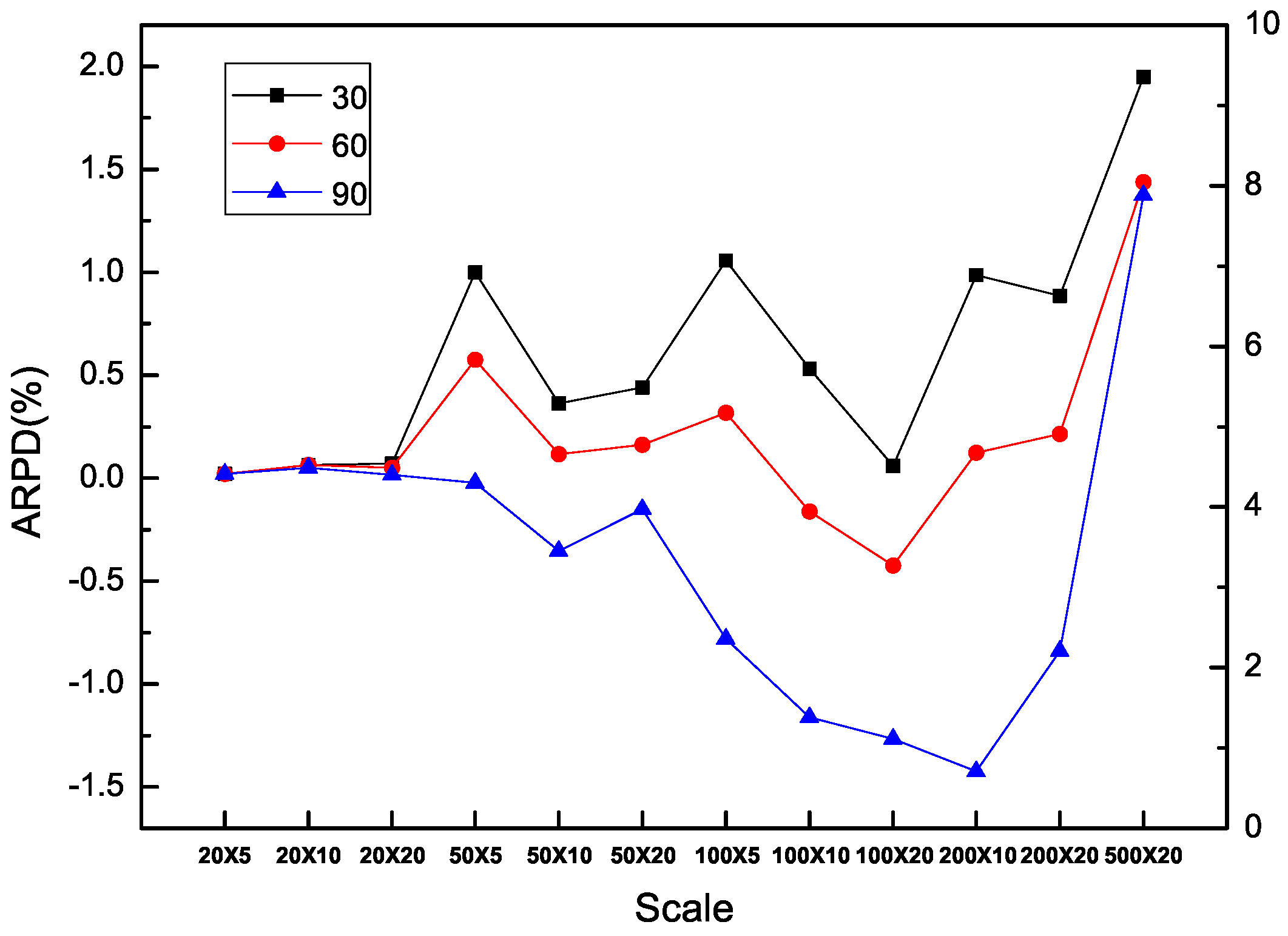
4.3.1. The Influence of the Population Size N
4.3.2. The Influence of the Maximal Number of GlobalSearch GSNum
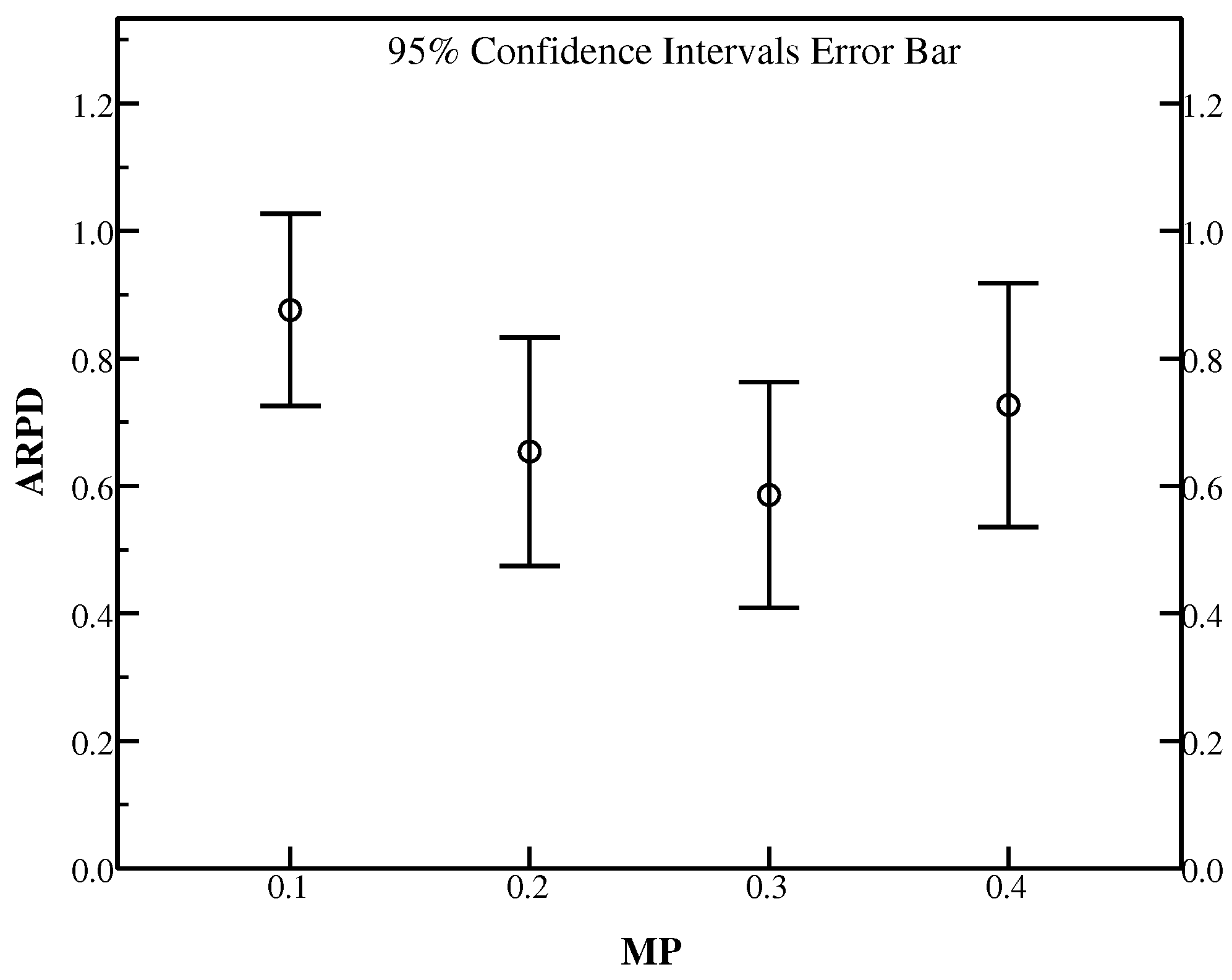
4.3.3. The Effect of the Mutation Probability
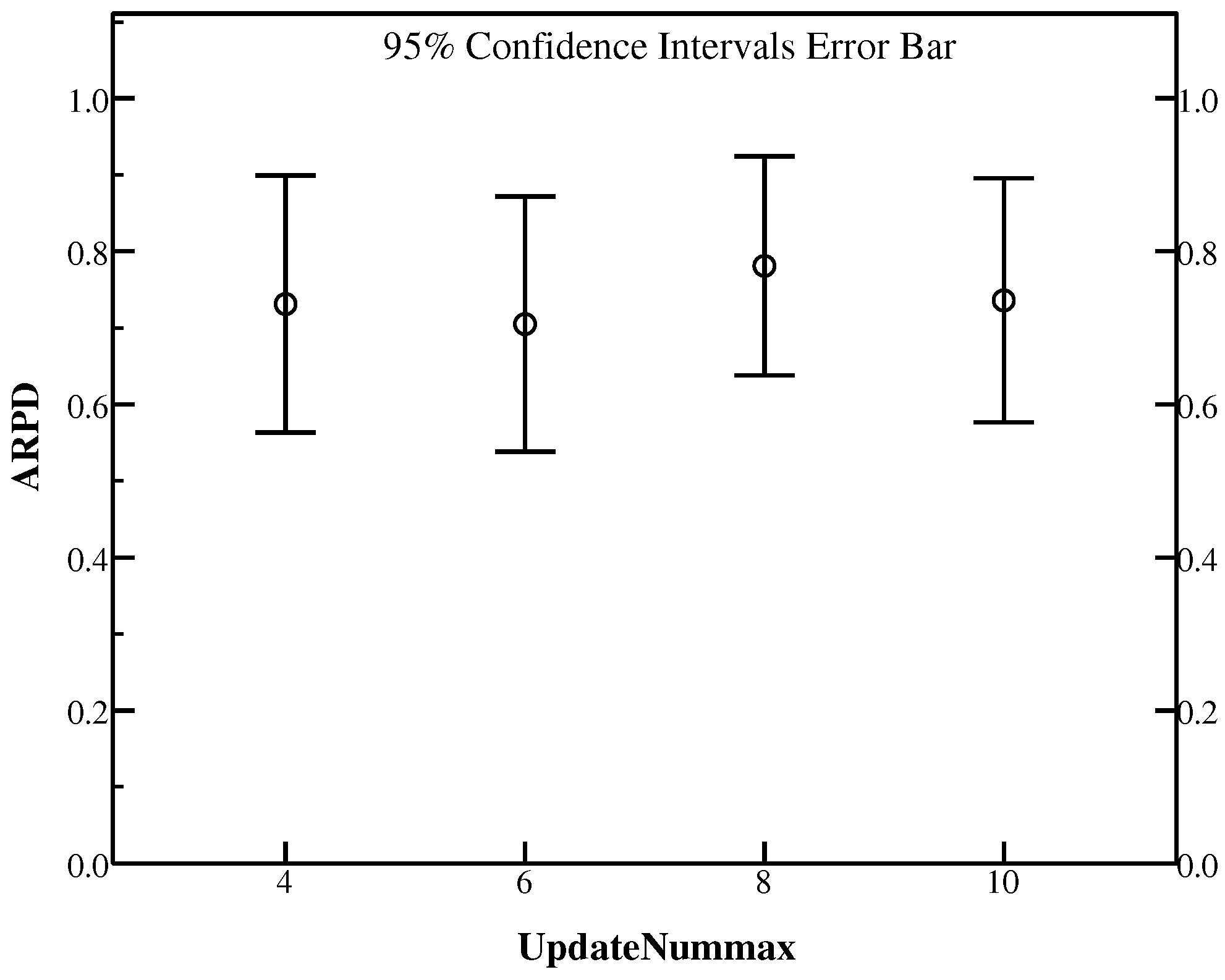
4.3.4. The Influence of the Maximal Number of Update UpdateNum
4.3.5. The Effect of the Maximum Number of Further Search FSNum
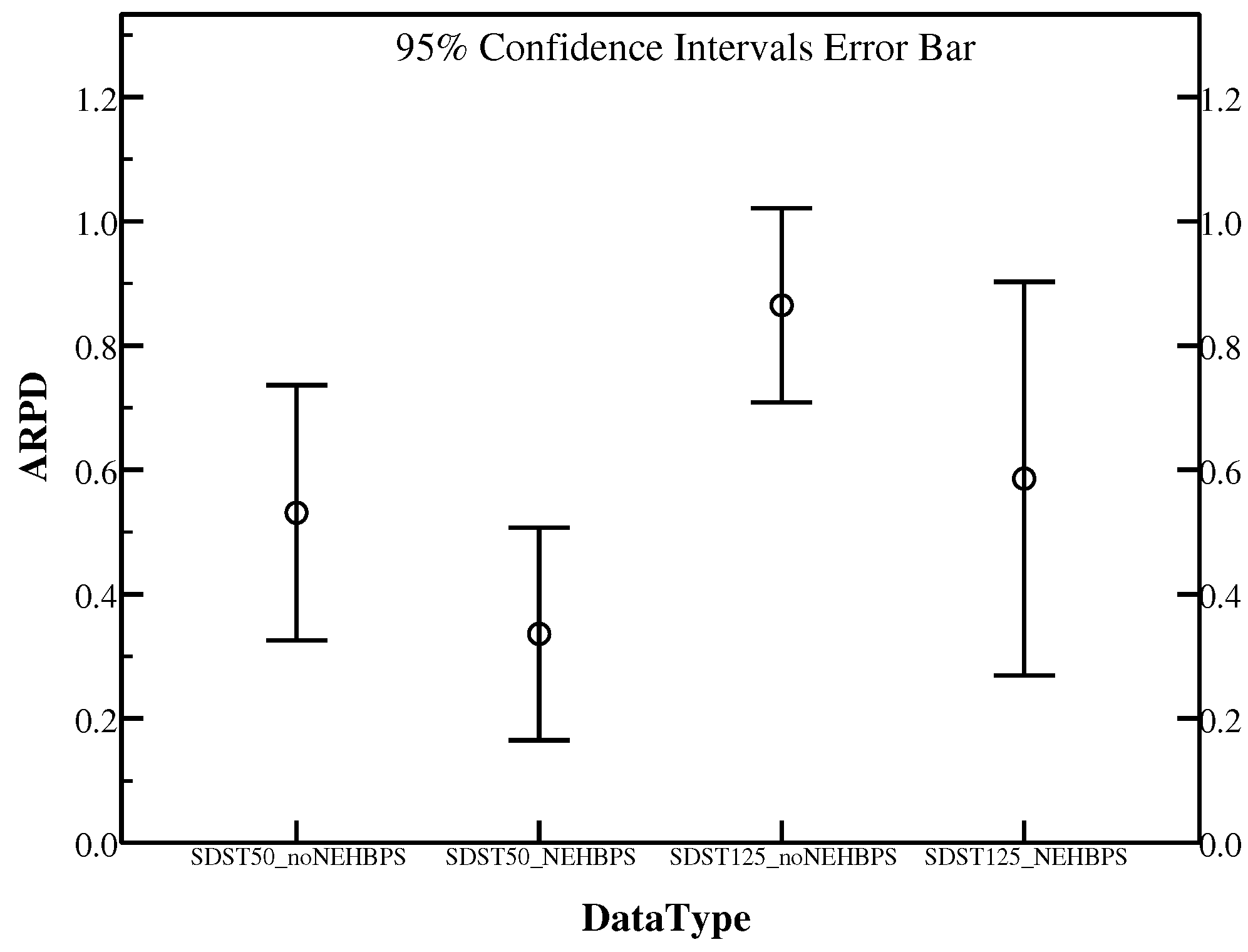
4.4. Effect of NEH Based Problem-Specific Heuristic
4.5. Effect of Different Perturbation Operators
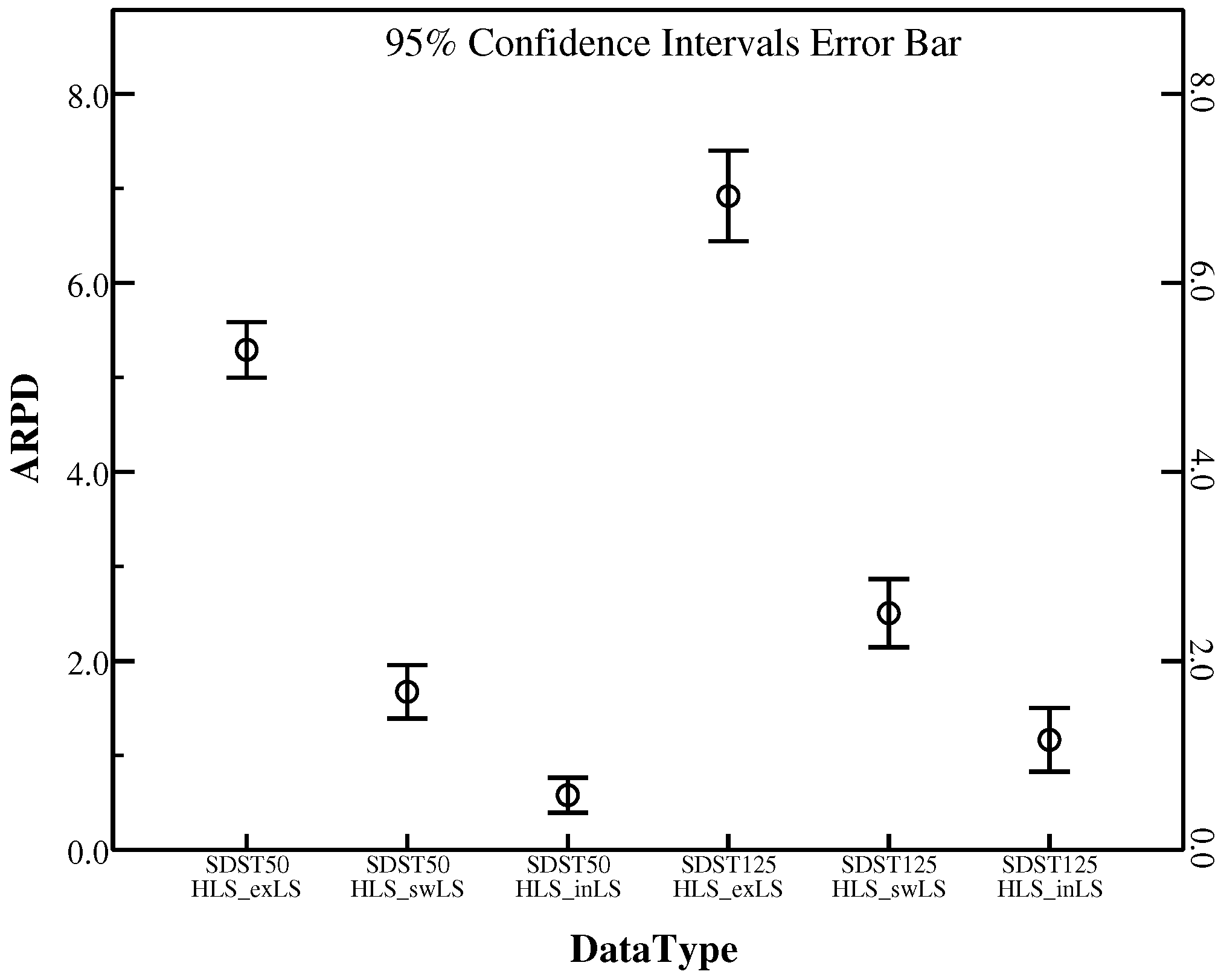
4.6. Effectiveness Evaluation of Different Local Search Operators
- (1)
- exchange_based local search: For the positions ranging from 1 to of the scheduling permutation, exchange the job in it with the job in the adjacent next position.
- (2)
- swap_based local search: For every position of the scheduling permutation (from 1 to n), swap the job in it with the job in the given position.
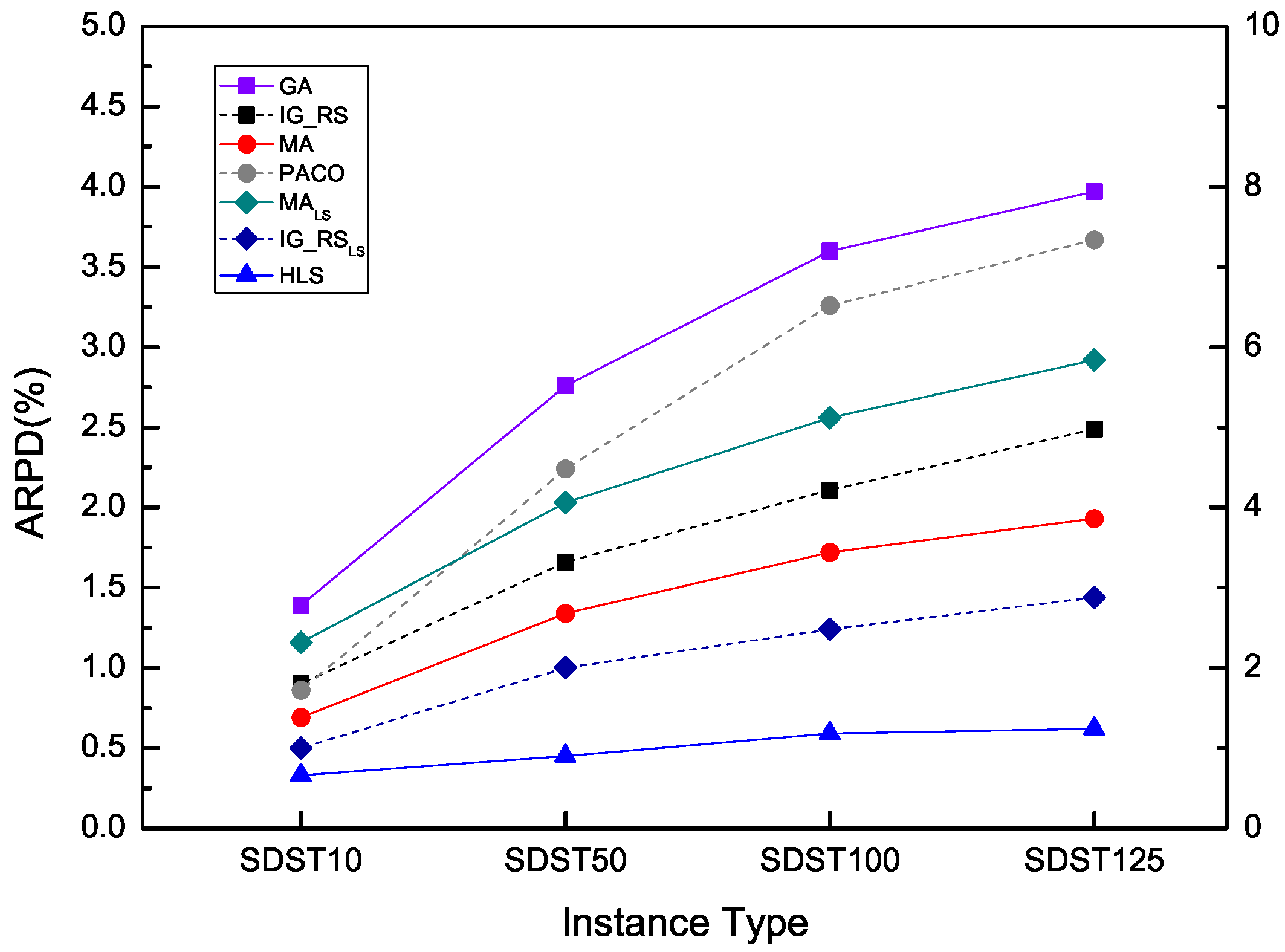
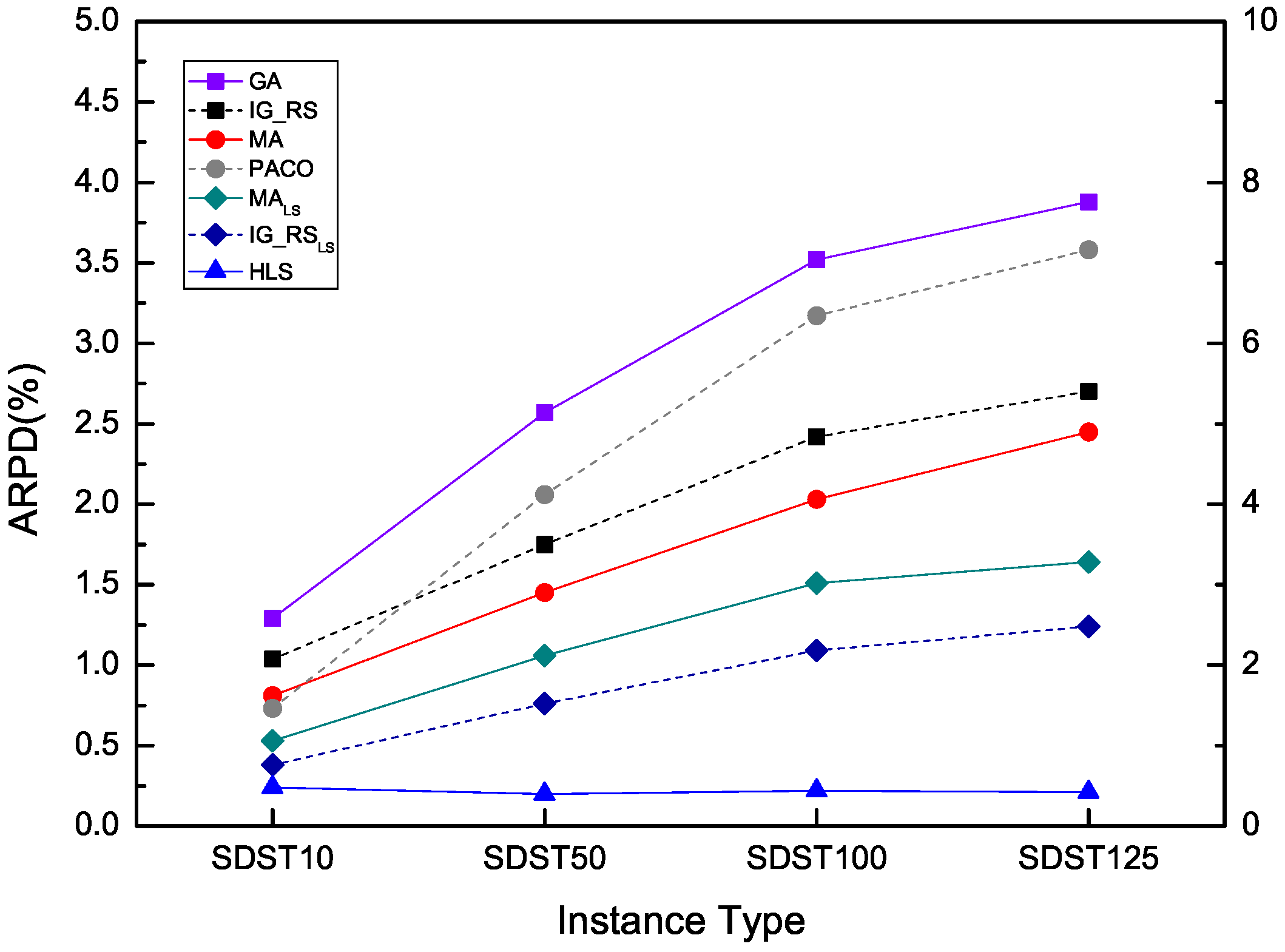
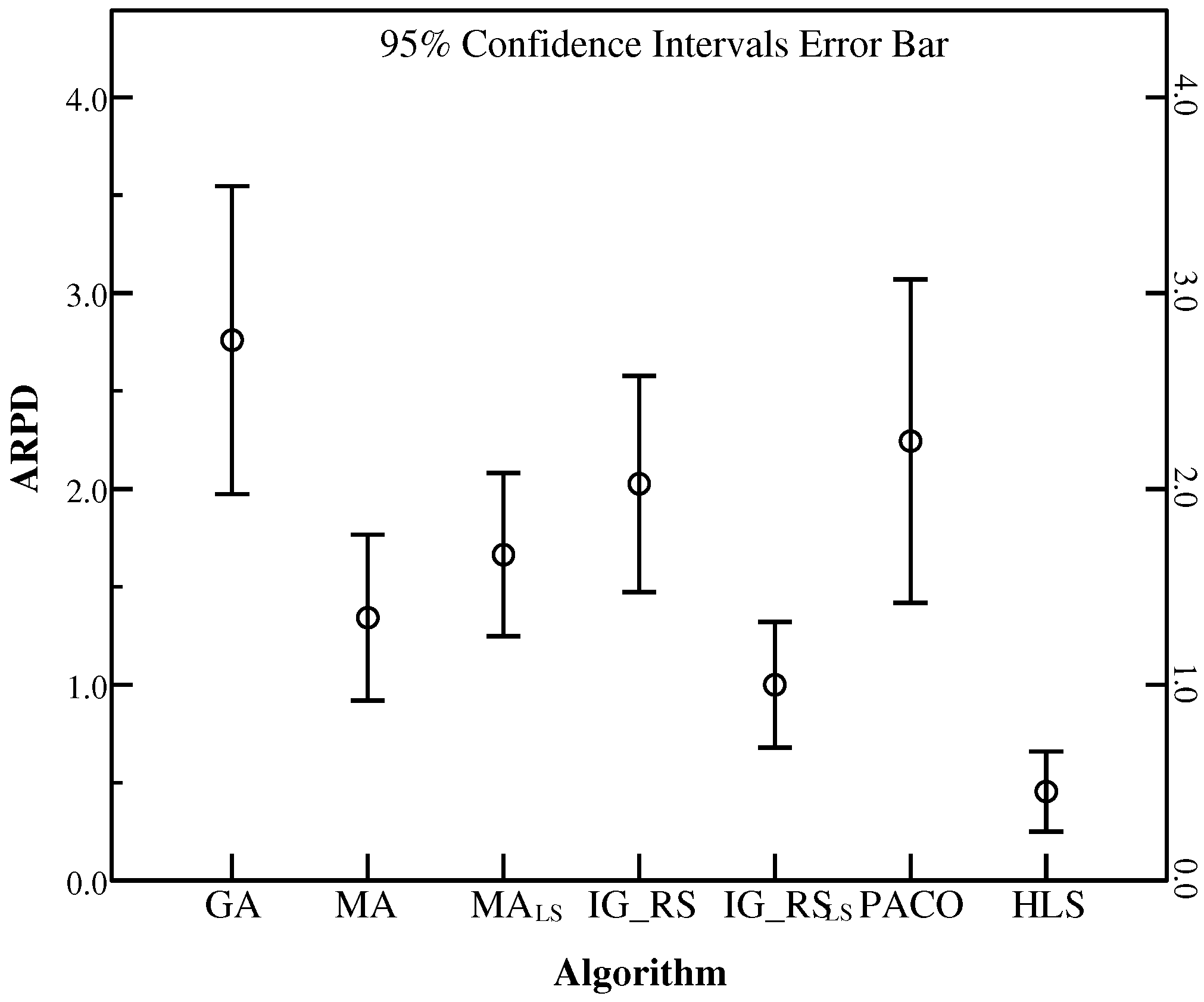
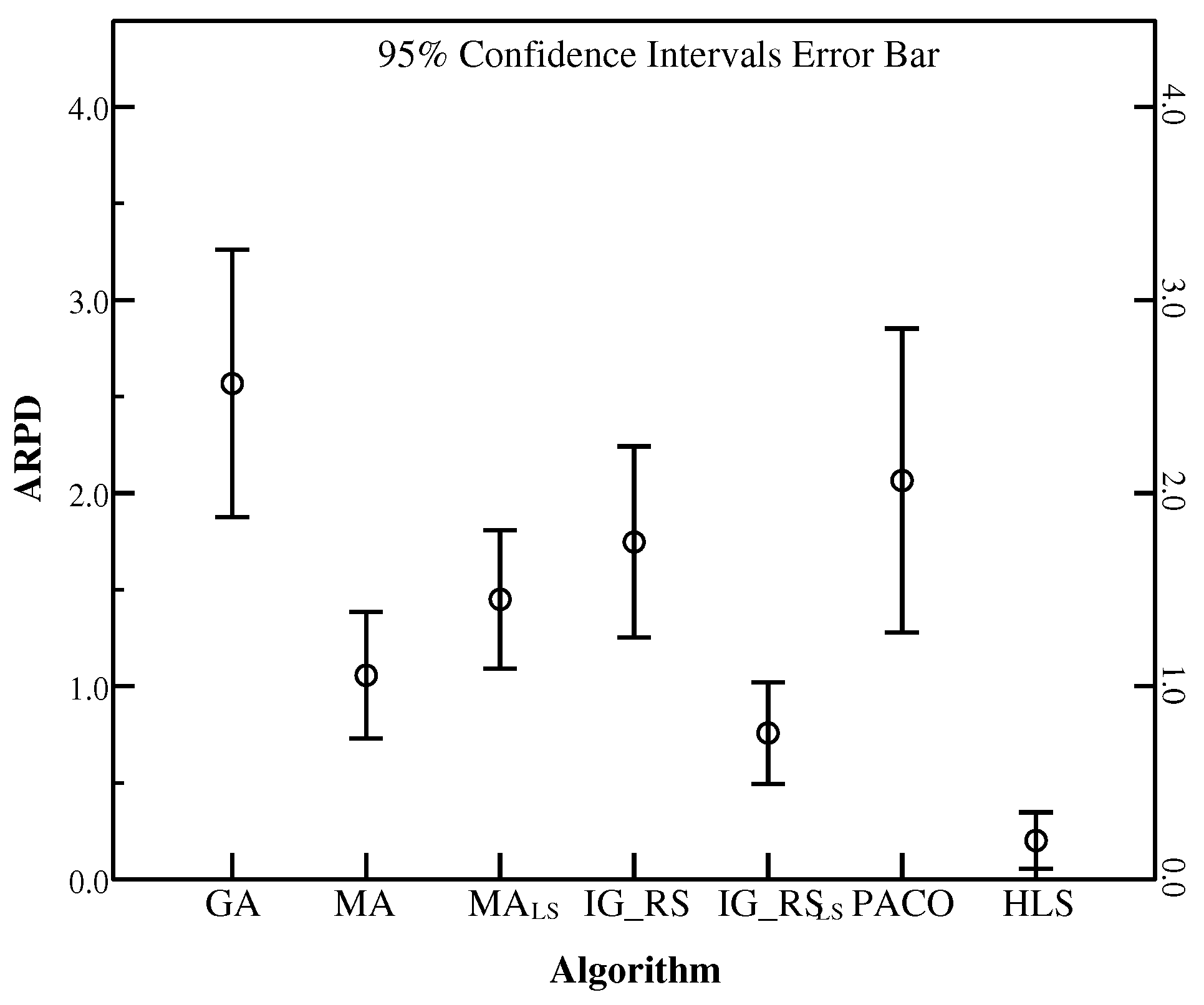
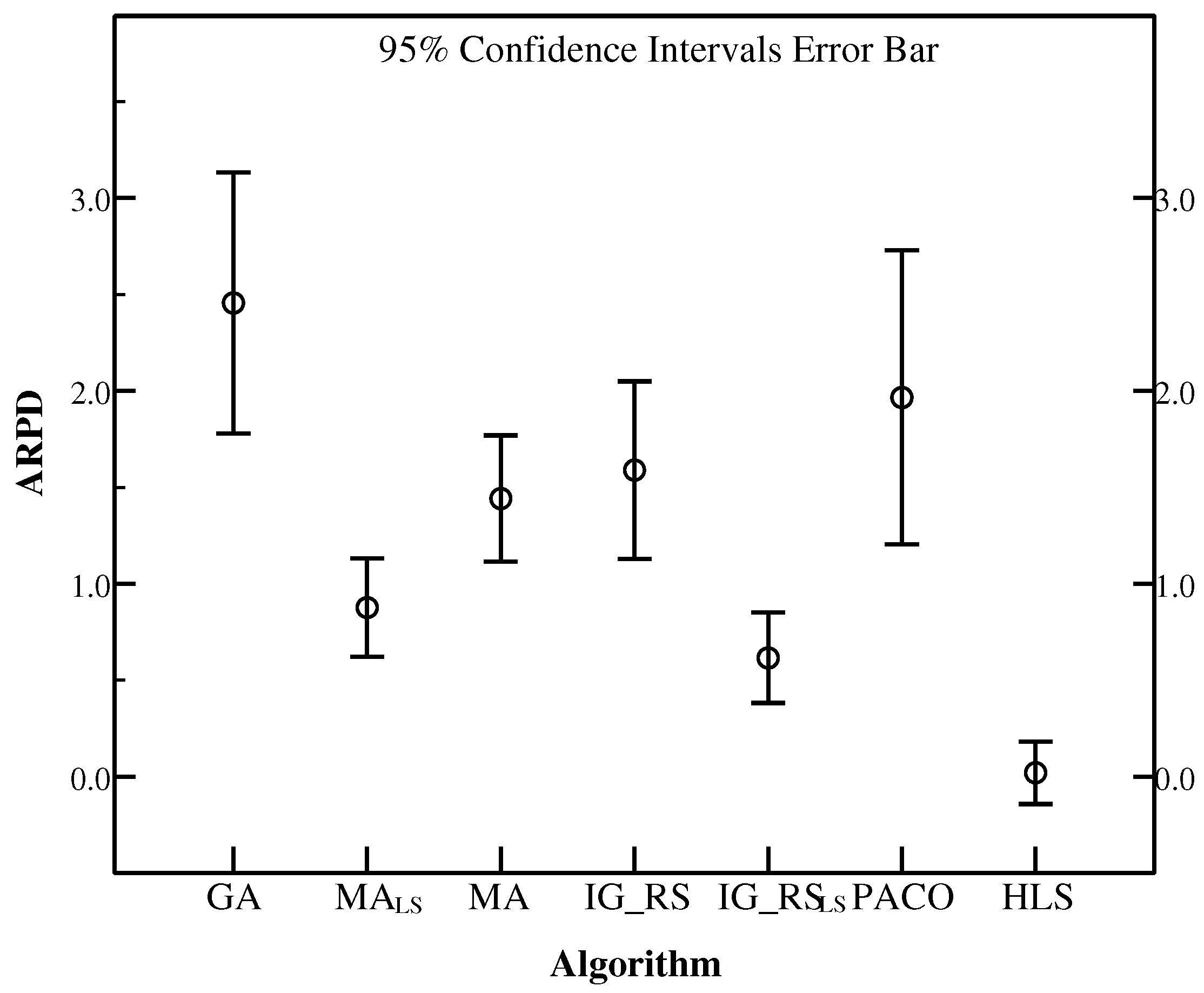
4.7. Comparison Results with Some State-Of-The-Art Approaches
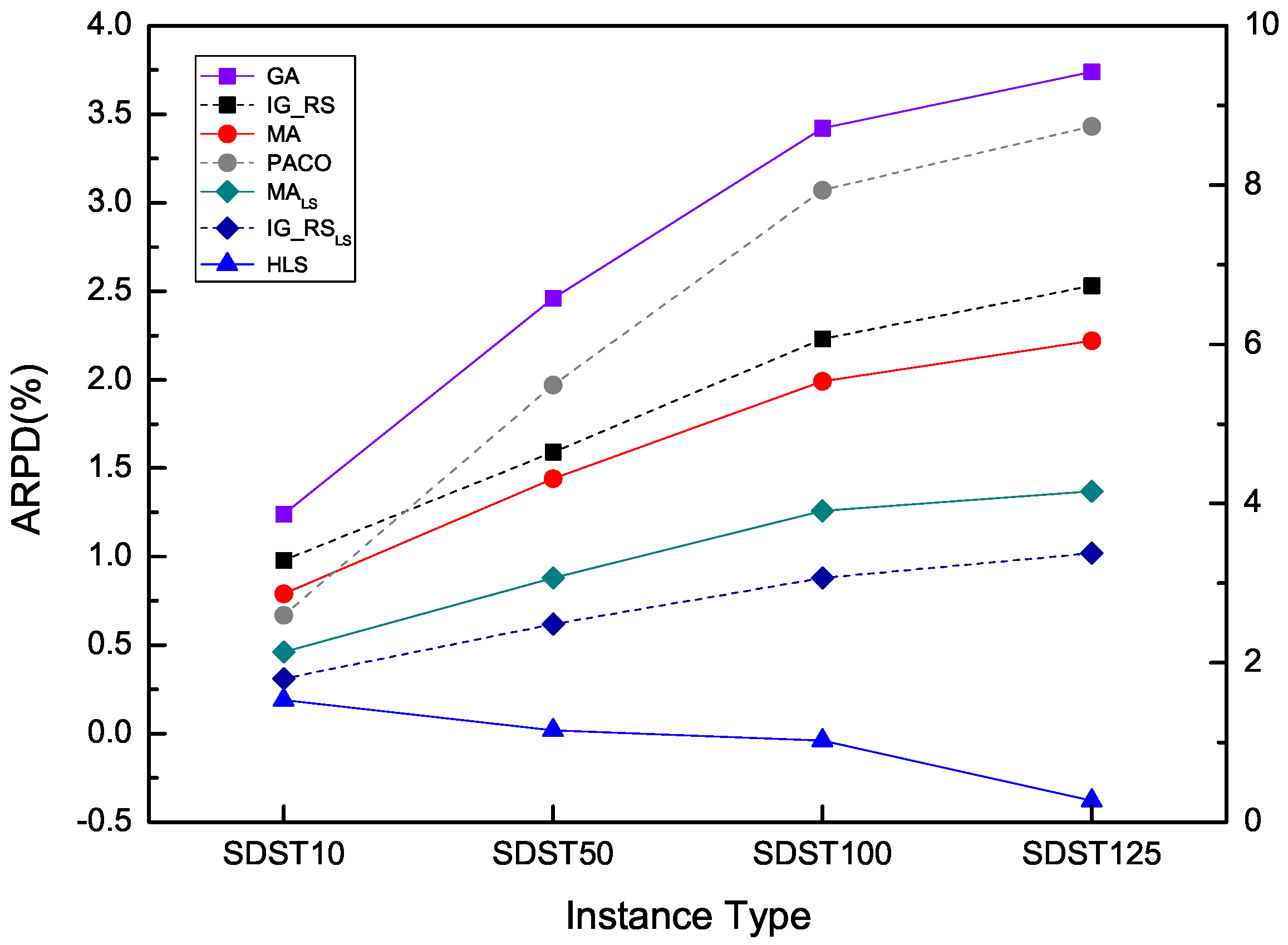
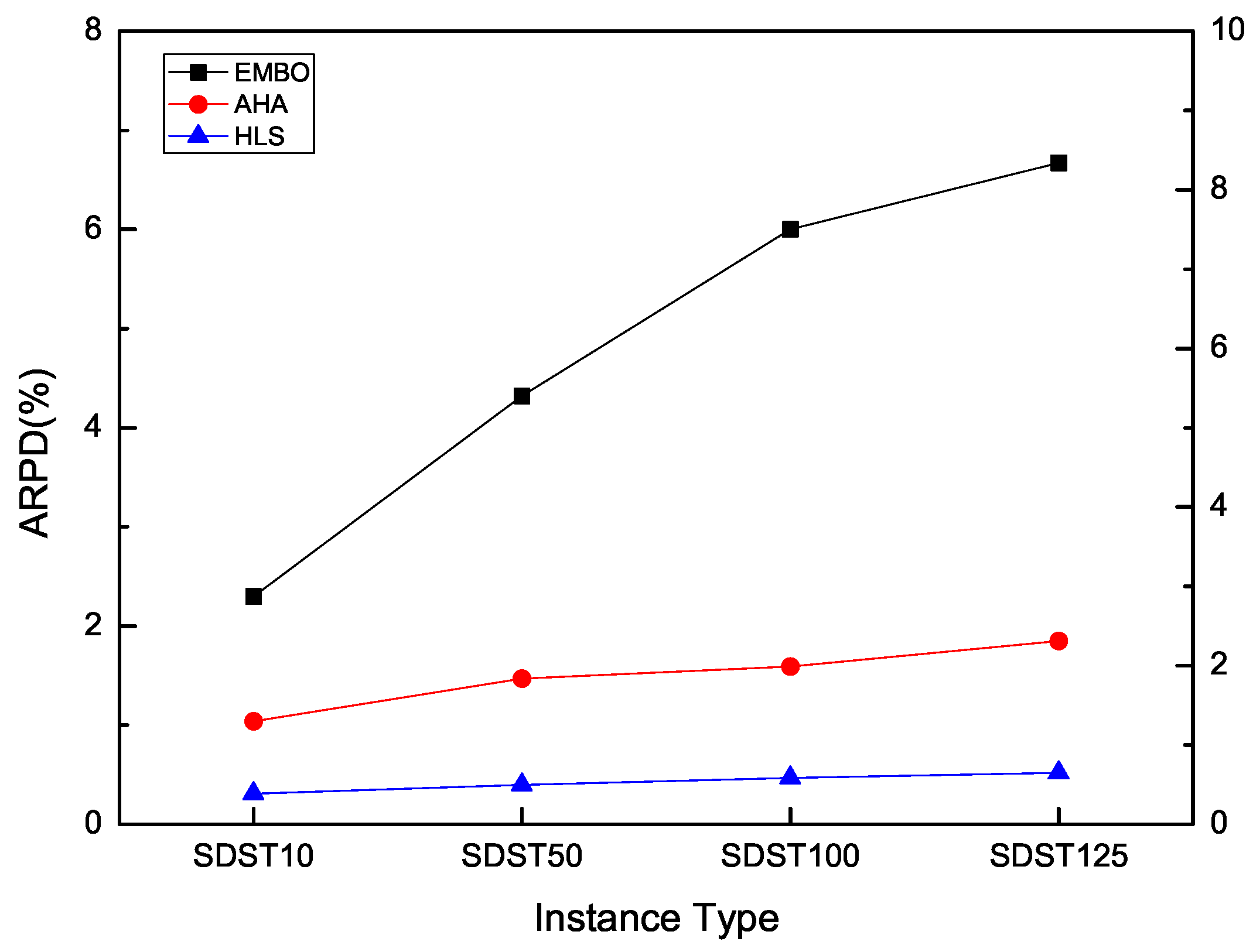
4.8. Comparison Results with Some Recent Algorithms
5. Conclusions and Future Work
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| FSSP-SDST | The flowshop scheduling problem with sequence dependent setup times |
| HLS | Hybrid local search algorithm |
| NEHBPS | Nawaz-Enscore-Hoam based problem-specific method |
| RPD | Relatively percentage deviation |
References
- Johnson, S.M. Optimal two- and three-stage production schedules with setup times included. Nav. Res. Logist. Q. 1954, 1, 61–68. [Google Scholar] [CrossRef]
- Cheng, T.C.E.; Gupta, J.N.D.; Wang, G. A review of flowshop scheduling reasearch with setup times. Prod. Oper. Manag. 2000, 9, 262–282. [Google Scholar] [CrossRef]
- Vanchipura, R.; Sridharan, R. Development and analysis of constructive heuristic algorithms for flow shop scheduling problems with sequence-dependent setup times. Int. J. Adv. Manuf. Technol. 2013, 67, 1337–1353. [Google Scholar] [CrossRef]
- Kheirkhah, A.; Navidi, H.; Bidgoli, M.M. Dynamic facility layout problem: A new bilevel formulation and some metaheuristic solution methods. IEEE Trans. Eng. Manag. 2015, 62, 396–410. [Google Scholar] [CrossRef]
- Balouka, N.; Cohen, I.; Shtub, A. Extending the Multimode Resource-Constrained Project Scheduling Problem by Including Value Considerations. IEEE Trans. Eng. Manag. 2016, 63, 4–15. [Google Scholar] [CrossRef]
- Li, S.; Wang, N.; Jia, T.; He, Z.; Liang, H. Multiobjective Optimization for Multiperiod Reverse Logistics Network Design. IEEE Trans. Eng. Manag. 2016, 63, 223–236. [Google Scholar] [CrossRef]
- Kheirkhah, A.; Navidi, H.; Bidgoli, M.M. An Improved Benders Decomposition Algorithm for an Arc Interdiction Vehicle Routing Problem. IEEE Trans. Eng. Manag. 2016, 63, 259–273. [Google Scholar] [CrossRef]
- Rios-Mercado, R.Z.; Bard, J.F. The flow shop scheduling polyhedron with setup times. J. Comb. Optim. 2003, 7, 291–318. [Google Scholar] [CrossRef]
- Nishi, T.; Hiranaka, Y. Lagrangian relaxation and cut generation for sequence-dependent setup time flowshop scheduling problems to minimise the total weighted tardiness. Int. J. Prod. Res. 2013, 51, 4778–4796. [Google Scholar] [CrossRef]
- Christian, B.; Andrea, R.; Michael, S. Hybrid Metaheuristics: An Emerging Approach to Optimization; Studies in Computational Intelligence; Springer: Berlin, Germany, 2008; Volume 114. [Google Scholar]
- Raidl, G.R.; Puchinger, J. Combining (Integer) Linear Programming Techniques and Metaheuristics for Combinatorial Optimization. Hybrid Metaheuristics 2008, 114, 31–62. [Google Scholar]
- Blum, C.; Cotta, C.; Fernandez, A.; Sampels, M. Hybridizations of metaheuristics with branch & bound derivates. Hybrid Metaheuristics 2008, 114, 85–116. [Google Scholar]
- D’Andreagiovanni, F.; Nardin, A. Towards the fast and robust optimal design of wireless body area networks. Appl. Soft Comput. 2015, 37, 971–982. [Google Scholar] [CrossRef]
- D’Andreagiovanni, F.; Krolikowski, J.; Pulaj, J. A fast hybrid primal heuristic for multiband robust capacitated network design with multiple time periods. Appl. Soft Comput. 2015, 26, 497–507. [Google Scholar] [CrossRef]
- Gambardella, L.M.; Montemanni, R.; Weyland, D. Coupling ant colony systems with strong local searches. Eur. J. Oper. Res. 2012, 220, 831–843. [Google Scholar] [CrossRef]
- Nawaz, M.; Enscore, E.E.; Ham, I. A heuristic algorithm for the m-machine, n-job flow-shop sequencing problem. Omega 1983, 11, 91–95. [Google Scholar] [CrossRef]
- Rios-Mercado, R.Z.; Bard, J.F. Heuristics for the flow line problem with setup costs. Eur. J. Oper. Res. 1998, 110, 76–98. [Google Scholar] [CrossRef]
- Ruiz, R.; Maroto, C.; Alcaraz, J. Solving the flowshop scheduling problem with sequence dependent setup times using advanced metaheuristics. Eur. J. Oper. Res. 2005, 165, 34–54. [Google Scholar] [CrossRef]
- Rios-Mercado, R.Z.; Bard, J.F. An Enhanced TSP-Based Heuristic for Makespan Minimization in a Flow Shop with Setup Times. J. Heuristics 1999, 5, 53–70. [Google Scholar] [CrossRef]
- Rajendran, C.; Ziegler, H. Ant-colony algorithms for permutation flowshop scheduling to minimize makespan/total flowtime of jobs. Eur. J. Oper. Res. 2004, 155, 426–438. [Google Scholar] [CrossRef]
- Gajpal, Y.; Rajendran, C.; Ziegler, H. An ant colony algorithm for scheduling in flowshops with sequence-dependent setup times of jobs. Int. J. Adv. Manuf. Technol. 2006, 30, 416–424. [Google Scholar] [CrossRef]
- Tseng, F.T.; Gupta, J.N.D.; Stafford, E.F. A penalty-based heuristic algorithm for the permutation flowshop scheduling problem with sequence-dependent set-up times. J. Oper. Res. Soc. 2006, 57, 541–551. [Google Scholar] [CrossRef]
- Benkalai, I.; Rebaine, D.; Gagne, C.; Baptiste, P. The migrating birds optimization metaheuristic for the permutation flow shop with sequence dependent setup times. IFAC PapersOnLine 2016, 49, 408–413. [Google Scholar] [CrossRef]
- Simons, J.V. Heuristics in flow shop scheduling with sequence dependent setup times. Omega 1992, 20, 215–225. [Google Scholar] [CrossRef]
- Jacobs, L.W.; Brusco, M.J. Note: A local-search heuristic for large set-covering problems. Nav. Res. Logist. 1995, 42, 1129–1140. [Google Scholar] [CrossRef]
- Ruizab, R. A simple and effective iterated greedy algorithm for the permutation flowshop scheduling problem. Eur. J. Oper. Res. 2007, 177, 2033–2049. [Google Scholar]
- Rajendran, C.; Ziegler, H. A heuristic for scheduling to minimize the sum of weighted flowtime of jobs in a flowshop with sequence-dependent setup times of jobs. Comput. Ind. Eng. 1997, 33, 281–284. [Google Scholar] [CrossRef]
- Wang, Y.; Dong, X.; Chen, P.; Lin, Y. Iterated Local Search Algorithms for the Sequence-Dependent Setup Times Flow Shop Scheduling Problem Minimizing Makespan. In Foundations of Intelligent Systems; Springer: Berlin/Heidelberg, Germany, 2014; pp. 329–338. [Google Scholar]
- Li, X.; Yin, M. An opposition-based differential evolution algorithm for permutation flow shop scheduling based on diversity measure. Adv. Eng. Softw. 2013, 55, 10–31. [Google Scholar] [CrossRef]
- Li, X.; Yin, M. A hybrid cuckoo search via Levy flights for the permutation flow shop scheduling problem. Int. J. Prod. Res. 2013, 51, 4732–4754. [Google Scholar] [CrossRef]
- Li, X.; Yin, M. A discrete artificial bee colony algorithm with composite mutation strategies for permutation flow shop scheduling problem. Sci. Iran. 2012, 19, 1921–1935. [Google Scholar] [CrossRef]
- Wang, L.; Fang, C. A hybrid estimation of distribution algorithm for solving the resource-constrained project scheduling problem. Expert Syst. Appl. 2012, 39, 2451–2460. [Google Scholar] [CrossRef]
- Fang, C.; Wang, L. An effective shuffled frog-leaping algorithm for resource-constrained project scheduling problem. Inf. Sci. 2011, 181, 4804–4822. [Google Scholar] [CrossRef]
- Pan, Q.K.; Wang, L. Effective heuristics for the blocking flowshop scheduling problem with makespan minimization. Omega 2012, 40, 218–229. [Google Scholar] [CrossRef]
- Li, X.; Wang, Q.; Wu, C. Efficient composite heuristics for total flowtime minimization in permutation flow shops. Omega 2009, 37, 155–164. [Google Scholar] [CrossRef]
- Li, X.; Ma, S. Multi-Objective Memetic Search Algorithm for Multi-Objective Permutation Flow Shop Scheduling Problem. IEEE Access 2017, 4, 2154–2165. [Google Scholar] [CrossRef]
- Li, X.; Li, M. Multiobjective Local Search Algorithm-Based Decomposition for Multiobjective Permutation Flow Shop Scheduling Problem. IEEE Trans. Eng. Manag. 2015, 62, 544–557. [Google Scholar] [CrossRef]
- Ruizab, R. An Iterated Greedy heuristic for the sequence dependent setup times flowshop problem with makespan and weighted tardiness objectives. Eur. J. Oper. Res. 2008, 187, 1143–1159. [Google Scholar]
- Li, X.; Zhang, Y. Adaptive hybrid algorithms for the sequence-dependent setup time permutation flow shop scheduling problem. IEEE Trans. Autom. Sci. Eng. 2012, 9, 578–595. [Google Scholar] [CrossRef]
- Benkalai, I.; Rebaine, D.; Gagne, C.; Baptiste, P. Improving the migrating birds optimization metaheuristic for the permutation flow shop with sequence-dependent set-up times. Int. J. Prod. Res. 2017, 1–13. [Google Scholar] [CrossRef]
- Duman, E.; Uysal, M.; Alkaya, A.F. Migrating Birds Optimization: A new metaheuristic approach and its performance on quadratic assignment problem. Inf. Sci. 2012, 217, 65–77. [Google Scholar] [CrossRef]
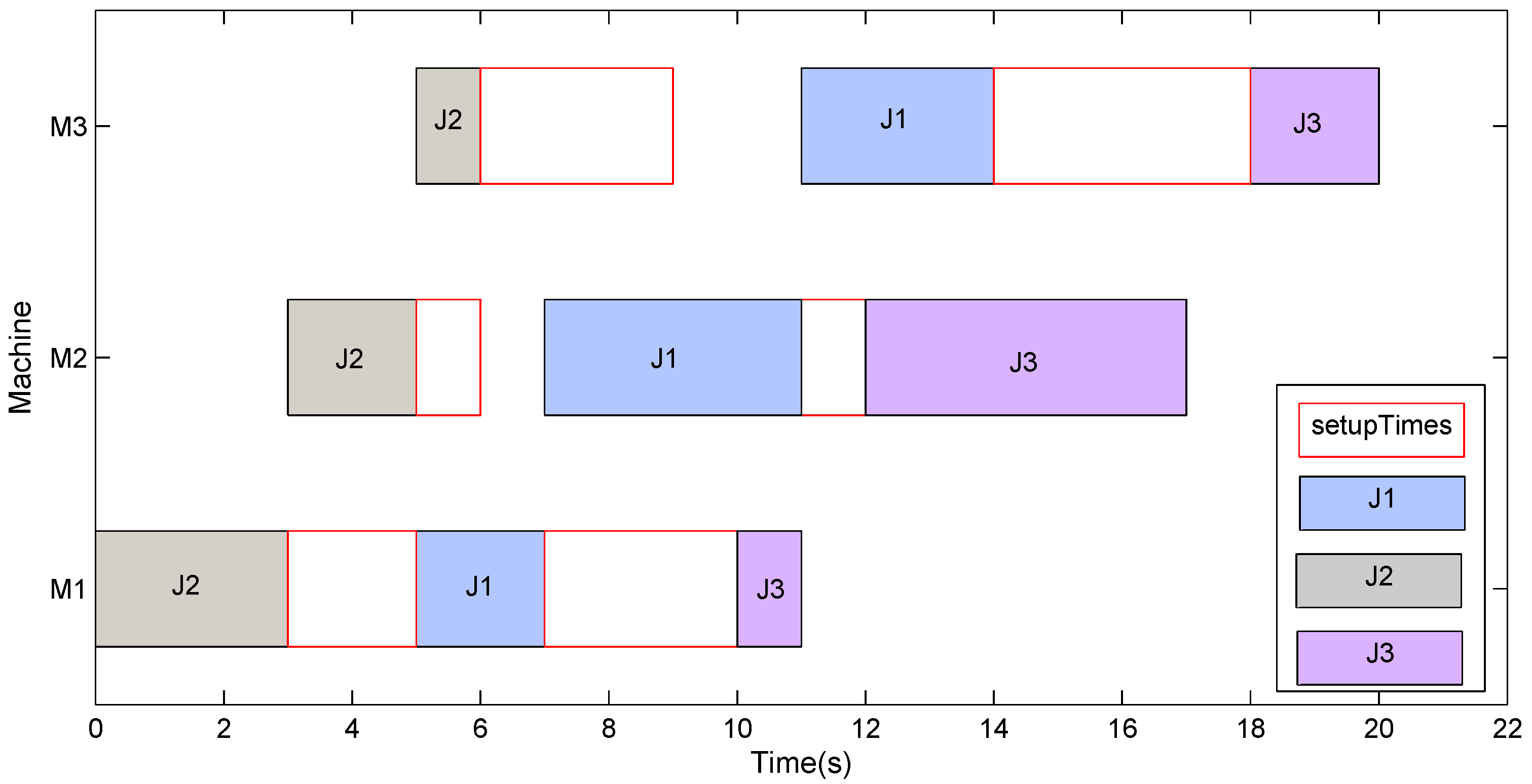




| J1 | J2 | J3 | |
|---|---|---|---|
| M1 | 2 | 3 | 1 |
| M2 | 4 | 2 | 5 |
| M3 | 3 | 1 | 2 |
| M1 | M2 | M3 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| J1 | J2 | J3 | J1 | J2 | J3 | J1 | J2 | J3 | |||
| J1 | – | 2 | 3 | J1 | – | 3 | 1 | J1 | – | 2 | 4 |
| J2 | 2 | – | 4 | J2 | 1 | – | 3 | J2 | 3 | – | 8 |
| J3 | 3 | 4 | – | J3 | 3 | 2 | – | J3 | 6 | 7 | – |
| DataNo. | 10 | 20 | 30 | 40 |
|---|---|---|---|---|
| Ta071 | 0.72 | 0.47 | 0.54 | 0.50 |
| Ta072 | 0.80 | 0.81 | 0.94 | 1.17 |
| Ta073 | 0.65 | 0.58 | 0.59 | 0.56 |
| Ta074 | 0.62 | 0.68 | 0.58 | 0.89 |
| Ta075 | 0.70 | 0.46 | 0.77 | 0.76 |
| Ta076 | 0.67 | 1.11 | 1.13 | 0.78 |
| Ta077 | 0.86 | 0.65 | 0.63 | 0.66 |
| Ta078 | 0.41 | 0.41 | 0.88 | 0.80 |
| Ta079 | 0.56 | 0.67 | 0.56 | 0.78 |
| Ta080 | 1.02 | 0.83 | 1.05 | 0.91 |
| Average | 0.70 | 0.67 | 0.77 | 0.78 |
| DataNo. | 3 | 4 | 5 | 6 |
|---|---|---|---|---|
| Ta071 | 0.42 | 0.55 | 0.62 | 0.60 |
| Ta072 | 1.22 | 0.91 | 0.94 | 0.90 |
| Ta073 | 0.76 | 0.73 | 0.59 | 0.65 |
| Ta074 | 1.10 | 0.65 | 0.23 | 0.83 |
| Ta075 | 0.86 | 0.22 | 0.77 | 0.62 |
| Ta076 | 0.92 | 0.62 | 1.05 | 0.86 |
| Ta077 | 0.87 | 0.69 | 0.63 | 0.91 |
| Ta078 | 0.82 | 0.29 | 0.40 | 0.55 |
| Ta079 | 0.93 | 0.54 | 0.55 | 0.74 |
| Ta080 | 1.05 | 0.54 | 1.05 | 0.90 |
| Average | 0.89 | 0.57 | 0.68 | 0.76 |
| DataNo. | 0.1 | 0.2 | 0.3 | 0.4 |
|---|---|---|---|---|
| Ta071 | 0.77 | 0.46 | 0.63 | 0.85 |
| Ta072 | 0.94 | 0.90 | 0.55 | 1.02 |
| Ta073 | 0.63 | 0.62 | 0.58 | 0.81 |
| Ta074 | 0.94 | 0.46 | 0.57 | 0.56 |
| Ta075 | 0.51 | 0.91 | 0.72 | 0.72 |
| Ta076 | 1.19 | 0.82 | 0.75 | 0.79 |
| Ta077 | 1.16 | 1.08 | 1.08 | 0.93 |
| Ta078 | 0.93 | 0.43 | 0.48 | 0.21 |
| Ta079 | 0.82 | 0.47 | 0.35 | 0.38 |
| Ta080 | 0.87 | 0.39 | 0.15 | 1.00 |
| Average | 0.88 | 0.65 | 0.59 | 0.73 |
| DataNo. | 4 | 6 | 8 | 10 |
|---|---|---|---|---|
| Ta071 | 0.67 | 0.54 | 0.83 | 0.66 |
| Ta072 | 0.78 | 0.80 | 0.78 | 0.91 |
| Ta073 | 0.33 | 0.59 | 0.37 | 0.39 |
| Ta074 | 0.94 | 0.58 | 0.74 | 0.99 |
| Ta075 | 0.79 | 0.77 | 0.64 | 0.68 |
| Ta076 | 0.92 | 1.13 | 0.78 | 0.69 |
| Ta077 | 1.08 | 0.63 | 1.18 | 0.97 |
| Ta078 | 0.78 | 0.40 | 0.82 | 0.37 |
| Ta079 | 0.40 | 0.56 | 0.81 | 0.79 |
| Ta080 | 0.62 | 1.05 | 0.86 | 0.91 |
| Average | 0.73 | 0.71 | 0.78 | 0.74 |
| DataNo. | 10 | 15 | 20 | 25 |
|---|---|---|---|---|
| Ta071 | 0.71 | 0.28 | 0.54 | 0.78 |
| Ta072 | 0.67 | 0.84 | 0.80 | 0.95 |
| Ta073 | 0.39 | 0.41 | 0.59 | 0.32 |
| Ta074 | 0.83 | 0.56 | 0.58 | 0.64 |
| Ta075 | 0.52 | 0.22 | 0.77 | 0.76 |
| Ta076 | 1.21 | 0.62 | 1.05 | 0.88 |
| Ta077 | 0.91 | 0.49 | 0.63 | 0.86 |
| Ta078 | 0.86 | 0.88 | 0.40 | 1.08 |
| Ta079 | 0.59 | 0.50 | 0.55 | 0.62 |
| Ta080 | 0.69 | 0.49 | 1.05 | 0.96 |
| Average | 0.74 | 0.53 | 0.70 | 0.78 |
| DataNo. | HLS_noNEHBPS | HLS_NEHBPS | ||
|---|---|---|---|---|
| SDST50 | SDST125 | SDST50 | SDST125 | |
| Ta071 | 0.08 | 0.43 | 0.59 | 0.55 |
| Ta072 | 0.80 | 0.86 | 0.38 | 0.60 |
| Ta073 | 0.29 | 1.05 | 0.14 | 1.41 |
| Ta074 | 0.60 | 0.99 | 0.52 | 0.70 |
| Ta075 | 0.33 | 0.90 | 0.15 | 0.41 |
| Ta076 | 0.42 | 1.09 | 0.23 | 0.78 |
| Ta077 | 0.90 | 1.13 | 0.21 | 0.79 |
| Ta078 | 0.77 | 0.78 | 0.47 | 0.42 |
| Ta079 | 0.28 | 0.63 | −0.05 | 0.58 |
| Ta080 | 0.84 | 0.79 | 0.72 | −0.38 |
| Average | 0.53 | 0.87 | 0.34 | 0.59 |
| DataNo. | HLS_heavy | HLS_light | ||
|---|---|---|---|---|
| SDST50 | SDST125 | SDST50 | SDST125 | |
| Ta071 | 0.63 | 0.59 | 0.59 | 0.75 |
| Ta072 | 0.55 | 1.61 | 0.64 | 0.60 |
| Ta073 | 0.84 | 1.85 | 0.48 | 1.41 |
| Ta074 | 0.57 | 0.92 | 0.74 | 0.73 |
| Ta075 | 0.72 | 1.78 | 0.64 | 0.69 |
| Ta076 | 0.75 | 1.30 | 0.69 | 1.00 |
| Ta077 | 1.11 | 1.14 | 0.28 | 1.07 |
| Ta078 | 0.43 | 0.92 | 0.58 | 0.42 |
| Ta079 | 0.35 | 0.46 | 0.25 | 0.79 |
| Ta080 | 0.15 | 0.95 | 0.75 | 0.32 |
| Average | 0.61 | 1.15 | 0.56 | 0.78 |
| DataNo. | HLS_exLS | HLS_swLS | HLS_inLS | |||
|---|---|---|---|---|---|---|
| SDST50 | SDST125 | SDST50 | SDST125 | SDST50 | SDST125 | |
| Ta071 | 4.89 | 6.64 | 1.02 | 1.93 | 0.63 | 0.59 |
| Ta072 | 5.69 | 7.67 | 2.29 | 2.58 | 0.55 | 1.61 |
| Ta073 | 5.11 | 7.60 | 1.39 | 3.21 | 0.58 | 1.85 |
| Ta074 | 4.82 | 6.78 | 2.05 | 2.03 | 0.57 | 0.92 |
| Ta075 | 4.94 | 6.22 | 1.59 | 2.67 | 0.72 | 1.78 |
| Ta076 | 5.60 | 7.69 | 1.95 | 3.16 | 0.75 | 1.30 |
| Ta077 | 5.85 | 7.24 | 2.06 | 1.66 | 1.11 | 1.14 |
| Ta078 | 4.83 | 5.74 | 1.55 | 2.68 | 0.43 | 1.05 |
| Ta079 | 5.69 | 7.19 | 1.44 | 2.48 | 0.31 | 0.46 |
| Ta080 | 5.50 | 6.42 | 1.40 | 2.65 | 0.15 | 0.95 |
| SD | 0.41 | 0.67 | 0.40 | 0.50 | 0.26 | 0.47 |
| Average | 5.29 | 6.92 | 1.67 | 2.50 | 0.58 | 1.16 |
| DataSet | GA | MA | MA | PACO | IG_RS | IG_RS | HLS(10) | HLS(30) | ||
|---|---|---|---|---|---|---|---|---|---|---|
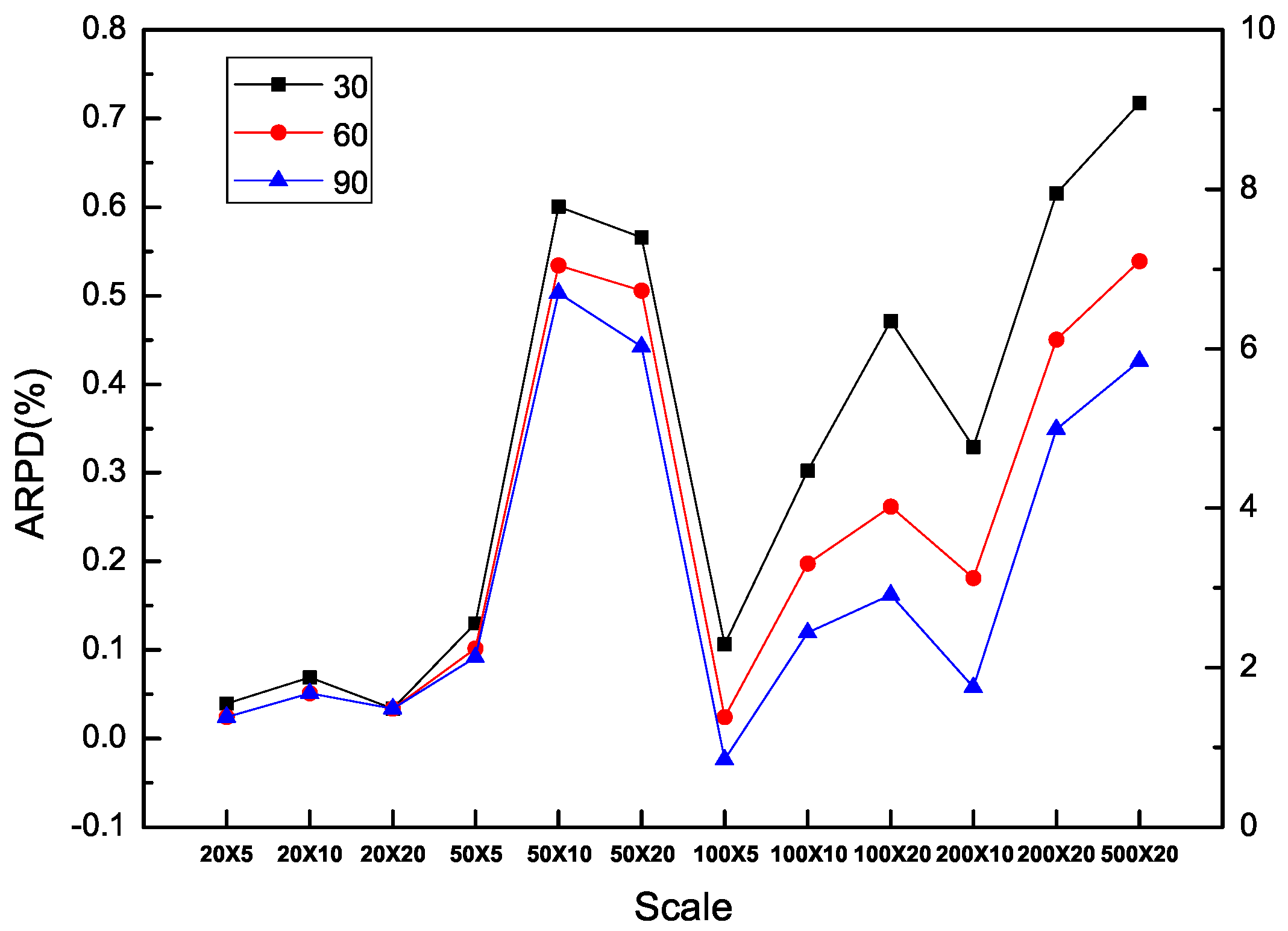
| SDST10 | 20 × 5 | Ta001–Ta010 | 0.43 | 0.49 | 0.12 | 0.18 | 0.21 | 0.08 | 0.04 | 0.04 |
| 20 × 10 | Ta011–Ta020 | 0.59 | 0.55 | 0.13 | 0.33 | 0.28 | 0.08 | 0.07 | 0.06 | |
| 20 × 20 | Ta021–Ta030 | 0.44 | 0.59 | 0.14 | 0.20 | 0.30 | 0.07 | 0.03 | 0.02 | |
| 50 × 5 | Ta031–Ta040 | 1.04 | 0.77 | 0.43 | 0.53 | 1.00 | 0.37 | 0.13 | 0.12 | |
| 50 × 10 | Ta041–Ta050 | 2.10 | 1.21 | 1.12 | 1.23 | 1.58 | 0.76 | 0.60 | 0.57 | |
| 50 × 20 | Ta051–Ta060 | 2.23 | 1.38 | 1.16 | 1.27 | 1.85 | 0.91 | 0.57 | 0.49 | |
| 100 × 5 | Ta061–Ta070 | 1.28 | 0.76 | 0.54 | 0.87 | 1.44 | 0.43 | 0.11 | 0.12 | |
| 100 × 10 | Ta071–Ta080 | 1.48 | 0.91 | 0.78 | 0.99 | 1.49 | 0.61 | 0.30 | 0.25 | |
| 100 × 20 | Ta081–Ta090 | 2.07 | 1.49 | 1.27 | 1.49 | 1.75 | 0.88 | 0.47 | 0.46 | |
| 200 × 10 | Ta091–Ta100 | 1.63 | 0.81 | 0.79 | 1.04 | 1.50 | 0.58 | 0.33 | 0.30 | |
| 200 × 20 | Ta101–Ta110 | 2.00 | 1.14 | 1.11 | 1.31 | 1.45 | 0.79 | 0.61 | 0.59 | |
| 500 × 20 | Ta111–Ta120 | 1.38 | 0.74 | 0.69 | 0.82 | 1.01 | 0.46 | 0.72 | 0.69 | |
| SD | 0.65 | 0.33 | 0.42 | 0.45 | 0.59 | 0.31 | 0.25 | 0.24 | ||
| ARPD | 1.39 | 0.90 | 0.69 | 0.86 | 1.16 | 0.50 | 0.33 | 0.31 | ||
| SDST50 | 20 × 5 | Ta001–Ta010 | 1.34 | 0.44 | 0.37 | 0.58 | 0.83 | 0.26 | 0.12 | 0.09 |
| 20 × 10 | Ta011–Ta020 | 1.21 | 0.92 | 0.41 | 0.49 | 0.66 | 0.28 | 0.05 | 0.03 | |
| 20 × 20 | Ta021–Ta030 | 0.57 | 0.87 | 0.20 | 0.35 | 0.60 | 0.10 | 0.06 | 0.05 | |
| 50 × 5 | Ta031–Ta040 | 3.85 | 2.27 | 1.79 | 2.52 | 2.99 | 1.41 | 0.60 | 0.48 | |
| 50 × 10 | Ta041–Ta050 | 3.24 | 1.81 | 1.49 | 2.15 | 2.44 | 1.33 | 0.44 | 0.40 | |
| 50 × 20 | Ta051–Ta060 | 2.57 | 1.93 | 1.33 | 1.65 | 2.34 | 1.16 | 0.41 | 0.32 | |
| 100 × 5 | Ta061–Ta070 | 4.64 | 2.64 | 2.23 | 4.37 | 2.93 | 1.51 | 0.66 | 0.63 | |
| 100 × 10 | Ta071–Ta080 | 3.61 | 2.20 | 1.84 | 3.44 | 2.69 | 1.37 | 0.38 | 0.22 | |
| 100 × 20 | Ta081–Ta090 | 2.96 | 2.00 | 1.73 | 2.87 | 2.38 | 1.29 | 0.30 | 0.12 | |
| 200 × 10 | Ta091–Ta100 | 3.95 | 1.98 | 1.88 | 3.62 | 2.59 | 1.33 | 0.71 | 0.54 | |
| 200 × 20 | Ta101–Ta110 | 3.04 | 1.62 | 1.61 | 2.89 | 2.07 | 1.10 | 0.54 | 0.65 | |
| 500 × 20 | Ta111–Ta120 | 2.14 | 1.29 | 1.23 | 2.00 | 1.79 | 0.86 | 1.19 | 1.28 | |
| SD | 1.24 | 0.66 | 0.67 | 1.30 | 0.87 | 0.50 | 0.32 | 0.36 | ||
| ARPD | 2.76 | 1.66 | 1.34 | 2.24 | 2.03 | 1.00 | 0.45 | 0.40 | ||
| DataSet | GA | MA | MA | PACO | IG_RS | IG_RS | HLS(10) | HLS(30) | ||
|---|---|---|---|---|---|---|---|---|---|---|
| SDST100 | 20 × 5 | Ta001–Ta010 | 2.01 | 1.29 | 0.43 | 0.82 | 1.53 | 0.30 | 0.02 | 0.02 |
| 20 × 10 | Ta011–Ta020 | 1.48 | 0.87 | 0.31 | 0.66 | 1.42 | 0.35 | 0.07 | 0.07 | |
| 20 × 20 | Ta021–Ta030 | 1.08 | 0.62 | 0.29 | 0.52 | 0.95 | 0.27 | 0.08 | 0.05 | |
| 50 × 5 | Ta031–Ta040 | 5.00 | 3.12 | 2.37 | 3.79 | 3.83 | 1.95 | 0.85 | 0.73 | |
| 50 × 10 | Ta041–Ta050 | 4.19 | 2.59 | 1.98 | 3.05 | 3.10 | 1.57 | 0.50 | 0.44 | |
| 50 × 20 | Ta051–Ta060 | 3.39 | 1.78 | 1.66 | 2.51 | 2.76 | 1.41 | 0.42 | 0.40 | |
| 100 × 5 | Ta061–Ta070 | 6.49 | 3.63 | 3.20 | 6.86 | 3.93 | 2.16 | 1.00 | 0.88 | |
| 100 × 10 | Ta071–Ta080 | 4.58 | 3.03 | 2.26 | 5.14 | 3.28 | 1.61 | 0.31 | 0.13 | |
| 100 × 20 | Ta081–Ta090 | 3.73 | 2.37 | 2.12 | 4.04 | 2.76 | 1.41 | 0.27 | 0.17 | |
| 200 × 10 | Ta091–Ta100 | 5.12 | 2.56 | 2.53 | 5.48 | 2.98 | 1.67 | 0.92 | 0.71 | |
| 200 × 20 | Ta101–Ta110 | 3.59 | 1.99 | 1.93 | 3.70 | 2.27 | 1.26 | 0.91 | 0.57 | |
| 500 × 20 | Ta111–Ta120 | 2.50 | 1.53 | 1.53 | 2.50 | 1.87 | 0.96 | 1.77 | 1.45 | |
| SD | 1.61 | 0.93 | 0.93 | 2.00 | 0.96 | 0.64 | 0.51 | 0.43 | ||
| ARPD | 3.60 | 2.11 | 1.72 | 3.26 | 2.56 | 1.24 | 0.59 | 0.47 | ||
| SDST125 | 20 × 5 | Ta001–Ta010 | 2.06 | 1.69 | 0.67 | 0.88 | 1.96 | 0.46 | 0.02 | 0.02 |
| 20 × 10 | Ta011–Ta020 | 1.74 | 1.02 | 0.51 | 0.85 | 1.62 | 0.53 | 0.07 | 0.04 | |
| 20 × 20 | Ta021–Ta030 | 1.06 | 1.37 | 0.28 | 0.47 | 0.94 | 0.26 | 0.07 | 0.04 | |
| 50 × 5 | Ta031–Ta040 | 6.09 | 3.71 | 2.97 | 4.59 | 4.57 | 2.37 | 1.00 | 0.80 | |
| 50 × 10 | Ta041–Ta050 | 4.64 | 3.14 | 2.07 | 3.60 | 3.95 | 1.94 | 0.36 | 0.22 | |
| 50 × 20 | Ta051–Ta060 | 3.32 | 2.16 | 1.59 | 2.55 | 2.77 | 1.42 | 0.44 | 0.21 | |
| 100 × 5 | Ta061–Ta070 | 7.33 | 4.38 | 3.55 | 8.19 | 4.70 | 2.41 | 1.06 | 1.00 | |
| 100 × 10 | Ta071–Ta080 | 5.33 | 3.24 | 2.78 | 6.02 | 3.66 | 2.07 | 0.53 | 0.34 | |
| 100 × 20 | Ta081–Ta090 | 3.99 | 2.56 | 2.31 | 4.37 | 2.91 | 1.52 | 0.06 | −0.07 | |
| 200 × 10 | Ta091–Ta100 | 5.53 | 2.81 | 2.73 | 5.80 | 3.33 | 1.79 | 0.99 | 0.98 | |
| 200 × 20 | Ta101–Ta110 | 3.86 | 2.08 | 2.04 | 3.93 | 2.51 | 1.38 | 0.89 | 0.77 | |
| 500 × 20 | Ta111–Ta120 | 2.71 | 1.71 | 1.70 | 2.77 | 2.13 | 1.08 | 1.95 | 1.92 | |
| SD | 1.90 | 1.00 | 1.03 | 2.33 | 1.17 | 0.73 | 0.58 | 0.59 | ||
| ARPD | 3.97 | 2.49 | 1.93 | 3.67 | 2.92 | 1.44 | 0.62 | 0.52 | ||
| DataSet | GA | MA | MA | PACO | IG_RS | IG_RS | HLS(10) | HLS(30) | ||
|---|---|---|---|---|---|---|---|---|---|---|
| SDST10 | 20 × 5 | Ta001–Ta010 | 0.46 | 0.90 | 0.10 | 0.21 | 0.19 | 0.05 | 0.02 | 0.02 |
| 20 × 10 | Ta011–Ta020 | 0.57 | 0.28 | 0.13 | 0.26 | 0.22 | 0.05 | 0.05 | 0.05 | |
| 20 × 20 | Ta021–Ta030 | 0.37 | 0.52 | 0.09 | 0.16 | 0.22 | 0.05 | 0.03 | 0.02 | |
| 50 × 5 | Ta031–Ta040 | 0.93 | 0.57 | 0.31 | 0.44 | 0.88 | 0.32 | 0.10 | 0.07 | |
| 50 × 10 | Ta041–Ta050 | 2.07 | 1.38 | 0.83 | 1.02 | 1.58 | 0.60 | 0.53 | 0.49 | |
| 50 × 20 | Ta051–Ta060 | 2.18 | 1.21 | 0.96 | 1.06 | 1.70 | 0.64 | 0.51 | 0.42 | |
| 100 × 5 | Ta061–Ta070 | 1.10 | 0.70 | 0.40 | 0.80 | 1.36 | 0.38 | 0.02 | 0.01 | |
| 100 × 10 | Ta071–Ta080 | 1.39 | 0.81 | 0.60 | 0.84 | 1.37 | 0.44 | 0.20 | 0.13 | |
| 100 × 20 | Ta081–Ta090 | 1.93 | 1.11 | 0.97 | 1.25 | 1.48 | 0.71 | 0.26 | 0.24 | |
| 200 × 10 | Ta091–Ta100 | 1.42 | 0.73 | 0.61 | 0.94 | 1.39 | 0.43 | 0.18 | 0.17 | |
| 200 × 20 | Ta101–Ta110 | 1.79 | 0.93 | 0.87 | 1.10 | 1.25 | 0.53 | 0.45 | 0.39 | |
| 500 × 20 | Ta111–Ta120 | 1.31 | 0.54 | 0.54 | 0.69 | 0.88 | 0.31 | 0.54 | 0.52 | |
| SD | 0.63 | 0.32 | 0.33 | 0.38 | 0.56 | 0.23 | 0.21 | 0.19 | ||
| ARPD | 1.29 | 0.81 | 0.53 | 0.73 | 1.04 | 0.38 | 0.24 | 0.21 | ||
| SDST50 | 20 × 5 | Ta001–Ta010 | 1.30 | 1.21 | 0.35 | 0.53 | 0.69 | 0.18 | 0.12 | 0.05 |
| 20 × 10 | Ta011–Ta020 | 1.16 | 0.87 | 0.31 | 0.43 | 0.62 | 0.20 | 0.05 | 0.03 | |
| 20 × 20 | Ta021–Ta030 | 0.57 | 0.23 | 0.16 | 0.32 | 0.41 | 0.09 | 0.04 | 0.04 | |
| 50 × 5 | Ta031–Ta040 | 3.57 | 1.65 | 1.39 | 2.05 | 2.61 | 1.13 | 0.42 | 0.30 | |
| 50 × 10 | Ta041–Ta050 | 3.15 | 1.96 | 1.24 | 1.81 | 2.23 | 1.17 | 0.31 | 0.19 | |
| 50 × 20 | Ta051–Ta060 | 2.49 | 1.61 | 1.07 | 1.42 | 2.06 | 0.93 | 0.23 | 0.12 | |
| 100 × 5 | Ta061–Ta070 | 4.06 | 2.35 | 1.72 | 4.11 | 2.67 | 1.27 | 0.29 | 0.24 | |
| 100 × 10 | Ta071–Ta080 | 3.24 | 1.82 | 1.53 | 3.19 | 2.23 | 1.04 | 0.03 | −0.10 | |
| 100 × 20 | Ta081–Ta090 | 2.71 | 1.66 | 1.35 | 2.66 | 2.01 | 0.96 | −0.07 | −0.22 | |
| 200 × 10 | Ta091–Ta100 | 3.64 | 1.71 | 1.43 | 3.48 | 2.19 | 0.88 | 0.10 | 0.00 | |
| 200 × 20 | Ta101–Ta110 | 2.82 | 1.34 | 1.17 | 2.78 | 1.77 | 0.74 | 0.12 | 0.15 | |
| 500 × 20 | Ta111–Ta120 | 2.09 | 0.99 | 0.96 | 2.00 | 1.47 | 0.50 | 0.78 | 0.89 | |
| SD | 1.09 | 0.56 | 0.51 | 1.24 | 0.78 | 0.41 | 0.23 | 0.28 | ||
| ARPD | 2.57 | 1.45 | 1.06 | 2.06 | 1.75 | 0.76 | 0.20 | 0.14 | ||
| DataSet | GA | MA | MA | PACO | IG_RS | IG_RS | HLS(10) | HLS(30) | ||
|---|---|---|---|---|---|---|---|---|---|---|
| SDST100 | 20 × 5 | Ta001–Ta010 | 1.88 | 1.73 | 0.37 | 0.71 | 1.48 | 0.25 | 0.02 | 0.02 |
| 20 × 10 | Ta011–Ta020 | 1.26 | 0.88 | 0.28 | 0.47 | 1.01 | 0.25 | 0.07 | 0.07 | |
| 20 × 20 | Ta021–Ta030 | 1.00 | 0.28 | 0.26 | 0.41 | 0.92 | 0.18 | 0.02 | 0.02 | |
| 50 × 5 | Ta031–Ta040 | 5.35 | 2.65 | 2.24 | 3.40 | 3.89 | 1.95 | 0.44 | 0.31 | |
| 50 × 10 | Ta041–Ta050 | 4.21 | 2.72 | 1.66 | 2.73 | 3.09 | 1.48 | 0.29 | 0.10 | |
| 50 × 20 | Ta051–Ta060 | 3.23 | 2.11 | 1.35 | 2.14 | 2.58 | 1.28 | 0.18 | 0.10 | |
| 100 × 5 | Ta061–Ta070 | 5.99 | 3.50 | 2.69 | 6.89 | 3.82 | 1.95 | 0.55 | 0.23 | |
| 100 × 10 | Ta071–Ta080 | 4.39 | 2.67 | 2.01 | 4.96 | 2.95 | 1.44 | −0.36 | −0.48 | |
| 100 × 20 | Ta081–Ta090 | 3.67 | 2.31 | 2.03 | 4.04 | 2.65 | 1.35 | −0.22 | −0.36 | |
| 200 × 10 | Ta091–Ta100 | 4.95 | 2.31 | 2.19 | 5.62 | 2.86 | 1.25 | 0.00 | −0.13 | |
| 200 × 20 | Ta101–Ta110 | 3.65 | 1.81 | 1.68 | 3.87 | 2.08 | 0.93 | 0.25 | −0.06 | |
| 500 × 20 | Ta111–Ta120 | 2.66 | 1.44 | 1.35 | 2.75 | 1.70 | 0.73 | 1.34 | 0.94 | |
| SD | 1.59 | 0.88 | 0.82 | 2.06 | 0.99 | 0.62 | 0.44 | 0.36 | ||
| ARPD | 3.52 | 2.03 | 1.51 | 3.17 | 2.42 | 1.09 | 0.22 | 0.06 | ||
| SDST125 | 20 × 5 | Ta001–Ta010 | 1.80 | 2.05 | 0.34 | 0.64 | 1.40 | 0.35 | 0.02 | 0.02 |
| 20 × 10 | Ta011–Ta020 | 1.66 | 1.48 | 0.42 | 0.68 | 1.39 | 0.41 | 0.07 | 0.04 | |
| 20 × 20 | Ta021–Ta030 | 0.97 | 0.96 | 0.22 | 0.39 | 0.84 | 0.22 | 0.05 | 0.03 | |
| 50 × 5 | Ta031–Ta040 | 5.83 | 3.97 | 2.47 | 4.07 | 4.25 | 2.18 | 0.57 | 0.47 | |
| 50 × 10 | Ta041–Ta050 | 4.73 | 2.13 | 1.78 | 3.16 | 3.60 | 1.67 | 0.12 | 0.02 | |
| 50 × 20 | Ta051–Ta060 | 3.41 | 2.50 | 1.43 | 2.43 | 2.71 | 1.45 | 0.16 | −0.03 | |
| 100 × 5 | Ta061–Ta070 | 6.86 | 4.45 | 3.02 | 7.89 | 4.58 | 2.27 | 0.32 | 0.18 | |
| 100 × 10 | Ta071–Ta080 | 5.14 | 3.10 | 2.37 | 5.89 | 3.43 | 1.65 | −0.16 | −0.31 | |
| 100 × 20 | Ta081–Ta090 | 3.79 | 2.40 | 1.80 | 4.32 | 2.69 | 1.22 | −0.42 | −0.55 | |
| 200 × 10 | Ta091–Ta100 | 5.65 | 2.76 | 2.51 | 6.27 | 3.17 | 1.60 | 0.12 | 0.08 | |
| 200 × 20 | Ta101–Ta110 | 3.88 | 1.94 | 1.74 | 4.20 | 2.40 | 1.06 | 0.21 | 0.12 | |
| 500 × 20 | Ta111–Ta120 | 2.89 | 1.66 | 1.53 | 3.03 | 1.91 | 0.83 | 1.44 | 1.39 | |
| SD | 1.84 | 1.01 | 0.91 | 2.36 | 1.17 | 0.69 | 0.46 | 0.47 | ||
| ARPD | 3.88 | 2.45 | 1.64 | 3.58 | 2.70 | 1.24 | 0.21 | 0.12 | ||
| DataSet | GA | MA | MA | PACO | IG_RS | IG_RS | HLS(10) | HLS(30) | ||
|---|---|---|---|---|---|---|---|---|---|---|
| SDST10 | 20 × 5 | Ta001–Ta010 | 0.41 | 0.70 | 0.08 | 0.18 | 0.14 | 0.04 | 0.02 | 0.02 |
| 20 × 10 | Ta011–Ta020 | 0.56 | 0.36 | 0.13 | 0.22 | 0.24 | 0.04 | 0.05 | 0.05 | |
| 20 × 20 | Ta021–Ta030 | 0.39 | 0.56 | 0.10 | 0.12 | 0.19 | 0.04 | 0.03 | 0.02 | |
| 50 × 5 | Ta031–Ta040 | 0.92 | 0.77 | 0.30 | 0.42 | 0.84 | 0.27 | 0.09 | 0.04 | |
| 50 × 10 | Ta041–Ta050 | 2.01 | 1.26 | 0.81 | 1.06 | 1.43 | 0.53 | 0.50 | 0.44 | |
| 50 × 20 | Ta051–Ta060 | 2.10 | 1.28 | 0.82 | 1.01 | 1.54 | 0.60 | 0.44 | 0.36 | |
| 100 × 5 | Ta061–Ta070 | 1.03 | 0.63 | 0.31 | 0.76 | 1.34 | 0.33 | −0.02 | −0.04 | |
| 100 × 10 | Ta071–Ta080 | 1.33 | 0.90 | 0.48 | 0.77 | 1.32 | 0.38 | 0.12 | 0.05 | |
| 100 × 20 | Ta081–Ta090 | 1.83 | 1.06 | 0.82 | 1.12 | 1.47 | 0.54 | 0.16 | 0.16 | |
| 200 × 10 | Ta091–Ta100 | 1.32 | 0.65 | 0.48 | 0.85 | 1.33 | 0.32 | 0.06 | 0.06 | |
| 200 × 20 | Ta101–Ta110 | 1.71 | 0.87 | 0.76 | 0.95 | 1.12 | 0.38 | 0.35 | 0.29 | |
| 500 × 20 | Ta111–Ta120 | 1.27 | 0.48 | 0.43 | 0.61 | 0.82 | 0.21 | 0.43 | 0.40 | |
| SD | 0.60 | 0.29 | 0.29 | 0.36 | 0.53 | 0.20 | 0.19 | 0.17 | ||
| ARPD | 1.24 | 0.79 | 0.46 | 0.67 | 0.98 | 0.31 | 0.19 | 0.15 | ||
| SDST50 | 20 × 5 | Ta001–Ta010 | 1.15 | 1.50 | 0.30 | 0.51 | 0.58 | 0.10 | 0.04 | 0.02 |
| 20 × 10 | Ta011–Ta020 | 1.17 | 0.77 | 0.32 | 0.44 | 0.58 | 0.19 | 0.05 | 0.03 | |
| 20 × 20 | Ta021–Ta030 | 0.49 | 0.78 | 0.16 | 0.25 | 0.37 | 0.07 | 0.04 | 0.03 | |
| 50 × 5 | Ta031–Ta040 | 3.43 | 2.18 | 1.13 | 1.98 | 2.42 | 1.04 | 0.29 | 0.22 | |
| 50 × 10 | Ta041–Ta050 | 3.01 | 1.68 | 1.08 | 1.62 | 2.12 | 0.92 | 0.14 | 0.07 | |
| 50 × 20 | Ta051–Ta060 | 2.43 | 1.69 | 0.89 | 1.28 | 2.03 | 0.82 | 0.17 | 0.07 | |
| 100 × 5 | Ta061–Ta070 | 3.98 | 2.34 | 1.38 | 3.95 | 2.33 | 1.09 | 0.03 | 0.00 | |
| 100 × 10 | Ta071–Ta080 | 3.07 | 1.52 | 1.21 | 3.10 | 2.13 | 0.88 | −0.10 | −0.25 | |
| 100 × 20 | Ta081–Ta090 | 2.51 | 1.54 | 1.03 | 2.45 | 1.82 | 0.81 | −0.34 | −0.42 | |
| 200 × 10 | Ta091–Ta100 | 3.49 | 1.35 | 1.21 | 3.37 | 1.90 | 0.63 | −0.39 | −0.40 | |
| 200 × 20 | Ta101–Ta110 | 2.67 | 1.19 | 1.02 | 2.64 | 1.51 | 0.53 | −0.20 | −0.12 | |
| 500 × 20 | Ta111–Ta120 | 2.07 | 0.76 | 0.79 | 2.00 | 1.28 | 0.31 | 0.51 | 0.65 | |
| SD | 1.06 | 0.51 | 0.40 | 1.20 | 0.73 | 0.37 | 0.25 | 0.29 | ||
| ARPD | 2.46 | 1.44 | 0.88 | 1.97 | 1.59 | 0.62 | 0.02 | −0.01 | ||
| DataSet | GA | MA | MA | PACO | IG_RS | IG_RS | HLS(10) | HLS(30) | ||
|---|---|---|---|---|---|---|---|---|---|---|
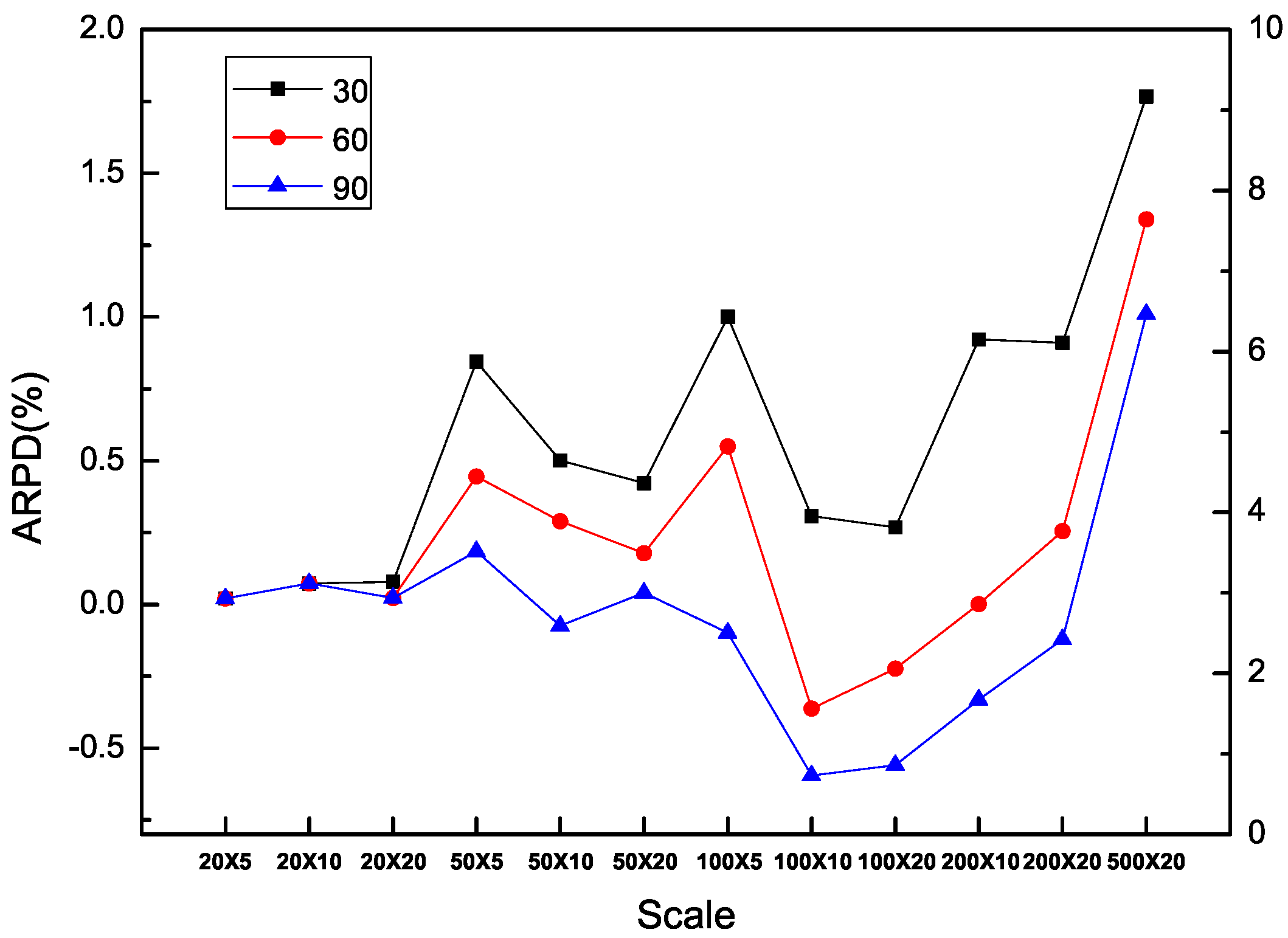
| SDST100 | 20 × 5 | Ta001–Ta010 | 1.82 | 1.43 | 0.39 | 0.61 | 1.24 | 0.17 | 0.02 | 0.02 |
| 20 × 10 | Ta011–Ta020 | 1.27 | 1.09 | 0.29 | 0.48 | 1.03 | 0.18 | 0.07 | 0.07 | |
| 20 × 20 | Ta021–Ta030 | 0.94 | 1.14 | 0.17 | 0.48 | 0.74 | 0.17 | 0.02 | 0.02 | |
| 50 × 5 | Ta031–Ta040 | 5.26 | 3.02 | 1.99 | 3.31 | 3.70 | 1.82 | 0.18 | 0.09 | |
| 50 × 10 | Ta041–Ta050 | 4.18 | 2.55 | 1.50 | 2.49 | 2.99 | 1.30 | −0.07 | −0.14 | |
| 50 × 20 | Ta051–Ta060 | 3.11 | 1.77 | 1.18 | 1.98 | 2.40 | 1.11 | 0.04 | −0.06 | |
| 100 × 5 | Ta061–Ta070 | 6.00 | 3.04 | 2.16 | 6.65 | 3.48 | 1.63 | −0.10 | −0.2 | |
| 100 × 10 | Ta071–Ta080 | 4.15 | 2.45 | 1.61 | 4.89 | 2.77 | 1.02 | −0.60 | −0.68 | |
| 100 × 20 | Ta081–Ta090 | 3.49 | 2.39 | 1.53 | 3.91 | 2.46 | 1.05 | −0.56 | −0.61 | |
| 200 × 10 | Ta091–Ta100 | 4.71 | 2.19 | 1.77 | 5.53 | 2.49 | 0.92 | −0.33 | −0.5 | |
| 200 × 20 | Ta101–Ta110 | 3.48 | 1.68 | 1.40 | 3.82 | 1.92 | 0.76 | −0.12 | −0.39 | |
| 500 × 20 | Ta111–Ta120 | 2.64 | 1.16 | 1.14 | 2.75 | 1.50 | 0.46 | 1.01 | 0.61 | |
| SD | 1.56 | 0.71 | 0.66 | 2.01 | 0.95 | 0.56 | 0.41 | 0.36 | ||
| Average | 3.42 | 1.99 | 1.26 | 3.07 | 2.23 | 0.88 | −0.04 | −0.15 | ||
| SDST125 | 20 × 5 | Ta001–Ta010 | 1.90 | 1.40 | 0.32 | 0.65 | 1.24 | 0.30 | 0.02 | 0.02 |
| 20 × 10 | Ta011–Ta020 | 1.52 | 1.24 | 0.37 | 0.56 | 1.44 | 0.36 | 0.05 | 0.03 | |
| 20 × 20 | Ta021–Ta030 | 0.95 | 1.21 | 0.24 | 0.39 | 0.81 | 0.19 | 0.02 | 0.02 | |
| 50 × 5 | Ta031–Ta040 | 5.63 | 3.48 | 1.97 | 3.67 | 4.00 | 2.01 | −0.02 | 0.04 | |
| 50 × 10 | Ta041–Ta050 | 4.59 | 3.35 | 1.50 | 2.96 | 3.47 | 1.54 | −0.35 | −0.34 | |
| 50 × 20 | Ta051–Ta060 | 3.25 | 1.63 | 1.26 | 2.06 | 2.59 | 1.18 | −0.15 | -0.16 | |
| 100 × 5 | Ta061–Ta070 | 6.82 | 3.65 | 2.52 | 7.75 | 4.14 | 1.91 | −0.78 | −0.28 | |
| 100 × 10 | Ta071–Ta080 | 4.80 | 2.84 | 1.94 | 5.61 | 3.26 | 1.34 | −1.16 | −0.85 | |
| 100 × 20 | Ta081–Ta090 | 3.50 | 2.16 | 1.50 | 4.15 | 2.60 | 1.00 | −1.27 | −1.05 | |
| 200 × 10 | Ta091–Ta100 | 5.37 | 2.63 | 2.14 | 6.20 | 2.94 | 1.17 | −1.42 | −0.84 | |
| 200 × 20 | Ta101–Ta110 | 3.69 | 1.69 | 1.49 | 4.16 | 2.24 | 0.76 | −0.84 | −0.55 | |
| 500 × 20 | Ta111–Ta120 | 2.83 | 1.36 | 1.23 | 3.02 | 1.64 | 0.52 | 1.37 | 1.15 | |
| SD | 1.78 | 0.93 | 0.74 | 2.33 | 1.09 | 0.61 | 0.78 | 0.58 | ||
| Average | 3.74 | 2.22 | 1.37 | 3.43 | 2.53 | 1.02 | −0.38 | −0.23 | ||
| Scale | Instances | NewBound | Best-Known_Bound | Difference |
|---|---|---|---|---|
| 50 × 5 | SDST10 | |||
| Ta031 | 2813 | 2814 | −1 | |
| Ta039 | 2671 | 2673 | −2 | |
| SDST100 | ||||
| Ta034 | 4019 | 4020 | −1 | |
| Ta037 | 3995 | 3999 | −4 | |
| Ta038 | 3939 | 3966 | −27 | |
| SDST125 | ||||
| Ta031 | 4212 | 4226 | −14 | |
| Ta034 | 4348 | 4356 | −8 | |
| Ta035 | 4340 | 4342 | −2 | |
| Ta039 | 4117 | 4145 | −28 | |
| Scale | Instances | NewBound | Best-Known_Bound | Difference |
|---|---|---|---|---|
| 50 × 10 | SDST50 | |||
| Ta045 | 3932 | 3939 | −7 | |
| Ta048 | 3942 | 3950 | −8 | |
| Ta050 | 3981 | 3983 | −2 | |
| SDST100 | ||||
| Ta041 | 4796 | 4812 | −16 | |
| Ta044 | 4813 | 4830 | −17 | |
| Ta045 | 4787 | 4812 | −25 | |
| Ta046 | 4809 | 4816 | −7 | |
| Ta047 | 4889 | 4898 | −9 | |
| Ta048 | 4839 | 4849 | −10 | |
| SDST125 | ||||
| Ta041 | 5215 | 5275 | −60 | |
| Ta042 | 5145 | 5177 | −32 | |
| Ta043 | 5164 | 5193 | −29 | |
| Ta044 | 5269 | 5286 | −17 | |
| Ta047 | 5309 | 5340 | −31 | |
| Ta048 | 5315 | 5317 | −2 | |
| Ta049 | 5173 | 5194 | −21 | |
| Ta050 | 5325 | 5334 | −9 | |
| Scale | Instances | NewBound | Best-Known_Bound | Difference |
|---|---|---|---|---|
| 100 × 5 | SDST10 | |||
| Ta061 | 5645 | 5647 | −2 | |
| Ta062 | 5463 | 5465 | −2 | |
| Ta063 | 5405 | 5406 | −1 | |
| Ta064 | 5208 | 5213 | −5 | |
| Ta065 | 5463 | 5466 | −3 | |
| Ta069 | 5636 | 5641 | −5 | |
| Ta070 | 5536 | 5537 | −1 | |
| SDST50 | ||||
| Ta061 | 6525 | 6542 | −17 | |
| Ta064 | 6175 | 6182 | −7 | |
| Ta066 | 6248 | 6270 | −22 | |
| Ta067 | 6385 | 6390 | −5 | |
| Ta069 | 6556 | 6576 | −20 | |
| SDST100 | ||||
| Ta061 | 7697 | 7714 | −17 | |
| Ta062 | 7591 | 7610 | −19 | |
| Ta063 | 7497 | 7539 | −42 | |
| Ta070 | 7664 | 7735 | −71 | |
| SDST125 | ||||
| Ta061 | 8246 | 8339 | −93 | |
| Ta062 | 8121 | 8230 | −109 | |
| Ta063 | 8085 | 8168 | −83 | |
| Ta064 | 7995 | 8005 | −10 | |
| Ta065 | 8197 | 8231 | −34 | |
| Ta066 | 8009 | 8082 | −73 | |
| Ta067 | 8188 | 8267 | −79 | |
| Ta068 | 7959 | 7993 | −34 | |
| Ta069 | 8324 | 8393 | −69 | |
| Ta070 | 8232 | 8290 | −58 | |
| Scale | Instances | NewBound | Best-Known_Bound | Difference |
|---|---|---|---|---|
| 100 × 10 | SDST10 | |||
| Ta072 | 5675 | 5683 | −8 | |
| Ta076 | 5606 | 5607 | −1 | |
| SDST50 | ||||
| Ta071 | 7442 | 7450 | −8 | |
| Ta072 | 7011 | 7033 | −22 | |
| Ta073 | 7254 | 7262 | −8 | |
| Ta074 | 7518 | 7549 | −31 | |
| Ta075 | 7232 | 7240 | −8 | |
| Ta076 | 6955 | 6964 | −9 | |
| Ta078 | 7273 | 7290 | −17 | |
| Ta079 | 7443 | 7452 | −9 | |
| SDST100 | ||||
| Ta071 | 9138 | 9201 | −63 | |
| Ta072 | 8758 | 8794 | −36 | |
| Ta073 | 8937 | 9004 | −67 | |
| Ta074 | 9186 | 9276 | −90 | |
| Ta075 | 8954 | 9002 | −48 | |
| Ta076 | 8671 | 8689 | −18 | |
| Ta077 | 8811 | 8858 | −47 | |
| Ta078 | 8948 | 9028 | −80 | |
| Ta079 | 9082 | 9133 | −51 | |
| Ta080 | 9075 | 9114 | −39 | |
| SDST125 | ||||
| Ta071 | 9930 | 10070 | −140 | |
| Ta072 | 9511 | 9631 | −120 | |
| Ta073 | 9772 | 9808 | −36 | |
| Ta074 | 10040 | 10168 | −128 | |
| Ta075 | 9770 | 9852 | −82 | |
| Ta076 | 9426 | 9529 | −103 | |
| Ta077 | 9580 | 9696 | −116 | |
| Ta078 | 9737 | 9891 | −154 | |
| Ta079 | 9885 | 10004 | −119 | |
| Ta080 | 9864 | 10013 | −149 | |
| Scale | Instances | NewBound | Best-Known_Bound | Difference |
|---|---|---|---|---|
| 100 × 20 | SDST50 | |||
| Ta081 | 8415 | 8437 | −22 | |
| Ta082 | 8364 | 8387 | −23 | |
| Ta084 | 8303 | 8389 | −86 | |
| Ta085 | 8431 | 8471 | −40 | |
| Ta086 | 8520 | 8548 | −28 | |
| Ta087 | 8457 | 8482 | −25 | |
| Ta088 | 8622 | 8662 | −40 | |
| Ta089 | 8464 | 8473 | −9 | |
| Ta090 | 8505 | 8519 | −14 | |
| SDST100 | ||||
| Ta081 | 10513 | 10578 | −65 | |
| Ta082 | 10492 | 10535 | −43 | |
| Ta083 | 10528 | 10552 | −24 | |
| Ta084 | 10451 | 10479 | −28 | |
| Ta085 | 10499 | 10539 | −40 | |
| Ta086 | 10600 | 10679 | −79 | |
| Ta087 | 10580 | 10645 | −65 | |
| Ta088 | 10694 | 10794 | −100 | |
| Ta089 | 10508 | 10612 | −104 | |
| Ta090 | 10605 | 10651 | −46 | |
| SDST125 | ||||
| Ta081 | 11572 | 11694 | −122 | |
| Ta082 | 11539 | 11679 | −140 | |
| Ta083 | 11566 | 11701 | −135 | |
| Ta084 | 11450 | 11634 | −184 | |
| Ta085 | 11489 | 11675 | −186 | |
| Ta086 | 11631 | 11740 | −109 | |
| Ta087 | 11630 | 11784 | −154 | |
| Ta088 | 11713 | 11883 | −170 | |
| Ta089 | 11581 | 11731 | −150 | |
| Ta090 | 11617 | 11753 | −136 | |
| Scale | Instances | NewBound | Best-Known_Bound | Difference |
|---|---|---|---|---|
| 200 × 10 | SDST10 | |||
| Ta095 | 11195 | 11207 | −12 | |
| Ta100 | 11276 | 11284 | −8 | |
| SDST50 | ||||
| Ta091 | 13908 | 14005 | −97 | |
| Ta092 | 13769 | 13902 | −133 | |
| Ta093 | 13972 | 14087 | −115 | |
| Ta094 | 13795 | 13873 | −78 | |
| Ta096 | 13625 | 13653 | −28 | |
| Ta097 | 14083 | 14115 | −32 | |
| Ta098 | 13988 | 14018 | −30 | |
| Ta099 | 13811 | 13857 | −46 | |
| Ta100 | 13885 | 13894 | −9 | |
| SDST100 | ||||
| Ta091 | 17199 | 17307 | −108 | |
| Ta092 | 17132 | 17210 | −78 | |
| Ta093 | 17354 | 17386 | −32 | |
| Ta094 | 17167 | 17206 | −39 | |
| Ta095 | 17185 | 17244 | −59 | |
| Ta096 | 16995 | 17022 | −27 | |
| Ta098 | 17298 | 17407 | −109 | |
| Ta099 | 17129 | 17194 | −65 | |
| Ta100 | 17195 | 17263 | −68 | |
| SDST125 | ||||
| Ta091 | 18589 | 18930 | −341 | |
| Ta092 | 18584 | 18876 | −292 | |
| Ta093 | 18747 | 19059 | −312 | |
| Ta094 | 18610 | 18934 | −324 | |
| Ta095 | 18608 | 18906 | −298 | |
| Ta096 | 18451 | 18659 | −208 | |
| Ta097 | 18857 | 19118 | −261 | |
| Ta098 | 18819 | 19058 | −239 | |
| Ta099 | 18576 | 18819 | −243 | |
| Ta100 | 18615 | 18793 | −178 | |
| Scale | Instances | NewBound | Best-Known_Bound | Difference |
|---|---|---|---|---|
| 200 × 20 | SDST50 | |||
| Ta102 | 15627 | 15644 | −17 | |
| Ta103 | 15585 | 15689 | −104 | |
| Ta104 | 15619 | 15627 | −8 | |
| Ta105 | 15435 | 15470 | −35 | |
| Ta106 | 15480 | 15514 | −34 | |
| Ta107 | 15640 | 15669 | −29 | |
| Ta108 | 15627 | 15645 | −18 | |
| Ta109 | 15538 | 15544 | −6 | |
| Ta110 | 15632 | 15694 | −62 | |
| SDST100 | ||||
| Ta101 | 19599 | 19618 | −19 | |
| Ta102 | 19787 | 19816 | −29 | |
| Ta103 | 19830 | 19881 | −51 | |
| Ta104 | 19714 | 19810 | −96 | |
| Ta107 | 19814 | 19888 | −74 | |
| Ta108 | 19797 | 19826 | −29 | |
| Ta109 | 19666 | 19757 | −91 | |
| SDST125 | ||||
| Ta101 | 21513 | 21765 | −252 | |
| Ta102 | 21714 | 21973 | −259 | |
| Ta103 | 21844 | 21975 | −131 | |
| Ta104 | 21810 | 21984 | −174 | |
| Ta105 | 21568 | 21773 | −205 | |
| Ta106 | 21625 | 21829 | −204 | |
| Ta107 | 21789 | 22055 | −266 | |
| Ta108 | 21814 | 21902 | −88 | |
| Ta109 | 21684 | 21821 | −137 | |
| Ta110 | 21854 | 21975 | −121 | |
| Scale | Instances | ||
|---|---|---|---|
| 50 × 5 | SDST10 | Permutation of Jobs | Makespan |
| Ta031 | 30 16 40 0 39 49 25 5 17 29 31 12 35 9 28 7 45 19 33 44 38 10 20 24 4 | 2813 | |
| 37 23 36 13 3 6 14 21 8 1 42 26 43 27 46 15 41 48 22 47 32 18 11 2 34 | |||
| Ta039 | 45 43 23 48 14 40 0 12 32 29 46 49 41 9 6 19 10 31 20 44 24 3 21 22 37 | 2671 | |
| 35 4 33 39 28 17 2 47 5 34 15 8 42 18 1 25 30 36 38 27 26 16 7 11 13 | |||
| SDST100 | Permutation of Jobs | ||
| Ta034 | 25 49 12 21 23 43 16 47 9 11 0 2 29 8 45 27 31 13 26 34 19 41 35 14 7 | 4019 | |
| 30 4 48 46 15 44 6 32 1 17 24 3 40 39 36 10 42 28 38 22 37 18 33 5 20 | |||
| Ta037 | 36 48 4 21 18 29 20 14 17 44 26 32 38 46 8 30 42 35 34 13 31 9 39 47 | 3995 | |
| 45 10 24 3 19 40 1 43 23 2 28 12 49 7 16 6 41 25 0 5 33 11 22 27 37 15 | |||
| Ta038 | 33 38 13 17 4 1 24 15 9 25 7 16 19 45 34 46 14 35 29 8 39 21 27 0 26 23 | 3939 | |
| 48 37 30 49 36 6 18 20 42 40 5 22 32 44 2 43 11 28 47 31 12 10 41 3 | |||
| DataSet | SDST10 | SDST50 | SDST100 | SDST125 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| EMBO | AHA | HLS | EMBO | AHA | HLS | EMBO | AHA | HLS | EMBO | AHA | HLS | |
| 20 × 5 | 0.67 | 0.34 | 0.04 | 1.88 | 0.51 | 0.09 | 3.71 | 0.62 | 0.02 | 3.05 | 1.01 | 0.02 |
| 20 × 10 | 1.10 | 0.46 | 0.06 | 1.87 | 0.92 | 0.03 | 2.64 | 0.99 | 0.07 | 3.63 | 1.29 | 0.04 |
| 20 × 20 | 1.09 | 0.71 | 0.02 | 1.46 | 1.04 | 0.05 | 2.17 | 1.23 | 0.05 | 2.12 | 1.38 | 0.04 |
| 50 × 5 | 1.83 | 0.92 | 0.12 | 5.88 | 0.99 | 0.48 | 9.27 | 1.05 | 0.73 | 10.73 | 1.32 | 0.80 |
| 50 × 10 | 3.50 | 1.30 | 0.57 | 5.92 | 1.20 | 0.40 | 7.54 | 1.82 | 0.44 | 8.91 | 2.04 | 0.22 |
| 50 × 20 | 3.93 | 1.48 | 0.49 | 5.05 | 1.78 | 0.32 | 5.82 | 1.92 | 0.40 | 6.31 | 2.41 | 0.21 |
| 100 × 5 | 2.15 | 0.78 | 0.12 | 7.35 | 1.58 | 0.63 | 10.36 | 1.75 | 0.88 | 11.96 | 2.00 | 1.00 |
| 100 × 10 | 2.91 | 1.23 | 0.25 | 5.75 | 2.56 | 0.22 | 7.83 | 2.56 | 0.13 | 9.47 | 2.29 | 0.34 |
| 100 × 20 | 3.48 | 1.74 | 0.46 | 5.28 | 2.54 | 0.12 | 6.87 | 2.29 | 0.17 | 6.60 | 2.66 | −0.07 |
| 200 × 10 | 2.24 | 0.94 | 0.30 | 5.22 | 1.32 | 0.54 | 7.26 | 1.55 | 0.71 | 8.08 | 2.11 | 0.98 |
| 200 × 20 | 3.03 | 1.35 | 0.59 | 3.74 | 1.75 | 0.65 | 5.18 | 1.81 | 0.57 | 5.55 | 1.98 | 0.77 |
| 500 × 20 | 1.63 | 1.17 | 0.69 | 2.48 | 1.43 | 1.28 | 3.37 | 1.50 | 1.45 | 3.66 | 1.73 | 1.92 |
| ARPD | 2.30 | 1.04 | 0.31 | 4.32 | 1.47 | 0.40 | 6.00 | 1.59 | 0.47 | 6.67 | 1.85 | 0.52 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Li, X.; Ma, Z. A Hybrid Local Search Algorithm for the Sequence Dependent Setup Times Flowshop Scheduling Problem with Makespan Criterion. Sustainability 2017, 9, 2318. https://doi.org/10.3390/su9122318
Wang Y, Li X, Ma Z. A Hybrid Local Search Algorithm for the Sequence Dependent Setup Times Flowshop Scheduling Problem with Makespan Criterion. Sustainability. 2017; 9(12):2318. https://doi.org/10.3390/su9122318
Chicago/Turabian StyleWang, Yunhe, Xiangtao Li, and Zhiqiang Ma. 2017. "A Hybrid Local Search Algorithm for the Sequence Dependent Setup Times Flowshop Scheduling Problem with Makespan Criterion" Sustainability 9, no. 12: 2318. https://doi.org/10.3390/su9122318





