Dual-Recycling Channel Decision in a Closed-Loop Supply Chain with Cost Disruptions
Abstract
:1. Introduction
- (1)
- What are the equilibrium strategies of dual-channel CLSC when facing cost disruptions of new and remanufactured products?
- (2)
- Which is the optimal recycling channel with respect to different disruption cases?
- (3)
- How does consumers’ preference to online-recycling channel affect the manufacturer’s production and collection strategies?
2. Literature Review
3. Model Assumptions and Notation
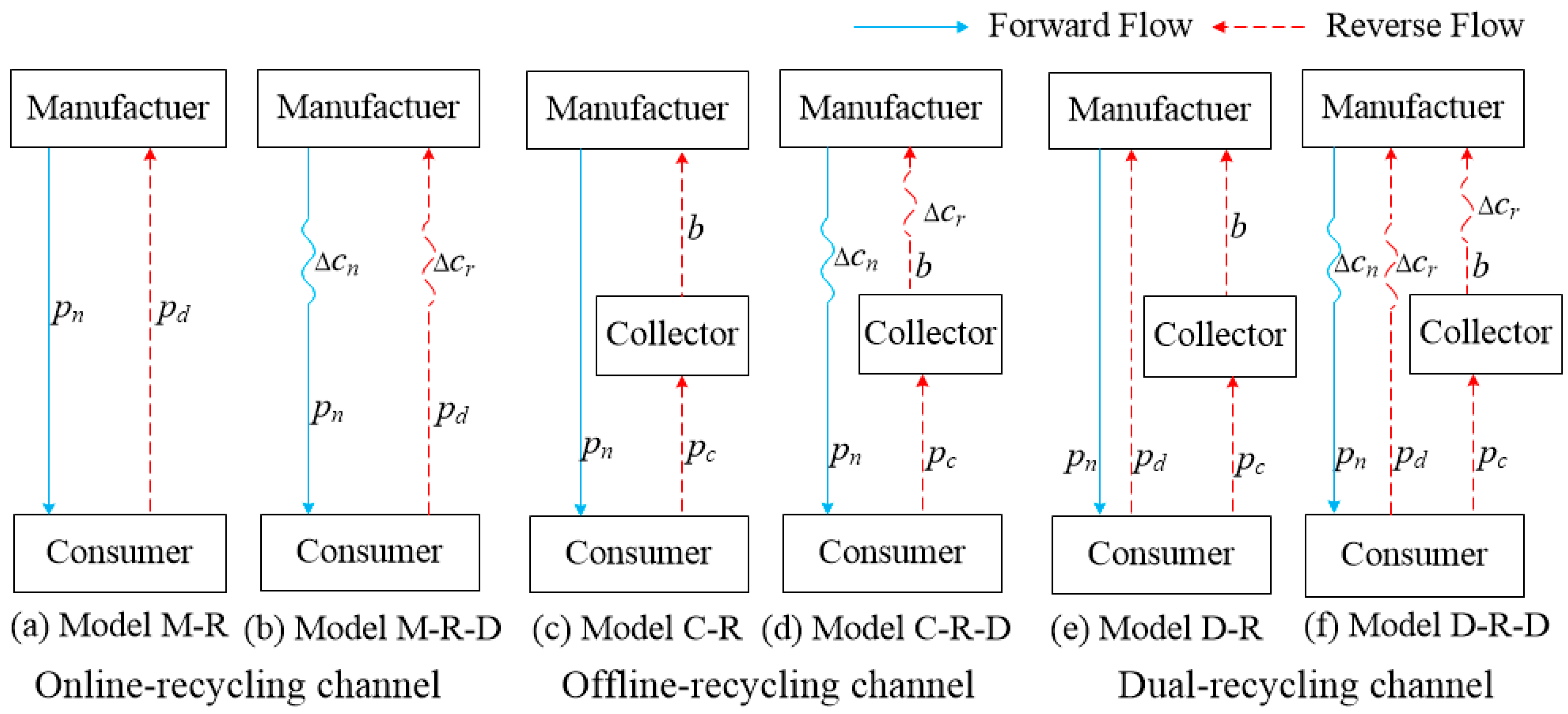
4. Models
4.1. Single Online-Recycling Channel
4.2. Single Offline-Recycling Channel
- (1)
- The manufacturer’s profit is joint concave in the selling price () and the transfer price ().
- (2)
- The collector’s profit is concave in the acquisition price ().
4.3. Dual-Recycling Channel
- (1)
- The manufacturer’s profit function is joint concave in the selling price , the transfer price and the acquisition price
- (2)
- The collector’s profit function is concave in the acquisition price .
5. The Analysis of Closed-Loop Supply Chain Models
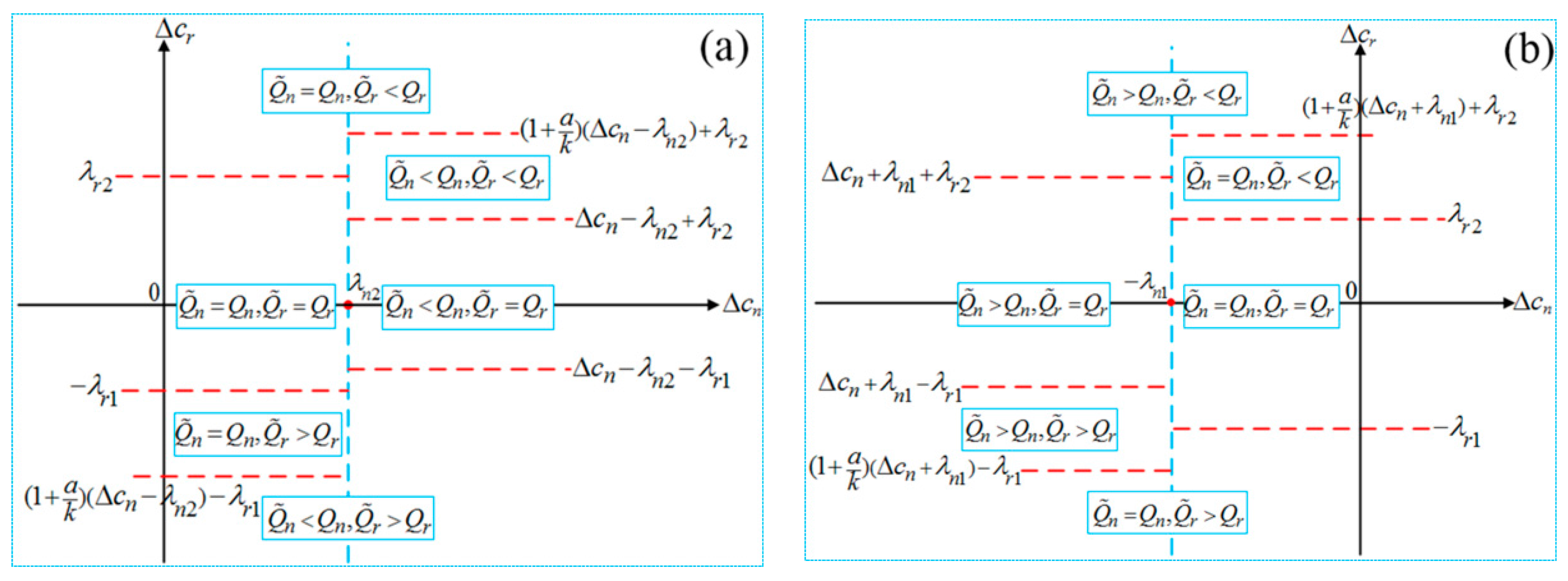
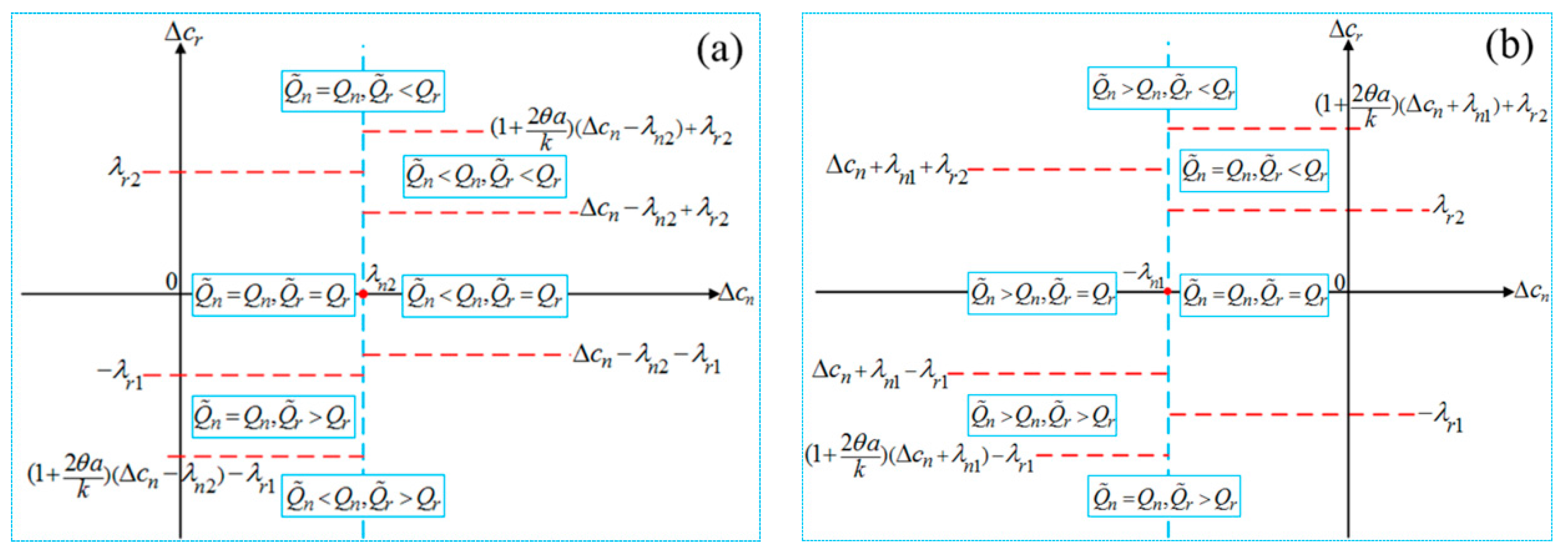
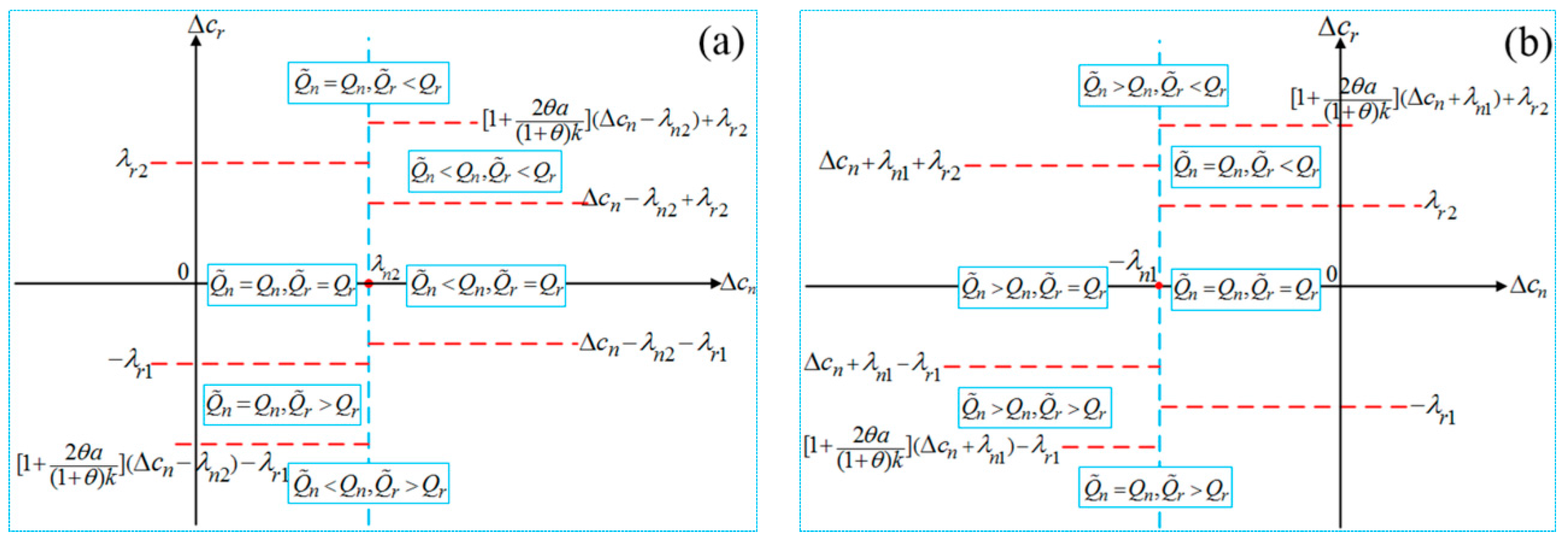
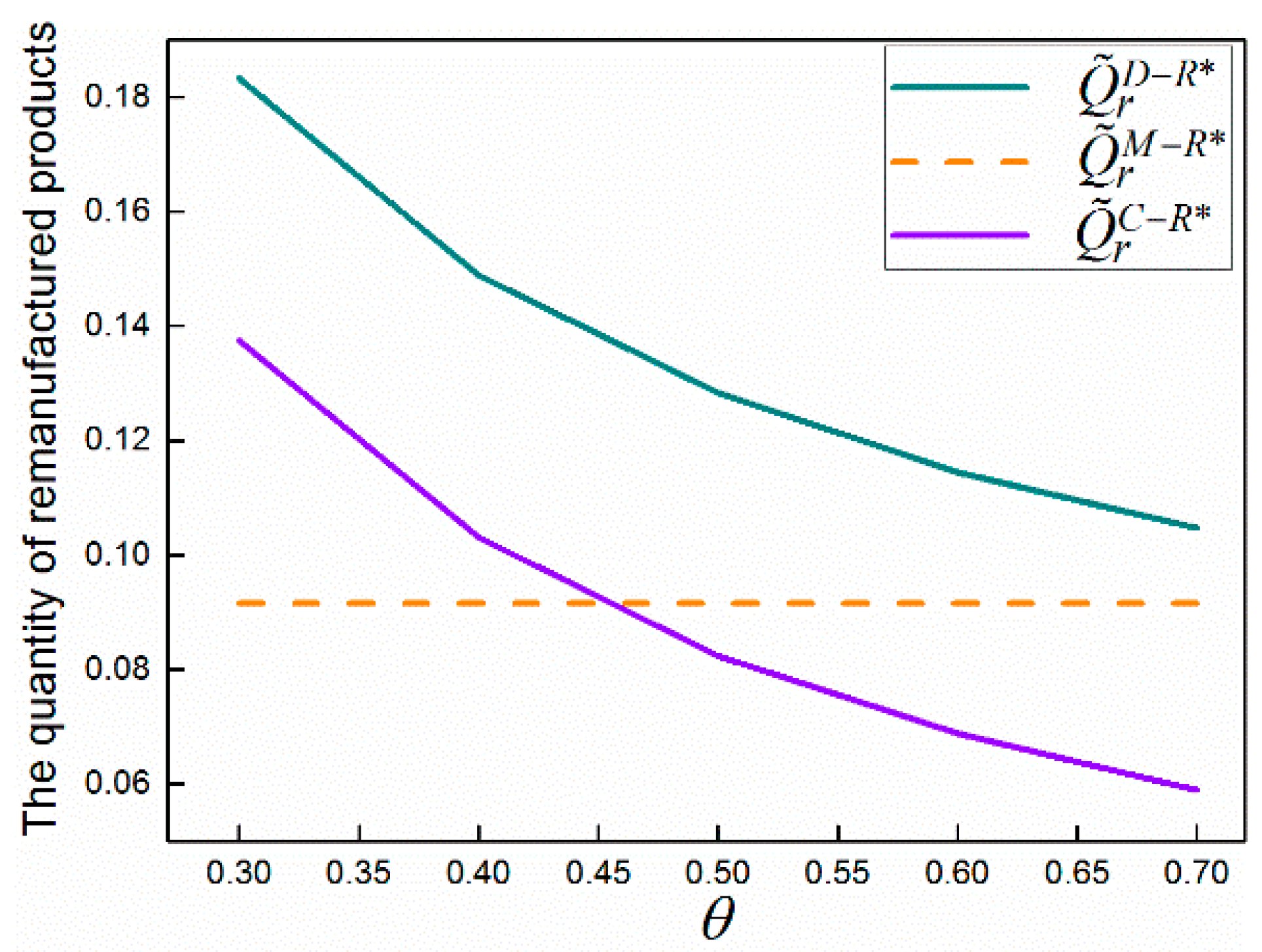
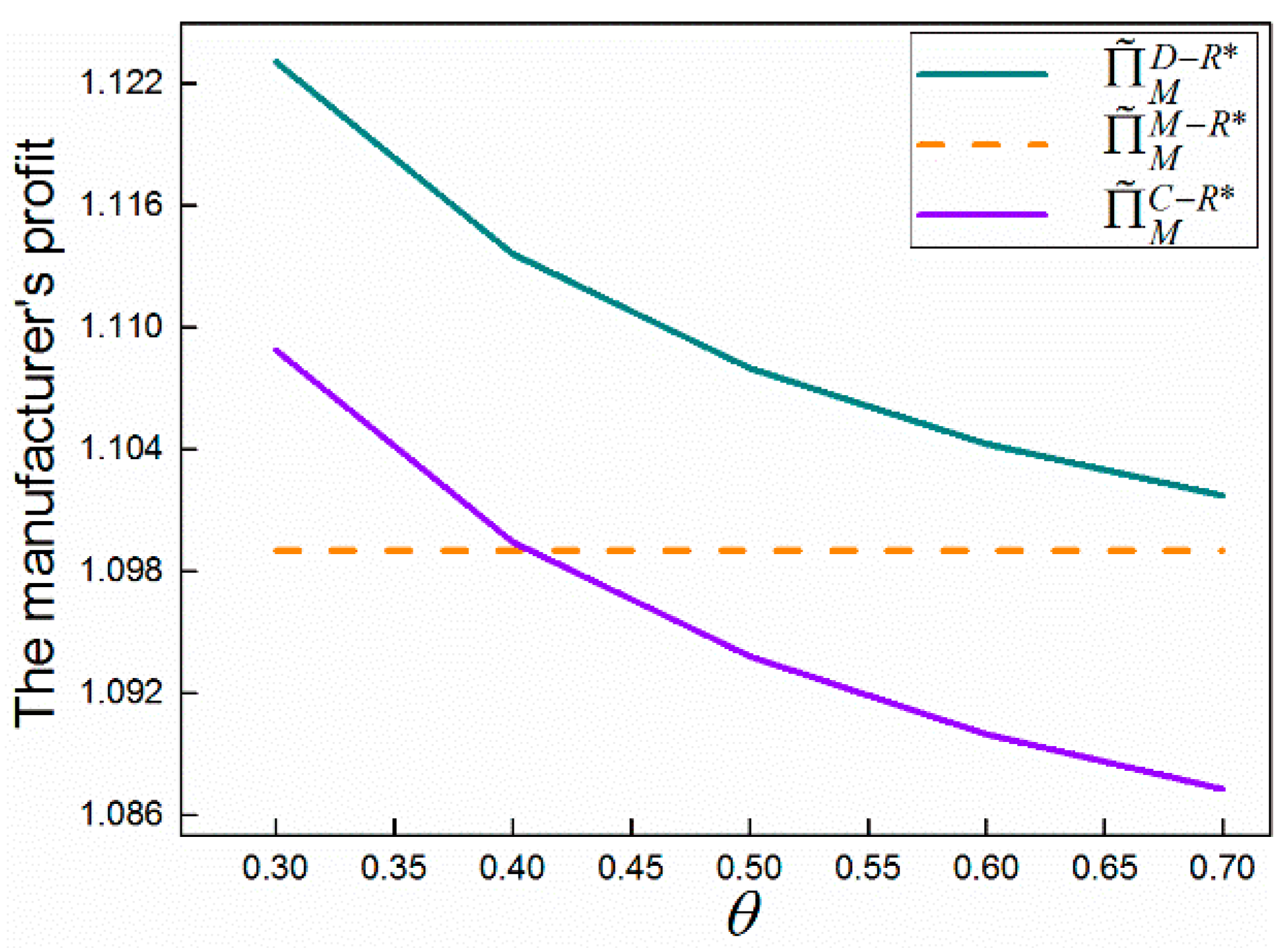
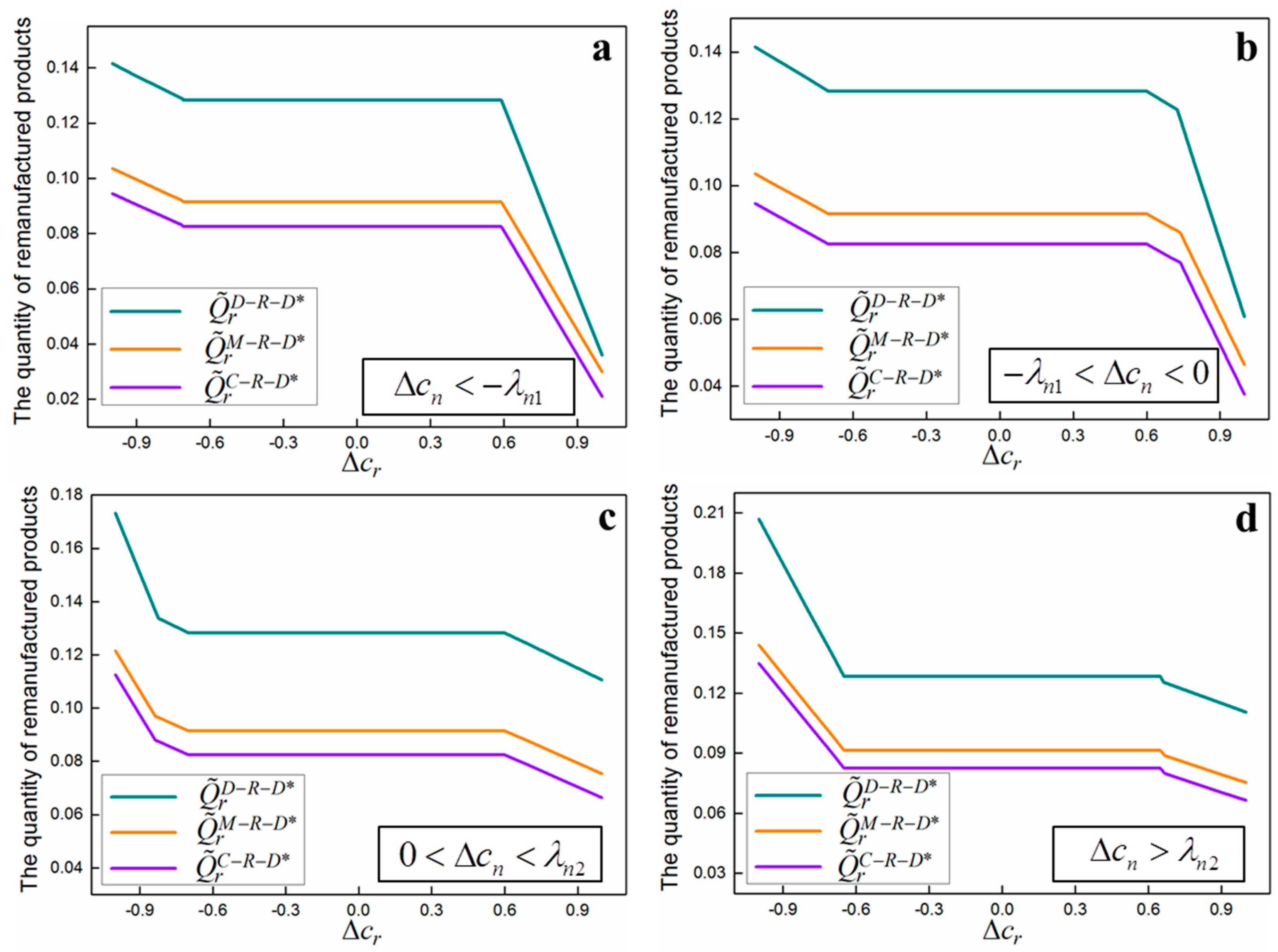
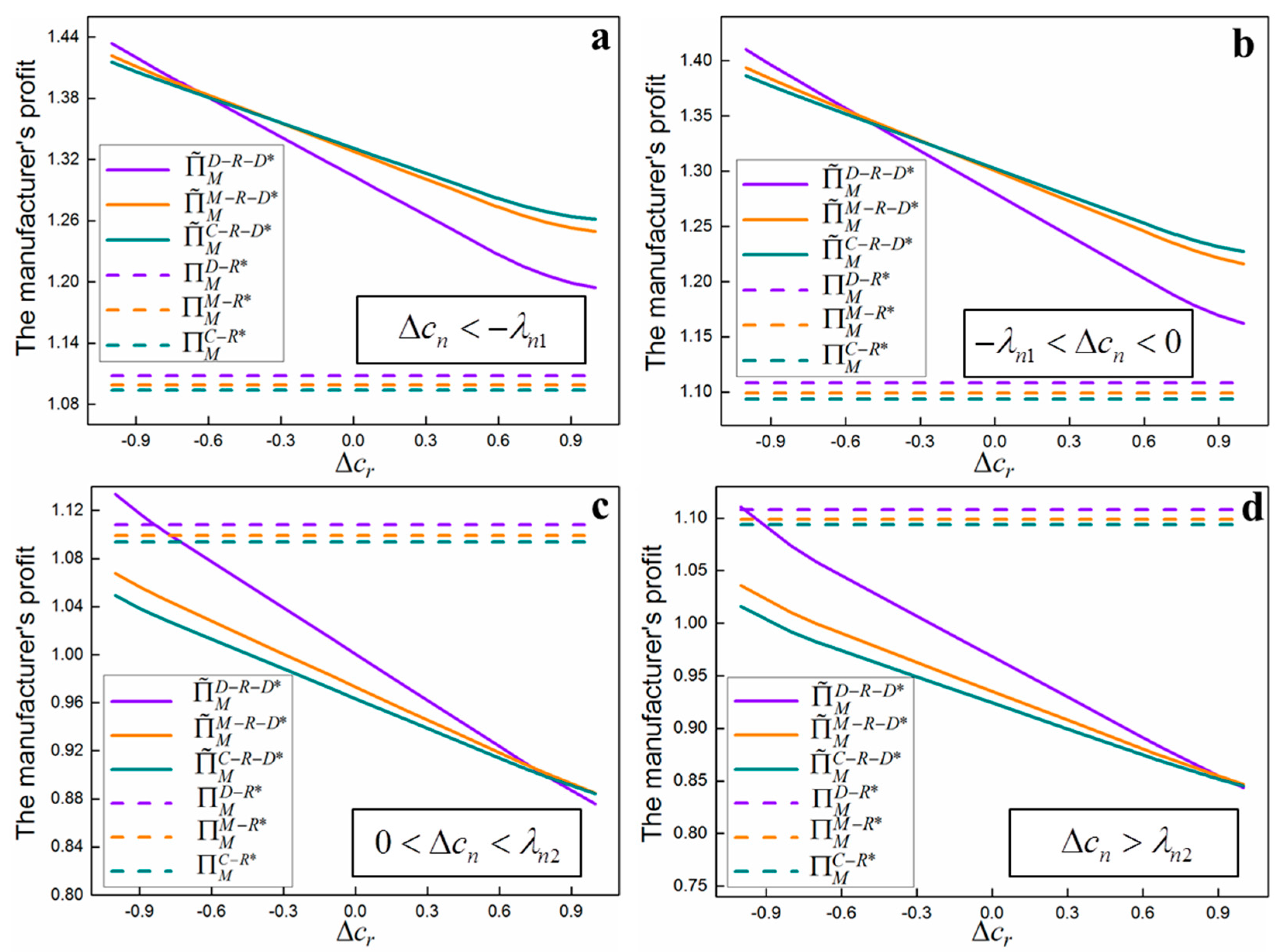
5.1. The Effect of Disruption
5.2. The Comparisons of Single-Recycling and Dual-Recycling Channels
- (1)
- In case 4, the optimal selling price and market demand satisfy the relations as follows:
- (i)
- , ; and , .
- (ii)
- If holds, then , ; else if holds, then , ; Specifically, if holds, then , .
- (2)
- In case 6, the optimal selling price and market demand satisfy the relations:
- (i)
- , ; and , .
- (ii)
- If holds, then , ; else if holds, then , ; Specifically, if holds, then , .
- (3)
- In other cases, the optimal selling price and market demand are the same:
- (1)
- In case 4, , .
- (2)
- In case 6, , .
- (3)
- In other cases, , .
6. Numerical Examples
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
| — — | , |
|---|---|
| case 1, 2 and 3 | |
| case 4 | |
| case 5 | |
| case 6 | |
| case 7, 8 and 9 |
| — — | , |
|---|---|
| case 1 | |
| case 2, 5 and 8 | , |
| case 3 | |
| case 4 | |
| case 6 | |
| case 7 | |
| case 9 |
| Case | |
|---|---|
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 |
| — — | , |
|---|---|
| case 1, 2 and 3 | |
| case 4 | |
| case 5 | |
| case 6 | |
| case 7, 8 and 9 |
| — — | , , , |
|---|---|
| case 1 | |
| case 2, 5 and 8 | |
| case 3 | . |
| case 4 | |
| case 6 | |
| case 7 | |
| case 9 | |
| Case | |
|---|---|
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 |
| — — | , |
|---|---|
| case 1, 2 and 3 | |
| case 4 | |
| case 5 | |
| case 6 | |
| case 7, 8 and 9 |
| Case | , , , , |
|---|---|
| 1 | |
| 2, 5, 8 | |
| 3 | |
| 4 | |
| 6 | |
| 7 | |
| 9 | |
| Case | |
|---|---|
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 |
References
- Gaur, J.; Amini, M.; Rao, A.K. Closed-loop supply chain configuration for new and reconditioned products: An integrated optimization model. Omega 2017, 66, 212–223. [Google Scholar] [CrossRef]
- Atasu, A.; Souza, G.C. How Does Product Recovery Affect Quality Choice? Prod. Oper. Manag. 2013, 22, 991–1010. [Google Scholar] [CrossRef]
- Polotski, V.; Kenne, J.-P.; Gharbi, A. Production and setup policy optimization for hybrid manufacturing–remanufacturing systems. Int. J. Prod. Econ. 2017, 183, 322–333. [Google Scholar] [CrossRef]
- Esenduran, G.; Kemahlıoğlu-Ziya, E.; Swaminathan, J.M. Impact of Take-Back Regulation on the Remanufacturing Industry. Prod. Oper. Manag. 2017, 26, 924–944. [Google Scholar] [CrossRef]
- Ferrer, G.; Swaminathan, J.M. Managing New and Remanufactured Products. Manag. Sci. 2006, 52, 15–26. [Google Scholar] [CrossRef] [Green Version]
- Kumar, A.; Chinnam, R.B.; Murat, A. Hazard rate models for core return modeling in auto parts remanufacturing. Int. J. Prod. Econ. 2017, 183, 354–361. [Google Scholar] [CrossRef]
- Guide Jr, V.D.R.; Van Wassenhove, L.N. OR FORUM-the evolution of closed-loop supply chain research. Oper. Res. 2009, 57, 10–18. [Google Scholar] [CrossRef]
- Jia, J.; Xu, S.H.; Guide, V.D.R. Addressing Supply-Demand Imbalance: Designing Efficient Remanufacturing Strategies. Prod. Oper. Manag. 2016, 25, 1958–1967. [Google Scholar] [CrossRef]
- Subramanian, R.; Ferguson, M.E.; Beril Toktay, L. Remanufacturing and the Component Commonality Decision. Prod. Oper. Manag. 2013, 22, 36–53. [Google Scholar] [CrossRef]
- Zhou, L.; Naim, M.M.; Disney, S.M. The impact of product returns and remanufacturing uncertainties on the dynamic performance of a multi-echelon closed-loop supply chain. Int. J. Prod. Econ. 2017, 183, 487–502. [Google Scholar] [CrossRef]
- Feng, L.; Govindan, K.; Li, C. Strategic planning: Design and coordination for dual-recycling channel reverse supply chain considering consumer behavior. Eur. J. Oper. Res. 2017, 260, 601–612. [Google Scholar] [CrossRef]
- Ma, Z.-J.; Nian, Z.; Ying, D.; Shu, H. Managing channel profits of different cooperative models in closed-loop supply chains. Omega 2016, 59, 251–262. [Google Scholar]
- Xiao, T.; Qi, X.; Yu, G. Coordination of supply chain after demand disruptions when retailers compete. Int. J. Prod. Econ. 2007, 109, 162–179. [Google Scholar] [CrossRef]
- Li, Y.; Zhen, X.; Qi, X.; Cai, G. Penalty and financial assistance in a supply chain with supply disruption. Omega 2016, 61, 167–181. [Google Scholar] [CrossRef]
- Paul, S.K.; Sarker, R.; Essam, D. A quantitative model for disruption mitigation in a supply chain. Eur. J. Oper. Res. 2017, 257, 881–895. [Google Scholar] [CrossRef]
- Park, Y.; Hong, P.; Roh, J.J. Supply chain lessons from the catastrophic natural disaster in Japan. Bus. Horiz. 2013, 56, 75–85. [Google Scholar] [CrossRef]
- Genc, T.S.; De Giovanni, P. Trade-in and save: A two-period closed-loop supply chain game with price and technology dependent returns. Int. J. Prod. Econ. 2017, 183, 514–527. [Google Scholar] [CrossRef]
- He, Y. Acquisition pricing and remanufacturing decisions in a closed-loop supply chain. Int. J. Prod. Econ. 2015, 163, 48–60. [Google Scholar] [CrossRef]
- Xiong, Y.; Li, G.; Zhou, Y.; Fernandes, K.; Harrison, R.; Xiong, Z. Dynamic pricing models for used products in remanufacturing with lost-sales and uncertain quality. Int. J. Prod. Econ. 2014, 147, 678–688. [Google Scholar] [CrossRef]
- Li, X.; Li, Y.; Cai, X. Remanufacturing and pricing decisions with random yield and random demand. Comput. Oper. Res. 2015, 54, 195–203. [Google Scholar] [CrossRef]
- Han, X.; Wu, H.; Yang, Q.; Shang, J. Reverse channel selection under remanufacturing risks: Balancing profitability and robustness. Int. J. Prod. Econ. 2016, 182, 63–72. [Google Scholar] [CrossRef]
- Savaskan, R.C.; Bhattacharya, S.; Van Wassenhove, L.N. Closed-Loop Supply Chain Models with Product Remanufacturing. Manag. Sci. 2004, 50, 239–252. [Google Scholar] [CrossRef]
- Choi, T.-M.; Li, Y.; Xu, L. Channel leadership, performance and coordination in closed loop supply chains. Int. J. Prod. Econ. 2013, 146, 371–380. [Google Scholar] [CrossRef]
- Atasu, A.; Toktay, L.B.; Van Wassenhove, L.N. How Collection Cost Structure Drives a Manufacturer’s Reverse Channel Choice. Prod. Oper. Manag. 2013, 22, 1089–1102. [Google Scholar] [CrossRef]
- Mutha, A.; Bansal, S.; Guide, V.D.R. Managing Demand Uncertainty through Core Acquisition in Remanufacturing. Prod. Oper. Manag. 2016, 25, 1449–1464. [Google Scholar] [CrossRef]
- Savaskan, R.C.; Van Wassenhove, L.N. Reverse Channel Design: The Case of Competing Retailers. Manag. Sci. 2006, 52, 1–14. [Google Scholar] [CrossRef]
- Huang, M.; Song, M.; Lee, L.H.; Ching, W.K. Analysis for strategy of closed-loop supply chain with dual recycling channel. Int. J. Prod. Econ. 2013, 144, 510–520. [Google Scholar] [CrossRef]
- Hong, X.; Wang, Z.; Wang, D.; Zhang, H. Decision models of closed-loop supply chain with remanufacturing under hybrid dual-channel collection. Int. J. Adv. Manuf. Technol. 2013, 68, 1851–1865. [Google Scholar] [CrossRef]
- Yi, P.; Huang, M.; Guo, L.; Shi, T. Dual recycling channel decision in retailer oriented closed-loop supply chain for construction machinery remanufacturing. J. Clean. Prod. 2016, 137, 1393–1405. [Google Scholar] [CrossRef]
- Yu, H.; Zeng, A.Z.; Zhao, L. Single or dual sourcing: Decision-making in the presence of supply chain disruption risks. Omega 2009, 37, 788–800. [Google Scholar] [CrossRef]
- Tomlin, B. On the Value of Mitigation and Contingency Strategies for Managing Supply Chain Disruption Risks. Manag. Sci. 2006, 52, 639–657. [Google Scholar] [CrossRef]
- Xiao, T.; Qi, X. Price competition, cost and demand disruptions and coordination of a supply chain with one manufacturer and two competing retailers. Omega 2008, 36, 741–753. [Google Scholar] [CrossRef]
- Zhang, W.-G.; Fu, J.; Li, H.; Xu, W. Coordination of supply chain with a revenue-sharing contract under demand disruptions when retailers compete. Int. J. Prod. Econ. 2012, 138, 68–75. [Google Scholar] [CrossRef]
- Sawik, T. Joint supplier selection and scheduling of customer orders under disruption risks: Single vs. dual sourcing. Omega 2014, 43, 83–95. [Google Scholar] [CrossRef]
- Giri, B.C.; Sarker, B.R. Improving performance by coordinating a supply chain with third party logistics outsourcing under production disruption. Comput. Ind. Eng. 2017, 103, 168–177. [Google Scholar] [CrossRef]
- Han, X.; Wu, H.; Yang, Q.; Shang, J. Collection channel and production decisions in a closed-loop supply chain with remanufacturing cost disruption. Int. J. Prod. Res. 2016, 55, 1147–1167. [Google Scholar] [CrossRef]
- Giri, B.C.; Sharma, S. Optimal production policy for a closed-loop hybrid system with uncertain demand and return under supply disruption. J. Clean. Prod. 2016, 112, 2015–2028. [Google Scholar] [CrossRef]
- De Giovanni, P.; Reddy, P.V.; Zaccour, G. Incentive strategies for an optimal recovery program in a closed-loop supply chain. Eur. J. Oper. Res. 2016, 249, 605–617. [Google Scholar] [CrossRef]
| Notation | Definition |
|---|---|
| The unit selling price | |
| The average unit cost of manufacturing new products by the manufacturer | |
| The average unit cost of remanufacturing returned products by the third party | |
| , | The unit acquisition prices of the manufacturer and the collector, respectively |
| The unit transfer price from the manufacturer to the collector | |
| The market demand function | |
| Sensitivity of consumers to the selling price | |
| The quantity of remanufactured products | |
| , | The collection quantity of used products under online-recycling and offline-recycling channels, respectively |
| Profit |
| , | , |
|---|---|
| , | case 1: |
| , | case 2: |
| (1) , (2) , | case 3: |
| (1) , (2) , (3) , | case 4: |
| , | case 5: , |
| (1) , ; (2) ,; (3) , ; | case 6: |
| (1) , (2) , | case 7: |
| , | case 8: |
| , | case 9: |
| — | vs. | vs. | — | vs. | vs. | — | vs. | vs. |
|---|---|---|---|---|---|---|---|---|
| Case 1 | > | > | Case 4 | = | > | Case 7 | < | > |
| Case 2 | > | = | Case 5 | = | = | Case 8 | < | = |
| Case 3 | > | < | Case 6 | = | < | Case 9 | < | < |
| , | , |
|---|---|
| , | case 1: |
| , | case 2: |
| (1) , (2) , | case 3: |
| (1) , (2) , (3) , | case 4: |
| , | case 5: , |
| (1) , (2) , (3) , | case 6: |
| (1) , (2) , | case 7: |
| , | case 8: |
| , | case 9: |
| , | , |
|---|---|
| , | case 1: |
| , | case 2: |
| (1) , (2) , | case 3: |
| (1) , (2) , (3) , | case 4: |
| , | case 5: , |
| (1) , (2) , (3) , | case 6: |
| (1) , (2) , | case 7: |
| , | case 8: |
| , | case 9: |
| Lemma 1 | Lemma 2 | Lemma 3 | Lemma 4 |
|---|---|---|---|
| If , | If , | If , | If , |
| Lemma 5 | Lemma 6 | Lemma 7 | Lemma 8 |
|---|---|---|---|
| If , | If , | If , | If , |
| Lemma 9 | Lemma 10 | Lemma 11 | Lemma 12 |
|---|---|---|---|
| If , | If , | If , | If , |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.; Wang, Z. Dual-Recycling Channel Decision in a Closed-Loop Supply Chain with Cost Disruptions. Sustainability 2017, 9, 2004. https://doi.org/10.3390/su9112004
Huang Y, Wang Z. Dual-Recycling Channel Decision in a Closed-Loop Supply Chain with Cost Disruptions. Sustainability. 2017; 9(11):2004. https://doi.org/10.3390/su9112004
Chicago/Turabian StyleHuang, Yanting, and Zongjun Wang. 2017. "Dual-Recycling Channel Decision in a Closed-Loop Supply Chain with Cost Disruptions" Sustainability 9, no. 11: 2004. https://doi.org/10.3390/su9112004




