1. Introduction
At the tenth meeting of the conference of parties to the Convention on Biological Diversity (CBD) in 2010 in Japan, the
Strategic Plan for Biodiversity 2011–2020 was developed [
1]. Governments, intergovernmental and non-governmental organisations and other representatives agreed on five strategic goals and 20 Aichi targets to protect biodiversity. Some years later, the United Nations (UN) acknowledged the protection of biodiversity in two of the published Sustainable Development Goals (SDGs), i.e., number 14 “life on land” and number 15 “life below water” [
2]. Protecting biodiversity is important because it affects humanity. It underpins and stabilises [
3] the functions of ecological systems that provide goods and services (called ecosystem services (ESS)) securing human life [
4]. The ESS include, e.g., the provision of food, regulating of floods or supporting soil formation [
4].
Biodiversity as such includes the genetic, the species and the ecosystem diversity (defined by the UN [
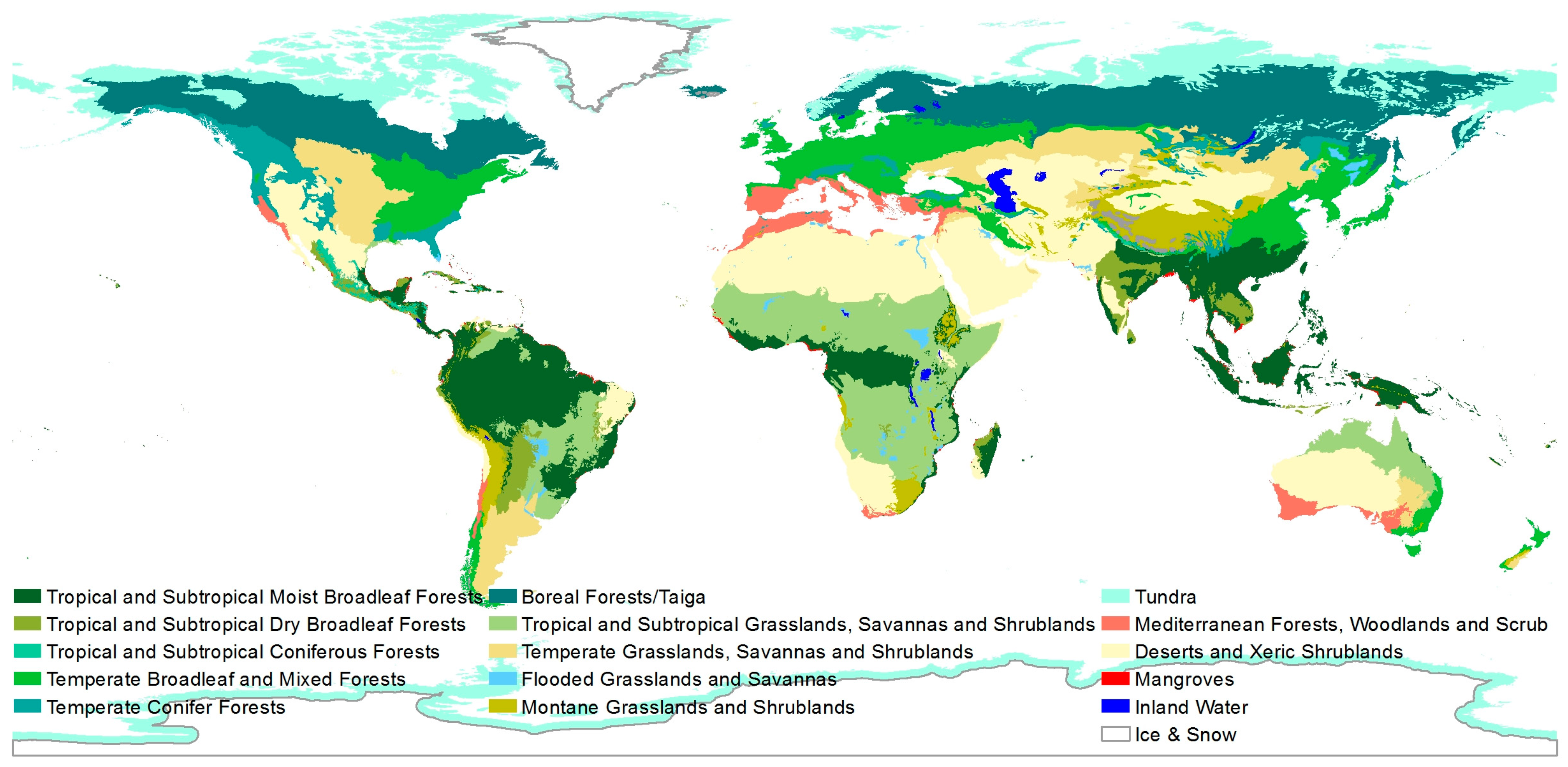
5]). It can be described on different spatial resolutions. For example, the World Wild Fund for Nature (WWF) uses a resolution of 14 major habitat types (MHT) (see
Figure 1) defined as “areas of the world that share similar environmental conditions, habitat structure, and patterns of biological complexity, and that contain similar communities and species adaptations” [
6].
To strengthen the protection of biodiversity, the impacts of anthropogenic pressures on it have to be measurable in order to be preventable. Anthropogenic pressures include, e.g., agriculture (land use, land transformation), emission of toxic substances, greenhouse gas (GHG) emissions, fertilization (i.e., phosphorus and nitrogen emissions), light and noise emissions or destructive harvesting practices [
8]. The anthropogenic pressures could have an effect, among others, on different environmental parameters. For instance the pH of soil and water can be affected by the release of acidifying substances [
9], the share of cultivated land is affected by agriculture and the mean global temperature can be influenced by man-made GHG emissions [
10]. In a second step, these altered environmental parameters can affect biodiversity due to, e.g., loss of species richness.
In recent years, several methods and tools have been developed to determine the impact of human activities (anthropogenic pressures) on biodiversity. One such method which has increasingly been used in the recent years is life cycle assessment (LCA) as set forth by the ISO 14040/14044 standards [
11,
12]. LCA is a comprehensive method, allowing for the assessment of the potential environmental impacts of products along their entire life cycle from raw material extraction through materials processing, manufacturing, distribution, use, repair and maintenance, to disposal [
11]. In LCA’s impact assessment phase, the potential impacts of anthropogenic pressures on, e.g., biodiversity are described at different levels in the cause–effect chain. For example, impacts of GHG emissions are assessed at the middle of the cause–effect chain (global warming potential [
13]) and at the end of the cause–effect chain at which damages to human health and biodiversity [
13] are quantified.
LCA has improved the possibility to quantify and analyse the potential environmental impacts associated with any given product system (including the impact on certain biodiversity aspects). However, the modelling of cause–effect chains leading, first, from anthropogenic pressures to changes in environmental parameters and, second, leading from altered environmental parameters to biodiversity impacts still needs improvements. Most of the models used in LCA are region specific (because specific species are used to assess the impacts on biodiversity) and consider land use only. Further, they consider one aspects of biodiversity only, namely species diversity. As data for indicators measuring biodiversity (e.g., species richness, genetic diversity) is lacking, the impact assessment is possible for few regions in the world only—but biodiversity should be protected globally. [
14].
To strengthen LCA in assessing impacts on biodiversity, the central goal of this paper is to analyse the relationship between environmental parameters and biodiversity allowing for a reliable description of cause–effect mechanisms. To meet this aim, three questions have to be answered. First, which parameters should be investigated? Second, how can biodiversity be measured? Third, what is the mathematical relationship between the considered parameters and biodiversity?
2. Method
As biodiversity varies in different regions, the MHTs have been used as a basis to assess the impacts of various parameters on biodiversity. The appropriateness of using the MHTs has been tested after (see
Section 2.3).
Usually, the relation of parameters and biodiversity should be considered on a high spatial resolution, e.g., on an ecoregion level as recommended by Coelho and Michelsen (2014) [
15]. However, data availability is a limiting factor. Thus, the effect of three parameters has been estimated on a low resolution (i.e., at MHT level) in this study. The data for the parameters and the biodiversity were collected for the 827 ecoregions and analysed with regard to every MHT because each of the 14 MHT includes several ecoregions [
16].
To analyse the relationship between the parameters and biodiversity, the following steps were conducted.
2.1. Parameters for Each Ecoregion
Many parameters affect biodiversity, but for most of them data availability on a global level are limited. Therefore, within this study, only parameters were examined for which data is available in a Geographical Information System (GIS) layer for the whole world. The parameters “soil pH”, “share of cultivated land” and “temperature in June” were considered. Data for other parameters, which also might affect the biodiversity, were not available for the whole world or with the resolution which is needed (i.e., on an ecoregion level) for the aim of the study. GIS data for the considered parameters are available as raster data for the whole world from the following sources:
- (a)
The “soil pH” was extracted from the Harmonized World Soil Database (HWSD) where the data is given with a grid cell resolution of 1 km [
17].
- (b)
The “share of cultivated land” with a grid cell resolution of 10 km is published online as supplementary materials to the HWSD [
17].
- (c)
The “mean temperature in June” with a grid cell resolution of 1 km is published online by Hijmans et al. [
18].
Besides the GIS data for the parameters, GIS data for the size, shape and location of the ecoregions proposed by Olsen et al. [
16] were collected. These data are available as polygon data at the ecoregion database website [
7]. The size of the ecoregions varies from few square kilometres to some thousands square kilometres [
7]. After collecting the GIS data, the different GIS layers (for the parameters (raster data) and the ecoregions (polygon data)) were overlaid and merged by means of the zonal statistic function in ArcGIS 10.4 [
19]. Thus, all parameter grid cell values which are located in one ecoregion polygon were summed up. This resulted in mean values for the considered parameters for every ecoregion.
2.2. Biodiversity Status (BS) for Each Ecoregion
Several indicators for the estimation of biodiversity are proposed by, e.g., [
20,
21,
22] but for only few of them data are available. To define biodiversity on a more generic level, a new index is defined within this study. The index, called biodiversity status (BS), was developed with indicators for which data are available for all ecoregions. It is meant to present the current situation of the genetic diversity (e.g., gene pool), the species diversity (e.g., species number) and the ecosystem diversity (e.g., landscape) in one ecoregion. Thus, all levels of biodiversity are included. For the BS, the “number of species per km
2” (data from the ecoregion database website [
7], which includes the taxa amphibians, reptiles, birds and mammals); “number of endemic species per km
2” (data from the ecoregion database website [
7], which also includes the taxa amphibians, reptiles, birds and mammals); and “mean share of grassland and forest” per ecoregion were used. The last indicator was calculated in the same way as the “mean share of cultivated land” (see
Section 2.1 with published data from the HWSD [
17].
As there is no definition of “good” and “bad” biodiversity, the index was normalised in order to have a highest BS (which has the value of one) and a lowest BS (which has the value of zero). For this, the individual indicators were normalised, summed up to the BS and normalised again (data and calculation steps are presented in
Supplementary Materials (
Table S1)). The outcome is a BS between zero and one for every ecoregion. The calculation of the BS is presented in Equation (1).
SER,n = normalised (n) number of species per km2 per ecoregion (ER);
ESER,n = normalised (n) number of endemic species per km2 per ecoregion (ER);
SGFER,n = normalised (n) mean share of grassland and forest per ecoregion (ER);
min = minimum value of the sum of the indicators of all ecoregions; and
max = maximum value of the sum of the indicators of all ecoregions.
2.3. Kruskal–Wallis Test
Biodiversity varies even in small ecosystems, but, as mentioned above, data for such a high spatial resolution are not available. To have any differentiation regarding biodiversity and not assuming even distribution of biodiversity all over the world, the MHTs were chosen as the considered regions. A Kruskal–Wallis test was performed using SPSS 24 [
23] to prove that this differentiation is appropriate. The Kruskal–Wallis test is a statistical analysis to compare two or more groups (in this case MHTs) and to find significant differences [
24]. After this test, a pairwise comparison was performed to highlight which MHTs differentiate from each other.
2.4. Curve Fitting
To analyse the relation of the BS and the three parameters, curve fitting was performed by means of SPSS 24 on a MHT level. This is possible because every MHT consists of several ecoregions. Each ecoregion (i.e., the data for the BS and the parameters) represents one point in the curve estimation models for the respective MHT. The best curve estimation model (depending on the coefficient of determination, the p-value (to characterise the significance) and a reasonable justification) serves as a function which describes the influence of the considered parameter on the BS within the considered MHT.
4. Discussion and Conclusions
4.1. Parameters for Each Ecoregion
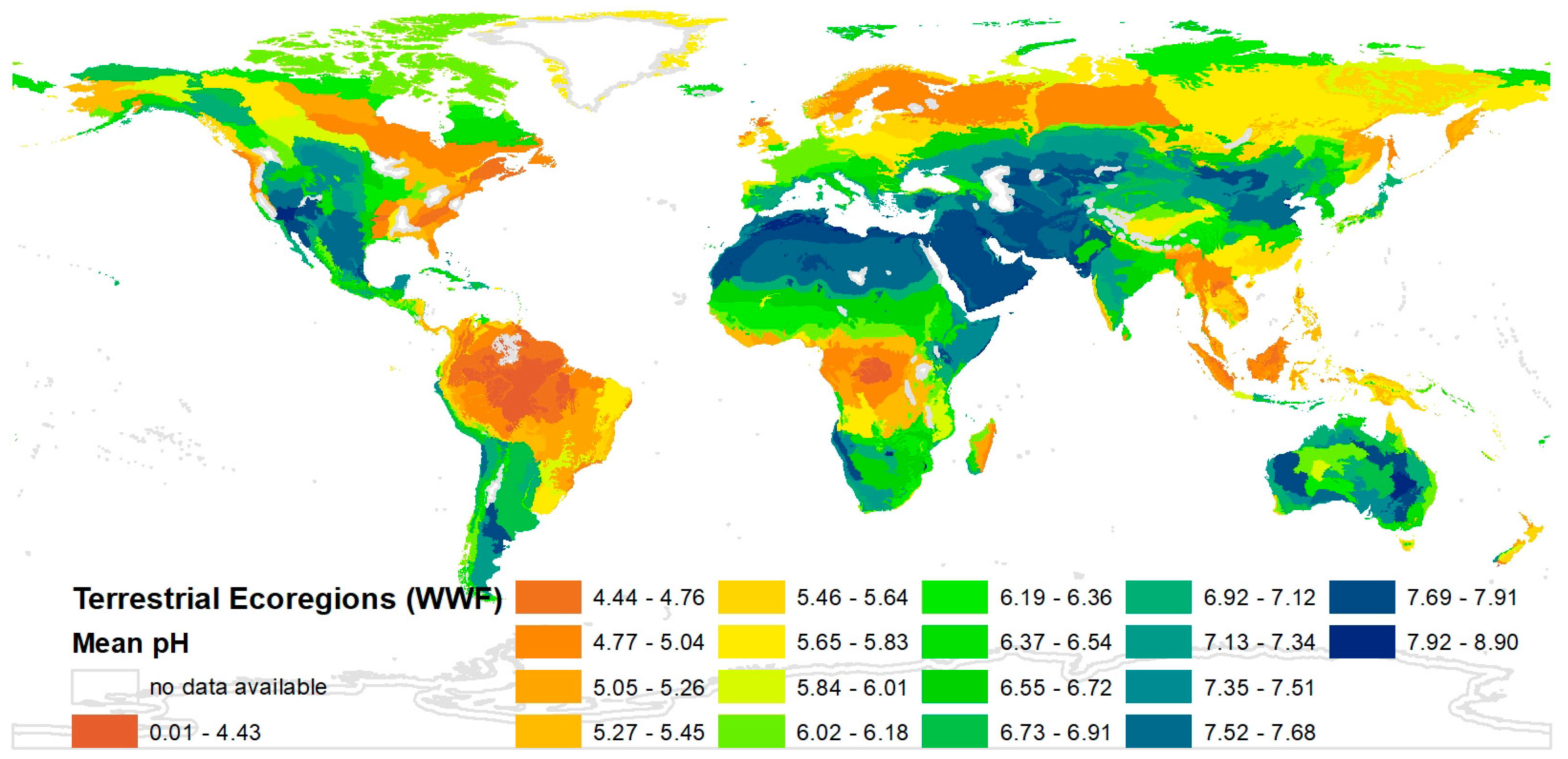
The “mean soil pH” varies a lot in the different regions, but it can be seen in
Figure 2 that usually neighbouring areas have similar soil pH values. As a tendency, it can be seen that the higher the population density the higher the “mean share of cultivated land” (see
Figure S2) in different areas, which is not surprising. Data for the “mean temperature” were available for all months. It would not be meaningful to use the average data for one year or months for which the temperature lies in between maxima and minima of the yearly temperature (e.g., months in autumn and spring) because the differences are not high all over the world. Thus, the month June was chosen. It would be possible to use other months. A comparison of the results of a correlation analysis between the mean temperature and the BS with data for January and for June shows only insignificant differences (the correlation coefficient is |0.206| for January and |0.216| for June).
The accuracy of the mean parameter values per ecoregion can be improved by using raster data with higher resolutions. This would mean to have more exact values for different region. However, such data were not available at the time the study was conducted.
4.2. Measuring Biodiversity
The BS presented in
Figure 3 shows biodiversity hotspots all over the world. The red marked ecoregions (i.e., high BS which means high biodiversity) are located, e.g., in South America and south-central China. The hotspots overlap with the hotspots identified by Myers et al. (2000) [
25].
As already mentioned, the UN defined biodiversity as genetic, species and ecosystem diversity [
5]. Within this study, these levels were implicitly considered (as completely as possible for the estimation of the BS) by selecting the appropriate indicators. Species diversity, for some taxa only, is covered by the “number of species per km” and the “number of endemic species per km”, while ecosystem diversity is covered by the “share of grassland and forest”. Thus far, genetic diversity is not covered explicitly, but is included implicitly in the indicators for species and ecosystem diversity because it is assumed that the genetic diversity increases with increasing number of (endemic) species and increasing number of ecosystems (i.e., grassland and forest). However, as this is not proven and only an assumption, it would be more scientifically robust to use an indicator for genetic diversity directly, but data are not yet available for such an indicator [
26]. Within the index of the BS equal weighting of all indicators was applied because there is no consensus within the research community which level of biodiversity is more important [
27].
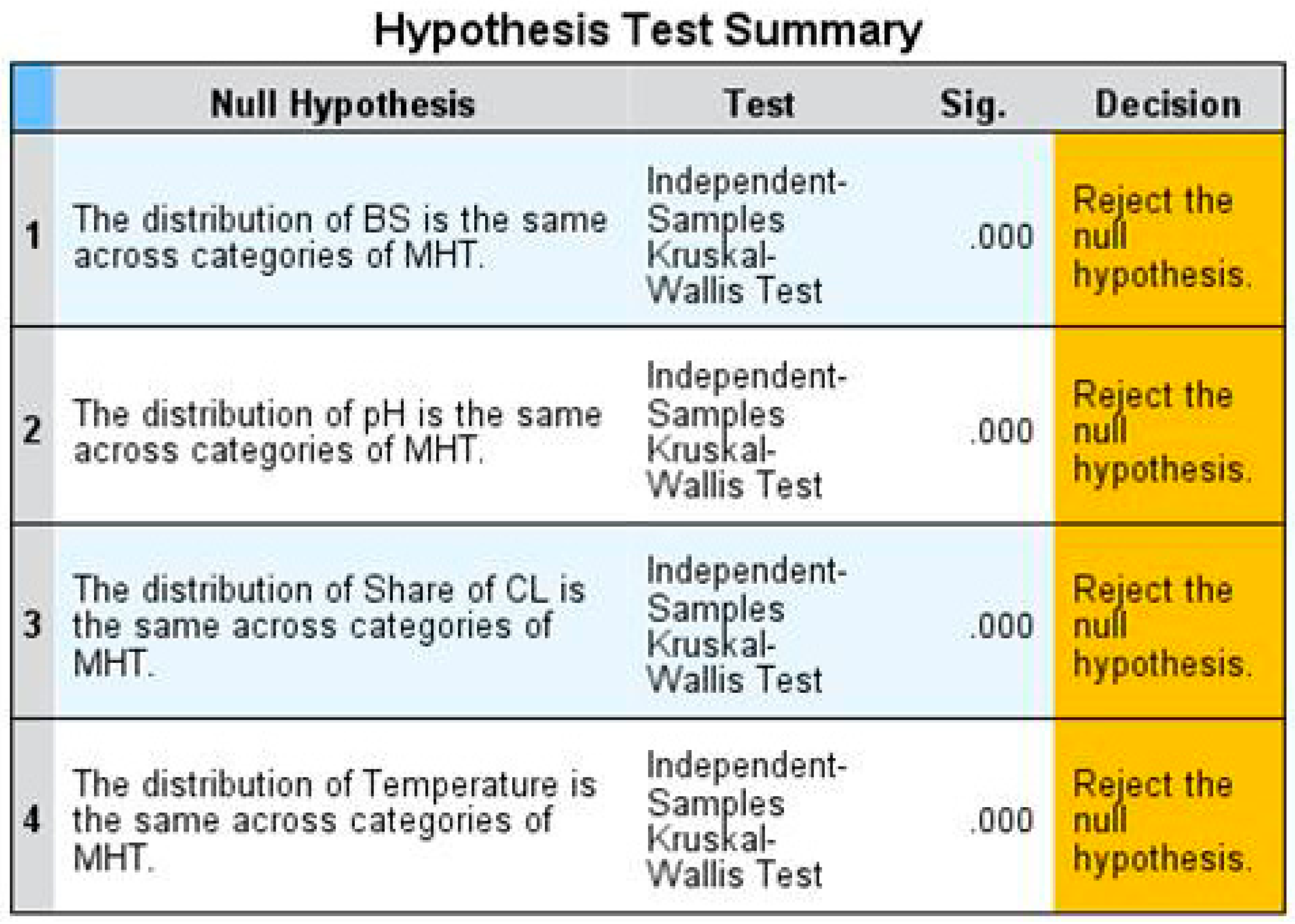
4.3. Kruskal–Wallis Test
The Kruskal–Wallis test shows that there is a statistically significant difference in the distribution of the BS, the “mean soil pH”, the “share of cultivated land” and the “mean temperature in June” across all MHTs. Even though the pairwise comparison of the MHTs regarding the respective variables (i.e., the BS and the parameters) reveals that the distribution of the BS and the parameters is the same in few MHTs (see
Supplementary Materials S1), it is relevant to differentiate the BS and the parameters on a MHT and not to analyse the impacts on a global level without any differentiation.
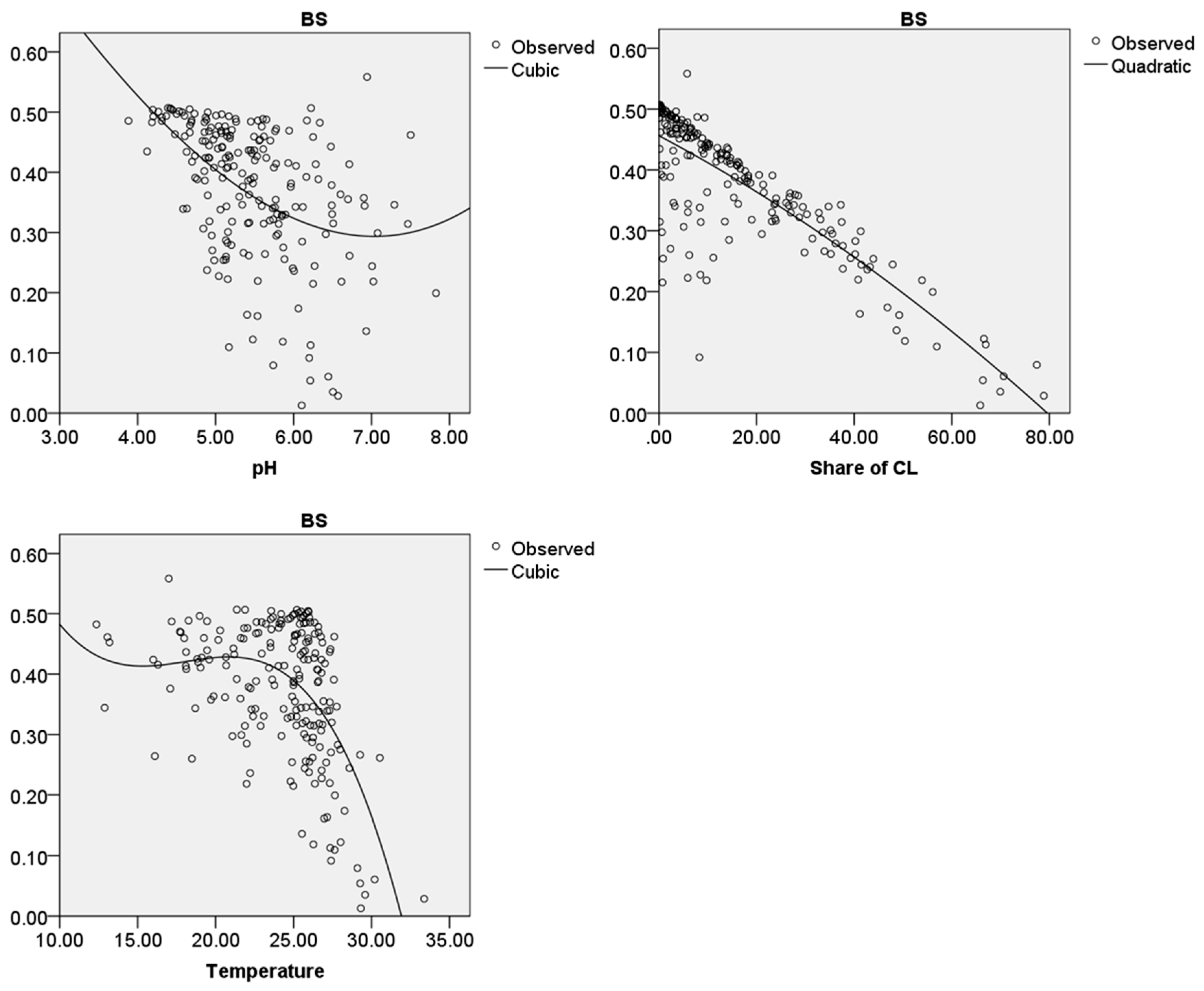
4.4. Curve Fitting
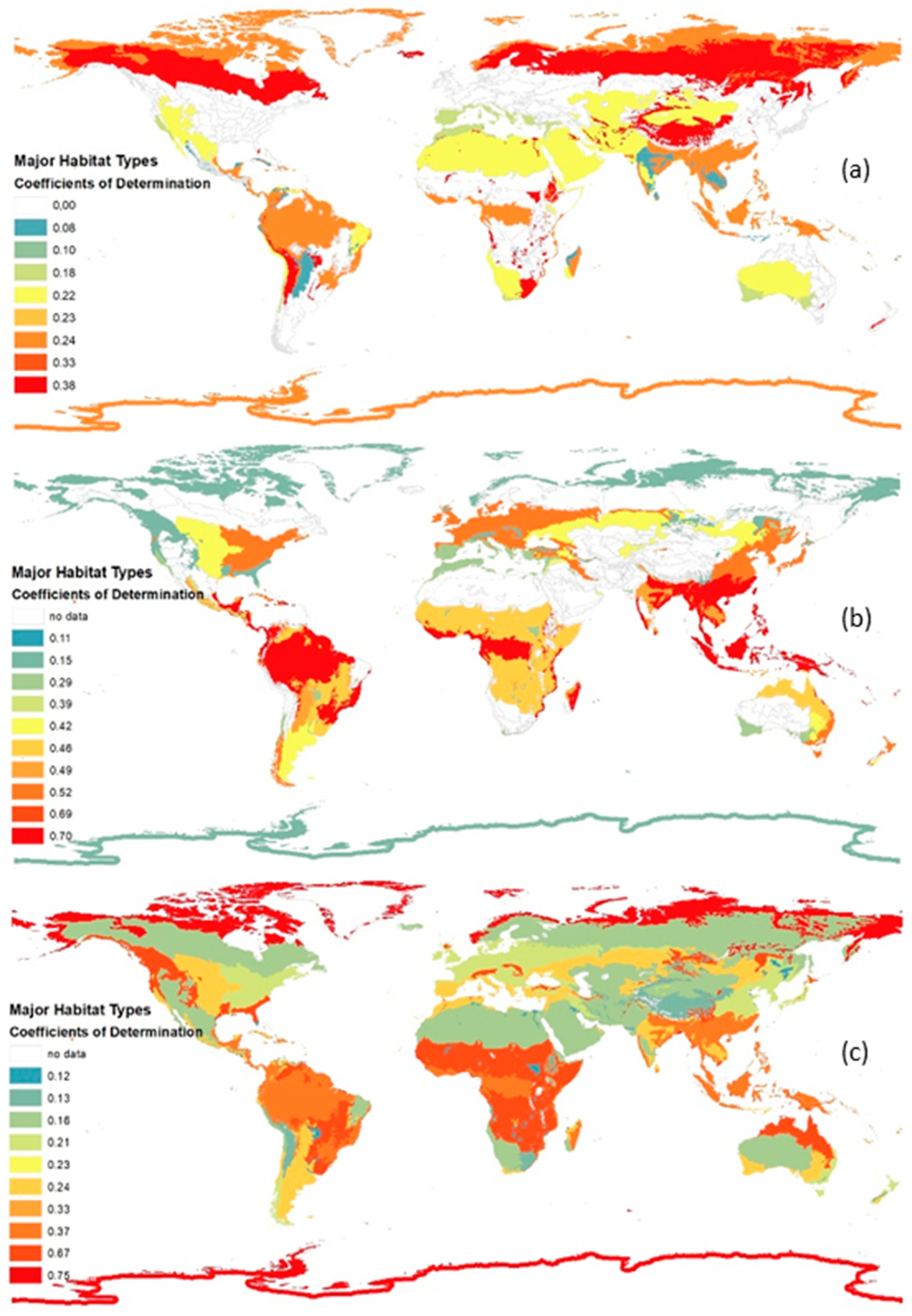
In most MHTs the parameter “mean share of cultivated land” has the highest coefficient of determination (see
Figure 5). It seems that this parameter has the most effect on biodiversity (of the considered parameters), which supports the hypothesis that land use can be regarded as the main pressure on biodiversity [
28]. However, in some MHTs, the parameters “mean temperature in June” and “mean soil pH” have a moderate to high coefficient of determination (e.g., 0.747 in MHT11 and 0.383 MHT10, respectively). Thus, these two parameters also have a moderate to strong relation to biodiversity.
In general, most of the obtained coefficients of determination are lower than 0.700 (see
Figure 5). For these models the strength of relationship cannot be stated as very strong. However, it is still justifiable to use the different models to explain the relation of the BS and the considered parameters. In this study the relation of the BS and one parameter only, e.g., “mean soil pH”, was considered. In reality, many parameters affect the biodiversity in a cumulative manner. However, so far it has not been possible to analyse the interrelation of different parameters and their cumulated impacts on biodiversity because of a lack of data. As the study at hand analysed the impact of individual parameters on the BS, the coefficient of determination is not expected to be high. Therefore, the models are still valuable. Additionally, the
p-value of the chosen models is mostly lower than 0.05, i.e., the chance that the respective model does not explain the relation of the considered parameter and the BS is lower than five per cent. Thus, most of the developed models are significant. However, for some models, the
p-value is higher (see MHT11 BS and “mean share of cultivated land”). For these models, one has to decide by means of the coefficient of determination if it is reasonable to use the model to explain the relation of the considered parameter and the BS or not. In general, for some MHTs and parameters no curve estimation model fits because neither the coefficient of determination is high, nor the
p-value is low (e.g., see
Supplementary Materials (S2) MHT5 BS and “mean soil pH”). One example is the relation of the BS and the “mean share of cultivated land” in MHT11 (displayed in
Figure 7). The coefficient of determination is relatively low (0.108) while the
p-value is high (0.301) for the quadratic model. Thus, the curve estimation model does not appear reliable. The other models for this relation have even worse coefficients of determination and p-values or do not seem to be reasonable (see
Supplementary Materials (S2)). A case specific decision has to be made whether a curve estimation model is useful or not.
The choice of the best curve estimation model for functionalising of the relation of the parameter and the BS has been made depending on the coefficient of determination, the significance and a reasonable justification. For example, even though the coefficient of determination of the cubic model for the relation of the BS and the “mean share of cultivated land” in MHT11 is higher (0.222) than the coefficient of determination for the quadratic model (0.108), it is reasonable to use the quadratic model. The cubic model would imply that, from a mean share of cultivated land of 40%, the BS increases with increasing mean share of cultivated land. As this is not justifiable, it was decided by the authors of this study that the quadratic model is more reasonable because the BS decreases from a mean share of cultivated land of 30%, which seems to be more reasonable.
All curve estimation models are restricted to a specific interval for the considered parameter. This is because the values of the considered parameters lie usually in specific intervals depending on the considered MHT. Thus, the calculation of the BS in dependence of the considered parameter in a specific MHT is only possible in the respective interval. For example, the curve estimation models of the parameter “mean temperature in June” differentiate regarding their temperature intervals in the different MHTs (e.g., MHT6, 4–14 °C; and MHT9, 10–35 °C).
The results of the curve fitting differentiate greatly between the different MHTs because of the differences in the number of ecoregions which are located in the MHTs. The number varies from 16 (see
Supplementary Materials (S2) MHT3) to 204 (see MHT1). The more ecoregions, the more data are available and, thus, the more meaningful is the regression analysis and the curve fitting.
4.5. Limitations and Conclusions
Many different pressures on biodiversity exist, but data availability was decisive for the selection of the parameters for this study. Additionally, the data used for this study (i.e., data for the considered parameters and data for the indicators defining the BS) are secondary (i.e., they were not collected by the authors of this paper). For these data, uncertainty exists. Such uncertainty cannot be decreased by the user and has to be accepted as is. Moreover, the time representativeness of the data is different. For instance, the data for the “mean soil pH” are from 2012, whereas the data for the “mean temperature in June” are for a period from 1950 to 2000.
Usually an ecosystem depends on so-called limiting factors (e.g., water or nutrients). These are decisive factors that are crucial for the development of an ecosystem. Within this study, it was not investigated whether a parameter could be decisive or not because of a lack of data. However, it would be valuable to analyse the influence of decisive factors on a MHT level, too.
The analysis on a MHT level is controversial and impacts on biodiversity are usually considered on a higher resolution (e.g., ecosystems). An assessment on such a low resolution implies great simplifications and assumptions. Even on an ecoregion level, huge differences exist regarding biodiversity [
15]. However, data on such a high resolution are not available. Thus, assumptions have to be made to assess impacts on biodiversity all over the world. The approach suggested in this paper is a simplification for estimating the influence of various parameters on biodiversity, but it is useful, e.g., to assess and compare impacts on a global level, as it is done in LCA. Two other approaches were also considered in this study (no differentiation at all and differentiation on a continent level). Firstly, as global data are available, an analysis could be done without differentiation on a MHT level. However, the results of the Kruskal–Wallis test and the curve fitting show obvious differences across the MHTs. For example, the range and the optimum values of the parameters differentiate a lot in the different MHTs. Additionally, since the MHT distinction is already a simplification, the analysis on a global level would not be reasonable. Secondly, it was considered to distinguish between the MHTs and the continents in combination, i.e., analysing the sections of a MHT located on different continents individually. However, for this, not enough data points are available because some areas would contain only few ecoregions. Thus, fragmented MHTs were considered as one MHT.
Despite the uncertainty of the suggested approach, this study provides a concept of how to assess impacts of several parameters, which can be anthropogenically influenced, on biodiversity on a MHT level for the whole world. The results (i.e., curve estimation models) can be used, e.g., in life cycle impact assessment. By describing changes in biodiversity as a consequence of changes in (anthropogenically influenced) parameters considered here, the curve estimation models can be a central part of impact assessment models (i.e., they can be used to develop the needed cause effect chain), which are urgently needed to comprehensively consider biodiversity impacts in LCA. It would help to identify and improve impact hotspots of production processes on biodiversity on a global level. However, a temporal resolution is not considered. The approach can be used, e.g., by policy makers for the identification of current pressures on biodiversity and, therefore, for their prevention. The strategic goal to “reduce the direct pressures on biodiversity and promote sustainable use” from the
Strategic Plan for Biodiversity 2011–2020 [
1] could be addressed.
Further research should be undertaken in several directions. First, data for other parameters, such as nitrogen concentration or water content, which affect biodiversity, should be generated. Second, more data points with regard to the parameters already used should be provided to enhance the certainty of the curve estimation models. Third, the BS should be developed further. Research on biodiversity indicators is currently developing towards the use of functional biodiversity [
29,
30] and ESS instead of the levels of biodiversity defined by the UN [
5]. However, as this research is in an early stage, and data are not available, in this study, the common understanding of biodiversity (i.e., the three levels of biodiversity) was used as a basis for the development of the BS. Fourth, the interrelation of the different parameters and their cumulative impact on biodiversity should be investigated. For this a multi regression analysis can be used. The main problem that has to be solved is to determine the mathematical relationship of the parameters. This step will be undertaken in further research by the authors.