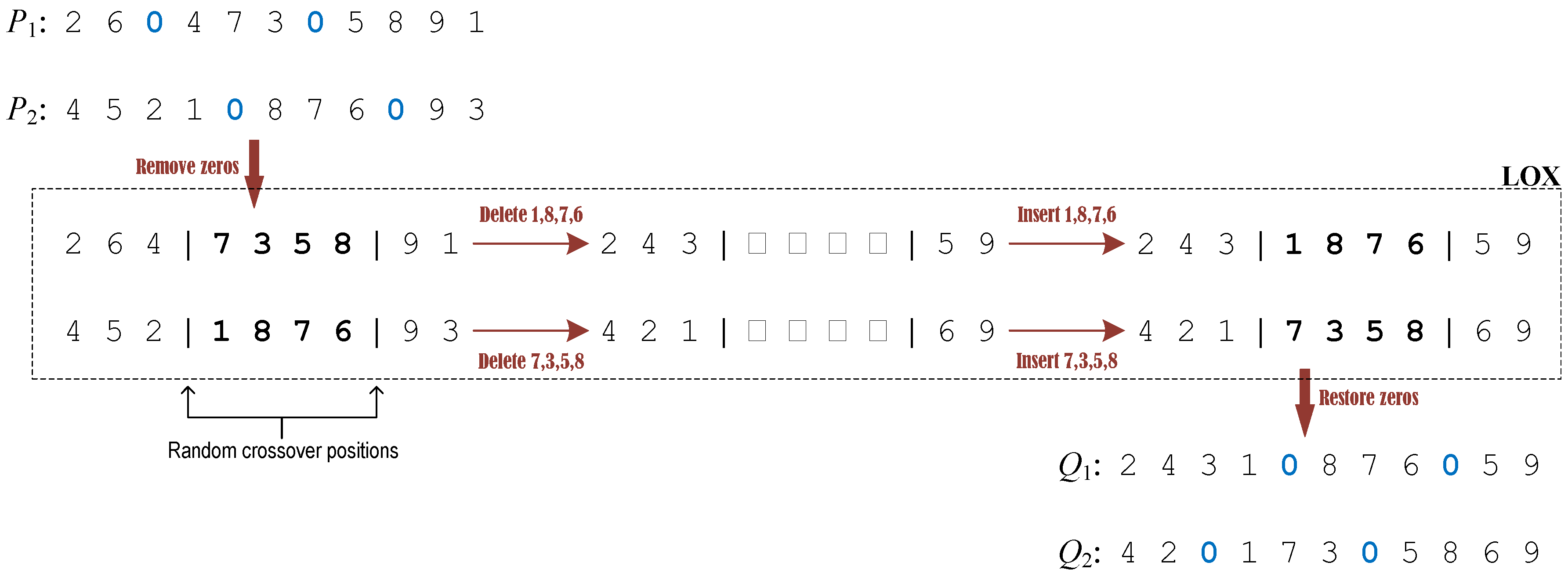1. Introduction
The increasing concerns over climate change and global warming has exerted great pressure on the manufacturing sector because it is believed to be a considerable source of pollutant and greenhouse gas emissions. Faced with stringent regulations and pollution taxes, manufacturing enterprises have been actively seeking for cost-effective strategies to reduce the discharge of pollutants in their production processes. Upgrading the relevant processing equipment, technological standards and pollutant treatment facilities certainly constitutes a feasible option, but it requires substantial investment for the purchasing and maintenance activities. As an alternative policy, sustainability-oriented production scheduling has been utilized in a growing variety of process industries as a system-level methodology for reducing pollutions and carbon emissions [
1,
2]. The related research on sustainable production scheduling has attracted increasing attention since the launch of a focused special issue in 2016 [
3].
The earliest effort for reducing energy consumption through production scheduling can be attributed to [
4]. The authors collected operational statistics of the CNC machines in a workshop and found that the non-bottleneck machines consumed considerable energy during the idle periods. To solve the issue, they proposed a turn-on/turn-off scheduling framework (which determines whether and when to turn off a machine or to keep it idle) to reduce the overall energy consumption of the machines. This framework has been utilized and extended in later research such as [
5,
6,
7,
8] for single machine scheduling or flow shop scheduling settings. Another research framework is based on machine speed scaling [
9]. In this framework, it is possible to let the machines work at different speed levels when processing jobs, and a higher speed is associated with shortened processing time but increased energy consumption. Therefore, a trade-off must be made between production efficiency and energy usage. The speed scaling framework has been utilized in subsequent research such as [
10,
11,
12,
13] for single machine or job shop production environments. The above-mentioned and many other existing works all focus on the minimization of energy consumption for achieving sustainable manufacturing (based on the fact that electricity generation will normally produce carbon emissions). However, manufacturing processes can influence the environment in more direct ways, e.g., discharge of toxic sewage and waste. The use of production scheduling to reduce these direct emissions certainly deserves more research efforts in the near future. The work presented here reflects such an attempt.
In this paper, we focus on the production scheduling of the cloth dyeing process, which is a core process in typical cloth-making and textile industries. It is noticed that pollutant emissions relating to this process have originated from two major sources. Firstly, the dyeing machines need to be cleaned thoroughly whenever they are prepared for processing jobs with a different color than that of the preceding jobs. The chemical cleaning process is accompanied by the use of polymer detergents in large amounts, resulting in considerable sewage discharge. Secondly, some machines may not be fully utilized during the dyeing process, for example, in the case where a machine with maximum capacity of 200 kg has been assigned to process a batch of jobs that weigh only 100 kg. The underutilization of dyeing equipment can lead to waste of dyes, which further increases the risk of polluting the environment if the unconsumed dyes have not been properly disposed of. It is crucial to realize that the pollutions resulting from these two major sources can be effectively reduced by means of production scheduling. In particular, scheduling could help to minimize the number of cleanings by arranging jobs with the same color to be processed consecutively, and likewise, scheduling can help to minimize the waste of dyeing resources by making the size of each batch close to the capacity of the assigned machine.
Meanwhile, it should be noticed that such objectives reflecting the environmental and sustainable goal may conflict with the traditional scheduling objectives (e.g., tardiness, which reflects the penalty on late completion of jobs), not to mention that these sustainable objectives are often mutually conflicting as well. Therefore, multi-objective optimization approaches are required for modeling and solving sustainable production scheduling problems. Under the multi-objective optimization framework, the algorithm must be able to output a set of solutions with equal quality (in the Pareto optimality sense) and widespread distribution (representing different trade-offs among the objectives) so that the decision maker can choose the most suitable solution according to practical conditions [
14]. In the following, we provide a quick literature review of the related publications on multi-objective parallel machine scheduling, considering that the production system studied in this paper is basically consistent with the parallel-machine settings, in which a number of machines are working in parallel to process the pending jobs.
Most existing publications are focused on theoretical problems which are extended from the standard single-objective parallel machine scheduling model. A modified NSGA-II (Non-dominated Sorting Genetic Algorithm II) was proposed for a parallel machine scheduling problem with three objectives including tardiness cost, deterioration cost and makespan [
15], and it was found that the modified algorithm outperforms the original NSGA-II and another universal multi-objective optimizer SPEA2. A multi-objective multi-point simulated annealing (MOMSA) algorithm [
16] and a tabu-enhanced iterated Pareto greedy (TIPG) algorithm [
17] were proposed for solving unrelated parallel machine scheduling problem in which the makespan, total weighted completion time and total weighted tardiness should be minimized simultaneously. It had been revealed that the proposed algorithms markedly outperformed the existing heuristics in terms of the adopted performance indicators. A bi-objective uniform parallel machine scheduling problem (minimizing makespan and machine hiring cost) with consideration of learning and adapting effects was studied in [
18], where the authors designed a highly modified particle swarm optimization (PSO) algorithm based on Lévy flights to implement an efficient search procedure. Experimental results showed that the proposed modifications had significantly helped the algorithm to escape from local optima, therefore resulting in an outstanding performance even when compared to exact solution methods. A multi-objective unrelated parallel machine scheduling problem (minimizing total completion time, number of tardy jobs, total flow time and machine load variation) with machine-dependent and job-sequence-dependent setup times was considered in [
19], where the authors presented an artificial immune mechanism enhanced NSGA-II called AI-NSGA-II to solve the complex scheduling problem. Robust performance of the proposed algorithm was verified by comparison with the conventional NSGA-II and a multi-objective particle swarm optimization (MOPSO) algorithm. A multi-phase heuristic algorithm, which iterates over a genetic algorithm in the first phase and three hybrid meta-heuristics (ACO, VNS and SA) in the second and third phases, was proposed for a parallel machine scheduling problem with sequence-dependent setup times to minimize both makespan and total earliness/tardiness in the due window [
20]. Experiments had shown that the multi-phase method approximates the Pareto front better than the global archive sub-population genetic algorithm (GSPG) presented earlier in [
21]. A bi-objective parallel machine scheduling model was built to deal with production scheduling and maintenance planning problems simultaneously, aiming at minimizing the total tardiness and the unavailability of the production system [
22]. The proposed solution method based on Pareto ant colony optimization was shown to outperform two universal multi-objective genetic algorithms (NSGA-II and SPEA2).
There are also some publications dealing with practical scheduling problems or problems with practical features. Motivated by a real-life production system with eligibility considerations (i.e., a job from a certain quality level can be processed by a machine of the same level or a higher level but the latter case incurs a penalty), the authors of [
23] investigated a bi-objective parallel machine scheduling problem with the aim of minimizing the final completion date (production plus delivery) and the total penalty generated by job level mismatches. Efficient heuristic search algorithms were proposed for the problem to obtain Pareto solutions which had been compared with the exact Pareto fronts. Inspired by a real-world scheduling problem in the shipyard, the authors of [
24] modeled an unrelated parallel machine scheduling problem with sequence-dependent setup times, release dates, machine eligibility and precedence constraints. Adaptive versions of the NSGA-II and a multi-objective ant colony optimization (MOACO) algorithm were developed for solving the problem, and the results had indicated that the improved MOACO statistically outperformed the proposed NSGA-II. To reflect the practical situation of “project crashing” in manufacturing activities (which means expediting the processing of certain jobs in the hope of shortening the makespan), a parallel machine scheduling problem with controllable processing times was investigated in [
25], in which the total manufacturing cost (associated with the shortened processing times), total weighted tardiness and makespan had been considered as objective functions. Pareto solutions were obtained by the lexicographic weighted Tchebycheff method, and it was found that the applied method had yielded more and better-spread non-dominated solutions than the weighted-sum method. Considering the inevitable uncertainty of processing times and due dates in real-world systems, a non-identical parallel machine multi-objective scheduling problem with both deterioration and learning effects was formulated as a fuzzy chance-constrained nonlinear programming model (with objectives of minimizing total earliness/tardiness and makespan) [
26]. A multi-objective branch and bound algorithm was proposed in order to obtain the Pareto front, and it was revealed by computational results that the algorithm had been efficient for solving large-scale instances.
It can be concluded from the literature review that multi-objective optimization approaches (based on Pareto optimality) have not yet been applied to parallel machine scheduling problems with sustainable or environmental requirements (the few existing works such as [
27] have treated the problem as single-objective by adding traditional scheduling cost and environmental cost together). There are even fewer publications that aim at sustainable scheduling of real-life parallel-machine production systems based on practically motivated definition of objective functions. Therefore, the work reported in this paper reflects a novel research attempt for modeling and solving a sustainable production scheduling problem that arises from the pollution-intensive cloth dyeing industry.
The remainder of the paper is organized as follows.
Section 2 describes the sustainable scheduling problem in detail and gives an exact mathematical programming formulation.
Section 3 introduces all aspects of the proposed solution approach, including the encoding/decoding scheme, initialization method, modified genetic operators, multi-objective handling functions, and the tabu-enhanced iterated greedy local search module.
Section 4 presents a series of computational experiments to verify the effectiveness of our algorithm, including DOE-based parameter test and systematic comparison with the recently proposed multi-objective evolutionary algorithms. Finally,
Section 5 concludes the paper with discussions on future research possibilities.
2. Problem Statement
2.1. Background
In the studied production system for textile dyeing, there are n jobs () waiting to be processed by m parallel batch-processing machines (). Each job has a series of attributes, namely, the processing time , the due date , the size and the weight . In addition, all the jobs are categorized into l families (each family represents a specific color for dyeing), and the family index of job i is denoted as . It is noteworthy that the processing time of each job is only determined by its family category but not affected by its size. Therefore, we could use to denote the processing time of any job that falls under family j. Each machine has a maximum volume, denoted by . A number of jobs in the same family can be processed in the form of a batch on machine k as long as the total size of the jobs does not exceed the capacity . The processing time of a batch of jobs from family j is equal to .
A setup operation is required whenever a machine is about to start processing the next batch with a different family than the previously finished batch. We assume that the setup time is identical and is denoted as s. Since the setup operation mainly concerns a thorough cleaning of the dyeing vat using a chemical detergent, sewage emissions are often incurred. We use to represent the environmental cost of a single setup operation. It is evident that the number of setup operations should be reduced, which means it is preferable to process the batches from the same family in a consecutive manner.
Meanwhile, it should be highlighted that the use of larger dyeing vats naturally leads to increased energy consumption in terms of electricity and excessive material consumption in terms of water and dyes (noting that unconsumed dyes are usually discharged in dissolved form). Therefore, it is more efficient to assign a 120 kg batch to a 150 kg machine than to a 200 kg machine. Formally speaking, when making scheduling decisions, we should consider maximizing the utilization rate of dyeing machines, which is equivalent to minimizing the total occupied capacity of machines.
Finally, due date performance is critical for any manufacturing company that adopts the make-to-order strategy. Hence, the total delivery tardiness should be minimized besides the above mentioned sustainability-oriented goals (setup reduction and utilization rate promotion). The three objectives, however, are usually conflicting (e.g., reducing the tardiness can cause a decrease in the machine utilization rate). Therefore, a multi-objective optimization approach is required to deal with such a scheduling problem.
2.2. The Linear Programming Formulation
We construct a mixed-integer linear programming (MILP) model to formulate the studied scheduling problem. Four sets of 0-1 decision variables are first defined as follows, where represents the h-th batch to be processed on machine k.
if job i is processed in , and otherwise.
if the jobs in belong to family j, and otherwise.
if the jobs in belong to a different family than the jobs in , and otherwise.
if there is at least one job assigned to , and otherwise.
The MILP model is then constructed based on these decision variables. The other variables in the model are all derived from these binary variables.
represents the family index of
.
denotes the finishing time of
.
and
indicate the completion time and the tardiness of job
i, respectively.
M is a very large positive number.
Equations (
1)–(
3) define the three objective functions to be minimized, i.e., the total weighted tardiness
, the total setup cost
(when a setup operation is performed on machine
k, an additional setup cost of
is incurred) and the total capacity utilization
(the sum of the capacity of all utilized batches). Constraint (4) requires that the total size of the jobs processed in a batch should not exceed the volume of the corresponding machine. Constraint (5) ensures that each job is assigned to one and only one batch. Constraint (6) guarantees that each batch must be associated with exactly one family (since the number of batches on each machine is unknown,
h is enumerated from 1 to
n for each machine
k, and
will be empty as
h becomes sufficiently large). Constraint (7) indicates that job
i can be assigned to
only if it complies with the family of the batch. Equation (8) is used to evaluate the family index of each batch, i.e.,
. Constraints (9) and (10) force
to take 1 if the family type of
is different from that of
. Equation (11) calculates the finishing time of the first batch on each machine (
), and then Equation (12) calculates the finishing time of each subsequent batch (
) by adding up the batch processing times and the setup times. Equation (13) defines the completion time (
) of job
i, which is equal to
if job
i has been allocated to
. Equations (14) and (15) define the tardiness (
) of job
i. Equation (16) forces
to take 1 if any job has been allocated to
. Constraint (17) requires that all empty batches should be placed after the non-empty batches.
2.3. Illustrative Example
An example instance of the scheduling problem is provided here for easier understanding. We have
,
(
);
,
;
,
;
;
(
). The other data regarding
,
and
are displayed as
Table 1.
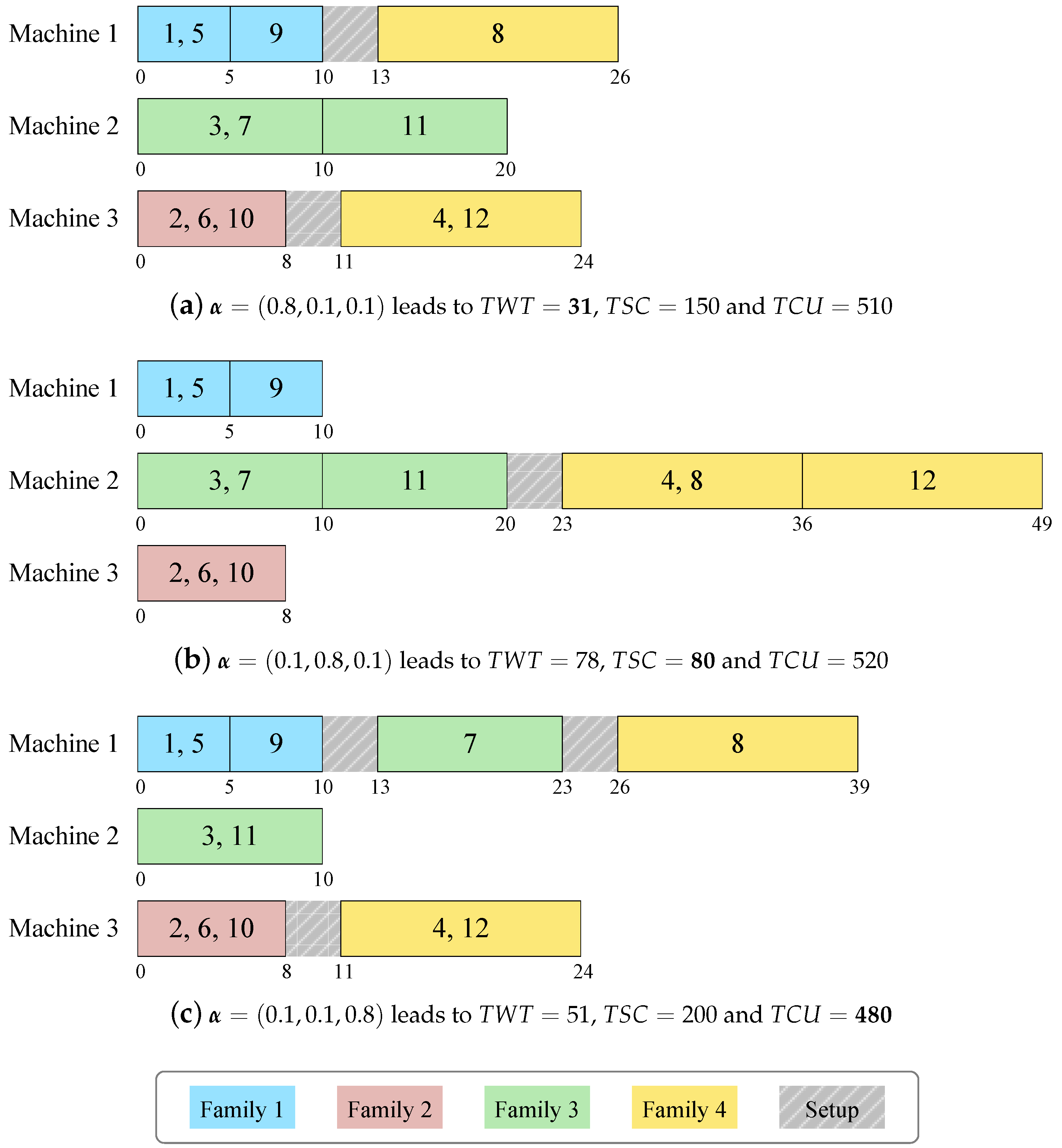
Using CPLEX to solve the model with different weighted sums of the three objectives, we could obtain a set of Pareto non-dominated solutions. Let the aggregated objective function be
, with
. Three schedules, for example, have been obtained under the settings
, respectively. They are shown as Gantt charts in
Figure 1. It complies with our intuition that the emphasized objective will get more bias in the optimization process. The minimum value of
(31),
(80) and
(480) is achieved respectively when each of the objectives is emphasized by the weight of 0.8.
This small instance is just used as an example to clarify the problem definition. It should be noted that the weighted sum method cannot generate all Pareto optimal solutions, and thus a systematic multi-objective optimization algorithm is required for solving practical-sized instances of the scheduling problem.
3. The Proposed MOGA-TIG Algorithm
In this section, a multi-objective genetic algorithm with tabu-enhanced iterated greedy local search (MOGA-TIG) is presented to solve the studied scheduling problem. In the following subsections, we will introduce the crucial components in our algorithm that have been designed to suit the features of this specific problem.
3.1. Encoding and Decoding of Solutions
We use a permutation sequence of n jobs and zeros to represent a possible solution to the problem. The zeros are interpreted as separators, and each sub-sequence indicates the preferential order of batching and processing the relevant jobs on the corresponding machine. To transform such a sequence into a feasible schedule, we devise the following heuristic procedure for quick decoding of solutions.
- Step 1:
Let . Use to denote the sub-sequence of jobs related to machine k.
- Step 2:
Let . Use to denote the i-th job in .
- Step 3:
Schedule job , the family index and the size of which are respectively denoted as and , by the following steps:
- (3.1)
If , return “infeasible” and terminate the procedure.
- (3.2)
Examine all the existing batches on machine k and try to identify the first batch which shares the same family with job and satisfies , where indicates the current total size of batch .
- (3.3)
If such a qualified batch does exist, insert job into this batch and accordingly update the total size of this batch.
- (3.4)
If there exists no batch satisfying the above conditions, create a new batch of family on machine k after all the existing batches. Insert job into the new batch and set the value of accordingly for this batch.
- Step 4:
If not all jobs in have been scheduled, let and repeat Step 3. Otherwise, proceed to the next step.
- Step 5:
Let . If , go back to Step 2, otherwise exit the procedure.
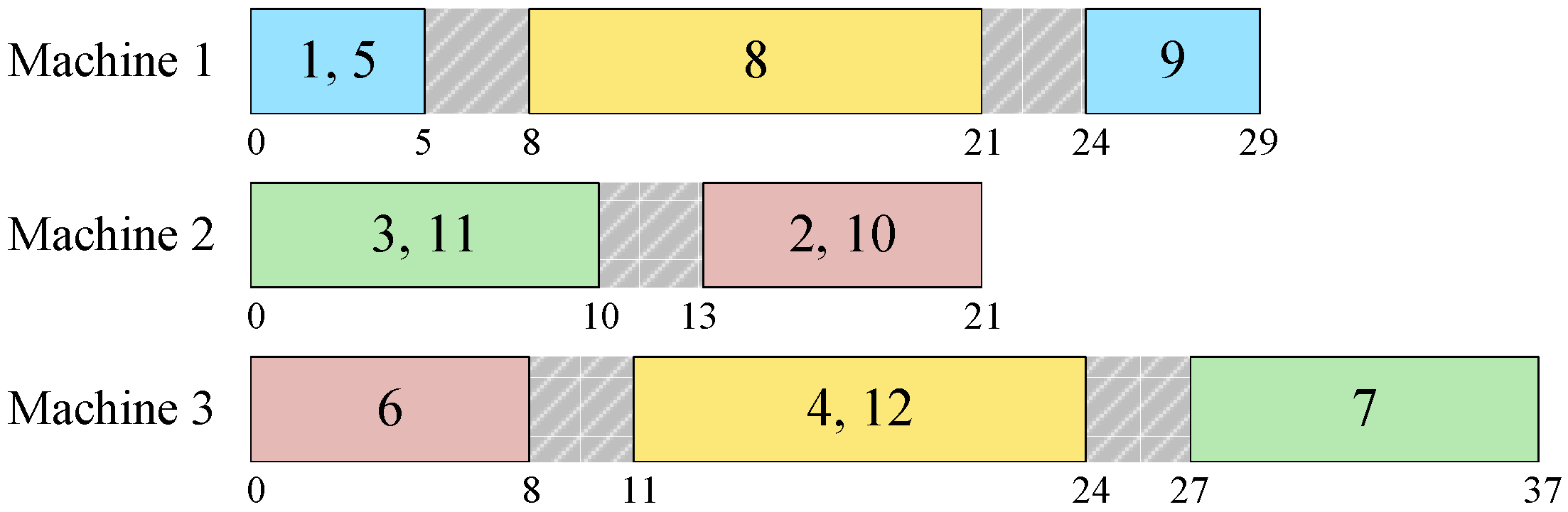
To illustrate the decoding procedure, we continue to use the example instance described in
Section 2.3. The schedule decoded from the given solution (1, 8, 9, 5, 0, 3, 10, 2, 11, 0, 6, 12, 7, 4) is shown in the form of a Gantt chart in
Figure 2. The first sub-sequence (1, 8, 9, 5) represents the jobs to be processed on machine 1, the second sub-sequence (3, 10, 2, 11) represents the jobs to be processed on machine 2, and the third sub-sequence (6, 12, 7, 4) represents the jobs to be processed on machine 3. When scheduling each machine, the jobs are scanned in the order specified by the corresponding sub-sequence and each job is always inserted into the earliest possible batch (in order to be started as early as possible).
3.2. Generation of Initial Solutions
Utilizing problem-specific domain knowledge, we have designed a heuristic procedure for generating a group of initial feasible solutions. The procedure consists of three critical steps, namely, job prioritization (determining the order of considering unscheduled jobs), machine selection (deciding which machine to use for the considered job), and batching (constructing a largest possible batch on the selected machine).
- Step 1:
Sort all jobs in non-decreasing order of their due dates (). The jobs with identical due dates are sorted in decreasing order of their weights (). The sorted job sequence is denoted as J.
- Step 2:
Select the first job in J, denoted as job . Determine the subset of machines which can be used to process (i.e., with a capacity no smaller than the size of ), denoted as .
- Step 3:
For each machine k in , independently perform a simulation of the following tasks:
- (3.1)
Create a batch with the family of and place it after all the existing batches on machine k. Insert into the batch.
- (3.2)
If there is surplus capacity in the batch, scan the subsequent jobs in J sequentially and add qualified jobs to the batch until no more job in the family can be fitted in.
- (3.3)
Evaluate the incremental costs related to this new batch: the total weighted tardiness of the jobs in the batch (), the setup cost incurred before starting the batch (), and the idle capacity of the machine in the course of processing this batch ().
- Step 4:
Define a weighted criterion based on the normalized values of , and as , where , and are random numbers in satisfying .
- Step 5:
Select from the machine associated with the minimum value of , and denote the machine as .
- Step 6:
Construct a batch on machine after existing batches. Assign job and subsequent jobs with the same family to the batch (subject to capacity limit ) in a sequential way and as many as possible.
- Step 7:
Delete from the list J the jobs that have just been assigned.
- Step 8:
If , go back to Step 2. Otherwise, terminate the procedure.
The above procedure can produce a group of different initial solutions because of the inbuilt randomization mechanism in Step 4. To generate more diverse solutions, we exert perturbations on the original ranking of jobs by randomly exchanging the positions of pairs of jobs in J (Step 1) before continuing to Step 2. In the initialization stage, of the required solutions are produced after performing such a random shuffling of the due date based job sequence.
The last issue is to transform a feasible schedule produced by the above initialization procedure to an encoded solution in order to be used by the optimization algorithm. We simply have to sort the jobs on each machine in increasing order of their starting times (jobs with smaller due dates or larger weights are prioritized in case of identical starting times) and use zeros as linkages in between to construct the encoded solution for any feasible schedule.
3.3. Pareto-Based Sorting of Solutions
In the multi-objective optimization setting, Pareto dominance is the major criterion to distinguish the quality of different solutions. Therefore, sorting a set of solutions
in the Pareto sense means dividing the set into
P subsets
such that: (1) Any solution
(
) is dominated by at least one solution
; and (2) any two solutions from the same subset are not dominated by each other. The sorting algorithm is essentially equivalent to a topological sort procedure and has been detailed in [
28].
It should be noted that, in practice, the number of solutions in each of these Pareto subsets can be considerably large, which means there often exist a number of solutions without mutual dominance relations. Hence, a more critical issue is to decide how the solutions within a non-dominated subset should be sorted and prioritized. The general idea is to suppress those solutions which are crowding around other solutions in the objective space, or equivalently, to give priority to the solutions which are sparsely located in the objective space. The motivation is to ensure that each solution maintained is sufficiently representative and thus the whole group of solutions can provide a wide variety of options for the decision makers. For the purpose of recognizing the degrees of crowdedness, a crowding distance measure must be defined. The following procedure is designed to evaluate the crowding distance value for each solution in a set .
- Step 1:
Calculate the distance between any two solutions and according to , where refers to the normalized difference between the two solutions with respect to the z-th dimension, i.e., , with and respectively denoting the maximal and minimal value of the z-th objective appearing in . Z represents the number of objectives ( for our problem).
- Step 2:
For each solution , identify the solutions that are located most closely to in the objective space, by the following steps:
- (2.1)
Let , .
- (2.2)
For , let , .
- Step 3:
For each solution , evaluate its crowding distance value according to .
Based on the discussions above, when ranking the solutions within a non-dominated set, we should sort them in a decreasing order of the value. The solutions in the back rank may have to be discarded during the evolutionary optimization progress due to limited archive size. In the process of evaluating , is an input parameter that should be properly set to balance accuracy with efficiency. It is recommended to set for the proposed algorithm.
3.4. Maintenance of Elite Solutions
The strategy of preserving the high-quality solutions that have been visited by the search process is known as “elitism” in the evolutionary computation field. Elitism is a critical function to guarantee theoretical convergence of an evolutionary algorithm. In our algorithm, there is such an elitism mechanism which helps to record the best-so-far solutions and thereby accelerate the convergence rate. The elitism strategy designed for the MOGA-TIG works in the following way. An independent archive
is used to store the high-quality non-dominated solutions that are found during the optimization process. The solutions stored in
will be mixed with each generation of individuals so that they will have chance to take part in the evolutionary operations. In addition, an enhanced local search algorithm (to be introduced in
Section 3.6) will be implemented to improve a certain part of solutions in
in each generation.
To control the computational burden, a hard limit is set for the maximal number of solutions that can be saved in , expressed as ( represents the population size). The procedure used to update with a new solution set is detailed as follows.
- Step 1:
Set .
- Step 2:
For each solution , test whether is dominated by .
- Step 3:
If is found to be dominated by any of the solutions in , go to Step 6.
- Step 4:
For each solution , if dominates , remove from .
- Step 5:
Let .
- Step 6:
Let . If go back to Step 2, otherwise proceed to the next step.
- Step 7:
If , sort all solutions in in a decreasing order of their crowding distance values (). Keep the first solutions and delete the rest of solutions.
3.5. Genetic Operators
- (1)
Selection. In the proposed algorithm, selection of individuals from the current population is required for conducting crossover and for constructing the new-generation population. The standard roulette-wheel selection method is adopted, and the crucial issue is to assign the probability of each solution being selected. We first divide the considered solution set
into a series of Pareto ranks
(c.f.
Section 3.3), and then assign the selection probabilities based on two simple principles: the solutions in
should have larger probability of being selected than the solutions in
if
, and the solutions within the same non-dominated subset
should be equally treated in the selection stage. We therefore assign the probabilities in the following way (linearly decreasing style), i.e., each solution in
(
) will be selected with probability
where
denotes the number of solutions in
.
- (2)
Crossover. The crossover operation is performed with probability
(a.k.a. the crossover probability) for two randomly selected individuals from the current population. According to the encoding policy (c.f.
Section 3.1), the crossover operator designed for the MOGA-TIG consists of three sequential steps, i.e., removal of zeros from the encoded solutions, LOX-based crossover on random positions of the parent solutions, and reinsertion of zeros to recover the correct encoded form of solutions. For illustration purpose, an example is given in
Figure 3. Firstly, the zeros (representing delimiters) are all removed from the parent solutions
and
. Subsequently, two random positions for crossover are determined, and the LOX (linear order crossover) operator [
29] is applied to perform crossover of the two intermediate solutions (the segments between the two identified positions are exchanged while the other elements are reorganized in a linear way). Finally, the zeros are inserted back to their original positions and thereby the two offspring individuals
and
are produced (note that the positions of zeros in the two solutions are also swapped, i.e., the positions of zeros in
are identical with those in
and the positions of zeros in
are the same as those in
). In this way, the characteristics of parent solutions are partially inherited by the offspring solutions.
- (3)
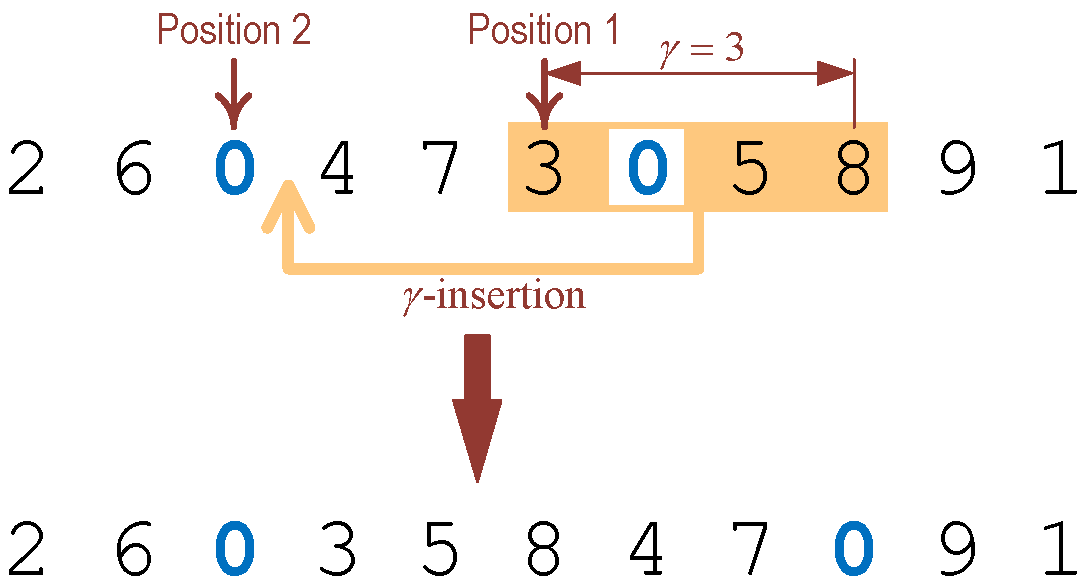
Mutation. The mutation operator designed for the MOGA-TIG is based on reinsertion of
consecutive jobs from the original sequence. This new operator is called
-insertion for short. The commonly used operators for mutation (e.g., swap of two elements, reinsertion of a single element) only lead to small variations of the current solution, which may not be sufficient for the implementation of an extensive search in large-scale solution space. The
-insertion operator is designed to overcome the limitation of traditional mutation operators. It extracts a series of
jobs (excluding zeros) from a certain location of the original sequence and reinsert them as a whole into another location of the sequence, respecting the relative order of these jobs. The length of a reinserted segment (i.e.,
) is randomly selected from
, where
is an input parameter for controlling the mutation level. For illustration purpose, an example is given in
Figure 4. Firstly, position 1 for job removal is randomly identified (
in this example) and, meanwhile, the length
is randomly selected (
in this example). Note that zeros are not counted into the length of extracted segments. Subsequently, position 2 for job insertion is randomly identified subject to the constraint that the selected position does not overlap with the segment to be extracted (
in this example). Finally, the segment (excluding zeros) is taken out and reinserted to the location immediately after position 2, and a new solution is thereby produced.
- (4)
Feasibility check. It should be noticed that crossover and mutation can produce infeasible solutions because of large-sized jobs being assigned to low-capacity machines. After new solutions are produced, we check each sub-sequence (related with each machine), and if any job exceeding the corresponding machine’s capacity is found, it is reassigned to another capable machine and reinserted to a random position in that sub-sequence. If more than one machines are applicable, the machine with minimum capacity will be chosen (assuming that machines are numbered in increasing order of their volumes, then choose machine for job i such that ).
3.6. The Embedded Local Search Function
Previous studies in the evolutionary computation field have suggested that an embedded local search component is usually crucial for achieving robust optimization performance. The reasons are twofold. On the one hand, the working mechanism of local search is believed to be complementary to that of population-based search (fine-granularity vs. coarse-granularity search). On the other hand, local search algorithms can exploit some structural properties of the specific problem, which is often difficult to be utilized by the evolutionary algorithm at the population level.
In this paper, we propose a tabu-enhanced iterated greedy (IG) algorithm as the local search module to be embedded into the multi-objective genetic algorithm framework. We start with the standard IG and then discuss how we have extended it to effectively cope with the multi-objective optimization context.
3.6.1. The Basic IG algorithm
The standard iterated greedy (IG) algorithm [
30] was intended for single-objective combinatorial optimization problems. The IG algorithm consists of two iterative phases, i.e., destruction and construction. In the destruction phase, some solution elements are removed from a complete solution, and in the subsequent construction phase, a greedy heuristic is applied to restore the removed elements so that a new candidate solution is constructed. The two phases are implemented iteratively until a predefined termination condition is met.
- Step 1:
Produce an initial solution .
- Step 2:
Conduct (optional) local search for improving the initial solution. The improved solution is denoted as .
- Step 3:
[Destruction] Randomly remove d elements from . The removed elements are stored in in the order they are picked out. The resulting partial solution is denoted as .
- Step 4:
[Construction] Insert the elements of back into in a sequential manner. For each element, first examine all the possible locations for insertion and then choose the best location. The newly constructed solution is denoted as .
- Step 5:
Conduct (optional) local search for improving . The improved solution is denoted as .
- Step 6:
Update , which records the best solution found so far, i.e., let only if turns out to be better than the original .
- Step 7:
Update the incumbent solution using an acceptance criterion which decides whether to replace with .
- Step 8:
If the termination criterion is not satisfied, go back to Step 3. Otherwise, output the best-so-far solution .
3.6.2. The Proposed Tabu-Enhanced Multi-Objective IG Algorithm
Since the basic IG algorithm can only handle single-objective optimization problems, the key issue of applying IG principles to our problem lies in effective maintenance of non-dominated solutions during the search process. Another limitation of the standard IG is the lack of a mechanism to prevent repeated search (it may so happen that the same jobs are being extracted repetitively by the destruction operator in consecutive iterations). Therefore, a tabu mechanism is designed to prohibit the same jobs being removed again in a certain number of subsequent iterations.
The proposed tabu-enhanced IG local search algorithm takes a set of solutions () as input, and conducts an in-depth exploitation based on these initial solutions with the aim of finding solutions that dominate the original ones. The complete local search algorithm is described as pseudo code in Algorithm 1 and is hereinafter abbreviated as TIG.
| Algorithm 1 Tabu-enhanced IG local search algorithm |
Input: A solution set denoted as together with parameters d, and - 1:
Let ; - 2:
for each do - 3:
Let ; - 4:
Record ; - 5:
end for - 6:
for do - 7:
Let ; - 8:
for each do - 9:
Let ; - 10:
Randomly select and remove d unrepeated jobs from (subject to the tabu list ). Denote the resulting partial solution as and the sequence of removed jobs as . - 11:
; // Update the tabu list using Procedure 1 - 12:
Let ; - 13:
for ddo - 14:
Let ; - 15:
for each do - 16:
Try inserting the q-th job from into the partial solution at every possible location. The obtained set of non-dominated partial solutions is denoted as . - 17:
; - 18:
end for - 19:
end for - 20:
for each do - 21:
Record ; - 22:
end for - 23:
; - 24:
end for - 25:
Let ; - 26:
end for
Output: The non-dominated solution set |
We provide the following remarks to further explain Algorithm 1.
- (1)
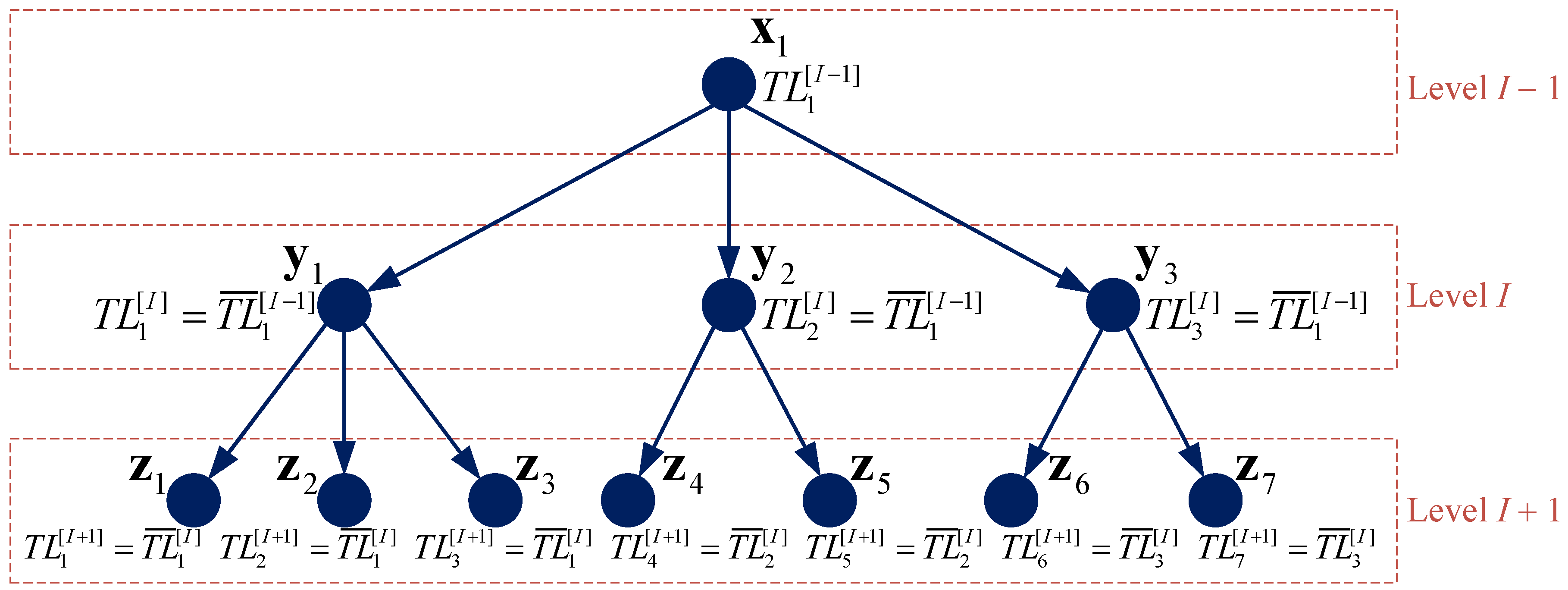
The proposed TIG differs from the basic IG mainly because the construction phase of TIG would produce more than one solutions at a time (Lines 13–19) based on the Pareto optimality criterion. As a result, the search pattern of the TIG is comparable to that of a breadth-first search. In each iteration , the nodes of level I are completely exploited and the nodes of the next level are generated. The maximum depth of the search trees is equal to (i.e., the number of iterations).
- (2)
Under the tree search framework, implementation of the tabu mechanism requires the use of a backtracking technique. In the TIG, we introduce a new attribute
for each solution to record the index of the tabu list which has been used for the destruction of its parent solution (thus leading to the current solution itself). In Lines 20–22, the
attribute of the new solutions produced based on the destruction of
are all pointed at
i. In Line 9, before solution
in the present iteration
I is randomly destructed, we build the corresponding tabu list
by inheriting the tabu list that has been updated after the destruction of its parent solution in the previous iteration
.
Figure 5 illustrates the inheriting of tabu lists between adjacent levels in the search tree, where
with a bar indicates updated tabu lists (c.f. Line 11).
- (3)
The tabu mechanism in the TIG relies on a short-term memory , which records the recently removed jobs and prevents these jobs from being removed again in a certain number of offspring generations. The number of subsequent generations in which removal of the same jobs are prohibited is defined as the tabu tenure. We use to represent this parameter. In Line 11, the tabu list gets updated after some jobs (different from those in the list) have been removed from the current solution. Procedure 1 provides details of this step. The jobs which have just been removed are added to the , and meanwhile the “age” of the existing jobs in the is increased by one, and finally if any jobs have grown to the upper limit age they will be eliminated from the (and can be freely considered for removal again). According to the definition of , we must ensure for the algorithm to work properly.
- (4)
The process of construction after removal of d jobs from solution starts from Line 12. The series of sets are used to store the non-dominated partial solutions obtained after q jobs have been reinserted (). In the process of reinserting the q-th job, all the partial solutions in should be tried one after another for possible insertions (Lines 15–18) and the resulting non-dominated partial solutions are assigned to . Obviously, consists of the non-dominated complete solutions constructed based on the previously destructed and thus it should be incorporated into the next generation of solutions (Line 23). The operator returns all the Pareto non-dominated (partial) solutions in a set.
| Procedure 1 UpdateTL |
- 1:
for each do - 2:
; - 3:
Set ; // the age of j in - 4:
end for - 5:
for each do - 6:
; - 7:
if then - 8:
; - 9:
end if - 10:
end for
Output: the updated tabu list |
3.7. Overall Structure of the MOGA-TIG Algorithm
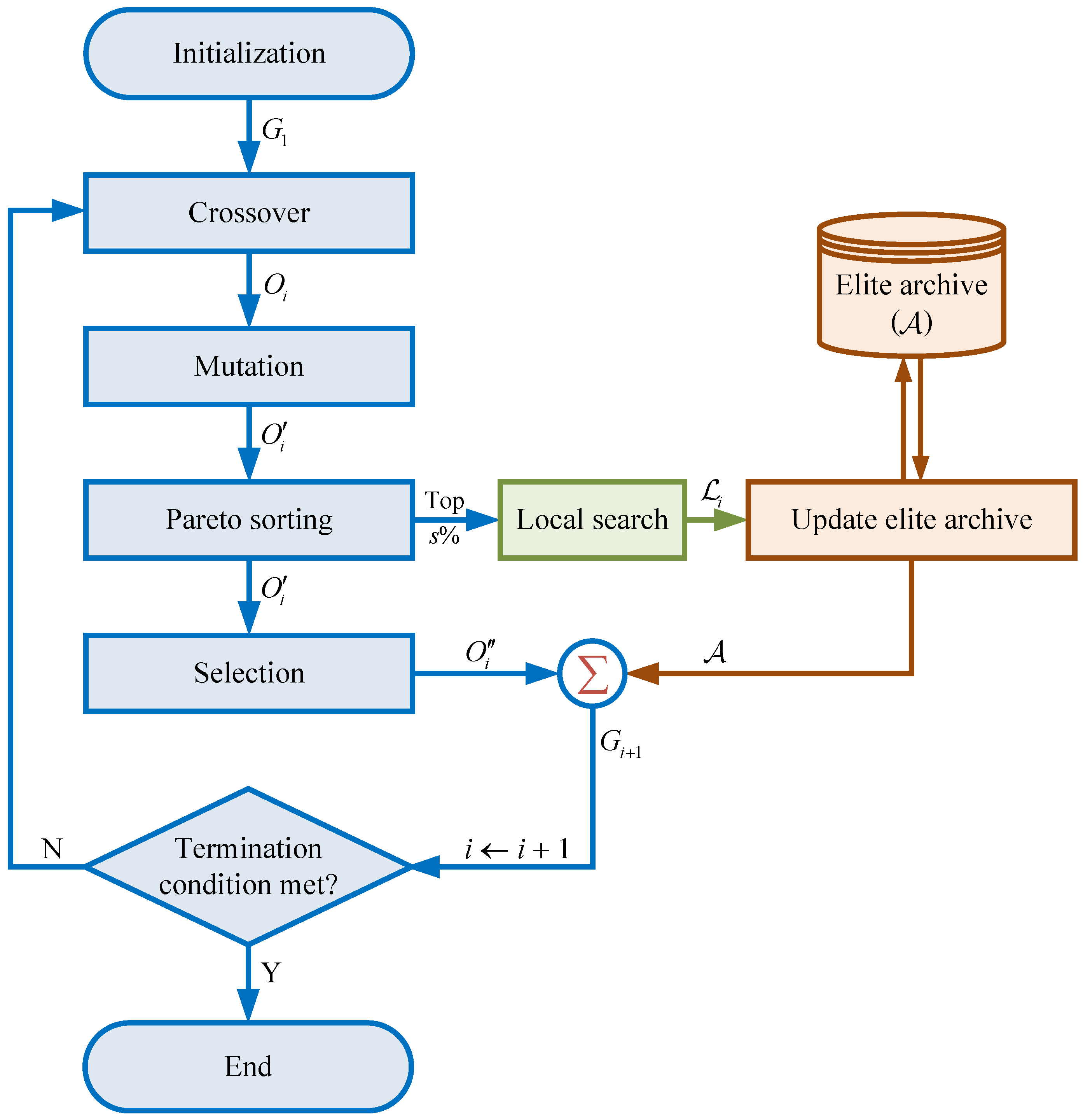
We now provide a comprehensive summary of the proposed MOGA-TIG algorithm. Meanwhile, a flowchart is given in
Figure 6 to facilitate the perception of the algorithm framework.
- Step 1:
[Initialization] Apply the procedure described in
Section 3.2 to generate a total of
initial solutions, which are then filled into the initial population
. Initialize the generation index
, and the elite archive
.
- Step 2:
[Crossover] Conduct the crossover operation for
times. For each time, two individuals are randomly selected from the current population
and then the crossover operator as described in
Section 3.5 (part 2) is executed with probability
. The obtained offspring individuals are denoted by the set
.
- Step 3:
[Mutation] Execute the mutation operator as described in
Section 3.5 (part 3) for each individual in
with probability
. The modified solution set is denoted by
.
- Step 4:
[Pareto sorting] Sort all the solutions in
using the procedure presented in
Section 3.3.
- Step 5:
[Local search] Conduct a local search for each solution that ranks in the top
of all solutions in
by using the TIG algorithm introduced in
Section 3.6. The solution set output by the local search is denoted by
.
- Step 6:
[Elitism] Update the elite archive
with
using the procedure detailed in
Section 3.4.
- Step 7:
[Selection] Using the selection method described in
Section 3.5 (part 1), randomly select
solutions from
. Denote the subset of selected solutions as
.
- Step 8:
[New generation] Let .
- Step 9:
[Loop/Termination] Let . If , return to Step 2. Otherwise, terminate the algorithm with (i.e., non-dominated solutions in ) as output solutions.
4. Computational Results
4.1. Experimental Setup
The instances for testing the proposed algorithm have been generated according to the specifications given below.
The number of jobs and the number of job families are to be considered in a coordinated manner at eight different levels, i.e., .
The family index for each job i is randomly selected from with uniform probability distribution. The size of job i is generated from the discrete uniform distribution . The due date of job i is set as , where follows the uniform distribution . The weight of job i is generated from the discrete uniform distribution .
The processing time required for any job in family j is produced from the discrete uniform distribution .
The number of machines m is to be considered at three levels, i.e., .
The volume of machine k is given as . The setup cost related with machine k is given as , where follows the uniform distribution . The setup time s required for a machine to switch between different families is drawn from the discrete uniform distribution .
We have generated a total of 120 test instances based on the above standards (there are 8 levels for and 3 levels for m, and 5 instances are generated for each combination ).
Following the standards for multi-objective optimization, we adopt four performance indicators for assessing the quality of obtained solutions. Given non-dominated solution sets and , which are achieved by different optimization algorithms respectively, the relevant performance indicators are formally defined as follows.
The first indicator reflects the number of solutions in the non-dominated solution set, which is also known as the overall non-dominated vector generation (ONVG) metric [
31]. Formally, we define
. Larger
suggests a wider range of choices for the decision makers and therefore represents a more desirable situation.
The second indicator reflects the mutual dominance relations between the two sets of solutions, which is called the coverage metric (CM) [
32]. Formally, CM is defined as
where
denotes the case where
either dominates or turns out identical to
. Hence,
characterizes the proportion of solutions in
that are dominated by (or equal to) some solutions in
. Note that
is usually less than 1 because there can exist a portion of solutions in
and
which are not mutually dominated.
The third indicator reflects the distance between the set of obtained solutions and a high-quality reference set (estimated Pareto frontier of the problem) in the objective space. Specifically, the distance metrics
and
[
33] are defined as:
where
R denotes the reference set, which is obtained by selecting all the non-dominated solutions found by the compared algorithms so as to approximate the Pareto frontier. Meanwhile,
where
refers to the value range of the
z-th objective function. For each solution in
R, there is an associated solution in
with the minimum distance to that solution. Clearly,
captures the average of such distances, while
records the maximum of such distances. Therefore, small values of
and
are preferable.
The fourth indicator measures the evenness of solution distribution. It is known as Tan’s Spacing (TS) metric [
34] and is defined as
where
and
stands for the Euclidean distance between
and its nearest neighboring solution in
(in the objective space). Since decision makers always prefer that the candidate solutions should be evenly distributed, smaller values of
indicate higher quality of the obtained solutions.
4.2. Experiment on Parameter Influence
To study the influence of the major parameters involved in the proposed algorithm, we adopt a DOE (design of experiments) approach based on the Taguchi design method [
35] which significantly reduces the number of scenarios to be tested. In the DOE stage, we focus on the distance metric
as the exclusive indicator of solution quality because
reflects the optimality of solutions in the most accurate way. The reference set
R is constructed by a combination of all the non-dominated solutions found by the compared algorithms after 20 independent runs with 1000 generations allowed for each run. The proposed MOGA-TIG algorithm is executed 20 times based on each set of parameter values required to be tested, and then the average value of
is used as the input of DOE analysis.
A randomly generated instance which involves 150 jobs (9 families) and 15 machines is used for the parameter experiments. The maximum execution time of the algorithm is set as 450 s per run.
(1) Central algorithm parameters
In the first experiment, we study the influence of the key parameters related to the MOGA (
,
,
,
,
) and temporarily neglect the local search module (by forcing the TIG to output the same solutions as what it receives as input). Each parameter has been tested at 4 different levels (
,
,
,
,
). The Taguchi design with an orthogonal array of
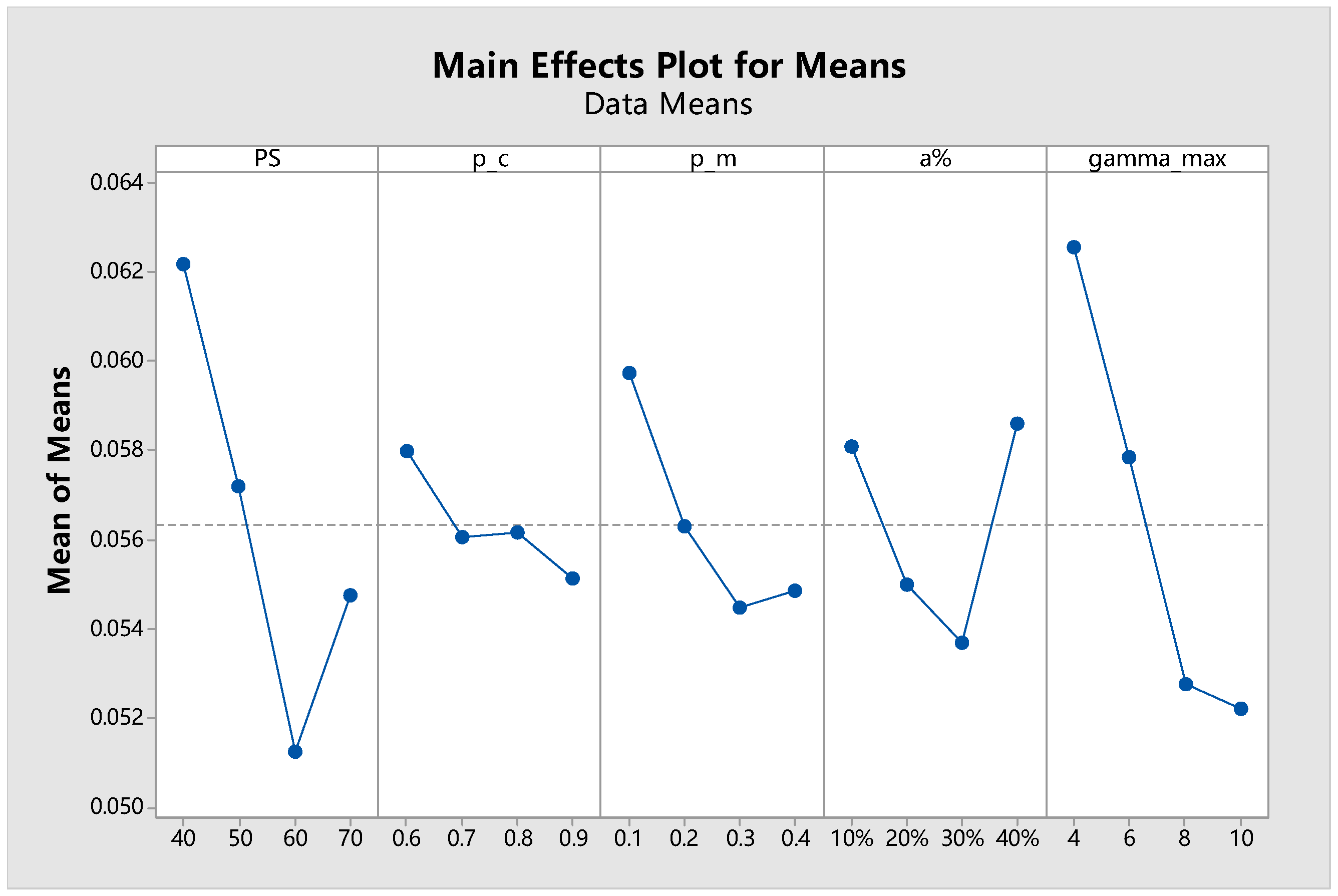
is adopted, which suggests that 16 scenarios need to be tested by experiments. The resulting main effects plot is shown in
Figure 7.
According to the results, the following comments can be made. It is observed that has a remarkable impact on the solution quality. When the population does not reach a sufficient size, the diversity of solutions is limited and the genetic operators including crossover and selection cannot function properly. On the other hand, a too large can also be unfavorable because in this case the number of generations evolved will be reduced (recalling that the computational time available is fixed) and consequently the solutions tend to be underdeveloped. The two parameters and are both related with the intensity of applying the mutation operator in the evolutionary process. The general trend is clear, i.e., the solution quality will improve as the frequency or the depth of mutation is increased (in the reasonable range). This validates the effectiveness of the proposed mutation strategy based on multiple insertions. Meanwhile, it is worth pointing out that the mutation rate cannot be set too large, otherwise the inheritance of solution characteristics between successive generations will be adversely affected. The parameter is used to control the maximum size of the elite archive. It is revealed that the preservation and reuse of elite solutions during the evolutionary process has clearly helped to accelerate the convergence and find higher quality solutions. However, the elite archive size should not exceed a certain limit because otherwise more diverse solutions will be crowded out, hindering the inherent optimization mechanisms of genetic algorithm. Finally, the crossover rate has not produced a high level of influence on the solution quality as long as it has been assigned a sufficiently large value. Crossover is the most essential form of genetic operations, and thus a high crossover rate ensures proper function of the evolutionary mechanism.
(2) Local search parameters
In the second experiment, we study the influence of the local search related parameters (
,
d,
,
) on the final solution quality. Each parameter has been tested at 4 different levels (
,
,
,
). The Taguchi design with an orthogonal array of
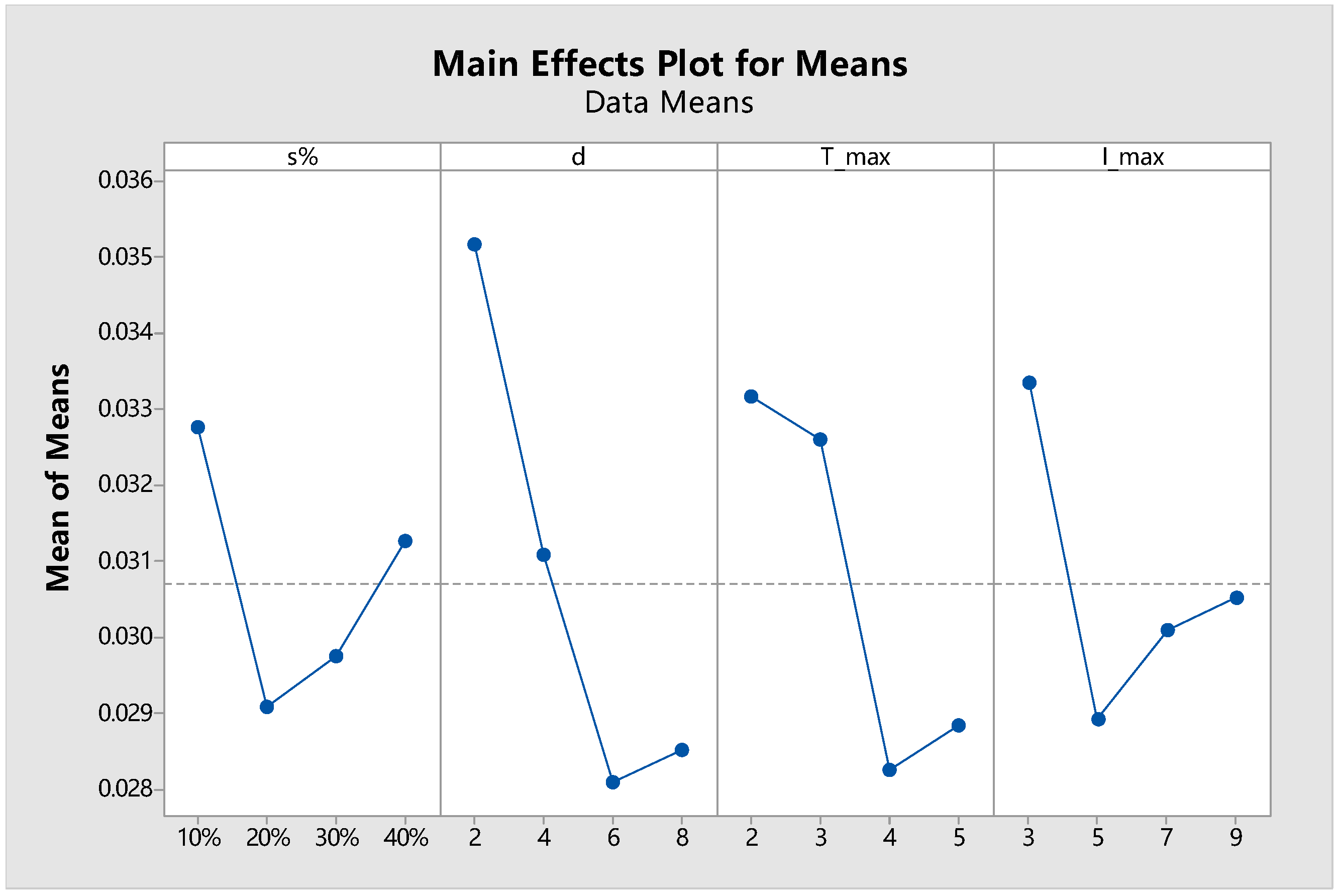
is adopted, which suggests that 16 scenarios need to be tested by experiments. The other parameters of the MOGA-TIG are all fixed at their recommended values which will be summarized before the end of this subsection. The resulting main effects plot is shown in
Figure 8.
Based on the results, the following remarks can be made. It is clearly seen that d produces a significant impact on the solution quality. Generally, a larger value is preferred for d because in such cases the solutions have greater opportunity to be improved (after an in-depth reconstruction) by the TIG algorithm. However, local search may lead to loss of diversity besides its notable ability of enhancing certain individual solutions. That’s probably why we observe a slight retracement when d is set to 8 (the anti-diversification effect has become dominant). The influence of the maximum iteration number is also noteworthy. Although increasing can bring about a more intensive local search, the resulting increase in computational burden should not be neglected. Because actually reflects the depth of the search tree, the complexity of the search process grows in an exponential manner with the increase of . Therefore, setting too large will inevitably occupy excessive computational time that could have been utilized by the evolutionary process and consequently deteriorate the solution quality. Meanwhile, the noticeable impact of the tabu tenure on the solution quality shows that the proposed tabu mechanism does help to avoid repeated search and contribute to effective exploitation of the neighborhood. Finally, the percentage of solutions participating local search () should represent an appropriate balance between exploration and exploitation. Considering the complexity and the effectiveness of the TIG algorithm, it is not recommended to set the frequency of calling local search at a level higher than 30%.
To further examine the effect of the local search module, we have conducted control experiments in which the local search function is completely removed, i.e., by setting
. The resulting MOGA and the original MOGA-TIG have been executed for 20 times, respectively, using the recommended parameter settings (except the difference in
). We report the average value of
obtained from each scenario in
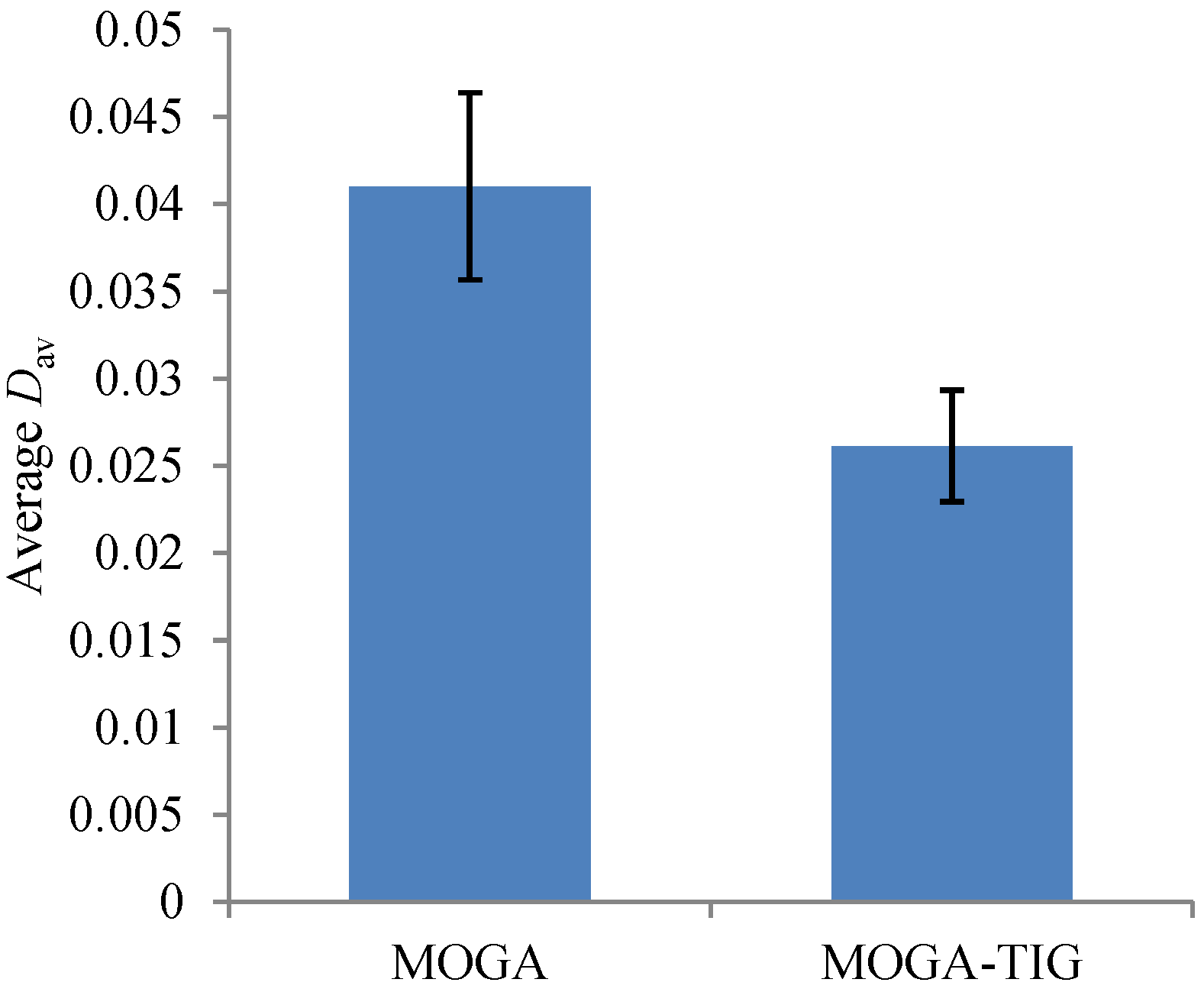
Figure 9, with the error bars indicating standard deviations. It is clear that the local search component not only helps to achieve higher solution quality in the average sense, but also improves the robustness of the obtained results (narrowing the standard deviation).
Now, we summarize the recommended parameter settings for the proposed algorithm in
Table 2 based on the above results and discussions.
4.3. Optimality Test on Small-Sized Instances
To examine the optimization ability of the proposed algorithm, we compare the results from MOGA-TIG with the solutions obtained by the CPLEX solver based on the weighted sum approach (the weighting vector is enumerated according to
with a step size of 0.01, i.e., from
,
, …, to
). Since the exact algorithm can only handle small instances within acceptable time, the group of instances with
is utilized for this experiment. The proposed algorithm has been executed for 20 times (150 s per run) independently on each instance and the performance indicator values have been averaged. The resulting data are displayed in
Table 3.
According to the results, it can be judged that the proposed algorithm has achieved satisfactory solution quality. On average, the solutions found by the MOGA-TIG is able to match 40% of the solutions output by CPLEX (i.e., having equal objective values). Meanwhile, the MOGA-TIG has maintained relatively low values for the and indicators (0.017 and 0.036, respectively), showing that the obtained solutions are situated closely to the CPLEX-based solutions. Although the number of solutions from the MOGA-TIG is a bit smaller than that of the CPLEX approach, the degree of solution distribution evenness is comparable. It is noteworthy that the weighted sum approach can miss some Pareto optimal solutions if the Pareto frontier is concave in certain parts. For this reason, is slightly less than 1 for three instances. Overall, it is evident that the proposed algorithm has performed well, especially when considering that it consumes much shorter computational time than the exact approach (which consumes more than two hours for each instance on average).
4.4. Comparison with MOEAs in the Literature
To evaluate the performance of the MOGA-TIG algorithm, we compare it with the well-known and state-of-the-art multi-objective evolutionary algorithms (MOEAs) in the literature. Considering that there are three objectives to be optimized in our problem, we adopt the latest MOEAs that are able to handle problems with “many” objectives (
). The compared algorithms include the NSGA-III [
36], which is an upgraded version of the famous NSGA-II, and the MOEA/DD [
37], which can be regarded as an enhanced version of the renowned MOEA/D.
To adapt the real-coded NSGA-III and MOEA/DD to our problem, we design a dedicated procedure for transforming a vector of real values () to a feasible schedule for our problem.
- Step 1:
Sort the n values in non-decreasing order, and then record the sequence of their subscripts as a permutation of , which is denoted as . Let .
- Step 2:
Denote the family index and the size of job as and , respectively.
- Step 3:
For to m, if , examine existing batches on machine k and find the earliest batch which complies with family and meets , where represents the current total size of batch . If such a qualified batch is found, stop the scan and immediately insert job into this batch (with the relevant item updated accordingly).
- Step 4:
If no qualified batch is found, identify the machine such that . Place a new batch of family on machine immediately after the existing batches, and insert job into this new batch (with the relevant item created).
- Step 5:
Let . If go back to Step 2, otherwise terminate the procedure.
The proposed algorithm MOGA-TIG together with the two compared algorithms NSGA-III and MOEA/DD have been implemented under Visual C++ 2015 based on a PC with Intel Core i7-4790 3.60 GHz CPU and 16 GB RAM. To ensure that the subsequent comparisons are fair, the computational time that is allowed for a single run of each algorithm is confined to a common level: at most seconds could be used to solve an instance with n jobs. Specifically, we will allocate
150 s for each attempt to solve a 50-job instance;
300 s for each attempt to solve a 100-job instance;
450 s for each attempt to solve a 150-job instance;
600 s for each attempt to solve a 200-job instance.
As soon as the time budget is consumed, the algorithm must stop and output the currently available non-dominated solutions. Under such a computational setting, the number of generations () finished by each algorithm is no longer a pre-determined constant but is affected by the relative efficiency of the algorithm.
The parameters of the two compared algorithms are determined by considering the suggestions from their developers, and then fine-tuned on the basis of problem-specific preliminary experiments so that they can achieve the best performance on our problem. The parameter settings for the NSGA-III and MOEA/DD are listed as follows.
The crossover probability: (distribution index ).
The mutation probability: (distribution index ).
The number of reference points (for NSGA-III) or the number of weight vectors (for MOEA/DD): .
The population size: for NSGA-III (smallest multiple of 4 above 91) and for MOEA/DD.
The penalty parameter in PBI (penalty-based boundary intersection [
38]):
.
The neighborhood size: .
The probability to choose mating partner in the neighborhood: .
Computational experiments have been conducted based on the specified settings. Each algorithm, including MOGA-TIG, NSGA-III and MOEA/DD, has been run for 20 independent times on each test instance. Average values of the performance indicators collected from the 20 runs are reported in groups of
n (the number of jobs) and are shown in
Tables S1–S8 (see the
Supplementary Materials). To verify the statistical significance of the resulting data, we have performed paired-sample
t-tests on the obtained indicator values (MOGA-TIG vs. NSGA-III and MOGA-TIG vs. MOEA/DD). The
p-values from the
t-tests are shown in
Table 4 and
Table 5.
When presenting the coverage metric (CM) data in
Tables S5–S8, we assume that
represents the solutions found by the MOGA-TIG,
represents the solutions obtained by the NSGA-III, and
represents the solutions output by the MOEA/DD. Meanwhile,
denotes the combined set of non-dominated solutions achieved by NSGA-III and MOEA/DD together.
Based on the presented computational results, the following remarks can be made.
Focusing on the ONVG metric, it is clearly observed that the number of Pareto solutions obtained by each algorithm grows steadily with the size of the test instances. This is because, as n and l increases, there will be more opportunities of making trade-offs between the three objectives by means of batching and sequencing. The number of solutions obtained by the MOGA-TIG exceeds the number of solutions from both compared algorithms on 81 out of the 120 instances. By a closer observation, it is found that most of the 81 cases have occurred on large-sized instances (e.g., covering 25 of the 30 instances with 150 jobs and all of the 30 instances with 200 jobs). Meanwhile, the NSGA-III is able to find more Pareto solutions than the MOEA/DD for smaller instances but becomes slightly weaker than the MOEA/DD when faced with larger instances.
Focusing on the distance metrics
and
, it is observed that the proposed MOGA-TIG has clearly outperformed the compared algorithms in the average sense. In fact, the MOGA-TIG achieves a smaller
than both compared algorithms on 94 out of the 120 instances, and achieves a smaller
than both compared algorithms on 96 out of the 120 instances. It is worth noting that, when calculating
and
according to Equations (
21) and (), the reference set which is used to approximate the true Pareto frontier has been given by the compared algorithms (NSGA-III and MOEA/DD) based on 1000 iterations per run, which means there has been a slight bias towards the NSGA-III and MOEA/DD in terms of the distance metrics. The performance of the proposed algorithm under such a circumstance is therefore quite satisfactory and convincing.
Focusing on the TS metric, it is found that the MOGA-TIG has achieved the smallest indicator value on 107 out of the 120 instances. This advantage can be attributed to the in-built sorting mechanism based on accurately defined crowding distances. In particular, we have adopted a normalized distance measure which is similar to the definition of Euclidean distance, while the compared algorithms employ a distance measure which is comparable to the taxicab distance ( norm). The fact that the TS indicator is defined on the basis of Euclidean distances clearly suggests that our distance measure is more suitable and pertinent for describing the distribution of solutions in the objective space. Meanwhile, it can be observed that the TS values tend to increase as the size of instances grows (most apparently for NSGA-III). The degradation is inevitably due to the exponential expansion of discrete solution spaces which aggravates the difficulty of finding equally spaced Pareto solutions.
Focusing on the CM metric, we can see that the average value of remains above 0.95 and the average value of remains above 0.90 for all the test instances, which clearly shows that the great majority of the solutions from NSGA-III () and MOEA/DD () are dominated by or at most identical (in terms of objective vector) to the solutions found by the MOGA-TIG (). On the other side, the relatively small average values of and (below 0.05 for all instances) again verify the superior quality of the solutions obtained by the proposed algorithm. In addition, we have also reported the CM values with respect to the integrated solution set (). In this case, we observe a slight drop in the average value of (compared to and ) and a marginal increase in the average value of (compared to and ), which shows that the combination of solutions does lead to noticeable improvement of quality. Another interesting fact to notice is that the averaged tends to increase with the instance sizes (from 0.89 to 0.93) while the averaged seems to decrease (from 0.05 to 0.03) with the instance sizes. Such a trend suggests that the proposed algorithm exhibits a degree of comparative advantage in handling large-scale instances with limited computational time.
According to the statistical results (one-tailed
p-values) shown in
Table 4 and
Table 5, 31 of the 32 paired samples tested are statistically different if we adopt a significance level of 0.01. The only insignificant case occurs on the group of 50-job instances when comparing the ONVG values between MOGA-TIG with NSGA-III. In summary, the overall statistical results have revealed that the proposed algorithm significantly outperforms the state-of-the-art MOEAs for solving the complex scheduling problem studied in this paper.
5. Conclusions
In this paper, we focus on modeling and solution of a production scheduling problem with explicit consideration of pollution-reduction objectives that are critical to the long-term goal of sustainable manufacturing. Two environmentally-related objective functions have been defined to capture the pollutant emissions during setup operations as well as the potential pollution caused by underutilized production equipment. These sustainable objectives are considered alongside with the conventional scheduling objective (i.e., total weighted tardiness, which reflects the penalty for delayed delivery of products) under a three-objective optimization framework. We have derived an exact mixed-integer programming formulation for the problem and verified the model by applying a commercial solver to small-sized instances based on weighted sum approximations. Due to the high complexity of the problem, a systematic multi-objective optimization algorithm is required to be able to solve practical-sized instances in the Pareto optimality sense. For this purpose, we have proposed a multi-objective genetic algorithm integrated with tabu-enhanced iterated greedy local search (abbreviated as MOGA-TIG) specifically for solving the studied scheduling problem.
The proposed MOGA-TIG algorithm features a sequence-based encoding/decoding scheme, a dedicated initialization procedure utilizing problem-specific information, a set of redesigned genetic operators to suit the search space of the problem, a number of novel functions to deal with Pareto optimality, and most importantly, an effective local search strategy for conducting in-depth exploitations around selected promising solutions in each generation. Using fine-tuned parameter settings, we have carried out extensive computational experiments with 120 different-sized test instances. The performance of the MOGA-TIG is compared with that of two state-of-the-art MOEAs under the same levels of computational time budget. According to the four adopted performance indicators, our approach is able to outperform the compared algorithms on a dominant number of instances and in a statistically significant sense.
The results have revealed the remarkable role that production scheduling could play in reducing the emissions of chemical pollutants from manufacturing processes. Our research has highlighted two major causes of pollution in the cloth-dyeing industry, i.e., avoidable setup activities and underutilized production capacity, which are, in fact, commonly observed issues in many other manufacturing industries (e.g., glass production, wafer fabrication and steel making) as well. Therefore, this work can shed a light on the definition of environmentally-oriented performance indicators and multi-objective formulation of sustainable production scheduling models for a variety of real-world manufacturing systems, with implicit goals of reducing the frequency of setup operations and improving the utilization rate of machines.
Future research will be focused on two aspects. First, it is interesting to investigate sustainable aspects in manufacturing from other perspectives such as electricity consumption and carbon footprint and then characterize these factors into the objective functions or constraints of relevant production scheduling models. Second, considering the fact that sustainable scheduling problems are often complex in nature (multi-objective or heavily constrained), it is of great importance to devise computationally efficient local search algorithms, especially the local improvement strategies that are built on the structural properties of the integer programming model of the problem.