Sustainable Design Operations in the Supply Chain: Non-Profit Manufacturer vs. For-Profit Manufacturer

Abstract

Sustainable design aims to reduce the negative impacts either on people (e.g., create healthy) or on planet (e.g., minimize waste). In other words, sustainable design is the philosophy that tends to improve design performance by incorporating health and safety attributes (for people), and environmental attributes (for planet) into products. In this paper, we develop an analytical model to examine the sustainable design operations in a supply chain which consists of one retailer and one manufacturer. The manufacturer designs the products by investigating sustainable design efforts, such that the products can better coordinate human needs. Motivated by the real industry practice, we consider two business modes for the manufacturer: a nonprofit organization (i.e., a demand quantity seeker) or a commercial firm (i.e., a profit seeker). We obtain the optimal operational decisions in both the decentralized case and the centralized case, and we also compare the results. Managerial insights are derived, and the efficiency of the sustainable design is also discussed.

1. Introduction

In recent years, sustainability has been gradually incorporated into product design. Sustainability refers to the Triple Bottom Line, namely, Profit, People, and Planet. Sustainable design refers to the design activities that incorporate the sustainable concepts and functions into the product design, such that the Triple Bottom Line can be achieved. The main feature of sustainable design is that it aims to reduce the negative impacts on people (e.g., create health) and planet (e.g., minimize waste). In other words, sustainable design is the philosophy which tends to improve the design performance by incorporating sustainable design factors, like health and safety attributes for people, or environmental attributes for planet [1]. Sustainable design focuses on satisfying customers’s needs under the umbrella of the three pillar of sustainability (i.e., economic, social and environmental). It is compatible to achieve a good sustainable design achieving profit (or zero profit) for everyone in the supply chain. Designers input the sustainable design efforts to connect and coordinate human needs and product designs [2]. For example, one tableware designer Sha Yao created a seven-piece tableware set with 20 unique features, which are specifically designed to meet the needs of the people with physical, motor, or cognitive impairments. Sha Yao’s design helps improve the healthy condition for these people [3]. Some firms may also use the green package or sustainable materials to enhance sustainable product design. The well-known examples include the sustainability practices in H&M (Stockholm, Sweden), where the organic cotton and the recycled materials are used in product development.

Nowadays, consumers are becoming increasingly aware of the sustainable design attributes in the products, and thus it is necessary that designers create more human centric products with sustainability considerations [2]. A great number of studies have shown that the sustainable practices have positive effect on the market demand [4], and consumers are more willing to purchase the products with sustainable design [5,6]. In other words, the firms can increase market demand by enhancing sustainable design. In the previous examples, consumers are willing to purchase the Sha Yao’s tableware set [3] or H&M’s organic cotton t-shirts [7], even if these sustainable designed ones are relatively more expensive than the regular products.

From the above discussion, there is no doubt that the sustainable design is important for our communities and now an emerging business practice in the industry. The sustainable design is a corporate socially responsible practice, which incorporates the socially and environmentally sustainable concepts and functions into products. It hence carries values that benefit the participating firms and organizations [8]. Motivated by the industrial practices, in this paper, we consider a supply chain where a manufacturer may investigate the efforts of sustainable design for enhancing market demand in the supply chain. We consider two possibilities of the business modes of the manufacturer. On one hand, the manufacturer may be a non-profit seeker, which aims to distribute the sustainable designed products to as many customers as possible, like a non-profit organization. On the other hand, the manufacturer may also be a profit seeker, which aims to maximize the profit by developing sustainable designed products. In this paper, we will analyze these two types of manufacturers. We find the optimal solutions of the supply chain under these two different business modes. We yield the optimal operational decisions under the realized demand quantity maximization objective and the profit maximization objective. We also conduct some comparison and obtained important managerial insights. To the best of our knowledge, this paper is the first one which examines the sustainable design operations in the supply chain with different types of manufacturers. All findings are derived in closed-form, and the results can provide important guidance and managerial implications to organizations interested in sustainable design.

The rest of the paper is organized as follows. In Section 2, we conduct a literature review. In Section 3, we introduce the model and find the optimal solutions in the decentralized setting and centralized setting. Section 4 compare all the optimal solutions and derive managerial insights, and Section 5 concludes the paper. All the proofs are regulated to the Appendix.

2. Literature Review

In this section, we review the related literature. In this paper, we consider the sustainable design effort investment for a manufacturer, which may aim at demand quantity maximization or profit maximization. Thus, our paper is related to three aspects: the sustainable design perspectives, the demand quantity maximization problem, and the profit maximization problem. We will review the related research work from these three aspects, respectively.

As mentioned above, sustainable design is the design activities that incorporate the sustainable concepts and functions into the product design, which also aims to meet people’s needs from environmental and social perspectives. Bhamra and Lofthouse [9] mention that the mission of sustainable design is undertaken from two perspectives: human well-being and natural environmental systems, and both aspects focus on the design phase, which may potentially affect the entire life cycle of the products. Thus, we can classify the objectives of sustainable design into (i) health and safety attributes, and (ii) environmental attributes [10]. The objective regarding the health and safety attributes is about how the sustainable product design helps community from the socially responsible perspective. It is important to apply out-of-the-box concept to product design with socially responsible sustainability [2]. Clark et al. [10] conduct a case study on new product design for Kamworks prototype Moonlight, which greatly improve life quality for people in rural Cambodia. The objective regarding the environmental attribute refers to how the sustainable design reduces the waste and enhances eco-system. Mollenkopf et al. [11] examine the impact of product design on supply chain with return policy. Under such a sustainable supply chain, they find that a more responsible product design would decrease the percentage of product return, enhance marketing channel, and increase supply chain performance. The Sweden fast fashion retailer H&M inputs the eco-friendly materials and packaging into clothes design, which will have less impact throughout the product lifecycle on ecosystem [7]. Niinimaki and Hassi [12] study the importance of design for sustainable fashion and explore the corresponding sustainable design strategies. They find that the textile and apparel industry promote sustainability in product design in terms of eco-materials and ethical issues. Curwen et al. [13] examine the product develop strategies for sustainable fashion by thirteen in-depth interviews from Eileen Fisher, a women’s apparel manufacturer. They find that sustainable design should be jointly developed by the manufacturer and the retailer. Zhao et al. [1] develop an integrated multi-attribute decision making approach to select the commercially available materials in sustainable design. This approach mainly focuses on the material selection that has less impact on the environment. They identify various key indicators to show the contexts of sustainable design. The sustainable design considered in this paper is a general form, and we only assume that the higher sustainable design efforts could enhance market demand, and it can represent either socially responsible attribute or environmentally responsible attribute.

A quantity maximization objective is typically adopted by non-profit organizations. Many scholars have investigated how the quantity maximization objective firms affect sustainable supply chain. In the early work of Ansari et al. [14], they examine the pricing strategies of a non-profit organization, which maximizes usage subject to a non-deficit constraint. Later, Liu and Weinberg [15] examine the duopoly price competition between a for-profit firm (i.e., profit maximization) and a non-profit organization (i.e., quantity maximization). They yield an interesting result that non-profit firms are more sensitive to fixed cost change than the for-profit firms. More recently, Zhao et al. [16] consider the distribution channel selection of a non-profit organization under decentralized and centralized systems, where the demand is sensitive to the market size and the selling price. They find that the non-profit organization is better off in the centralized channel system with strong market competition. In our paper, demand is sensitive to both selling price as well as the design effort investment. The design effort issue is not considered by the above mentioned demand quantity maximization problems. Regarding the approach of solving the demand quantity maximization problem, we adopt the Lagrangian method, which is also used by these works. Bian et al. [17] investigate the equilibrium channel strategies in a mixed market, consisting of a private firm and a public firm. The former aims at profit maximization, and the latter aims at social welfare maximization. The social welfare they considered is constructed jointly from the demand quantities for the private firm and the public firm.

Compared with the research on the quantity maximization models, profit maximization in a sustainable supply chain has been extensively examined in the literature. For a comprehensive review on the quantitative models in sustainable supply chain (please refer to the review paper by Brandenburg et al. [18]). Recently, Swami and Shah [5] study a two echelon supply chain in which both supply chain parties can input greening efforts into product design. They find the two-part tariff contract can coordinate supply chain, namely, maximize the total chain profitability. Zhang and Liu [19] investigate the supply chain coordination contracts under the assumption that the market demand is related to the green degree of the products. Dong et al. [6] study a two-echelon sustainable supply chain with the consideration of sustainable design efforts, which can reduce the amount of carbon emission in production.

3. The Model

The main feature of our model is that we incorporate the sustainable design effort investment into the manufacturer’s decision problem. We assume that the manufacturer can invest some sustainable design effort to improve the functionality of the products, which is costly but can make the products be suitable for more needed people. Thus, more investment on the sustainable design effort will have positive effect on the demand. We also assume that the demand is sensitive in the selling price. Specifically, we let $D(p,e)$ be the realized demand quantity, where p and e are the selling price and the sustainable design effort, respectively. We consider the following demand function

$$\begin{array}{c}\hfill D(p,e)=a-bp+\beta e,\end{array}$$

(1)

where $a>0$ is the market size, $b>0$ is the price sensitive parameter, and $\beta >0$ is the design-effort sensitive parameter. In our setting, the market size a is fixed, the sensitive parameters b and β are given, and the selling price p and the design effort e are the decision variables. If the design effort is not considered, this kind of demand function is commonly adopted (see, e.g., Zhao et al. [16], Dong et al. [6]). On the other hand, the sustainable design effort investment is costly. We assume that if the sustainable design effort investment is e, then the sustainable design cost is $\frac{1}{2}\theta e^2$, where θ is the cost sensitive parameter. The design investment cost is a quadratic function and increasing in the sustainable design effort. This kind of cost associated with sustainability analysis is commonly used (see, e.g., Savaskan and Van Wassenhove [20], Gurnani and Drkoc [21], Dong et al. [6]). To avoid a non-trial case, we assume that $2b\theta -{\beta }^2>0$. The other cost parameters include the unit production cost c and the fixed production cost F. We assume that the fixed production cost cannot be too large. Specifically, we assume $F<\frac{{(a-bc)}^2\theta }{2(4b\theta -{\beta }^2)}$. It is easy to check that this is the upper bound on F such that the manufacturer can at least achieve non-negative profit in the centralized case.

Regarding the manufacturer’s business pattern, we consider two cases: it can be a commonly seen for-profit company, or it can be a non-profit organization. The purpose of a non-profit organization is usually to help disadvantage people or improve social benefit rather than maximize profit. It typically aims to distribute the products to as many needed people as possible. Thus, in the second case, we take the objective as maximizing the realized demand if only the profit is non-negative. This objective is also adopted in many other research works, like Zhao et al. [16].

Regarding the product distribution channel for the manufacturer, we also consider two cases: the decentralized case, where the products is distributed through a separate retailer, and the centralized case, where the products is distributed through the manufacturer’s own retailing channel. We will find the optimal solutions in the different cases and also compare the results. In the following sections, we will first consider the decentralized case and then the centralized case.

3.1. The Decentralized Case

In the decentralized case, the manufacturer designs and wholesales the products to a separate retailer, and the retailer sells the products to the end market. We assume a Stackelberg game between the manufacturer and the retailer, where the former is the leader. Specifically, we assume that the manufacturer first determine the unit wholesale price w and the sustainable design effort investment e, and then the retailer determines the unit selling price p. We assume the retailer is always profit seeking, but the manufacturer aims at maximizing either the realized demand or the profit.

To formulate the problem, we denote ${\Pi }_{\mathrm{R}}\left(p\right)$ as the retailer’s profit given that the selling price is p. Since the retailer is profit seeking, the retailer’s problem can be formulated as

$$\begin{array}{c}\hfill {\mathbf{P}}_{\mathrm{R}}:\underset{p}{max}{\Pi }_{\mathrm{R}}\left(p\right)=(p-w)D(p,e).\end{array}$$

We denote $p^{*}(w,e)$ as the retailer’s best response given the manufacturer’s decisions.

We denote ${\Pi }_{\mathrm{M}}(w,e)$ as the manufacturer’s profit given that the wholesale price is w and the sustainable design effort investment is e. We have

$$\begin{array}{c}\hfill {\Pi }_{\mathrm{M}}(w,e)=(w-c)D(p(w,e),e)-F-\frac{1}{2}\theta e^2,\end{array}$$

(2)

where $(w-c)D\left(p\right(w,e),e)$ is the revenue from selling the products, F is the fixed cost, and $\frac{1}{2}\theta e^2$ is the sustainable design effort investment cost. We denote the manufacturer’s decision problem as ${\mathbf{P}}_{\mathrm{M}}$ when the manufacturer is not for profit, and we denote the decision problem as ${{\mathbf{P}}^{\prime }}_{\mathrm{M}}$ when the manufacturer is profit seeking. Then, problem ${\mathbf{P}}_{\mathrm{M}}$ can be mathematically formulated as

$$\begin{array}{cc}\hfill {\mathbf{P}}_{\mathrm{M}}:\underset{w,e}{max}& D\left(p\right(w,e),e),\hfill \\ \hfill s.t.& {\Pi }_{\mathrm{M}}(w,e)\ge 0,\hfill \end{array}$$

and problem ${{\mathbf{P}}^{\prime }}_{\mathrm{M}}$ can be formulated as

$$\begin{array}{c}\hfill {{\mathbf{P}}^{\prime }}_{\mathrm{M}}:\underset{w,e}{max}{\Pi }_{\mathrm{M}}(w,e).\end{array}$$

Since the retailer and the manufacturer perform in a Stackelberg game, we find the optimal solutions by backwards induction. We first solve the problem ${\mathbf{P}}_{\mathrm{R}}$ and then the problem ${\mathbf{P}}_{\mathrm{M}}$ (${{\mathbf{P}}^{\prime }}_{\mathrm{M}}$). Consider the retailer’s decision problem ${\mathbf{P}}_{\mathrm{R}}$. From the demand function (1), the retailer’s profit function ${\Pi }_{\mathrm{R}}\left(p\right)$ can be written as

$${\Pi }_{\mathrm{R}}\left(p\right)=(p-w)(a-bp+\beta e)=-b{p}^2+(a+\beta e+bw)p-w(a+\beta e).$$

This is a quadratic function and the second order derivative of ${\Pi }_{\mathrm{R}}\left(p\right)$ versus p is $-b<0$, which implies that ${\Pi }_{\mathrm{R}}\left(p\right)$ is concave in p, and thus the retailer’s best response can be determined by the first order condition. We have

$$\begin{array}{c}\hfill p^{*}(w,e)=\frac{a+\beta e+bw}{2b}.\end{array}$$

(3)

Next, we submit the optimal price $p^{*}(w,e)$ into the manufacturer’s problem. We will first solve the quantity maximization problem ${\mathbf{P}}_{\mathrm{M}}$, and then the profit maximization problem ${{\mathbf{P}}^{\prime }}_{\mathrm{M}}$.

Consider the quantity maximization problem ${\mathbf{P}}_{\mathrm{M}}$. From Equations (1)–(3), problem ${\mathbf{P}}_{\mathrm{M}}$ can be reformulated in terms of w and e as follows:

$$\begin{array}{ccc}\hfill {\mathbf{P}}_{\mathrm{M}}:& \hfill \underset{w,e}{max}& D(p(w,e),e)=\frac{1}{2}(-bw+\beta e+a),\hfill \\ & \hfill s.t.& {\Pi }_{\mathrm{M}}(w,e)=\frac{1}{2}\left[-b{w}^2-\theta e^2+\beta we+(a+bc)w-\beta ce-ac-2F\right]\ge 0.\hfill \end{array}$$

(4)

Note that problem ${\mathbf{P}}_{\mathrm{M}}$ is a constraint maximization problem. Thus, we can use a Lagrangian method to solve it. To apply a Lagrangian method, we first investigate the properties of the objective function and the constraint. First note that the objective function (4) is a linear function of w and e, which implies that the objective function is jointly concave over w and e. Regarding the constraint function ${\Pi }_{\mathrm{M}}(w,e)$ given by Equation (5), it is easy to check that its Hessian matrix is

$$\begin{array}{c}\hfill \left(\begin{array}{cc}-b& \frac{1}{2}\beta \\ \frac{1}{2}\beta & -\theta \end{array}\right),\end{array}$$

where $-b<0$, $-\theta <0$, and the determinate

$$b\theta -\frac{1}{4}{\beta }^2=\frac{1}{4}(4b\theta -{\beta }^2)>\frac{1}{4}(2b\theta -{\beta }^2)>0,$$

where the last inequality holds from our assumption that $2b\theta -{\beta }^2>0$. Thus, this Hessian matrix is negatively definite, which implies that the constraint (5) is also jointly convex in w and e. Therefore, the Karush–Kuhn–Tucker point of problem ${\mathbf{P}}_{\mathrm{M}}$ is also its optimal solution. The Karush–Kuhn–Tucker point can be determined by using a Lagrangian parameter, and the results are summarized in the following proposition.

Proposition 1. 

In the decentralized case, if the manufacturer aims to maximize the realized demand quantity, then (i) the manufacturer’s optimal decisions are

$$\begin{array}{c}\hfill e^{*}=\frac{b\beta }{{\lambda }^{*}(4b\theta -{\beta }^2)}+\frac{\beta (a-bc)}{4b\theta -{\beta }^2}and{w}^{*}=\frac{-2\theta b+{\beta }^2}{{\lambda }^{*}(4b\theta -{\beta }^2)}+\frac{2\theta (a-bc)}{4b\theta -{\beta }^2}+c,\end{array}$$

where ${\lambda }^{*}=\sqrt{\frac{b^2\theta }{{(a-bc)}^2\theta -2F(4b\theta -{\beta }^2)}}$, (ii) the retailer’s optimal price is

$$p^{*}=\frac{-\theta b+{\beta }^2}{{\lambda }^{*}(4b\theta -{\beta }^2)}+\frac{3\theta (a-bc)}{4b\theta -{\beta }^2}+c,$$

(iii) the realized demand is

$$D^{*}=\frac{\theta b^2}{{\lambda }^{*}(4b\theta -{\beta }^2)}+\frac{b\theta (a-bc)}{4b\theta -{\beta }^2},$$

and (iv) the constraint (5) is binding.

Proposition 1(iv) indicates that the manufacturer’s profit is zero. The retailer’s profit can be obtained as

$$\begin{array}{c}\hfill {\Pi }_{\mathrm{R}}^{*}=(p^{*}-w^{*})D^{*}={\left[\frac{\theta b^2}{{\lambda }^{*}(4b\theta -{\beta }^2)}+\frac{b\theta (a-bc)}{4b\theta -{\beta }^2}\right]}^2.\end{array}$$

Sensitivity analysis can be conducted regarding the above optimal solution, as summarized in the following proposition.

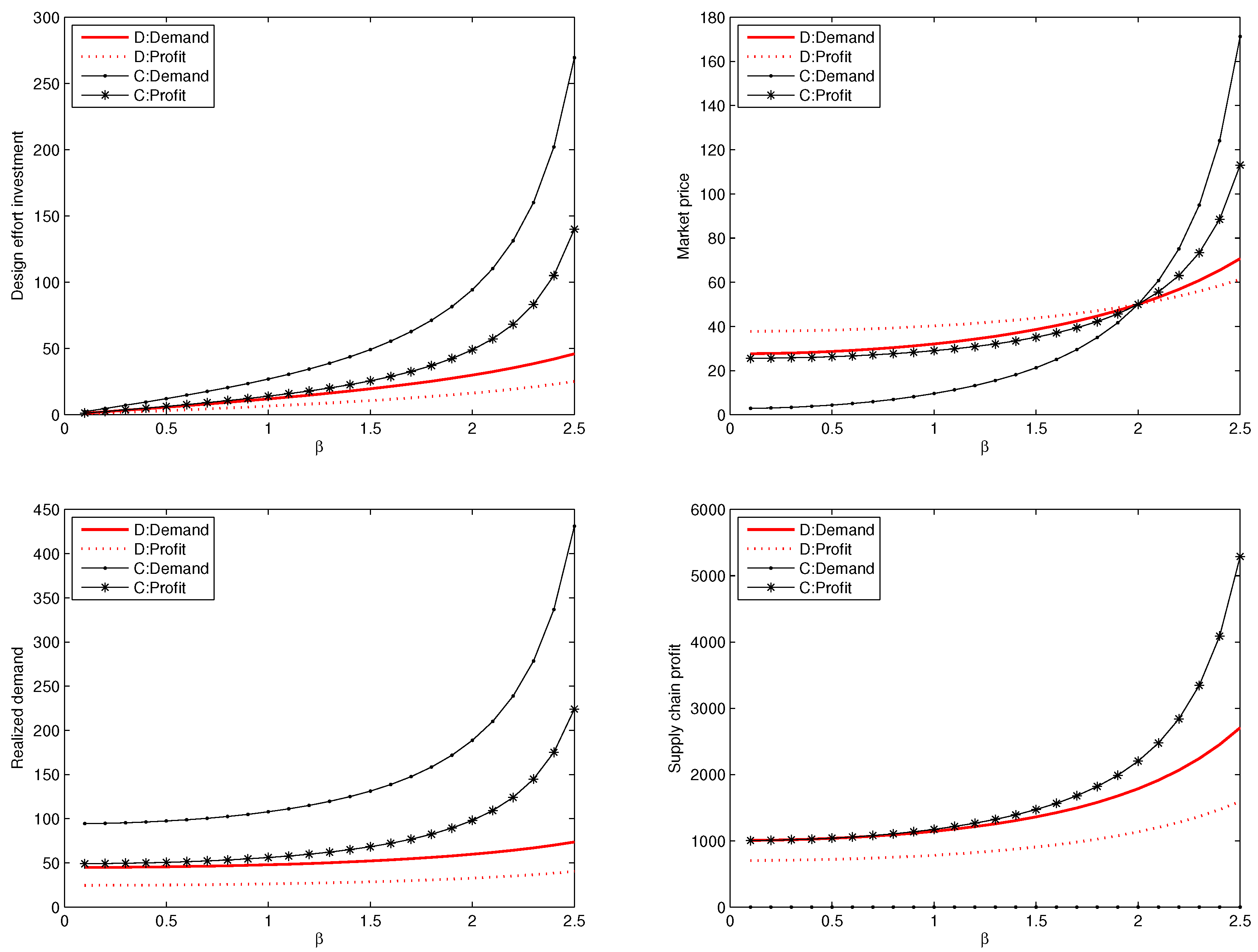
Proposition 2. 

Regarding the optimal decision variables to the decentralized problem, we have the following sensitivity analysis results: (i) the optimal price $p^{*}$ decreases in b and θ but increases in β; (ii) the optimal wholesale price $w^{*}$ decreases in b and θ but increases in β; (iii) the optimal sustainable design effort investment $e^{*}$ decreases in b and θ but increases in β; (iv) the optimal demand $D^{*}$ decreases in θ but increases in β, and (v) the retailer’s profit ${\Pi }_{\mathrm{R}}^{*}$ also increases in β but decreases in θ.

Next, we solve the profit maximization problem ${{\mathbf{P}}^{\prime }}_{\mathrm{M}}$. Recall that the manufacturer’s profit is

$$\begin{array}{c}\hfill {{\mathbf{P}}^{\prime }}_{\mathrm{M}}:\underset{w,e}{max}{\Pi }_{\mathrm{M}}(w,e)=(w-c)D(p(w,e),e)-F-\frac{1}{2}\theta e^2.\end{array}$$

When solving problem ${\mathbf{P}}_{\mathrm{M}}$, we have checked that the Hessian matrix of the profit function ${\Pi }_{\mathrm{M}}(w,e)$ is jointly convex in w and e. Therefore, the optimal solution to problem ${{\mathbf{P}}^{\prime }}_{\mathrm{M}}$ can be determined by considering the first order derivatives of ${\Pi }_{\mathrm{M}}(w,e)$ over w and e. The results are summarized in the following proposition.

Proposition 3. 

In the decentralized case, if the manufacturer aims to maximize the profit, then (i) the manufacturer’s optimal decisions are

$$\begin{array}{c}\hfill e^{\prime *}=\frac{\beta (a-bc)}{4b\theta -{\beta }^2}and{w}^{\prime *}=\frac{2\theta (a-bc)}{4b\theta -{\beta }^2}+c,\end{array}$$

(ii) the retailer’s optimal price is

$$p^{\prime *}=\frac{3\theta (a-bc)}{4b\theta -{\beta }^2}+c,$$

and (iii) the realized demand is

$$D^{\prime *}=\frac{b\theta (a-bc)}{4b\theta -{\beta }^2}.$$

From Proposition 3, if the manufacturer aims at profit maximization, then the retailer’s profit is

$$\begin{array}{c}\hfill {\Pi }_{\mathrm{R}}^{\prime *}=(p^{*}-w^{*})D^{*}=\frac{b{\theta }^2{(a-bc)}^2}{{(4b\theta -{\beta }^2)}^2},\end{array}$$

and the manufacturer’s profit is

$$\begin{array}{cc}\hfill {\Pi }_{\mathrm{M}}^{\prime *}=& (w^{*}-c)D^{*}-F-\frac{1}{2}\theta e^{*2}=\frac{2b{\theta }^2{(a-bc)}^2}{{(4b\theta -{\beta }^2)}^2}-F-\frac{1}{2}\theta {\left[\frac{\beta (a-bc)}{4b\theta -{\beta }^2}\right]}^2\hfill \\ \hfill =& \frac{\theta {(a-bc)}^2}{{(4b\theta -{\beta }^2)}^2}(2b\theta -\frac{1}{2}{\beta }^2)-F=\frac{\theta {(a-bc)}^2}{2(4b\theta -{\beta }^2)}-F.\hfill \end{array}$$

Recall that ${\mathbf{P}}_{\mathrm{M}}$ is a demand quantity maximization problem, and that ${{\mathbf{P}}^{\prime }}_{\mathrm{M}}$ is a profit maximization problem. Thus, it follows straightforwardly that

$$D^{*}>D^{\prime *}\text{and}{\Pi }_{\mathrm{M}}^{*}<{\Pi }_{\mathrm{M}}^{\prime *},$$

which can also be easily double checked from the optimal solutions in Propositions 1 and 3. Furthermore, from Propositions 1 and 3, we can obtain the following results by some simple algebra by using the assumption that $2b\theta -{\beta }^2>0$ and the fact that ${\lambda }^{*}>0$, the proof is thus omitted.

Proposition 4. 

(i) $e^{*}>e^{\prime *}$, $w^{*}<w^{\prime *}$, ${\Pi }_{\mathrm{R}}^{*}>{\Pi }_{\mathrm{R}}^{\prime *}$; (ii) $p^{*}>p^{\prime *}$ if $\theta b-{\beta }^2<0$, and $p^{*}<p^{\prime *}$ otherwise.

Proposition 4(i) shows that when the manufacturer aims at maximizing the demand quantity rather than maximizing the profit, then he shall invest more on the sustainable design effort and set a lower wholesale price. Proposition 4(i) also shows that when the manufacturer aims at the demand quantity maximization, the retailer can achieve a better profit. Recall that the realized demand in this case is also greater than that in the profit-maximization case. Thus, when the manufacturer is not for profit, we can regard that the manufacturer split his own benefit into two parts. One part becomes the retailer’s profit, and the other part goes to benefit more customers.

Regarding the two optimal prices, the relation has different cases depending on the value of $\theta b-{\beta }^2$. This implies that the selling price in the profit maximization case may not necessarily be greater than that in the demand quantity maximization model.

3.2. The Centralized Case

In this subsection, we consider the centralized case, where the manufacturer distribute the products through its own channel, and the manufacturer determines both the sustainable design effort e as well as the selling price p. Similarly, we will also consider the optimal solutions in two different settings: the demand quantity maximization problem and the profit maximization problem. Note that the manufacturer makes all the decisions, we can regard this centralized case as a decision problem for the supply chain (consisting of the manufacturer and the retailer). Thus, we will use a subscript “SC" to denote the manufacturer’s problems and the profit.

Let ${\Pi }_{\text{SC}}$ be the manufacturer’s profit. We have

$$\begin{array}{c}\hfill {\Pi }_{\text{SC}}(p,e)=(p-c)D(p,e)-F-\frac{1}{2}\theta e^2.\end{array}$$

(6)

If the manufacturer is not for profit and aims to maximize the demand quantity, then the problem is formulated as

$$\begin{array}{cc}\hfill {\mathbf{P}}_{\text{SC}}:max& D(p,e)=a-bp+\beta e,\hfill \\ \hfill s.t.& {\Pi }_{\text{SC}}(p,e)\ge 0,\hfill \end{array}$$

and if the manufacturer is for profit and aims to maximize the profit, then the problem is formulated as

$$\begin{array}{c}\hfill {{\mathbf{P}}^{\prime }}_{\text{SC}}:\underset{p,e}{max}{\Pi }_{\text{SC}}(p,e).\end{array}$$

We first solve problem ${\mathbf{P}}_{\text{SC}}$ and then the problem ${{\mathbf{P}}^{\prime }}_{\text{SC}}$.

Problem ${\mathbf{P}}_{\text{SC}}$ is a constraint maximization problem, and thus we can also use a Lagrangian method to solve it. We first investigate the properties of the objective and the constraint of problem ${\mathbf{P}}_{\text{SC}}$. First note that the objective $D(p,e)$ is a linear function in both p and e, which implies that $D(p,e)$ must be jointly convex in p and e. Regarding the constraint ${\Pi }_{\text{SC}}(p,e)$, from Equations (1) and (6), we have

$$\begin{array}{c}\hfill {\Pi }_{\text{SC}}(p,e)=-b{p}^2+\beta pe+(a+bc)p-ac-\beta ce-F-\frac{1}{2}\theta e^2,\end{array}$$

the Hessian matrix of which is

$$\begin{array}{c}\hfill \left(\begin{array}{cc}-2b& \beta \\ \beta & -\theta \end{array}\right).\end{array}$$

Note that $-2b<0$, $-\theta <0$, and the determinate $2b\theta -{\beta }^2>0$, where the last inequality holds from our assumption. Thus, this Hessian matrix is negatively definite, which implies that the constraint is also jointly convex in p and e. Therefore, the Karush–Kuhn–Tucker point determined by the Lagrangian method is also the optimal solution to problem ${\mathbf{P}}_{\text{SC}}$. The results are summarized in the following proposition. Note that to differentiate from the optimal solutions in the decentralized setting, we use a “hat" for all the optimal solutions in the centralized setting.

Proposition 5. 

In the centralized model, if the manufacturer aims to maximize the demand quantity, then (i) the optimal solution is

$$\begin{array}{c}\hfill {\widehat{e}}^{*}=\frac{b\beta }{{\widehat{\lambda }}^{*}(2b\theta -{\beta }^2)}+\frac{\beta (a-bc)}{2b\theta -{\beta }^2}and{\widehat{p}}^{*}=\frac{-b\theta +{\beta }^2}{{\widehat{\lambda }}^{*}(2b\theta -{\beta }^2)}+\frac{\theta (a-bc)}{2b\theta -{\beta }^2}+c,\end{array}$$

where ${\widehat{\lambda }}^{*}=\sqrt{\frac{b^2\theta }{{(a-bc)}^2\theta -2F(2b\theta -{\beta }^2)}}$, (ii) the optimal demand quantity is

$$\begin{array}{c}\hfill {\widehat{D}}^{*}=\frac{b^2\theta }{{\widehat{\lambda }}^{*}(2b\theta -{\beta }^2)}+\frac{b\theta (a-bc)}{2b\theta -{\beta }^2},\end{array}$$

and (iii) the constraint is blinded at the optimal solution.

Note that, in this case, the profit for the supply chain is zero, i.e., ${\Pi }_{\text{SC}}^{*}=0$, as indicated by Proposition 5(iii).

The following sensitivity results can be determined similarly to those in Proposition 2, and thus the proof is omitted.

Proposition 6. 

Regarding the optimal decision variables to the centralized problem, we have the following sensitivity analysis results: (i) the optimal price ${\widehat{p}}^{*}$ decreases in b and θ but increases in β; (ii) the optimal wholesale price ${\widehat{w}}^{*}$ decreases in b and θ but increases in β; (iii) the optimal sustainable design effort investment ${\widehat{e}}^{*}$ decreases in b and θ but increases in β; and (iv) the optimal demand ${\widehat{D}}^{*}$ decreases in θ but increases in β.

Next, we solve the profit maximization problem ${{\mathbf{P}}^{\prime }}_{\text{SC}}$. Recall that when investigating the properties of the constraint in problem ${\mathbf{P}}_{\text{SC}}$, we have shown that the Hessian matrix of the profit function ${\Pi }_{\text{SC}}(p,e)$ is jointly convex in p and e. Thus, the optimal solution can be obtained by considering the first-order derivatives. The results are summarized in the following proposition.

Proposition 7. 

In the centralized model, if the manufacturer aims to maximize the profit, then (i) the optimal solutions are

$$\begin{array}{c}\hfill {\widehat{e}}^{\prime *}=\frac{\beta (a-bc)}{2b\theta -{\beta }^2}and{\widehat{p}}^{\prime *}=\frac{\theta (a-bc)}{2b\theta -{\beta }^2}+c,\end{array}$$

and (ii) the optimal demand quantity is

$$\begin{array}{c}\hfill {\widehat{D}}^{\prime *}=\frac{b\theta (a-bc)}{2b\theta -{\beta }^2}.\end{array}$$

From Proposition 7, in the centralized case, the manufacturer’s (i.e., supply chain’s) optimal profit is given by

$$\begin{array}{c}\hfill {\widehat{\Pi }}_{\text{SC}}^{\prime *}=({\widehat{p}}^{\prime *}-c){\widehat{D}}^{\prime *}-F-\frac{1}{2}\theta {\widehat{e}}^{\prime 2}=\theta {\left[\frac{\theta (a-bc)}{2b\theta -{\beta }^2}\right]}^2(b\theta -\frac{1}{2}{\beta }^2)-F=\frac{\theta {(a-bc)}^2}{2(2b\theta -{\beta }^2)}-F.\end{array}$$

Recall that ${\mathbf{P}}_{\text{SC}}$ is a demand quantity maximization problem, and that ${{\mathbf{P}}^{\prime }}_{\text{SC}}$ is a profit maximization problem. Thus, it follows straightforwardly that

$${\widehat{D}}^{*}>{\widehat{D}}^{\prime *}\text{and}{\widehat{\Pi }}_{\text{SC}}^{*}<{\widehat{\Pi }}_{\text{SC}}^{\prime *},$$

which can also be easily double checked from the optimal solutions in Propositions 5 and 7. Furthermore, from Propositions 5 and 7, we can obtain the following results by conducting some simple algebra and using the assumption that $2b\theta -{\beta }^2>0$ and the fact that ${\widehat{\lambda }}^{*}>0$, the proof is thus omitted.

Proposition 8. 

(i) ${\widehat{e}}^{*}>{\widehat{e}}^{\prime *}$; (ii) ${\widehat{p}}^{*}>{\widehat{p}}^{\prime *}$ if $\theta b-{\beta }^2<0$, and ${\widehat{p}}^{*}<{\widehat{p}}^{\prime *}$ otherwise.

Proposition 8 shows that, in the centralized case, if the manufacturer is not for profit, then he will invest more on the sustainable design effort. However, the relation of the optimal prices of the two cases depends on the sign of $\theta b-{\beta }^2$, just like the case in the decentralized model.

Comparing Propositions 4 with 8, we can see that the relations of the optimal solutions look similar in the two cases. Either the supply chain is decentralized or centralized, the manufacturer will devote greater sustainable design effort if he is not for profit, and the relation of the optimal product selling prices, when the manufacturer’s objective differs, depends on the system parameters.

4. The Comparison and Insights

In the last section, we have considered the decentralized case and the centralized case, respectively. In each case, we determine the optimal solutions to the demand quantity maximization problem as well as the profit maximization problem, and we also compare the results when the manufacturer has different goals. In this section, we will compare the results of the decentralized and centralized case, to see which distribution pattern outperforms when the manufacturer has different business modes.

First note that in the demand quantity maximization problems, ${\mathbf{P}}_{\mathrm{M}}$ and ${\mathbf{P}}_{\text{SC}}$, the optimal solutions depends on the optimal Lagrangian parameters ${\lambda }^{*}$ and ${\widehat{\lambda }}^{*}$, respectively ( see Propositions 1 and 5). Thus, to compare the results in the decentralized and centralized case, we first conduct a comparison of ${\lambda }^{*}$ and ${\widehat{\lambda }}^{*}$. From the expressions given by Equations (A3) and (A6), we have

$$\begin{array}{c}\hfill {\lambda }^{*}=\sqrt{\frac{b^2\theta }{{(a-bc)}^2\theta -2F(4b\theta -{\beta }^2)}}>\sqrt{\frac{b^2\theta }{{(a-bc)}^2\theta -2F(2b\theta -{\beta }^2)}}={\widehat{\lambda }}^{*}.\end{array}$$

We now have the relationship between ${\lambda }^{*}$ and ${\widehat{\lambda }}^{*}$. For ease of comparing the optimal solutions in the different cases, we summarize all the optimal results in

Table 1. The comparison of the optimal solutions.

	Decentralized Case		Centralized Case
	Quantity Maximization	Profit Maximization	Quantity Maximization	Profit Maximization
$D^{*}$	$\frac{\theta b^2}{{\lambda }^{*}(4b\theta -{\beta }^2)}+\frac{b\theta (a-bc)}{4b\theta -{\beta }^2}$	$\frac{b\theta (a-bc)}{4b\theta -{\beta }^2}$	$\frac{b^2\theta }{{\widehat{\lambda }}^{*}(2b\theta -{\beta }^2)}+\frac{b\theta (a-bc)}{2b\theta -{\beta }^2}$	$\frac{b\theta (a-bc)}{2b\theta -{\beta }^2}$
$e^{*}$	$\frac{b\beta }{{\lambda }^{*}(4b\theta -{\beta }^2)}+\frac{\beta (a-bc)}{4b\theta -{\beta }^2}$	$\frac{\beta (a-bc)}{4b\theta -{\beta }^2}$	$\frac{b\beta }{{\widehat{\lambda }}^{*}(2b\theta -{\beta }^2)}+\frac{\beta (a-bc)}{2b\theta -{\beta }^2}$	$\frac{\beta (a-bc)}{2b\theta -{\beta }^2}$
$p^{*}$	$\frac{-\theta b+{\beta }^2}{{\lambda }^{*}(4b\theta -{\beta }^2)}+\frac{3\theta (a-bc)}{4b\theta -{\beta }^2}+c$	$\frac{3\theta (a-bc)}{4b\theta -{\beta }^2}+c$	$\frac{-b\theta +{\beta }^2}{{\widehat{\lambda }}^{*}(2b\theta -{\beta }^2)}+\frac{\theta (a-bc)}{2b\theta -{\beta }^2}+c$	$\frac{\theta (a-bc)}{2b\theta -{\beta }^2}+c$
$w^{*}$	$\frac{-2\theta b+{\beta }^2}{{\lambda }^{*}(4b\theta -{\beta }^2)}+\frac{2\theta (a-bc)}{4b\theta -{\beta }^2}+c$	$\frac{2\theta (a-bc)}{4b\theta -{\beta }^2}+c$	N.A.	N.A.
${\Pi }_{\mathrm{R}}^{*}$	$b{\left[\frac{\theta b}{{\lambda }^{*}(4b\theta -{\beta }^2)}+\frac{\theta (a-bc)}{4b\theta -{\beta }^2}\right]}^2$	$b{\left[\frac{\theta (a-bc)}{(4b\theta -{\beta }^2)}\right]}^2$	N.A.	N.A.
${\Pi }_{\mathrm{M}}^{*}$	0	$\frac{\theta {(a-bc)}^2}{2(4b\theta -{\beta }^2)}-F$	N.A.	N.A.
${\Pi }_{\text{SC}}^{*}$	$b{\left[\frac{\theta b}{{\lambda }^{*}(4b\theta -{\beta }^2)}+\frac{\theta (a-bc)}{4b\theta -{\beta }^2}\right]}^2$	$b{\left[\frac{\theta (a-bc)}{(4b\theta -{\beta }^2)}\right]}^2+\frac{\theta {(a-bc)}^2}{2(4b\theta -{\beta }^2)}-F$	0	$\frac{\theta {(a-bc)}^2}{2(2b\theta -{\beta }^2)}-F$

.

By using the relation ${\lambda }^{*}>{\widehat{\lambda }}^{*}$ and conducting some simple algebra, we can obtain the following results.

Proposition 9. 

(i) $D^{*}<{\widehat{D}}^{*}$, $e^{*}<{\widehat{e}}^{*}$; (ii) $D^{\prime *}<{\widehat{D}}^{\prime *}$, $e^{\prime *}<{\widehat{e}}^{\prime *}$; (iii) if $b\theta -{\beta }^2=0$, then $p^{*}=p^{\prime *}=\widehat{p}*={\widehat{p}}^{\prime *}$.

Proposition 9 implies that no matter if the manufacturer is for profit or not for profit, if the supply chain is centralized, the manufacturer has greater incentive to invest in the sustainable design effort, and more customers will consume the sustainable products. In other words, a centralized supply chain will always benefit the supply chain from the perspective of sustainable design operations. To more intuitively illustrate the relations of the optimal solutions among different cases, we present a numerical example. Note that in Propositions 2 and 4, and in Propositions 6 and 8, we present some theoretical analysis regarding the comparison of the optimal solutions. Therefore, in this numerical example, we simply take the design effort sensitivity parameter β as an example. In Figure 1, we depict the optimal solutions, including the design effort investment, market selling price, realized demand, and supply chain profit, versus β. Note that in the legend of the figure, we use “D:Demand" and “D:Profit” to refer to the decentralized cases with the objectives of maximizing the realized demand and maximizing the profit, respectively; and we also use “C:Demand” and “C:Profit” to refer to the centralized cases with the two objectives, respectively. In this example, we set $a=100$, $b=2$, $c=1$, $\theta =2$, $F=200$, and we let β vary from 0.1 to 2.5. These parameters satisfy the constraints we assumed in the model setting. It is interesting to notice that in the subfigure about the optimal price versus β, all the curves cross at $\beta =2$. This is the threshold that $b\theta -{\beta }^2=0$, and this generally holds as indicated from Proposition 9(iii).

5. Conclusions

In this paper, we develop an analytical model to examine a supply chain consisting of one manufacturer and one retailer, where the manufacturer designs the products by investigating sustainable design efforts and produces the products. A greater sustainable design effort investment increases the market demand. We consider two business modes for the manufacturer: the manufacturer may be a non-profit one, which aims to maximize the demand quantity, and the manufacturer may also be a for-profit one, which targets maximizing the profit. We consider these two objectives under a decentralized supply chain setting and a centralized setting, respectively. The optimal operational decisions are derived and compared.

Our findings can be summarized in three aspects.

(i) Benefit allocation: in the decentralized supply chain setting, if the manufacturer is a non-profit one rather than a for-profit one, then he will split his benefits between the customers and the retailer. With the non-profit manufacturer, the products will have higher demand and the retailer will have a greater profit. This finding gives us an important industrial implication that if Sha Yao is a non-profit manufacturer, her sustainable tableware sets market demand would be higher, and her retailer would earn more. Compared with the non-profit manufacturer Sha Yao, H&M may not be successful in market demand and profit.

(ii) Sustainable design investment: no matter the supply chain is decentralized or centralized, the manufacturer will put more effort into sustainable design when he is a non-profit one rather than a for-profit one. Meanwhile, the realized demand quantity will be higher. This implies that a non-profit manufacturer (e.g., Sha Yao) will do a better job if he wants to insist on a better sustainable design product and distribute the products to more customers.

(iii) Channel management: no matter the manufacturer is not for profit or for profit, a greater design effort investment and a higher realized demand quantity will be attained in the centralized supply chain setting rather than a decentralized one. This implies that a centralized supply chain will have greater efficiency in the sustainable design investment. This finding implies that if Sha Yao and H&M integrate their supply chain to be a centralized one, the efficiency of the sustainable design investment would be significantly improved.

Our study is subject to two main limitations that also point toward potential future research directions. Firstly, we assume that our market demand is deterministic and depends on the retail price and sustainable design effort. This assumption provides us with neat and tractable results but may not be consistent with the reality that the market always faces randomness. Thus, it would be interesting to investigate the random market demand case in future research. Secondly, we assume that the manufacturer takes either quantity maximization or profit maximization as the objective. In reality, the manufacturer may have mixed maximization problems. It would be interesting to examine the optimization problem in a sustainable design driven supply chain with the mixed maximization objectives. Thirdly, the current supply chain structure is a classic one consisting of one manufacturer and one retailer. Other important parts such as waste managers (in reverse logistics) and third-party logistics do not fall into the scope of this paper. Thus, it would also be interesting to investigate more complicated supply structures with such parties.

no