Neimark–Sacker Bifurcation Analysis and 0–1 Chaos Test of an Interactions Model between Industrial Production and Environmental Quality in a Closed Area
Abstract
:1. Introduction
2. Model
2.1. Notations
| Variables/Parameters | Descriptions |
|---|---|
| the environmental quality index at period n; | |
| indicates the change of environmentalquality, either improvement or deterioration; | |
| the production amount at period n; | |
| indicates the change of production amount, which represents a production decision, either an increase or a decrease; | |
| a | the low threshold of environmental quality; |
| c | the high threshold of environmental quality; |
| b | the payment on the pollution emission right; |
| δ | the step size of a decision or measurement; |
| ϵ | a general, small parameter. |
2.2. Assumptions
| Assumptions | Descriptions | Expressions |
|---|---|---|
| Assumption 1 | The environmental quality has a positive linear impact on the production decision. | |
| Assumption 2 | The last production amount has a negative linear impact on the current production decision due to congestion in the product market. | |
| Assumption 3 | The payment on the pollution emission right has a negative linear impact on the production decision. | |
| Assumption 4 | The production amount has a negative linear impact on the change of environmental quality. | |
| Assumption 5 | The change of environmental quality is affected simultaneously by the last environmental quality and deviations from its low and high thresholds. |
2.3. Model Formulation
3. Stability of the Fixed Points
- (i)
- locally asymptotically-stable if and only ifand;
- (ii)
- a saddle if and only if ;
- (iii)
- locally unstable if and only if and ;
- (iv)
- non-hyperbolic if either and or and .
4. Neimark–Sacker Bifurcation
4.1. Existence of Neimark–Sacker Bifurcation
- (H1)
- Eigenvalue assignment when n is even (or odd, respectively),
- (H2)
- Transversality condition
- (H3)
- Non-resonance condition or resonance condition , where and then a Neimark–Sacker bifurcation occurs at .
4.2. Direction and Stability of the Neimark–Sacker Bifurcations
4.3. Numerical Example
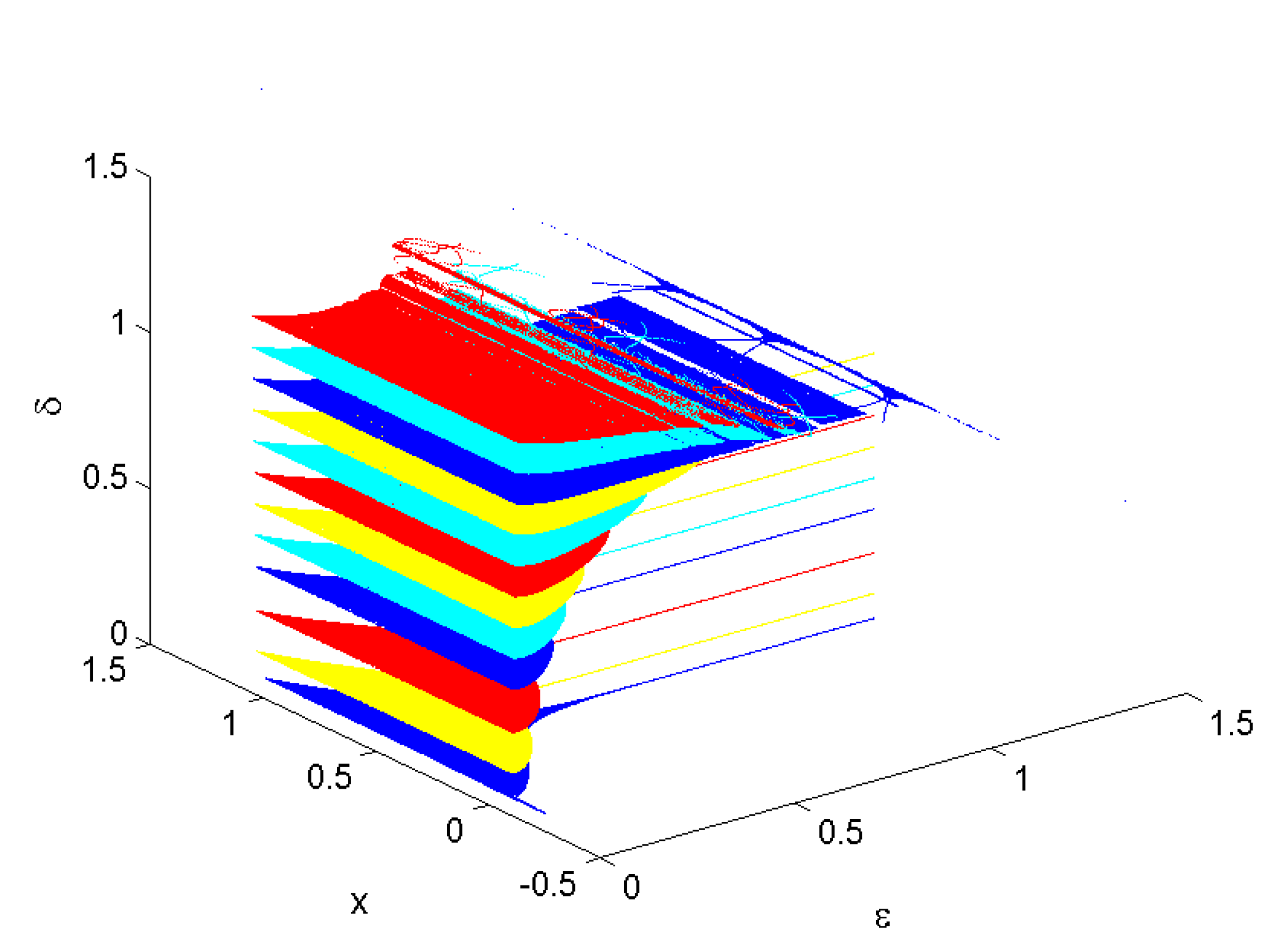
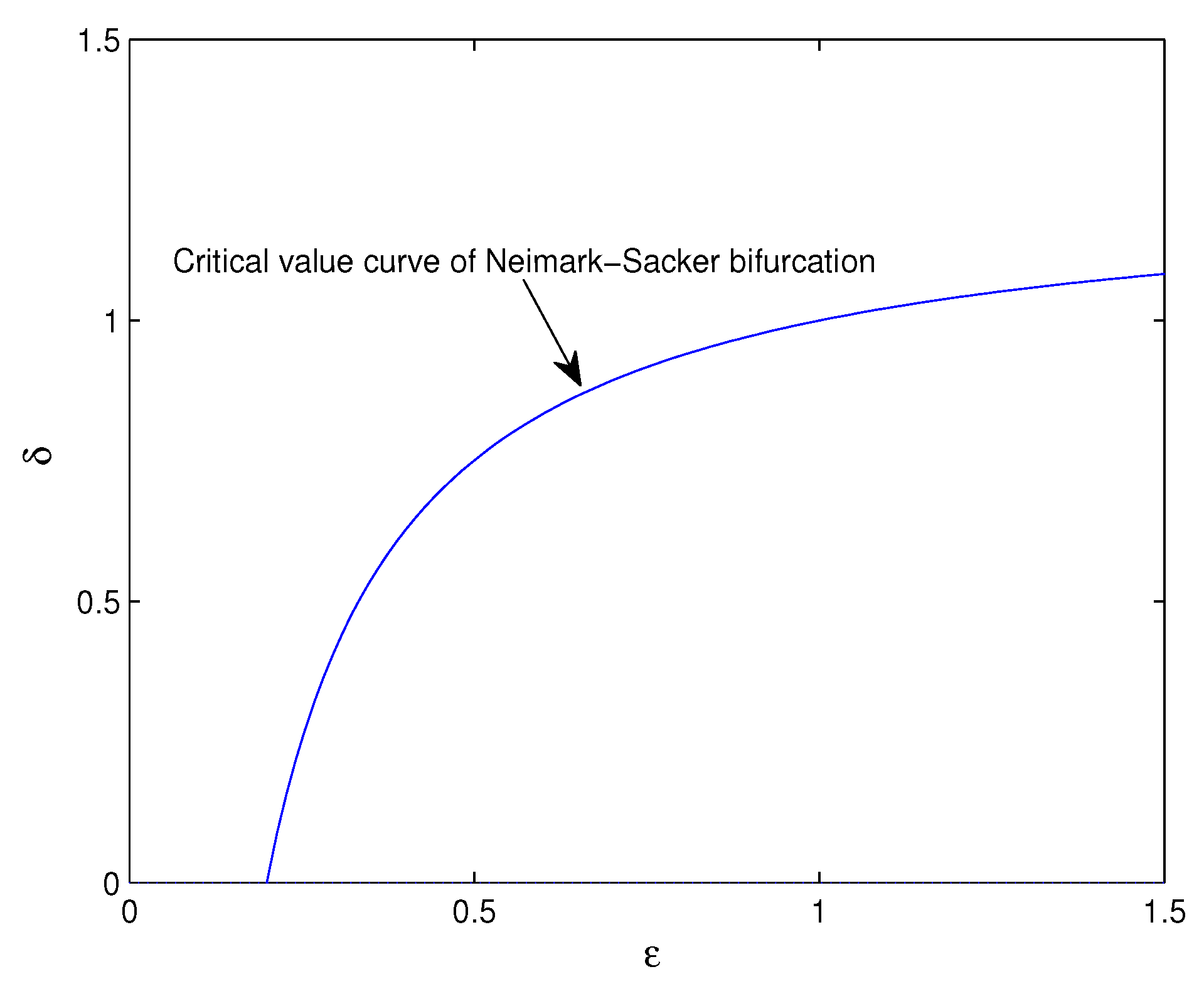
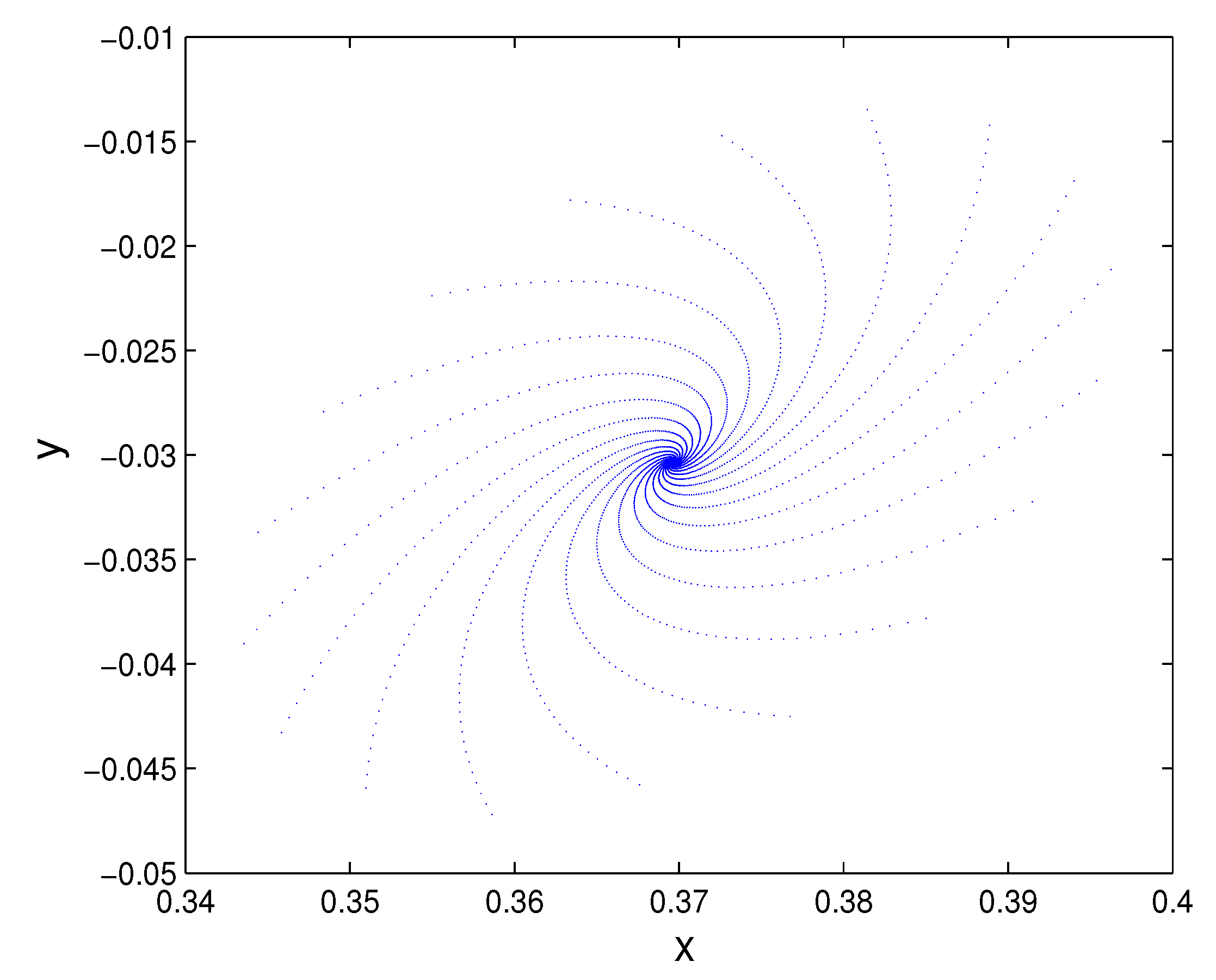



5. Chaos
5.1. 0–1 Test Algorithm for Chaos
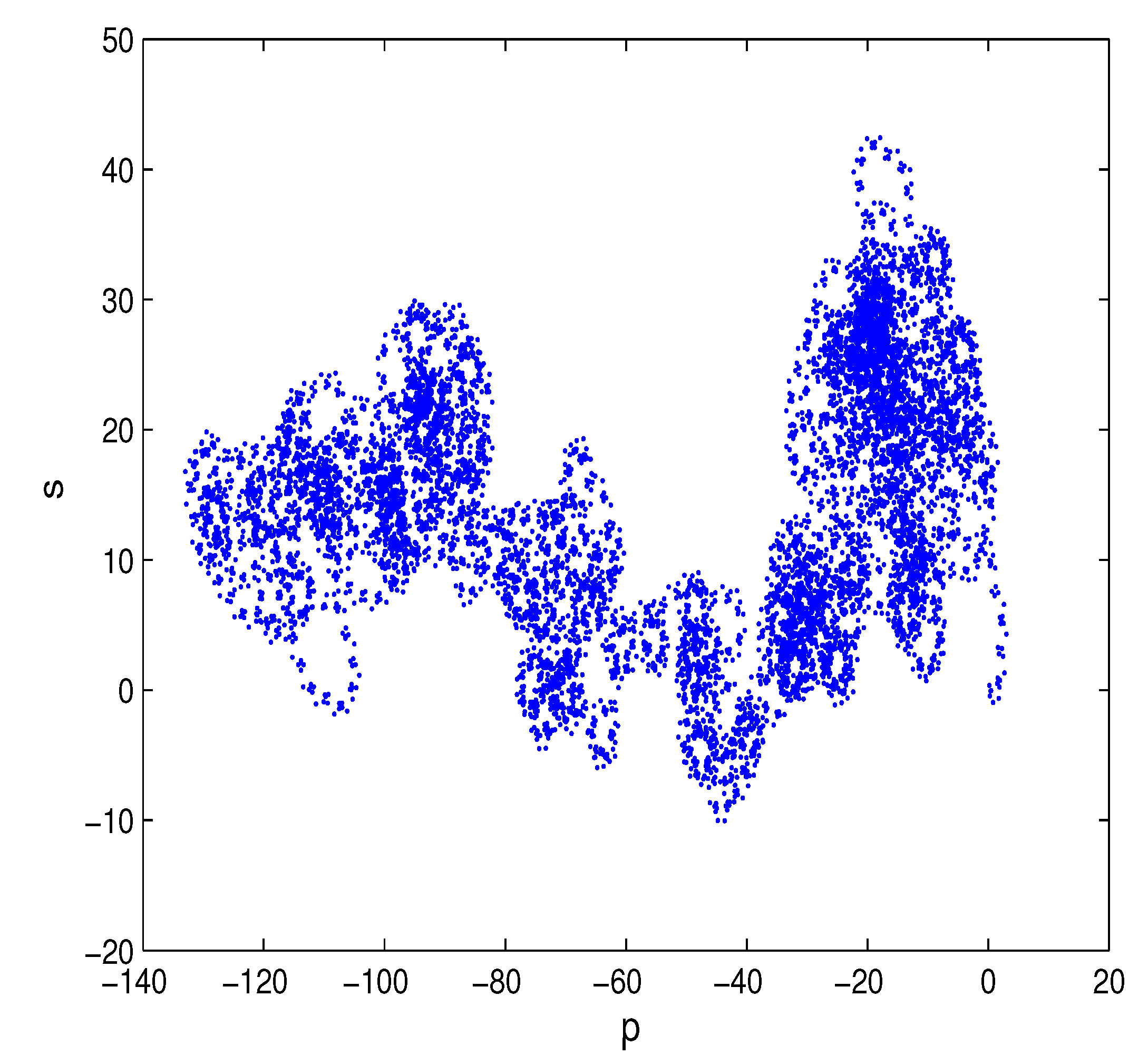
5.2. Numerical Example
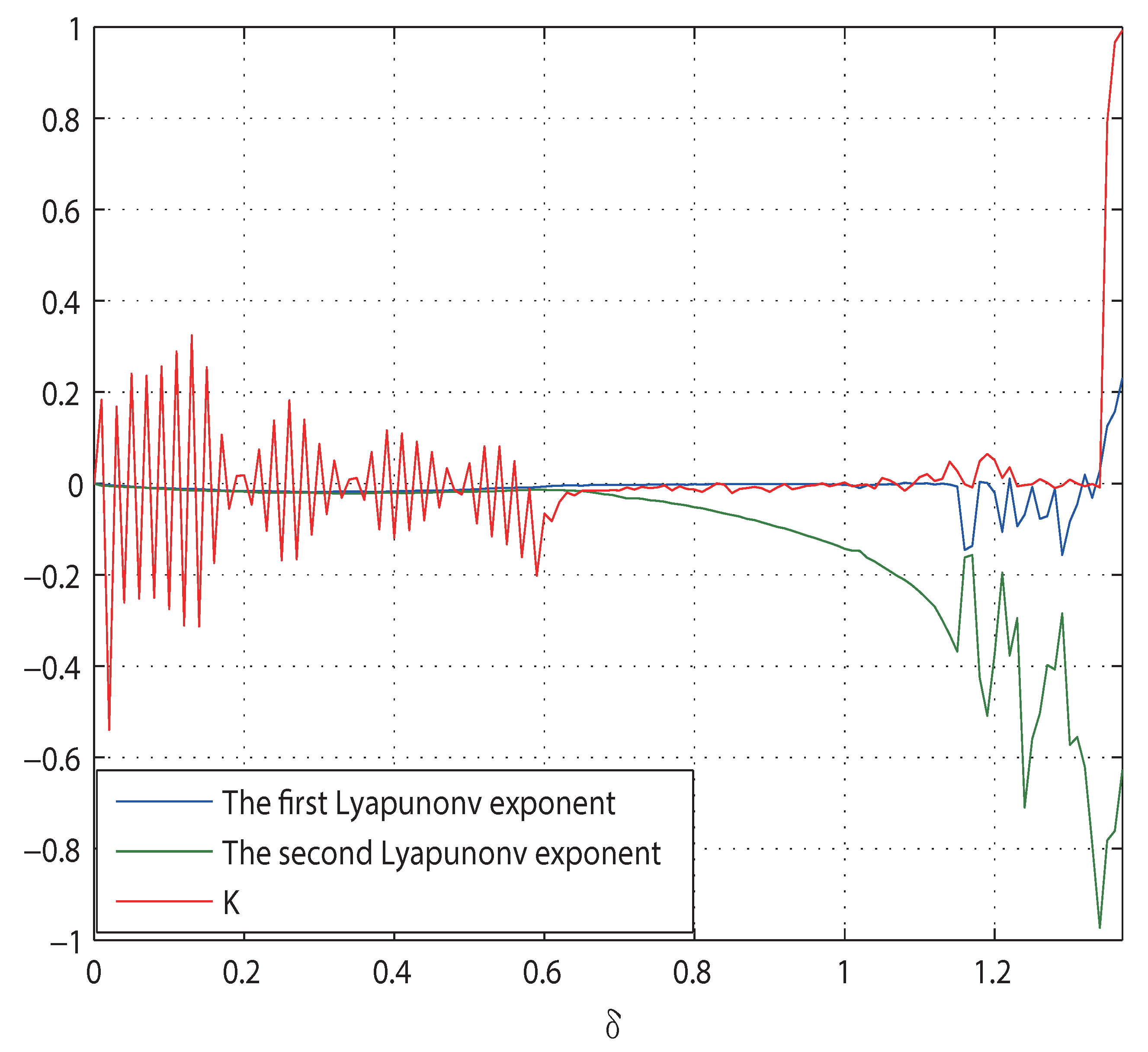

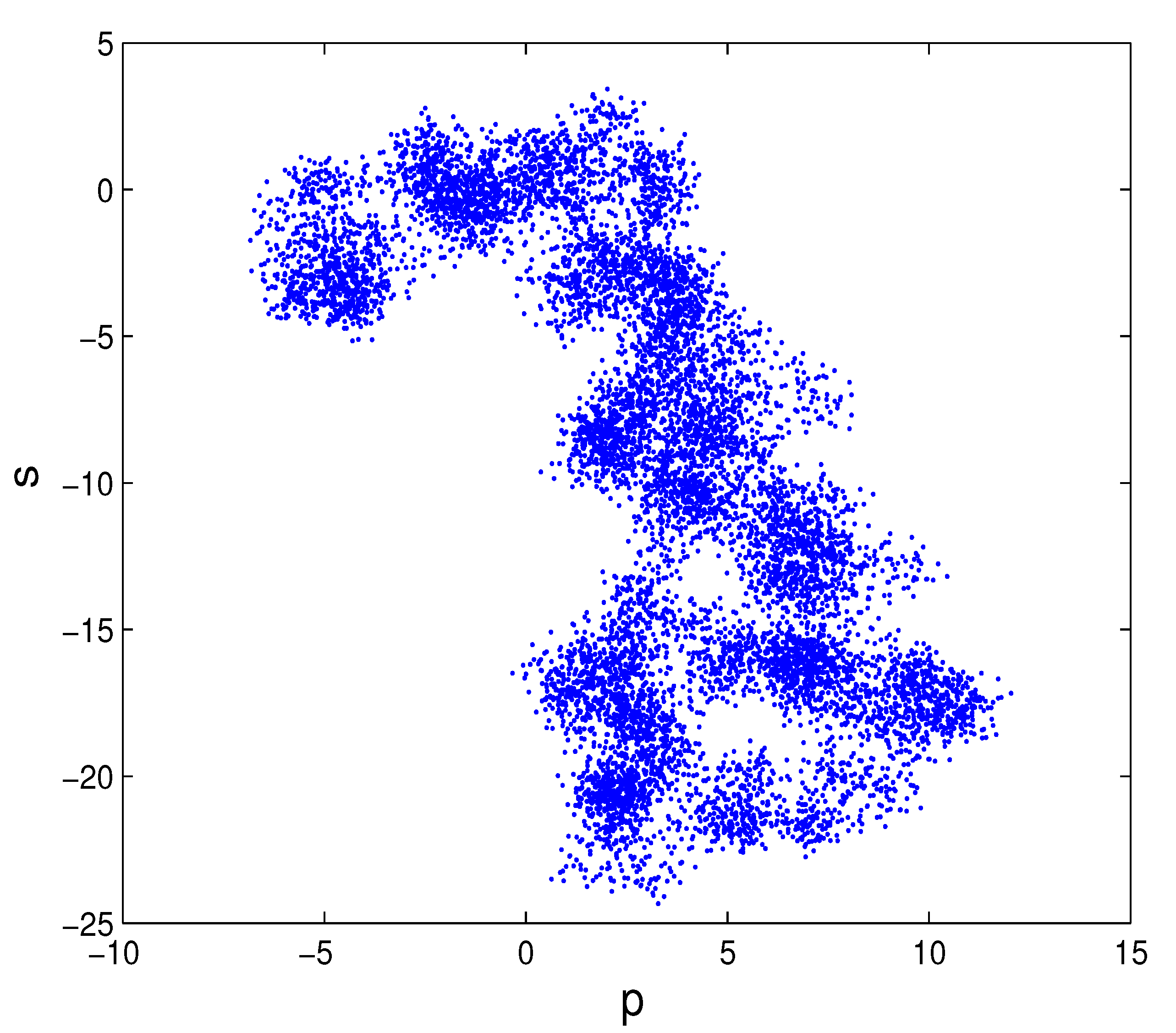
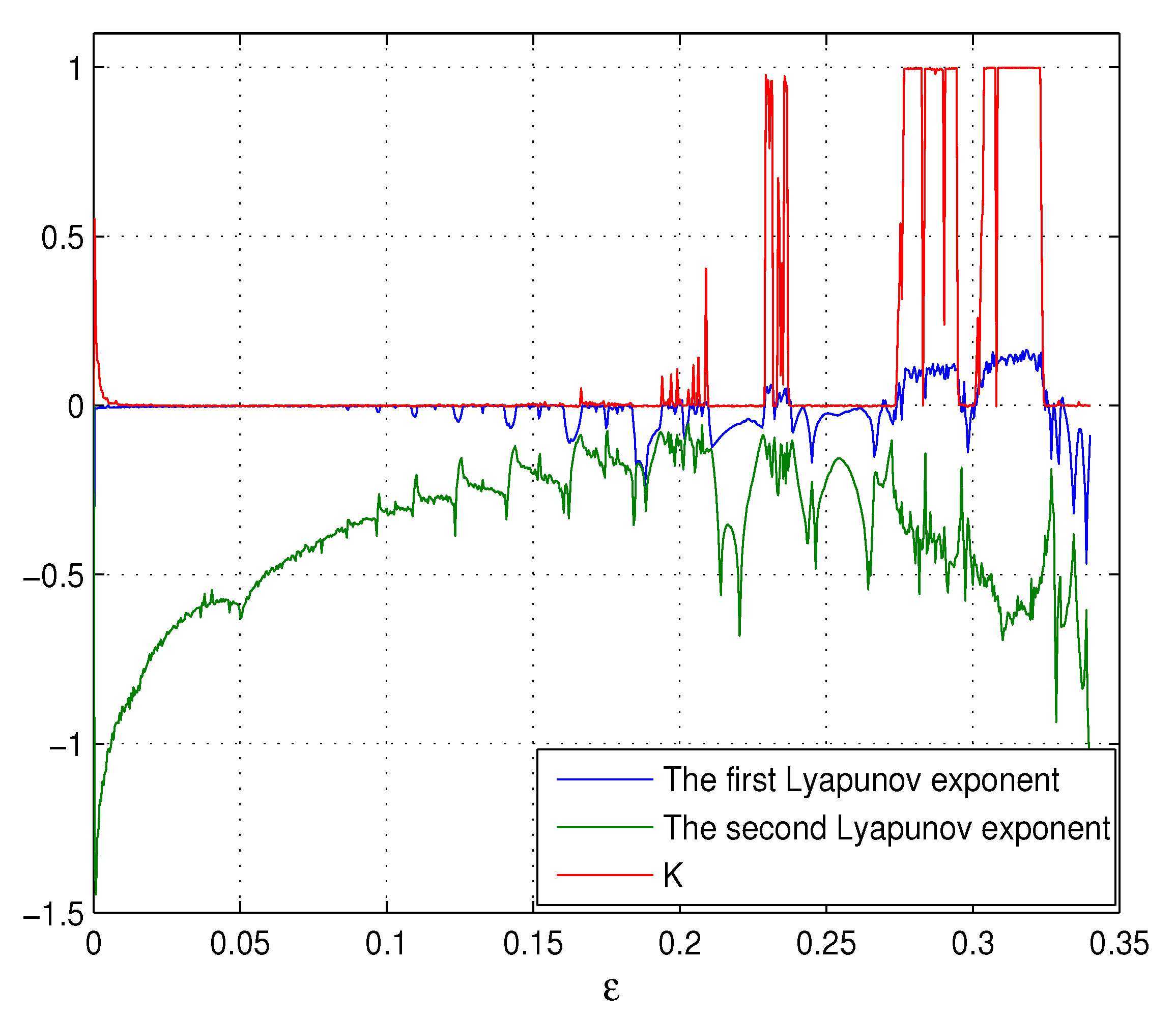
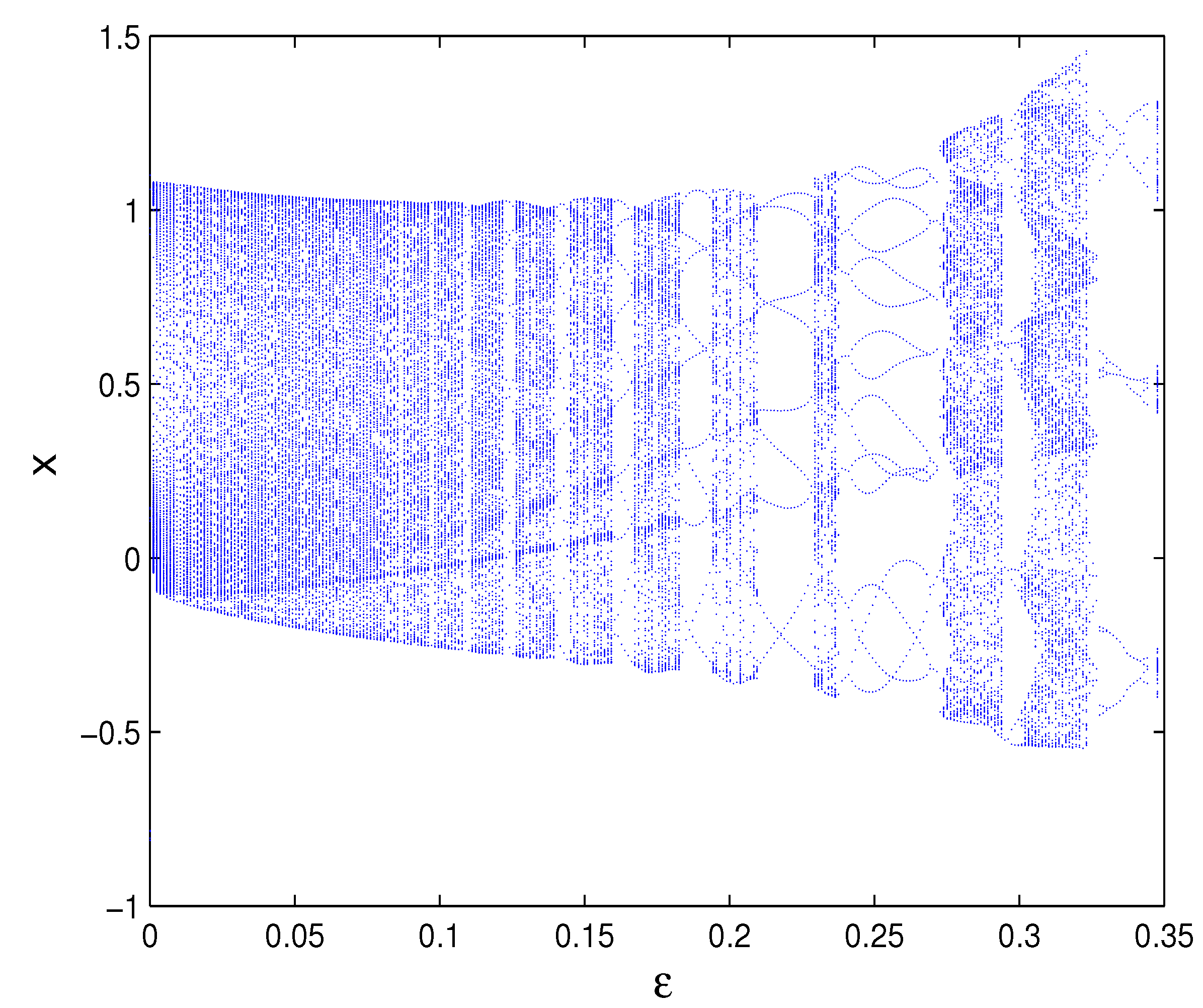
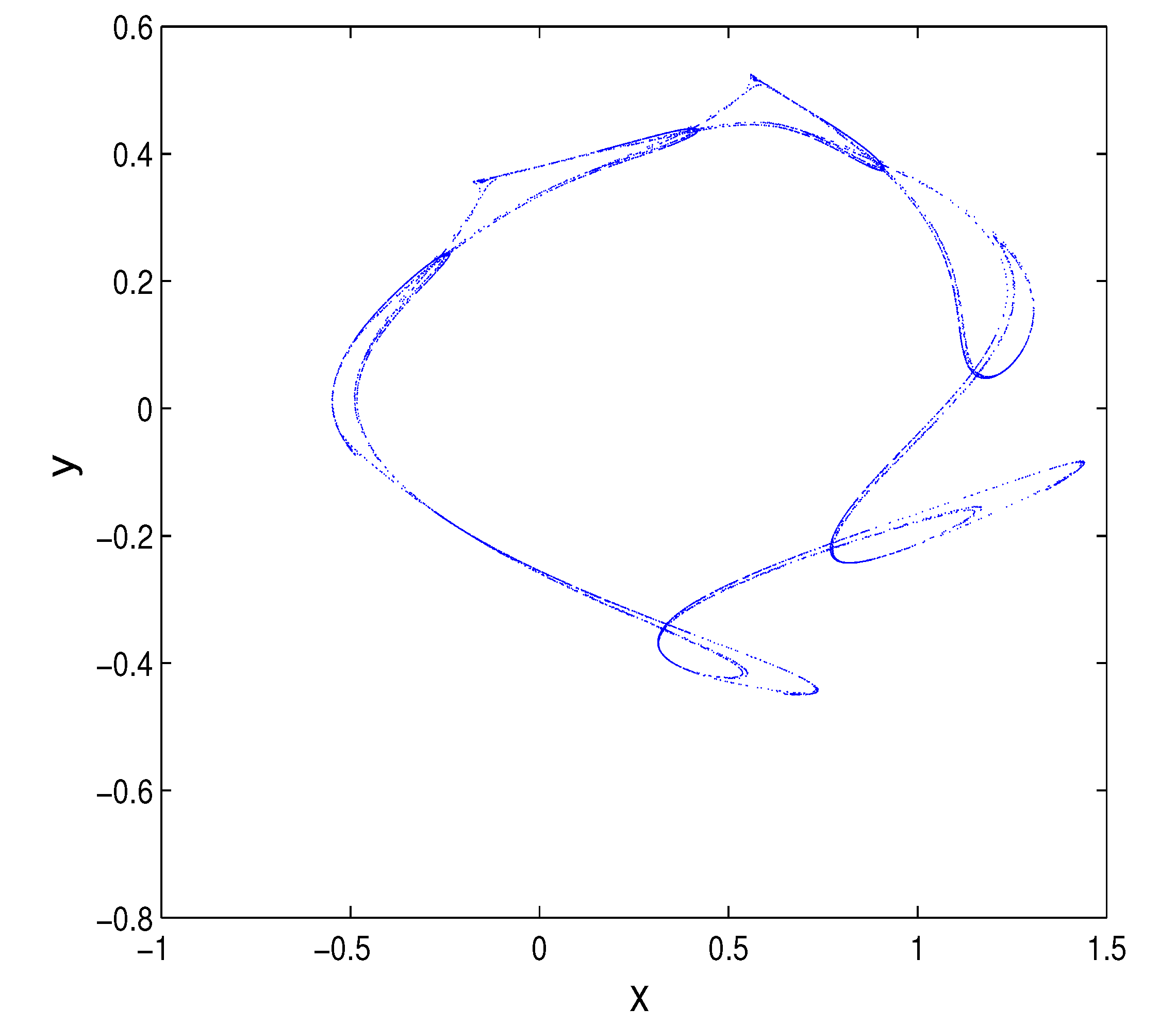
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Salomone, R.; Clasadonte, M.; Proto, M.; Raggi, A. (Eds.) Product-oriented environmental management system (POEMS): A sustainable management framework for the food industry. Available online http://www.lcm2011.org/papers.html?file=tl_files/pdf/poster/day1/Salomone-Product-Oriented_Environmental_Management_System-651_b.pdf (accesseed on 24 July 2015).
- Salomone, R.; Ioppolo, G.; Saija, G. Product-Oriented Environmental Management Systems (POEMS); Springer: Dordrecht, The Netherlands, 2013; pp. 257–302. [Google Scholar]
- Salomone, R.; Ioppolo, G. Environmental impacts of olive oil production: A Life Cycle Assessment case study in the province of Messina (Sicily). J. Clean Prod. 2012, 28, 88–100. [Google Scholar] [CrossRef]
- Zhao, N.; Liu, Y.; Chen, J. Regional industrial production's spatial distribution and water pollution control: A plant-level aggregation method for the case of a small region in China. Sci. Total Environ. 2009, 407, 4946–4953. [Google Scholar] [CrossRef] [PubMed]
- Aşıcı, A. Economic growth and its impact on environment: A panel data analysis. Ecological. Indic. 2013, 24, 324–333. [Google Scholar] [CrossRef] [Green Version]
- Dinda, S. Environmental Kuznets curve hypothesis: A survey. Ecol. Econ. 2004, 49, 431–455. [Google Scholar] [CrossRef] [Green Version]
- Copeland, B.; Taylor, M. Trade, growth, and the environment. J. Econ. Literat. 2004, 42, 7–71. [Google Scholar] [CrossRef]
- Paraschiv, D.; Tudor, C.; Petrariu, R. The Textile Industry and Sustainable Development: A Holt-Winters Forecasting Investigation for the Eastern European Area. Sustainability 2015, 7, 1280–1291. [Google Scholar] [CrossRef]
- Aliehyaei, M.; Atabi, F.; Khorshidvand, M.; Rosen, M. Exergy, Economic and Environmental Analysis for Simple and Combined Heat and Power IC Engines. Sustainability 2015, 7, 4411–4424. [Google Scholar]
- Kuznetsov, J. Elements of Applied Bifurcation Theory; Springer: New York, NY, USA, 1998. [Google Scholar]
- Wen, G.; Xu, D.; Han, X. On creation of Hopf bifurcations in discrete-time nonlinear systems. Chaos 2002, 12, 350–355. [Google Scholar] [CrossRef] [PubMed]
- Wen, G. Criterion to identify Hopf bifurcations in maps of arbitrary dimension. Phys. Rev. E 2005, 72, 26201. [Google Scholar] [CrossRef]
- Xin, B.; Chen, T.; Ma, J. Neimark–Sacker Bifurcation in a Discrete-Time Financial System. Discrete Dynam. Nat. Soc. 2010, 2010, 405639. [Google Scholar] [CrossRef]
- Xin, B.; Ma, J.; Gao, Q. The complexity of an investment competition dynamical model with imperfect information in a security market. Chaos Soliton. Fract. 2009, 42, 2425–2438. [Google Scholar] [CrossRef]
- Li, E.; Li, G.; Wen, G.; Wang, H. Hopf bifurcation of the third-order He´non system based on an explicit criterion. Nonlinear Anal Theor. Meth. Appl. 2009, 70, 3227–3235. [Google Scholar] [CrossRef]
- Gottwald, G.; Melbourne, I. A new test for chaos in deterministic systems. Proc. R. Soc. Lond. Ser. A 2004, 460, 603–611. [Google Scholar] [CrossRef]
- Xin, B.; Li, Y. 0–1 test for chaos in a fractional order financial system with investment incentive. Abstr. Appl. Anal. 2013, 2013, 876298. [Google Scholar] [CrossRef]
- Xin, B.; Li, Y. Bifurcation and Chaos in a Price Game of Irrigation Water in a Coastal Irrigation District. Discrete Dynam. Nat. Soc. 2013, 2013, 408904. [Google Scholar] [CrossRef]
- Xin, B.; Wu, Z. Projective Synchronization of Chaotic Discrete Dynamical Systems via Linear State Error Feedback Control. Entropy 2015, 17, 2677–2687. [Google Scholar] [CrossRef]
- Gottwald, G.; Melbourne, I. On the Implementation of the 0–1 Test for Chaos. SIAM J. Appl. Dynam. Syst. 2009, 8, 129–145. [Google Scholar] [CrossRef] [Green Version]
- Falconer, I.; Gottwald, G.; Melbourne, I.; Wormnes, K. Application of the 0-1 test for chaos to experimental data. SIAM J. Appl. Dynam. Syst. 2007, 6, 395–402. [Google Scholar] [CrossRef] [Green Version]
- Gottwald, G.; Melbourne, I. On the validity of the 0–1 test for chaos. Nonlinearity 2009, 22, 1367–1382. [Google Scholar] [CrossRef]
- Litak, G.; Syta, A.; Wiercigroch, M. Identification of chaos in a cutting process by the 0–1 test. Chaos Soliton. Fract. 2009, 40, 2095–2101. [Google Scholar] [CrossRef]
- Bizjan, B.; Sirok, B.; Govekar, E. Nonlinear Analysis of Mineral Wool Fiberization Process. J. Comput. Nonlinear Dynam. 2015, 10, 021005. [Google Scholar] [CrossRef]
- Krese, B.; Govekar, E. Nonlinear analysis of laser droplet generation by means of 0–1 test for chaos. Nonlinear Dynam. 2012, 67, 2101–2109. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xin, B.; Wu, Z. Neimark–Sacker Bifurcation Analysis and 0–1 Chaos Test of an Interactions Model between Industrial Production and Environmental Quality in a Closed Area. Sustainability 2015, 7, 10191-10209. https://doi.org/10.3390/su70810191
Xin B, Wu Z. Neimark–Sacker Bifurcation Analysis and 0–1 Chaos Test of an Interactions Model between Industrial Production and Environmental Quality in a Closed Area. Sustainability. 2015; 7(8):10191-10209. https://doi.org/10.3390/su70810191
Chicago/Turabian StyleXin, Baogui, and Zhiheng Wu. 2015. "Neimark–Sacker Bifurcation Analysis and 0–1 Chaos Test of an Interactions Model between Industrial Production and Environmental Quality in a Closed Area" Sustainability 7, no. 8: 10191-10209. https://doi.org/10.3390/su70810191








