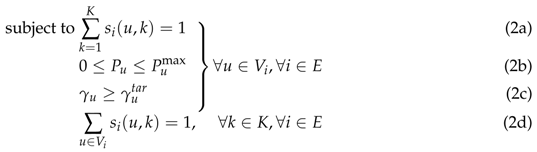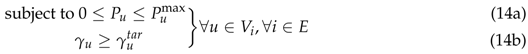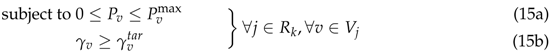1. Introduction
Device to Device (D2D) communication has emerged as an add-on communication paradigm to the modern 5G wireless cellular networks [
1]. In these networks, two types of users exist. The first type of users are the cellular users who communicate conventionally via the intervention of the evolved nodeB (eNB). The second type of users concerns the D2D users who are able to communicate directly with each other [
2].
D2D communications can take place either overlaying or underlaying inband a cellular network or outband [
3]. D2D users can act cooperatively, form clusters and facilitate content dissemination [
4,
5]. In the overlay case, D2D communications use dedicated resources, while in the underlay case D2D communications share common resources with the residual cellular network. In this paper, we focus on the underlay policy, where the cellular and the D2D users share common radio resources, organized into resource blocks (RBs). RBs are combinations of frequency and time symbols which are allocated to the users of the network [
6]. All users of the network belong to a cell, where the central entity, i.e., the eNB, is in charge of the efficient RBs assignment to the users. RBs assignment and power control are key factors for the efficient operation of the network in terms of spectral and power efficiency. Though significant research efforts have been devoted to the RBs and power allocation in a single-cell environment [
7,
8,
9,
10,
11,
12], the impact and consideration of multi-cell environment in the case of D2D underlay cellular network has been considerably neglected.
In this paper, we aim at closing this gap in the literature and study the joint problem of RB and power allocation in a multicell D2D underlay cellular environment. Multiple neighbouring cells exist serving the users of the network. Every cell is assumed to use the same spectrum band with the other cells for reasons of spectrum economy. In every cell, both cellular and D2D users co-exist and share common RBs. D2D users may share RBs with several other D2D users and with at most one cellular user in a given cell. Though a RB can be used by only one cellular user in a cell, yet interference may occur either by the reuse of the same RB by other cellular users in neighbouring cells, or by several other pairs of D2D users reusing the same RB either in the same cell or neighbouring cells.
In this setting, efficient RBs assignment and power control are of fundamental importance. On one hand RBs reuse promotes spectrum economy, but on the other hand causes signal to interference and noise ratio (SINR) degradation to the co-sharing users. The users of the network establish connections to either the eNB or their D2D receiver and try to obtain a minimum quality of service (QoS) at their receiver. QoS is expressed at the physical layer via the SINR at the receiver of each link. Users may have multiple different requirements with respect to the SINR at their receiver.
The rest of the paper is structured as follows.
Section 1.1 discusses the related work and
Section 1.2 summarizes and introduces our contributions.
Section 2 presents the system model adopted, while in
Section 3 the problem under consideration is formally presented. Subsequently,
Section 4 and
Section 5 present the first and second stage of the proposed approach respectively, where the problems of RB allocation and power control are described and solved. Finally, in
Section 6 detailed numerical results are presented demonstrating the operational effectiveness and efficiency of the proposed methodology, while
Section 7 concludes the paper.
1.1. Related Work
RB allocation approaches in the uplink of Long Term Evolution (LTE) networks have gained a lot of interest in the literature [
13,
14,
15]. In this setting, the eNB needs to determine in an efficient and timely manner the assignment of RBs to the users of the network. The optimization objective of the RBs assignment process could be the total throughput maximization, the interference mitigation [
16,
17], or the spectral efficiency improvement.
The approaches above concern the traditional cellular networks, where the users communicate via the eNB. Towards 5G networks and enabling the D2D communication capabilities of the users [
18,
19,
20], respective RB allocation approaches can be found in [
21,
22,
23]. In [
21] the importance of RB allocation approaches in various and emerging network architectures is stressed via presenting different approaches in LTE and LTE-Advanced networks. In [
22] the authors propose scheduling algorithms for the problem of RB allocation in D2D enabled networks taking into account each user’s delay requirement. Here the eNB needs to determine the optimal assignment of resources to the users at time scales of milliseconds according to 3rd Generation Partnership Project (3GPP) specifications including devices that may communicate directly. In [
23] the authors are proposing an efficient resource allocation scheme in clustered D2D enabled networks.
Focusing on the uplink RB allocation problem for the D2D enabled networks most of the related work is restricted to single cell environments [
7,
8,
9,
10,
11,
12], while very little attention has been paid so far to the respective multi-cell case. Specifically, in [
24,
25] the D2D RB selection problem is analysed as a game, in a simple scenario with one cellular user per cell. The players of the game are the BSs and they compete with each other in order to serve the D2D users with less harm. However, the existence of the Nash Equilibrium (NE) point of the game is not analytically proven, and it is only examined via numerical simulations.
The previous works focus on maximizing the total sum of rates in the network via game theoretic approaches and pricing for the resources. In [
26], the authors address only the problem of RB allocation in a D2D underlay multicell network, via formulating a potential game with the objective of optimizing the total sum of rates in the network. In [
27] the problem of total throughput maximization for the D2D users in a multicell D2D underlay cellular network is addressed under a Multiple Input Multiple Output (MIMO) setting. In [
28] the problem of both RB and power allocation is addressed. Initially, the authors aim at minimizing the interference caused by the D2D links to the cellular links of the network, and subsequently a power control approach is applied in order to maximize total system throughput.
1.2. Paper Contributions
In this paper, we address the joint problem of optimal RB and power allocation in the uplink communication of multicell D2D enabled networks, where the optimization objective is the minimization of the total interference of the network. Due to the inherent complexity of the nature of the combined problem, a two step approach is followed. At the first step the RB allocation problem is solved considering that all users of the network transmit at fixed power. At the second step, taking the RB allocation vector of the first stage as an input, the total interference minimization problem is decomposed into multiple interference minimization problems per available RB.
Specifically, at the first step the problem is formulated as a non-cooperative game which is proven to be a bilateral symmetric interaction game. This type of games are exact potential games. Every player of the game is one of the potential receivers of the system. The receiver of the network can be either an eNB or a D2D receiver. The eNB is in charge of deciding the optimal RB assignment to the cellular users who belong to the respective cell. The D2D receiver decides the optimal RB for the respective D2D transmitter. Leveraging the highly desirable properties of potential games, we prove that at least one NE of the game exists. A best response algorithm is proposed which converges after a finite number of iterations to the identified NE point of the game.
It is noted that in our approach and methodology, in contrast to the majority of existing literature, we do not restrict a priori the number of D2D pairs that can reuse a RB, allocated to a cellular link. This is determined dynamically by the objective of interference minimization. Thus, a RB reserved by a cellular link can be potentially reused multiple times by different D2D links in order to increase spectrum efficiency.
During the second step of our approach each uplink power allocation problem per RB is formulated as a linear programming problem. This optimization problem is shown that is equivalent to the total power minimization problem for every available RB. For this reason, the well known Foschini-Miljanic algorithm [
29], which solves the total power minimization problem [
30], is properly adopted to solve our problem in a distributed way. This algorithm finds either a feasible solution or pushes the users who cannot satisfy their SINR requirement to the maximum transmission power level in order to achieve a SINR level as close as possible to their SINR requirement.
Finally, the efficiency of the overall proposed framework is evaluated through numerical simulations, especially with respect to significantly decreasing the total power consumption in the network, while increasing the network capacity in terms of number of users who are able to satisfy their SINR requirement.
2. System Model
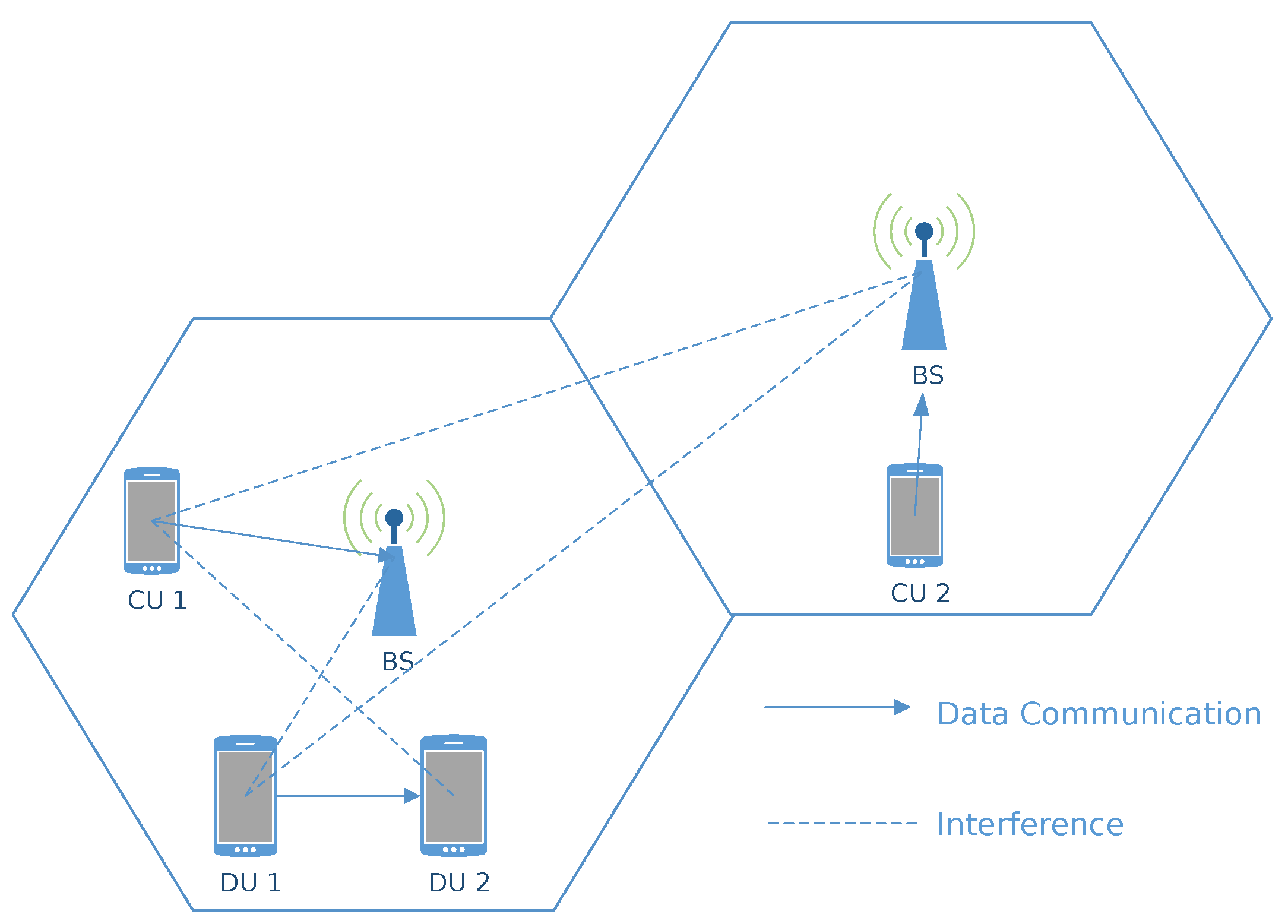
We consider a multicell D2D underlay cellular network, where
L neighbouring cells co-exist. The UEs and the eNBs are assumed to be equipped with a single omni-directional antenna. Each cell contains two types of users, cellular users (CUs) and D2D users (DUs), where their communication modes are assumed that have already been selected. The CUs communicate through the eNB of their serving cell, while the DUs communicate directly to each other in pairs, where the DUs of every D2D pair are adequately close to each other, thus forming a D2D link. The corresponding reference topology is shown in
Figure 1.
We assume that each cell has access to a fixed number of K RBs. Every cellular user of each cell uses one of those RBs which are orthogonal to each other. This means that there is no interference between cellular users of the same cell. The number of cellular users at each cell requesting a RB can be variable from cell to cell. Considering that the set of cellular users of cell i will be requesting and assigned a non-overlapping set of RBs, each cellular user of the same cell will occupy a different RB. Apart from the cellular users, D2D users reside in the network and each of them has to decide which RB to choose in order to transmit. The D2D users reuse one of the available K RBs at each cell. Multiple D2D users may share the same RB with one cellular user in each cell. As mentioned before, RBs reuse takes place between cellular users from different cells and between cellular and D2D users from the same or different cell. In principle, a RB may be occupied simultaneously from only one cellular user per eNB, and from multiple D2D users.
In this multicell D2D underlay architecture, in order to treat cellular and D2D users in a homogeneous and holistic manner from RB allocation point of view, apart from the cellular cells i.e., eNBs, we consider the D2D receivers as virtual cells. Each D2D receiver can play the role of a (virtual) cell, where the serving users of this cell is exactly one i.e., the D2D transmitter of the respective D2D pair. From this point and on, when we refer to a cell, we may consider either the eNB of a cell or the D2D receiver of the respective D2D pair (that is we refer to either the physical L neighbouring cells or the considered virtual cells as defined above).
Let
E be the set of all the cells (including the virtual ones) and
be its cardinality that represents the number of the considered cells in the network. Let
be the set of users of cell
i and let also
be the set of the available RBs at cell
i which a user
u can use. We define the SINR at the receiver of every user
u of cell
i, either cellular or D2D, using RB
k, as follows:
where
, i.e., the set of users who belong to cell
i,
denotes the channel gain between user
u of the cell
i and the receiver-cell
i at RB
k,
is the transmission power of user
u at RB
k,
is the set of users who belong to cell
j,
is the channel gain between user
v of the cell
j and the receiver of cell
i at RB
k,
is the transmission power of user
v at RB
k and
refers to the thermal background noise power at the receiver of each link.
3. Problem Formulation
In the following, we formulate the problem of interference minimization in the joint space of RBs and uplink transmission power.
where
is the total sensed interference from all users at cell
i, caused by any other user of the other cells of the system who share common RBs with the users of cell
i and
User u belongs to cell i and user v belongs to cell j. denotes the transmission power of user u of the cell i at the chosen RB from user u. Since every user is assumed to use exactly one RB we can omit the exponent k from without disambiguation. is the maximum transmission power of user u. is the SINR at the receiver of user u. Similarly the exponent k is omitted from . is a positive real number denoting the SINR requirement of user u.
and , where is the number of the cells in the network.
The first Constraint (2a) concerns the fact that each user of each cell (either physical or virtual) chooses exactly one RB. Constraints (2b) and (2c) concern the acceptable range of values for the transmission power and SINR levels. The final Constraint (2d) is related to the orthogonality requirement between users of the same cell. It is stressed here that based on the consideration of the additional virtual cells, a D2D user belongs to the corresponding cell (which essentially is a single user cell) and not to the physical cell that is placed within. In a nutshell, in order to solve the aforementioned optimization problem we search for feasible combinations of RB and transmission power assignments which minimize the total interference in the network.
The above problem is a mixed integer programming problem since some of the decision variables are integer numbers and the rest of them i.e. transmission powers, continuous variables. This problem is a combinatorial optimization problem and its complexity is known to be NP-hard [
31]. For this reason, we aim at efficient approximation algorithms to solve the problem. The proposed approach is to solve the problem in two stages. In the first stage, we consider that all users have chosen a fixed transmission power and we search for the optimal RB assignment. We propose a game theoretic approach which solves the problem iteratively. At each iteration every player of the game makes a decision regarding its RB which maximizes its utility function while simultaneously minimizes the total interference in the network. After a finite number of iterations the algorithm converges to the desirable NE point of the game. At the second stage, the problem of total interference minimization can be decomposed to multiple interference minimization problems per RB. Certain number of users share a RB and create interference one to another. Our goal is to determine users’ optimal transmission power allocation towards minimizing the total interference per RB while satisfying the minimum SINR requirements of the respective users.
4. RB Allocation
4.1. RB Problem Formulation and Solution
In this subsection we describe the first stage of our proposed approach which concerns the RB allocation. It is assumed that every user of the cell (either cellular or D2D) has a fixed transmission power value. Thus the problem, expressed in Equation (2), may be simplified and take the following form
where
is defined as in Equation (
3) and
has been assumed a fixed value for every
and
The above problem is a combinatorial optimization problem since the decision variables of the problem i.e., the assignment matrices of each cell are integer. In the literature, efficient algorithms for the exact solution of this type of problems do not exist. For this reason, we search for approximation algorithms which provide suboptimal solutions in a time efficient manner.
For this problem, our idea is to model it, as an exact potential game. The players of this game will be the cells—either physical or virtual (D2D)—of the system and the strategies will be the assignment matrices of the cells. Formally, we define the game
where
N is the set of the players of the game G, , i.e., the set of the receivers in the system—either the eNBs or the D2D receivers,
S denotes the set of the strategies of the players,
i.e., the set of the assignment matrices of each cell-receiver,
, defined in Equation (
4) and
U denotes the set of the utility functions of the players of the game G.
The utility function
of the player
i is defined as follows:
where
is defined in Equation (
3) and repeated here for clarity reasons
is defined as follows
denotes the total interference caused by all users of cell
i to all other cells using at least one common RB with cell
i.
Theorem 1. Game G is a bilateral symmetric interaction game [32]. Proof of Theorem 1. A bilateral symmetric interaction game has the following form
, where
and
where
.
The utility function of the player
i of the game
G, defined in Equation (
7), can be mapped to the utility function defined in Equation (
9), if
. It is observed that the bilateral symmetric property of Equation (
10) also holds. ☐
Bilateral symmetric interaction games exhibit certain desirable properties since they are exact potential games. The potential function of the game
G according to [
32] is the following:
We observe that there is a symmetry between the interactions of one player i and another player j. This holds, because the total interference sensed and caused by the users of cell i to the cell j is equal to the respective interference from the users of cell j to the cell i. We characterize as a non overlapping set of users, the users who are allocated orthogonal RBs. The interference sensed by a non overlapping set of users of the cell i, due to the cell j, is the total interference that a non overlapping set of users of the cell j create to the cell i. The inverse is also true.
Since the game
G is an exact potential game, this means that this game has at least one NE point and this NE point is a local optimum of the potential function defined in Equation (
11). The potential function, defined in Equation (
11), can be easily proven (change of variables
i and
j for the second term) that it coincides with minus the total interference sensed by every cell in the network. Thus, every NE point of the game
G is a local minimum of the total interference.
4.2. RB Allocation Iterative Algorithm
In this subsection, we will present a best response algorithm which is proven to converge after a finite number of iterations to one of the NEs of the game G. We consider that initially all players of the game, i.e., the cells, have chosen an initial RB assignment for all users who reside inside them. Below the respective algorithm is presented.
In Algorithm 1, every player of the game, i.e., each cell acts in a sequential order. This assures that Algorithm 1 will converge to the NE of the game i.e., minimum of the total interference after a finite number of iterations. It chooses the optimal RB assignment to its users, based on the equation of Line 4 in the Algorithm 1. All other users are considered that they have already chosen a RB assignment to their users and then the current cell according to Line 4 chooses the new optimal RB assignment for its users. This step is repeated until all players of the game conclude to a common RB assignment for all users of the network.
| Algorithm 1: RB allocation |
| 1: | Counter , Converged = false, ite(i) = 0 |
| 2: | for all cells do |
| 3: | if then |
| 4: | |
| 5: | if then |
| 6: | |
| 7: | else |
| 8: | |
| 9: | end if |
| 10: | |
| 11: | if then |
| 12: | |
| 13: | end if |
| 14: | end if |
| 15: | end for |
More precisely, from Equation (
7) and considering that all other cells, apart from cell
i, have chosen RB assignment the decision problem of cell
i takes the following form:
where
and
.
Problem (12) is an integer linear programming problem and even the relaxed version of it always has an integer optimal value since the constraint matrix is totally unimodular. This problem can be solved via the well known Hungarian algorithm [
33] in polynomial time with respect to the number of the available RBs at each cell. Leveraging the potential game properties, Algorithm 1 converges after a finite number of iterations. Moreover, at each step, Algorithm 1 improves not only the utility function of each cell but also the potential function of the game i.e., the total interference. After a finite number of iterations, a RB assignment is selected which minimizes the total interference of the network.
In order for Algorithm 1 to be practically implementable, there is a need for a communication control channel between the different cells i.e., the eNBs and the D2D cells. This control channel will carry the necessary information in order for the cells to execute Algorithm 1. For the case of eNBs, this can be done using the X2 interface [
34] which has been already designed to implement this type of communication between the eNBs in LTE networks. For the D2D cells it can be assumed that there is a control channel between the D2D receivers and the respective serving eNB they reside in [
19]. The complexity of Algorithm 1 belongs to the class of Polynomial local search (PLS) problems [
35]. At each step, each eNB runs the Hungarian algorithm in order to update its RB assignment. The complexity of the Hungarian algorithm is
with respect to the number of the available RBs. For the D2D cells the complexity of the update step is
since the number of served users is only one i.e., the respective D2D transmitter. The convergence of the above algorithm is guaranteed but not necessarily in polynomial time. However, at every step of the Algorithm 1 the total interference is being reduced. As it will be seen in
Section 6.1.1 the required number of iterations for convergence was quite low with respect to the number of players involved. By applying Algorithm 1, we will obtain a RB assignment for all cells of the network which minimizes the total interference in the network.
5. Power Control
In this section, we present the second stage of our approach for the power control problem in multicell D2D underlay network architectures, considering that the RBs have already been assigned to the cellular and the D2D users according to the output of the first stage of our approach. Thus, capitalizing on the outcome of the RB allocation approach, Problem (2) takes the following form:
All cells have already chosen their RB assignment matrices and thus Problem (14) can be decomposed to multiple optimization problems per available RB since we assume that there is no interference between different RBs due to their orthogonality. Problem (14) is equivalent to multiple interference minimization problems per RB
k. Then each problem for every RB
k can be written as:
is the set of cells who occupy RB
k and
v the user of cell
j who occupies RB
k. There is no other user who uses the same RB at the same cell since we assume orthogonality of the available RBs. Let
be the transmission power of the the user
v of cell
j who uses RB
k.
The objective is to minimize total interference at every RB k under the constraints of feasible transmission power and SINR requirement satisfaction of the users. Problem (15) is a typical linear programming problem. Thus, if this problem has a feasible solution this lies at the point of intersection of the Constraints (15a) and (15b). The gradient of the objective function shows the direction of the optimal change of the objective Function with respect to the independent variables of the problem i.e., transmission powers of the users sharing RB k. The gradient of the objective Function (15) is positive with respect to the transmission power of every user of each cell who uses common RB k. Thus, the minimum power which satisfies all Conditions (15a) and (15b) is the optimal feasible solution which minimizes the objective function of Problem (15).
The gradient of the objective function of Problem (15) has the same sign to the total power minimization problem under the same SINR and transmission power constraints. For the problem of total power minimization, as it is already known from the literature [
29], there is a distributed algorithm which converges to the optimal solution, if this solution is feasible i.e., satisfies Constraints (15a) and (15b). Thus, by applying this algorithm to Problem (15), we can find the required optimal solution.
Let be the initial transmission power vector of all users of the network. This is a fixed transmission power vector which could be the maximum transmission power value for each user of the network. At Line 4 of Algorithm 2, each user updates its current power in a parallel fashion. After the execution of this step, a coordination mechanism is needed in order to check the power convergence of each user.
| Algorithm 2: Distributed Power Control per RB k |
| 1: | Counter , , |
| 2: | if then |
| 3: | for all do |
| 4: | |
| 5: | end for |
| 6: | if then |
| 7: | |
| 8: | end if |
| 9: | |
| 10: | end if |
6. Performance Evaluation
In this section, we provide a series of numerical results evaluating the operational features and the performance of the proposed approach. Initially, in
Section 6.1, we focus on the operation performance achievements of our proposed methodology, in terms of interference, uplink transmission power and achievable data rate. The achievable performance and contribution of the proposed RB allocation process (i.e., first step) is examined and evaluated in
Section 6.1.1, while subsequently in
Section 6.1.2 the additional benefits obtained by the second stage of our approach (i.e., power control) are studied and its fast convergence to the final optimal power values is shown. Then, in
Section 6.2 we provide a comparative evaluation of our proposed approach against another existing approach in the recent literature that targets rate maximization [
26], through the efficient resource allocation in a multi-cell network supporting D2D communication. The aforementioned approaches are thoroughly compared in order to illustrate the obtained gain of our proposed approach in terms of uplink transmission power required to meet the users’ SINR requirements, number of users that can be supported by each approach (i.e., users that their SINR meets or exceeds the pre-specified threshold), rate and interference. It should be noted that unless otherwise is explicitly mentioned, the majority of the numerical results is the statistical average outcome of several random topologies with respect to the distribution of the cellular and D2D users within each cell.
6.1. Proposed Approach Properties and Operation
6.1.1. RB Allocation
In this subsection, the effectiveness and efficiency of the first step of our approach i.e., Algorithm 1 is shown. The simulation setup and the corresponding parameters considered are shown in
Table 1.
We consider an initial random RB assignment to all users of all cells (both cellular and D2D users) of the network, where each user is assumed to use exactly one RB. Cellular users of the same cell use different RBs in order to satisfy the orthogonality requirement for every cell. The channel gains between a user
u of cell
i and the receiver at cell
j is computed as
. In
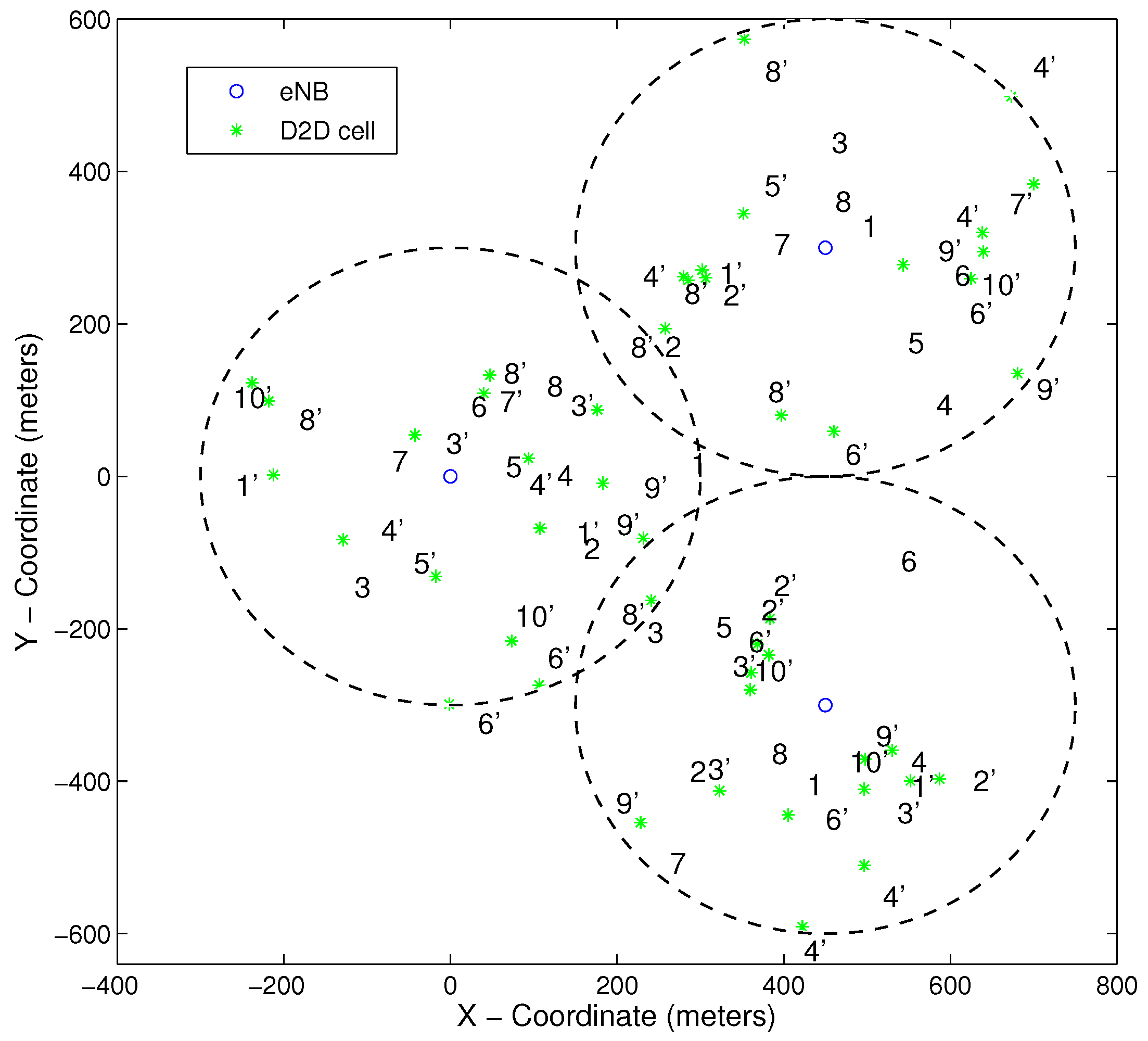
Figure 2, the specific topology under consideration in this experiment along with the initial RB assignment is presented. The corresponding numbers represent the RB assigned to the respective users, therefore this figure practically shows a graphical representation of the reuse of each RB. In
Figure 2 and
Figure 3, the numbers without the special character ’ refer to cellular users while the numbers followed by ’ refer to D2D users.
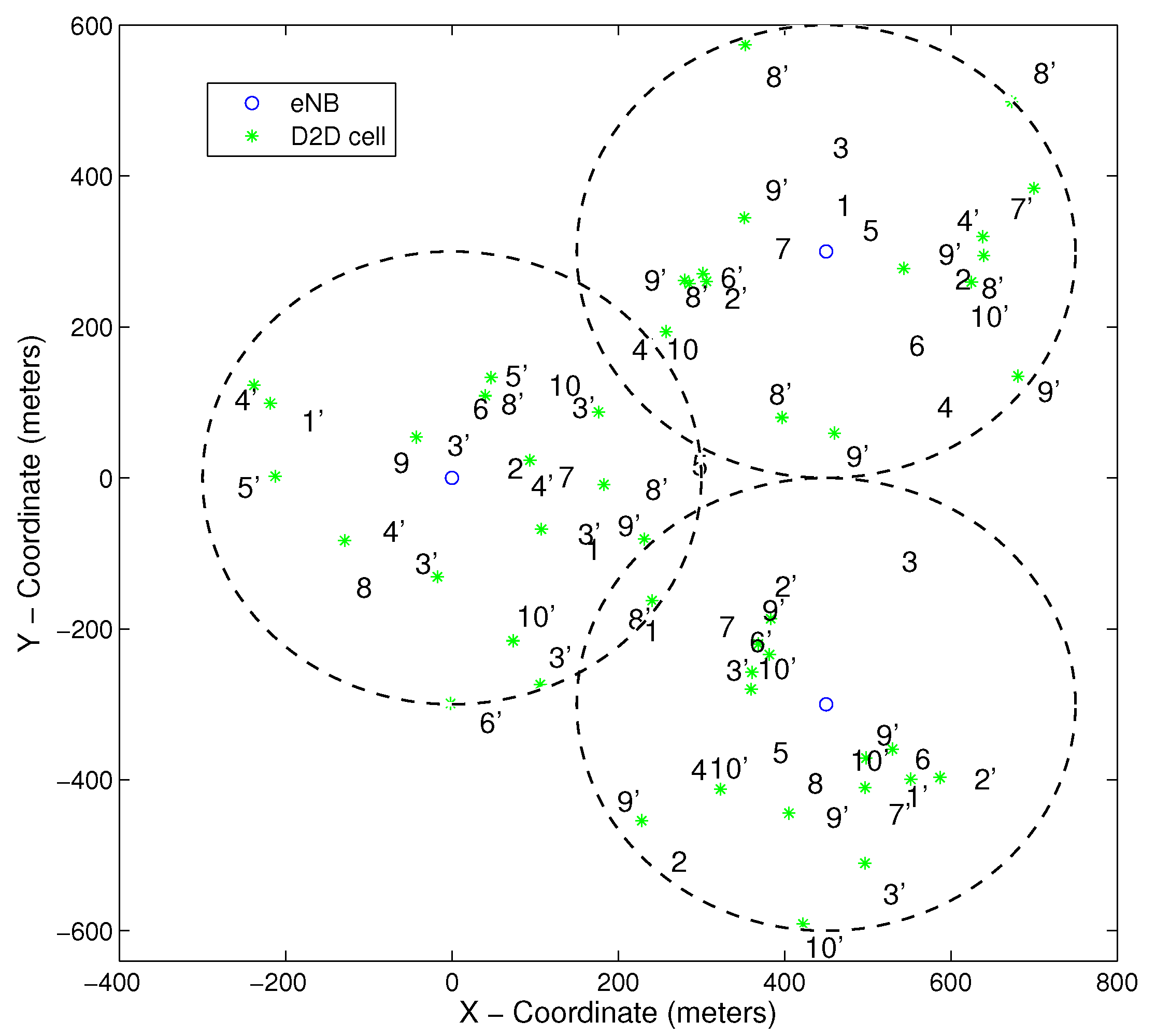
Similarly, in
Figure 3, the final RB allocation as the outcome of the application of the first step of our approach (i.e., Algorithm 1) to all users of the network is shown. It is clearly demonstrated that the RB reuse efficiency has been significantly improved. Specifically, considering as metric of such efficiency the achieved reuse distance of a common RB—denoting the distance between a transmitter and a different D2D receiver who share the same RB—it is observed that the reuse distance of all RBs increases drastically. Precisely, the average minimum reuse distance of every RB, before the application of Algorithm 1, was approximately 15 m and after the application of Algorithm 1 it increases to approximately 35 m, corresponding to an improvement of 133%.
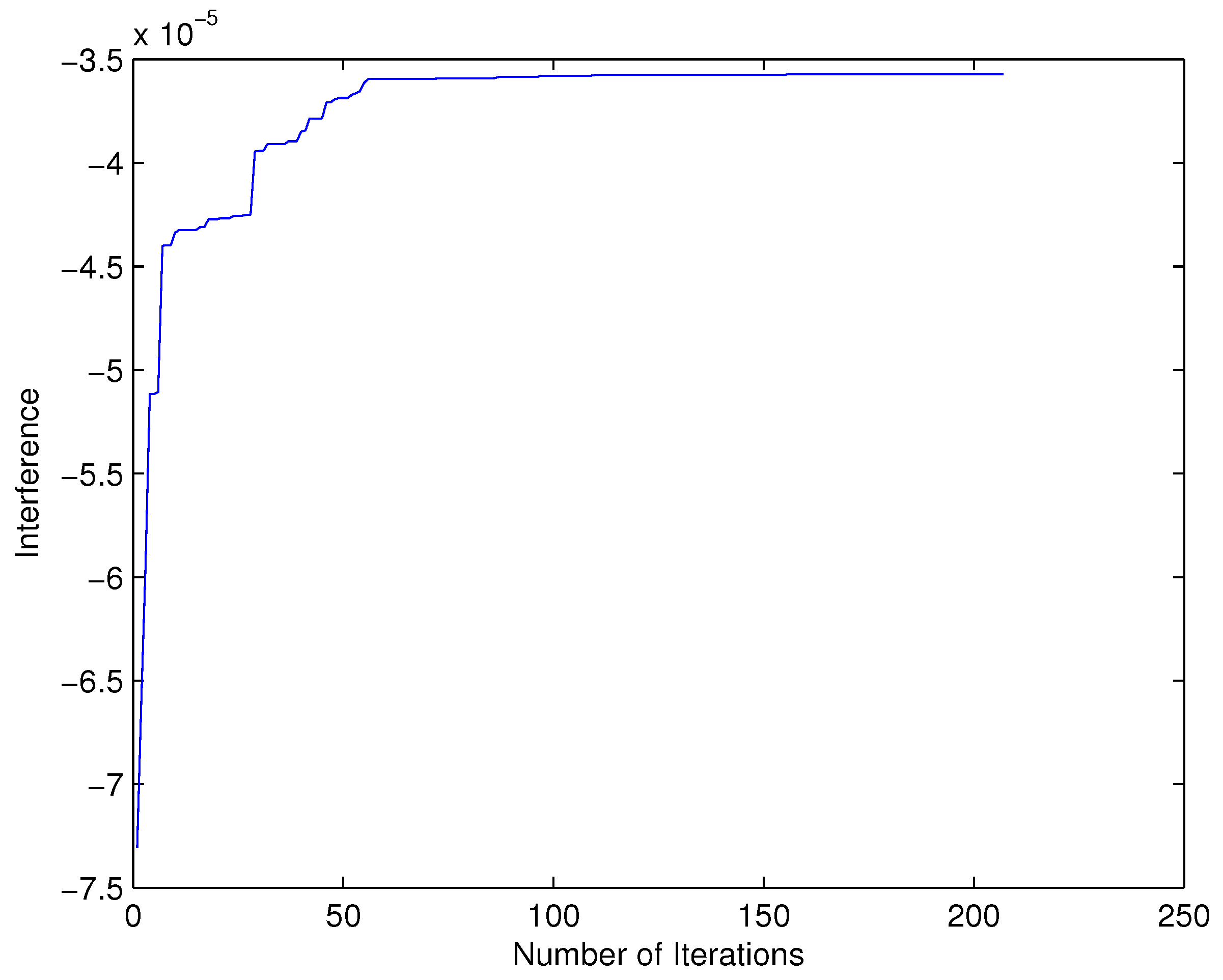
In
Figure 4, the evolution of the total interference in the network is demonstrated with respect to the number of iterations needed for Algorithm 1 to converge. It is shown that Algorithm 1 always reduces the total interference after each step of its execution. This also verifies experimentally the respective theoretical property of potential games [
32], as the one considered in this paper. The required number of iterations for convergence was quite low with respect to the total number of players of the game. Precisely, the required number was about 3–4 times the total number of players involved in the game. The total interference reduction compared to the corresponding value based on the initial random allocation is approximately 80%. It is noted that we have also verified experimentally that Algorithm 1 converges to a stable outcome under any initial RB allocation, while the range of the optimal values of the total interference was within 5% difference of the observed maximum value.
Subsequently, in
Figure 5, we show the average interference reduction for every user of the network after the application of Algorithm 1. For clarity reasons, it is mentioned that users 1–24 in all figures represent cellular users, while the users 25 and beyond represent D2D users.
Based on these results, we observe that Algorithm 1 achieves a significant reduction to the interference, sensed at every user of the network. Precisely, the mean interference reduction is on average 93%. This in turn can be translated to significant improvements in the achievable transmission rate as well, as it is observed in
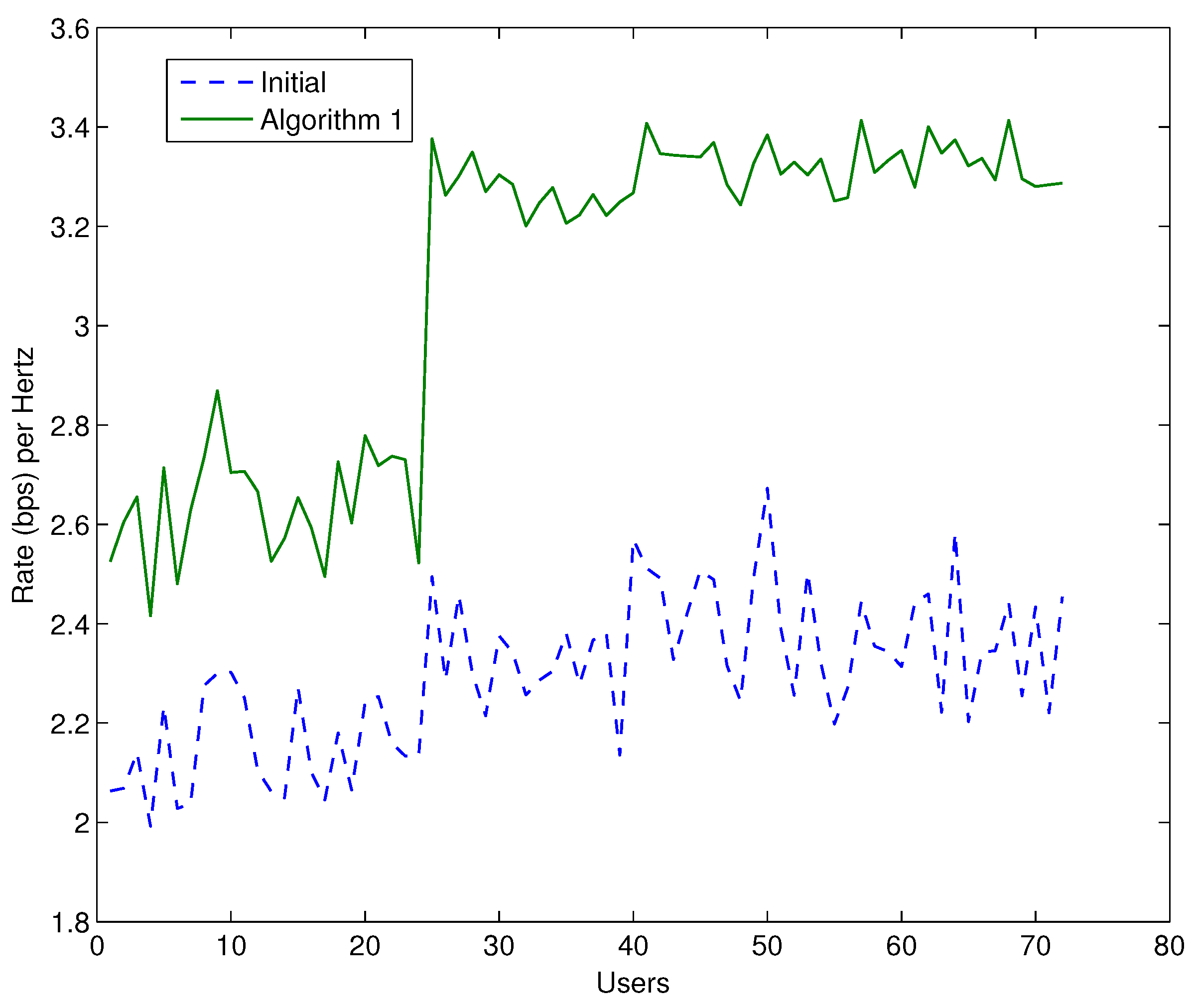
Figure 6, where the achieved transmission rate per used bandwidth unit (i.e., spectral efficiency) is shown for every user of the network. The mean rate increase with respect to the initial achievable transmission rate is calculated at approximately 34% .
6.1.2. Power Allocation
In this subsection, the second step of our approach i.e. the power allocation Algorithm 2 is evaluated. After the application of Algorithm 1, a RB selection for all users of the network is obtained. Then as explained before, we apply Algorithm 2 for every co-sharing RB. The simulation setup for this section of our experimentation is the same as presented in
Table 1. It is noted that in principle users may have different SINR requirements depending on the type of service they request. For demonstration only purposes in the set of results presented here, we have assumed a common SINR requirement for all users of the network equal to 10. Algorithm 2 instructs users who share a common RB to act in a parallel fashion. The convergence of Algorithm 2 takes place after a quite low number of iterations. All users start from an initial power allocation which is their maximum transmission power. This is considered to be 2 watts for the cellular users and 0.1 watts for the D2D users. During the convergence process of Algorithm 2, each user tries to find the minimum necessary transmission power in order to satisfy his SINR requirement. In case this is not found, it transmits at his maximum power.
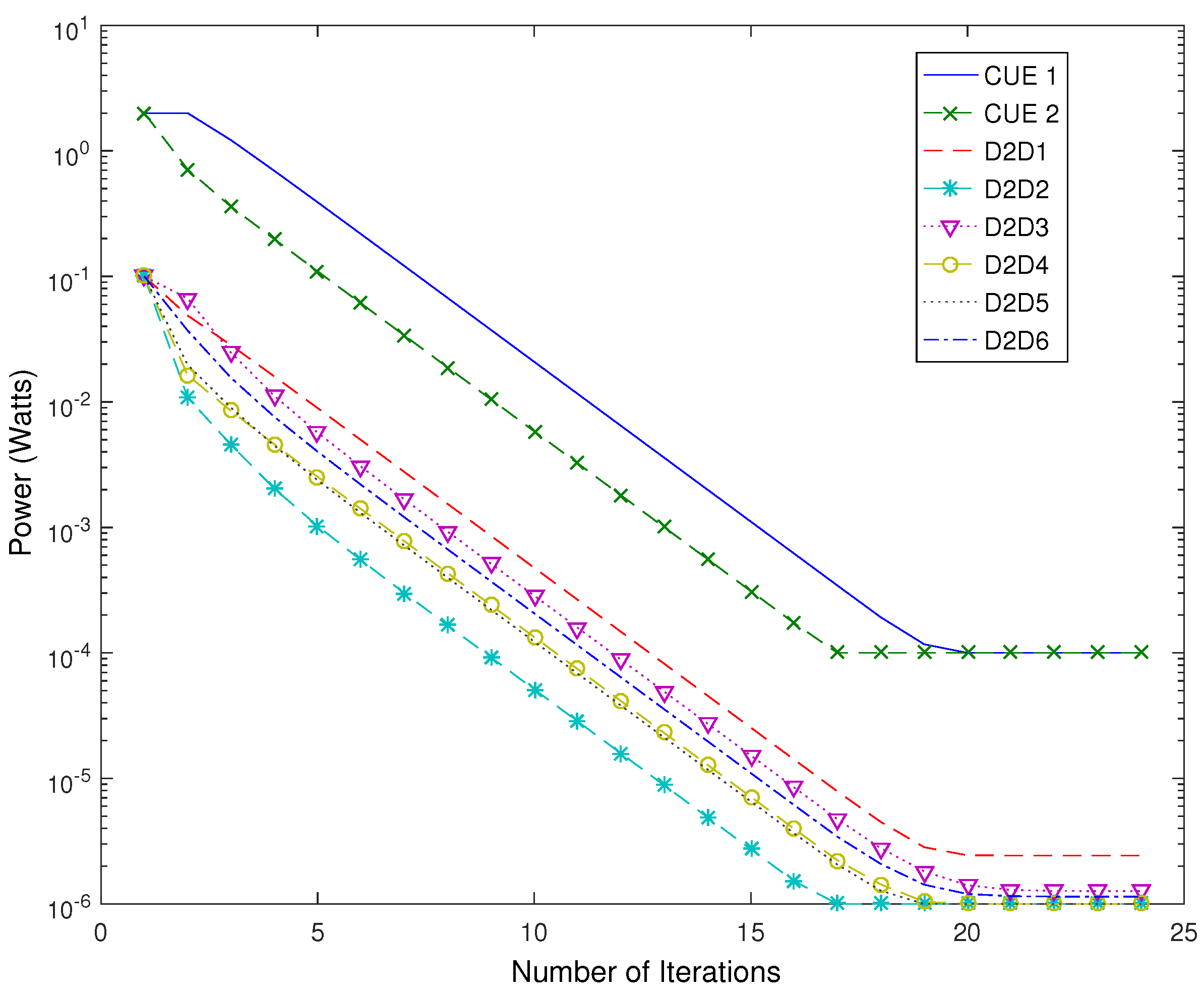
In
Figure 7, the transmit power convergence is shown for a randomly selected RB, that is RB 6. It is shown that all users of the network who share RB 6 converge to their desired transmission power values. All users of this RB either meet or exceed their SINR requirement. The transmit power radically reduces for all users, and as a result the total power consumption decreases by 57% with respect to the initial power values. Moreover the average number of users, throughout the whole network, who satisfy their SINR requirement increases from 29.15 to 55.35 after the application of Algorithm 1 corresponding to an increase of approximately 90%, and finally to 61.19 users after the combined application of Algorithms 1 and 2, raising this improvement to 110% in total.
6.2. Comparative Results
In this subsection our proposed approach is compared against a state of the art approach in the recent literature [
26]. The latter concerns the RB allocation in a multicell D2D underlay network, with the objective of optimizing the total sum of transmission rates of all users of the network, through an approximate better response algorithm under a potential game formulation. In the following, we refer to this approach as Rate Max approach.
The comparative process and evaluation is performed in a gradual manner in order to clearly demonstrate and quantify the benefits obtained by the application of each step of our approach, while maintaining fairness in the comparisons. Our approach aims at total interference minimization while the approach of [
26] aims at throughput maximization in the RB allocations space. The first step of our approach i.e., Algorithm 1 achieves on average better results with respect to the interference at the receiver of each user compared to [
26]. This gives the users the opportunity as it will be shown next, by applying Algorithm 2 to transmit at lower levels on average while a larger number of them satisfies their SINR requirements. Specifically, the following four scenarios are considered and compared:
the application of only Algorithm 1 i.e., our proposed algorithm for the RB allocation phase of the problem
the application of approach [
26] for the RB allocation phase of the problem
the combined application of Algorithms 1 and 2
the combined application of approach [
26] and Algorithm 2 of our approach (for power control).
In this subsection, the above approaches are tested and evaluated under the simulation setup used in previous
Section 6.1.2, that is the one presented in
Table 1 with the SINR requirement equal to 10. As mentioned before, all the numerical results presented in the following refer to statistical average values, as they are obtained by several repetitions of the simulation, with the locations of the cellular and D2D users varying uniformly and randomly in the network topology. The combined application concerns the sequential application of a RB allocation approach and then the application of our proposed power control approach (i.e., Algorithm 2).
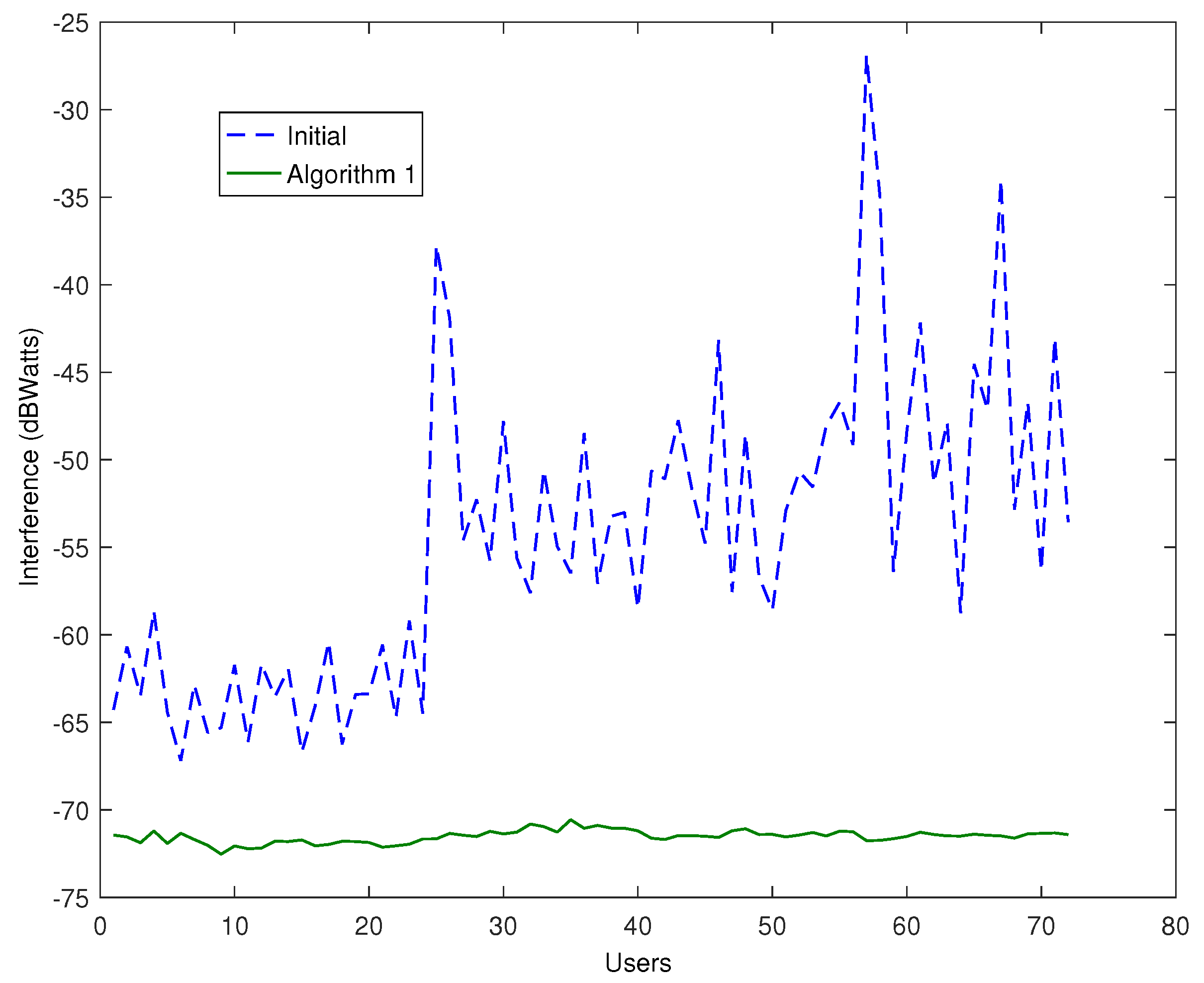
In
Figure 8, the first step of our approach i.e. Algorithm 1 is compared directly to approach [
26] in terms of observed interference. As clearly indicated by the corresponding results Algorithm 1 achieves a considerable interference reduction compared to [
26]. Specifically, the average reduction of our approach with respect to [
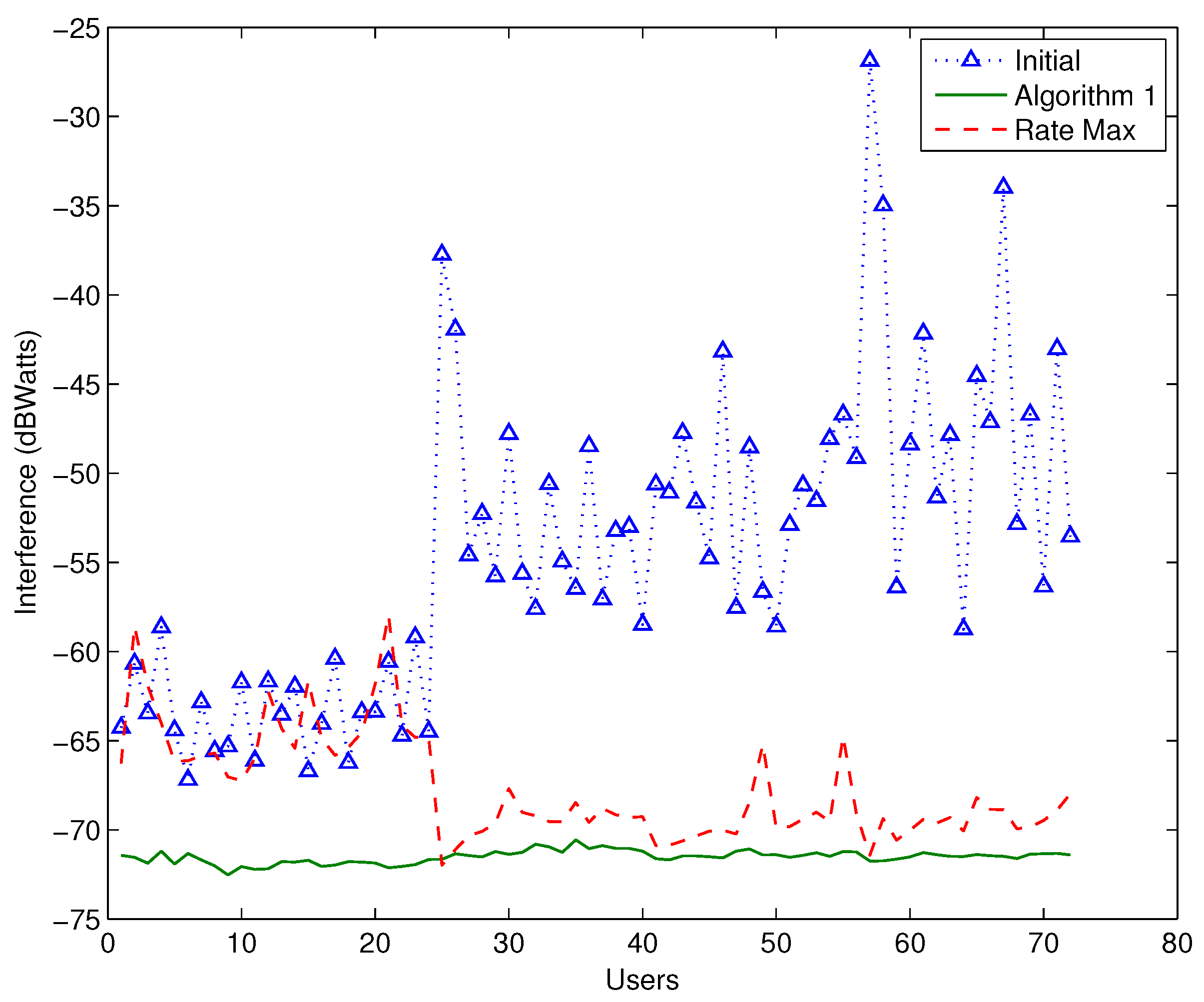
26] is calculated as approximately 50% per user. It should be clarified that this value refers to the net value of interference, while the vertical axis of
Figure 8 is expressed in decibel Watts (dBWatts). It can be seen that the largest benefit concerns the cellular users, where the respective reduction is almost 80%. In
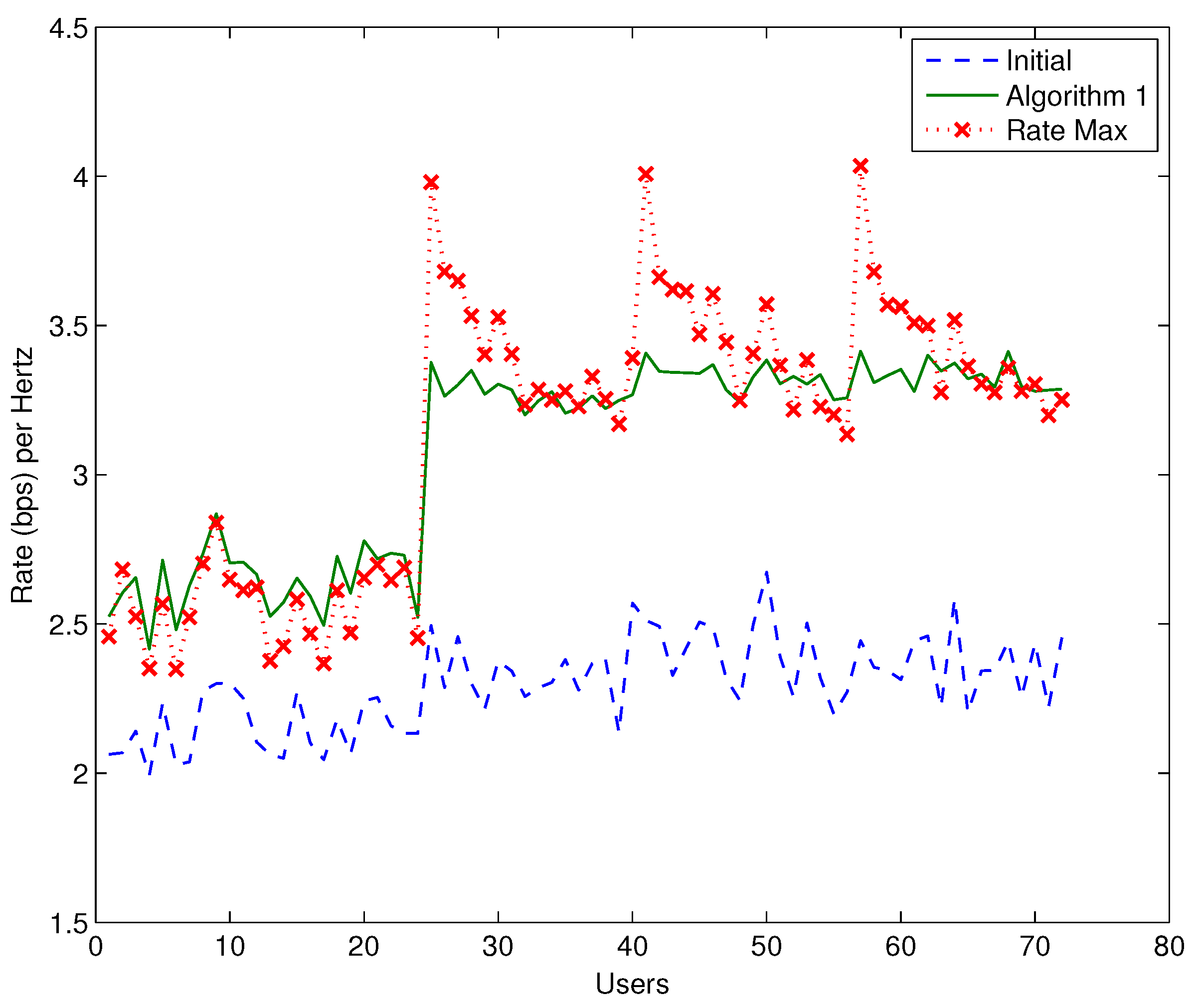
Figure 9, the respective transmission rates per Hertz for each user are shown. It can be seen that although Algorithm 1 targets at interference minimization, under fixed transmission power obtains comparable to [
26] performance with respect to the achievable transmission rate.
By applying Algorithm 2 after the execution of Algorithm 1 and approach [
26] respectively, we compare and analyse the averaging results with respect to the transmission power and the number of users satisfying their SINR requirements. In
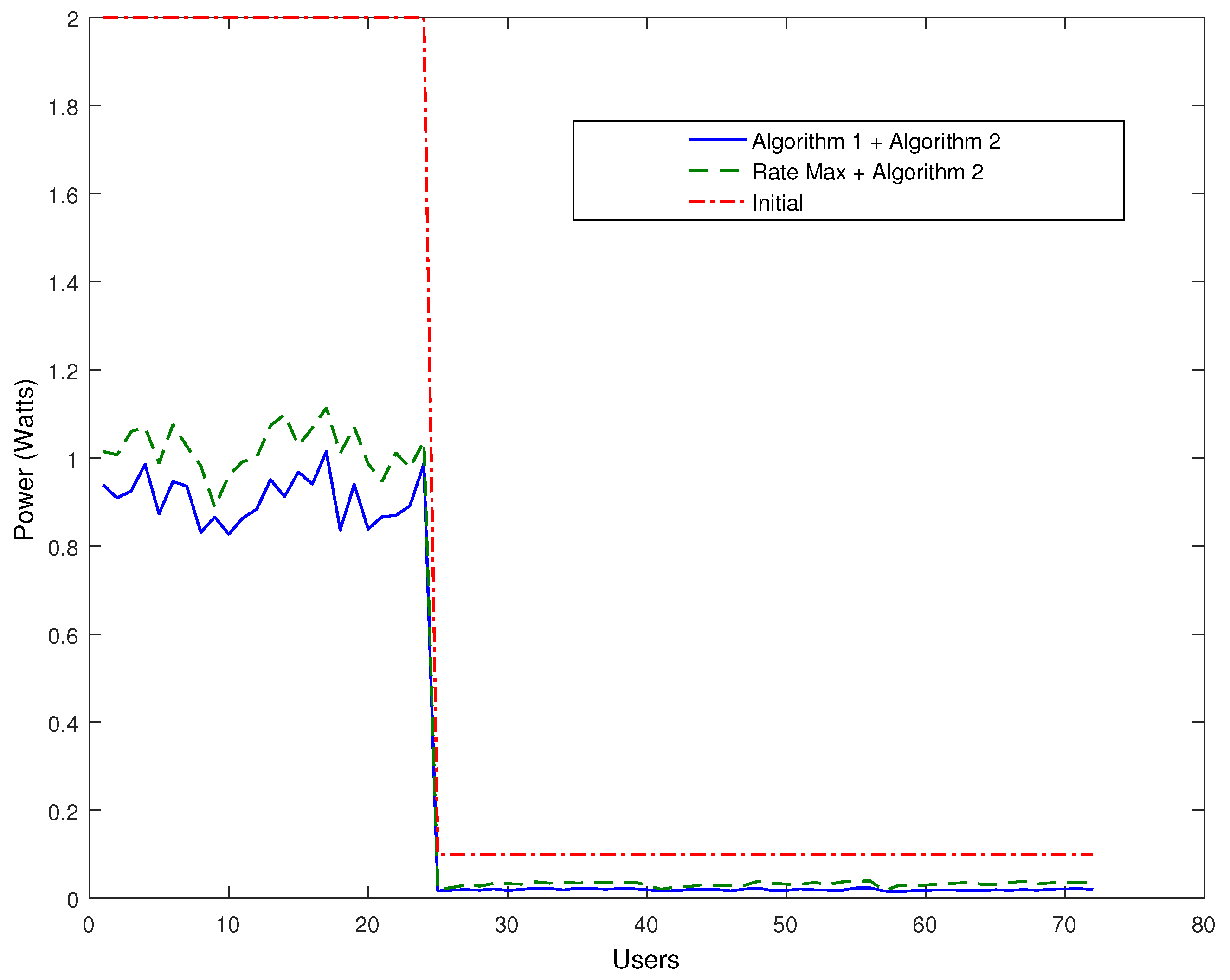
Figure 10, it is demonstrated that the required transmission power under our proposed approach reduces radically, i.e., by 70% on average with respect to the initial transmission power values and by 30% with respect to the combined approach (Rate Max + Algorithm 2). Lastly, the number of users in the system who are able to satisfy their SINR requirement also increases following both approaches, with our approach outperforming by 12% the (Rate Max + Algorithm 2) (
Figure 11).
Similarly in
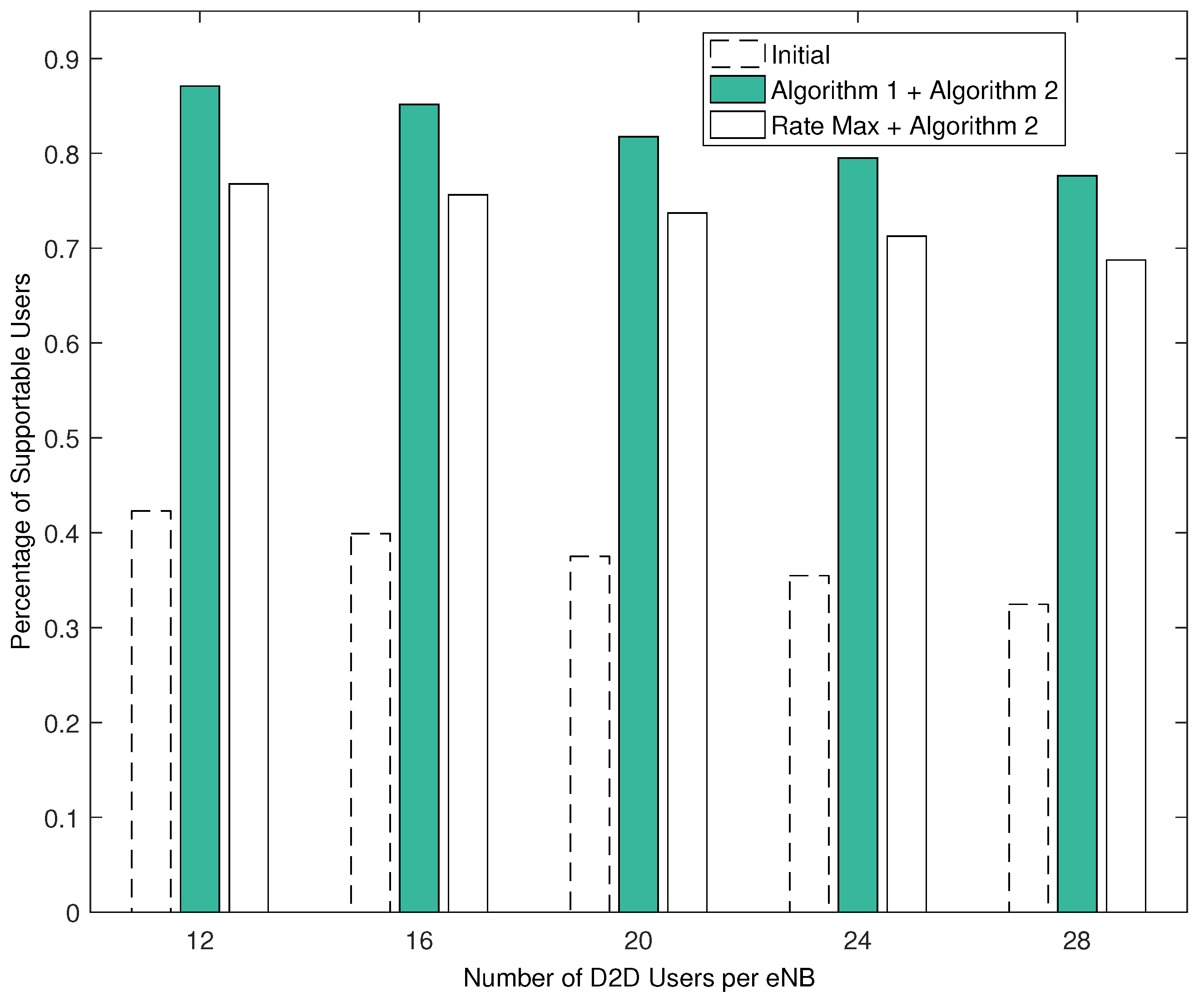
Figure 12, the total number of users who satisfy their SINR requirements as a function of increasing number of D2D users per eNB is presented. It is clearly observed that our approach sustains its significant capacity improvement in terms of number of users that can be supported by the network resources even both for low and high density networks (i.e., increasing number of D2D users per eNB).
7. Conclusions
In this paper, the problem of interference mitigation in a multi-cell D2D underlay cellular network is addressed. To deal with the complexity introduced by the multiple cell environment and the existence of D2D users, a two step approach has been proposed and adopted. As the first step, the RB allocation problem is solved by formulating it as a non-cooperative game which is proven to be a bilateral symmetric interaction game. We show that at least one NE of the game exists and a best response algorithm is introduced which converges after a finite number of iterations to the identified NE point of the game. Subsequently, at the second step the total interference minimization problem is decomposed into multiple interference minimization problems per available RB, and power control is applied by each user in a distributed manner in order to identify the lowest required transmission power to satisfy its SINR, if possible. Extensive numerical results are presented that verify several properties and operational characteristics of our proposed approach. Specifically it is demonstrated that our proposed approach manages to reduce significantly the total interference in the network as well as the interference at the receiver of every user, either cellular or D2D. Furthermore, by comparing our approach to another existing approach in the recent literature that targets rate maximization, it is shown that though our approach targets interference minimization, it still obtains comparable performance in terms of total throughput, and as a consequence significant spectral efficiency improvement is finally achieved. This enhanced performance translates directly to system capacity increase in terms of number of users that can be supported by the network resources and transmission power reduction.