Physical Layer Network Coding Based on Integer Forcing Precoded Compute and Forward
Abstract
:1. Introduction
1.1. Main Contributions
- We propose a novel precoding technique to implement physical layer network coding using CF. Our precoder design is based on integer forcing and allows bypassing the self-noise limitation of existing formulations, thus providing higher achievable rates than existent relaying schemes.
- We developed a decoder for relays of CF and characterized it using the generalization of Bezout’s theorem. We also made an analytical derivation of the end-to-end probability of error for cubic lattices.
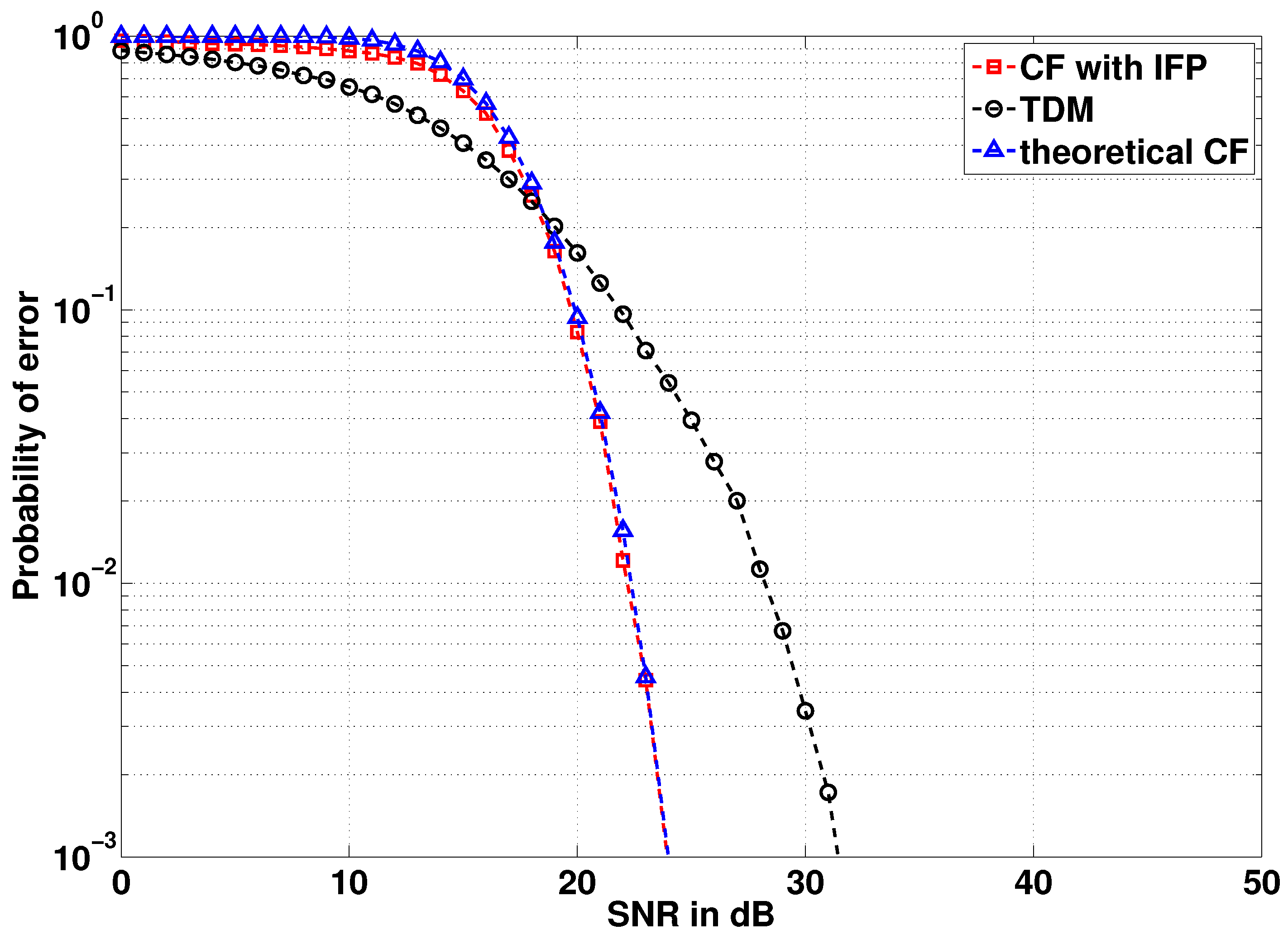
- We analyze the two phases of transmission in the CF scheme, thereby characterizing the end-to-end behavior of the CF based on different performance metrics and not only one-phase behavior, as in available studies. Compared to conventional designs, we obtain a gain of approximately 5 dB in terms of probability of error as compared to conventional time division multiplexing (TDM) transmission.
1.2. Outline of the Paper
1.3. Notations
2. System Model
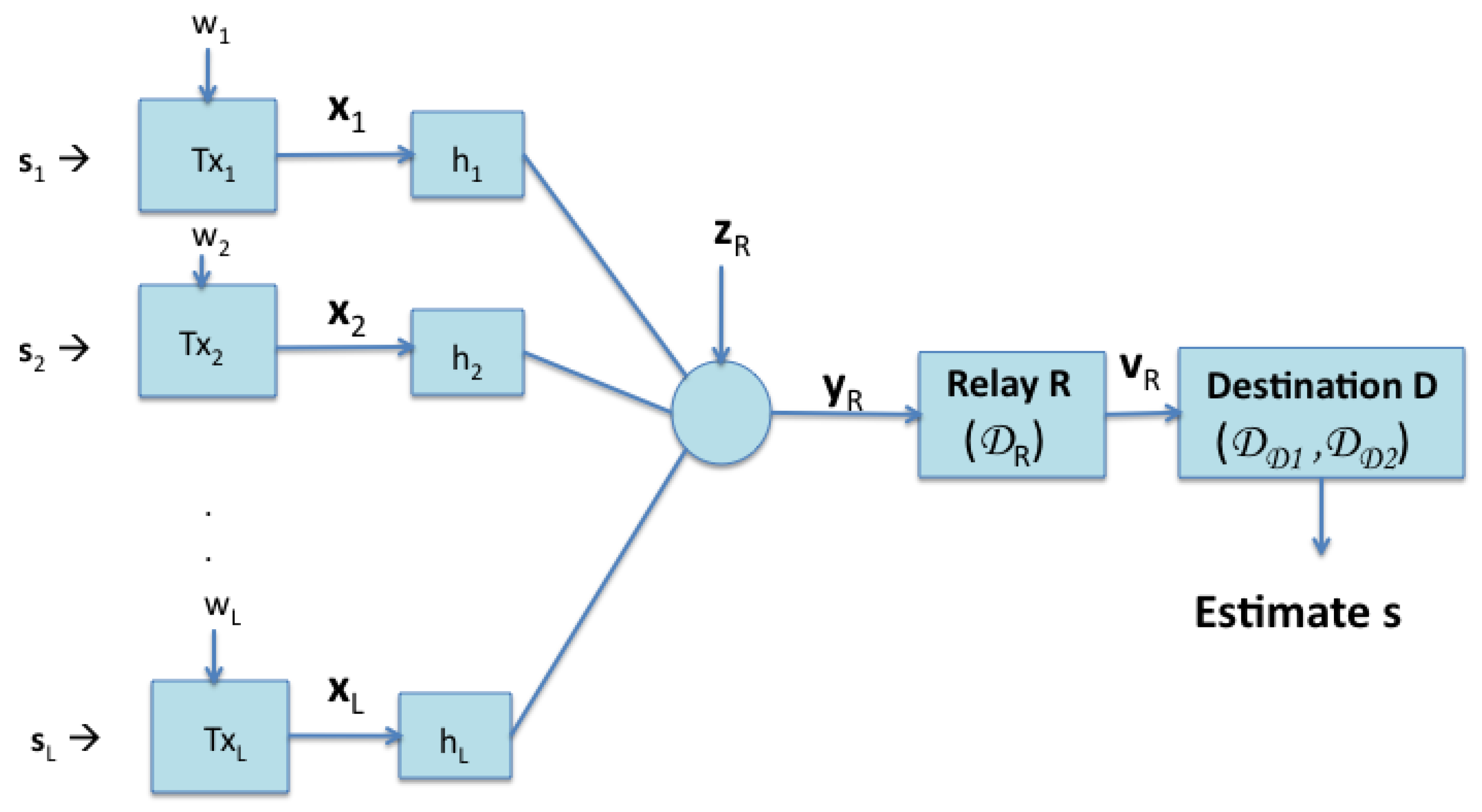
2.1. Phase I: Source to Relay Multiple Access Channel
2.2. Phase II: Relay-to-Destination Point-to-Point Channel
3. Phase I : Proposed Precoding-Based Source to Relay Transmission
3.1. Problem Formulation
3.2. Proposed Integer Forcing Precoder
3.3. Decoding at the Relay
4. Phase II: Proposed Point-to-Point Relay-to-Destination Transmission
4.1. Problem Formulation
4.2. Decoding Linear Combination at the Destination
4.3. Decoding Original Signals at the Destination
5. Performance Analysis
5.1. Probability of Error from Source to Relay Node
5.2. Probability of Error from Relay-to-Destination Node
5.3. Overall End-to-End Probability of Error
6. Numerical Results
6.1. Probability of Error
6.1.1. Probability of Error at the Relay
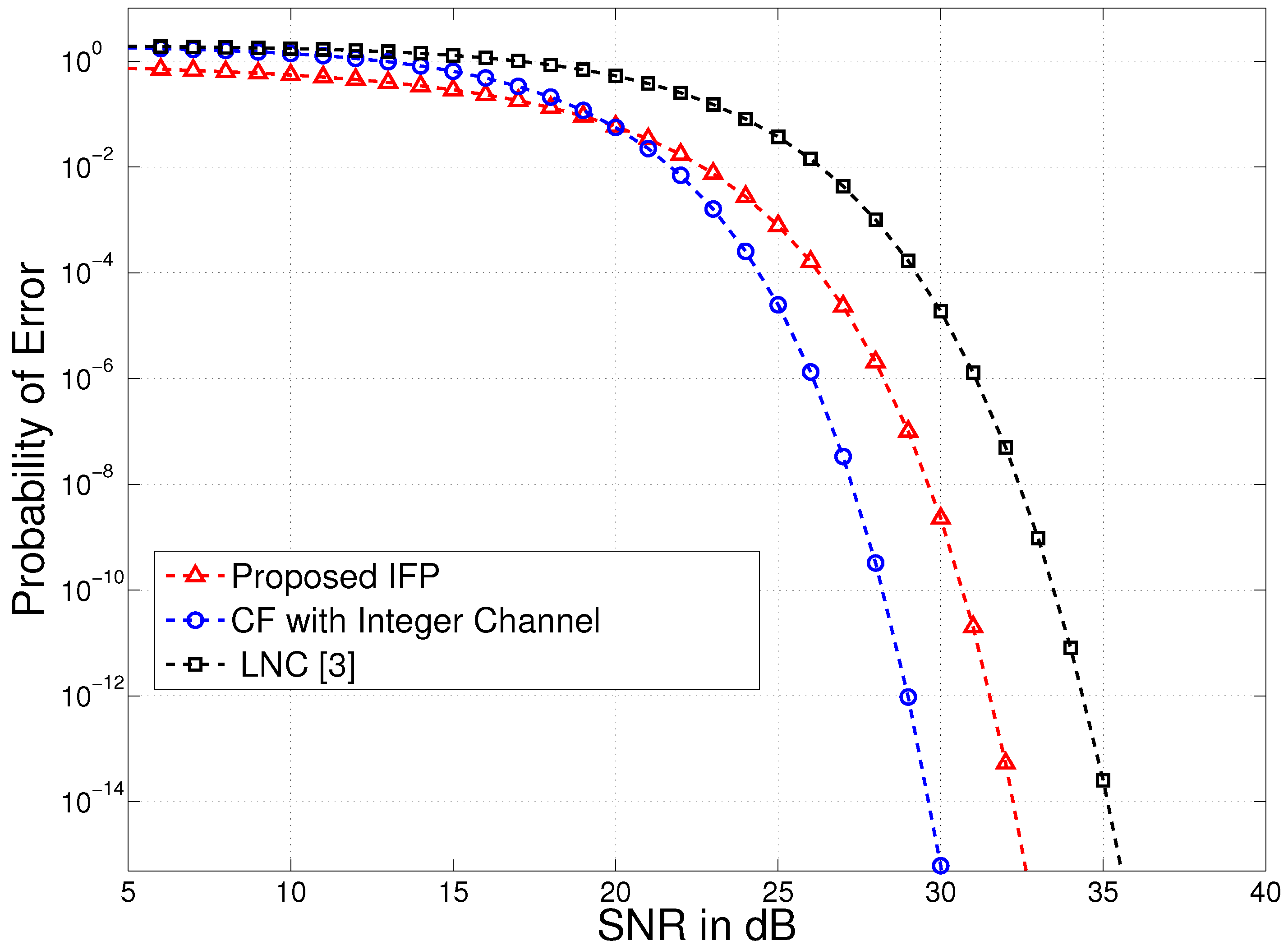
6.1.2. Probability of Error at the Destination
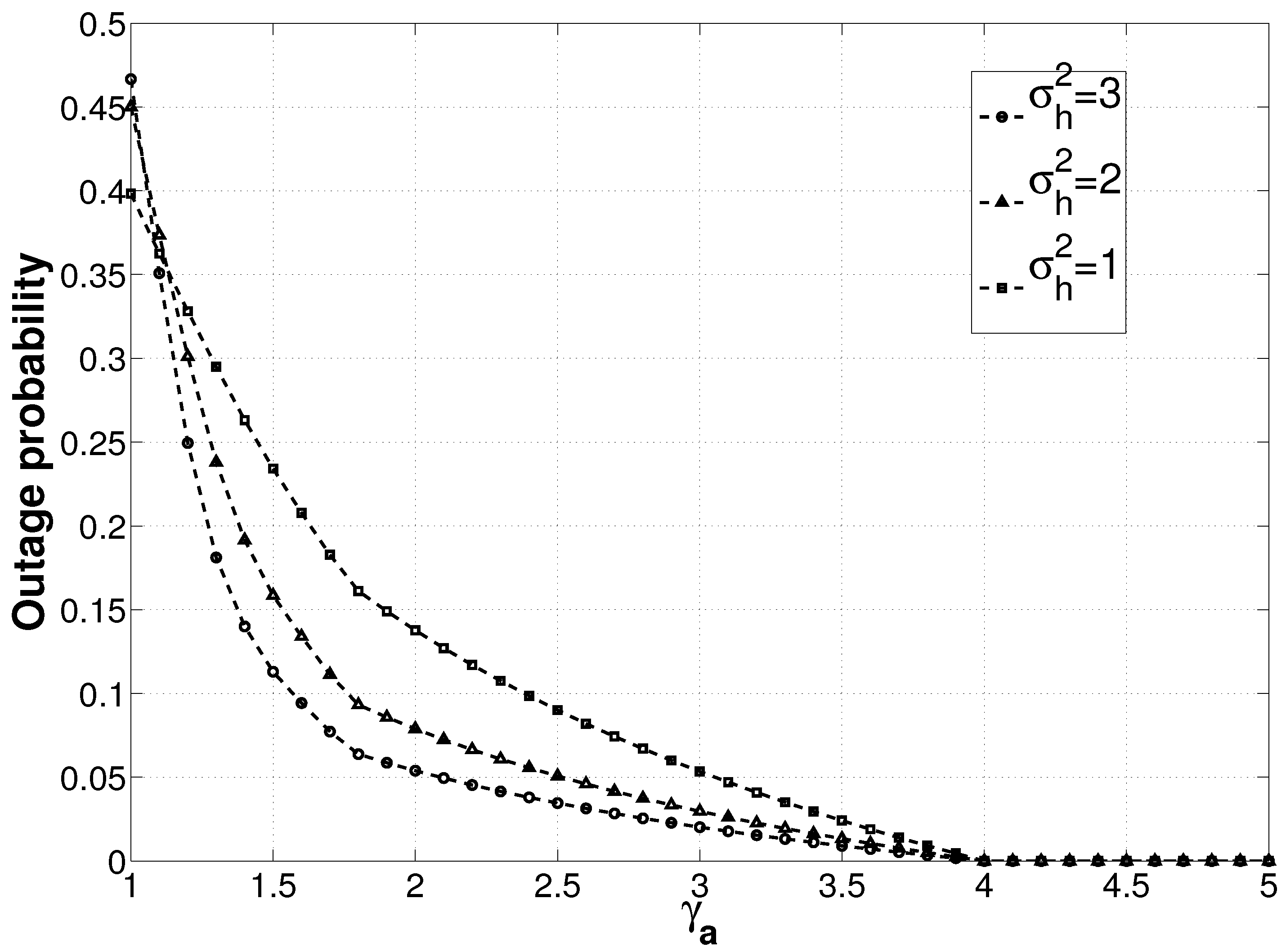
6.2. Outage Probability
6.3. Achievable Rates
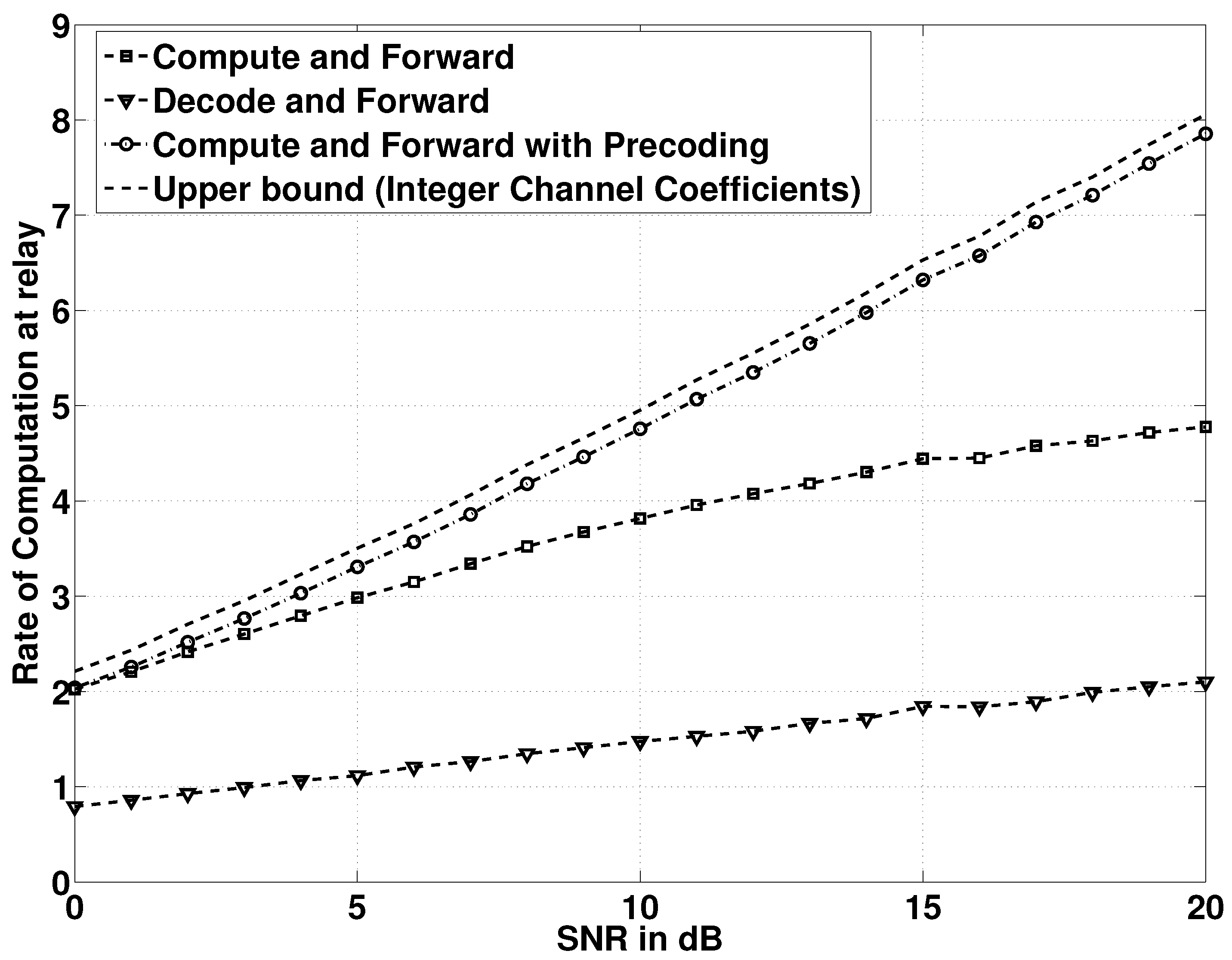
7. Conclusions
References
- Zhang, S.; Liew, S.; Lam, P. Physical Layer Network Coding. 2006. arXiv.org Website. Available online: http://arxiv.org/abs/0704.2475 (accessed on 12 August 2013).
- Nazer, B.; Gastpar, M. Compute and forward: Harnessing interference through structured codes. IEEE Trans. Inf. Theory 2011, 57, 6463–6486. [Google Scholar] [CrossRef]
- Feng, C.; Silva, D.; Kschischang, F. An Algebraic Approach to Physical-Layer Network Coding. In Proceedings of 2010 IEEE International Symposium on Information Theory Proceedings (ISIT), Austin, TX, USA, 13–18 June 2010.
- Niesen, U.; Whiting, P. The degrees of freedom of compute-and-forward. IEEE Trans. Inf. Theory 2012, 58, 5214–5232. [Google Scholar] [CrossRef]
- Belfiore, J.-C. Lattice Codes for the Compute-and-Forward Protocol: The Flatness Factor. In Proceedings of the IEEE Information Theory Workshop (ITW), Paraty, Brazil, 16–20 October 2011; pp. 1–4.
- Nazer, B.; Gastpar, M. Reliable physical layer network coding. Proc. IEEE 2011, 99, 438–460. [Google Scholar] [CrossRef]
- Chen, F.; Silva, D.; Kschischang, F.R. Blind Compute-and-Forward. In Proceedings of the IEEE International Symposium on Information Theory Proceedings (ISIT), Cambridge, MA, USA, 1–6 July 2012; pp. 403–407.
- Hong, S.-N.; Caire, G. Reverse Compute and Forward: A Low-Complexity Architecture for Downlink Distributed Antenna Systems. In Proceedings of the IEEE International Symposium on Information Theory Proceedings (ISIT), Cambridge, MA, USA, 1–6 July 2012; pp. 1147–1151.
- Yang, T.; Yuan, X.; Li, P.; Collings, I.B.; Yuan, J. A new physical-layer network coding scheme with eigen-direction alignment precoding for mimo two-way relaying. IEEE Trans. Commun. 2013, 61, 973–986. [Google Scholar] [CrossRef]
- Gupta, S.; Vazquez-Castro, M.A. Physical-Layer Network Coding based on Integer-forcing Precoded Compute and Forward. In Proceedings of the IEEE 8th International Conference on Wireless and Mobile Computing, Networking and Communications (WiMob), Barcelona, Spain, 8–10 October 2012; pp. 600–605.
- Wiesel, A.; Eldar, Y.; Shamai, S. Zero-forcing precoding and generalized inverses. IEEE Trans. Signal Process. 2008, 56, 4409–4441. [Google Scholar] [CrossRef]
- Hassibi, B.; Vikalo, H. On the sphere-decoding algorithm I. Expected complexity. IEEE Trans. Signal Process. 2005, 53, 2806–2818. [Google Scholar] [CrossRef]
- Zamir, R. Lattices are Everywhere. In Proceedings of the Information Theory and Applications Workshop, San Diego, CA, USA, 8–13 February 2009; pp. 392–421.
- Forney, G.D., Jr. Coset codes-I: Introduction and geometrical classification. IEEE Trans. Inf. Theory 1988, 34, 1123–1151. [Google Scholar] [CrossRef]
- Monteiro, F.A.; Wassell, I.J. Dual-Lattice-Aided MIMO Detection for Slow Fading Channel. In Proceedings of the IEEE International Symposium on Signal Processing and Information Technology, Bilbao, Spain, 14–17 December 2011; pp. 502–507.
- Tarokh, V.; Vardy, A.; Zeger, K. Universal bound on the performance of lattice codes. IEEE Trans. Inf. Theory 1999, 45, 670–681. [Google Scholar] [CrossRef]
- Shub, M.; Smale, S. Complexity of Bezout’s theorem. I. Geometric aspects. J. Am. Math. Soc. 1993, 6, 459–501. [Google Scholar] [CrossRef]
- Papoulis, A. Probability, Random Variables, and Stochastic Processes, 2nd ed.; McGraw-Hill: New York, NY, USA, 1984; p. 104. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Gupta, S.; Vázquez-Castro, M.A. Physical Layer Network Coding Based on Integer Forcing Precoded Compute and Forward. Future Internet 2013, 5, 439-459. https://doi.org/10.3390/fi5030439
Gupta S, Vázquez-Castro MA. Physical Layer Network Coding Based on Integer Forcing Precoded Compute and Forward. Future Internet. 2013; 5(3):439-459. https://doi.org/10.3390/fi5030439
Chicago/Turabian StyleGupta, Smrati, and M. A. Vázquez-Castro. 2013. "Physical Layer Network Coding Based on Integer Forcing Precoded Compute and Forward" Future Internet 5, no. 3: 439-459. https://doi.org/10.3390/fi5030439



