Dual-Filter Estimation for Rotating-Panel Sample Designs
Abstract
:1. Introduction
- n = T − k + 1;
- = an n row by n column co-variance matrix for ;
- = an (n − 3) row by (n − 3) column sub-matrix of , using rows and columns from 4 to n;
- R = an (n − 3) row by n column constraint matrix, appropriate for the quadratic model, which has zeros everywhere except that each row t has the sequence [1,−3,3,−1] beginning in column t.
2. Materials and Methods
2.1. Simulated Populations
2.2. Sampling the Simulated Populations
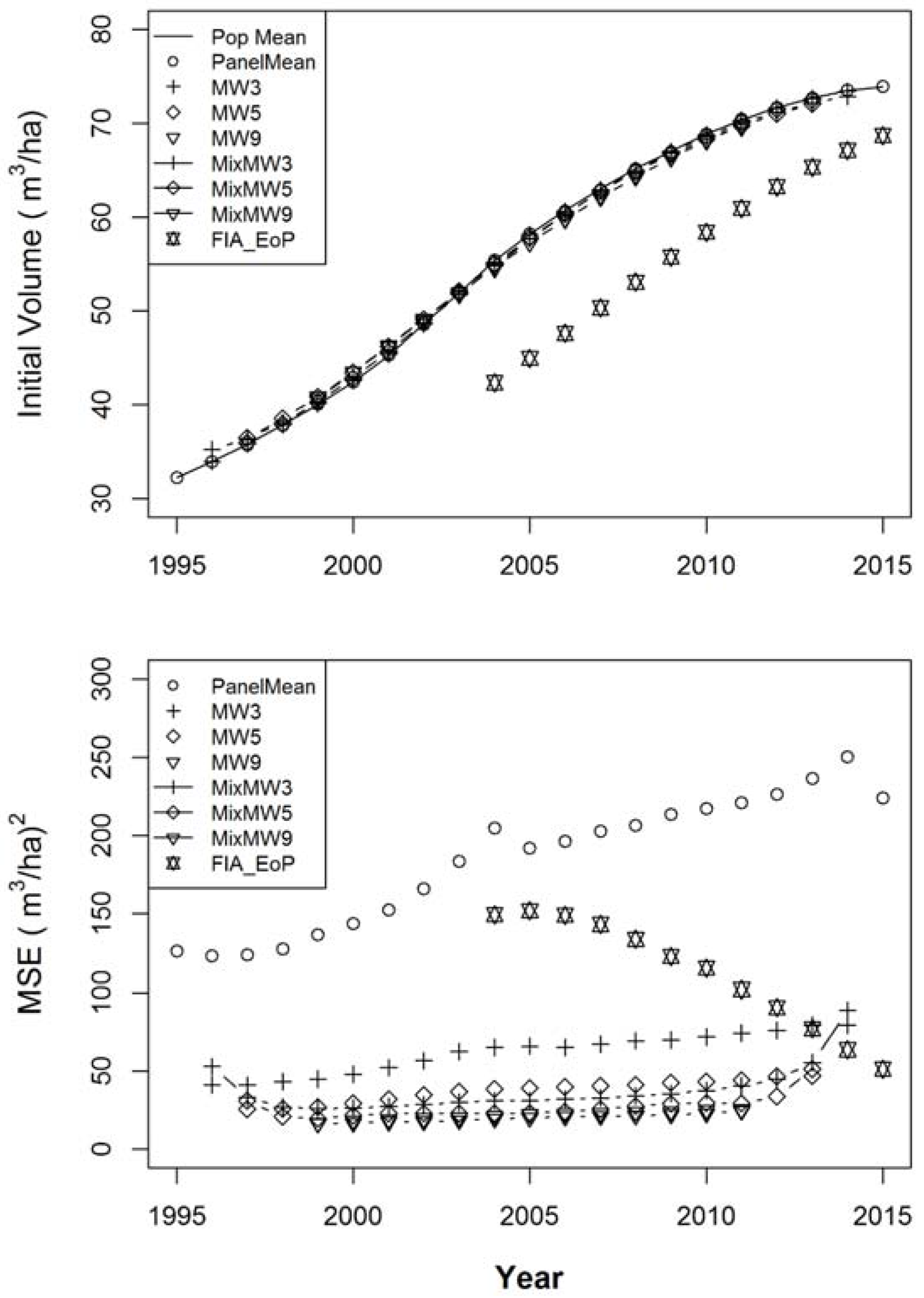
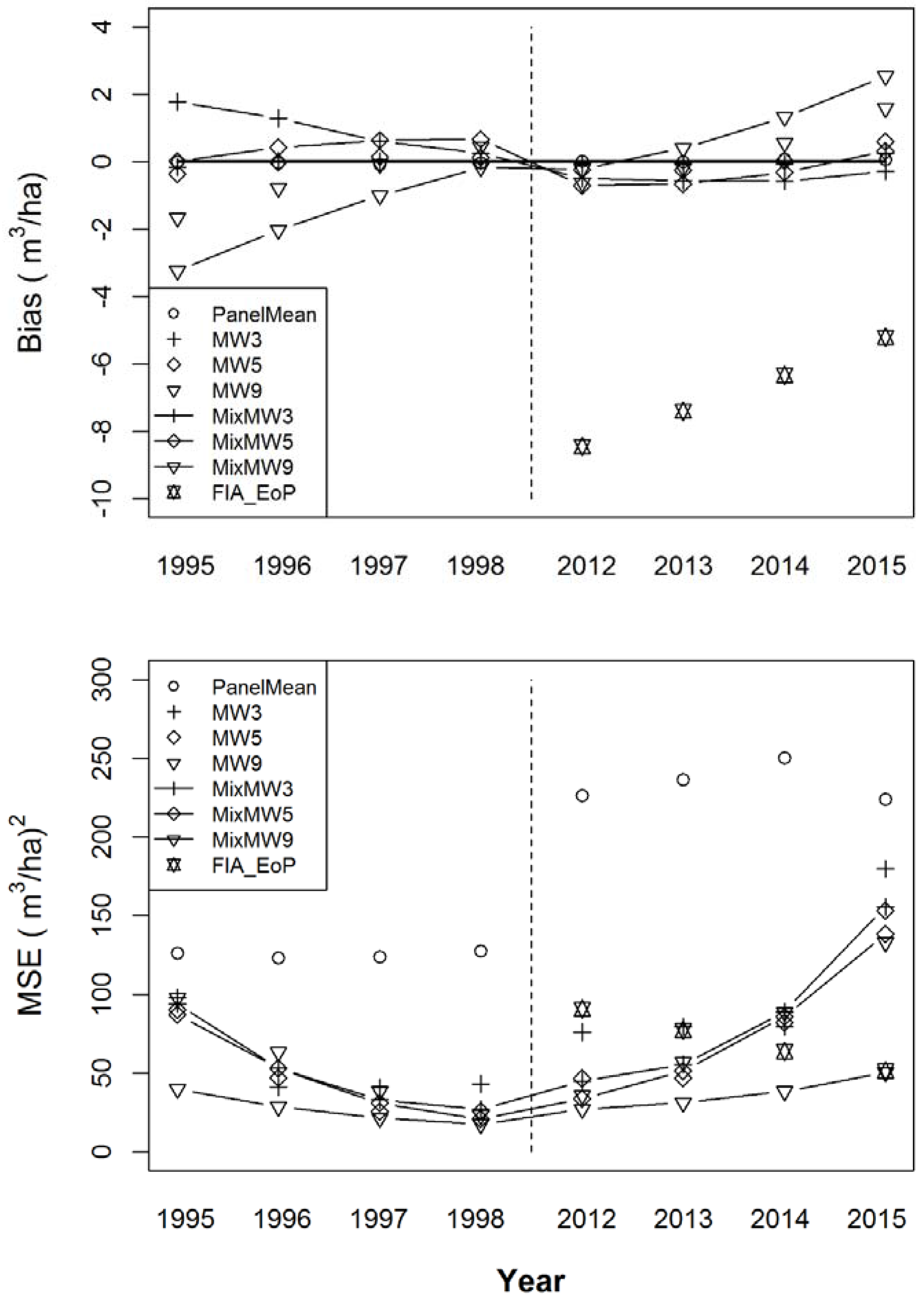
3. Results
4. Discussion and Conclusions
Acknowledgments
Conflicts of Interest
Appendix A
| FIA State Code | Number of Units |
|---|---|
| AL | 6 |
| AR | 5 |
| CA | 6 |
| CT | 1 |
| DE | 1 |
| FL | 4 |
| GA | 5 |
| IL | 3 |
| IN | 4 |
| IA | 4 |
| KS | 3 |
| KY | 7 |
| LA | 5 |
| ME | 9 |
| MD | 4 |
| MA | 1 |
| MI | 4 |
| MN | 4 |
| MO | 5 |
| NE | 2 |
| NH | 2 |
| NJ | 1 |
| NY | 8 |
| NC | 4 |
| ND | 1 |
| OH | 6 |
| OR | 5 |
| PA | 6 |
| RI | 1 |
| SC | 3 |
| SD | 2 |
| TN | 5 |
| TX | 2 |
| VT | 2 |
| VA | 5 |
| WA | 5 |
| WV | 3 |
| WI | 5 |
| PR | 3 |
References
- Bechtold, W.A.; Patterson, P.L. (Eds.) The Enhanced Forest Inventory and Analysis Program-National Sampling Design and Estimation Procedures; Gen. Tech. Rep. SRS-80; U.S. Department of Agriculture Forest Service, Southern Research Station: Asheville, NC, USA, 2005. Available online: http://www.srs.fs.fed.us/pubs/20371 (accessed on 24 May 2017).
- Theil, H. On the use of incomplete prior information in regression analysis. J. Am. Stat. Assoc. 1963, 58, 401–414. [Google Scholar] [CrossRef]
- Van Deusen, P.C. Incorporating predictions into an annual forest inventory. Can. J. For. Res. 1996, 26, 1709–1713. [Google Scholar] [CrossRef]
- Van Deusen, P.C. Modeling trends with annual survey data. Can. J. For. Res. 1999, 29, 1824–1828. [Google Scholar] [CrossRef]
- Roesch, F. Spatial-Temporal Models for Improved County-Level Annual Estimates. In 2008 Forest Inventory and Analysis (FIA) Symposium, Proceedings of the RMRS-P-56CD, Park City, UT, USA, 21–23 October 2008; McWilliams, W., Moisen, G., Czaplewski, R., Eds.; comps. 2009; Department of Agriculture, Forest Service, Rocky Mountain Research Station: Fort Collins, CO, USA, 2009. [Google Scholar]
- Roesch, F.A. A simulation of Image-Assisted Forest Monitoring for National Inventories. Forests 2016, 7, 204. Available online: https://www.mdpi.com/1999-4907/7/9/204/htm (accessed on 31 May 2017). [CrossRef]
- Roesch, F.A.; Coulston, J.W.; Van Deusen, P.C.; Podlaski, R. Evaluation of Image-Assisted Forest Monitoring: A Simulation. Forests 2015, 6, 2897–2917. Available online: https://www.mdpi.com/1999-4907/6/9/2897/htm (accessed on 31 May 2017). [CrossRef]
- Roesch, F.A. Toward robust estimation of the components of forest population change. For. Sci. 2014, 60, 1029–1049. [Google Scholar] [CrossRef]
- Box, G.E.P. Robustness in the strategy of scientific model building. In Army Research Office Workshop on Robustness in Statistics, 11–12 April 1978; No. MRC-TSR-1954; Research Triangle Park: Durham, NC, USA, 1979; WISCONSIN UNIV-MADISON MATHEMATICS RESEARCH CENTER, 1979. [Google Scholar]
- Van Deusen, P.C. An Alternative View of Some FIA Sample Design and Analysis Issues. In Gen. Tech. Rep. NC-252, Proceedings of the Fourth Annual Forest Inventory and Analysis Symposium, New Orleans, LA, USA, 19–21 November 2002; McRoberts, R.E., Reams, G.A., Van Deusen, P.C., McWilliams, W.H., Cieszewski, C.J., Eds.; U.S. Department of Agriculture, Forest Service, North Central Research Station: St. Paul, MN, USA, 2005; 258p. [Google Scholar]
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roesch, F.A. Dual-Filter Estimation for Rotating-Panel Sample Designs. Forests 2017, 8, 192. https://doi.org/10.3390/f8060192
Roesch FA. Dual-Filter Estimation for Rotating-Panel Sample Designs. Forests. 2017; 8(6):192. https://doi.org/10.3390/f8060192
Chicago/Turabian StyleRoesch, Francis A. 2017. "Dual-Filter Estimation for Rotating-Panel Sample Designs" Forests 8, no. 6: 192. https://doi.org/10.3390/f8060192





