Next Article in Journal / Special Issue
Assessment of Low Density Full-Waveform Airborne Laser Scanning for Individual Tree Detection and Tree Species Classification
Previous Article in Journal
Redefining Secondary Forests in the Mexican Forest Code: Implications for Management, Restoration, and Conservation
Previous Article in Special Issue
Analysis of the Influence of Plot Size and LiDAR Density on Forest Structure Attribute Estimates
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Forests
Volume 5
Issue 5
10.3390/f5050992
forests-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Low-Density LiDAR and Optical Imagery for Biomass Estimation over Boreal Forest in Sweden

by
Iurii Shendryk
1,2,*,
Margareta Hellström
2,
Leif Klemedtsson
3 and
Natascha Kljun
4
1
Center for Ecosystem Science, School of Biological, Earth and Environmental Sciences, University of New South Wales, Sydney 2052, Australia
2
Department of Physical Geography and Ecosystem Science, Lund University, Lund 22362, Sweden
3
Department of Earth Sciences, University of Gothenburg, Gothenburg 40530, Sweden
4
Department of Geography, College of Science, Swansea University, Swansea SA28PP, UK
*
Author to whom correspondence should be addressed.
Forests 2014, 5(5), 992-1010; https://doi.org/10.3390/f5050992
Submission received: 24 February 2014 / Revised: 22 April 2014 / Accepted: 14 May 2014 / Published: 21 May 2014
(This article belongs to the Special Issue LiDAR and Other Remote Sensing Applications in Mapping and Monitoring of Forests Structure and Biomass)
Browse Figures
Versions Notes

Abstract

:
Knowledge of the forest biomass and its change in time is crucial to understanding the carbon cycle and its interactions with climate change. LiDAR (Light Detection and Ranging) technology, in this respect, has proven to be a valuable tool, providing reliable estimates of aboveground biomass (AGB). The overall goal of this study was to develop a method for assessing AGB using a synergy of low point density LiDAR-derived point cloud data and multi-spectral imagery in conifer-dominated forest in the southwest of Sweden. Different treetop detection algorithms were applied for forest inventory parameter extraction from a LiDAR-derived canopy height model. Estimation of AGB was based on the power functions derived from tree parameters measured in the field, while vegetation classification of a multi-spectral image (SPOT-5) was performed in order to account for dependences of AGB estimates on vegetation types. Linear regression confirmed good performance of a newly developed grid-based approach for biomass estimation (R2 = 0.80). Results showed AGB to vary from below 1 kg/m2 in very young forests to 94 kg/m2 in mature spruce forests, with RMSE of 4.7 kg/m2. These AGB estimates build a basis for further studies on carbon stocks as well as for monitoring this forest ecosystem in respect of disturbance and change in time. The methodology developed in this study can be easily adopted for assessing biomass of other conifer-dominated forests on the basis of low-density LiDAR and multispectral imagery. This methodology is hence of much wider applicability than biomass derivation based on expensive and currently still scarce high-density LiDAR data.

Graphical Abstract

1. Introduction

Biomass assessment of forest ecosystems gained importance and attention in connection with the Climate Convention and the Kyoto Protocol [1]. In this context, biomass is of huge interest, as it can be combined with estimates of vegetation productivity in order to assess the magnitude and rate of carbon sequestration, autotrophic respiration as well as the amount of carbon emitted to the atmosphere when the ecosystem is disturbed [2]. Therefore, improved and comprehensive estimation of the biomass stored in forests can be considered as a key area of research for understanding the global carbon cycle [3]. However, accurate estimation of forest biomass remains a challenging task. So far, our understanding of terrestrial biomass quantity and distribution has been primarily based on ground measurements of limited areas with many regions remaining unmeasured [2]. At the same time, direct estimation of AGB (aboveground biomass) via ground surveys is both time-consuming and expensive and generally repeated only at ten-year intervals [4]. Therefore, the possibility of biomass estimation using remote sensing is considered a promising alternative or complement to conventional ground-based methods [5], even more so in view of recent initiatives to create publicly available national LiDAR datasets of several European countries and the USA [6,7].
It is widely recognized that LiDAR (Light Detection and Ranging) technology represents the future of biomass estimation, and, as such, has become widely used in vegetation studies [4,8,9,10,11,12,13]. LiDAR is an active remote sensing system which transmits pulses of laser light toward the ground by means of a scanning mirror. The time difference between sent and reflected pulses is measured and converted into a distance measurement [3,10]. A LiDAR pulse is in the near infrared or visible part of the electromagnetic spectrum (900–1064 nm). The active LiDAR system allows recording of several returns per pulse [10]. In a forested area, first returns are usually associated with the tree canopy top and the last returns with the underlying ground surface. Hence the so-called canopy height model (CHM) can be derived [14]. Intermediate returns allow the derivation of structural characteristics of the tree canopy. Although there were many successful attempts to utilize LiDAR data for AGB estimations, it is still considered a challenging task, especially when using low density laser scanning systems due to its inability to reflect canopy structure comprehensively [15]. Generally, AGB estimation at individual tree level requires high point densities of more than 5 points/m2 and is based on regression models using LiDAR-derived parameters, such as tree height and estimates of AGB measured in the field [11,12,13]. A comparison of commonly-used algorithms for individual tree delineation from a high point density LiDAR data, such as FUSION, TreeVaW and watershed segmentation was undertaken by Edson and Wing [16], where they emphasized the inability of these methods to use laser hits from trees located under the primary canopy in rendering the canopy height model (CHM) surface. The low density LiDAR is considered to be even less effective for the estimation of forest variables and is usually problematic in delineation of individual trees due to under-sampling and thus suitable for plot- and stand-wise studies [10,17]. Furthermore, the research in the area of LiDAR data integration with vegetation classes derived from satellite imagery for estimation of AGB is not well documented. This study addresses the possibility of integrating LiDAR-derived tree heights with vegetation types derived from satellite imagery. According to Andersen et al. [18] and Chen et al. [9] the integration of optical imagery and LiDAR data can result in substantial improvement of biomass estimates compared to the use of LiDAR data alone. Thus, the objective of this study is to investigate how low point density LiDAR data (<1 points/m2) from airborne systems in combination with spectral information from satellite imagery may allow reliable estimation of AGB on a plot level in conifer-dominated forest in the southwest of Sweden.

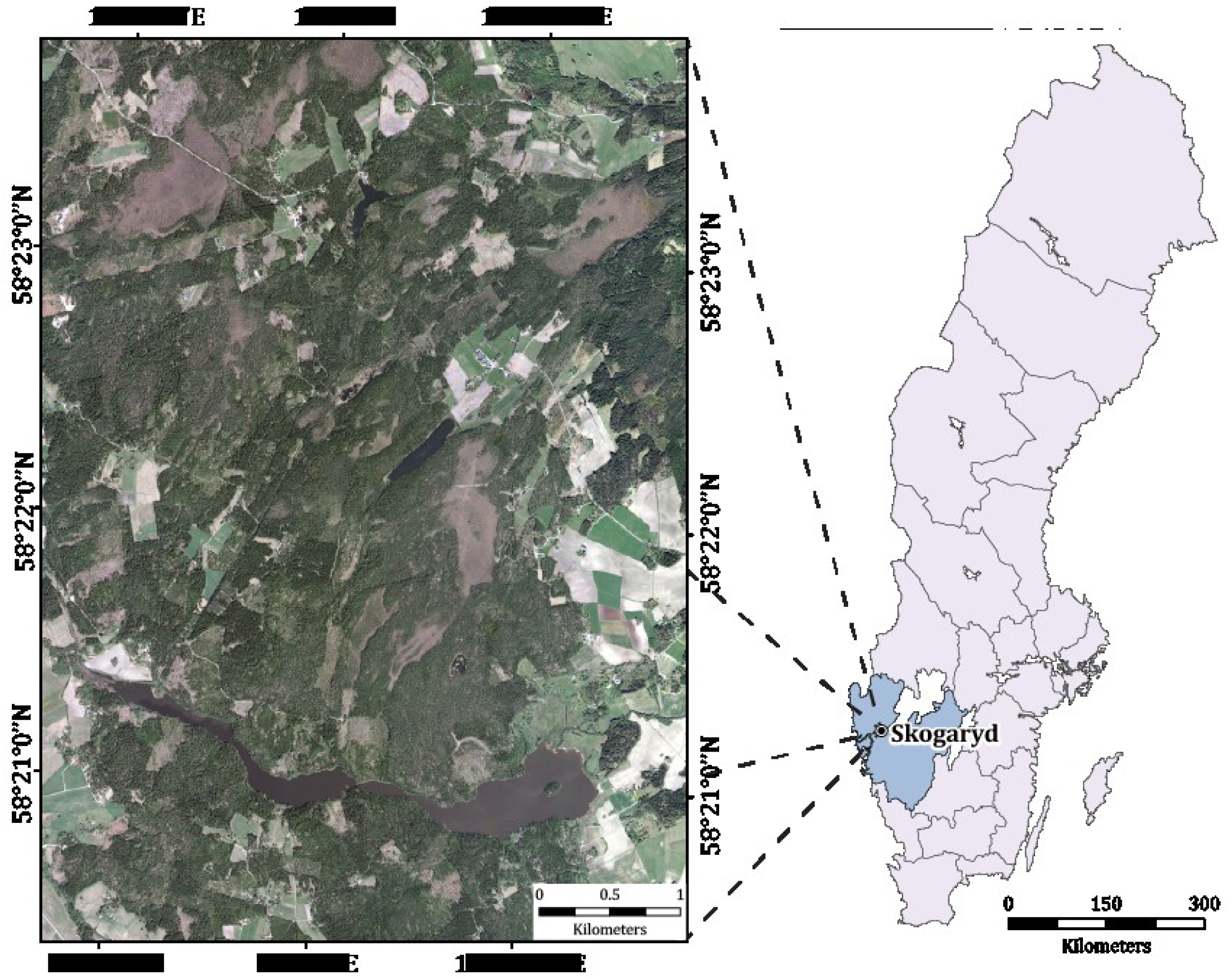
2. Study Area

The study site (58°22′10″ N, 12°08′47″ E), named Skogaryd Research Catchment (SRC), is located in the southwest Sweden (Västra Götaland county) near lake Vänern and extends to an area of approximately 30 km2 (Figure 1). SRC is a part of the Swedish Infrastructure for Ecosystem Sciences (SITES) station network. The topography of this region is characterized by an average elevation of 80 m asl and predominately gentle slopes. The soils in the area are highly fertile covered by stands of spruce, pine and birch of varying age. Coniferous trees dominate the landscape ranging from approximately 2 m to 30 m in height. The typical representatives of flora beneath the tree canopy layer consists of species such as juniper, blueberry shrub and feather moss. Lakes and bogs as well as agricultural fields are scattered throughout the region. Such a fragmented landscape has historically been formed due to farming and rural development [19].
Forests 05 00992 g001 1024
Figure 1. Map of Sweden, divided into counties, showing the location of the Skogaryd Research Catchment; the RGB orthophoto on the left details the study area.
Figure 1. Map of Sweden, divided into counties, showing the location of the Skogaryd Research Catchment; the RGB orthophoto on the left details the study area.
Forests 05 00992 g001

3. Data and Methods

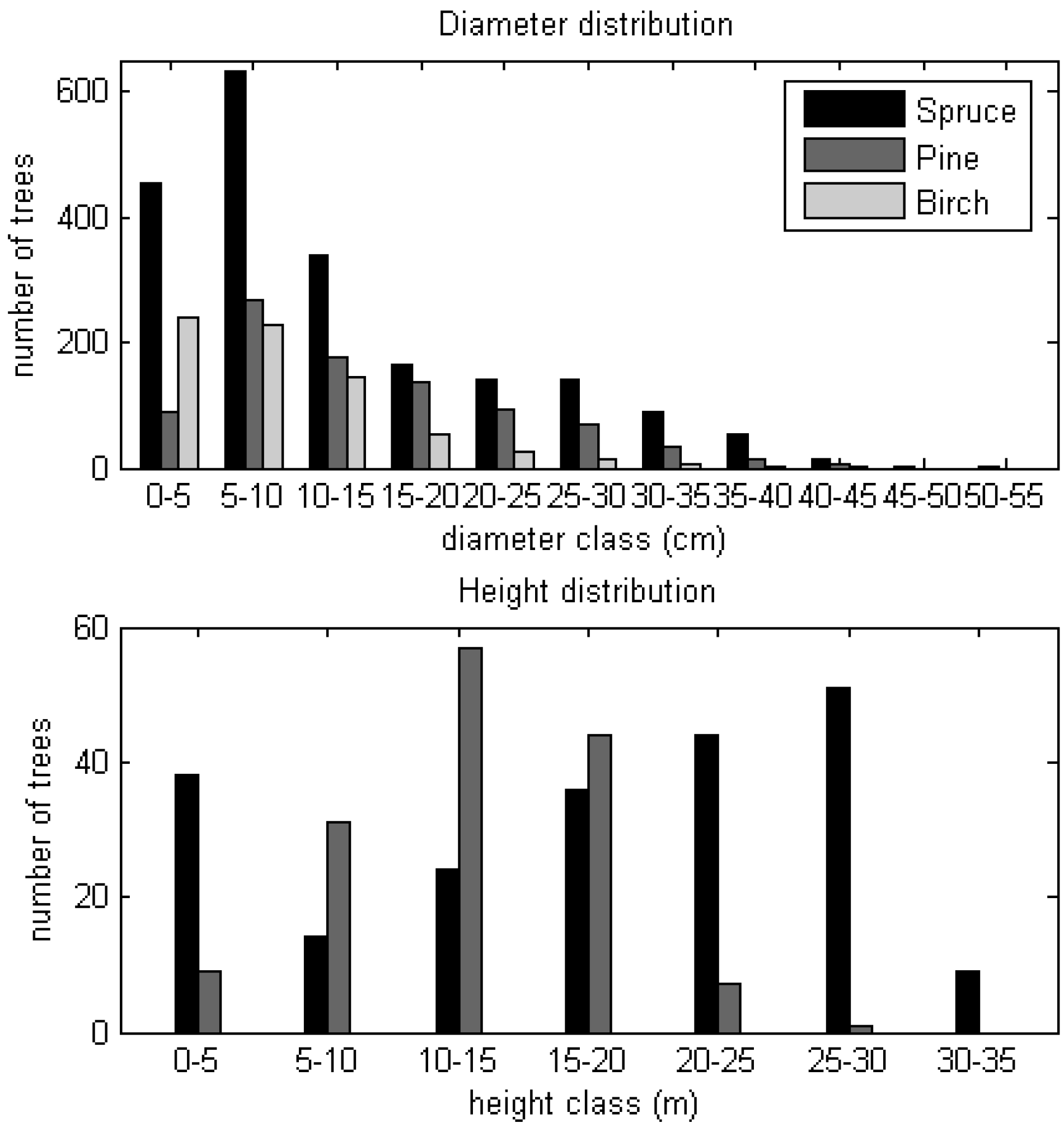
3.1. Field Measurements

Collection of ground truth data was carried out during summer 2012 in two phases. The first phase ran from 26th June till 6th July and the second phase was performed from 21st August till 27th August. Plots of the forested areas of SRC were selected on the basis of a random sampling scheme applied to a preliminary vegetation classification (cf. Section 3.3) by assigning each pixel with a unique reference number. Then, based on randomly generated numbers, samples were drawn from the preliminary vegetation classification map. A total of 230 points distributed in equal number within all vegetation classes were generated. These points were verified for species in the field and used for validation of the final vegetation classification. During both fieldwork phases an additional (randomly selected) 83 plots were surveyed for modeling and validation of the AGB. These plot data were also used for delineation of training samples for the final vegetation classification. All individual trees within each plot of approximately 15 m × 15 m were measured for diameter at breast height (DBH) and recorded for species. Tree height measurements were performed only in 18 of the surveyed plots, mainly due to time constraint and difficulties associated with treetop detection in the highly dense forest stands. The selection of plots covered all ranges of species and ages of trees typically found within SRC. Tree diameter measurements were performed with callipers, while tree heights were measured using a highly accurate Vertex IV ultrasonic hypsometer with a height resolution of 0.1 m [20]. The delimitation of plots in the field was done using a measuring tape and was sometimes subjected to inaccuracies (up to 1 m) due to forest obstructions. The coordinates of the plot centers were derived using a standard GPS unit “Magellan Explorist 510” with accuracy of about 5 m (according to GPS readings) in forested areas (geodetic quality GPS system was not available for this study).

3.2. Remotely Sensed Data

The discrete return airborne LiDAR data used in this study represent a part of the Swedish national LiDAR dataset. The data, available as a multiple return point cloud, were collected on 3rd July 2011 using a Leica ALS50-II system. The point density varied from 0.06 to 1 points/m2 with an average density of 0.8 points/m2. This varying point density of the LiDAR data can be attributed to the overlapping flight strips and spherical scan geometry of the instrument [11,12,21]. The flight height varied between 1740 m and 2300 m and was constant for each flight line. The scanning angle was ±20°. The laser system had a beam divergence of 0.22 mrad, producing a footprint of 0.5 m in diameter at an altitude of 2000 m. The vertical precision of the individual laser points was in general better than 10 cm on planar, open surfaces, while the horizontal precision was around 30 cm. The point cloud was pre-classified into three classes by the Swedish Land Survey: unclassified, ground, and water, using automated routines of TerraScan [22].
In addition to the LiDAR data, optical imagery of the same area included orthorectified multispectral SPOT-5 image with 10 m spatial resolution acquired on 29th July 2011 and aerial orthophoto with 1 m spatial resolution from 2009. All remotely sensed data available to this project were provided by the Swedish Land Survey.

3.3. Vegetation Mapping Using Maximum-Likelihood Classification

The application of SPOT-5 data for derivation of vegetation classes was motivated by its availability for this project. For similar studies, SPOT-5 data can be substituted by any other imagery with similar spectral characteristics, with imperative coverage in the near-infrared to maximize spectral discrimination between vegetation types [23].
Initially, a preliminary vegetation classification was performed as a basis for the fieldwork planning. In a second step, the data collected in the field served as an input for the final classification. In both instances similar methodologies were applied. The influence of non-vegetated pixels in the image on the classification results was minimized by delineation of up-to-date boundaries of forest stands (LiDAR-derived vegetation mask). The classification scheme adopted for this study consisted of three main classes: pine, spruce and deciduous forest. By analyzing spectral information (orthophoto) available from the study site and data collected in the field, training samples for preliminary and final vegetation classifications, respectively, were selected. The GPS-induced position uncertainty posed only a minor problem since all ground-truth points were collected exclusively within homogeneous forest stands. For the final classification both spruce and pine classes were additionally divided into two age classes based on field measurements and using a threshold of 15 cm in DBH for determination of tree maturity. Such a separation allows, for example, the monitoring of young forest stands only, which can be important for growth projections [16]. The usage of height as a common metric defining tree maturity was not used in this study due to the lack of sufficient measurements of tree height in the field. Supervised Maximum Likelihood classification was used for identifying the different vegetation types from the orthorectified SPOT-5 image, which calculates the probability of the information class membership for each pixel based on the probability density function [23].
Thereafter, an independent sample of ground validation points located across the investigation area with a random spatial distribution pattern was used for a statistical accuracy assessment of vegetation classification. The vegetation classification was validated against 196 ground truth points, which were not used for training the classifier. The accuracy assessment of classification was carried out by calculating the kappa coefficient in addition to obtaining the overall accuracy using an error matrix. Both user’s and producer’s accuracies were also derived, which respectively corresponds to error of commission and omission [24].

3.4. Derivation of Amount of Trees and Their Heights from Airborne LiDAR

The pre-classified LiDAR data were supplemented by two additional classes, high vegetation and buildings, by applying automated algorithms of Merrick’s MARS Explorer software. The high vegetation class was defined to include all points in the range from 2 to 40 m as calculated from a triangular irregular network (TIN) ground surface. This range of heights was chosen based on the lowest (2 m) and highest (35 m) trees measured in the field. All points having a height value of less than 2 m remained unclassified and potentially represent points reflected from very young trees, bushes or boulders. Buildings were classified using a filter able to identify points comprising relatively planar surfaces in the high vegetation class [25].
A digital terrain model (DTM) with cell size of 3 m was derived on the basis of all ground-class LiDAR points. A digital surface model (DSM) was then constructed using only the first returns of the LiDAR data in the high vegetation class. Other returns were considered to be not representative of canopy height but rather provided information on canopy structure [16]. When creating the DSM, only LiDAR points with maximum elevation in 0.5 m × 0.5 m cells were used to preserve an accurate characterization of the top canopy surface, following Popescu [7]. It was decided to create the DTM with a coarser resolution due to lower point density of LiDAR ground returns. Finally, a canopy height model (CHM) was derived by simple subtraction of DTM from DSM [7,13].
The delineation of individual trees was based on a well-established local maximum algorithm implemented in the TreeVaW software, which calculates a window size based on a height value of each CHM pixel to search for the local maximum [7]. Thus, it is potentially able to delineate distinct trees by using a window size directly proportional to tree height. The polynomial crown width model to predict variable window size was derived from the fieldwork carried out by Popescu and Wynne [26] within mixed coniferous-deciduous stands in the Piedmont region of Virginia:
CW = 2.51503 + 0.00901H2
where CW: crown width and H: tree height. The minimum tree height was set to 2 m in order to exclude understory from prediction of variable window size for tree top detection.
In this study, we compared the above with a grid-based approach for individual tree detection, based on the extraction of the highest pixel values from CHM within the grid cells of predefined size. Thus, each cell in a grid was approximated to an individual tree with a height corresponding to the maximum CHM value within a grid cell. The main disadvantage of extraction from the grid in comparison to TreeVaW is that the approximation process introduces substantial error into the estimation of the tree number depending on the grid cell size used. However, it is assumed that such approximation of individual trees would allow cancelling out the impact of undetected trees due to LiDAR under-sampling. In this way, the part of points identified as belonging to the same trees was used to represent suppressed trees. Grid cell sizes of 2 m × 2 m, 3 m × 3 m and 4 m × 4 m were tested in order to examine their influence on biomass estimation. Estimated cell values representing individual trees were fed into allometric equations for AGB estimation. To allow for a more rigorous estimate of errors of biomass estimates, almost 1/4 of the field data (18 plots with height measurements) were used to build the model (Figure 4), while the remaining 3/4 (65 plots without height measurements) were used to independently test the performance of the predicted AGB.

3.5. Reference Biomass Estimation

AGB estimates on plot level were obtained by applying species allometric relationships derived from harvested stands in Sweden (Table 1). In this study, AGB represents the sum of tree stem, bark, branch and foliage biomasses excluding understorey, and biomass is defined in dry weight terms. Height-AGB allometric functions were derived only for the dominant tree species in the SRC, which are Norway spruce (Picea abies), Scots pine (Pinus sylvestris) and Silver birch (Betula pendula). Other minor species encountered during fieldwork, such as rowan, were treated as birch. Pine and spruce biomass were derived as suggested by Marklund [27], while birch allometry was provided by Johansson [28]. The calculation of AGB was based on biomass functions for different tree components [17]:
AGB = CR + ST
where AGB—total aboveground biomass, CR—crown biomass (branch and foliage biomass) and ST—total stem biomass (stem wood and bark biomass). CR and ST were derived using allometric measures of Table 1 with tree height (H), and diameter at breast height (DBH), provided by field measurements.
Table
Table 1. Biomass equations for tree species in Sweden. Number of sampled trees (n), coefficients of determination (R2), diameter at breast height (DBH), height (H) of sampled trees and a, b, c, d are model parameters [17].
Table 1. Biomass equations for tree species in Sweden. Number of sampled trees (n), coefficients of determination (R2), diameter at breast height (DBH), height (H) of sampled trees and a, b, c, d are model parameters [17].
Biomass (kg)DBHHnR2Equationabcd
Spruceln(CR)cm-5440.95a + b × [DBH/(DBH + 13)]−1.2808.524--
Spruceln(CR)cmm5440.95a + b × [DBH/(DBH + 13)] + c × H + d × ln(H)−1.20610.971−0.012−0.492
Spruceln(ST)cm-5460.99a + b × [DBH/(DBH + 14)]−2.05711.334--
Spruceln(ST)cmm5460.99a + b × [DBH/(DBH + 14)] + c × H + d × ln(H)−2.1707.4690.0290.686
Pineln(CR)cm-4820.90a + b ×[DBH/(DBH + 10)]−2.8609.102--
Pineln(CR)cmm4820.92a + b·[DBH/(DBH + 10)] + c × ln(H)−2.54113.396−1.196-
Pineln(ST)cm-4880.98a + b × [DBH/(DBH + 13)]−2.33911.326--
Pineln(ST)cmm4880.99a + b × [DBH/(DBH + 13)] + c × H + d × ln(H)−2.6777.5940.0150.880
BirchAGBmm--0.99a × DBH b0.00092.2864--

4. Results and Discussion

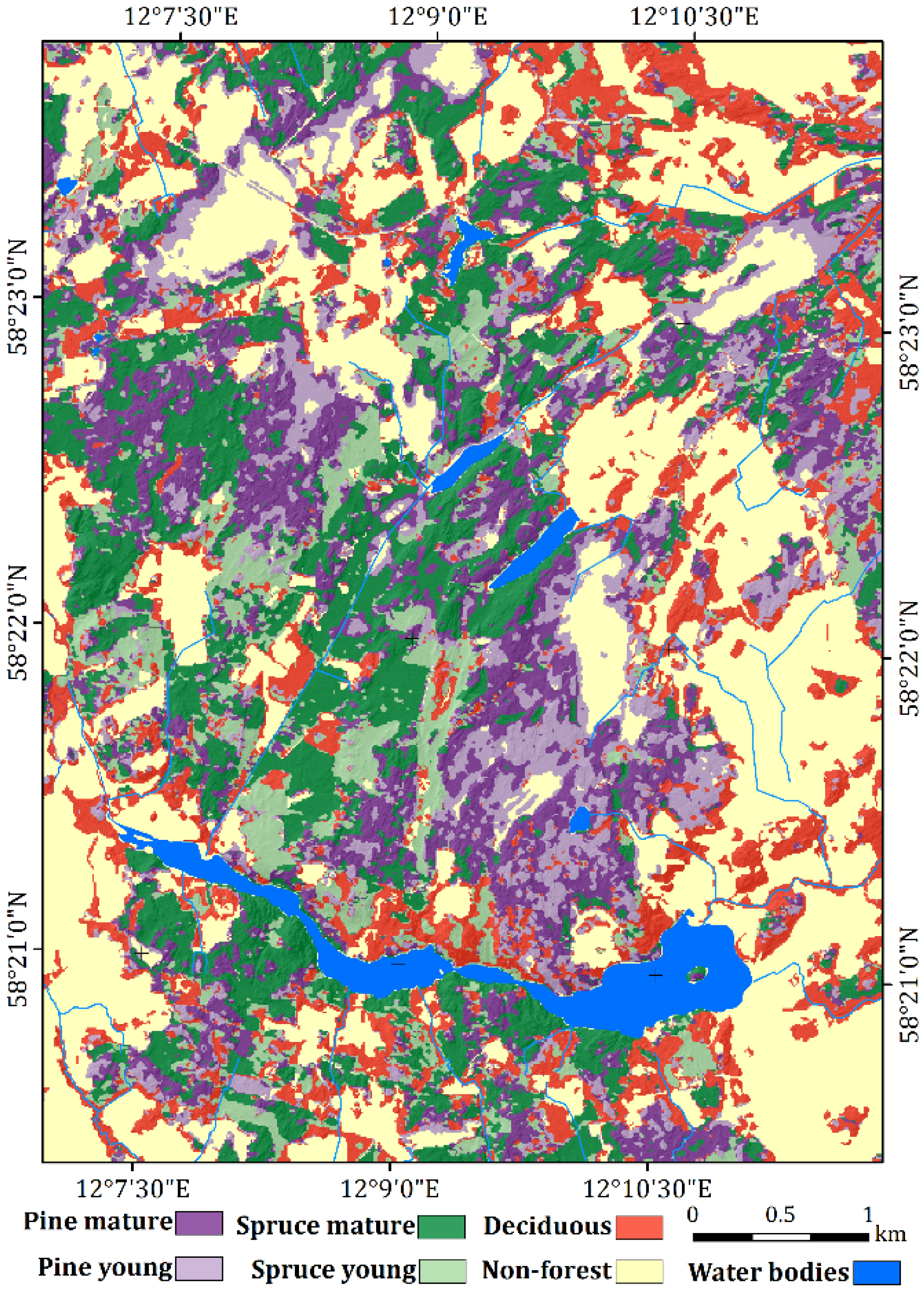
4.1. Vegetation Classes

A map of vegetation types based on maximum likelihood classification (cf. Section 3.3) for the SRC area is presented in Figure 2. According to the classification, the dominant species in the total forested area of slightly more than 20 km2 were spruce and pine, which each occupying areas of around 8 km2. In contrast, deciduous forest covered only 4.6 km2 and was mostly found in inhabited areas. The accuracy assessment of this classification is presented in Table 2.
Table
Table 2. Accuracy assessment for SPOT-5 image, using classification metrics from Congalton [24].
Table 2. Accuracy assessment for SPOT-5 image, using classification metrics from Congalton [24].
Spruce MatureSpruce YoungPine MaturePine YoungDeciduousTotalProducer’s accuracy (%)Area (km2)Area (%)
Spruce Mature67350176925.426.6
Spruce Young22530131862.512.3
Pine Mature41328045684.622.7
Pine Young00710017503.215.7
Deciduous00022527934.622.7
Total7329472027196
User’s accuracy (%)8881715993 Total accuracy (%)81
Kappa coefficient0.75
Forests 05 00992 g002 1024
Figure 2. Vegetation map from SPOT-5 data for 29th July 2011 using maximum likelihood classification (10 m pixel resolution); here, deciduous forest consists mostly of birch trees.
Figure 2. Vegetation map from SPOT-5 data for 29th July 2011 using maximum likelihood classification (10 m pixel resolution); here, deciduous forest consists mostly of birch trees.
Forests 05 00992 g002
According to Table 2, the main misclassification occurred among young and mature pine classes, while all the other classes were identified with accuracies higher than 80%. The result of 81% for the total accuracy of the maximum likelihood classification can be considered as good for optical type of data, while user’s and producer’s accuracies showed that all forest types were identified reliably, being only a little underclassified or overclassified. Although there was a time gap of one year between satellite data capture and the ground-truthing survey, we conclude that this is likely to have only a minor impact on the performed classification, as the average growth in height for coniferous trees taller than 230 cm was found to be roughly 30 cm per year in a similar climate zone [29]. Therefore, the one year time gap may be considered as negligible in terms of forest age structure change. Although the accuracy of the AGB prediction could have been affected due to the forest disturbance in the form of clear-cutting, thinning and storms between 2011 (remote sensing data capture) and 2012 (ground-truthing survey), the effect of land cover change was assumed to be insignificant due to minor harvesting activity in this region.
With regards to the spectral separability of the different vegetation types, seasonality and phenology are the main drivers of the spectral variation in the optical satellite imagery allowing a differentiation between vegetation classes. In this study, the main misclassification occurred between mature and young pine forests. This might have been caused by the substantial spectral overlap between these two classes, most probably caused by the density of the forest influencing the spectral signature in areas of pine stands or due to the limited training samples. Another consideration when assessing the classification output was the difference in understorey composition of forested areas affecting the spectral separability of vegetation classes. This is an issue in forest stands of the same species with different understorey type, varying from grassy and shrubby to bare soils and soils covered by litter leading to a large standard deviation for each of the vegetation classes.

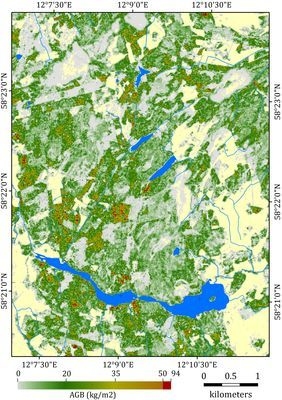
4.2. Reference Aboveground Biomass Estimates

The number of trees with their diameter and height measured in the field plots varied substantially with forest type, tree maturity and density. For example, the number of trees per plot ranged from only six trees in sparse mature spruce forest to more than one hundred trees in highly dense young birch forest (Figure 3).
Forests 05 00992 g003 1024
Figure 3. Tree diameter at breast height (top) and height distribution (bottom) of the plots surveyed in the field; Note: no height measurements were performed for birch trees.
Figure 3. Tree diameter at breast height (top) and height distribution (bottom) of the plots surveyed in the field; Note: no height measurements were performed for birch trees.
Forests 05 00992 g003
In this study, AGB prediction was not based on DBH, as DBH cannot be directly captured by the LiDAR technique. However, tree height derived from active remote sensing sensor measurements, such as LiDAR, has been shown to be highly correlated with biomass [18,30]. Therefore, AGB prediction was accomplished by deriving an additional allometric equation on the basis of field measurements. Following [17,31], the relation between tree height and biomass can be described as a power function of the form y = a × xc. For this study:
AGBSPRUCE = 0.1183 × H2.528
AGBPINE = 0.6696 × H1.996
Unfortunately, height measurements of deciduous trees were not available. Therefore, we applied an empirically derived relationship from forest yield tables of coniferous and broadleaf tree species in Middle Europe for AGB estimation of birch [30]:
AGBBIRCH = 0.8 × H1.748
The regression analysis showed satisfactory goodness of fit statistics for predicting AGB based on a sample of 145 pine trees and 189 spruce trees, with R2 values of 0.65 and 0.76, respectively (Figure 4). The estimated coefficient of the best-fit models developed for estimating AGB as a function of tree height were highly significant (P < 0.001).
Forests 05 00992 g004 1024
Figure 4. Power model for AGB prediction from LiDAR-derived height estimates for spruce and pine trees.
Figure 4. Power model for AGB prediction from LiDAR-derived height estimates for spruce and pine trees.
Forests 05 00992 g004
Trees with heights and species class recorded during fieldwork served as an input for allometric regression models and thus reference biomass over plots was calculated. Reference AGB was averaged in 15 m × 15 m squares and varied from 2.5 kg/m2 in very young sparse forest stands to 44 kg/m2 in mature dense forest stands.
The percentage of AGB stored in understory was derived based on field data (83 plots). On average 0.1% of biomass per plot was present in tree stands below 2 m in height and 3 cm in DBH, reaching a maximum of 5% in dense young forest. On the other hand, 0.7% of AGB was present in trees below 3 m in height and 4 cm in DBH with a maximum of 25% in dense young forest. Therefore, by applying a height threshold of 2 m for canopy extraction we can assume to account for at least 95% of the AGB in forest stands dominated by coniferous species.
The main parameters used for AGB estimation across surveyed plots were DBH and tree height. It was suggested that the use of both parameters would result in improved AGB estimates. However, as shown in Johansson [28] and Marklund [27], the introduction of a tree height variable leads to less than 1% increase in the R2 value of the prediction models. Thus, the absence of height measurements for the majority of plots introduced a minor error in the prediction of AGB.
Established relationships between AGB and field-measured tree heights approximated the first order power function, which introduced errors in the AGB calculation. As can be clearly seen from Figure 4, the model developed for pine overestimated AGB of young trees. Moreover, the uncertainty in AGB prediction increases with increasing canopy height due to small sample size of tall trees. Nevertheless, the ability to predict AGB on the basis of tree heights may be considered as quite strong (R2spruce = 0.76 and R2pine = 0.65).
Further investigation of allometric models for AGB estimation revealed that AGB estimates are critically dependent on tree species. This dependence can particularly be observed when comparing coniferous and deciduous species, though the relation used in this study for the estimation of AGB in deciduous trees represents a generalized relationship developed for both broadleaf and coniferous species. The estimates for deciduous trees might be improved by deriving AGB-height allometry equations from the relationship between DBH and height as shown in Mehtätalo [32].

4.3. LiDAR-Derived Forest Inventory Parameters

4.3.1. Tree Density

The main drawback of using low point density LiDAR data for individual tree modeling is its inability to accurately and consistently detect trees hidden within or under the main canopy. We hence restricted the comparison between the amount of trees recorded in the field and derived by TreeVaW to dominant trees. Dominant trees were defined as the tallest trees in the stand with a DBH wider than plot average. The TreeVaW algorithm for tree top detection showed better ability to detect the amount of dominant trees across mature forest than across young forest (Figure 5). It was able to identify 65% of dominant trees measured during fieldwork. The TreeVaW algorithm further was able to detect only dominant trees in the upper canopy with relatively good accuracies, while shorter trees remained undetected (Figure 5a). Note that most of the plots where the number of trees was accurately detected were located in areas with LiDAR density higher than 0.5 point/m2. Young forest stands exhibit more homogeneous and smooth canopy surfaces and thus it is unreasonable to expect that a TreeVaW algorithm would be able to accurately delineate separate tree objects from a CHM with 50 cm spatial resolution [33]. Random overestimation might be associated with imprecision of GPS measurements in locating the plot centers. The grid-based approach on the other hand approximates the highest pulse return within a user-defined grid cell to an individual tree and thus cannot provide reliable information on number of trees within a plot.
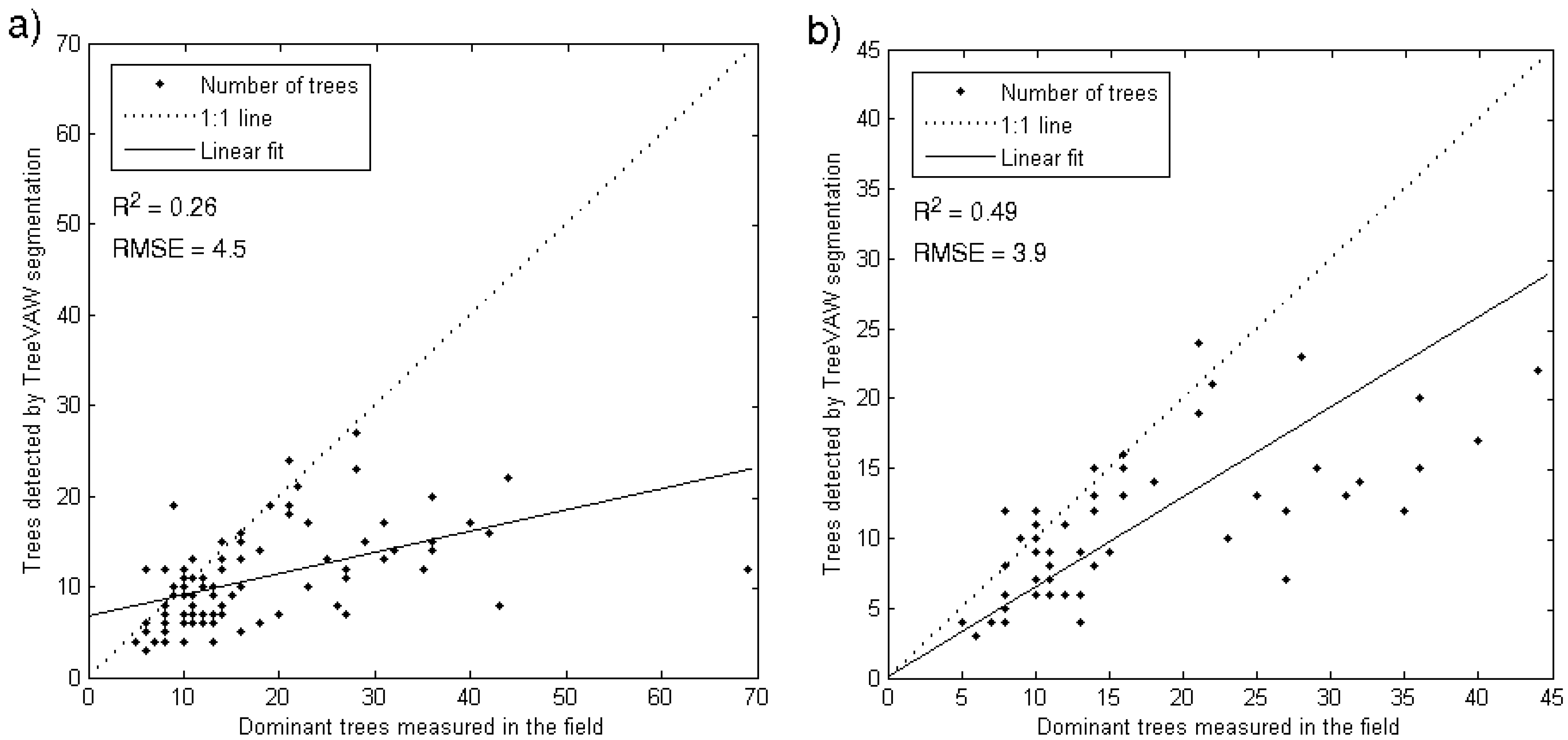
Forests 05 00992 g005 1024
Figure 5. Performance of the TreeVaW tree top detection algorithm applied to (a) all plot data; and to (b) plots classified as mature forest only.
Figure 5. Performance of the TreeVaW tree top detection algorithm applied to (a) all plot data; and to (b) plots classified as mature forest only.
Forests 05 00992 g005
These findings suggest the inability of the TreeVaW algorithm to detect treetops from low density LiDAR scanning data, as this is too coarse to allow the detection of individual tree crowns. Moreover, the crown width model of TreeVaW was derived from the tree metrics of forest stands in the Piedmont region of Virginia, USA, which can be morphologically different to those in the SRC area.
Because of the failure of the TreeVaW algorithm to account for suppressed trees, the tree densities extracted by this method are expected to lead to highly underestimated values of AGB. To overcome this problem, a simplistic grid-based algorithm was applied which while introducing substantial shortcomings in the delineation of individual tree canopies, nevertheless resulted in a good approximation of the forest biomass over plots (R2 = 0.80, RMSE = 4.7 kg/m2).

4.3.2. Tree Height

LiDAR-derived tree height was calculated using the maximum value of the CHM cells that coincided with the respective plot areas. In the following, it was evaluated against measured tree height, keeping in mind limitations and uncertainties of GPS measurements for individual trees of up to 5 m (Figure 6).
Forests 05 00992 g006 1024
Figure 6. LiDAR-derived vs. field-measured maximum tree height per plot; the GPS-introduced uncertainty was accounted for by the variance in maximum canopy model-based tree height when shifting the plot center by 5 m in any direction.
Figure 6. LiDAR-derived vs. field-measured maximum tree height per plot; the GPS-introduced uncertainty was accounted for by the variance in maximum canopy model-based tree height when shifting the plot center by 5 m in any direction.
Forests 05 00992 g006
As can be seen from Figure 6, LiDAR predictions underestimated tree height on average by 14%, ranging from 0.2% to 34%. This finding is consistent with several other studies indicating a similar correlation, but substantially smaller RMSE values of about 0.5 m were obtained when using high density LiDAR data [34,35]. Underestimation of tree heights is a common characteristic of LiDAR-derived tree height models [10,34] and is usually attributed to the laser beam missing the tree tops, instead striking the tree crowns due to the size of the LiDAR footprint and low scanning density [35]. This effect is particularly pronounced for trees with a large crown diameter. The relatively small footprint (0.5 m in diameter) of the LiDAR sensor also implies that there was a chance of complete beam absorption by the tree canopy before it reached the ground [36]. A combination of these factors could result in the observed underestimation of measured tree height. It should also be noted that there are distinct outliers in the field measurements; resulting in differences between LiDAR-derived and field-measured tree heights of more than 5 m. Checking suspicious outliers in the field therefore could have improved the overall correlation. The use of a tree height correction linear regression formula following for example of Maltamo et al. [4], is not possible as the forest stands investigated in this study are of varying shapes, ages and densities and hence the biases are not expected to be consistent. Another drawback of using low point density LiDAR is its inability to accurately and consistently detect the number of trees within sampling plots. Even though the TreeVaW algorithm was able to detect the amount of dominant trees in the upper canopy with relatively good accuracies, smaller and suppressed trees remained undetected (Figure 5), proving the application of individual treetop detection algorithms to be inappropriate when dealing with low point density LiDAR. On the other hand, a simplistic grid-based algorithm introduced substantial shortcomings in delineation of individual tree canopies, but presented a good approximation of the forest biomass over plots.

4.4. Aboveground Biomass Estimates over the Study Area

LiDAR-derived tree height (CHM) and species class from multi-spectral imagery served as input to allometric regression models to calculate biomass (AGB). Using tree metrics estimated by the TreeVaW algorithm as input to the allometric equations produced, as expected, highly underestimated AGB values. In contrast, the tree metrics extracted using the grid-based approach were successfully applied in equations for AGB estimation showing the model’s good predictive ability on a plot level. The best AGB estimate was achieved by using a grid-based approach for treetop detection with 3 m × 3 m cells (Figure 7), while the same approach with 2 m × 2 m and 4 m × 4 m cells yielded highly overestimated and underestimated AGB values respectively. A similar “fitting” technique for determination of the optimal cell resolution can be used at other forest sites when only low-density LiDAR data is available.
Forests 05 00992 g007 1024
Figure 7. Field-measured vs. predicted AGB using the grid-based approach with 3 m × 3 m cell size.
Figure 7. Field-measured vs. predicted AGB using the grid-based approach with 3 m × 3 m cell size.
Forests 05 00992 g007
Using the best performance grid-based approach for treetop detection and averaging the biomass in 15 m × 15 m to match the resolution of plots delineated in the field, the AGB over the study area was estimated to vary from slightly less than 1 kg/m2 in very young forests up to 94 kg/m2 in mature spruce forests (Figure 8). However, it is important to note that the mean AGB over the SRC area was equal to 9.4 kg/m2 and that values of more than 50 kg/m2 were quite rare and occupied only 1% of the area. Overall, the Skogaryd Research Catchment area is characterized by a patchy AGB distribution with high values of more than 50 kg/m2 located strictly in mature spruce forest stands. The performance of our model for AGB derivation is consistent with the findings of a similar project where a national low density LiDAR dataset was utilized [6]. The slightly higher coefficient of determination of AGB prediction in our study as pointed out by Nord-Larsen and Shumacher [6] can be attributed to the stratification of the study area into vegetation species using satellite imagery.
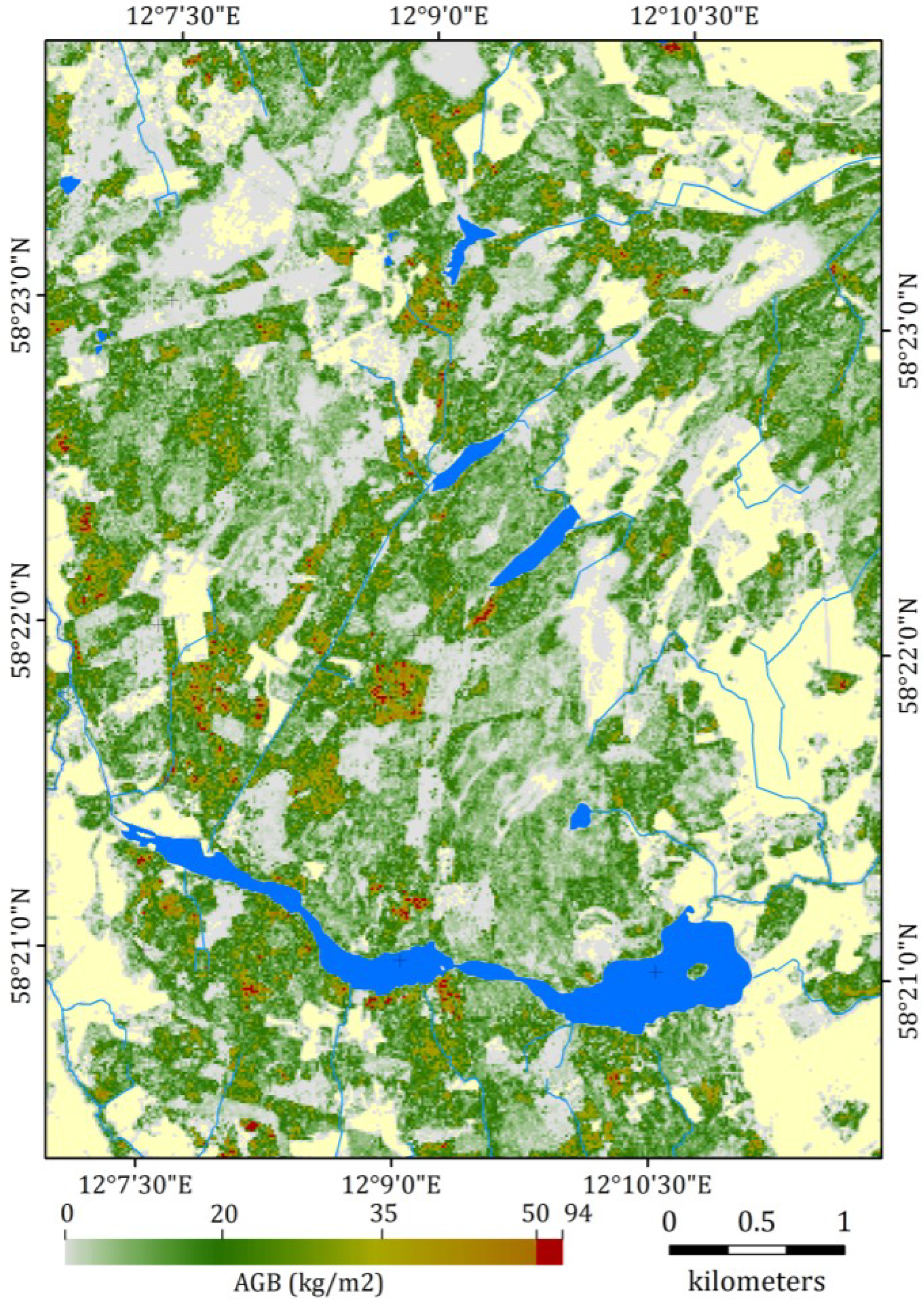
Forests 05 00992 g008 1024
Figure 8. Aboveground biomass map for June 2011 over the SRC area based on the grid-based approach with 3 m × 3 m cell size (within plot R2 = 0.80, 15 m pixel resolution).
Figure 8. Aboveground biomass map for June 2011 over the SRC area based on the grid-based approach with 3 m × 3 m cell size (within plot R2 = 0.80, 15 m pixel resolution).
Forests 05 00992 g008
It should also be noted that the low accuracy of the GPS measurements suggests that estimated plot AGB could have been located within at least a 5 m radius from the recorded plot center. The GPS accuracy deteriorates under dense forest canopy, where GPS systems tend to yield from 1.5 to 3 times less accurate solutions [26]. Therefore, the use of a high precision GPS receiver would be highly beneficial for future projects of similar nature.

5. Conclusions

We present estimates of above ground biomass (AGB) with reasonably high accuracy for conifer-dominated forests in Västra Götaland County using a fusion of low-density discrete-return airborne LiDAR and a multi-spectral satellite image (SPOT-5). SPOT-5 data provided reliable mapping of tree species, which was subsequently combined with LiDAR-derived canopy height (CHM) to derive forest inventory parameters for the main tree species of the area. Using a grid-based approach with 3 m × 3 m cells produced the most accurate estimation of AGB (R2 = 0.80), while application of the TreVaW algorithm for individual tree delineation showed to be inappropriate when dealing with low point density LiDAR data (<1 points/m2). Results show AGB to vary from slightly less than 1 kg/m2 in very young forests up to 94 kg/m2 in mature spruce forests, with RMSE of 4.7 kg/m2. We suggest that the methodology developed in this study can be applied across similar conifer-dominated forests, specifically where low density national LiDAR scanning has been performed, by “fitting” an optimal cell resolution to approximate individual trees. However, extensive field campaigns should be conducted to derive site-specific AGB-tree height allometry before applying our methodology to regions of different climatic and growth conditions.
Availability of baseline AGB estimates allows further monitoring of this forest ecosystem regarding disturbance and changes in time, though re-occurring airborne surveys would be required in order to collect adequate amounts of data. Furthermore, suggested AGB values can be directly used in future studies of carbon stocks in the Skogaryd Research Catchment, assuming carbon to account for 45% of total biomass [37]. Potentially, the algorithm developed in this study may be used for assessment of individual tree components of biomass, such as foliage or stem wood, since allometry for tree components is readily available.

Acknowledgments

The study was funded by the Landscape Greenhouse Gas Exchange (LAGGE) project led by the Department of Earth Sciences, Gothenburg University and the Department of Physical Geography and Ecosystem Science, Lund University, as well as the strategic research area BECC (Biodiversity and Ecosystem services in a Changing Climate, [38]). The authors acknowledge support from Lund University and from LUCCI (Lund University Centre for Studies of Carbon Cycle and Climate Interactions, [39]), a Linnaeus center funded by the Swedish Research Council VR. The authors also thank Elin Julen from Gothenburg University for her valuable contribution with the inventory of the Skogaryd Research Catchment forest and two reviewers for their helpful comments.

Author Contributions

Iurii Shendryk and Margareta Hellström identified the research questions and designed the study. Iurii Shendryk collected the data and performed the analyses with guidance from the co-authors. All authors contributed to the writing and revising successive drafts.

Conflicts of Interest

The authors declare no conflict of interest.

References and Notes

  1. IPCC. Climate Change 2007: Mitigation of Climate Change. IPCC Fourth Assessment Report (AR4); Contribution of Working Group III to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change, 2007; Metz, B., Davidson, O.R., Bosch, P.R., Dave, R., Meyer, L.A., Eds.; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
  2. Houghton, R.A.; Hall, F.; Goetz, S.J. Importance of biomass in the global carbon cycle. J. Geophys. Res. 2009, 114, 1–13. [Google Scholar]
  3. Lefsky, M.A.; Cohen, W.B.; Harding, D.J.; Parker, G.G.; Acker, S.A.; Gower, S.T. LiDAR remote sensing of aboveground biomass in three biomes. Glob. Ecol. Biogeogr. 2002, 11, 393–399. [Google Scholar] [CrossRef]
  4. Maltamo, M.; Mustonen, K.; Hyyppä, J.; Pitkänen, J.; Yu, X. The accuracy of estimating individual tree variables with airborne laser scanning in a boreal nature reserve. Can. J. For. Res. 2004, 34, 1791–1801. [Google Scholar] [CrossRef]
  5. Hese, S.; Lucht, W.; Schmullius, C. Global biomass mapping for an improved understanding of the CO2 balance-the Earth observation mission carbon-3D. Remote Sens. Environ. 2005, 94, 94–104. [Google Scholar] [CrossRef]
  6. Nord-Larsen, T.; Shumacher, J. Estimation of forest resources from a country wide laser scanning survey and national forest inventory data. Remote Sens. Environ. 2012, 119, 148–157. [Google Scholar] [CrossRef]
  7. Popescu, S.C. Estimating biomass of individual pine trees using airborne LiDAR. Biomass Bioenergy 2007, 31, 646–655. [Google Scholar] [CrossRef]
  8. Bortolot, Z.J.; Wynne, R.H. Estimating forest biomass using small footprint LiDAR data: An individual tree-based approach that incorporates training data. ISPRS J. Photogramm. Remote Sens. 2005, 59, 342–360. [Google Scholar] [CrossRef]
  9. Chen, Q.; Laurin, G.V.; Battles, J.J.; Saah, D. Integration of airborne LiDAR and vegetation types derived from aerial photography for mapping aboveground live biomass. Remote Sens. Environ. 2012, 121, 108–117. [Google Scholar] [CrossRef]
  10. Evans, J.S.; Hudak, A.T.; Faux, R.; Smith, A.M.S. Discrete return LiDAR in natural resources: Recommendations for project planning, data processing, and deliverables. Remote Sens. 2009, 1, 776–794. [Google Scholar] [CrossRef]
  11. Hopkinson, C.; Chasmer, L.; Colville, D.; Fournier, R.A.; Hall, R.J.; Luther, J.E.; Milne, T.; Petrone, R.M.; St-onge, B. Moving toward consistent ALS monitoring of forest attributes across Canada: A consortium approach. Photogramm. Eng. Remote Sens. 2013, 79, 159–173. [Google Scholar] [CrossRef]
  12. Jochem, A.; Hollaus, M.; Rutzinger, M.; Höfle, B. Estimation of aboveground biomass in alpine forests: A semi-empirical approach considering canopy transparency derived from airborne LiDAR data. Sensors 2011, 11, 278–295. [Google Scholar]
  13. Luther, J.E.; Skinner, R.; Fournier, R.A.; van Lier, O.R.; Bowers, W.W.; Cote, J.F.; Hopkinson, C.; Moulton, T. Predicting wood quantity and quality attributes of balsam fir and black spruce using airborne laser scanner data. Forestry 2014, 87, 313–326. [Google Scholar]
  14. Ramdani, F. Urban vegetation mapping from fused hyperspectral image and LiDAR data with application to monitor urban tree heights. J. Geogr. Inf. Syst. 2013, 5, 404–408. [Google Scholar]
  15. Lin, Y.; Jaakkola, A.; Hyyppä, J.; Kaartinen, H. From TLS to VLS: Biomass estimation at individual tree level. Remote Sens. 2010, 2, 1864–1879. [Google Scholar] [CrossRef]
  16. Edson, C.; Wing, M.G. Airborne light detection and ranging (LiDAR) for individual tree stem location, height, and biomass measurements. Remote Sens. 2011, 3, 2494–2528. [Google Scholar] [CrossRef] [Green Version]
  17. Zianis, D.; Muukkonen, P.; Mäkipää, R.; Mencuccini, M. Biomass and stem volume equations for tree species in Europe. Silva Fenn. Monogr. 2005, 4, 1–63. [Google Scholar]
  18. Andersen, H.E.; Strunk, J.; Temesgcn, H.; Atwood, D.; Winterberger, K. Using multilevel remote sensing and ground data to estimate forest biomass resources in remote regions: A case study in the boreal forests of interior Alaska. Can. J. Remote Sens. 2011, 37, 1–16. [Google Scholar]
  19. Meyer, A.; Tarvainen, L.; Nousratpour, A.; Björk, R.G.; Ernfors, M.; Grelle, A.; Klemedtsson, Å.K.; Lindroth, A.; Räntfors, M.; Rütting, T.; Wallin, G.; Weslien, P.; Klemedtsson, L.A. Fertile peatland forest does not constitute a major greenhouse gas sink. Biogeosciences 2013, 10, 7739–7758. [Google Scholar] [CrossRef]
  20. Vertex IV; Vertex IV and Transponder T3 Manual 2007. Vertex: Långsele, Sweden, 2007. Available online: http://www.haglofcg.com/index.php?option=com_content&view=article&id=49&Itemid=82&lang=en (accessed on 10 January).
  21. Bucksch, A.; Lindenbergh, R.; Menenti, M. Robust skeleton extraction from imperfect point clouds. Vis. Comput. 2010, 26, 1283–1300. [Google Scholar] [CrossRef]
  22. Lantmäteriet. Produktbeskrivning Laserdata, Dokumentversion: 1.6. Available online: http://www.lantmateriet.se/Global/Kartor%20och%20geografisk%20information/H%C3%B6jddata/Produktbeskrivningar/laserdat.pdf (accessed on 12 December 2012).
  23. Mehner, H.; Cutler, M.; Fairbairn, D.; Thompson, G. Remote sensing of upland vegetation: The potential of high spatial resolution satellite sensors. Glob. Ecol. Biogeogr. 2004, 13, 359–369. [Google Scholar] [CrossRef]
  24. Congalton, R.G. A review of assessing the accuracy of classifications of remotely sensed data. Remote Sens. Environ. 1991, 37, 35–46. [Google Scholar] [CrossRef]
  25. MARS Explorer, Mars 7.1 Help Manual 2012; MARS: Greenwood Village, CO, USA, 2012.
  26. Popescu, S.C.; Wynne, R.H. Seeing the trees in the forest: Using LiDAR and multispectral data fusion with local filtering and variable window size for estimating tree height. Photogramm. Eng. Remote Sens. 2004, 70, 589–604. [Google Scholar] [CrossRef]
  27. Marklund, L.G. Biomassafunktioner för tall, gran och björk i Sverige. Sveriges Lantbruksuniversitet, Institutionen för Skogstaxering. Rapport 1988, 45, 1–73. (in Swedish). [Google Scholar]
  28. Johansson, T. Biomass equations for determining functions of pendula and pubescent birches growing on abandoned farmland and some practical implications. Biomass Bioenergy 1999, 16, 223–238. [Google Scholar] [CrossRef]
  29. Lieffers, V.J.; Stadt, K.J.; Navratil, S. Age structure and growth of understory white spruce under aspen. Can. J. For. Res. 1996, 26, 1002–1007. [Google Scholar] [CrossRef]
  30. Mette, T.; Papathanassiou, K.; Hajnsek, I. Biomass estimation from polarimetric SAR interferometry over heterogeneous forest terrain. In Geoscience and Remote Sensing Symposium, 2004. IGARSS '04. Proceedings. 2004 IEEE International, Anchorage, AK, USA, 20–24 September 2004; pp. 511–514.
  31. Mette, T. Forest Biomass Estimation from Polarimetric SAR Interferometry. Ph.D. Thesis, Center of Life and Food Sciences Weihenstephan, Technical University of Munich, Munich, Germany, 2006. [Google Scholar]
  32. Mehtätalo, L. Height-Diameter Models for Scots Pine and Birch in Finland. Silva Fennica 2005, 39, 55–66. [Google Scholar]
  33. Gebreslasie, M.T.; Ahmed, F.B.; van Aardt, J.A.N.; Blakeway, F. Individual tree detection based on variable and fixed window size local maxima filtering applied to IKONOS imagery for even-aged Eucalyptus plantation forests. Int. J. Remote Sens. 2011, 32, 4141–4154. [Google Scholar] [CrossRef]
  34. Morsdorf, F.; Meier, E.; Kötz, B.; Itten, K.I.; Dobbertin, M.; Allgöwer, B. Lidar-based geometric reconstruction of boreal type forest stands at single tree level for forest and wildland fire management. Remote Sens. Environ. 2004, 92, 353–362. [Google Scholar] [CrossRef]
  35. Roberts, S.D.; Dean, T.J.; Evans, D.L.; McCombs, J.W.; Harrington, R.L.; Glass, P.A. Estimating individual tree leaf area in loblolly pine plantations using LiDAR-derived measurements of height and crown dimensions. For. Ecol. Manag. 2005, 213, 54–70. [Google Scholar] [CrossRef]
  36. Zimble, D.A.; Evans, D.L.; Carlson, G.C.; Parker, R.C.; Grado, S.C.; Gerard, P.D. Characterising vertical forest structure using small-footprint airborne LiDAR. Remote Sens. Environ. 2003, 87, 171–182. [Google Scholar] [CrossRef]
  37. Whittaker, R.H. Communities and Ecosystems, 2nd ed.; MacMillan Publishing: New York, NY, USA, 1975. [Google Scholar]
  38. Available online: www.cec.lu.se/research/becc (accessed on 10 January 2014).
  39. Available online: www.lucci.lu.se (accessed on 10 January 2014).

Share and Cite

MDPI and ACS Style

Shendryk, I.; Hellström, M.; Klemedtsson, L.; Kljun, N. Low-Density LiDAR and Optical Imagery for Biomass Estimation over Boreal Forest in Sweden. Forests 2014, 5, 992-1010. https://doi.org/10.3390/f5050992

AMA Style

Shendryk I, Hellström M, Klemedtsson L, Kljun N. Low-Density LiDAR and Optical Imagery for Biomass Estimation over Boreal Forest in Sweden. Forests. 2014; 5(5):992-1010. https://doi.org/10.3390/f5050992

Chicago/Turabian Style

Shendryk, Iurii, Margareta Hellström, Leif Klemedtsson, and Natascha Kljun. 2014. "Low-Density LiDAR and Optical Imagery for Biomass Estimation over Boreal Forest in Sweden" Forests 5, no. 5: 992-1010. https://doi.org/10.3390/f5050992

Article Metrics

Back to TopTop