Improved Direct Linear Transformation for Parameter Decoupling in Camera Calibration
Abstract
:1. Introduction
2. Parameter Coupling Analysis
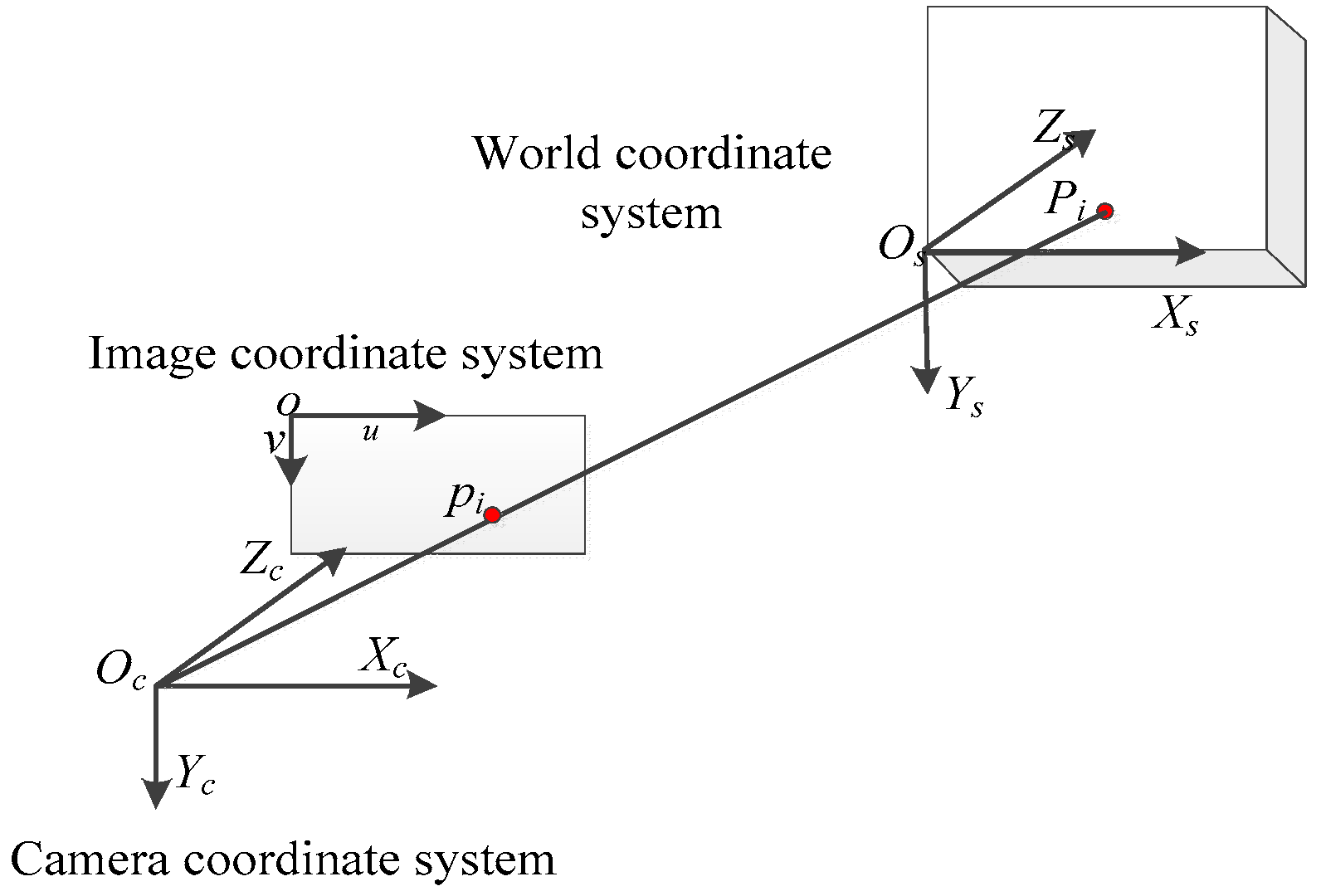
2.1. Camera Model
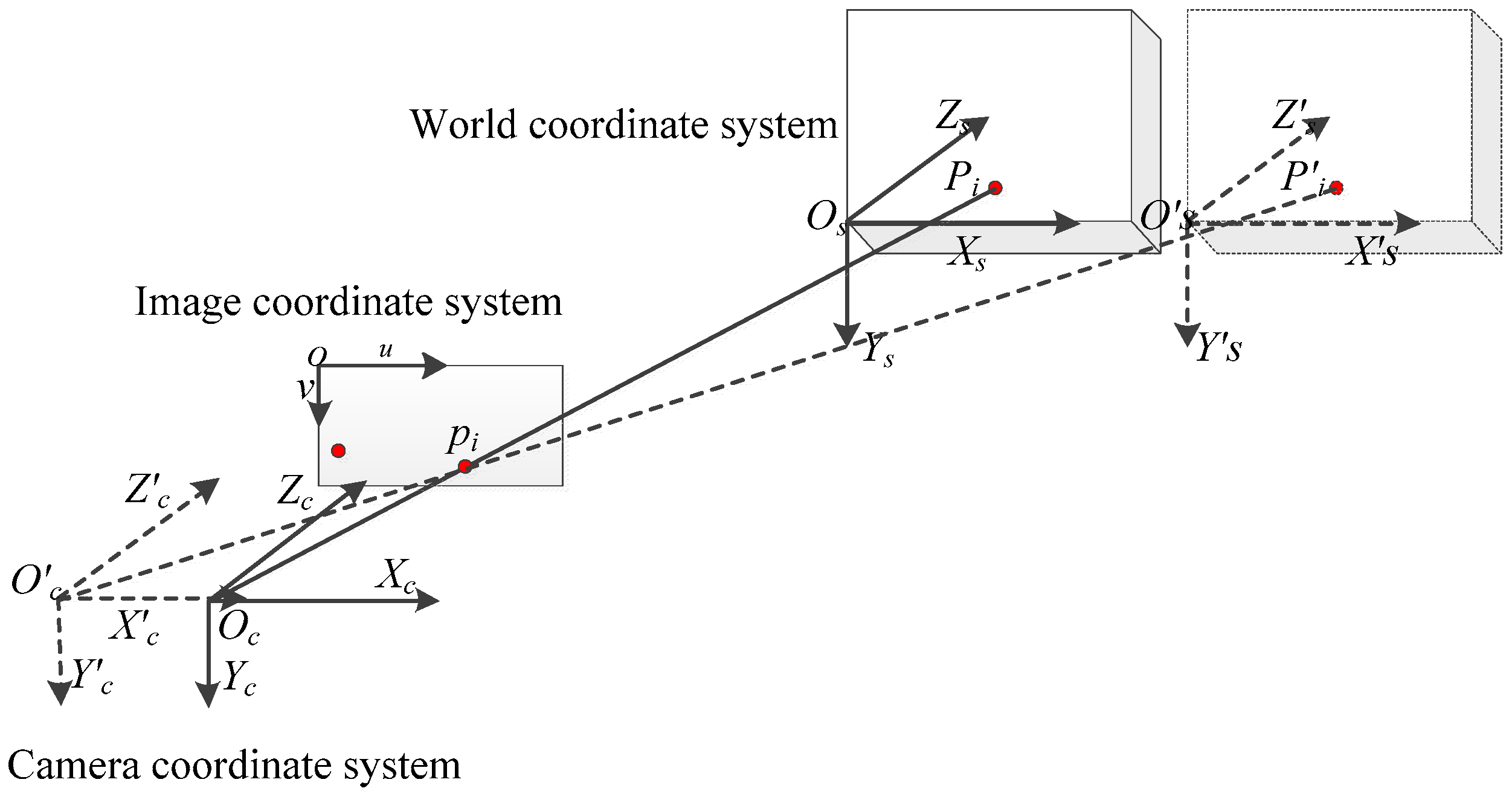
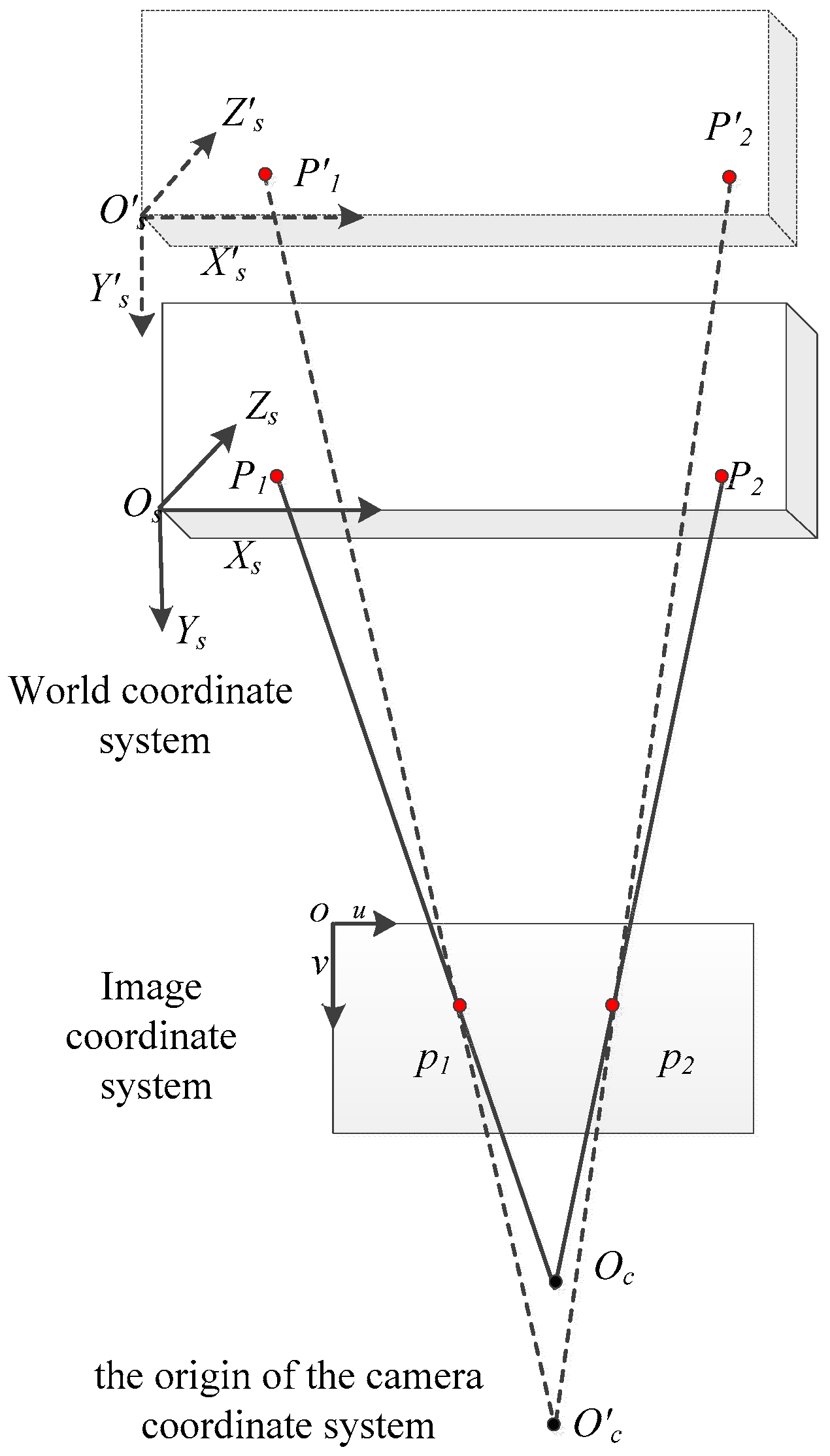
2.2. Error Coupling Analysis
3. Improved Direct Linear Transformation
3.1. Direct Linear Transformation
3.2. Improved Direct Linear Transformation
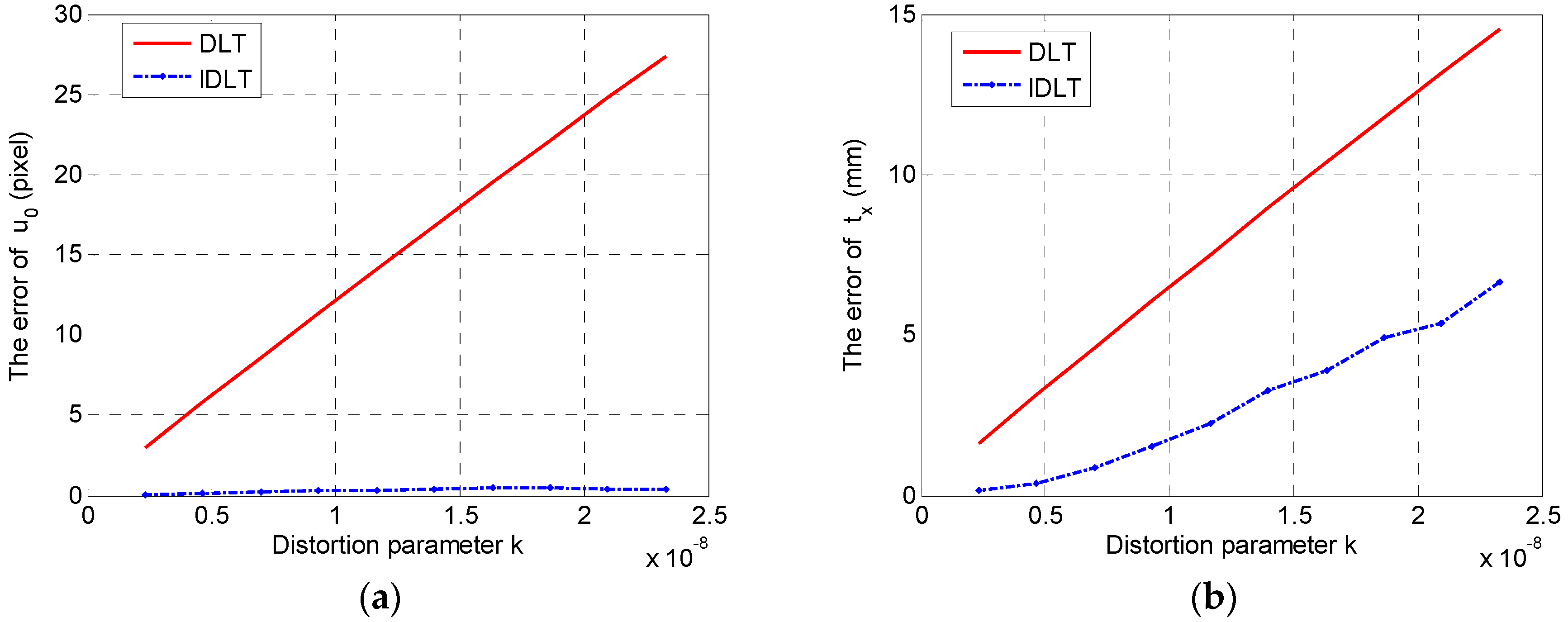
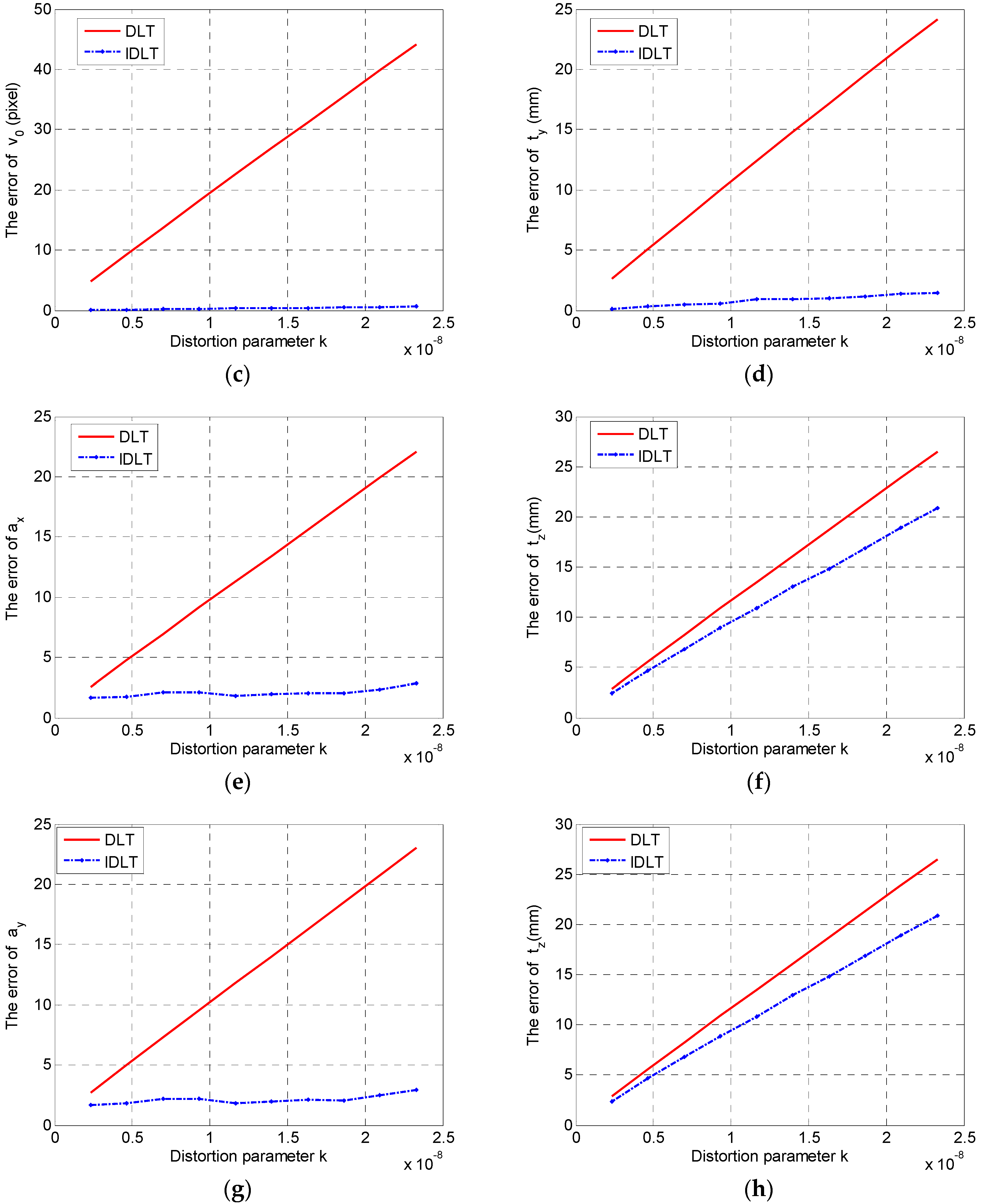
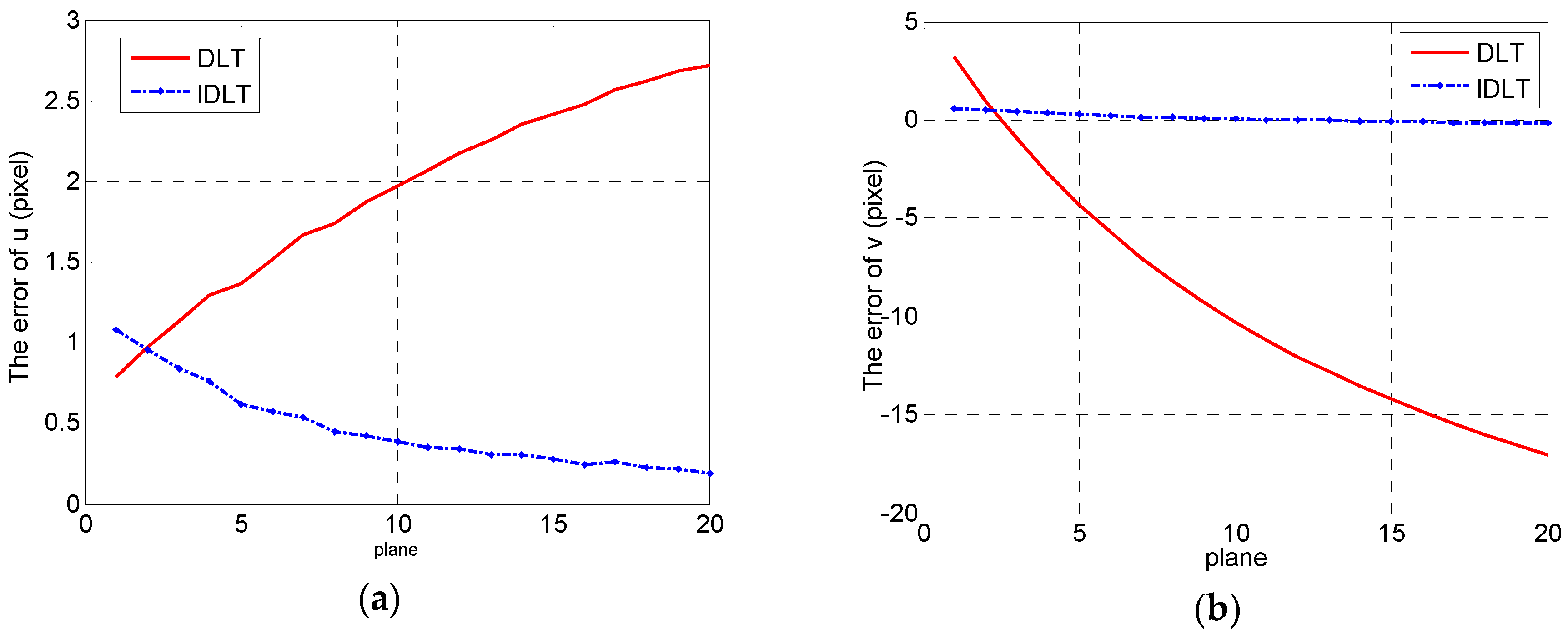
4. Experimental Section
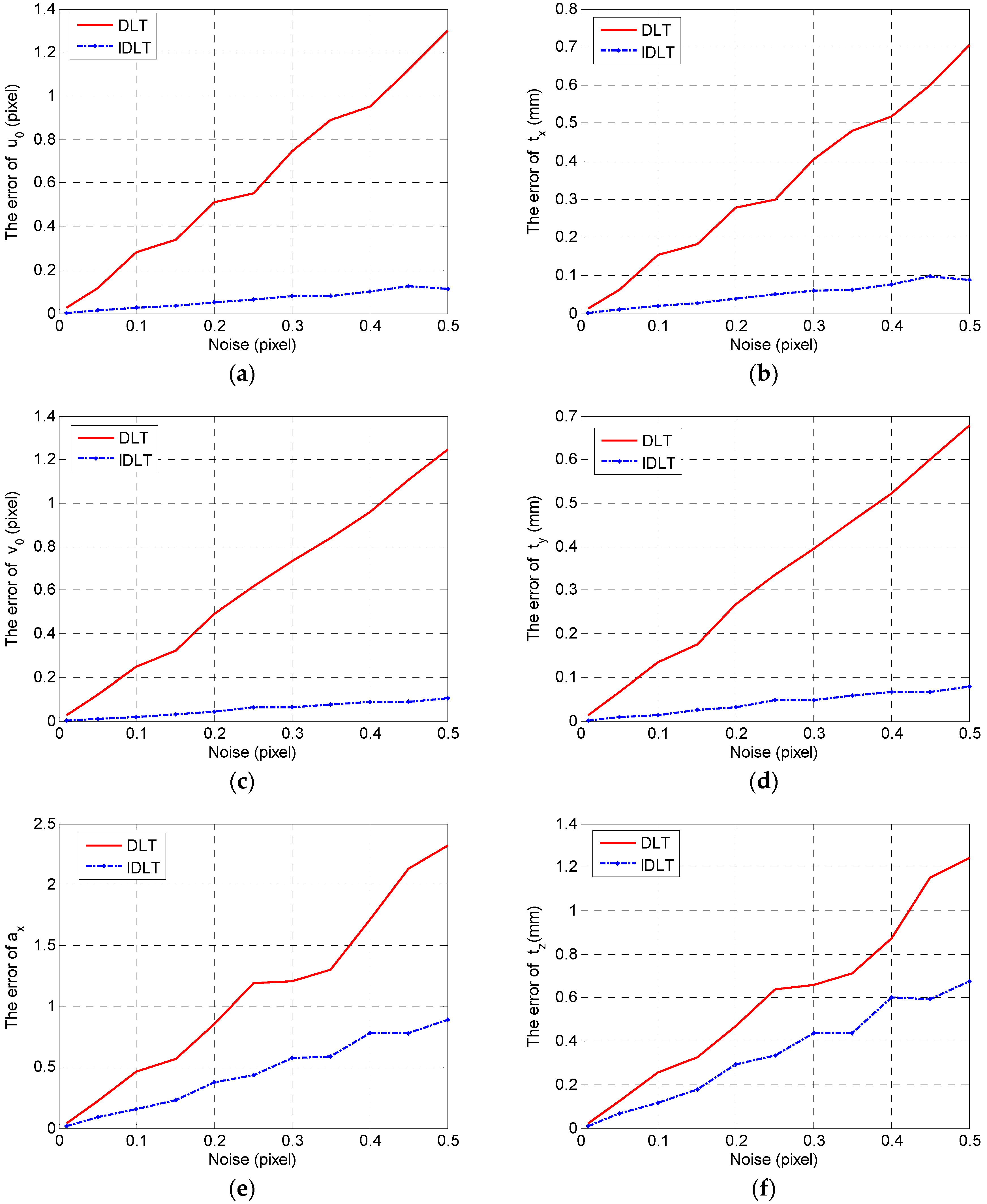
4.1. Simulation Experiment
4.2. Physical Experiment
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Chen, I.H.; Wang, S.J. An efficient approach for dynamic calibration of multiple cameras. IEEE Trans. Autom. Sci. Eng. 2009, 6, 187–194. [Google Scholar] [CrossRef]
- Ly, D.S.; Demonceaux, C.; Vasseur, P.; Pegard, C. Extrinsic calibration of heterogeneous cameras by line images. Mach. Vis. Appl. 2014, 25, 1601–1614. [Google Scholar] [CrossRef]
- Peng, E.; Li, L. Camera calibration using one-dimensional information and its applications in both controlled and uncontrolled environments. Pattern Recogn. 2010, 43, 1188–1198. [Google Scholar] [CrossRef]
- Abdel-Aziz, Y.I.; Karara, H.M. Direct linear transformation from comparator coordinates into object space coordinates in close-range photo grammetry. In Proceedings of the Symposium on Close-Range Photogrammetry, University of Illinois at Urbana-Champaign, Champaign, IL, USA, 1971; pp. 1–18.
- Tsai, R.Y. A versatile camera calibration technique for high-accuracy 3D machine vision metrology using off-the-shelf TV cameras and lenses. IEEE J. Robot Autom 1987, 3, 323–344. [Google Scholar] [CrossRef]
- Zhang, Z.Y. A flexible new technique for camera calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef]
- Chen, G.; Guo, Y.B.; Wang, H.P.; Ye, D.; Gu, Y.F. Stereo vision sensor calibration based on random spatial points given by CMM. Optik 2012, 123, 731–734. [Google Scholar] [CrossRef]
- Samper, D.; Santolaria, J.; Brosed, F.J.; Majarena, A.C.; Aguilar, J.J. Analysis of Tsai calibration method using two- and three-dimensional calibration objects. Mach. Vis. Appl. 2013, 24, 117–131. [Google Scholar] [CrossRef]
- Sun, W.; Cooperstock, J.R. An empirical evaluation of factors influencing camera calibration accuracy using three publicly available techniques. Mach. Vis. Appl. 2006, 17, 51–67. [Google Scholar] [CrossRef]
- Huang, J.H.; Wang, Z.; Xue, Q.; Gao, J.M. Calibration of a camera projector measurement system and error impact analysis. Meas. Sci. Technol. 2012, 23, 125402. [Google Scholar] [CrossRef]
- Zhou, F.Q.; Cui, Y.; Wang, Y.X.; Liu, L.; Gao, H. Accurate and robust estimation of camera parameters using RANSAC. Opt. Laser Eng. 2013, 51, 197–212. [Google Scholar] [CrossRef]
- Ricolfe-Viala, C.; Sanchez-Salmeron, A. Camera calibration under optimal conditions. J. Opt. Soc. Am. 2011, 19, 10769–10775. [Google Scholar] [CrossRef] [PubMed]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision; Cambridge University Press: Cambridge, UK, 2000; pp. 110–115. [Google Scholar]
- Batista, J.; Araujo, H.; Almeida, A.T. Iterative multistep explicit camera calibration. IEEE Trans. Robot. Autom. 1999, 15, 897–917. [Google Scholar] [CrossRef]
- Ricolfe-Viala, C.; Sanchez-Salmeron, A.; Valera, A. Efficient lens distortion correction for decoupling in calibration of wide angle lens cameras. IEEE Sens. J. 2013, 13, 854–863. [Google Scholar] [CrossRef]
- Guillemaut, J.Y.; Aguado, A.S.; Illingworth, J. Using points at infinity for parameter decoupling in camera calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 265–270. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Caprile, B.; Torre, V. Using vanishing points for camera calibration. Int. J. Comput. Vis. 1990, 4, 127–140. [Google Scholar] [CrossRef]
- He, B.W.; Zhou, X.L.; Li, Y.F. A new camera calibration method from vanishing points in a vision system. Trans. Inst. Meas. Control 2011, 33, 806–822. [Google Scholar] [CrossRef]
- Devernay, F.; Faugeras, O. Straight lines have to be straight. Mach. Vis. Appl. 2001, 13, 14–24. [Google Scholar] [CrossRef]
- Zhang, G.J.; He, J.J.; Yang, X.M. Calibrating camera radial distortion with cross-ratio invariability. Opt. Laser Technol. 2003, 35, 457–461. [Google Scholar] [CrossRef]
- Li, D.D.; Wen, G.J.; Hui, B.W.; Qiu, S.H.; Wang, W.F. Cross-ratio invariant based line scan camera geometric calibration with static linear data. Opt. Laser Eng. 2014, 62, 119–125. [Google Scholar] [CrossRef]
- Hartley, R.I. In defense of the eight-point algorithm. IEEE Trans. Pattern Anal. Mach. Intell. 1997, 19, 580–593. [Google Scholar] [CrossRef]
- Xu, Q.Y.; Ye, D.; Chen, H.; Che, R.S.; Chen, G.; Huang, Y. A valid camera calibration based on the maximum likelihood using virtual stereo calibration pattern. In Proceedings of the International Conference on Sensing, Computing and Automation, Chongqing, China, 8–11 May 2006; pp. 2346–2351.




| ax | ay | u0 (pixel) | v0 (pixel) | tx (mm) | ty (mm) | tz (mm) | (°) | (°) | (°) | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1735.90 | 1735.56 | 701.09 | 522.07 | −363.52 | −319.10 | 1705.86 | 1.11 | −0.13 | 1.36 |
| 2 | 1736.97 | 1736.67 | 700.97 | 522.59 | −363.67 | −317.70 | 1806.84 | 1.10 | −0.13 | 1.36 |
| 3 | 1738.26 | 1737.96 | 701.66 | 523.22 | −364.68 | −316.48 | 1908.12 | 1.08 | −0.13 | 1.36 |
| 4 | 1736.34 | 1736.05 | 701.59 | 523.46 | −364.90 | −314.87 | 2005.89 | 1.07 | −0.13 | 1.36 |
| 5 | 1737.88 | 1737.58 | 700.65 | 523.91 | −364.05 | −313.54 | 2107.60 | 1.06 | −0.13 | 1.36 |
| 6 | 1738.41 | 1738.15 | 700.71 | 523.93 | −364.39 | −311.73 | 2208.32 | 1.06 | −0.12 | 1.36 |
| 7 | 1737.42 | 1737.20 | 700.71 | 524.02 | −364.65 | −310.01 | 2307.00 | 1.05 | −0.12 | 1.36 |
| 8 | 1737.75 | 1737.60 | 700.58 | 524.17 | −364.72 | −308.38 | 2407.47 | 1.05 | −0.12 | 1.36 |
| 9 | 1737.21 | 1737.07 | 700.71 | 524.16 | −365.17 | −306.53 | 2506.68 | 1.05 | −0.13 | 1.36 |
| 0 | 1737.17 | 1737.05 | 700.54 | 524.10 | −365.18 | −304.62 | 2606.64 | 1.05 | −0.12 | 1.35 |
| 1 | 1736.76 | 1736.63 | 700.66 | 524.31 | −365.61 | −303.12 | 2705.92 | 1.04 | −0.12 | 1.35 |
| 2 | 1737.09 | 1737.00 | 700.74 | 524.76 | −365.99 | −302.02 | 2806.35 | 1.03 | −0.13 | 1.35 |
| 3 | 1737.19 | 1737.11 | 700.97 | 524.85 | −366.63 | −300.39 | 2906.44 | 1.03 | −0.13 | 1.35 |
| 4 | 1736.94 | 1736.86 | 700.96 | 524.60 | −366.89 | −298.18 | 3006.04 | 1.03 | −0.13 | 1.36 |
| 5 | 1737.05 | 1736.98 | 700.83 | 524.52 | −366.94 | −296.22 | 3106.31 | 1.04 | −0.13 | 1.36 |
| 6 | 1736.63 | 1736.56 | 700.75 | 524.32 | −367.06 | −294.05 | 3205.58 | 1.05 | −0.13 | 1.35 |
| 7 | 1736.33 | 1736.27 | 700.88 | 524.43 | −367.58 | −292.43 | 3304.94 | 1.04 | −0.13 | 1.35 |
| 8 | 1736.79 | 1736.77 | 701.40 | 524.66 | −368.87 | −291.07 | 3405.76 | 1.03 | −0.14 | 1.35 |
| ax | ay | u0 (pixel) | v0 (pixel) | tx (mm) | ty (mm) | Tz (mm) |
|---|---|---|---|---|---|---|
| 1738.11 | 1738.33 | 696.27 | 555.55 | −358.82 | −352.39 | 1708.23 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Z.; Ye, D.; Zhang, X.; Chen, G.; Zhang, B. Improved Direct Linear Transformation for Parameter Decoupling in Camera Calibration. Algorithms 2016, 9, 31. https://doi.org/10.3390/a9020031
Zhao Z, Ye D, Zhang X, Chen G, Zhang B. Improved Direct Linear Transformation for Parameter Decoupling in Camera Calibration. Algorithms. 2016; 9(2):31. https://doi.org/10.3390/a9020031
Chicago/Turabian StyleZhao, Zhenqing, Dong Ye, Xin Zhang, Gang Chen, and Bin Zhang. 2016. "Improved Direct Linear Transformation for Parameter Decoupling in Camera Calibration" Algorithms 9, no. 2: 31. https://doi.org/10.3390/a9020031






