Target Channel Visiting Order Design Using Particle Swarm Optimization for Spectrum Handoff in Cognitive Radio Networks
Abstract
:1. Introduction
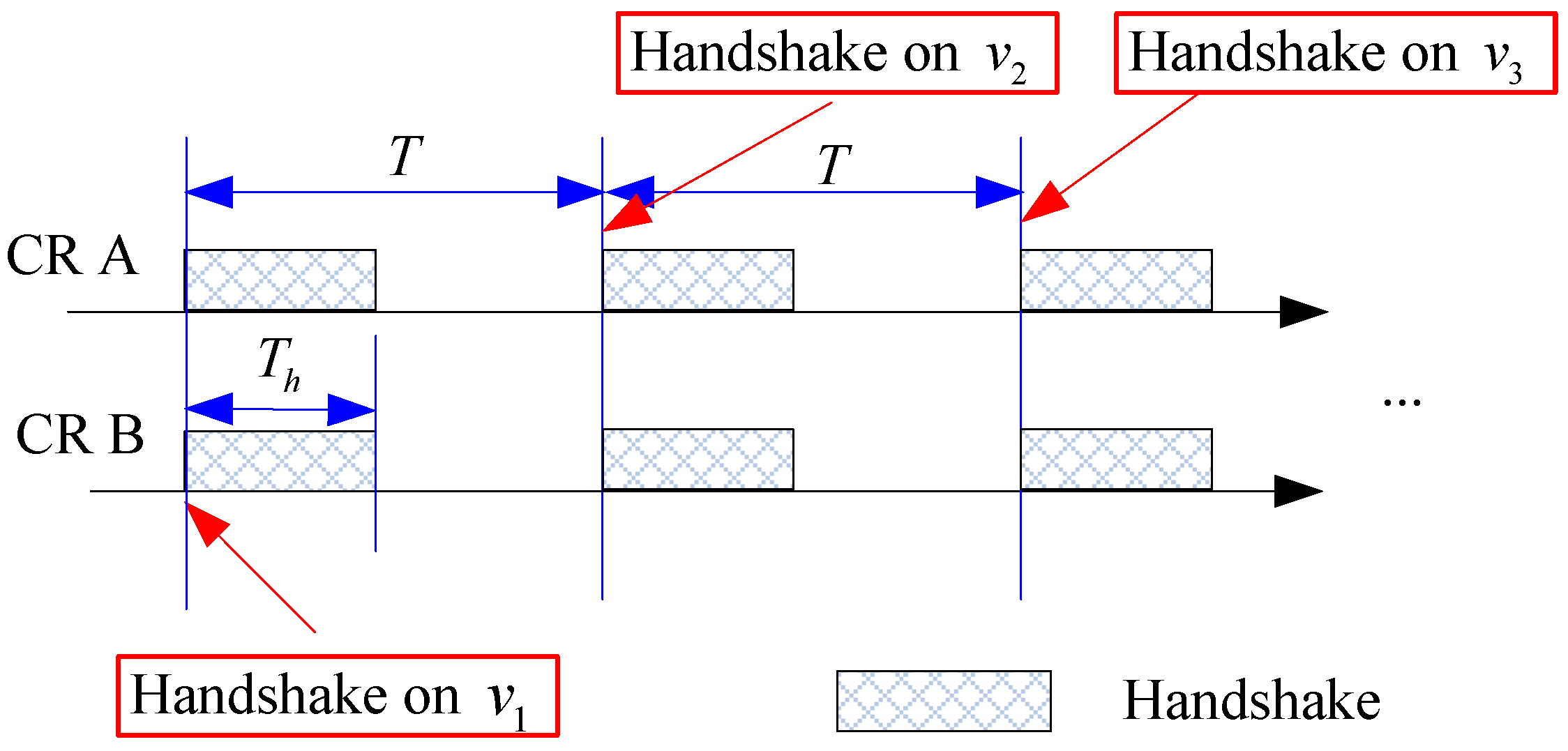
2. Problem Formulation
| Distribution | ρi | |
|---|---|---|
| Uniform ( ) | ||
| Exponential ( ) | ||
| Generalized Pareto ( , ) | ||
| Rayleigh ( ) | ||
| Weibull ( , ) |
3. Proposed Target Channel Visiting Order Design Algorithm
3.1. Introduction of PSO
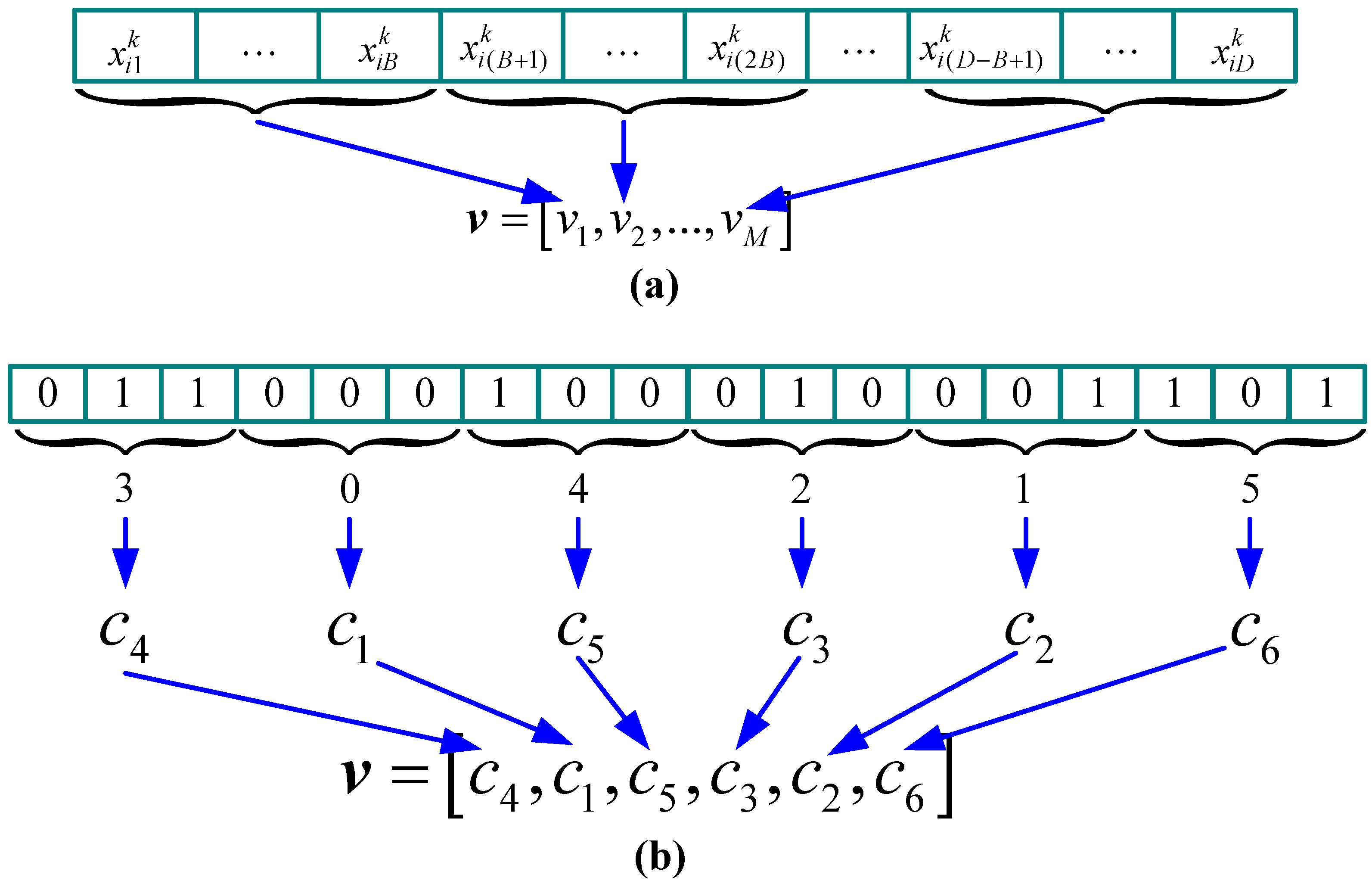
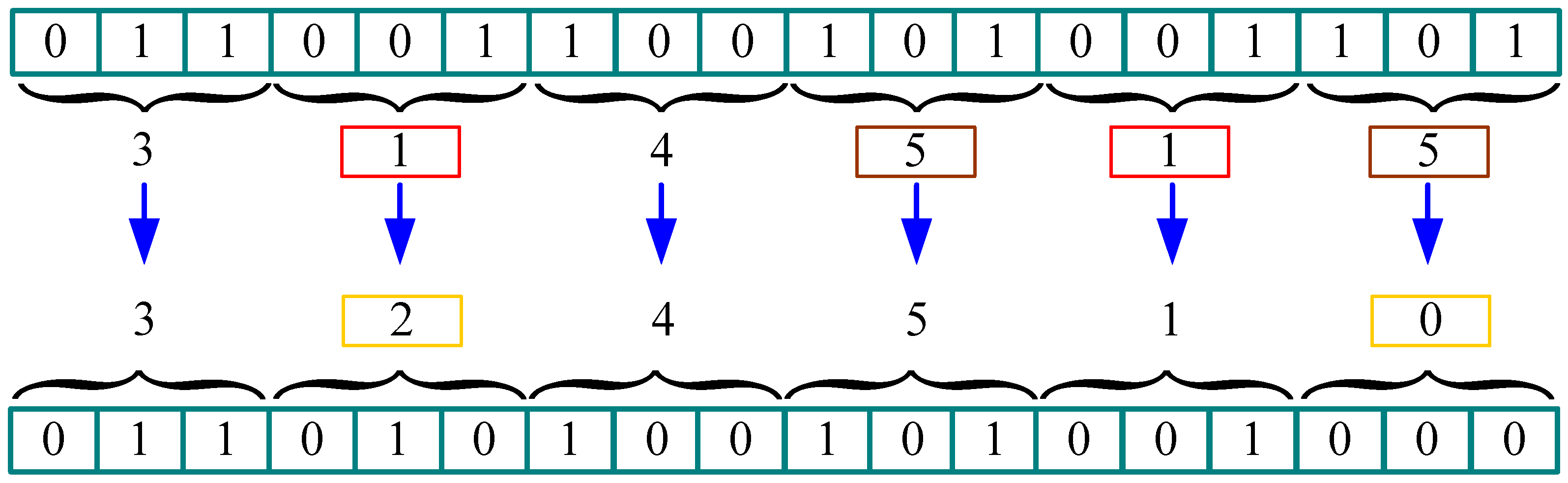
3.2. Proposed PSO Based Algorithm for Target Channel Visiting Order Design
| Steps | Procedures |
|---|---|
| 1 | Swarm initialization. Set k = 0, and randomly generate and , where , , and 1 ≤ i ≤ S. Apply “position correction” procedure to all particles in the swarm. |
| 2 | Fitness evaluation. Compute the fitness value of each particle according to (2). Set and , where g is the index of the particle which has the highest fitness value. |
| 3 | Velocity updating. Set k = k + 1, and update the velocity of the particle according to (6). If , set ; if , set . |
| 4 | Position updating. Update the position of the particle according to (7). Apply “position correction” procedure to all particles in the swarm. |
| 5 | Fitness evaluation. Compute the fitness value of each particle according to (2). For particle i, if it’s fitness value is greater than the fitness value of , then set ; if it’s fitness value is greater than the fitness value of , then set . |
| 6 | Stop criteria evaluation. If k equals to the predefined maximum iteration, the algorithm is terminated; otherwise, go to step 3. |
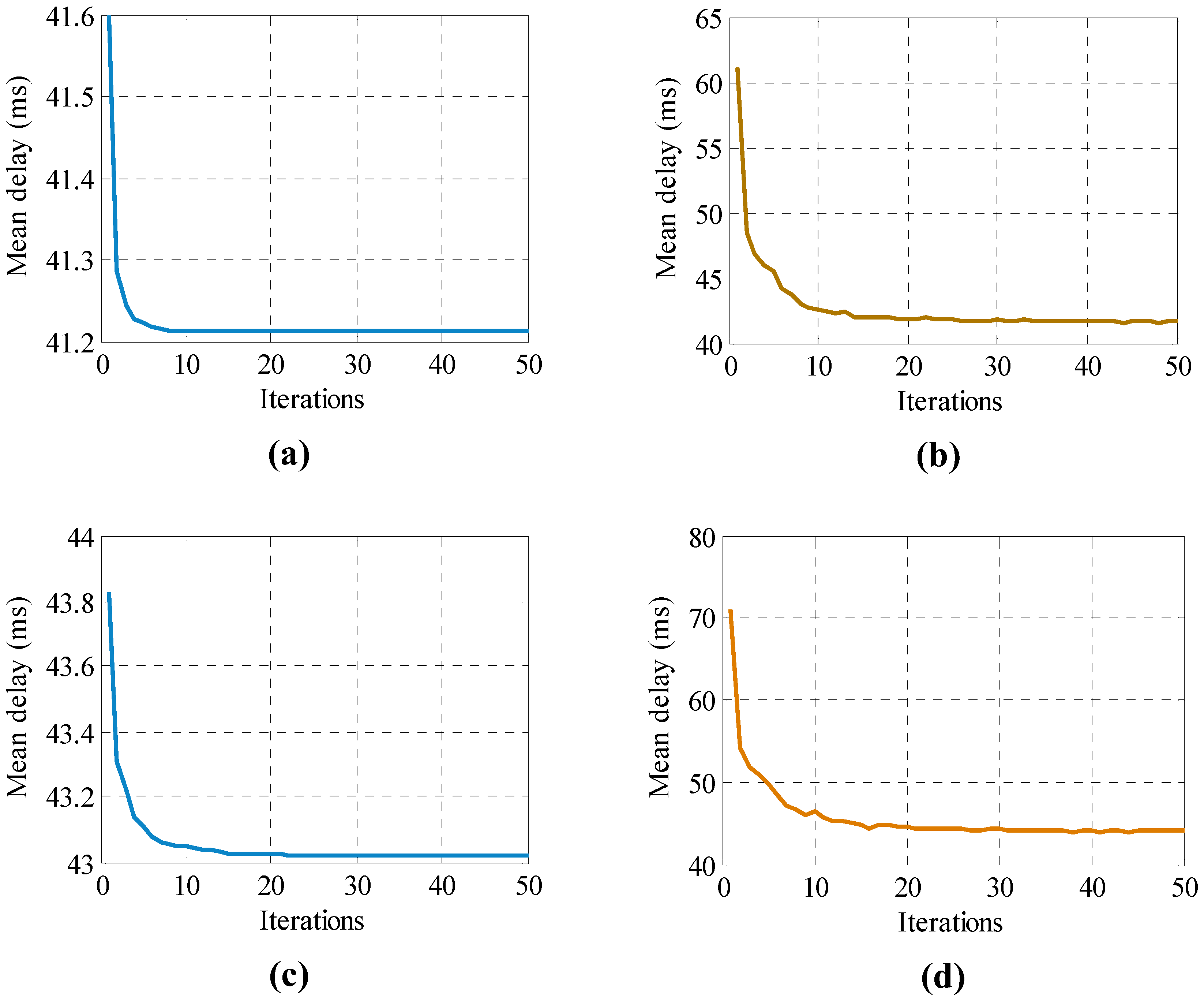
4. Simulation Results
| Distribution | Uniform | Exponential | Pareto | Rayleigh | Weibull | |
|---|---|---|---|---|---|---|
| Mean | Random | 47.1070 | 50.5568 | 43.1053 | 42.9436 | 44.4931 |
| Optimal | 40.4067 | 40.9428 | 40.3052 | 40.0660 | 40.0651 | |
| Proposed10 | 40.4411 | 41.0199 | 40.3109 | 40.0062 | 40.0694 | |
| Proposed50 | 40.4159 | 40.9638 | 40.3063 | 40.0060 | 40.0660 | |
| Standard Deviation | Random | 13.6106 | 16.2251 | 4.8572 | 8.5445 | 11.0222 |
| Proposed10 | 0.0269 | 0.0483 | 0.0048 | 1.2614 × 10−4 | 0.0035 | |
| Proposed50 | 0.0119 | 0.0255 | 0.0011 | 3.0954 × 10−5 | 0.0012 | |
| Distribution | Uniform | Exponential | Pareto | Rayleigh | Weibull | |
|---|---|---|---|---|---|---|
| Mean | Random | 60.8031 | 70.3932 | 46.3667 | 49.4641 | 54.7102 |
| Optimal | 41.2141 | 43.0155 | 40.6554 | 40.0270 | 40.2594 | |
| Proposed10 | 41.2141 | 43.0481 | 40.6614 | 40.0270 | 40.2604 | |
| Proposed50 | 41.2141 | 43.0222 | 40.6568 | 40.0270 | 40.2595 | |
| Standard Deviation | Random | 31.9083 | 35.4822 | 7.3149 | 22.8160 | 27.3215 |
| Proposed10 | 7.1776 × 10−15 | 0.0449 | 0.0061 | 1.9842 × 10−5 | 0.0021 | |
| Proposed50 | 7.1776 × 10−15 | 0.0125 | 0.0022 | 1.8236 × 10−6 | 3.6255 × 10−4 | |
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Federal Communications Commissions. Spectrum Policy Task Force Report; ET Docket No. 02-135; Federal Communications Commissions: Washington, DC, USA, 2002.
- Mitola, J. Cognitive radio for flexible mobile multimedia communications. In Proceedings of the 6th International Workshop on Mobile Multimedia Communications, San Diego, CA, USA, 15–17 November 1999; pp. 3–10.
- Akyildiz, I.F.; Lee, W.-Y.; Vuran, M.C.; Mohanty, S. Next generation/dynamic spectrum access/cognitive radio wireless networks: A survey. Comput. Netw. 2006, 50, 2127–2159. [Google Scholar] [CrossRef]
- Wang, L.-C.; Wang, C.-W.; Chang, C.-J. Optimal target channel sequence design for multiple spectrum handoffs in cognitive radio networks. IEEE Trans. Commun. 2012, 60, 2444–2455. [Google Scholar] [CrossRef]
- Kim, H.; Shin, K.G. Efficient discovery of spectrum opportunities with MAC-layer sensing in cognitive radio networks. IEEE Trans. Mob. Comput. 2008, 7, 533–545. [Google Scholar]
- Jiang, H.; Lai, L.; Fan, R.; Poor, H.V. Optimal selection of channel sensing order in cognitive radio. IEEE Trans. Wirel. Commun. 2009, 8, 297–307. [Google Scholar] [CrossRef]
- Wu, C.; He, C.; Jiang, L. Spectrum handoff scheme based on recommended channel sensing sequence. China Commun. 2013, 10, 18–26. [Google Scholar]
- Yoon, S.-U.; Ekici, E. Voluntary spectrum handoff: A novel approach to spectrum management in CRNs. In Proceedings of 2010 IEEE International Conference on Communications (ICC), Cape Town, South Africa, 23–27 May 2010; pp. 1–5.
- Zhang, W.; Yeo, C.K. Sequential sensing based spectrum handoff in cognitive radio networks with multiple users. Comput. Netw. 2014, 58, 87–98. [Google Scholar] [CrossRef]
- Song, Y.; Xie, J. ProSpect: A proactive spectrum handoff framework for cognitive radio ad hoc networks without common control channel. IEEE Trans. Mob. Comput. 2012, 11, 1127–1139. [Google Scholar] [CrossRef]
- Oo, T.Z.; Hong, C.S.; Lee, S. Alternating renewal framework for estimation in spectrum sensing policy and proactive spectrum handoff. In Proceedings of International Conference on Information Networking, Bangkok, Thailand, 28–30 January 2013; pp. 330–335.
- Zheng, S.; Yang, X.; Chen, S.; Lou, C. Target channel sequence selection scheme for proactive-decision spectrum handoff. IEEE Commun. Lett. 2011, 15, 1332–1334. [Google Scholar] [CrossRef]
- Zhao, Z.; Peng, Z.; Zheng, S.; Shang, J. Cognitive radio spectrum allocation using evolutionary algorithms. IEEE Trans. Wirel. Commun. 2009, 8, 4421–4425. [Google Scholar] [CrossRef]
- Zhao, Z.; Xu, S.; Zheng, S.; Shang, J. Cognitive radio adaptation using particle swarm optimization. Wirel. Commun. Mob. Comput. 2009, 9, 875–881. [Google Scholar] [CrossRef]
- Zheng, S.; Lou, C.; Yang, X. Cooperative spectrum sensing using particle swarm optimization. Electron. Lett. 2010, 46, 1525–1526. [Google Scholar] [CrossRef]
- Wang, L.-C.; Wang, C.-W.; Chang, C.-J. Modeling and analysis for spectrum handoff in cognitive radio networks. IEEE Trans. Mob. Comput. 2012, 11, 1499–1513. [Google Scholar] [CrossRef]
- Zhou, X.; Li, Y.; Kwon, Y.H.; Soong, A.C.K. Detection timing and channel selection for periodic spectrum sensing in cognitive radio. In Proceedings of IEEE Global Telecommunications Conference, New Orleans, LO, USA, 30 November–4 December 2008; pp. 1–5.
- Geirhofer, S.; Tong, L.; Sadler, B.M. A measurement-based model for dynamic spectrum access in WLAN channels. In Proceedings of IEEE Military Conference, Washington, DC, USA, 23–25 October 2006; pp. 1–7.
- Pawelczak, P.; Pollin, S.; So, H.-S.; Motamedi, A.; Bahai, A.; Prasad, R.V.; Hekmat, R. State of the art in opportunistic spectrum access medium access control design. In Proceedings of 3rd International Conference on Cognitive Radio Oriented Wireless Networks and Communications, Singapore, 15–17 May 2008; pp. 1–6.
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of IEEE International Conference on Neural Networks, Perth, Australia, 27 November–01 December 1995; pp. 1942–1948.
- Kennedy, J.; Eberhart, R. A discrete binary version of the particle swarm algorithm. In Proceedings of the Conference on Systems, Man, and Cybernetics, Orlando, FL, USA, 12–15 October 1997; pp. 4104–4109.
- Yang, X.S.; Deb, S. Engineering optimisation by cuckoo search. Int. J. Math. Model. Numer. Optim. 2010, 1, 330–343. [Google Scholar] [CrossRef]
- Yang, X.S.; Gandomi, A.H. Bat algorithm: A novel approach for global engineering optimization. Eng. Comput. 2012, 29, 464–483. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Zheng, S.; Zhao, Z.; Luo, C.; Yang, X. Target Channel Visiting Order Design Using Particle Swarm Optimization for Spectrum Handoff in Cognitive Radio Networks. Algorithms 2014, 7, 418-428. https://doi.org/10.3390/a7030418
Zheng S, Zhao Z, Luo C, Yang X. Target Channel Visiting Order Design Using Particle Swarm Optimization for Spectrum Handoff in Cognitive Radio Networks. Algorithms. 2014; 7(3):418-428. https://doi.org/10.3390/a7030418
Chicago/Turabian StyleZheng, Shilian, Zhijin Zhao, Changlin Luo, and Xiaoniu Yang. 2014. "Target Channel Visiting Order Design Using Particle Swarm Optimization for Spectrum Handoff in Cognitive Radio Networks" Algorithms 7, no. 3: 418-428. https://doi.org/10.3390/a7030418




