Tensor Completion Based on Triple Tubal Nuclear Norm
Abstract
:1. Introduction
2. Notations and Preliminaries
2.1. Notations
2.2. Tensor Singular Value Decomposition
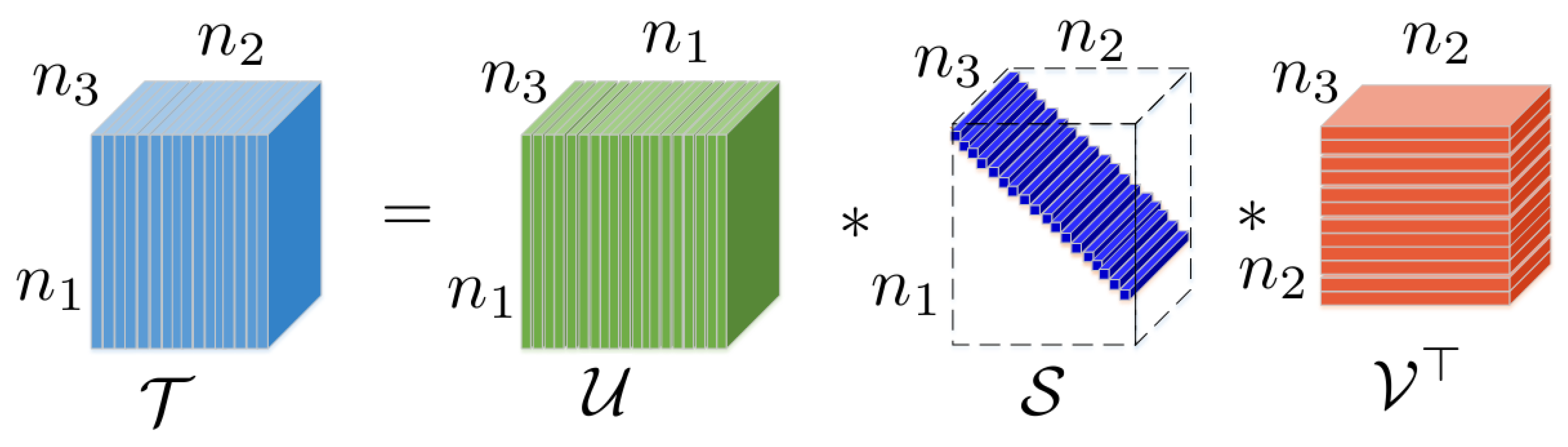
3. The Triple Tubal Nuclear Norm
3.1. Tubal Nuclear Norm
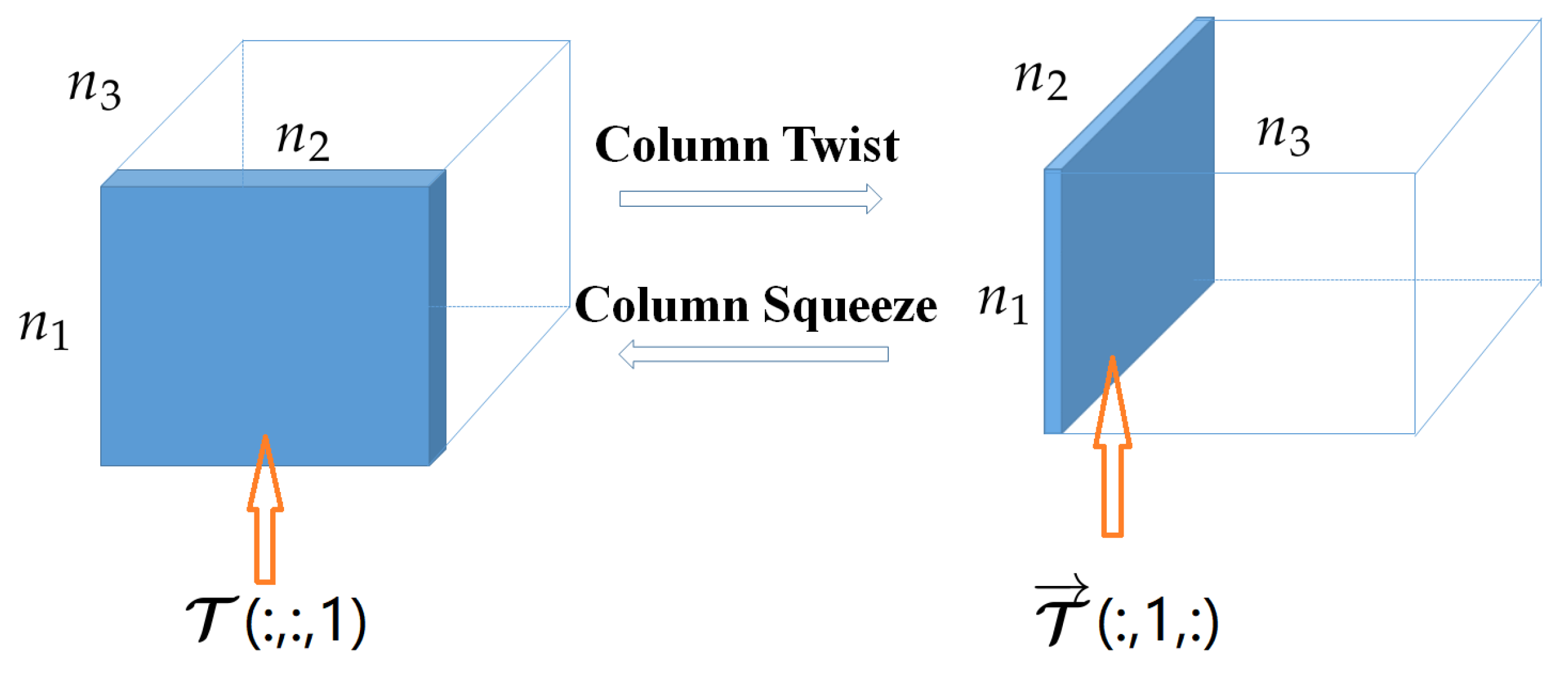
3.2. Twist Tubal Nuclear Norm
3.3. A Circular Interpretation of TNN and t-TNN
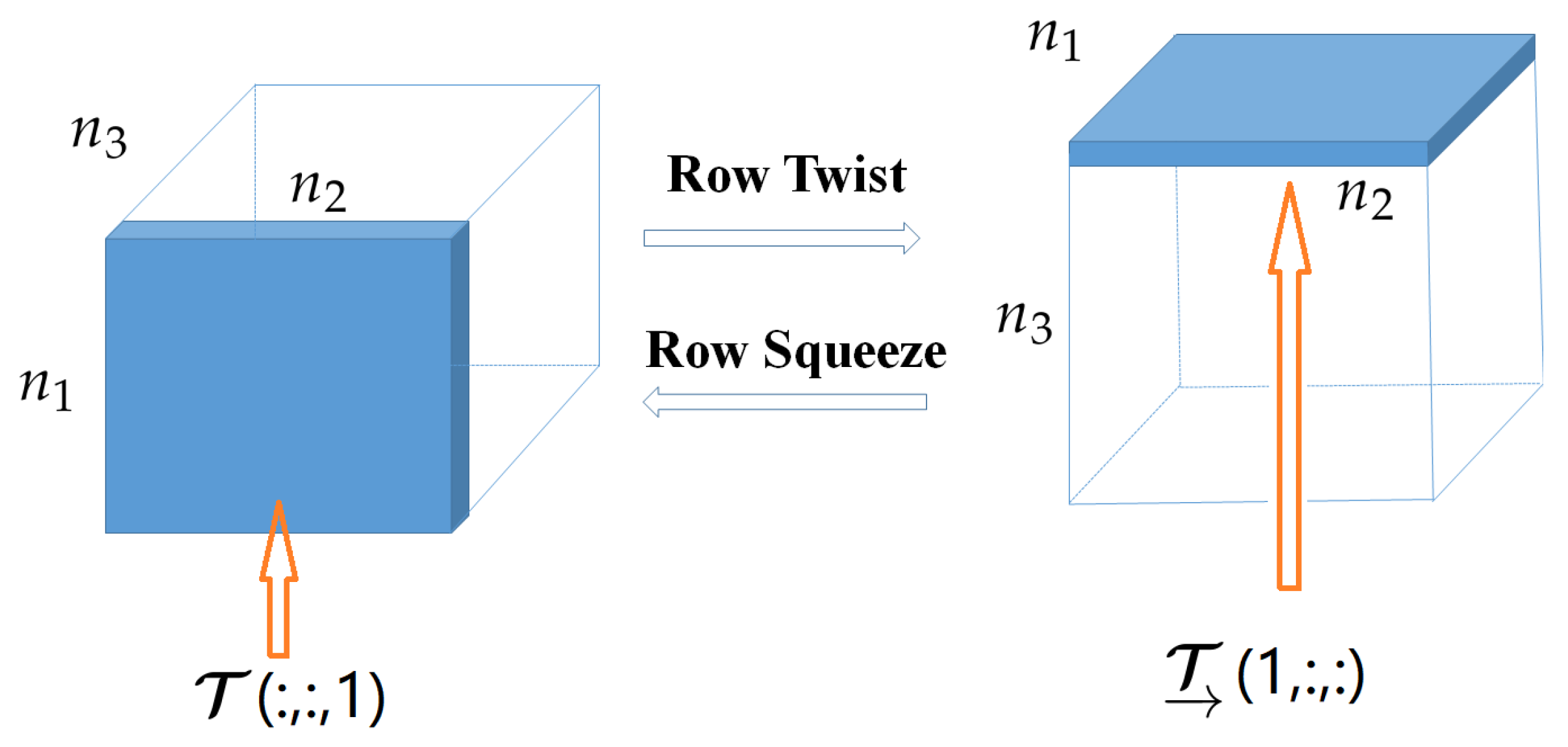
3.4. The Proposed Row Twist Tubal Nuclear Norm and Triple Tubal Nuclear Norm
4. TriTNN-Based Tensor Completion
4.1. Problem Formulation
4.2. An ADMM Solver to Problem (21)
| Algorithm 1 Solving Problem (21) using ADMM. |
| Input: The observed tensor , the parameters . |
| Output:. |
4.3. Convergence of Algorithm 1
4.4. Differences from Prior Work
5. Experiments
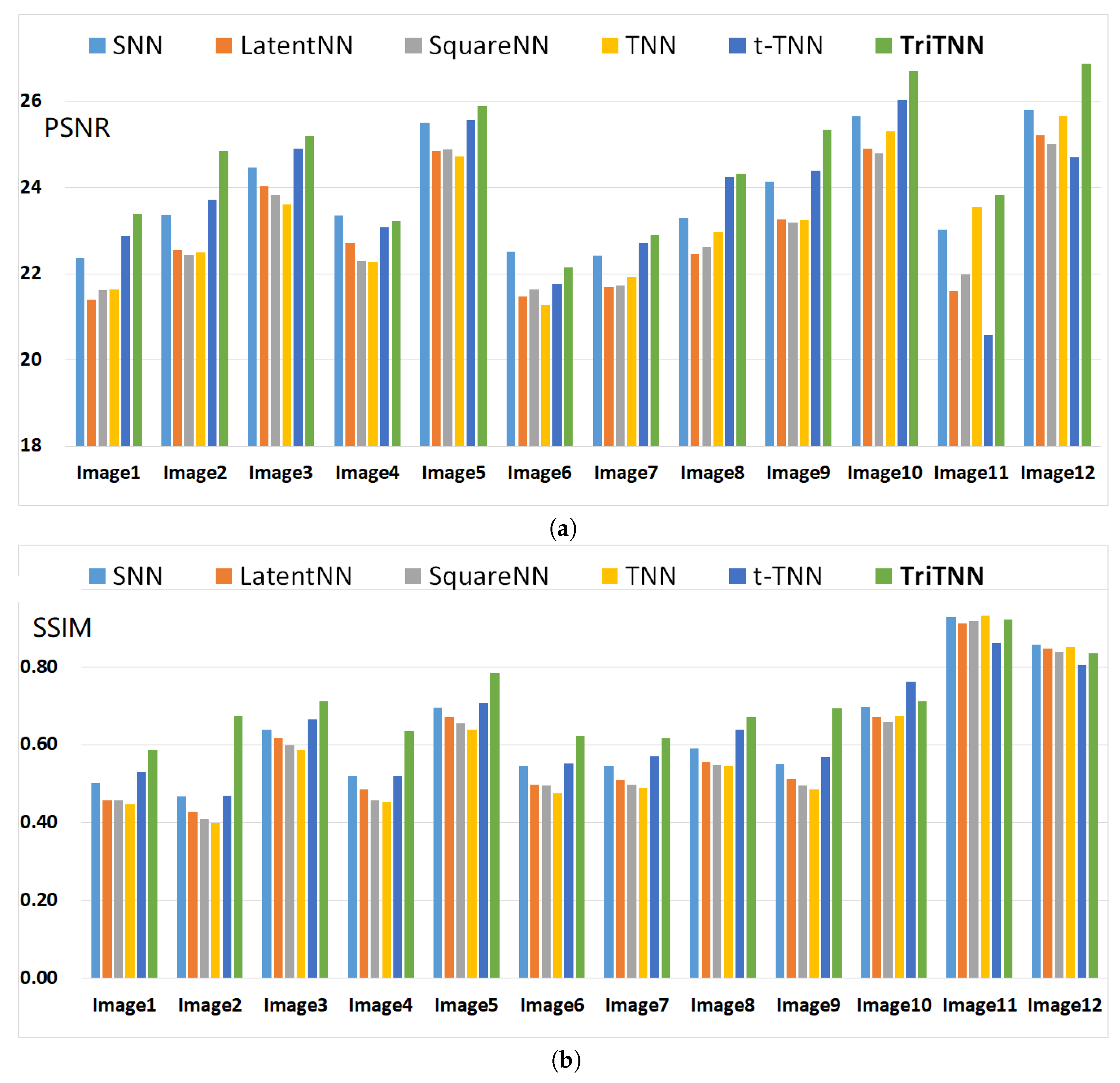
- The tensor nuclear norm-based model with ADMM solver: high accuracy low-rank tensor completion (HaLRTC, denoted by SNNin this paper) (code available: http://www.cs.rochester.edu/u/jliu/publications.html) [2], The tensor nuclear norm is defined as the weighted sum of nuclear norms of the unfolding matrices along each mode (thus, we denote this model as SNN):where , are positive parameters and , , is the unfolding matrix of tensor along the i-th mode [2].
- The latent tensor nuclear norm-based model (LatentNN) (code available: https://github.com/ryotat/tensor) [21]. The latent tensor nuclear norm is defined as:where and are the first-mode, second-mode and third-mode unfoldings of latent tensors and , respectively.
- The square nuclear norm-based model (SquareNN) (code available: https://sites.google.com/site/mucun1988/publi) [23]. The square nuclear norm of a tensor is defined as the nuclear norm of the most balanced unfolding of a tensor (see [7,23]).
- The most related tubal nuclear norm-based model (TNN) (code available: https://github.com/jamiezeminzhang/) [30] and the twist tubal nuclear norm-based model (t-TNN) [16].
5.1. Color Image Inpainting
5.2. Video Inpainting
5.3. A Dataset for Autonomous Driving
6. Conclusions
- Computational inefficiency: Compared to TNN and t-TNN, it is more time-consuming since it involves computing TNN, t-TNN and rt-TNN (see Equation (18)).
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Kilmer, M.E.; Braman, K.; Hao, N.; Hoover, R.C. Third-order tensors as operators on matrices: A theoretical and computational framework with applications in imaging. SIAM J. Matrix Anal. Appl. 2013, 34, 148–172. [Google Scholar] [CrossRef]
- Liu, J.; Musialski, P.; Wonka, P.; Ye, J. Tensor completion for estimating missing values in visual data. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 208–220. [Google Scholar] [CrossRef] [PubMed]
- Wang, A.; Jin, Z. Near-optimal Noisy Low-tubal-rank Tensor Completion via Singular Tube Thresholding. In Proceedings of the IEEE International Conference on Data Mining Workshop (ICDMW), New Orleans, LA, USA, 18–21 November 2017; pp. 553–560. [Google Scholar]
- Signoretto, M.; Dinh, Q.T.; Lathauwer, L.D.; Suykens, J.A.K. Learning with tensors: a framework based on convex optimization and spectral regularization. Mach. Learn. 2014, 94, 303–351. [Google Scholar] [CrossRef]
- Cichocki, A.; Mandic, D.; De Lathauwer, L.; Zhou, G.; Zhao, Q.; Caiafa, C.; Phan, H.A. Tensor decompositions for signal processing applications: From two-way to multiway component analysis. IEEE Signal Process. Mag. 2015, 32, 145–163. [Google Scholar] [CrossRef]
- Lu, C.; Feng, J.; Chen, Y.; Liu, W.; Lin, Z.; Yan, S. Tensor Robust Principal Component Analysis: Exact Recovery of Corrupted Low-Rank Tensors via Convex Optimization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 5249–5257. [Google Scholar]
- Wei, D.; Wang, A.; Wang, B.; Feng, X. Tensor Completion Using Spectral (k, p) -Support Norm. IEEE Access 2018, 6, 11559–11572. [Google Scholar] [CrossRef]
- Liu, Y.; Shang, F. An Efficient Matrix Factorization Method for Tensor Completion. IEEE Signal Process. Lett. 2013, 20, 307–310. [Google Scholar] [CrossRef]
- Song, X.; Lu, H. Multilinear Regression for Embedded Feature Selection with Application to fMRI Analysis. In Proceedings of the AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; pp. 2562–2568. [Google Scholar]
- Tan, H.; Feng, G.; Feng, J.; Wang, W.; Zhang, Y.J.; Li, F. A tensor-based method for missing traffic data completion. Transp. Res. Part C 2013, 28, 15–27. [Google Scholar] [CrossRef]
- Zhao, Q.; Zhang, L.; Cichocki, A. Bayesian CP Factorization of Incomplete Tensors with Automatic Rank Determination. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 1751–1763. [Google Scholar] [CrossRef] [PubMed]
- Cichocki, A.; Lee, N.; Oseledets, I.; Phan, A.H.; Zhao, Q.; Mandic, D.P. Tensor Networks for Dimensionality Reduction and Large-scale Optimization: Part 1 Low-Rank Tensor Decompositions. Found. Trends Mach. Learn. 2016, 9, 249–429. [Google Scholar] [CrossRef] [Green Version]
- Harshman, R.A. Foundations of the PARAFAC Procedure: Models and Conditions for an “Explanatory” Multi-Modal Factor Analysis; University of California: Los Angeles, CA, USA, 1970. [Google Scholar]
- Kolda, T.G.; Bader, B.W. Tensor decompositions and applications. SIAM Rev. 2009, 51, 455–500. [Google Scholar] [CrossRef]
- Tucker, L.R. Some mathematical notes on three-mode factor analysis. Psychometrika 1966, 31, 279–311. [Google Scholar] [CrossRef] [PubMed]
- Hu, W.; Tao, D.; Zhang, W. The twist tensor nuclear norm for video completion. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 2961–2973. [Google Scholar] [CrossRef] [PubMed]
- Yuan, M.; Zhang, C.H. Incoherent Tensor Norms and Their Applications in Higher Order Tensor Completion. IEEE Trans. Inf. Theory 2017, 63, 6753–6766. [Google Scholar] [CrossRef] [Green Version]
- Song, Q.; Ge, H.; Caverlee, J.; Hu, X. Tensor Completion Algorithms in Big Data Analytics. arXiv, 2017; arXiv:1711.10105. [Google Scholar]
- Candès, E.J.; Tao, T. The power of convex relaxation: near-optimal matrix completion. IEEE Trans. Inf. Theory 2010, 56, 2053–2080. [Google Scholar] [CrossRef]
- Hillar, C.J.; Lim, L. Most Tensor Problems Are NP-Hard. J. ACM 2009, 60, 45. [Google Scholar] [CrossRef]
- Tomioka, R.; Suzuki, T. Convex tensor decomposition via structured schatten norm regularization. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 5–10 December 2013; pp. 1331–1339. [Google Scholar]
- Semerci, O.; Hao, N.; Kilmer, M.E.; Miller, E.L. Tensor-Based Formulation and Nuclear Norm Regularization for Multienergy Computed Tomography. IEEE Trans. Image Process. 2014, 23, 1678–1693. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mu, C.; Huang, B.; Wright, J.; Goldfarb, D. Square Deal: Lower Bounds and Improved Relaxations for Tensor Recovery. In Proceedings of the International Conference on Machine Learning, Beijing, China, 21–26 June 2014; pp. 73–81. [Google Scholar]
- Zhao, Q.; Meng, D.; Kong, X.; Xie, Q.; Cao, W.; Wang, Y.; Xu, Z. A Novel Sparsity Measure for Tensor Recovery. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 271–279. [Google Scholar]
- Tomioka, R.; Hayashi, K.; Kashima, H. Estimation of low-rank tensors via convex optimization. arXiv, 2010; arXiv:1010.0789. [Google Scholar]
- Chretien, S.; Wei, T. Sensing tensors with Gaussian filters. IEEE Trans. Inf. Theory 2017, 63, 843–852. [Google Scholar] [CrossRef]
- Ghadermarzy, N.; Plan, Y.; Yılmaz, Ö. Near-optimal sample complexity for convex tensor completion. arXiv, 2017; arXiv:1711.04965. [Google Scholar]
- Ghadermarzy, N.; Plan, Y.; Yılmaz, Ö. Learning tensors from partial binary measurements. arXiv, 2018; arXiv:1804.00108. [Google Scholar]
- Liu, Y.; Shang, F.; Fan, W.; Cheng, J.; Cheng, H. Generalized Higher-Order Orthogonal Iteration for Tensor Decomposition and Completion. In Proceedings of the Advances in Neural Information Processing Systems, Palais des Congrès de Montréal, Montréal, Canada, 8–13 December 2014; pp. 1763–1771. [Google Scholar]
- Zhang, Z.; Ely, G.; Aeron, S.; Hao, N.; Kilmer, M. Novel methods for multilinear data completion and de-noising based on tensor-SVD. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 3842–3849. [Google Scholar]
- Zhang, Z.; Aeron, S. Exact Tensor Completion Using t-SVD. IEEE Trans. Signal Process. 2017, 65, 1511–1526. [Google Scholar] [CrossRef]
- Sun, W.; Chen, Y.; Huang, L.; So, H.C. Tensor Completion via Generalized Tensor Tubal Rank Minimization using General Unfolding. IEEE Signal Process. Lett. 2018. [Google Scholar] [CrossRef]
- Zhou, P.; Lu, C.; Lin, Z.; Zhang, C. Tensor Factorization for Low-Rank Tensor Completion. IEEE Trans. Image Process. 2018, 27, 1152–1163. [Google Scholar] [CrossRef] [PubMed]
- Ely, G.T.; Aeron, S.; Hao, N.; Kilmer, M.E. 5D seismic data completion and denoising using a novel class of tensor decompositions. Geophysics 2015, 80, V83–V95. [Google Scholar] [CrossRef]
- Liu, X.; Aeron, S.; Aggarwal, V.; Wang, X.; Wu, M. Adaptive Sampling of RF Fingerprints for Fine-grained Indoor Localization. IEEE Trans. Mob. Comput. 2016, 15, 2411–2423. [Google Scholar] [CrossRef]
- Jiang, J.Q.; Ng, M.K. Exact Tensor Completion from Sparsely Corrupted Observations via Convex Optimization. arXiv, 2017; arXiv:1708.00601. [Google Scholar]
- Liu, X.Y.; Aeron, S.; Aggarwal, V.; Wang, X. Low-tubal-rank tensor completion using alternating minimization. arXiv, 2016; arXiv:1610.01690. [Google Scholar]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends Mach. Learn. 2011, 3, 1–122. [Google Scholar] [CrossRef]
- Zhou, P.; Feng, J. Outlier-Robust Tensor PCA. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Cai, J.F.; Candès, E.J.; Shen, Z. A singular value thresholding algorithm for matrix completion. SIAM J. Opt. 2010, 20, 1956–1982. [Google Scholar] [CrossRef]
- Gleich, D.F.; Greif, C.; Varah, J.M. The power and Arnoldi methods in an algebra of circulants. Numer. Linear Algebra Appl. 2013, 20, 809–831. [Google Scholar] [CrossRef]
- Granata, J.; Conner, M.; Tolimieri, R. The tensor product: a mathematical programming language for FFTs and other fast DSP operations. IEEE Signal Process. Mag. 1992, 9, 40–48. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: from error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Oymak, S.; Jalali, A.; Fazel, M.; Eldar, Y.C.; Hassibi, B. Simultaneously structured models with application to sparse and low-rank matrices. IEEE Trans. Inf. Theory 2015, 61, 2886–2908. [Google Scholar] [CrossRef]
- Mu, C.; Zhang, Y.; Wright, J.; Goldfarb, D. Scalable Robust Matrix Recovery: Frank-Wolfe Meets Proximal Methods. SIAM J. Sci. Comput. 2016, 38, A3291–A3317. [Google Scholar] [CrossRef]
- Richard, E.; Obozinski, G.R.; Vert, J.P. Tight convex relaxations for sparse matrix factorization. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; pp. 3284–3292. [Google Scholar]
- Yokota, T.; Zhao, Q.; Cichocki, A. Smooth PARAFAC Decomposition for Tensor Completion. IEEE Trans. Signal Process. 2016, 64, 5423–5436. [Google Scholar] [CrossRef]
- Chen, Y.L.; Hsu, C.T.; Liao, H.Y.M. Simultaneous Tensor Decomposition and Completion Using Factor Priors. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 577–591. [Google Scholar] [CrossRef] [PubMed]
- Xutao Li, Y.Y.; Xu, X. Low-Rank Tensor Completion with Total Variation for Visual Data Inpainting. In Proceedings of the AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; pp. 2210–2216. [Google Scholar]
- Yokota, T.; Erem, B.; Guler, S.; Warfield, S.K.; Hontani, H. Missing Slice Recovery for Tensors Using a Low-rank Model in Embedded Space. arXiv, 2018; arXiv:1804.01736. [Google Scholar]
- Fan, J.; Cheng, J. Matrix completion by deep matrix factorization. Neural Netw. 2018, 98, 34–41. [Google Scholar] [CrossRef] [PubMed]
- Martin, C.D.; Shafer, R.; Larue, B. An Order-p Tensor Factorization with Applications in Imaging. SIAM J. Sci. Comput. 2013, 35, A474–A490. [Google Scholar] [CrossRef]
- Liu, X.Y.; Wang, X. Fourth-order tensors with multidimensional discrete transforms. arXiv, 2017; arXiv:1705.01576. [Google Scholar]




| Video | SNN [2] | LatentNN [21] | SquareNN [23] | TNN [31] | t-TNN [16] | TriTNN |
|---|---|---|---|---|---|---|
| salesman_qcif | 21.10 | 24.21 | 20.31 | 25.56 | 25.73 | 26.18 |
| silent_qcif | 24.07 | 23.95 | 22.98 | 27.93 | 28.03 | 28.47 |
| suzie_qcif | 25.79 | 24.63 | 24.48 | 27.92 | 29.47 | 29.70 |
| tempete_cif | 19.10 | 18.45 | 19.23 | 20.65 | 21.21 | 21.46 |
| waterfall_cif | 24.10 | 22.39 | 24.06 | 26.71 | 27.44 | 28.22 |
| Sampling Ratio | SNN [2] | LatentNN [21] | SquareNN [23] | TNN [31] | t-TNN [16] | TriTNN |
|---|---|---|---|---|---|---|
| 14.58 | 15.50 | 17.27 | 17.23 | 17.29 | 17.45 | |
| 17.79 | 17.27 | 18.16 | 18.32 | 18.59 | 18.74 | |
| 18.74 | 18.36 | 18.80 | 19.04 | 19.12 | 19.53 | |
| 19.29 | 19.02 | 19.21 | 19.50 | 19.44 | 20.02 | |
| 19.61 | 19.43 | 19.49 | 19.82 | 19.64 | 20.28 | |
| 19.80 | 19.70 | 19.69 | 20.06 | 19.76 | 22.01 | |
| 19.90 | 19.83 | 19.84 | 20.23 | 19.85 | 22.41 |
| Sampling Ratio | SNN [2] | LatentNN [21] | SquareNN [23] | TNN [31] | t-TNN [16] | TriTNN |
|---|---|---|---|---|---|---|
| 17.80 | 16.90 | 17.64 | 19.03 | 18.67 | 18.91 | |
| 19.26 | 18.48 | 18.94 | 20.04 | 19.60 | 20.09 | |
| 20.33 | 19.71 | 19.94 | 20.93 | 20.41 | 21.04 | |
| 21.24 | 20.67 | 20.89 | 21.74 | 21.17 | 21.92 | |
| 22.05 | 21.55 | 21.75 | 22.47 | 21.88 | 22.72 | |
| 22.82 | 22.39 | 22.56 | 23.16 | 22.61 | 23.68 | |
| 23.54 | 23.21 | 23.34 | 23.79 | 23.35 | 24.51 |
| Sampling Ratio | SNN [2] | LatentNN [21] | SquareNN [23] | TNN [31] | t-TNN [16] | TriTNN |
|---|---|---|---|---|---|---|
| 17.30 | 17.63 | 17.57 | 18.31 | 18.62 | 18.36 | |
| 18.79 | 19.30 | 18.92 | 19.50 | 19.61 | 19.63 | |
| 19.85 | 20.29 | 19.93 | 20.38 | 20.37 | 20.45 | |
| 20.84 | 21.11 | 20.90 | 21.24 | 21.08 | 21.30 | |
| 21.72 | 21.86 | 21.76 | 22.05 | 21.78 | 22.18 | |
| 22.51 | 22.62 | 22.53 | 22.79 | 22.50 | 22.94 | |
| 23.39 | 23.40 | 23.39 | 23.59 | 23.27 | 23.80 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, D.; Wang, A.; Feng, X.; Wang, B.; Wang, B. Tensor Completion Based on Triple Tubal Nuclear Norm. Algorithms 2018, 11, 94. https://doi.org/10.3390/a11070094
Wei D, Wang A, Feng X, Wang B, Wang B. Tensor Completion Based on Triple Tubal Nuclear Norm. Algorithms. 2018; 11(7):94. https://doi.org/10.3390/a11070094
Chicago/Turabian StyleWei, Dongxu, Andong Wang, Xiaoqin Feng, Boyu Wang, and Bo Wang. 2018. "Tensor Completion Based on Triple Tubal Nuclear Norm" Algorithms 11, no. 7: 94. https://doi.org/10.3390/a11070094





