The basic idea behind the AVQ algorithm is to subdivide the input image in variable-sized blocks. Each one of these latter blocks is substituted by an index, which represents a pointer to a similar block (according to a given distortion measure), stored into the dictionary. During the encoding, the AVQ algorithm dynamically updates the dictionary D, by adding new blocks to it. The new blocks are derived from the already processed blocks and from the already coded parts of the input data. These new blocks are essential to continue the encoding of the input image, since they can be used for the encoding of the not yet processed parts of the input image.
2.1. Logical Architecture
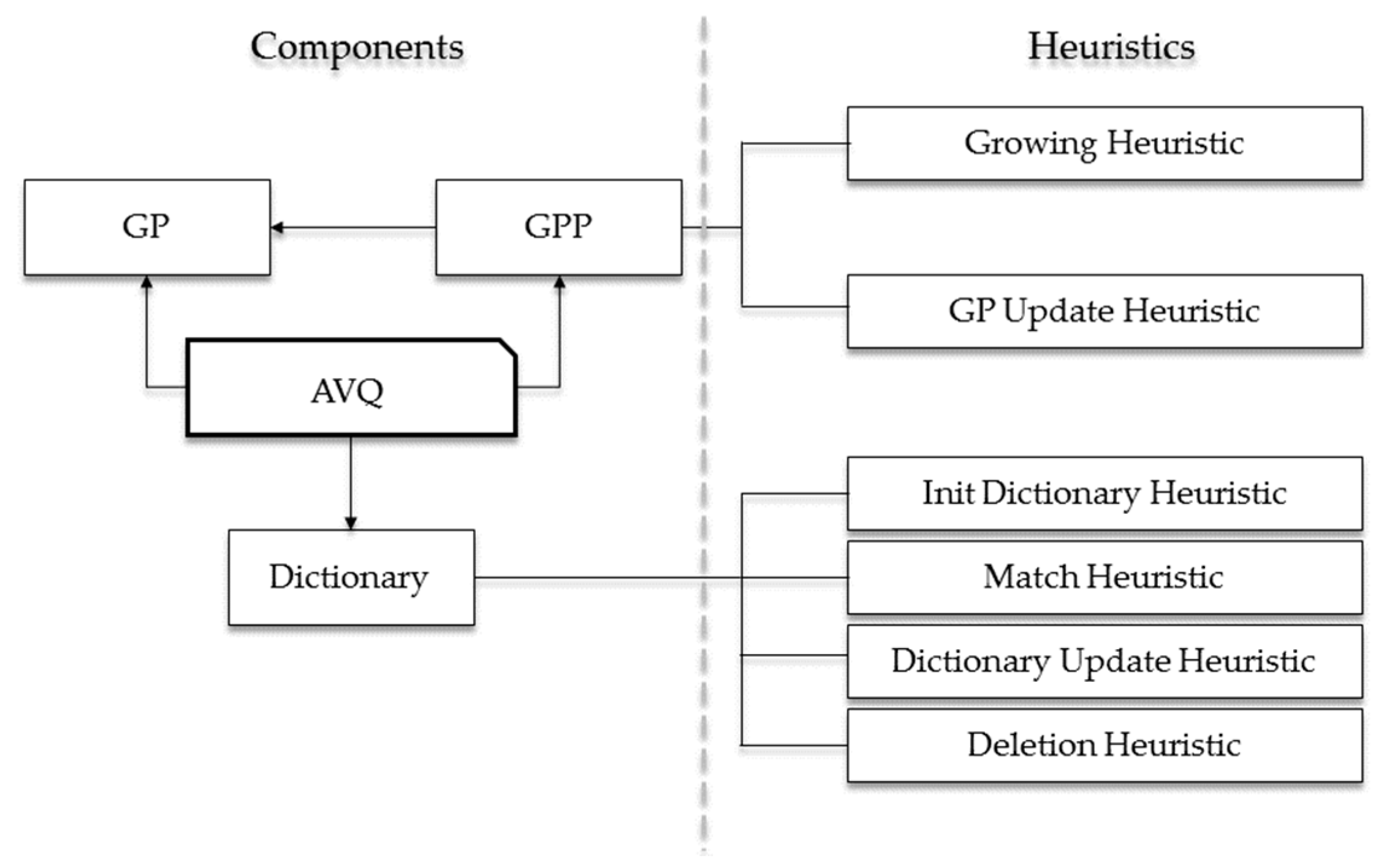
In
Figure 2, we graphically highlight the logical architecture of the AVQ algorithm. As it is noticeable from this figure, the key elements can be subdivided into two distinct categories:
A component is a data structure involved in the compression (or in the decompression) phase of the AVQ algorithm. The main components are the following:
• Growing Points (GPs)
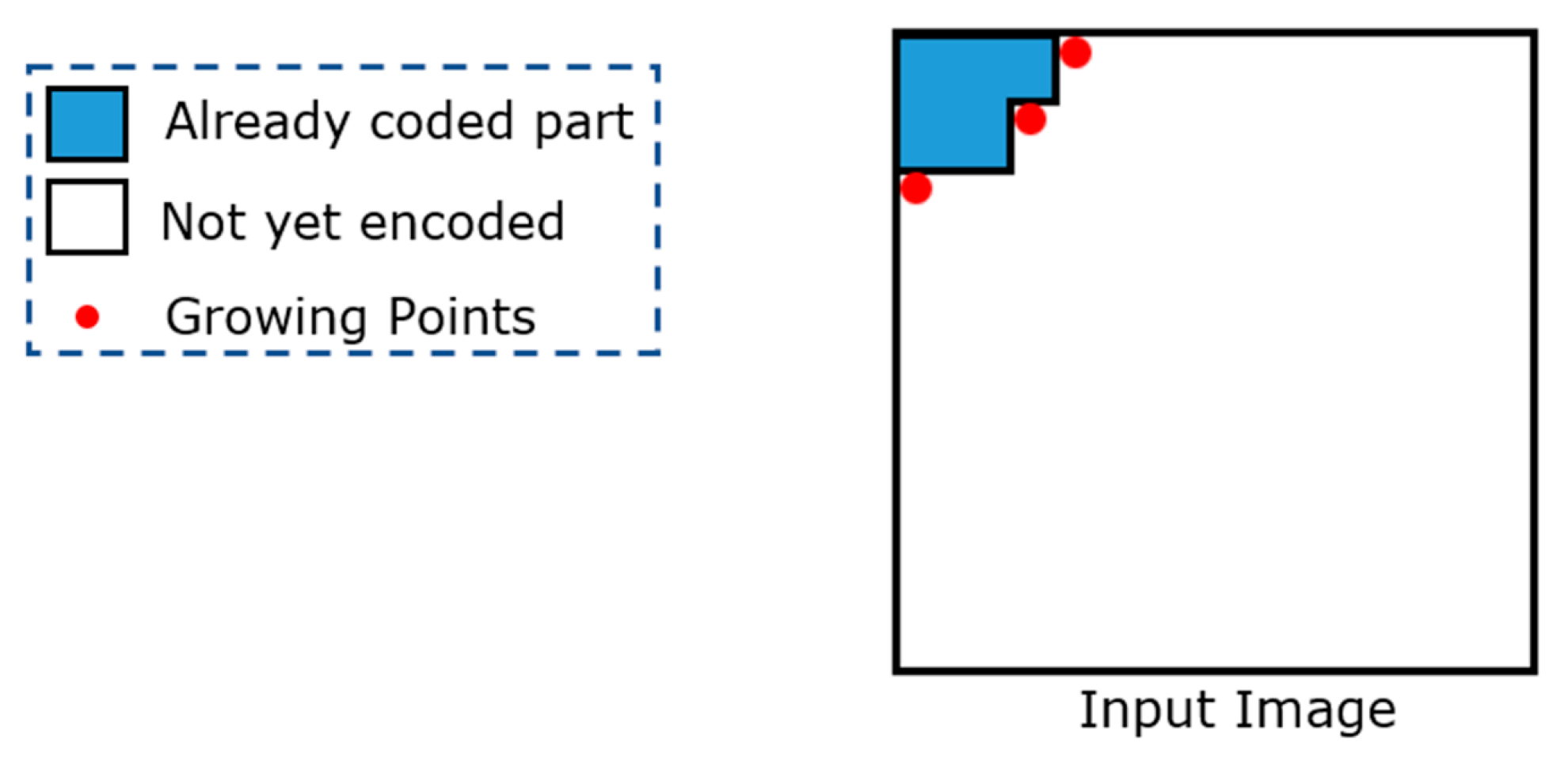
In contrast with one-dimensional data, two-dimensional data can have several uncoded points, from which an encoding algorithm can continue its encoding process. These points are referred to as
growing points (GPs).
Figure 3 shows a graphical example in which three GPs are highlighted in red.
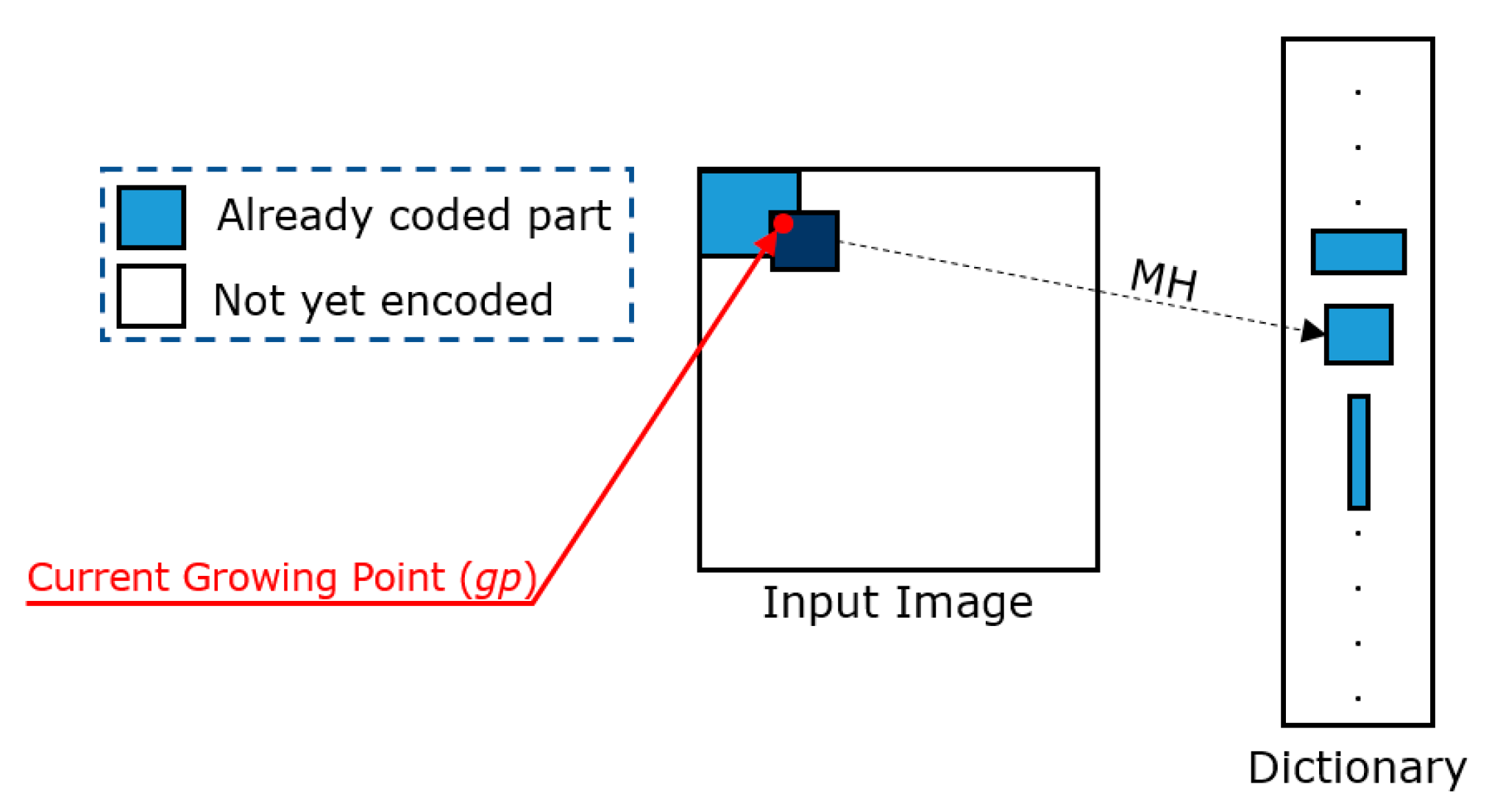
The encoder selects one GP at each step and identifies a match between the block anchored to the selected GP (we denote the selected GP as gp from now on) and a similar block (according to a given distortion measure) contained in the dictionary. Therefore, by using the GPs, the AVQ algorithm can continue its encoding process in a deterministic manner.
• Growing Point Pool (GPP)
A GPP is a data structure in which all the Growing Points (GPs) are maintained.
• Dictionary (D)
All the blocks derived from the already coded parts of the input image are stored in the dictionary. Such blocks are used to find a match with a block (anchored to a GP) in the not yet coded portion of the input image. It should be noted that the dictionary plays an important role for the compression (and the decompression) of the input image.
We can informally define a heuristic as a set of rules that describes the behavior of the AVQ algorithm and its architectural element. Mainly, the heuristics are related to the GPP and the dictionary, and are the following:
• Growing Heuristic (GH)
A GH highlights the behavior related to the identification of the next GP, which will be extracted from the GPP. Such a GP will be the next one that will be processed by the AVQ algorithm. Several strategies can be adopted to define a GH. The ones used in literature are the following:
– Wave Growing Heuristic
The Wave GH selects a GP in which the coordinates,
, satisfies the following relationship:
With this heuristic, the GPP is initialized in this manner: GPP . The point is the pixel at the left top corner. In addition, the image coverage follows perpendicular to the main diagonal by a wavelike trend.
– Diagonal Growing Heuristic
The Diagonal GH selects a GP in which the coordinates,
, which satisfies the following relationship:
In this scenario, the GPP is initialized in the same way of the initialization of the Wave GH and the image coverage follows perpendicular to the main diagonal.
– LIFO Growing Heuristic
A GP is selected from the GPP in Last-In-First-Out (LIFO) order.
• Growing Point Update Heuristic (GPUH)
A GPUH defines the behavior related to the updating of the GPP. Indeed, a GPUH defines the set of adding one or more GP to the GPP.
• Init Dictionary Heuristic (IDH)
An IDH is a set of rules that define in which manner the dictionary, D, will be initialized.
• Match Heuristic (MH)
An MH is used by the AVQ algorithm to identify a match between the block
b, anchored to the GP that is undergoing the process (we referred to as
gp), and a block in the dictionary
D. Generally, a
distance is used (e.g.,
Mean Squared Error - MSE [
9], etc.) to define the similarity between a block in the dictionary and the block anchored to
gp.
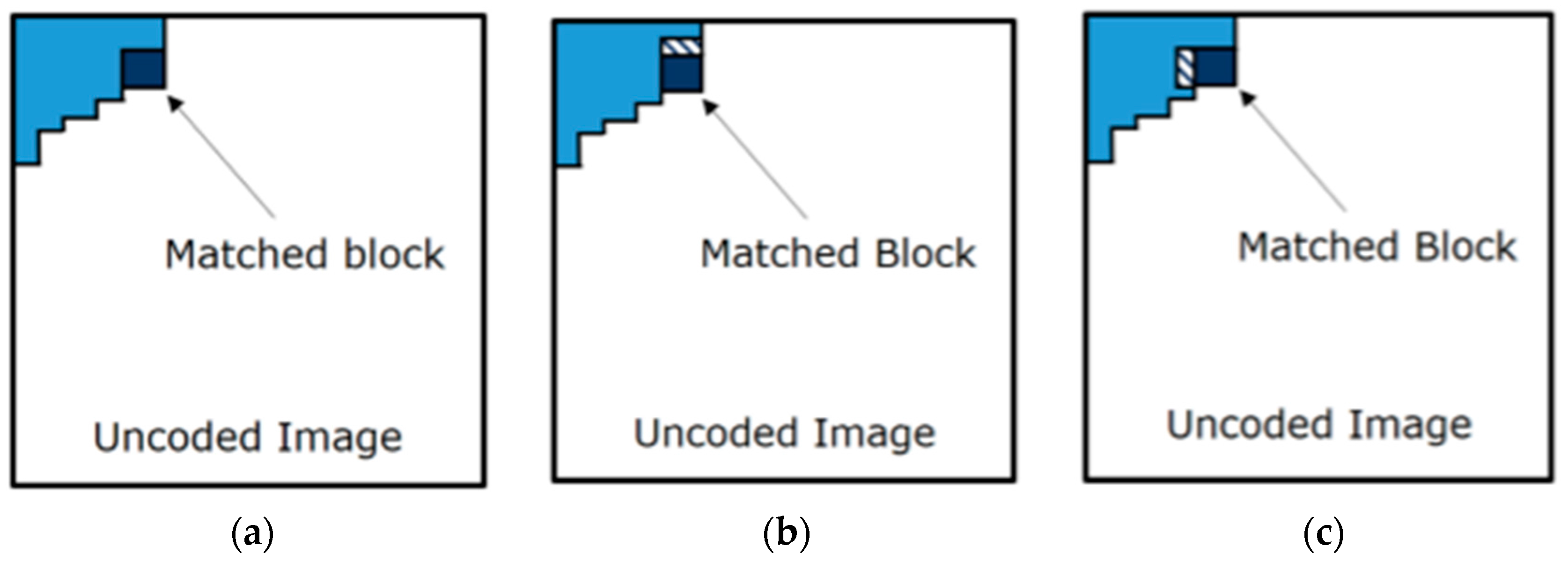
• Dictionary Update Heuristic (DUH)
A DUH is a set of rules that defines which new block(s) can be added to the dictionary
D. Several DUH are explained in literature, as, for instance, the
OneRow + OneColumn DUH (outlined in [
5]). This heuristic adds two new blocks to the dictionary, if possible. The first block and the second block are obtained by adding a row to the matched block, in the already coded part of the image, as shown in
Figure 4.
• Deletion Heuristic (DH)
A DH is used when all of the entries of the dictionary D are used. Such a heuristic defines which blocks in the dictionary should be deleted in order to make space.
2.2. Compression and Decompression Phases
Algorithm 1 highlights the pseudo-code of the AVQ compression phase. Firstly, the dictionary D and the GPP are initialized. The dictionary D is initialized by one entry for each value that a pixel can assume (i.e., in the case of grayscale images, D will be initialized with 256 values, from 0 to 255).
| Algorithm 1. Pseudo-code of the compression stage (AVQ algorithm). |
| 1. | GPP ← Initial GPs (e.g., the at coordinates ) |
| 2. | D ← Use an IDH for the initialization |
| 3. | while GPP has more elements do |
| 4. | Use a GH to identify the next GP |
| 5. | Let gp be the current GP |
| 6. | Use an MH to find a block b in D that matches the sub- block anchored to gp |
| 7. | Transmit bits for the index of b |
| 8. | Update
D with a DUH |
| 9. | if D is full then |
| 10. | Use a DH |
| 11. | endif |
| 12. | By using a GPUH, update the GPP |
| 13. | Remove gp from GPP |
| 14. | end while |
At each step, the AVQ algorithm selects a growing point from the growing point pool GPP (we referred to as gp), according to a specified growing heuristic (GH). The algorithm ends when there are no further selectable growing points (i.e., the GPP is empty).
Subsequently, the encoder uses a match heuristic (MH) to individuate which block, stored in the local dictionary
D, is the best match for the one anchored to
gp (see
Figure 5). In general, the matching heuristics prefer the largest block in
D, which presents a distortion measure that is less than or equal to a threshold
T, when compared with the block anchored to
gp. The threshold
T can be fixed for the whole image or can be dynamically adjusted by considering the image content, in order to improve the quality perception.
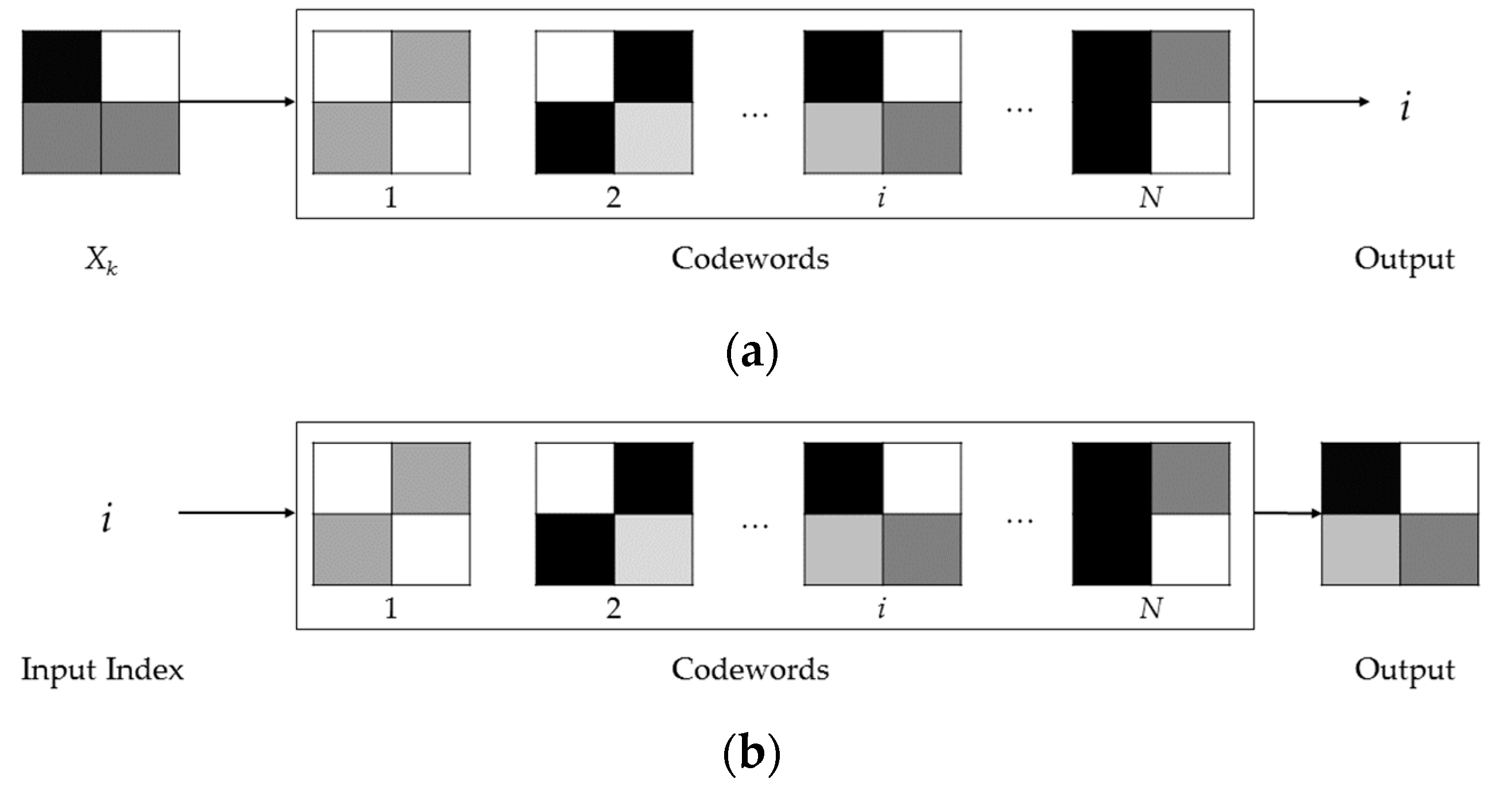
Once the match is performed and a block in D is identified, the index of this block (denoted as b in Algorithm 1) can be stored or transmitted. An index can be represented with bits ( is the size of the dictionary D). After that, the dictionary D is updated, by adding one or more blocks to it. The update is directed by the rules defined by a dictionary update heuristic (DUH). If D is full, a deletion heuristic (DH) is invoked to eventually make space in D.
Finally, the GPP is also updated by using a growing update heuristic (GUH). The processed growing point (i.e., gp) is removed from the GPP. Thus, such a growing point will not be further processed.
It is important to point out that the compression performances are strictly dependent on the number of indexes that will be stored or transmitted by the encoder. Indeed, by considering that each block is represented by its index in the dictionary, more blocks will be necessary to cover the input image, and it will be necessary for more indices to be stored or transmitted. Vice versa, less blocks will be necessary to cover the input image, and it will be necessary for less indices to be stored or transmitted. Consequently, even the dimensions of the matched blocks can influence the compression performances. In fact, the matched blocks with larger dimensions can increase the compression performances, since they cover larger portions of the input image.
Algorithm 2 reports the pseudo-code related to the AVQ decompression phase. Substantially, the pseudo-code is symmetrical, except for the fact that the decompression phase does not need to identify the match, since it receives the indices from the encoder (or reads the indices from a file).
| Algorithm 2. Pseudo-code of the decompression stage (AVQ algorithm). |
| 1. | GPP ← Initial GPs (e.g., the at coordinates ) |
| 2. | D ← Use an IDH for the initialization |
| 3. | while GPP has more elements do |
| 4. | Use a GH to identify the next GP |
| 5. | Let gp be the current GP |
| 7. | Receive bits representing the index of a block b into the dictionary D |
| | Anchor b to the current GP, gp, in order to reconstruct the output image |
| 8. | Update D with a DUH |
| 9. | if D is full then |
| 10. | Use a DH |
| 11. | endif |
| 12. | By using a GPUH, update the GPP |
| 13. | Remove gp from GPP |
| 14. | end while |
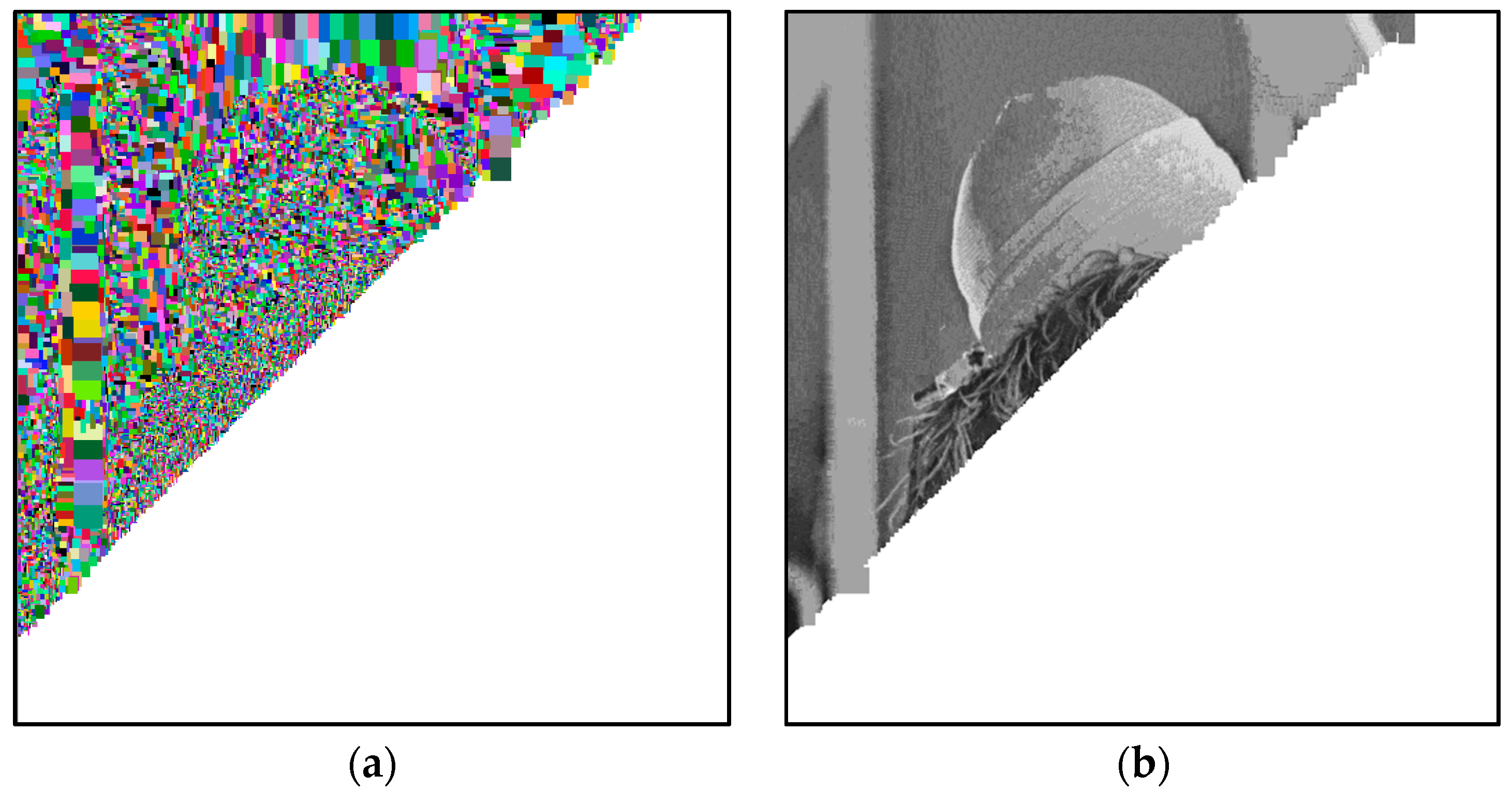
In
Figure 6a, we graphically show, in
false-colors, the progress of Algorithm 1, on the image denoted as
Lena. In detail, each block visually indicates the dimensions of the corresponding block, identified in the dictionary
D. In
Figure 6b, we graphically show the progress of the decompression phase (Algorithm 2).
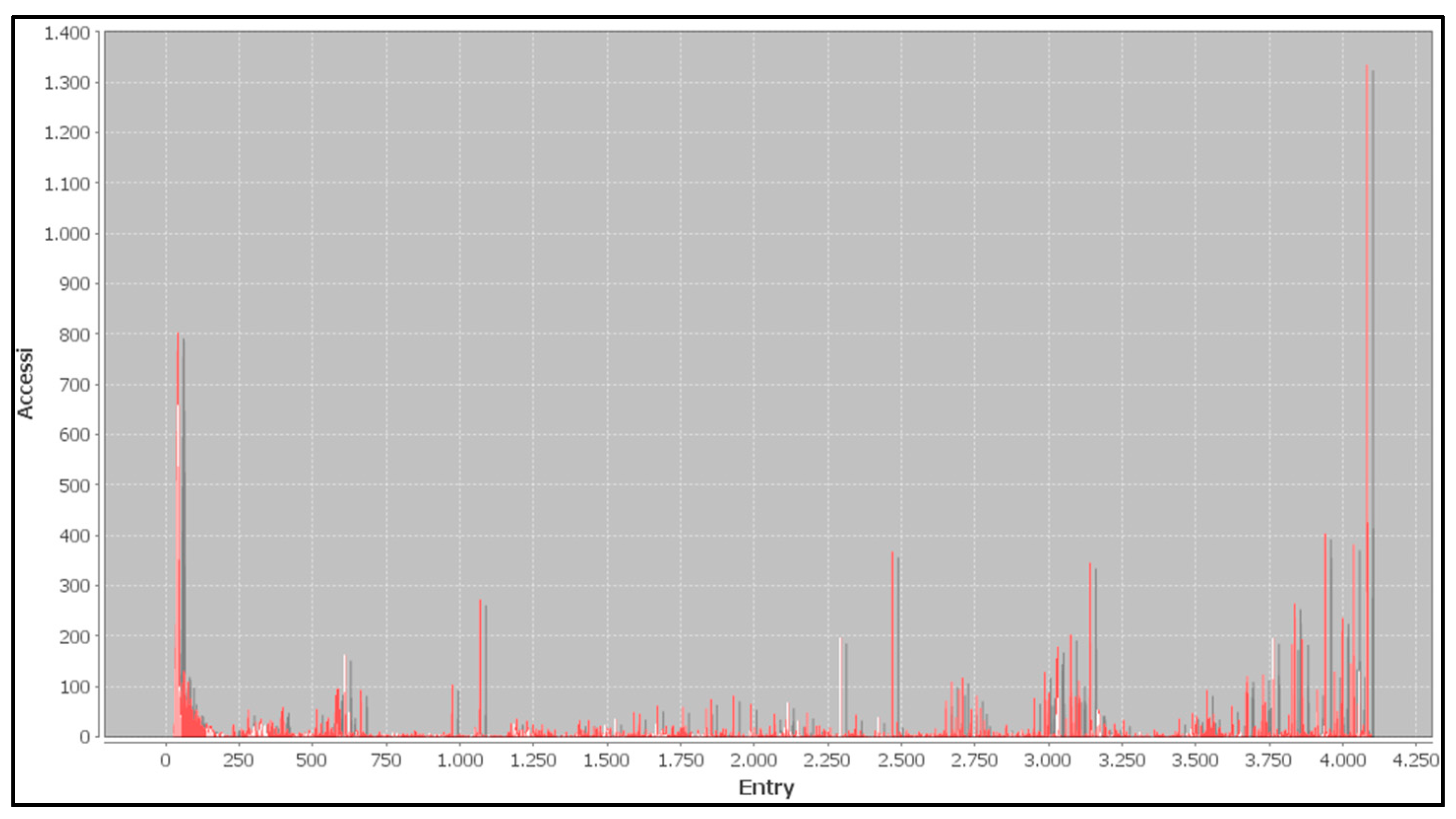
The graph in
Figure 7 shows the number of access (on the
y-axis) to a specific index of the dictionary
D (on the
x-axis), during the compression phase.