Generalized Effective Medium Theory for Particulate Nanocomposite Materials
Abstract
:1. Introduction
2. Framework of the Generalized Effective Medium Theory
2.1. Effective Medium Theory for Composites with Multiple Inclusions
2.2. Effect of Nanometer-Sized Inclusions on Matrix and Inclusion Thermal Conductivities
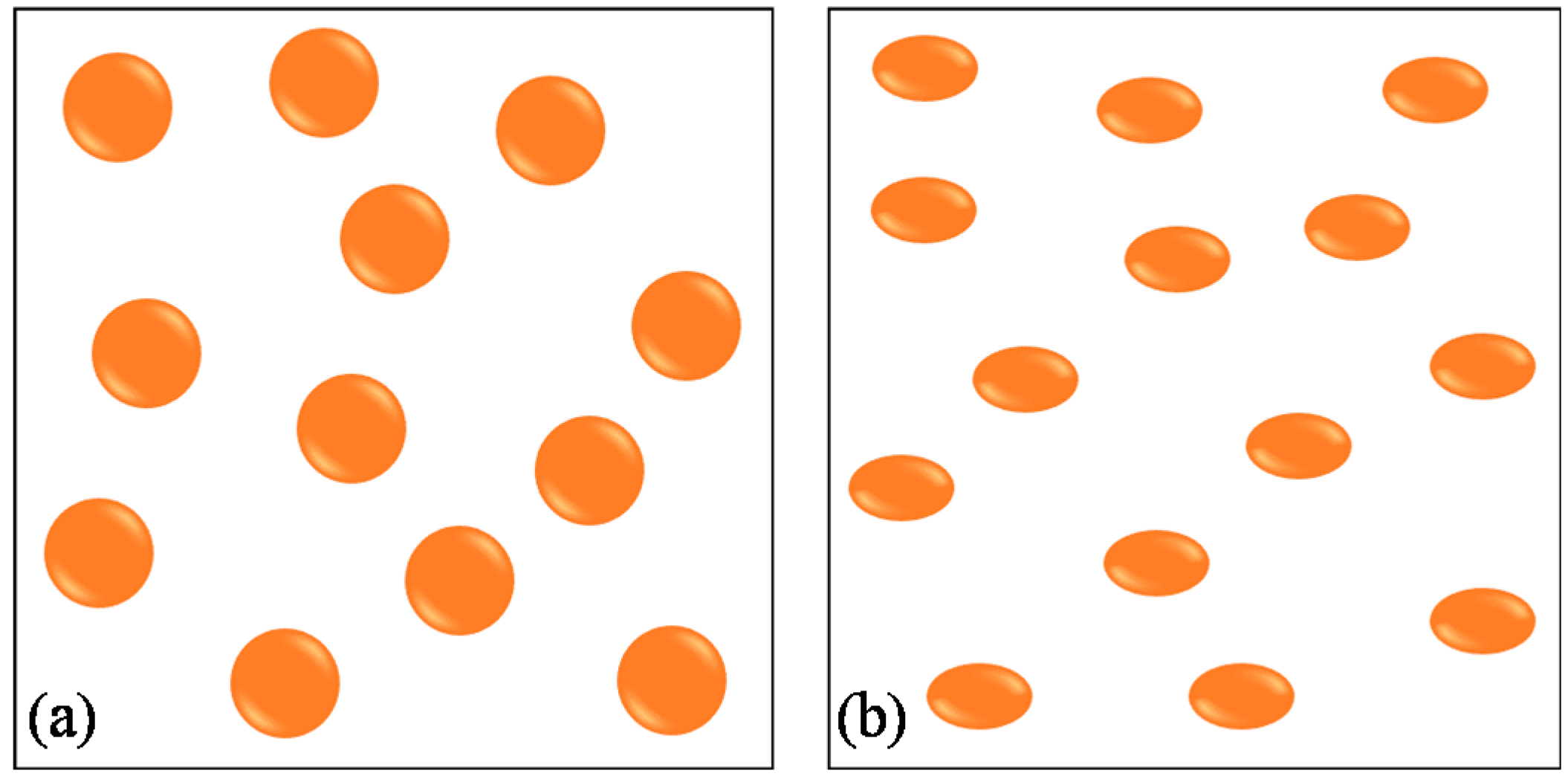
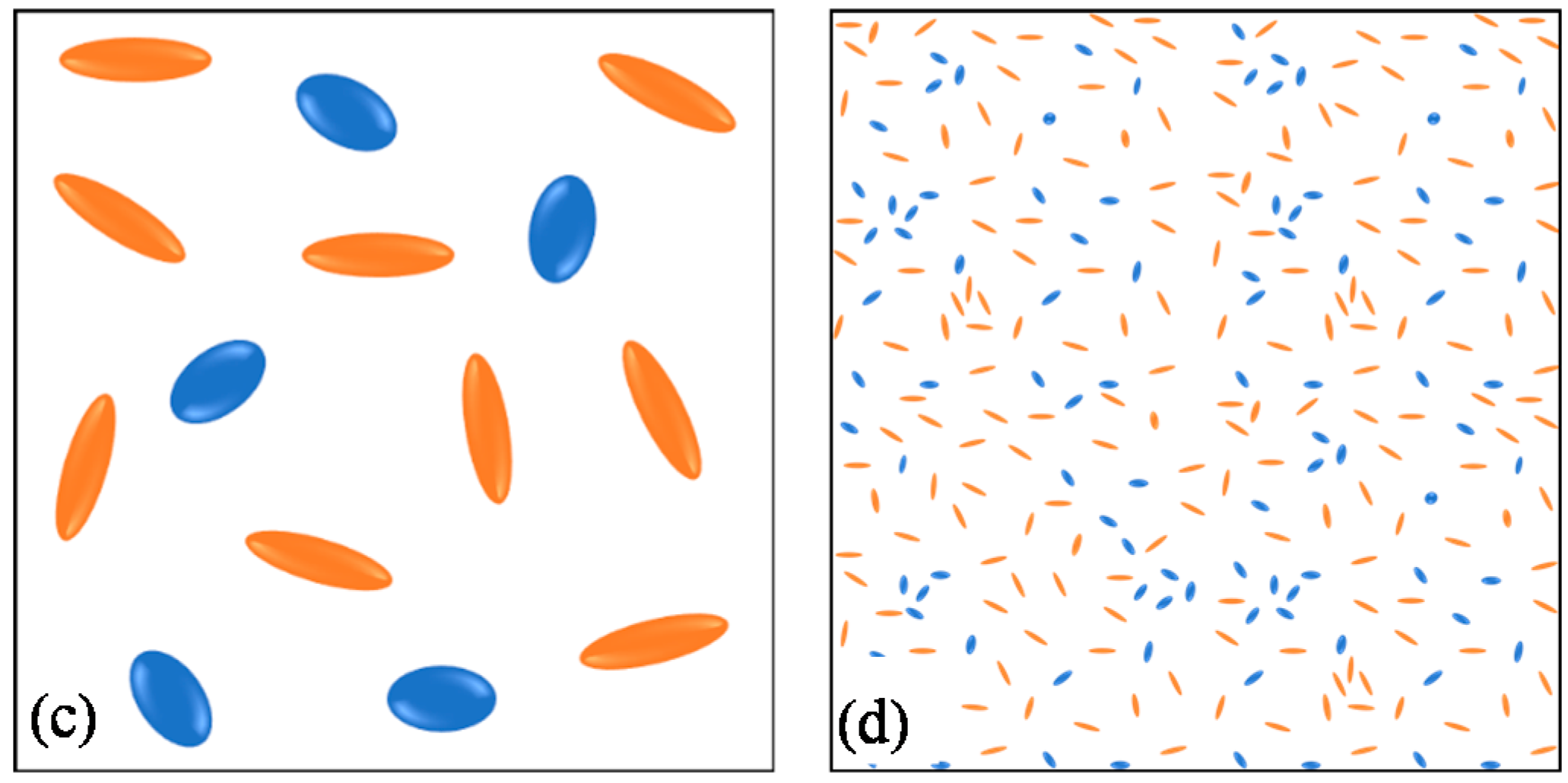
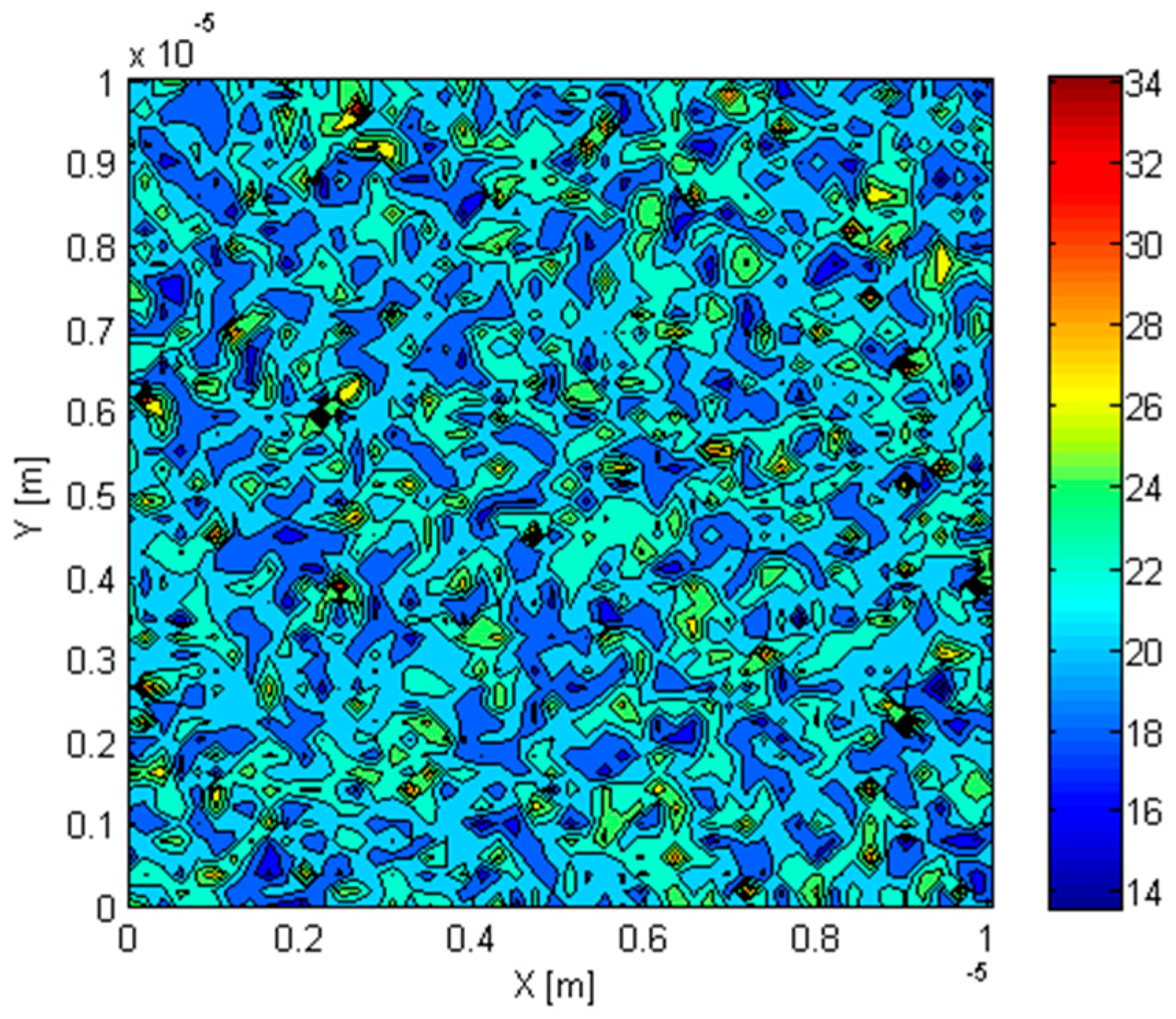
2.3. Two-Scale Approach for Non-Uniformly Distributed Inclusions
3. Applications of the Generalized Effective Medium Theory
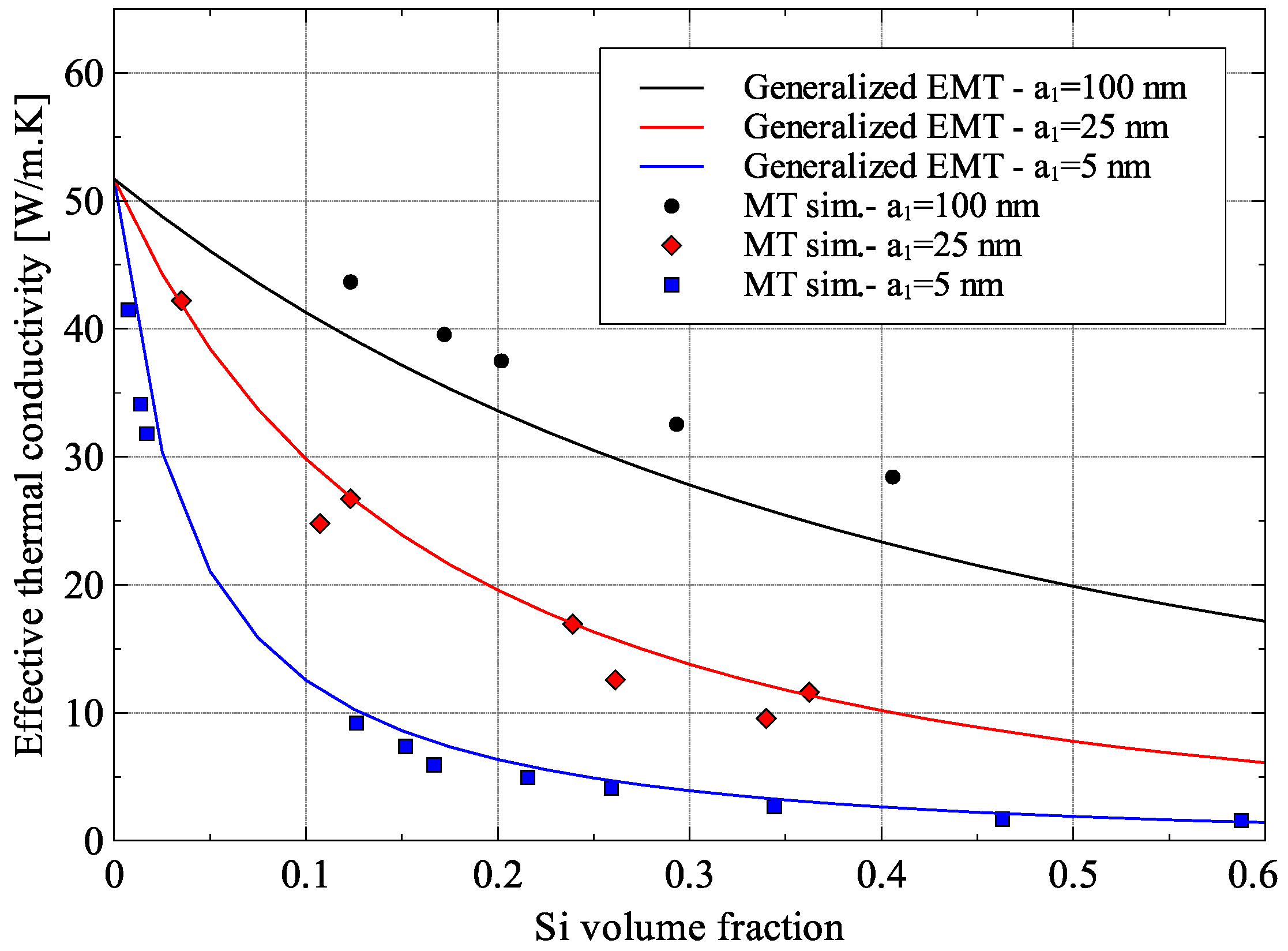
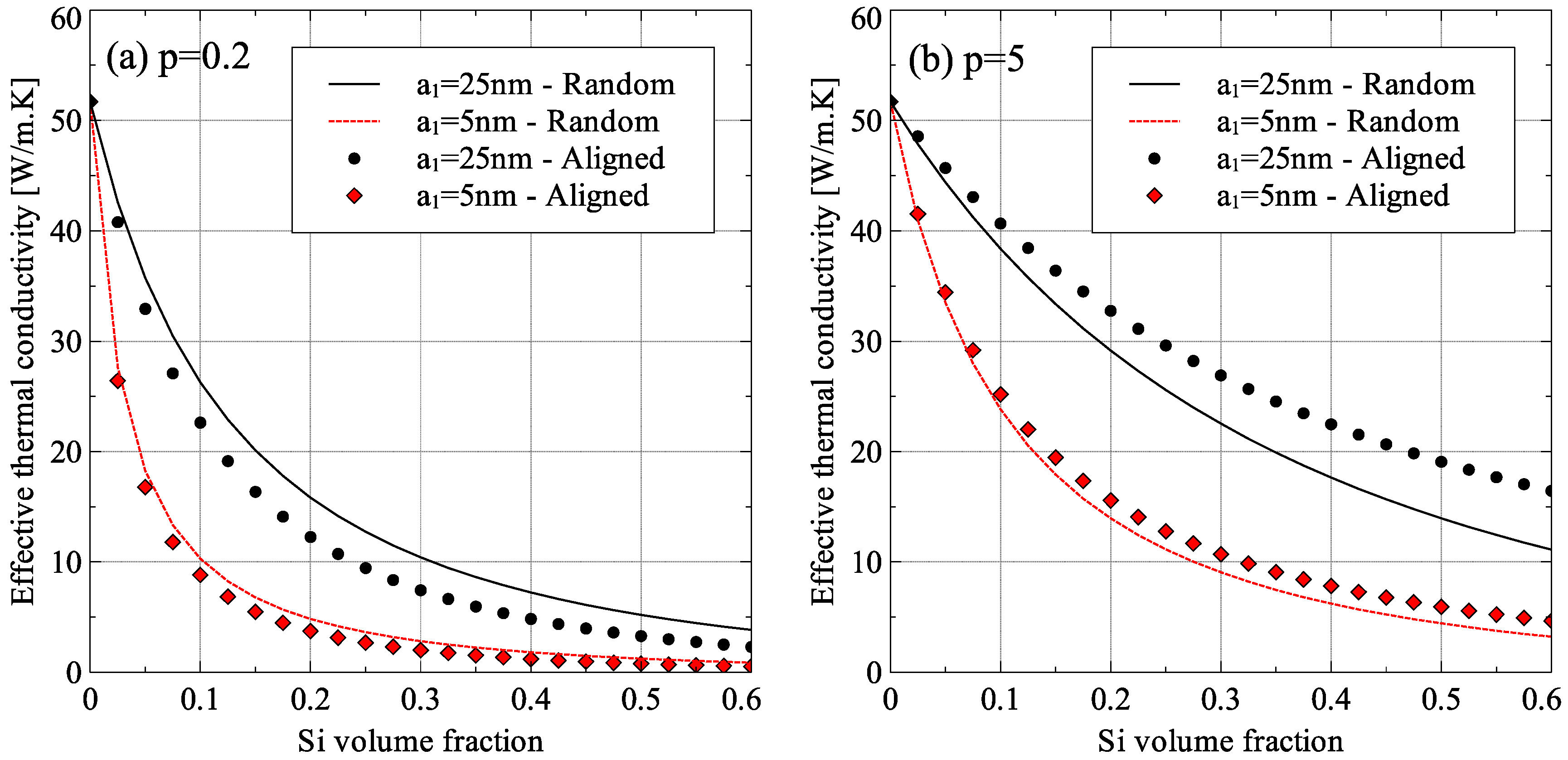
3.1. Effect of Nanometer-Sized Inclusions
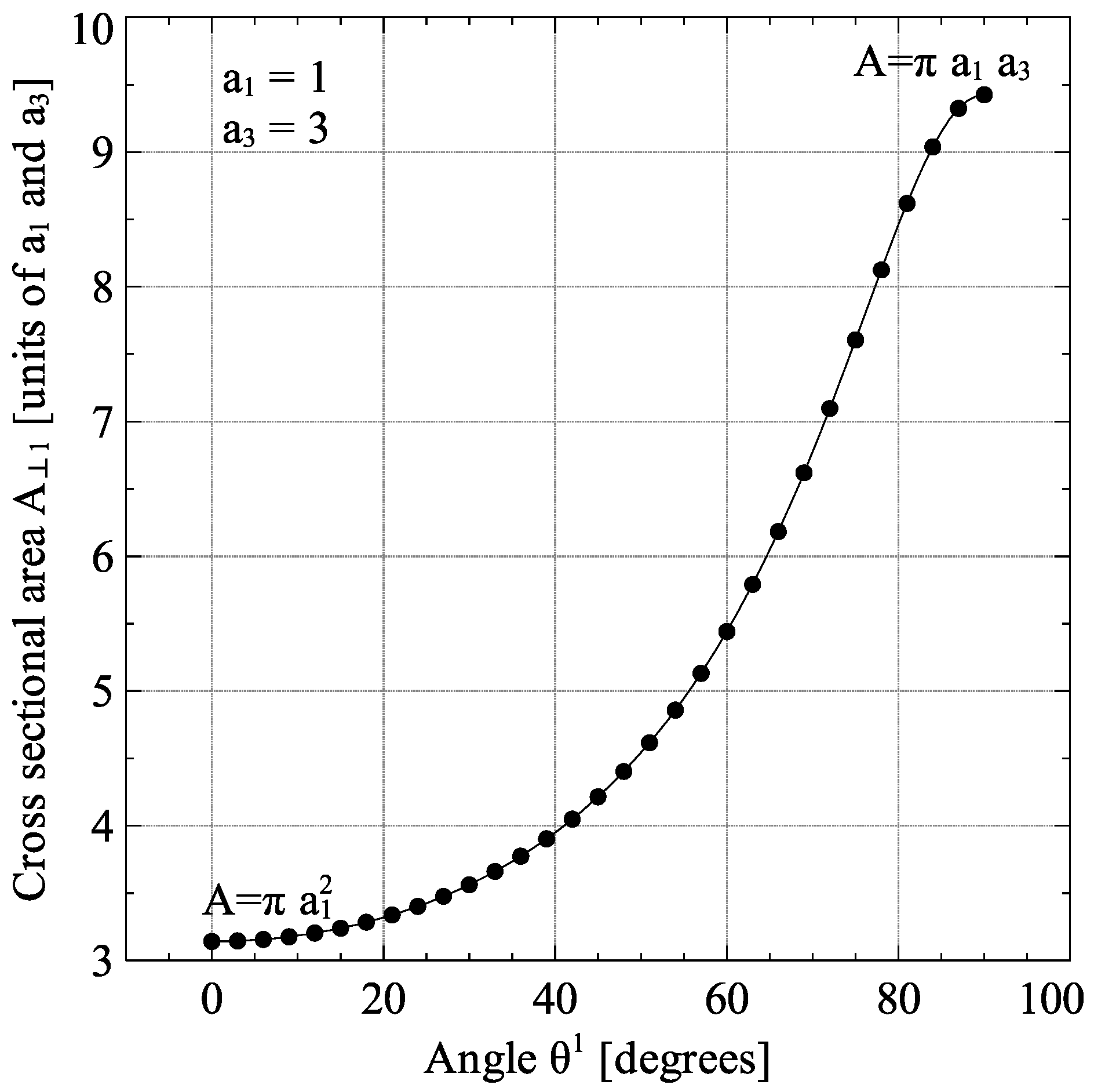
3.2. Effect of Inclusion Aspect Ratio
3.3. Effect of Inclusion Orientation
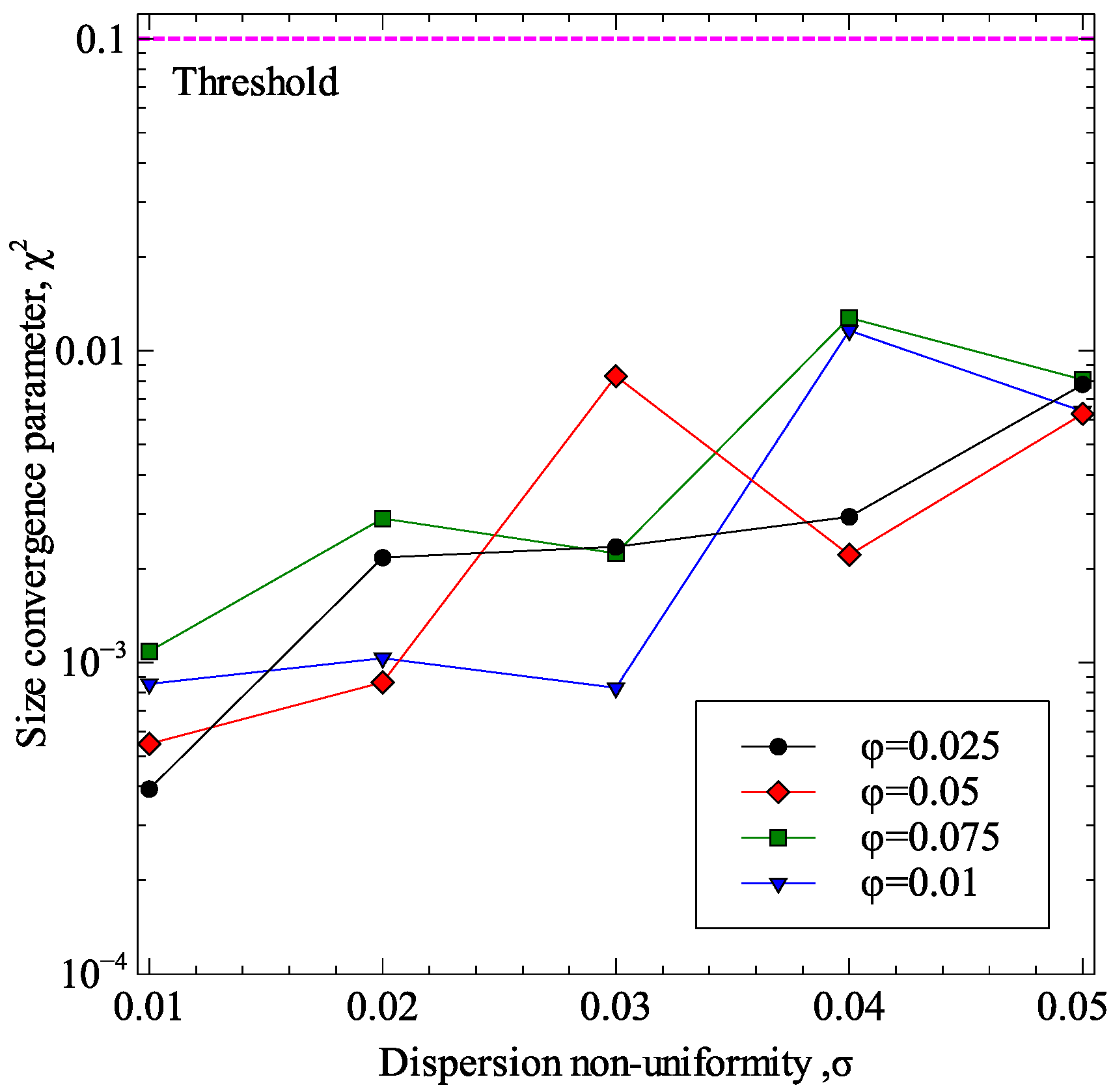
3.4. Effect of Non-Uniform Dispersion of Inclusions
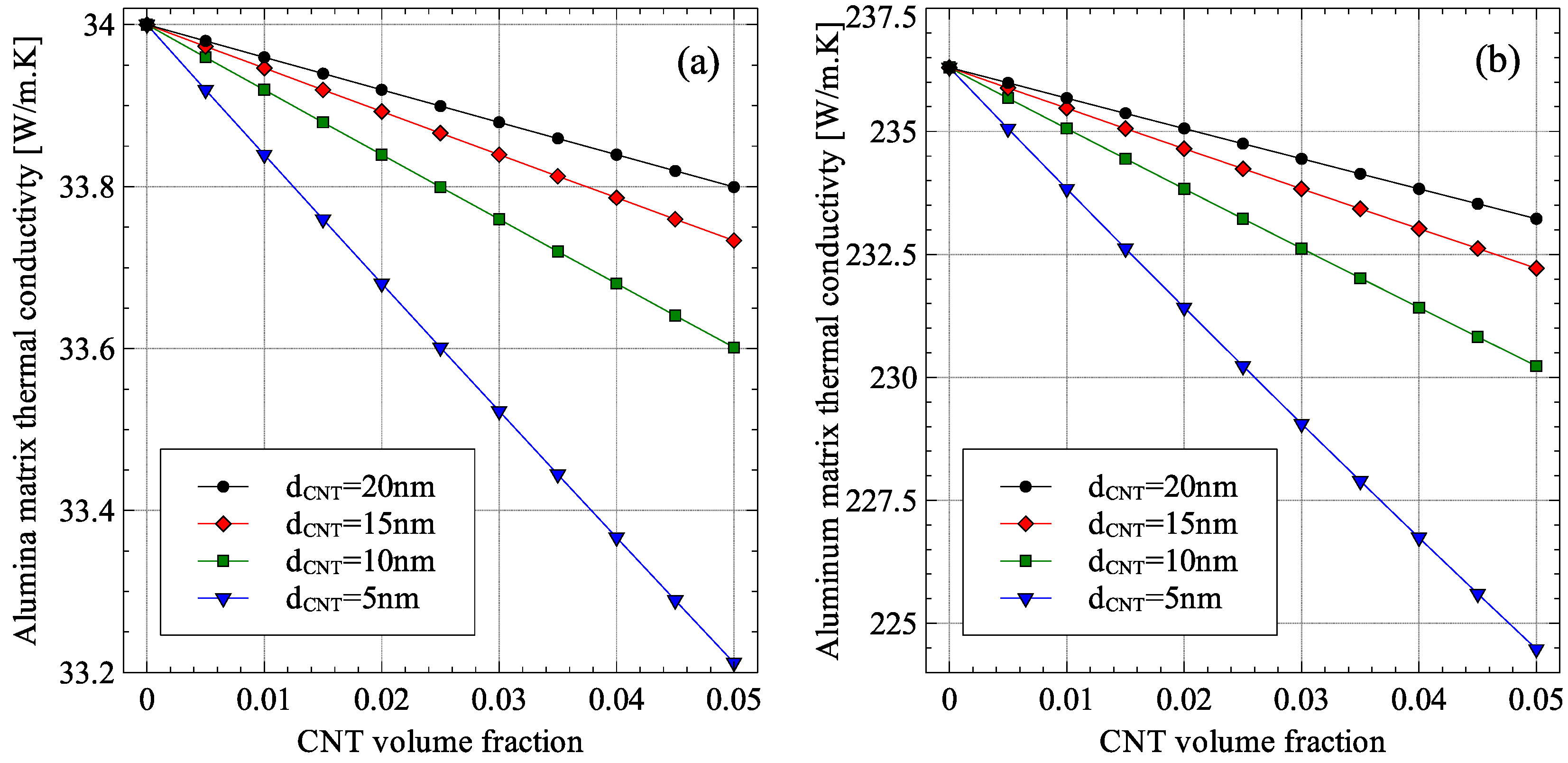
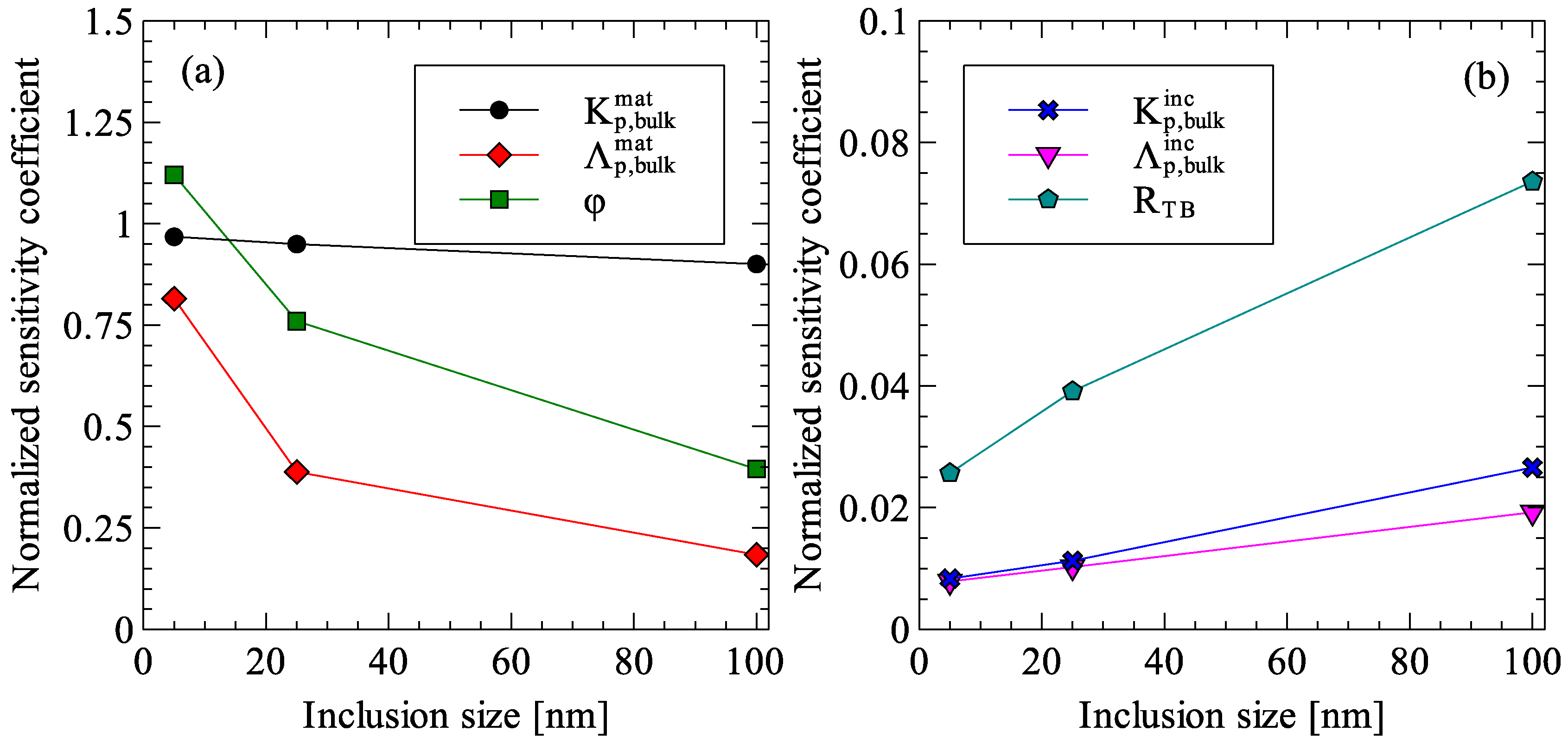
4. Sensitivity Analysis of the Generalized Effective Medium Theory
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
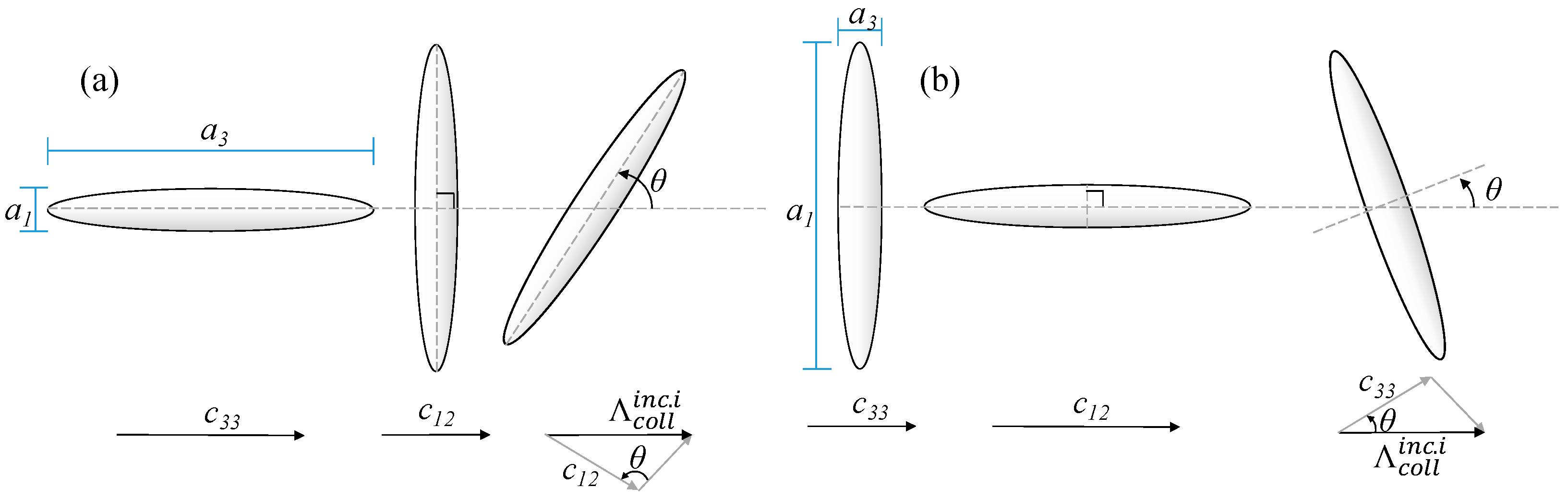
Appendix A. Calculation of the Collision Cross-Section Area
References
- Chen, G. Particularities of heat conduction in nanostructures. J. Nanopart. Res. 2000, 2, 199–204. [Google Scholar] [CrossRef]
- Maxwell, J. A Treatise on Electricity and Magnetism, 2nd ed.; Oxford University Press: Oxford, UK, 1904. [Google Scholar]
- Rayleigh, L. On the influence of obstacles arranged in rectangular order upon the properties of a medium. Philos. Mag. Ser. 5 1892, 34, 481–502. [Google Scholar] [CrossRef]
- Hasselman, D.P.H.; Johnson, L.F. Effective thermal conductivity of composites with interfacial thermal barrier resistance. J. Compos. Mater. 1987, 21, 508–515. [Google Scholar] [CrossRef]
- Benveniste, Y. Effective thermal conductivity of composites with a thermal contact resistance between the constituents: Nondilute case. J. Appl. Phys. 1987, 61. [Google Scholar] [CrossRef]
- Bruggeman, D.A.G. Berechnung verschiedener physikalischer Konstanten von heterogenen Substanzen. I. Dielektrizitätskonstanten und Leitfähigkeiten der Mischkörper aus isotropen Substanzen. Ann. Phys. 1935, 416, 636–664. [Google Scholar] [CrossRef]
- Every, A.G.; Tzou, Y.; Hasselman, D.P.H.; Raj, R. The effect of particle size on the thermal conductivity of ZnS/diamond composites. Acta Metall. Mater. 1992, 40, 123–129. [Google Scholar] [CrossRef]
- Wang, J.; Yi, X. Effects of interfacial thermal barrier resistance and particle shape and size on the thermal conductivity of AlN/PI composites. Compos. Sci. Technol. 2004, 64, 1623–1628. [Google Scholar]
- Nan, C.-W.; Birringer, R.; Clarke, D.R.; Gleiter, H. Effective thermal conductivity of particulate composites with interfacial thermal resistance. J. Appl. Phys. 1997, 81, 6692–6699. [Google Scholar] [CrossRef]
- Prasher, R.; Phelan, P.E.; Bhattacharya, P. Effect of aggregation kinetics on the thermal conductivity of nanoscale colloidal solutions (nanofluid). Nano Lett. 2006, 6, 1529–1534. [Google Scholar] [CrossRef] [PubMed]
- Prasher, R.; Evans, W.; Meakin, P.; Fish, J.; Phelan, P.; Keblinski, P. Effect of aggregation on thermal conduction in colloidal nanofluids. Appl. Phys. Lett. 2006, 89, 88–90. [Google Scholar] [CrossRef]
- Evans, W.; Prasher, R.; Fish, J.; Meakin, P.; Phelan, P.; Keblinski, P. Effect of aggregation and interfacial thermal resistance on thermal conductivity of nanocomposites and colloidal nanofluids. Int. J. Heat Mass Transf. 2008, 51, 1431–1438. [Google Scholar] [CrossRef]
- Shuvra Basu, T.; Yang, R.; Joottu Thiagarajan, S.; Ghosh, S.; Gierlotka, S.; Ray, M. Remarkable thermal conductivity reduction in metal-semiconductor nanocomposites. Appl. Phys. Lett. 2013, 103, 083115. [Google Scholar] [CrossRef]
- Jeng, M.-S.; Yang, R.; Song, D.; Chen, G. Modeling the thermal conductivity and phonon transport in nanoparticle composites using monte carlo simulation. J. Heat Transf. 2008, 130, 042410. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, H.; Zhang, Y.; Wang, X. Mechanical and thermal properties of carbon nanotube/aluminum composites consolidated by spark plasma sintering. Mater. Des. 2012, 41, 344–348. [Google Scholar] [CrossRef]
- Ahmad, K.; Wei, P.; Wan, C. Thermal conductivities of alumina-based multiwall carbon nanotube ceramic composites. J. Mater. Sci. 2014, 49, 6048–6055. [Google Scholar] [CrossRef]
- Nan, C.W.; Shi, Z.; Lin, Y. A simple model for thermal conductivity of carbon nanotube-based composites. Chem. Phys. Lett. 2003, 375, 666–669. [Google Scholar] [CrossRef]
- Minnich, A.; Chen, G. Modified effective medium formulation for the thermal conductivity of nanocomposites. Appl. Phys. Lett. 2007, 91, 4–7. [Google Scholar] [CrossRef]
- Ordonez-Miranda, J.; Yang, R.; Alvarado-Gil, J.J. On the thermal conductivity of particulate nanocomposites. Appl. Phys. Lett. 2011, 98, 2009–2012. [Google Scholar] [CrossRef]
- Tian, W.; Yang, R. Thermal conductivity modeling of compacted nanowire composites. J. Appl. Phys. 2007, 101, 22–27. [Google Scholar] [CrossRef]
- Duong, H.M.; Papavassiliou, D.V.; Mullen, K.J.; Maruyama, S. Computational modeling of the thermal conductivity of single-walled carbon nanotube-polymer composites. Nanotechnology 2008, 19, 065702. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Huai, X.; Liang, S.; Wang, X. Thermal transport in Si/Ge nanocomposites. J. Phys. D Appl. Phys. 2009, 42, 095416. [Google Scholar] [CrossRef]
- Yang, R.; Chen, G. Thermal conductivity modeling of periodic two-dimensional nanocomposites. Phys. Rev. B 2004, 69, 1–10. [Google Scholar] [CrossRef]
- Hsieh, T.Y.; Yang, J.Y.; Hong, Z.C. Thermal conductivity modeling of compacted type nanocomposites. J. Appl. Phys. 2009, 106. [Google Scholar] [CrossRef]
- Xu, Y.; Li, G. Strain effect analysis on phonon thermal conductivity of two-dimensional nanocomposites. J. Appl. Phys. 2009, 106. [Google Scholar] [CrossRef]
- Lee, P.; Yang, R.; Maute, K. An extended finite element method for the analysis of submicron heat transfer phenomena. In Multiscale Methods in Computational Mechanics; Springer Science & Business Media: Houten, The Netherlands, 2011; pp. 195–212. [Google Scholar]
- Maute, K.; Kreissl, S.; Makhija, D.; Yang, R. Topology optimization of heat conduction problems. In Proceedings of the 9th World Congress on Structural and Multidisciplinary Optimization, Shizouka, Japan, 13–17 June 2011; pp. 1–17.
- Nan, C.-W. Physics of inhomogeneous inorganic materials. Prog. Mater. Sci. 1993, 37, 1–116. [Google Scholar] [CrossRef]
- Nan, C.W. Effective-medium theory of piezoelectric composites. J. Appl. Phys. 1994, 76, 1155–1163. [Google Scholar] [CrossRef]
- Moumen, A.E.; Kanit, T.; Imad, A.; Minor, H. El Computational thermal conductivity in porous materials using homogenization techniques: Numerical and statistical approaches. Comput. Mater. Sci. 2015, 97, 148–158. [Google Scholar] [CrossRef]
- Wu, T.; Temizer, İ.; Wriggers, P. Computational thermal homogenization of concrete. Cem. Concr. Compos. 2013, 35, 59–70. [Google Scholar] [CrossRef] [Green Version]
- Gitman, I.M.; Askes, H.; Sluys, L.J. Representative volume: Existence and size determination. Eng. Fract. Mech. 2007, 74, 2518–2534. [Google Scholar] [CrossRef]
- Barea, R.; Belmonte, M.; Osendi, M.I.; Miranzo, P. Thermal conductivity of Al2O3/SiC platelet composites. J. Eur. Ceram. Soc. 2003, 23, 1773–1778. [Google Scholar] [CrossRef]
- Sivakumar, R.; Guo, S.; Nishimura, T.; Kagawa, Y. Thermal conductivity in multi-wall carbon nanotube/silica-based nanocomposites. Scr. Mater. 2007, 56, 265–268. [Google Scholar] [CrossRef]
- Balandin, A.A. Thermal properties of graphene and nanostructured carbon materials. Nat. Mater. 2011, 10, 569–581. [Google Scholar] [CrossRef] [PubMed]
- Nan, C.-W.; Liu, G.; Lin, Y.; Li, M. Interface effect on thermal conductivity of carbon nanotube composites. Appl. Phys. Lett. 2004, 85, 3549–3551. [Google Scholar] [CrossRef]
- Siddiqui, M.U.; Arif, A.F.M.; Bilton, A.M.; Dubowsky, S.; Elshafei, M. An improved electric circuit model for photovoltaic modules based on sensitivity analysis. Sol. Energy 2013, 90, 29–42. [Google Scholar] [CrossRef]
- Masi, M.; Fogliani, S.; Carra, S. Sensitivity analysis on indium phosphide liquid encapsulated czochralski growth. Cryst. Res. Technol. 1999, 34, 1157–1167. [Google Scholar] [CrossRef]









| Material | Bulk Thermal Conductivity (W/m·K) | Bulk Phonon Mean-Free-Path (nm) | Phonon Group Velocity (m/s) | Volumetric Specific Heat Capacity (J/m3·K) |
|---|---|---|---|---|
| Silicon | 150 | 268 | 1804 | 0.93 × 106 |
| Germanium | 51.7 | 171 | 1042 | 0.87 × 106 |
| Material | Bulk Phonon Thermal Conductivity (W/m·K) | Bulk Electron Thermal Conductivity (W/m·K) | Bulk Phonon Mean-Free-Path (nm) | Bulk Electron Mean-Free-Path (nm) | Diameter (nm) | Length (μm) |
|---|---|---|---|---|---|---|
| Alumina | 34 | - | 4.6 | - | - | - |
| Aluminum | 11.3 | 225 | 2.3 | 14.1 | - | - |
| MWCNT | 3000 | - | 2.2 | - | 10 | 2 |
| Parameter | a1 = 5 nm | = 6.3443 W/m·K | ||||||
| X+ | X− | Y+ | Y− | ΔX | ΔY | NSC | ||
| 51.70 | 56.87 | 46.53 | 6.98 | 5.75 | 10.34 | 1.23 | 0.97 | |
| 150.00 | 165.00 | 135.00 | 6.37 | 6.36 | 30.00 | 0.01 | 8.35 × 10−3 | |
| 1.71 × 10−7 | 1.88 × 10−7 | 1.54 × 10−7 | 5.89 | 6.92 | 3.42 × 10−8 | 1.04 | 0.82 | |
| 2.68 × 10−7 | 2.95 × 10−7 | 2.41 × 10−7 | 6.36 | 6.37 | 5.36 × 10−8 | 0.01 | 7.88 × 10−3 | |
| RTB | 6.80 × 10−9 | 7.48 × 10−9 | 6.12 × 10−9 | 6.33 | 6.36 | 1.36 × 10−9 | 0.03 | 25.69 × 10−3 |
| φ | 0.20 | 0.22 | 0.18 | 5.70 | 7.12 | 0.04 | 1.42 | 1.12 |
| Parameter | a1 = 25 nm | = 19.58 W/m·K | ||||||
| X+ | X− | Y+ | Y− | ΔX | ΔY | NSC | ||
| 51.70 | 56.87 | 46.53 | 21.44 | 17.72 | 10.34 | 3.72 | 0.95 | |
| 150.00 | 165.00 | 135.00 | 19.60 | 19.56 | 30.00 | 0.04 | 11.26 × 10−2 | |
| 1.71 × 10−7 | 1.88 × 10−7 | 1.54 × 10−7 | 19.04 | 20.57 | 3.42 × 10−8 | 1.52 | 0.39 | |
| 2.68 × 10−7 | 2.95 × 10−7 | 2.41 × 10−7 | 19.56 | 19.60 | 5.36 × 10−8 | 0.04 | 10.27 × 10−2 | |
| RTB | 6.80 × 10−9 | 7.48 × 10−9 | 6.12 × 10−9 | 19.51 | 19.66 | 1.36 × 10−9 | 0.15 | 39.15 × 10−2 |
| φ | 0.20 | 0.22 | 0.18 | 18.26 | 21.23 | 0.04 | 2.98 | 0.76 |
| Parameter | a1 = 100 nm | = 33.5943 W/m·K | ||||||
| X+ | X− | Y+ | Y− | ΔX | ΔY | NSC | ||
| 51.70 | 56.87 | 46.53 | 36.62 | 30.57 | 10.34 | 6.05 | 0.90 | |
| 150.00 | 165.00 | 135.00 | 33.68 | 33.50 | 30.00 | 0.18 | 26.60 × 10−2 | |
| 1.71 × 10−7 | 1.88 × 10−7 | 1.54 × 10−7 | 32.99 | 34.22 | 3.42 × 10−8 | 1.24 | 0.18 | |
| 2.68 × 10−7 | 2.95 × 10−7 | 2.41 × −7 | 33.53 | 33.66 | 5.36 × 10−8 | 0.13 | 19.26 × 10−2 | |
| RTB | 6.80 × 10−9 | 7.48 × 10−9 | 6.12 × 10−9 | 33.36 | 33.86 | 1.36 × 10−9 | 0.49 | 73.60 × 10−2 |
| φ | 0.2 | 0.22 | 0.18 | 32.30 | 34.96 | 0.04 | 2.65 | 0.40 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Siddiqui, M.U.; Arif, A.F.M. Generalized Effective Medium Theory for Particulate Nanocomposite Materials. Materials 2016, 9, 694. https://doi.org/10.3390/ma9080694
Siddiqui MU, Arif AFM. Generalized Effective Medium Theory for Particulate Nanocomposite Materials. Materials. 2016; 9(8):694. https://doi.org/10.3390/ma9080694
Chicago/Turabian StyleSiddiqui, Muhammad Usama, and Abul Fazal M. Arif. 2016. "Generalized Effective Medium Theory for Particulate Nanocomposite Materials" Materials 9, no. 8: 694. https://doi.org/10.3390/ma9080694






