Stress Wave Propagation in Viscoelastic-Plastic Rock-Like Materials
Abstract
:1. Introduction
2. Analytic Solution for Stress Wave Propagation in Viscoelastic-Plastic Rock-Like Materials
2.1. Constitutive Equation of Viscoelastic-Plastic Rock-Like Materials
2.2. The Wave Equation of Viscoelastic-Plastic Rock-Like Materials
3. Verification of the Analytic Solution for Stress Wave Propagation
3.1. An Experimental Test Using the SHPB and an Inverse Analysis
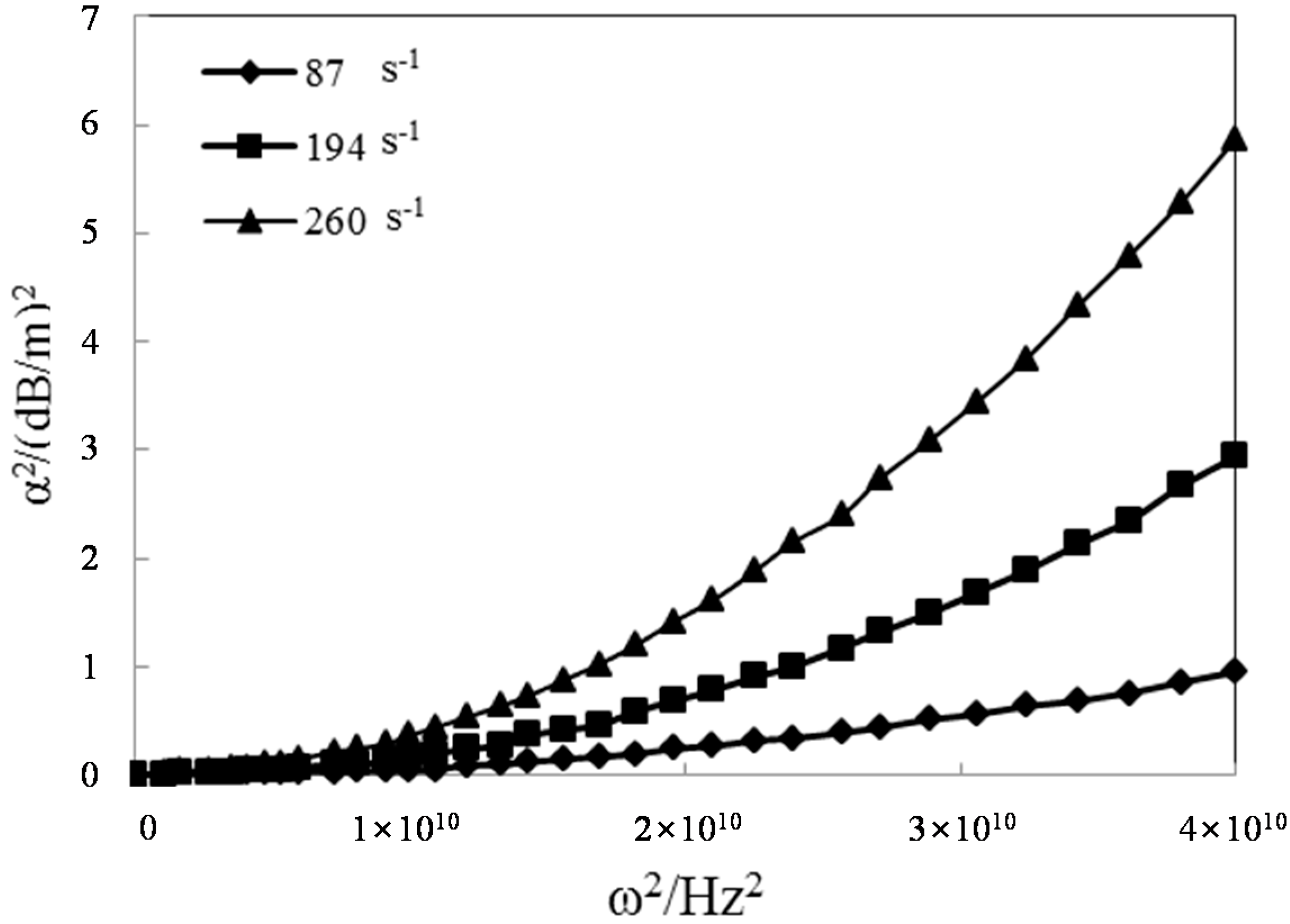
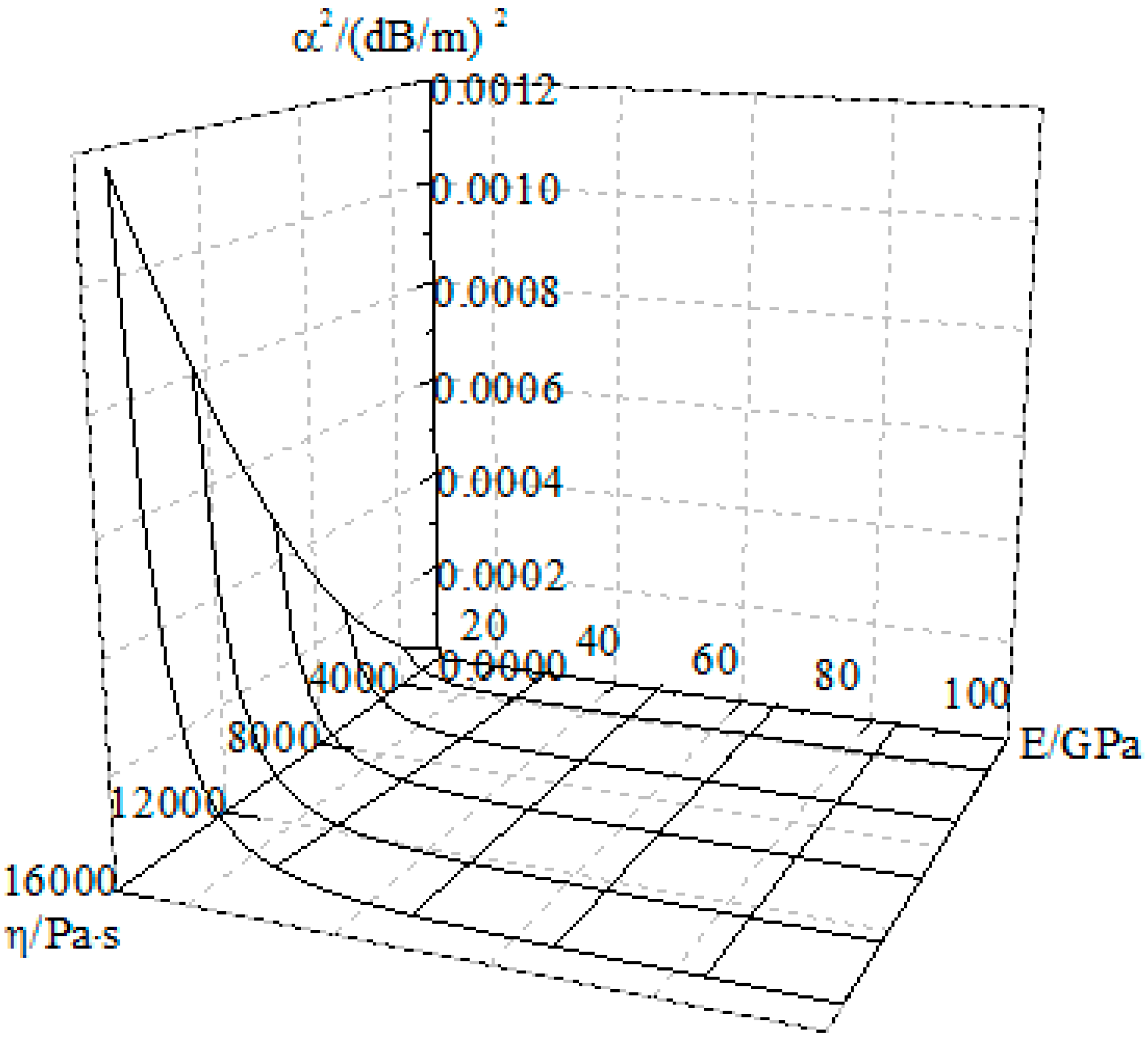
3.2. Attenuation Factors in the Stress Wave Equation
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Follansbee, P.S.; Frantz, C. Wave propagation in the split Hopkinson pressure bar. J. Eng. Mater. Technol. 1983, 105, 61–66. [Google Scholar] [CrossRef]
- Li, X.B.; Lo, T.S.; Zhao, J.; Zhao, P.J. Oscillation elimination in the Hopkinson bar apparatus and resultant complete dynamic stress-strain curve for rocks. Int. J. Rock Mech. Min. Sci. 2000, 37, 1055–1060. [Google Scholar] [CrossRef]
- Mustaqim, M.N.M.; Song, K.I.; Cho, G.C.; Zainab, M. Long-Wavelength Elastic Wave Propagation across Naturally Fractured Rock Masses. Rock Mech. Rock Eng. 2014, 47, 561–573. [Google Scholar]
- Zhai, Y.; Ma, G.W.; Zhao, J.H. Dynamic capability of granite and concrete under impact compressive loading. Chin. J. Rock Mech. Eng. 2007, 26, 762–768. [Google Scholar]
- Zhai, Y.; Zhao, J.H.; Li, X.C. Study on damage viscoelasticplastic dynamic constitutive model of rock-like materials. Chin. J. Rock Mech. Eng. 2011, 30, 3820–3824. [Google Scholar]
- Ozbolt, J.; Sharma, A. Numerical simulation of reinforced concrete beams with different shear reinforcements under dynamic impact loads. Int. J. Impact Eng. 2011, 38, 940–949. [Google Scholar] [CrossRef]
- Zhou, F.H.; Chen, L.; Wang, L.L. Two approaches for analyzing one-dimensional viscoelastic wave propagations. Eng. Mech. 2010, 7, 45–51. [Google Scholar]
- Graham, G.A.C.; Sabin, G.C.W. The correspondence principle of linear viscoelasticity for problems that involve time-dependent regions. Int. J. Eng. Sci. 1973, 11, 123–140. [Google Scholar] [CrossRef]
- Raymond, S.; Lemiale, V.; Ibrahim, R.; Lau, R. A mesh free study of the Kalthoff-Winkler experiment in 3D at room and low temperatures under dynamic loading using viscoplasticmodeling. Eng. Anal. Bound. Elem. 2014, 48, 20–25. [Google Scholar] [CrossRef]
- Liu, H.S.; Tang, L.; Bo, J.S.; Feng, Z. Elastic-viscoplastic analysis of explicit FEM for simulating wave motions in rock mass. Coal Geol. Explor. 2009, 37, 38–42. [Google Scholar]
- Passaris, E.K.S. The rheological behavior of rock salt as determined in an in situ pressure test cavity. In Proceedings of the 4th Conference on International Society for Rock Mechanics, Montreux, Switzerland, 2–3 September 1979; pp. 257–264.
- Ding, J.Y.; Zhou, H.W.; Liu, D. Research on fractional derivative three elements model of salt rock. Chin. J. Rock Mech. Eng. 2014, 34, 672–678. [Google Scholar]
- Xie, L.; Zhao, G.M.; Meng, X.R. Research on damage viscoelastic dynamic constitutive model of soft rock and concrete materials. Chin. J. Rock Mech. Eng. 2014, 34, 857–864. [Google Scholar]
- Liu, S.; Xu, J.Y.; Chen, T.F.; Wang, P. Study on dynamic response of rock based on split Hopkinson pressure bar test. Chin. J. Undergr. Space Eng. 2013, 9, 992–995. [Google Scholar]
- Yan, S.H.; Duan, J.X.; Yin, F.L.; Qian, Q.H. SHPB test on high-strength concrete. J. PLA Univ. Sci. Technol. 2000, 1, 6–9. [Google Scholar]
- Zhao, H.; Gray, G. On the use of SHPB techniques to determine the dynamic behavior of materials in the range of small strains. Int. J. Solids Struct. 1996, 33, 3363–3375. [Google Scholar] [CrossRef]
- Hertlein, B.H. Stress wave testing of concrete: A 25-year review and a peek into the future. Construct. Build. Mater. 2013, 38, 1240–1245. [Google Scholar] [CrossRef]
- Wang, L.L. Foundations of Stress Waves; National Defense Press: Beijing, China, 2005. (In Chinese) [Google Scholar]
- Li, Z.Q.; Chen, W.Y.; Wang, Z.H. Study on the effect of striker bar length on the SHPB measurements. J. Mech. Strength 2010, 32, 942–945. [Google Scholar]
- Liu, L.; Song, K.I.; Lao, D.Z.; Kwon, T.H. Rheological properties of cemented tailing backfill and the construction of a prediction. Model. Mater. 2015, 8, 2076–2092. [Google Scholar]
- Zhou, J.; Li, X.B.; Shi, X.Z. Long-term prediction model of rockburst in underground openings using heuristic algorithms and support vector machines. Saf. Sci. 2012, 50, 629–644. [Google Scholar] [CrossRef]
- Li, J.G.; Cheng, G.Q.; Zou, Y.H. Study on the Stress Wave Propagation Attenuation Laws in the Elastoplastic Coal and Rock. Master’s Thesis, Shandong University of Science and Technology, Qingdao, China, 2008; pp. 20–60. [Google Scholar]
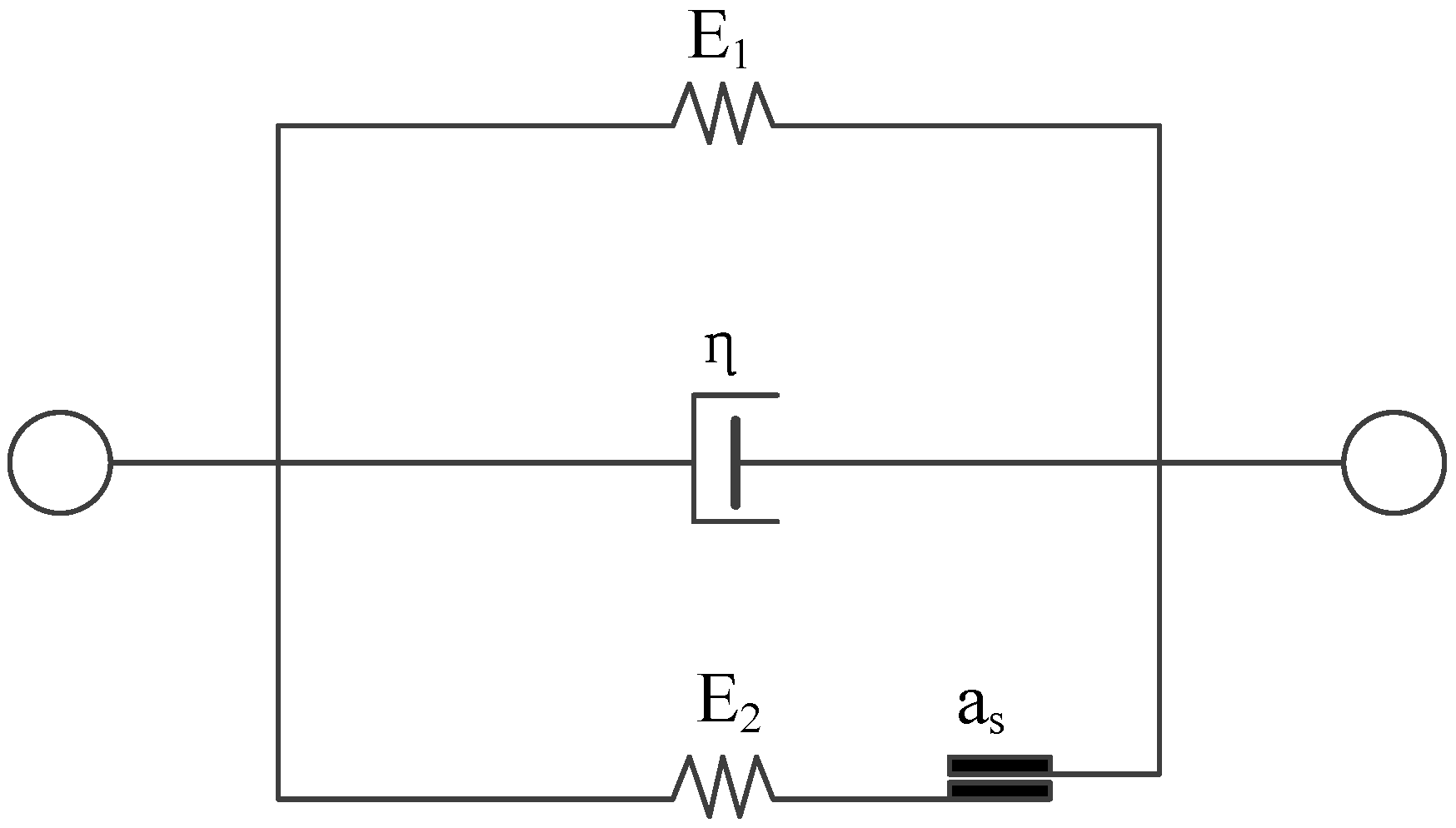




| Sample Number | Mean Strain Rate (s−1) | Estimated Parameters from Inverse Analysis | |||
|---|---|---|---|---|---|
| Elastic Modulus (N/m2) | Viscosity Coefficient, η | Variance, | |||
| E1 | E2 | ||||
| C01 | 87 | 3.499 × 1010 | 3.217 × 1010 | 1.200 × 104 | 9.077 × 10−2 |
| C02 | 194 | 3.498 × 1010 | 3.368 × 1010 | 1.093 × 104 | 8.572 × 10−3 |
| C03 | 260 | 3.488 × 1010 | 3.457 × 1010 | 8.311 × 103 | 2.239 × 10−2 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lang, L.; Song, K.-I.; Zhai, Y.; Lao, D.; Lee, H.-L. Stress Wave Propagation in Viscoelastic-Plastic Rock-Like Materials. Materials 2016, 9, 377. https://doi.org/10.3390/ma9050377
Lang L, Song K-I, Zhai Y, Lao D, Lee H-L. Stress Wave Propagation in Viscoelastic-Plastic Rock-Like Materials. Materials. 2016; 9(5):377. https://doi.org/10.3390/ma9050377
Chicago/Turabian StyleLang, Liu, KI-IL Song, Yue Zhai, Dezheng Lao, and Hang-Lo Lee. 2016. "Stress Wave Propagation in Viscoelastic-Plastic Rock-Like Materials" Materials 9, no. 5: 377. https://doi.org/10.3390/ma9050377







