Mechanical Properties of Auxetic Cellular Material Consisting of Re-Entrant Hexagonal Honeycombs
Abstract
:1. Introduction
2. Effects of Parameters on Bearing Capacity of the Auxetic Cellular Material
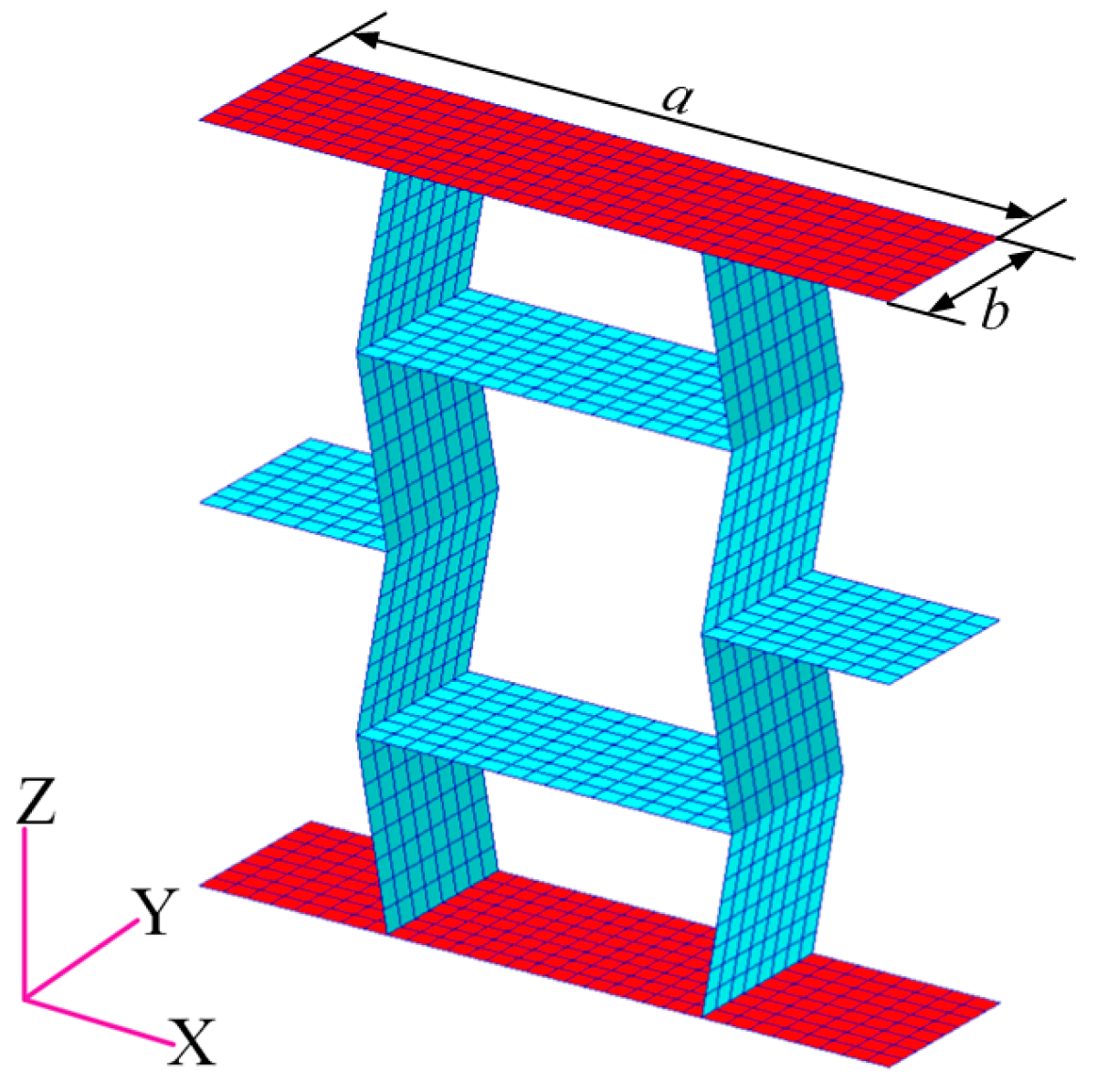
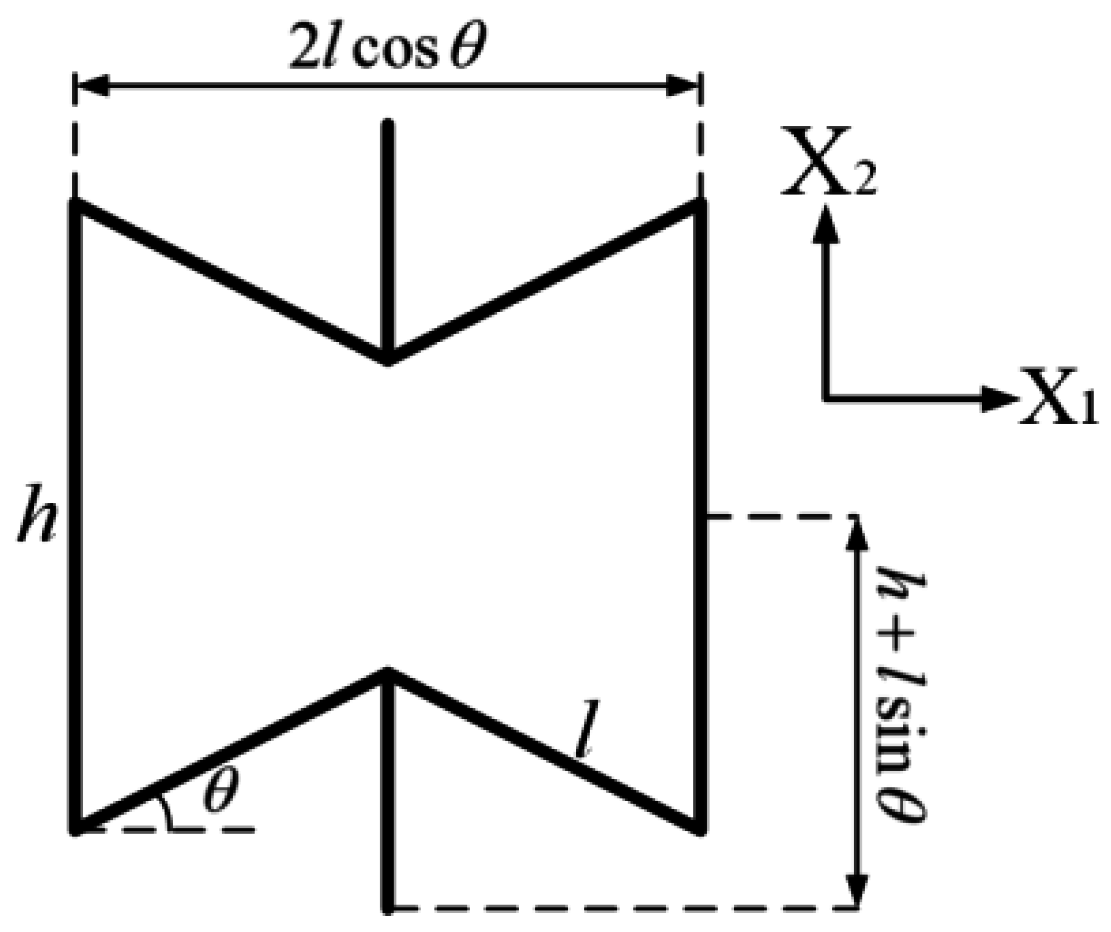
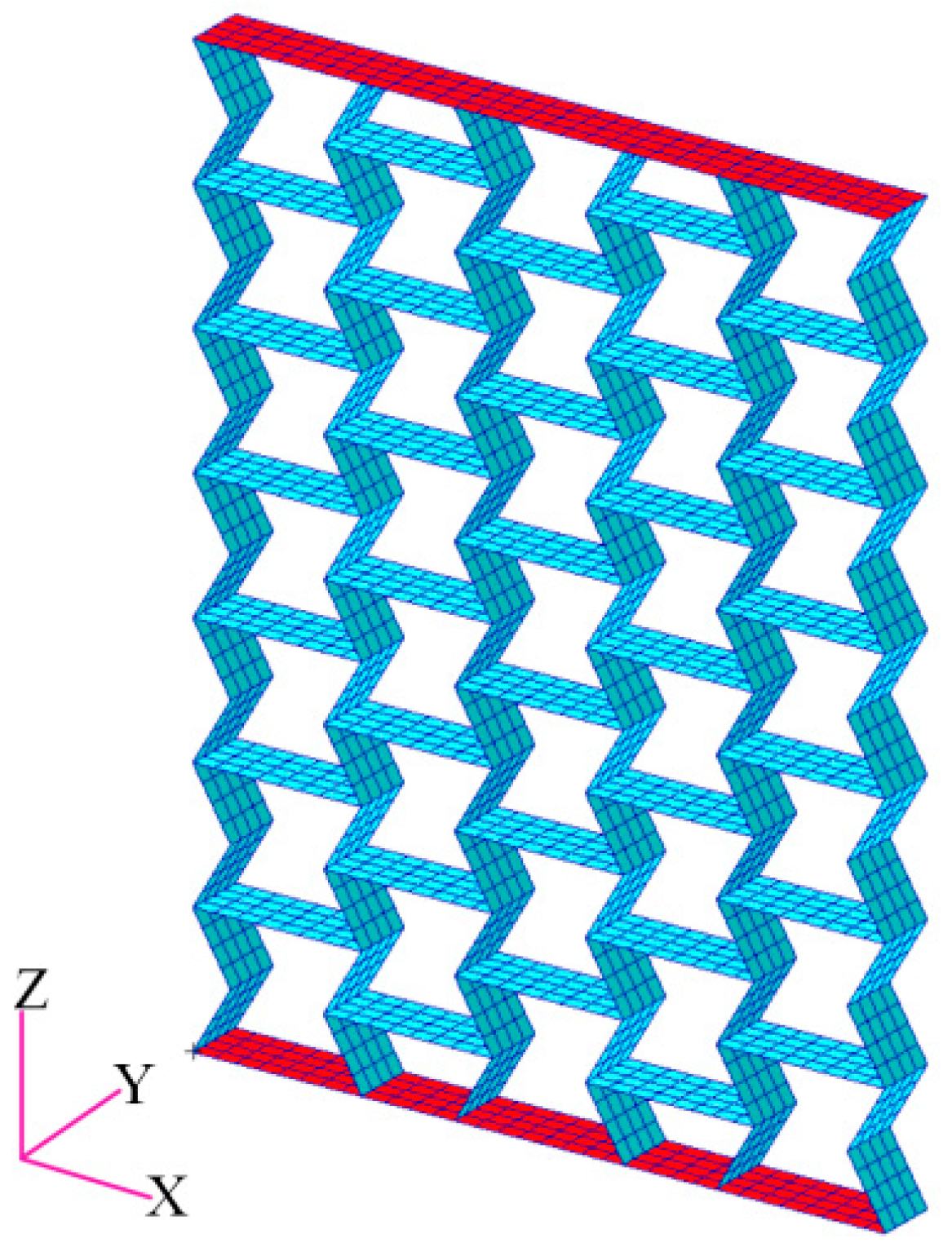
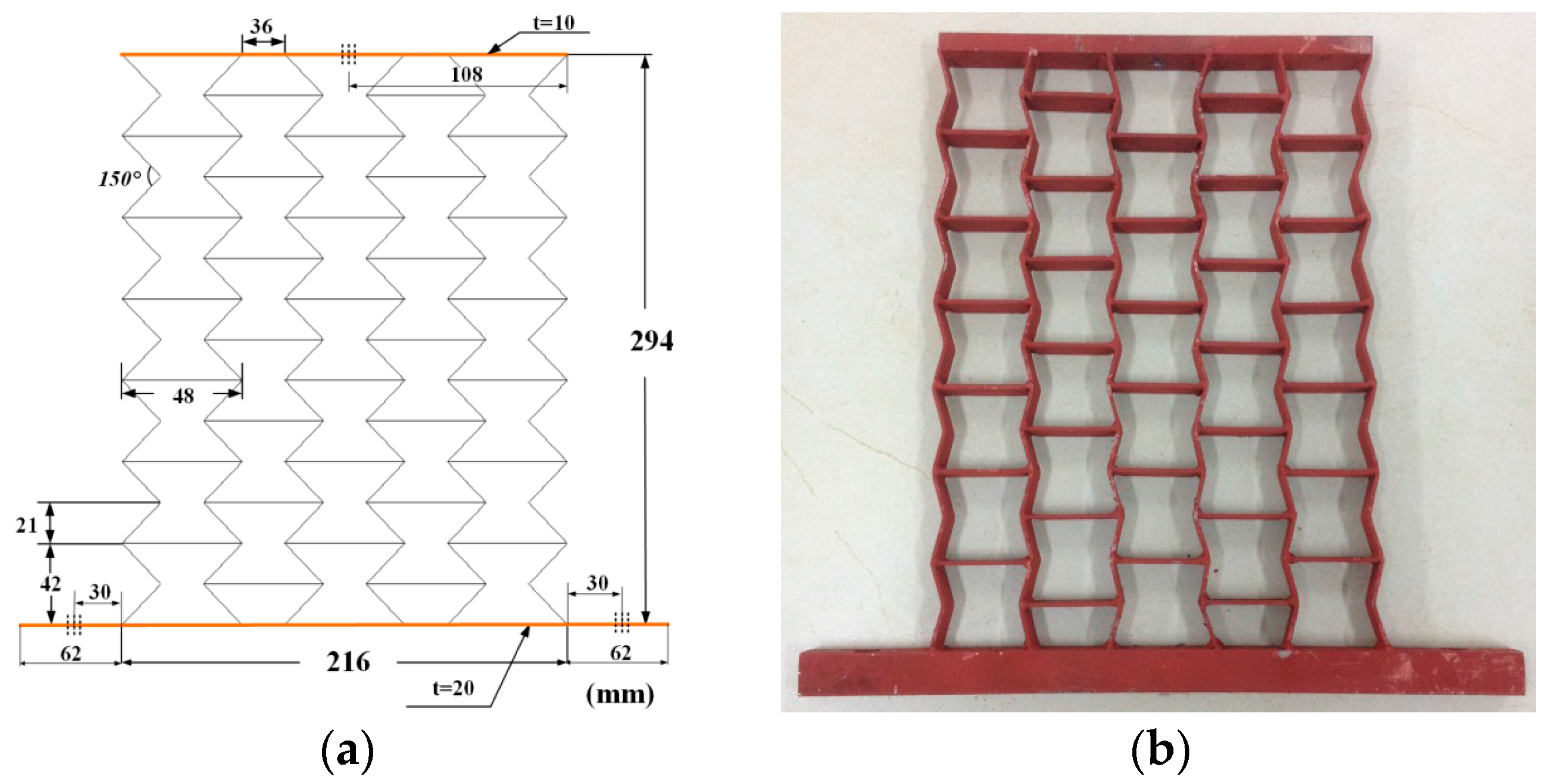
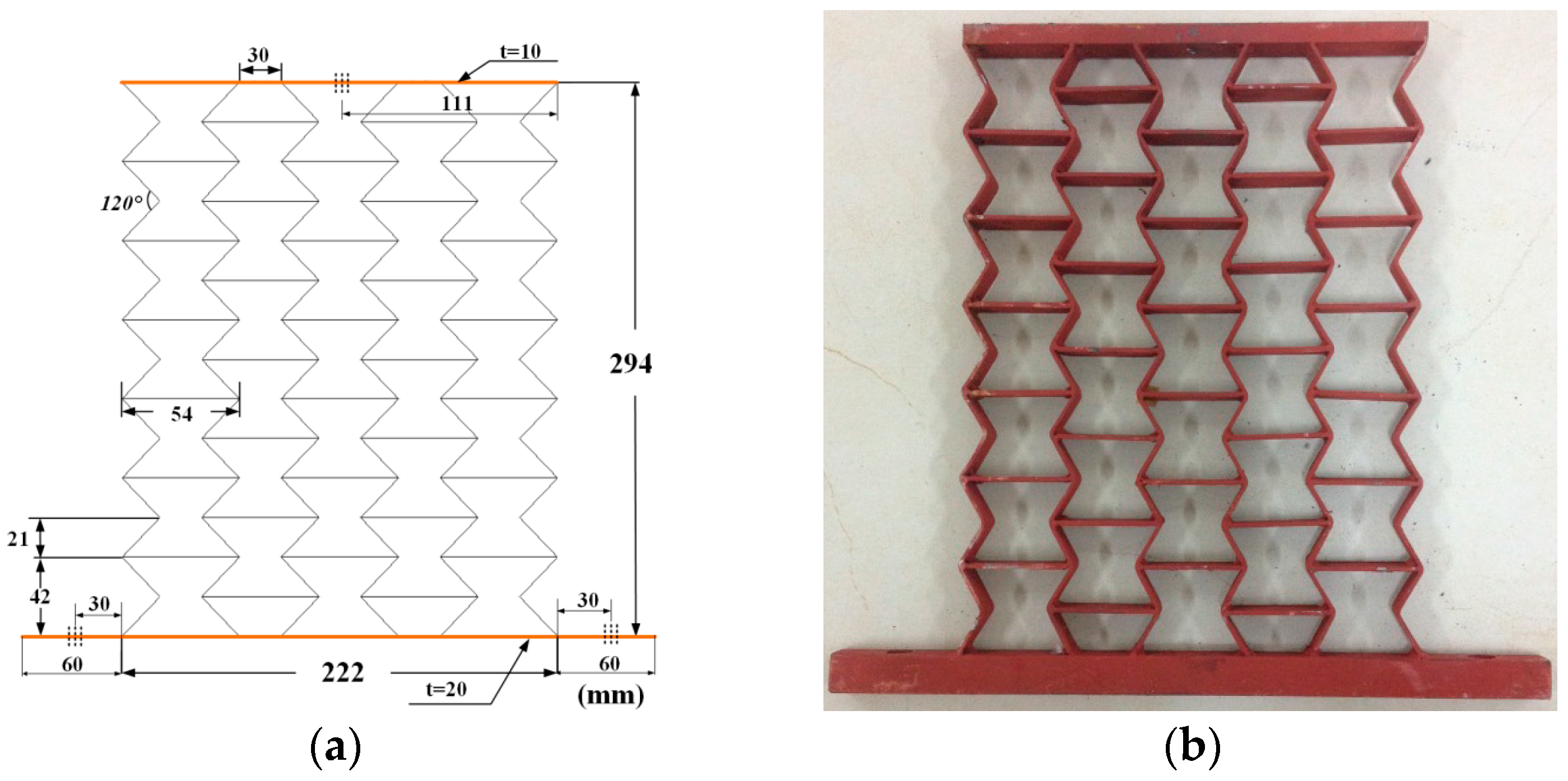
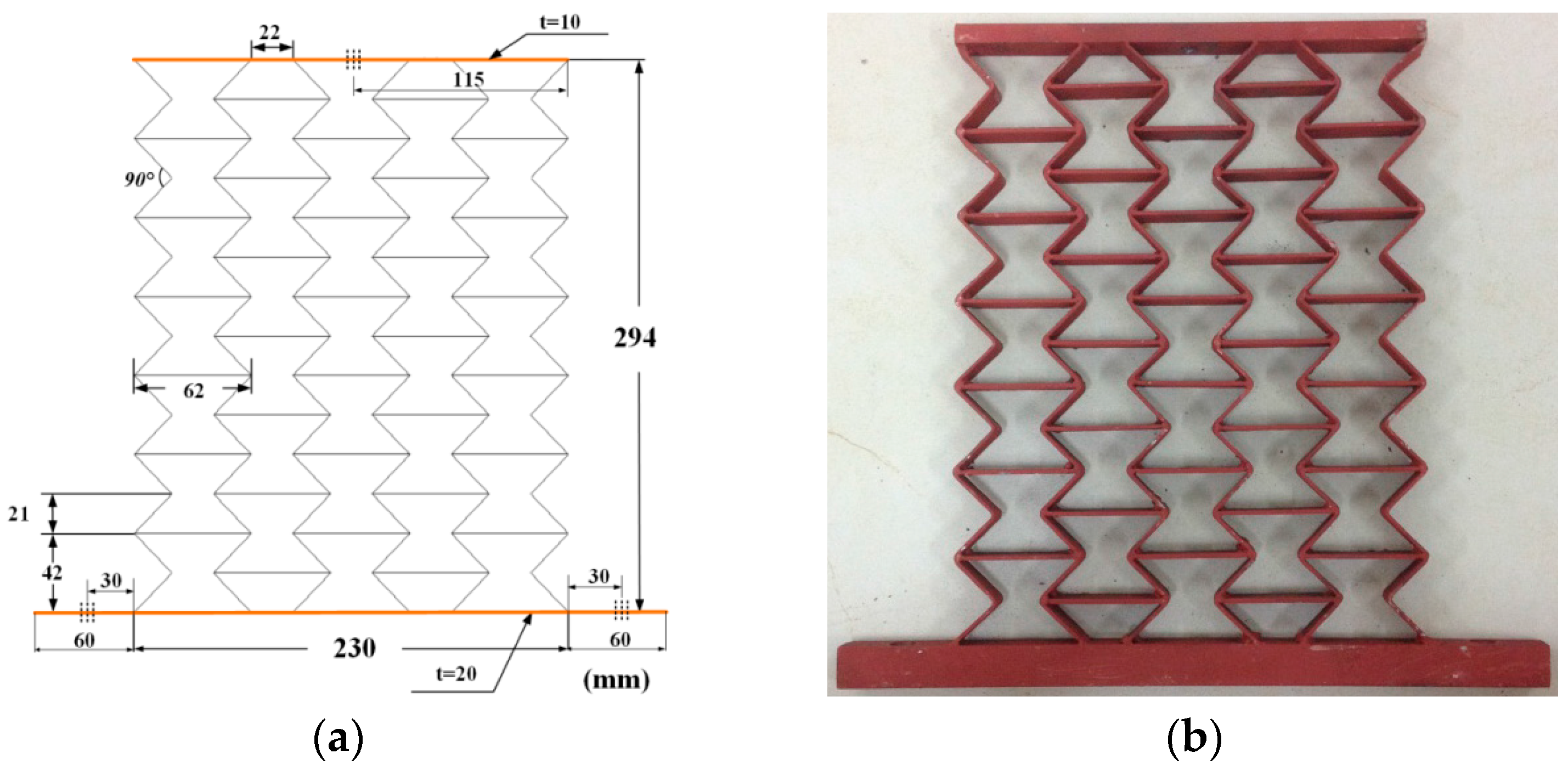
2.1. Finite Element Model Description
2.2. The Accuracy of Finite Element Models
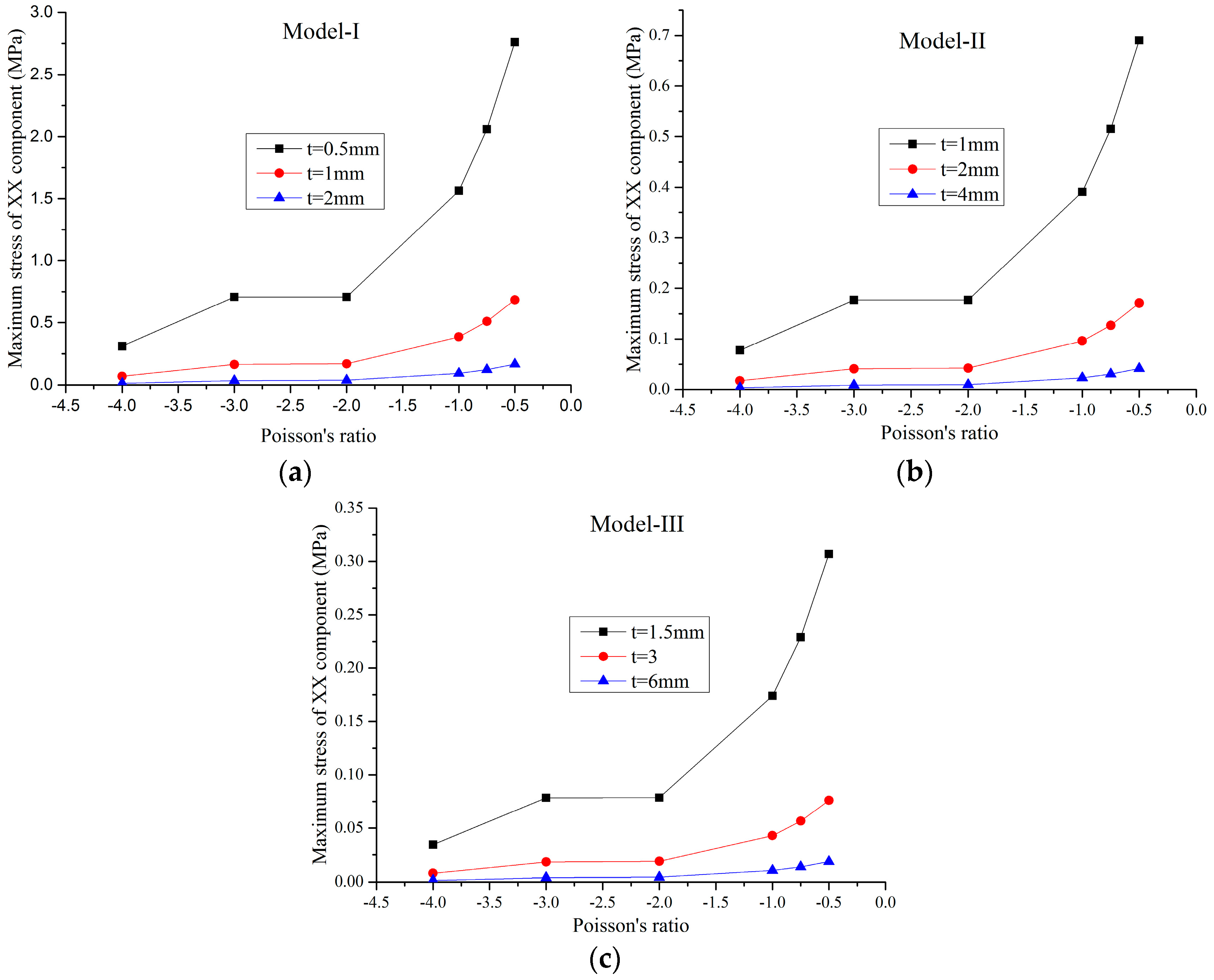
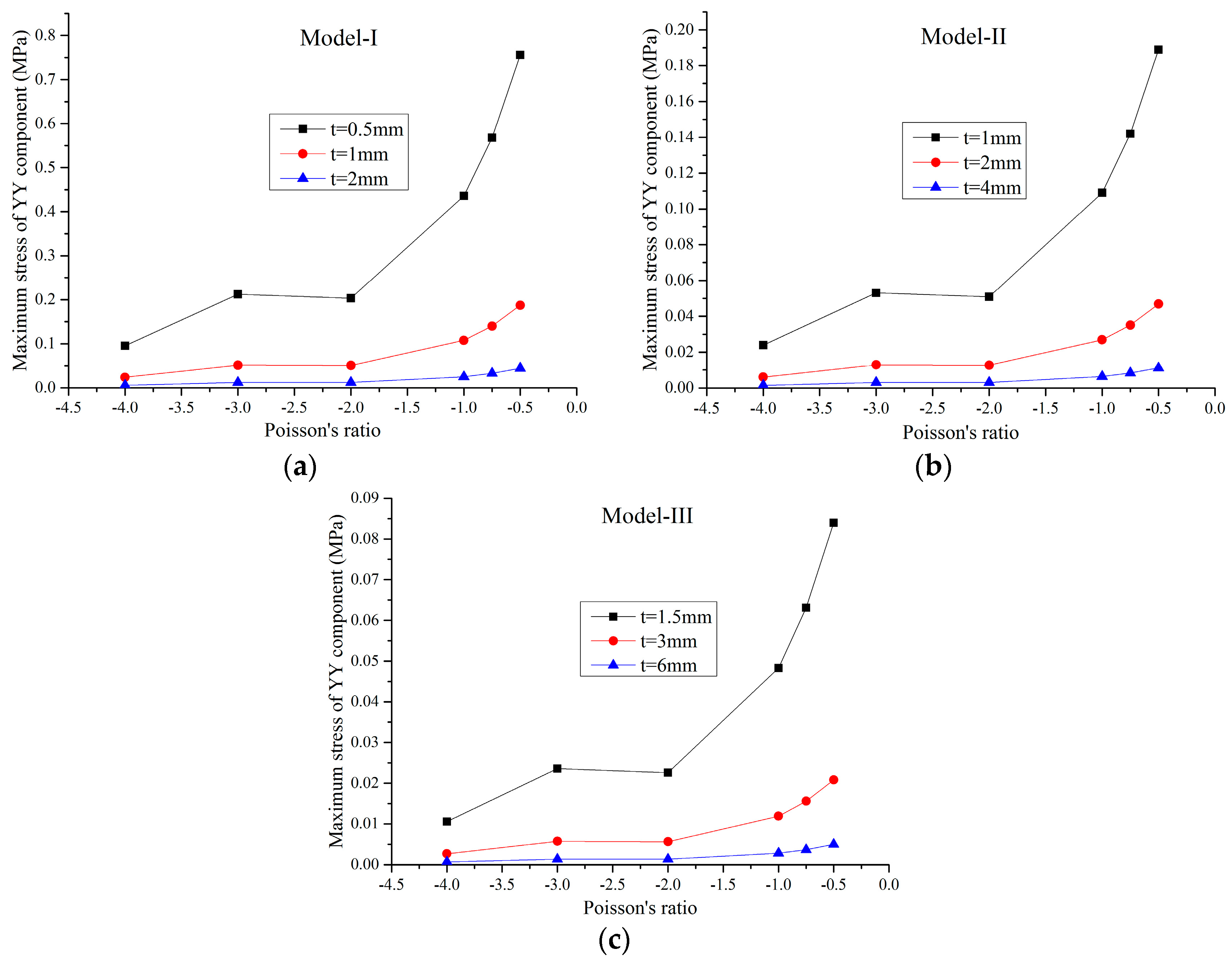
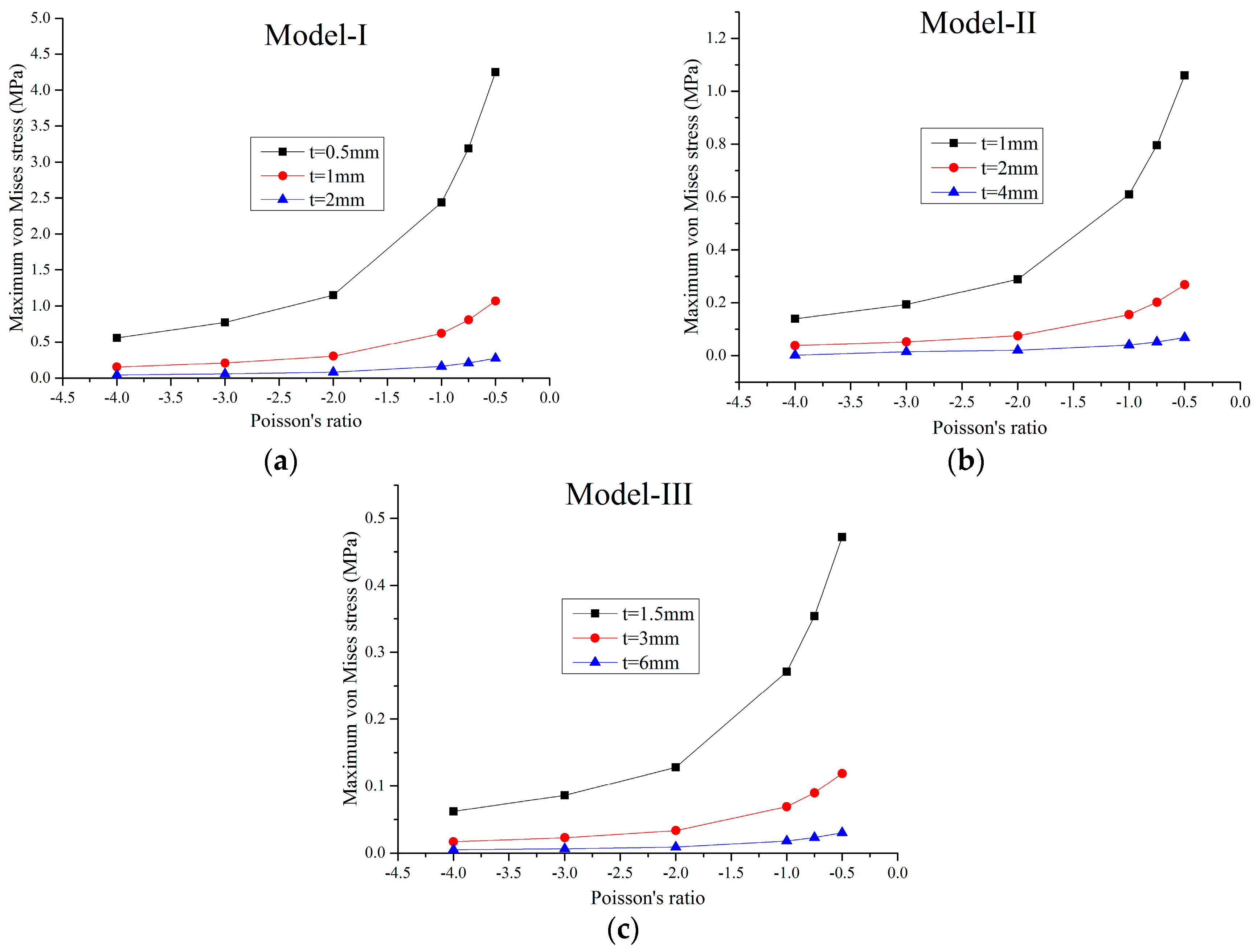
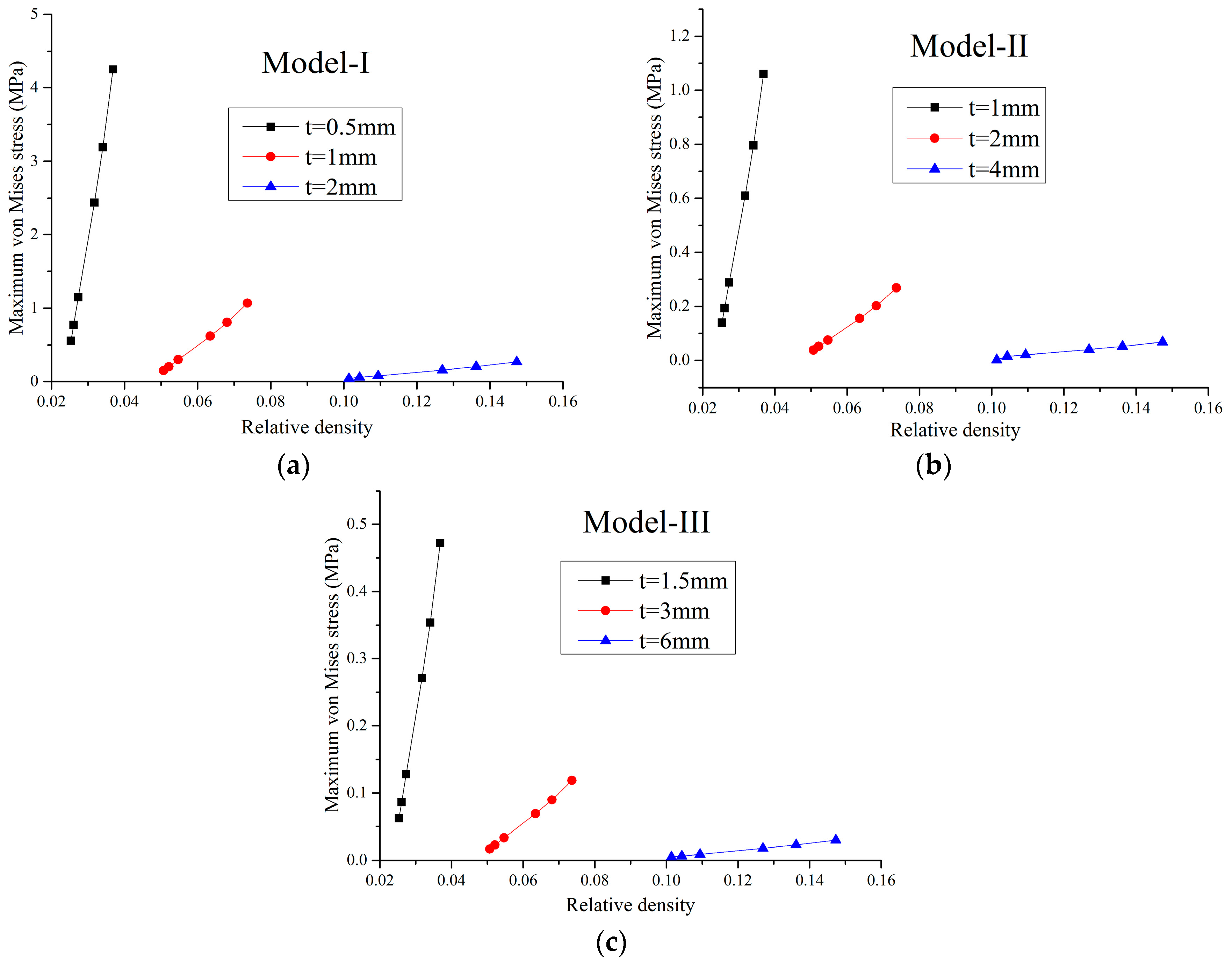
2.3. Linear Static Properties
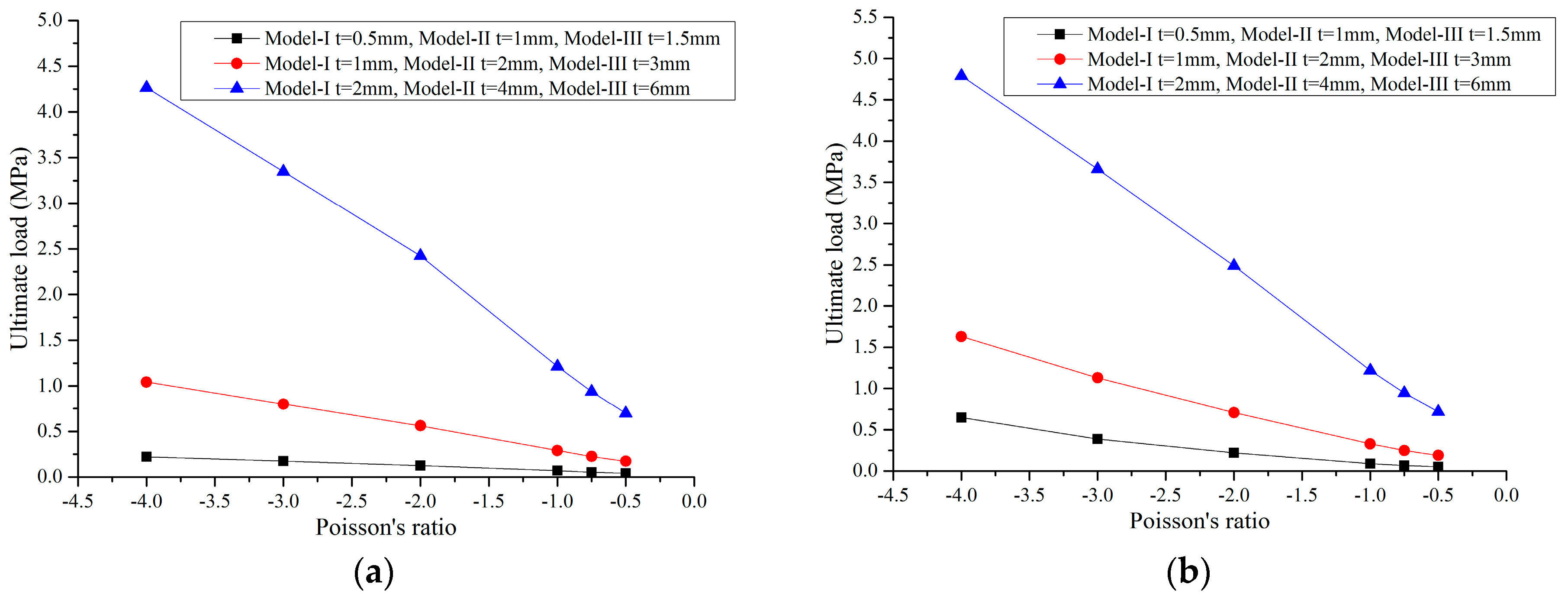
2.4. Nonlinear Static Properties
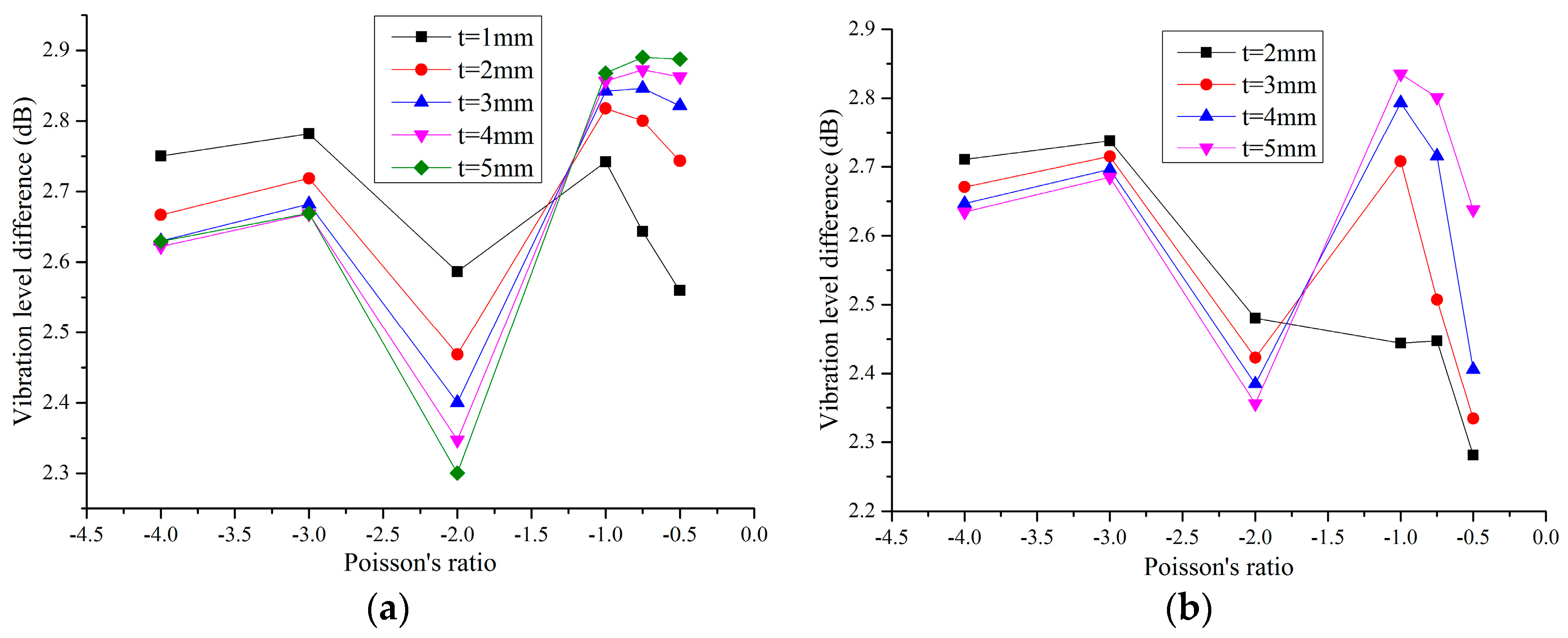
3. Effects of Parameters on Vibration Reduction Performance of the Auxetic Cellular Material
3.1. Numerical Analysis
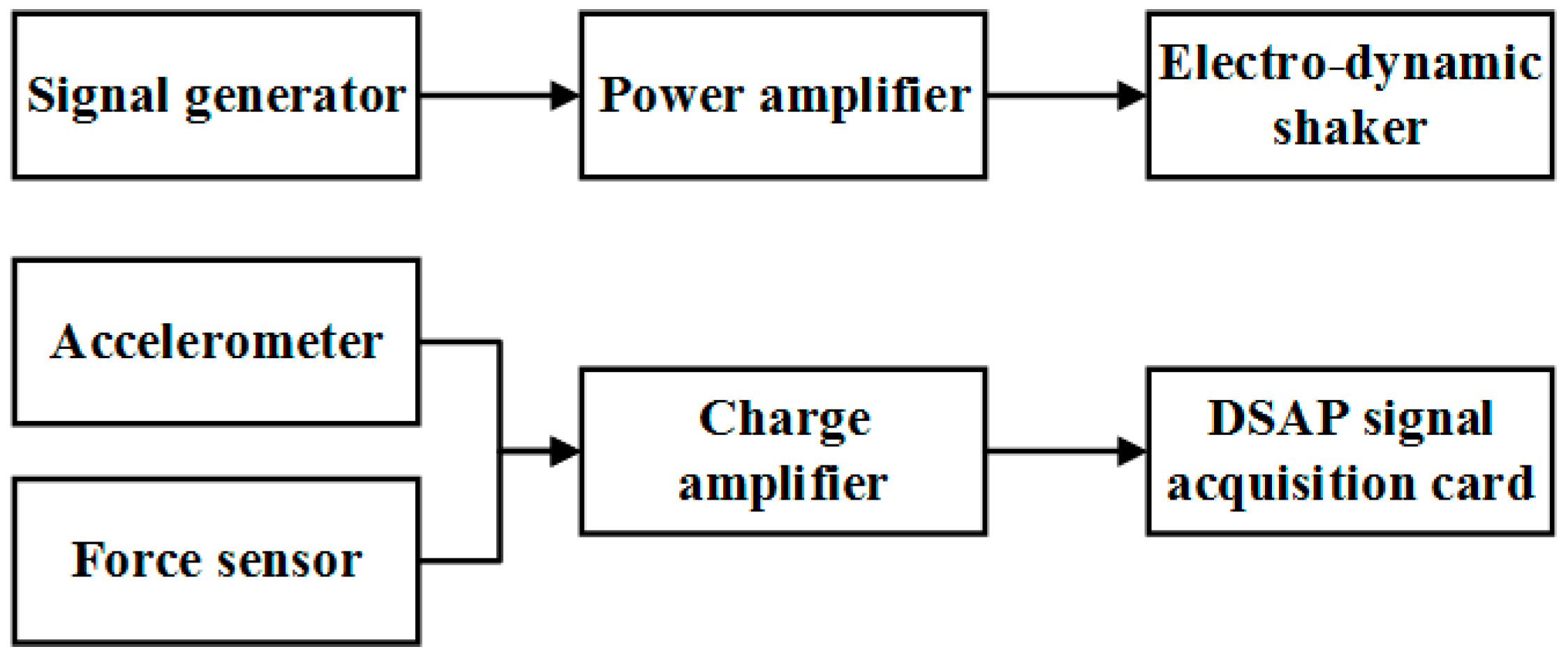
3.2. Experimental Testing
4. Conclusions
- For constant cell thickness, the maximum static stress of the honeycombs increases nonlinearly with the decrease of the Poisson’s ratio, and decreases linearly with the decrease of the relative density.
- Along with decreasing values of the Poisson’s ratio, the ultimate bearing capacity of the honeycombs decreases linearly under both compression and tension conditions, and the tensile ultimate bearing capacity is higher than the compressed one.
- When the Poisson’s ratio and relative density are kept constant, the ultimate bearing capacity of the auxetic materials is scale-independent.
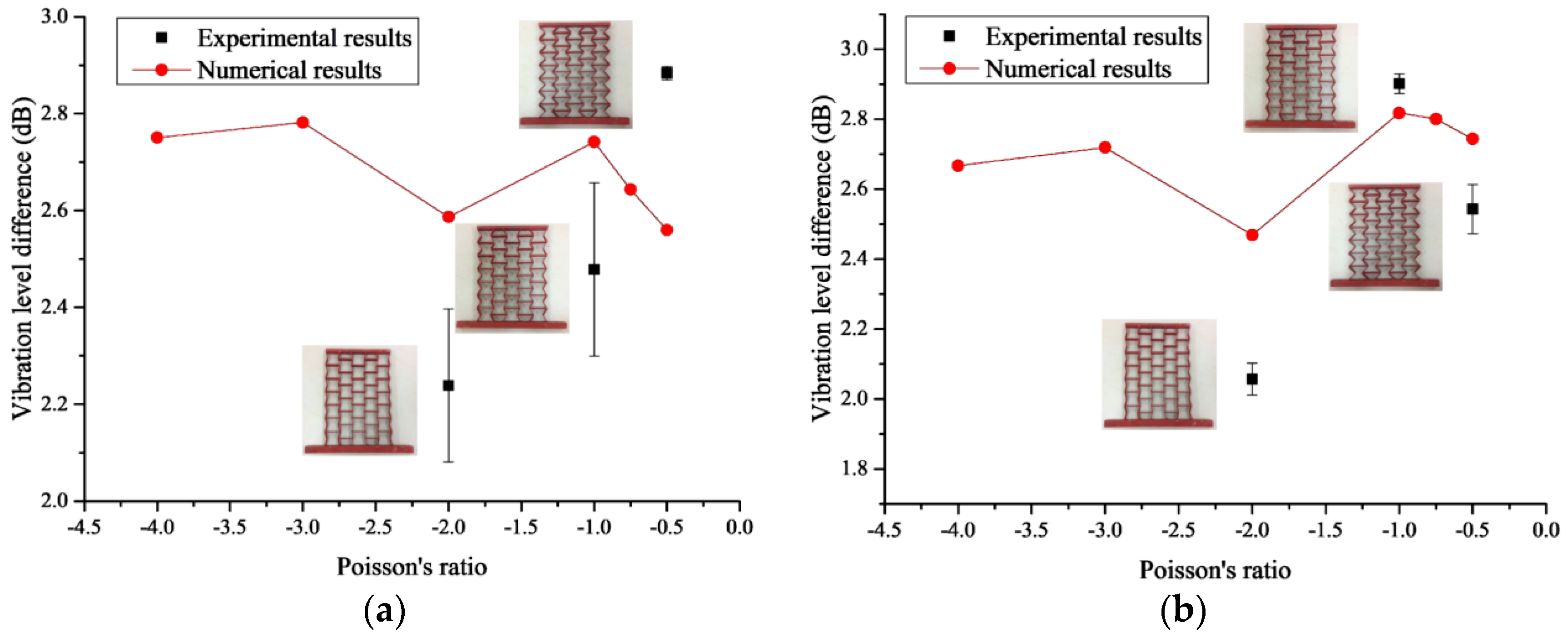
- When the Poisson’s ratio is larger than −1.5, the thinner the cell thickness, the better the dynamic performance of the honeycombs. Conversely, when it is smaller than −1.5, increasing the cell thickness leads to an increase in the vibration level difference of the honeycombs. Moreover, changing the scale has a great influence on the dynamic performance of thin-walled honeycombs, especially for the ones with small Poisson’s ratio.
- To improve the accuracy of experiments, casting or integral cutting technologies are suggested for the manufacture of experimental samples. In the near future, work will focus on the acoustic characteristics and dispersive properties of the materials.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Greaves, G.N. Poisson’s ratio over two centuries: Challenging hypotheses. Notes Rec. R. Soc. 2013, 67, 37–58. [Google Scholar] [CrossRef]
- Evans, K.E.; Nkansah, M.A.; Hutchinson, I.J.; Rogers, S.C. Molecular network design. Nature 1991, 353, 124–125. [Google Scholar] [CrossRef]
- Grima, J.N.; Attard, D.; Gatt, R.; Cassar, R.N. A novel process for the manufacture of auxetic foams and for their re-convention to conventional form. Adv. Eng. Mater. 2009, 11, 533–535. [Google Scholar] [CrossRef]
- Baughman, R.H.; Shacklette, J.M.; Zakhidev, A.A.; Stafström, S. Negative Poisson’s ratio as a common feature of cubic metals. Nature 1998, 392, 362–365. [Google Scholar] [CrossRef]
- Scarpa, F.; Panayiotou, P.; Tomlinson, G. Numerical and experimental uniaxial loading on in-plane auxetic honeycombs. J. Strain Anal. Eng. Des. 2000, 35, 383–388. [Google Scholar] [CrossRef]
- Ghaedizadeh, A.; Shen, J.; Ren, X.; Xie, Y.M. Tuning the performance of metallic auxetic metamaterials by using buckling and plasticity. Materials 2016, 9, 54. [Google Scholar] [CrossRef]
- Grima, J.N.; Attard, D.; Cassar, R.N.; Farrugia, L.; Trapani, L.; Gatt, R. On the mechanical properties and auxetic potential of various organic networked polymers. Mol. Simul. 2008, 34, 1149–1158. [Google Scholar] [CrossRef]
- Spagnoli, A.; Brighenti, R.; Lanfranchi, M.; Soncini, F. On the auxetic behaviour of metamaterials with re-entrant cell structures. Proced. Eng. 2015, 109, 410–417. [Google Scholar] [CrossRef]
- Azoti, W.L.; Koutsawa, Y.; Bonfoh, N.; Lipinski, P.; Belouettar, S. Analytical modeling of multilayered dynamic sandwich composites embedded with auxetic layers. Eng. Struct. 2013, 57, 248–253. [Google Scholar] [CrossRef]
- Alderson, K.L.; Pickles, A.P.; Neale, P.J.; Evans, K.E. Auxetic polyethylene: The effect of a negative Poisson’s ratio on hardness. Acta Metall. Mater. 1994, 42, 2261–2266. [Google Scholar] [CrossRef]
- Prawoto, Y. Seeing auxetic materials from the mechanics point of view: A structural review on the negative Poisson’s ratio. Comput. Mater. Sci. 2012, 58, 140–153. [Google Scholar] [CrossRef]
- Chekkal, I.; Remillat, C.; Scarpa, F. Acoustic properties of auxetic foams. High Perform. Struct. Mater. 2012, 124, 119–129. [Google Scholar] [CrossRef]
- Scarpa, F.; Ciffo, L.G.; Yates, J.R. Dynamic properties of high structural integrity auxetic open cell foam. Smart Mater. Struct. 2004, 13, 49–56. [Google Scholar] [CrossRef]
- Tee, K.F.; Spadoni, A.; Scarpa, F.; Ruzzene, M. Vibroacoustics and wave propagation of novel chiral honeycombs. In Proceedings of the Active and Passive Smart Structures and Integrated Systems, San Diego, CA, USA, 9 March 2008.
- Scarpa, F.; Tomlinson, G. Vibro-acoustics and damping analysis of negative Poisson’s ratio honeycombs. In Proceedings of the Smart Structures and Materials, San Diego, CA, USA, 1 March 1998; pp. 339–348.
- Alderson, A.; Alderson, K.L. Auxetic materials. In Proceedings of the Institution of Mechanical Engineers, Birmingham, UK, 1 April 2007; pp. 565–575. [CrossRef]
- Prall, D.; Lakes, R.S. Properties of a chiral honeycomb with Poisson’s ratio −1. Int. J. Mech. Sci. 1997, 39, 305–314. [Google Scholar] [CrossRef]
- Zhang, X.W.; Yang, D.Q. Numerical and experimental studies of a light-weight auxetic cellular vibration isolation base. Shock Vib. 2016. [Google Scholar] [CrossRef]
- Grima, J.N.; Gatt, R.; Farrugia, P.S.; Alderson, A.; Evans, K.E. Auxetic cellular materials and structures. In Proceedings of the ASME 2005 International Mechanical Engineering Congress and Exposition, Orlando, FL, USA, 5–11 November 2005; pp. 489–495. [CrossRef]
- Dascalu, C.; Bilbie, G.; Agiasofitou, E.K. Damage and size effects in elastic solids: A homogenization approach. Int. J. Solids Struct. 2008, 45, 409–430. [Google Scholar] [CrossRef]
- Gilat, R.; Aboudi, J. Behavior of elastoplastic auxetic microstructural arrays. Materials 2013, 6, 726–737. [Google Scholar] [CrossRef]
- Wan, H.; Ohtaki, H.; Kotosaka, S.; Hu, G. A study of negative Poisson’s ratios in auxetic honeycombs based on a large deflection model. Eur. J. Mech. A-Sol. 2004, 23, 95–106. [Google Scholar] [CrossRef]
- Liu, W.; Wang, N.; Huang, J.; Zhong, H. The effect of irregularity, residual convex units and stresses on the effective mechanical properties of 2D auxetic cellular structure. Mater. Sci. Eng. A 2014, 609, 26–33. [Google Scholar] [CrossRef]
- Grima, J.N.; Manicaro, E.; Attard, D. Auxetic Behavior from Connected Different-Sized Squares and Rectangles; Proceedings of the Royal Society A: London, UK, 2011; pp. 439–458. [Google Scholar] [CrossRef]
- Chetcuti, E.; Ellul, B.; Manicaro, E.; Brincat, J.; Attard, D.; Gatt, R.; Grima, J.N. Modeling auxetic foams through semi-rigid rotating triangles. Phys. Status Solidi (B) 2014, 251, 297–306. [Google Scholar] [CrossRef]
- Rad, M.S.; Ahmad, Z.; Alias, A. Computational approach in formulating mechanical characteristics of 3D star honeycomb auxetic structure. Adv. Mater. Sci. Eng. 2015. [Google Scholar] [CrossRef]
- Grima, J.N.; Alderson, A.; Gatt, R.; Evans, K.E. On the potential of connected stars as auxetic systems. Mol. Simul. 2005, 31, 925–935. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties, 2nd ed.; Pergamon Press: London, UK, 1988; pp. 93–159. [Google Scholar]
- Masters, I.G.; Evans, K.E. Models for the elastic deformation of honeycombs. Compos. Struct. 1996, 35, 403–408. [Google Scholar] [CrossRef]
- Mir, M.; Ali, M.N.; Sami, J.; Ansari, U. Review of mechanics and applications of auxetic structures. Adv. Mater. Sci. Eng. 2014. [Google Scholar] [CrossRef]

| Cell Angle | ||||||
| FE Model | −3.71 | −2.88 | −2.06 | −1.06 | −0.80 | −0.49 |
| Theory | −4.00 | −3.00 | −2.00 | −1.00 | −0.75 | −0.50 |
| Relative Error | −7.3% | −4.0% | 3.2% | 6.1% | 7.0% | −0.2% |
| Force | 4 N | 6 N | 8 N | Average | Relative Error with FEM Result |
|---|---|---|---|---|---|
| 1.78 | 2.18 | 2.75 | 2.24 | −13.44% | |
| 2.04 | 2.34 | 3.05 | 2.48 | −9.61% | |
| 2.73 | 2.91 | 3.01 | 2.88 | 12.64% |
| Force | 4 N | 6 N | 8 N | Average | Relative Error with FEM Result |
|---|---|---|---|---|---|
| 1.83 | 1.99 | 2.34 | 2.06 | −16.69% | |
| 2.73 | 2.85 | 3.13 | 2.90 | 2.98% | |
| 2.27 | 2.46 | 2.90 | 2.54 | −7.32% |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Yang, D. Mechanical Properties of Auxetic Cellular Material Consisting of Re-Entrant Hexagonal Honeycombs. Materials 2016, 9, 900. https://doi.org/10.3390/ma9110900
Zhang X, Yang D. Mechanical Properties of Auxetic Cellular Material Consisting of Re-Entrant Hexagonal Honeycombs. Materials. 2016; 9(11):900. https://doi.org/10.3390/ma9110900
Chicago/Turabian StyleZhang, Xiangwen, and Deqing Yang. 2016. "Mechanical Properties of Auxetic Cellular Material Consisting of Re-Entrant Hexagonal Honeycombs" Materials 9, no. 11: 900. https://doi.org/10.3390/ma9110900






