Tuning the Performance of Metallic Auxetic Metamaterials by Using Buckling and Plasticity
Abstract
:1. Introduction
2. A General Approach to Tuning the Performance of 2D Metallic Auxetic Metamaterial
2.1. Initial Geometric Design of Microstructures Modified from a Regular Pattern
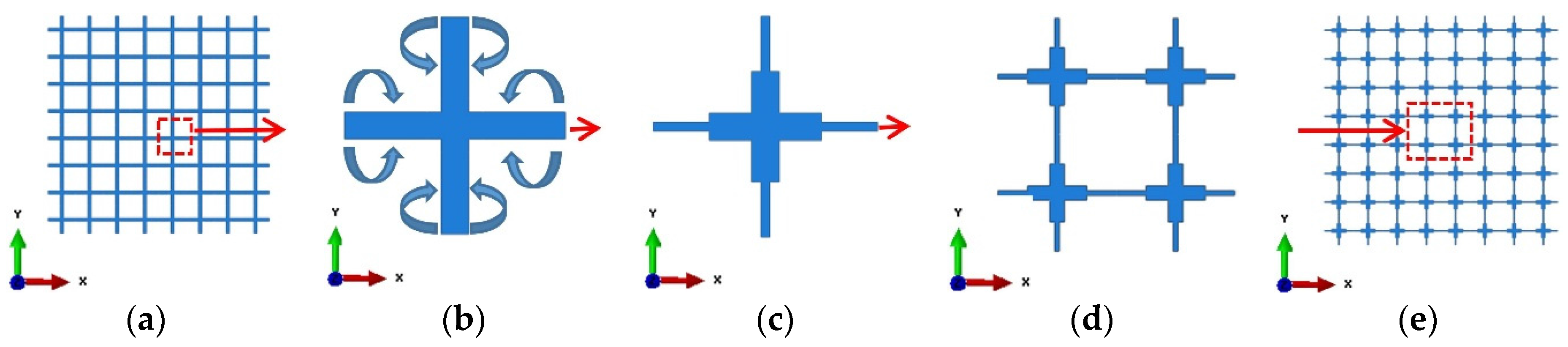
2.2. Investigation of the Instability of Initial 2D Auxetic Metamaterial Using a Linear Perturbation Procedure (Linear Buckling Analysis)
2.3. Identification of the Desired Buckling Pattern from an Elastic Instability Analysis
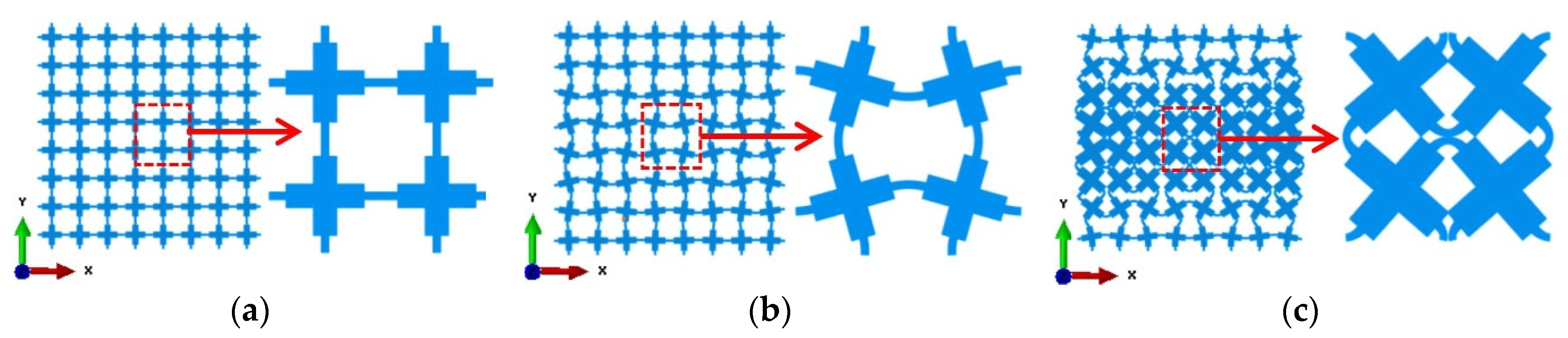
2.4. Design New Metamaterials through Superposition of Desired Buckling Mode
3. Experiments
3.1. Fabrication of 2D Metamaterials for Experiments
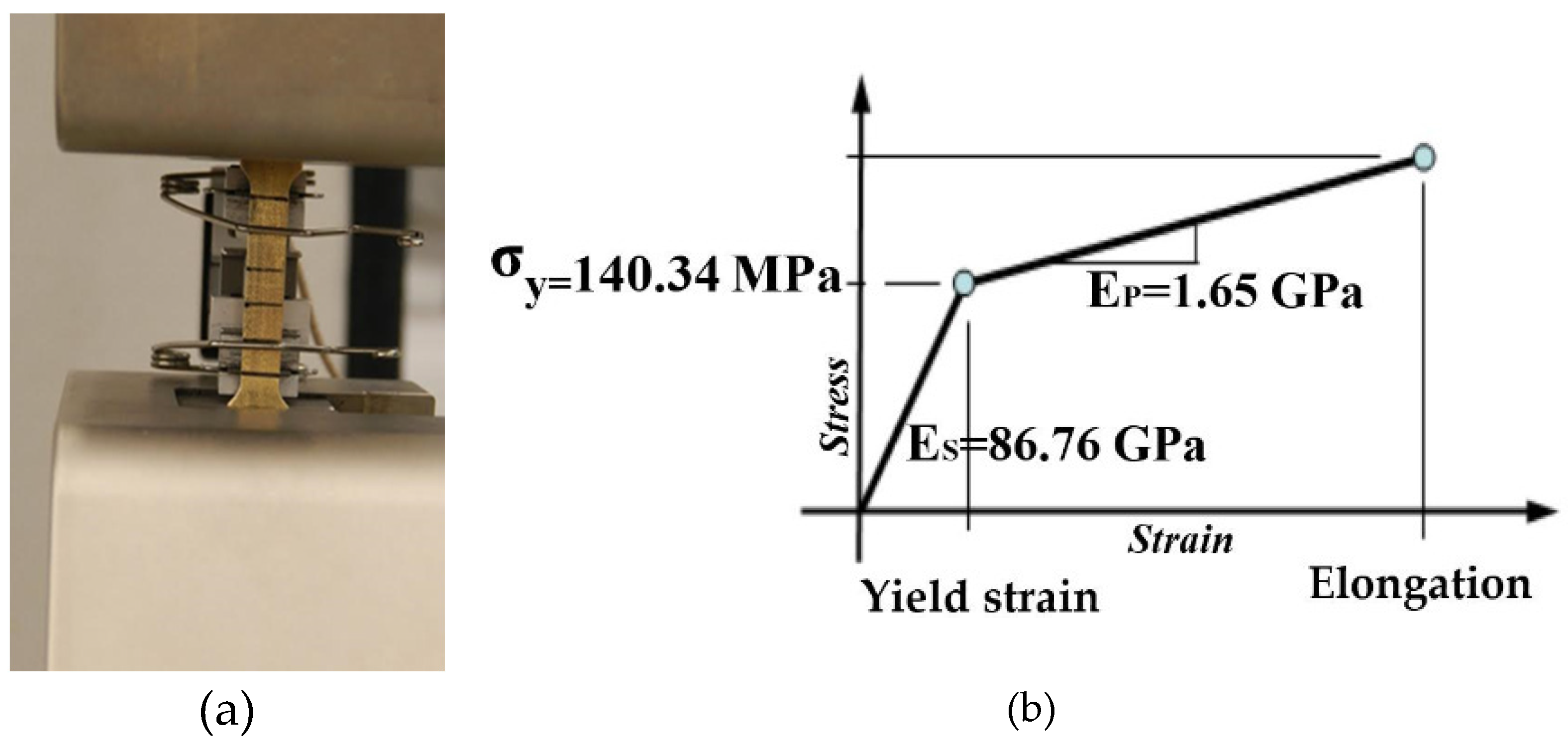
| Modulus of Elasticity (GPa) | Yield Stress (MPa) | Strain Hardening Modulus (GPa) | Density (GPa) |
|---|---|---|---|
| 86.76 | 140.34 | 1.65 | 8720 |

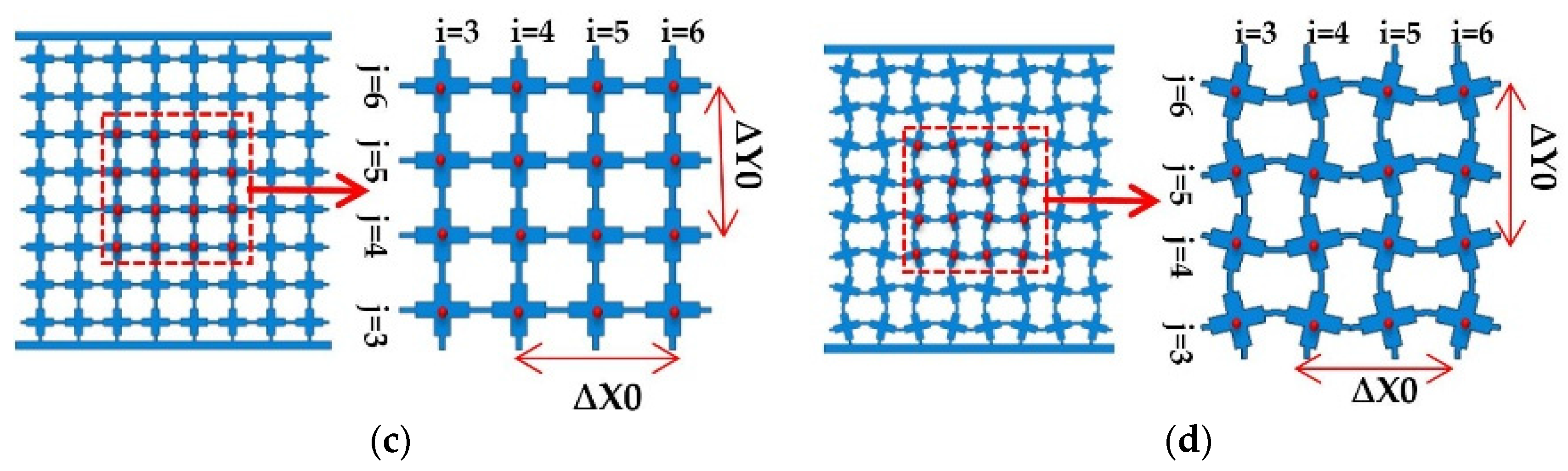

3.2. Experimental Setup for Uniaxial Compression Testing of 2D Metallic Metamaterials
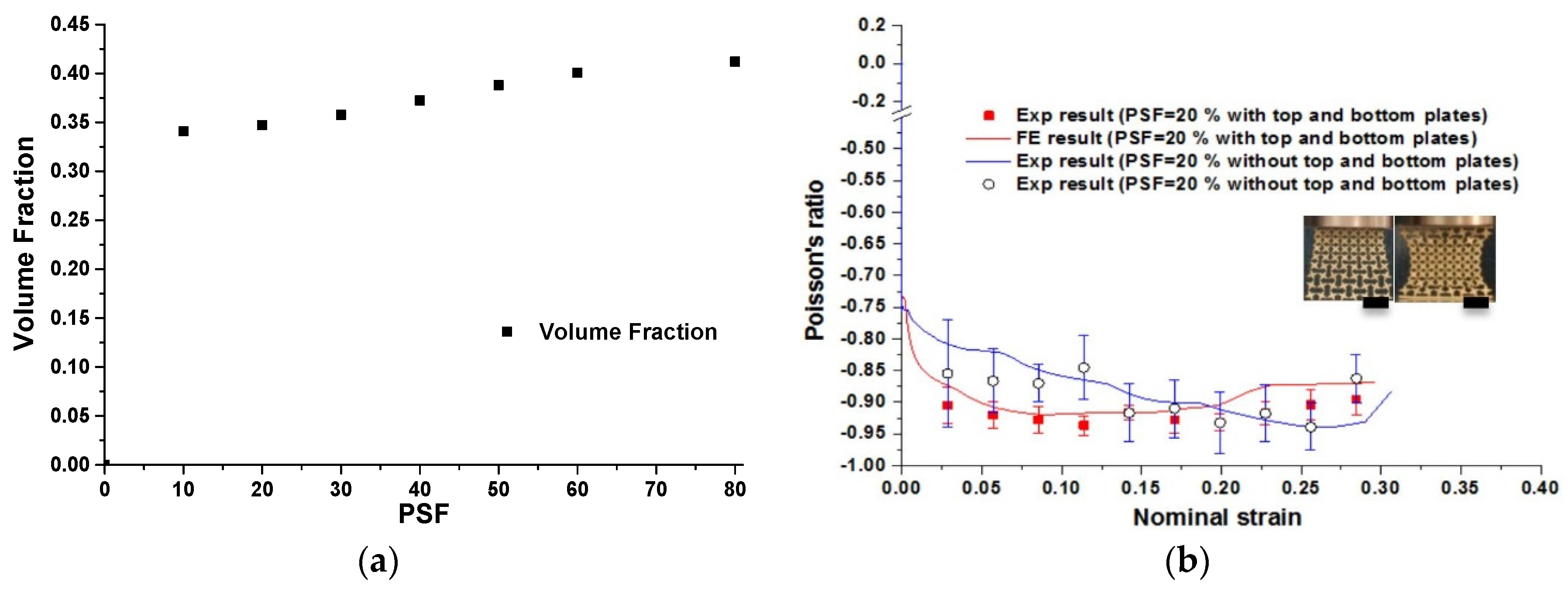
3.3. Experimental Results
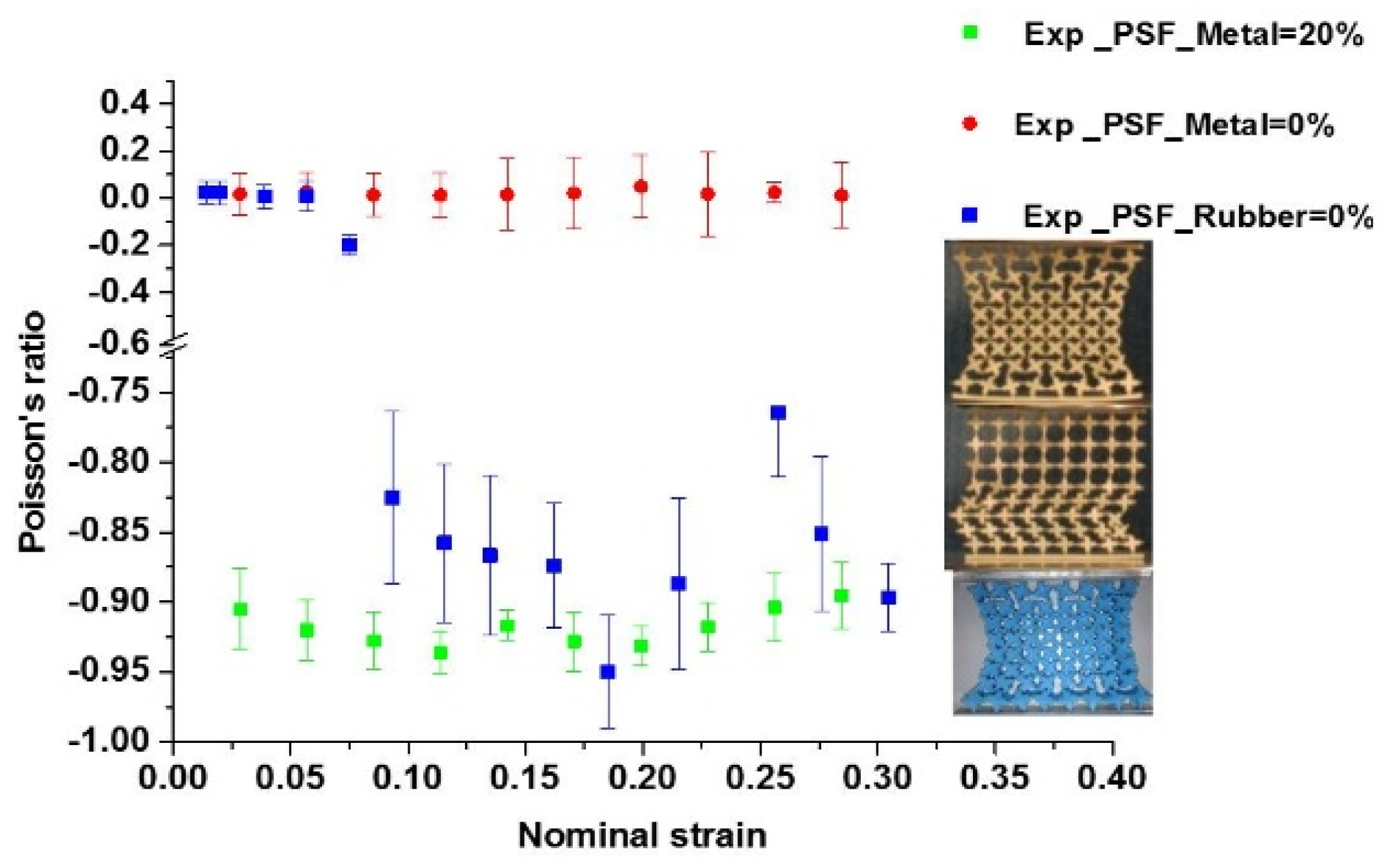
4. FE Simulations
4.1. Post-Buckling Analysis and Validation of Numerical Models
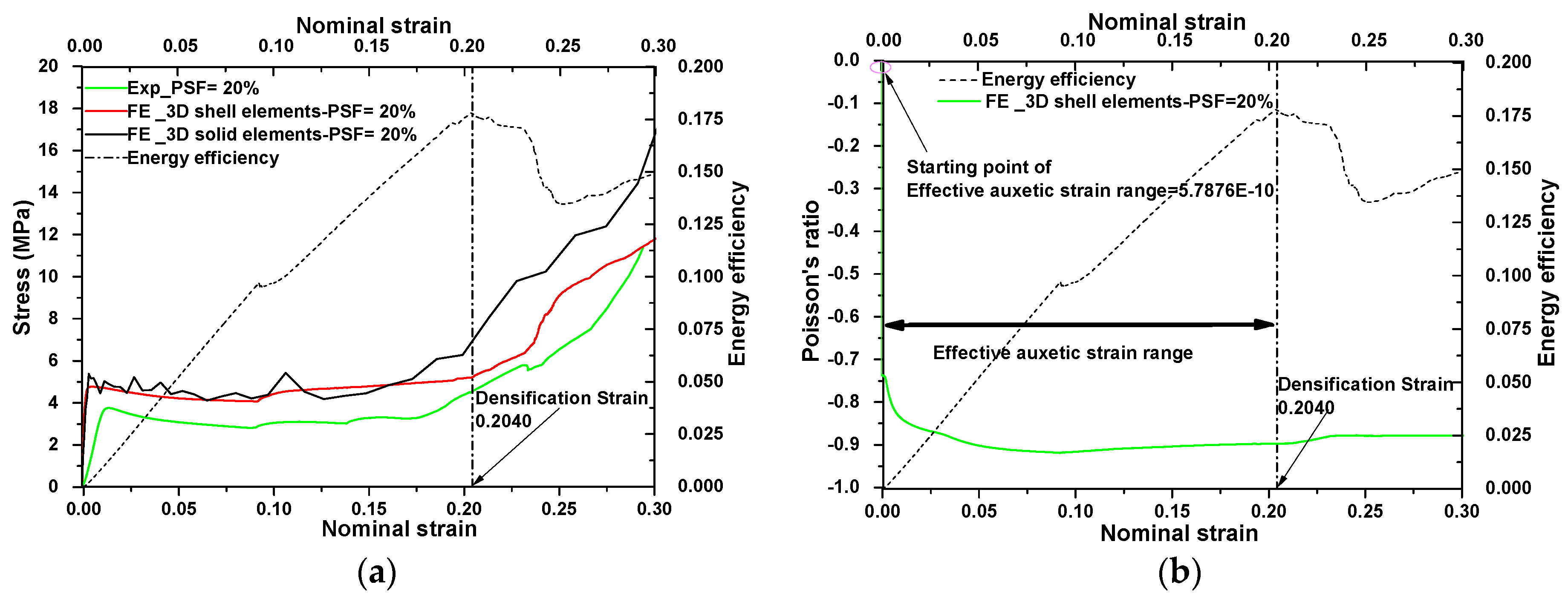
4.2. Defining a Strain Range for Auxetic Metamaterials Using the Energy Efficiency Method
4.3. Parametric Studies
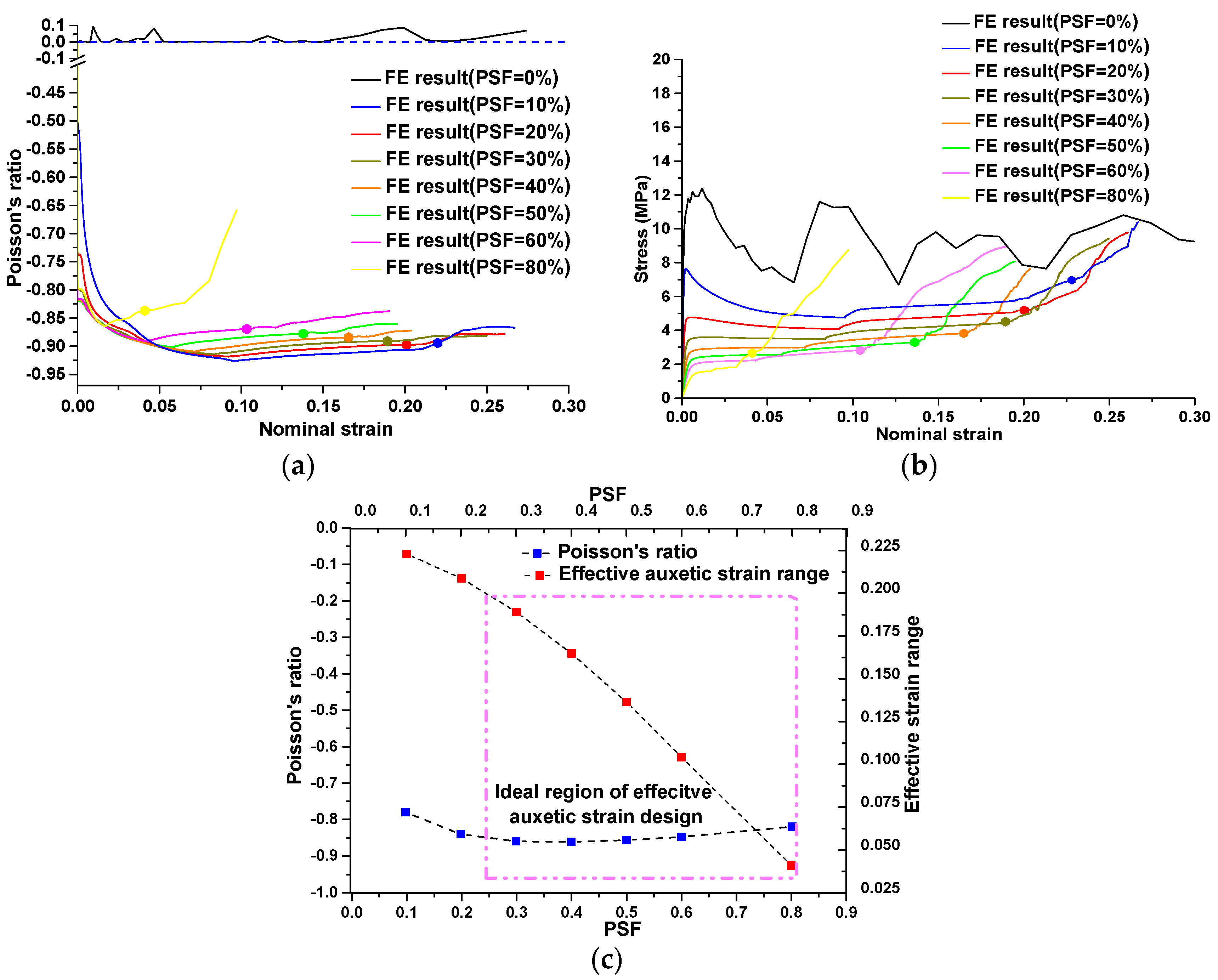
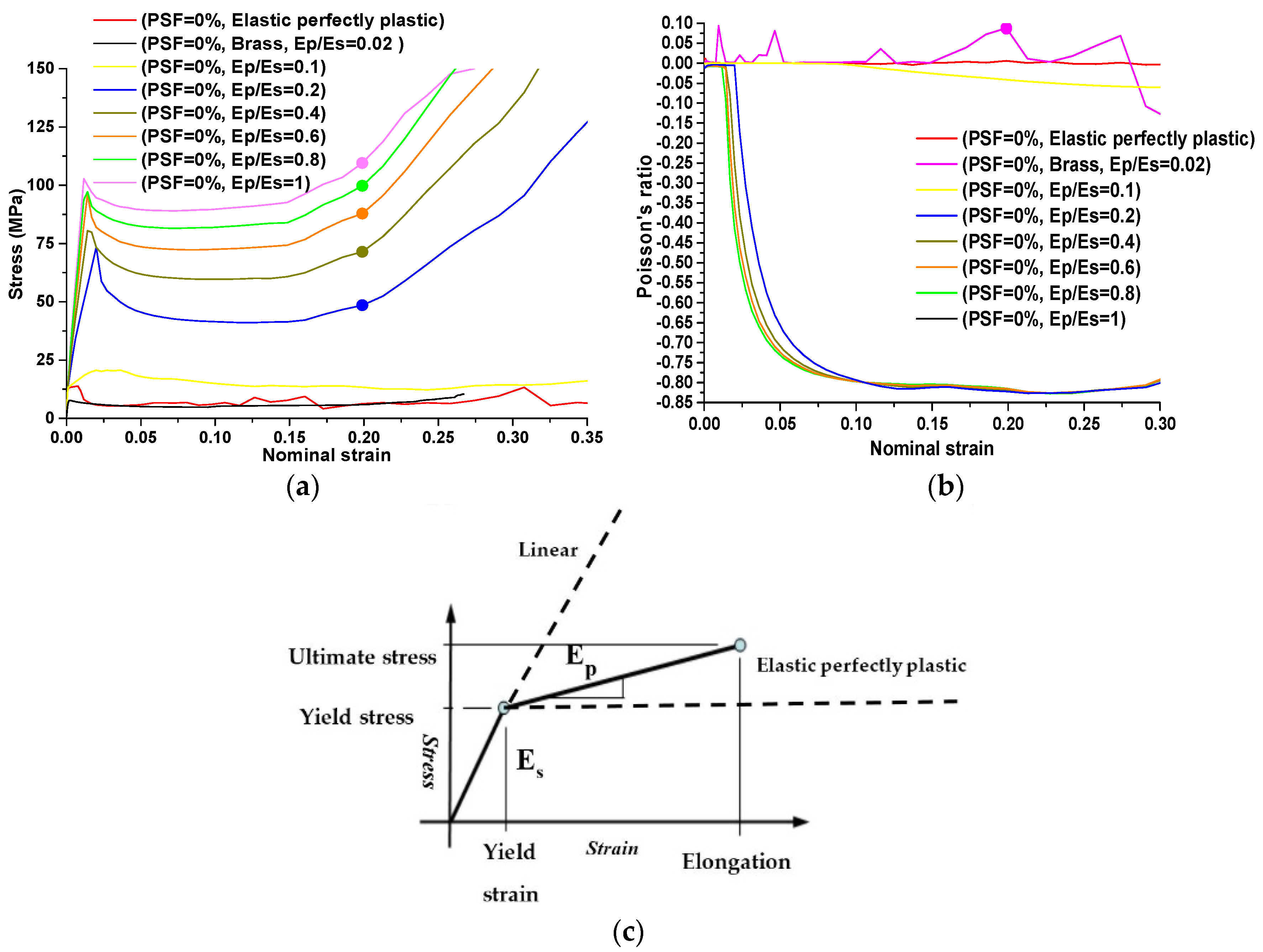
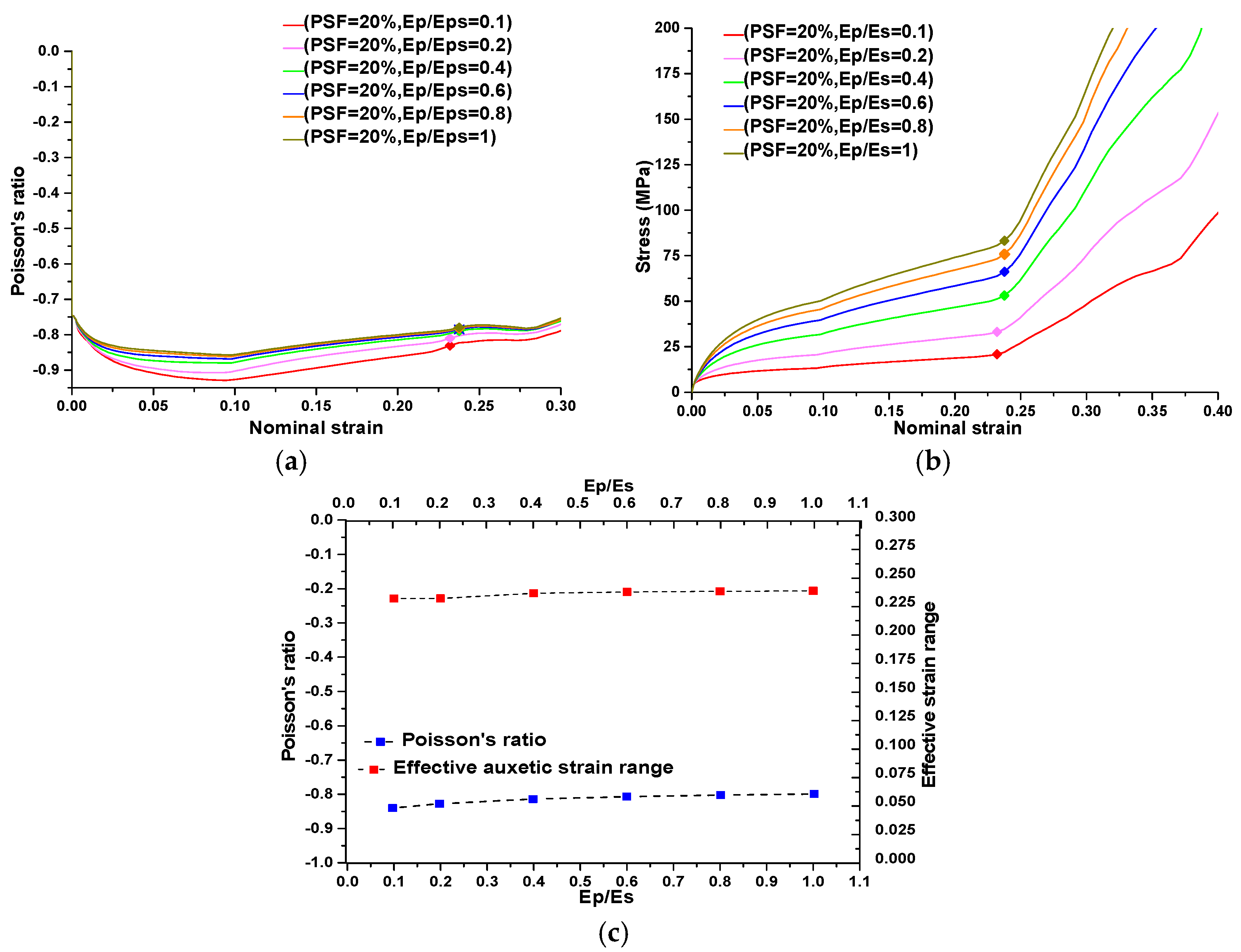
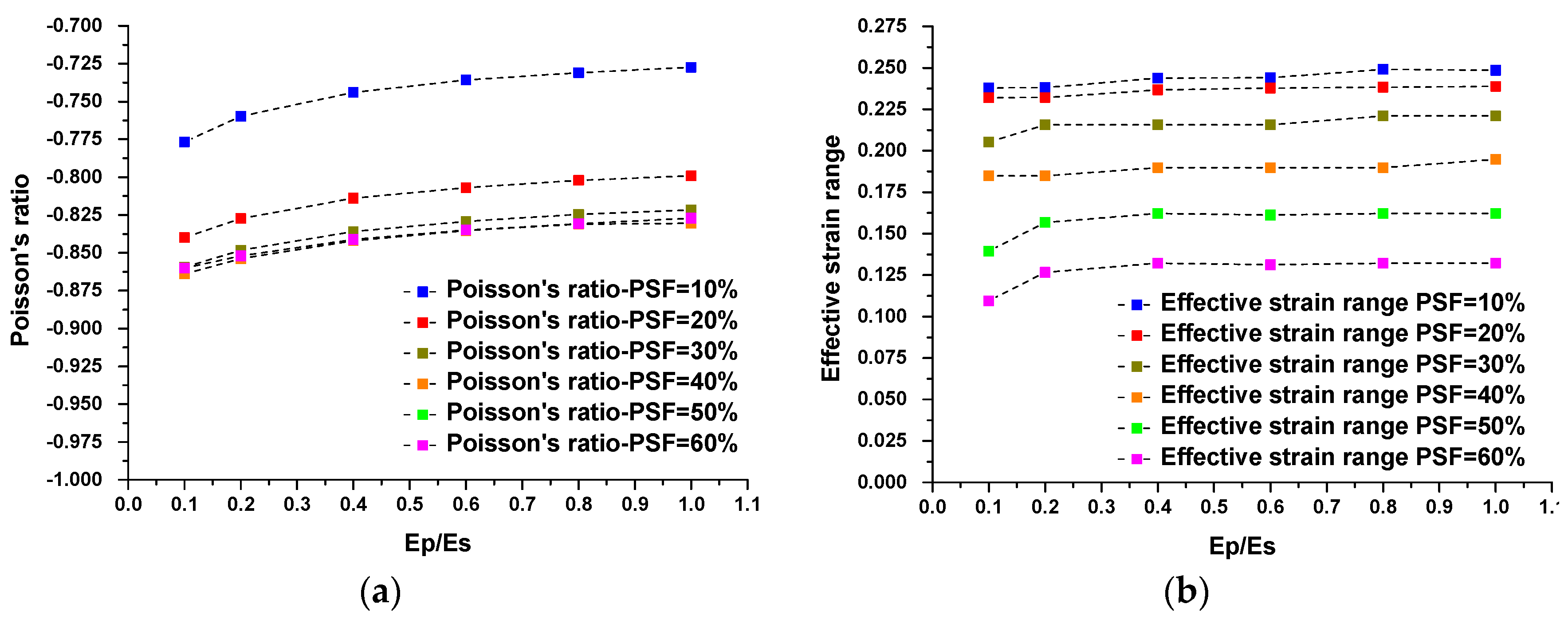
5. Discussion and Conclusions
- (1)
- The deformation process of the metallic auxetic metamaterial is influenced by boundary conditions; however, the auxetic behavior and its performance corresponding to different deformation processes are insensitive to boundary conditions.
- (2)
- The auxetic behavior of our designed metallic metamaterial remains within the effective auxetic strain range.
- (3)
- The effective auxetic strain can be controlled individually by PSF while maintaining a similarly negative value of Poisson’s ratio, especially when the PSF is in the range of 10% to 60%.
- (4)
- The stiffness and strength of the metallic auxetic metamaterials can be individually controlled through adjustment of the properties of the base materials, while the negative value of Poisson’s ratio remains relatively constant.
- (5)
- The loss of auxetic behavior in the metallic buckling-induced metamaterial is attributed to the localization of plastic collapse of RVEs.
- (6)
- The results from FE simulation confirmed that the buckling-induced metamaterial would have auxetic behavior after the plastic hardening modulus is large than a certain value determined by the microstructures of metamaterials. These results confirm that the effectiveness of increasing plastic hardening ratio will restore the auxetic behavior of buckling-induced metamaterials.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Evans, K.E.; Alderson, A. Auxetic materials: Functional materials and structures from lateral thinking! Adv. Mater. 2000, 12, 617–628. [Google Scholar] [CrossRef]
- Fozdar, D.Y.; Soman, P.; Lee, J.W.; Han, L.-H.; Chen, S. Three dimensional polymer constructs exhibiting a tunable negative poisson’s ratio. Adv. Mater. 2011, 21, 2712–2720. [Google Scholar] [CrossRef] [PubMed]
- Lakes, R. Foam structures with a negative Poisson’s ratio. Science 1987, 235, 1038–1040. [Google Scholar] [CrossRef] [PubMed]
- Evans, K.E.; Nkansah, M.A.; Hutchinson, I.J.; Rogers, S.C. Molecular network design. Nature 1991, 353, 124. [Google Scholar] [CrossRef]
- Friis, E.A.; Lakes, R.S.; Park, J.B. Negative Poisson’s ratio polymeric and metallic foams. J. Mater. Sci. 1988, 23, 4406–4414. [Google Scholar] [CrossRef]
- Evans, K.E.; Caddock, B.D. Microporous materials with negative Poisson’s ratios. I. Microstructure and mechanical properties. J. Phys. D Appl. Phys. 1989, 22, 1877–1882. [Google Scholar] [CrossRef]
- Evans, K.E.; Caddock, B.D. Microporous materials with negative Poisson’s ratios. II. Mechanisms and interpretation. J. Phys. D Appl. Phys. 1989, 22, 1883–1887. [Google Scholar] [CrossRef]
- Yang, W.; Li, Z.M.; Shi, W.; Xie, B.H.; Yang, M.B. Review on auxetic materials. J. Mater. Sci. 2004, 39, 3269–3279. [Google Scholar] [CrossRef]
- Critchley, R.; Corni, I.; Wharton, J.A.; Walsh, F.C.; Wood, R.J.K.; Stokes, K.R. A review of the manufacture, mechanical properties and potential applications of auxetic foams. Phys. Status Solidi B 2013, 250, 1963–1982. [Google Scholar] [CrossRef]
- Shen, J.; Zhou, S.; Huang, X.; Xie, Y.M. Simple cubic three-dimensional auxetic metamaterials. Phys. Status Solidi B 2014, 251, 1515–1522. [Google Scholar] [CrossRef]
- Bertoldi, K.; Reis, P.M.; Willshaw, S.; Mullin, T. Negative Poisson’s ratio behaviour induced by an elastic instability. Adv. Mater. 2010, 22, 361–366. [Google Scholar] [CrossRef] [PubMed]
- Mancusi, G.; Feo, L. A refined finite element formulation for the microstructure-dependent analysis of two-dimensional (2D) lattice materials. Materials 2013, 6, 1–17. [Google Scholar] [CrossRef]
- Choi, J.B.; Lakes, R.S. Design of a fastener based on negative Poisson’s ratio foam. Cell. Polym. 1991, 10, 205–212. [Google Scholar]
- Scarpa, F. Auxetic materials for bioprostheses. IEEE Sig. Proc. Mag. 2008, 25, 128–126. [Google Scholar] [CrossRef]
- Chen, C.P.; Lakes, R.S. Micromechanical analysis of dynamic behavior of conventional and negative Poisson’s ratio foams. J. Eng. Mater. Technol. 1996, 118, 285–288. [Google Scholar] [CrossRef]
- Scarpa, F.; Ciffo, L.; Yates, J. Dynamic properties of high structural integrity auxetic open cell foam. Smart Mater. Struct. 2004, 13. [Google Scholar] [CrossRef]
- Alderson, A.; Rasburn, J.; Ameer-Beg, S.; Mullarkey, P.G.; Perrie, W.; Evans, K.E. An auxetic filter: A tuneable filter displaying enhanced size selectivity or defouling properties. Ind. Eng. Chem. Res. 2000, 39, 654–665. [Google Scholar] [CrossRef]
- Sun, Y.; Pugno, N. Hierarchical fibers with a negative Poisson’s Ratio for tougher composites. Materials 2013, 6, 699–712. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F.; Schajer, G.S.; Robertson, C.I. The mechanics of two-dimensional cellular materials. Proc. R. Soc. Lond. A 1982, 382, 25–42. [Google Scholar] [CrossRef]
- Theocaris, P.S.; Stavroulakis, G.E.; Panagiotopoulos, P.D. Negative Poisson's ratios in composites with star-shaped inclusions: A numerical homogenization approach. Arch. Appl. Mech. 1997, 67, 274–286. [Google Scholar] [CrossRef]
- Smith, C.W.; Grima, J.N.; Evans, K.E. A novel mechanism for generating auxetic behaviour in reticulated foams: Missing rib foam model. Acta Mater. 2000, 48, 4349–4356. [Google Scholar] [CrossRef]
- Gaspar, N.; Ren, X.J.; Smith, C.W.; Grima, J.N.; Evans, K.E. Novel honeycombs with auxetic behaviour. Acta Mater. 2005, 53, 2439–2445. [Google Scholar] [CrossRef]
- Babaee, S.; Shim, J.; Weaver, J.C.; Chen, E.R.; Pate, N.; Bertoldi, K. Soft metamaterials with negative Poisson’s Ratio. Adv. Mater. 2013, 25, 5044–5049. [Google Scholar] [CrossRef] [PubMed]
- Taylor, M.; Francesconi, L.; Gerendás, M.; Shanian, A.; Carson, C.; Bertoldi, K. Low porosity metallic periodic structures with negative Poisson’s ratio. Adv. Mater. 2014, 26, 2365–2370. [Google Scholar] [CrossRef] [PubMed]
- Dirrenberger, J.; Forest, S.; Jeulin, D. Elastoplasticity of auxetic materials. Comp. Mater. Sci. 2012, 64, 57–61. [Google Scholar] [CrossRef]
- Gilat, R.; Aboudi, J. Behavior of elastoplastic auxetic microstructural arrays. Materials 2013, 6, 726–737. [Google Scholar] [CrossRef]
- Bertoldi, K.; Boyce, M.C.; Deschanel, S.; Prange, S.M.; Mullin, T. Mechanics of deformation-triggered pattern transformations and superelastic behavior in periodic elastomeric structures. J. Mech. Phys. Solids 2008, 56, 2642–2668. [Google Scholar] [CrossRef]
- Mullin, T.; Willshaw, S.; Box, F. Pattern switching in soft cellular solids under compression. Soft Matter 2013, 9, 4951–4955. [Google Scholar] [CrossRef]
- Ren, X.; Shen, J.; Ghaedizadeh, A.; Tian, H.; Xie, Y.M. Experiments and parametric studies on 3D metallic auxetic metamaterials with tuneable mechanical properties. Smart Mater. Struct. 2015, 24. [Google Scholar] [CrossRef]
- Singamaneni, S.; Tsukruk, V.V. Buckling instabilities in periodic composite polymeric materials. Soft Matter 2010, 6, 5681–5692. [Google Scholar] [CrossRef]
- Ho, D.T.; Park, S.-D.; Kwon, S.-Y.; Park, K.; Kim, S.Y. Negative Poisson’s ratios in metal nanoplates. Nat. Commun. 2014, 5. [Google Scholar] [CrossRef] [PubMed]
- Jiang, J.W.; Park, H.S. Negative Poisson’s ratio in single-layer black phosphorus. Nat. Commun. 2014, 5. [Google Scholar] [CrossRef] [PubMed]
- Mullin, T.; Deschanel, S.; Bertoldi, K.; Boyce, M.C. Pattern transformation triggered by deformation. Phys. Rev. Lett. 2007, 9. [Google Scholar] [CrossRef] [PubMed]
- Wu, G.; Xia, Y.; Yang, S. Buckling, symmetry breaking, and cavitation in periodically micro-structured hydrogel membranes. Soft Matter 2014, 10, 1392–1399. [Google Scholar] [CrossRef] [PubMed]
- Körner, C.; Liebold-Ribeiro, Y. A systematic approach to identify cellular auxetic materials. Smart Mater. Struct. 2015, 24. [Google Scholar] [CrossRef]
- Shen, J.; Xie, Y.M.; Huang, X.D.; Zhou, S.W.; Ruan, D. Mechanical properties of luffa sponge. J. Mech. Behav. Biomed. Mater. 2012, 15, 141–152. [Google Scholar] [CrossRef] [PubMed]
- Hanssen, A.G.; Hopperstad, O.S.; Langseth, M.; Ilstad, H. Validation of constitutive models applicable to aluminium foams. Int. J. Mech. Sci. 2002, 44, 359–406. [Google Scholar] [CrossRef]
- Avalle, M.; Belingardi, G.; Montanini, R. Characterization of polymeric structural foams under compressive impact loading by means of energy-absorption diagram. Int. J. Impact. Eng. 2001, 25, 455–472. [Google Scholar] [CrossRef]
- Grima, J.N.; Alderson, A.; Evans, K.E. Auxetic behaviour from rotating rigid units. Phys. Status Solidi B 2005, 242, 561–575. [Google Scholar] [CrossRef]
- Wu, G.; Cho, Y.; Choi, I.-S.; Ge, D.; Li, J.; Han, H.N.; Lubensky, T.; Yang, S. Directing the deformation paths of soft metamaterials with prescribed a symmetric units. Adv. Mater. 2015, 27, 2747–2752. [Google Scholar] [CrossRef] [PubMed]
- Ishibashi, Y.; Iwata, M.A. Microscopic model of a negative poisson’s ratio in some crystals. J. Phys. Soc. Jpn. 2000, 69, 2702–2703. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghaedizadeh, A.; Shen, J.; Ren, X.; Xie, Y.M. Tuning the Performance of Metallic Auxetic Metamaterials by Using Buckling and Plasticity. Materials 2016, 9, 54. https://doi.org/10.3390/ma9010054
Ghaedizadeh A, Shen J, Ren X, Xie YM. Tuning the Performance of Metallic Auxetic Metamaterials by Using Buckling and Plasticity. Materials. 2016; 9(1):54. https://doi.org/10.3390/ma9010054
Chicago/Turabian StyleGhaedizadeh, Arash, Jianhu Shen, Xin Ren, and Yi Min Xie. 2016. "Tuning the Performance of Metallic Auxetic Metamaterials by Using Buckling and Plasticity" Materials 9, no. 1: 54. https://doi.org/10.3390/ma9010054







