On the Passivity of Hysteretic Systems with Double Hysteretic Loops
Abstract
:1. Introduction
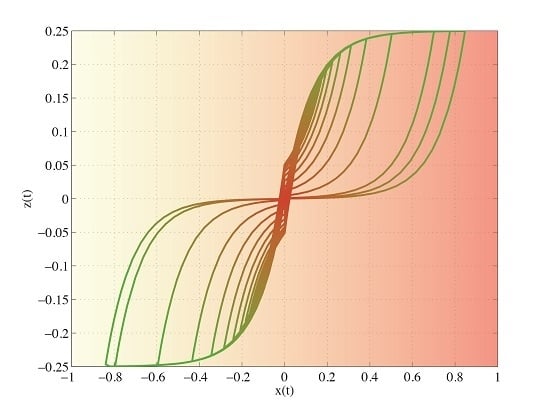
2. The Double-Loop Bouc-Model Model
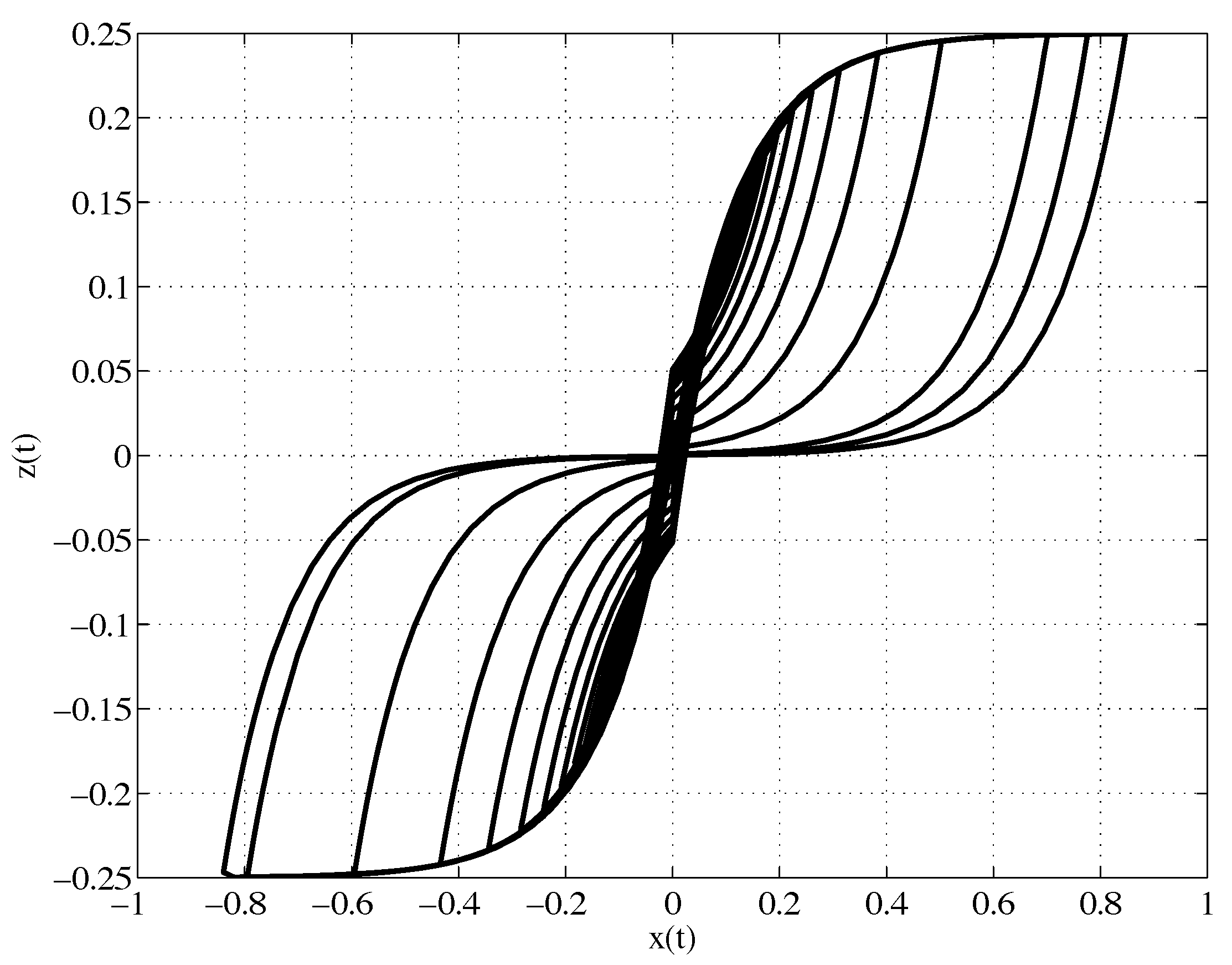
2.1. Bounded-Input Bounded-Output (BIBO) stability
| Class | Parameters | Ω | Upper Bound |
|---|---|---|---|
| I | , , | ||
| II | , , , | ||
| III | , , | ||
| IV | , , , | ||
| V | , , | ||
| VI | All other cases | ∅ |
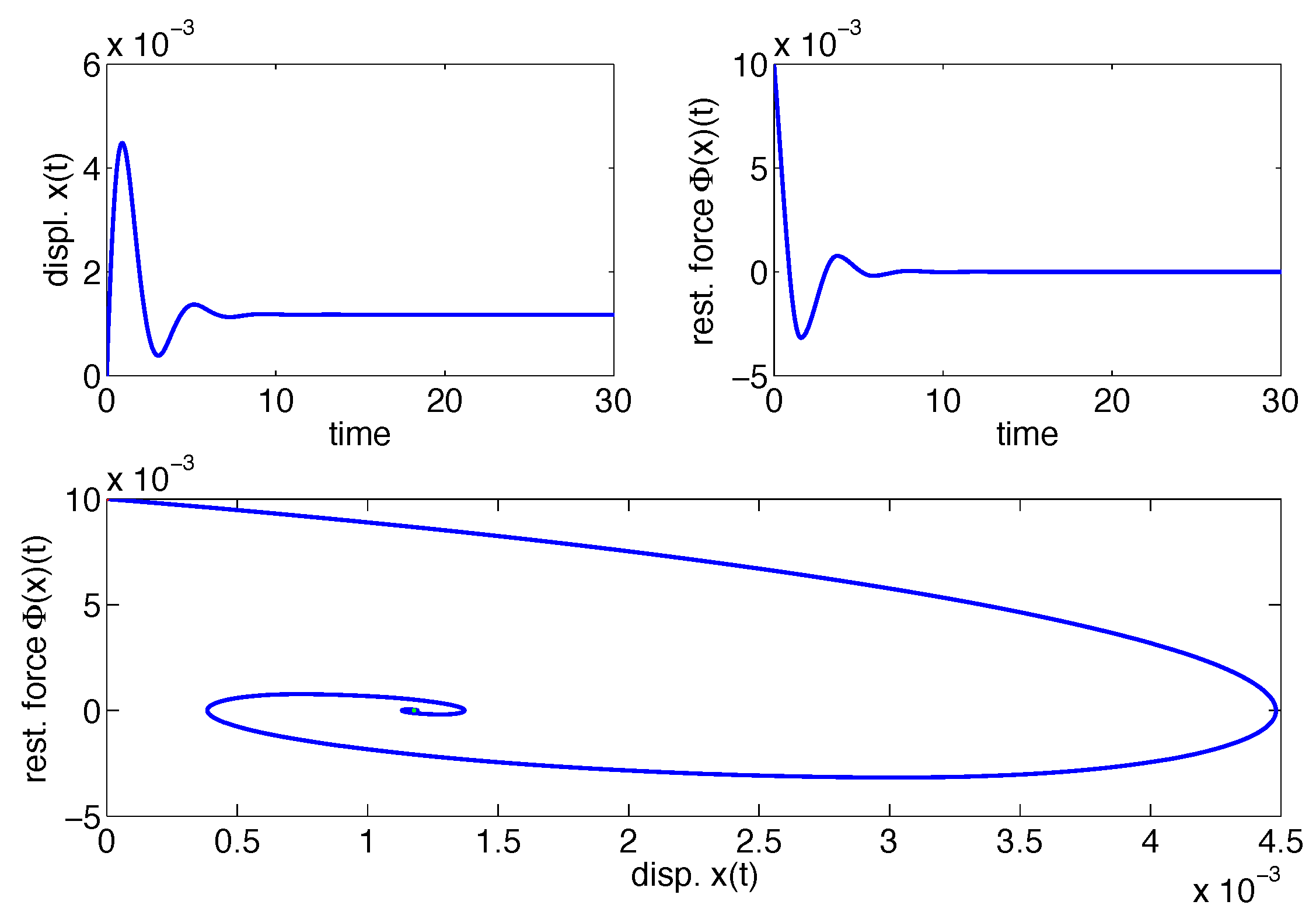

3. Passivity
3.1. Definition
3.2. Passivity of the Double-Loop Bouc–Wen Model Using Acceleration Information
3.3. Passivity Proof of the Double-Loop Bouc–Wen Model Using Position Information
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Aguirre, N.; Ikhouane, F.; Rodellar, J.; Christenson, R. Parametric identification of the Dahl model for large-scale MR dampers. Struct. Control Health Monit. 2012, 19, 332–347. [Google Scholar] [CrossRef]
- Lu, Q.; Zhao, C.; Mu, Y.; Zhao, C.Z.; Taylor, S.; Chalker, P.R. Hysteresis in lanthanide zirconium oxides observed using a pulse CV technique and including the effect of high temperature annealing. Materials 2015, 8, 4829–4842. [Google Scholar] [CrossRef]
- Oh, J.H.; Bernstein, S. Semilinear Duhem model for rate-independent and rate-dependent hysteresis. IEEE Trans. Autom. Control 2005, 50, 631–645. [Google Scholar]
- Rodríguez, A.; Pozo, F.; Bahar, A.; Acho, L.; Vidal, Y.; Rodellar, J. Force-derivative feedback semi-active control of base-isolated buildings using large-scale MR fluid dampers. Struct. Control Health Monit. 2012, 19, 120–145. [Google Scholar] [CrossRef]
- Zapateiro, M.; Karimi, H.R.; Luo, N.; Spencer, B.F., Jr. Real-time hybrid testing of semiactive control strategies for vibration reduction in a structure with MR damper. Struct. Control Health Monit. 2010, 17, 427–451. [Google Scholar] [CrossRef]
- Zhao, C.; Zhao, C.Z.; Lu, Q.; Yan, X.; Taylor, S.; Chalker, P.R. Hysteresis in lanthanide aluminum oxides observed by fast pulse CV measurement. Materials 2014, 7, 6965–6981. [Google Scholar] [CrossRef]
- Choi, H.J.; Zhang, W.L.; Kim, S.; Seo, Y. Core-shell structured electro- and magneto-responsive materials: Fabrication and characteristics. Materials 2014, 7, 7460–7471. [Google Scholar] [CrossRef]
- Aguirre, N.; Ikhouane, F.; Rodellar, J.; Wagg, D.; Neild, S. Modeling and identification of a small scale magnetorheological damper. In Proceedings of the 10th IFAC International Workshop on the Adaptation and Learning in Control and Signal Processing, Bogazici University, Istanbul, Turkey, 26–28 August 2010.
- Zapateiro, M.; Luo, N.; Taylor, E.; Dyke, S.J. Modeling and identification of a class of MR fluid foam dampers. Smart Struct. Syst. 2010, 6, 101–113. [Google Scholar] [CrossRef]
- Wen, Y.K. Method of random vibration for hysterestic systems. J. Eng. Mech. 1976, 102, 246–263. [Google Scholar]
- Ismail, M.; Ikhouane, F.; Rodellar, J. The hysteresis Bouc–Wen model: A survey. Arch. Comput. Methods Eng. 2009, 16, 161–188. [Google Scholar] [CrossRef]
- Ikhouane, F.; Rodellar, J. Systems with Hysteresis: Analysis Identification and Control Using the Bouc–Wen Model; Wiley: Chichester, UK, 2007. [Google Scholar]
- Erlicher, S.; Point, N. Thermodynamic admissibility of Bouc–Wen type hysteresis models. Comptes Rendus Méc. 2004, 332, 51–57. [Google Scholar] [CrossRef] [Green Version]
- Bruno, S.; Valente, C. Comparative response analysis of conventional and innovative seismic protection strategies. Earthq. Eng. Struct. Dyn. 2002, 31, 1067–1092. [Google Scholar] [CrossRef]
- Dolce, M.; Cardone, D.; Ponzo, F.C.; Valente, C. Shaking table tests on reinforced concrete frames without and with passive control systems. Earthq. Eng. Struct. Dyn. 2005, 34, 1687–1717. [Google Scholar] [CrossRef]
- Palermo, A.; Pampanin, S.; Marriott, D. Design, modeling and experimental response of seismic resistant bridge piers with posttensioned dissipating connections. J. Struct. Eng. 2007, 133, 1648–1661. [Google Scholar] [CrossRef]
- Pastor, N.; Rodríguez-Ferran, A. Hysteretic modeling of X-braced shear walls. Thin-Walled Struct. 2005, 43, 1567–1588. [Google Scholar] [CrossRef]
- Dobson, S.; Noori, M.; Hou, Z.; Dimentberg, M.; Baber, T. Modeling and random vibration analysis of SDOF systems with asymmetric hysteresis. Int. J. Non-Linear Mech. 1997, 32, 669–680. [Google Scholar] [CrossRef]
- Li, S.J.; Suzuki, Y.; Noori, M. Improvement of parameter estimation for non-linear hysteretic systems with slip by a fast Bayesian bootstrap filter. Int. J. Non-Linear Mech. 2004, 39, 1435–1445. [Google Scholar] [CrossRef]
- Pozo, F.; Acho, L.; Rodríguez, A.; Pujol, G. Nonlinear modeling of hysteretic systems with double hysteretic loops using position and acceleration information. Nonlinear Dyn. 2009, 57, 1–12. [Google Scholar] [CrossRef]
- Baber, T.T.; Noori, M.N. Random vibration of degrading, pinching systems. J. Eng. Mech. 1985, 111, 1010–1026. [Google Scholar] [CrossRef]
- Zinober, A.; Owens, D. Nonlinear and Adaptive Control; Lecture Notes in Control and Information Sciences; Springer: Berlin, Germany, 2003; Volume 281, pp. 181–194. [Google Scholar]
- Sepulchre, R.; Janković, M.; Kokotović, P. Constructive Nonlinear Control; Springer-Verlag: London, UK, 1997. [Google Scholar]
- Willems, J.C. The Analysis of Feedback Systems; MIT Press: Cambdridge, MA, USA, 1971. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pozo, F.; Zapateiro, M. On the Passivity of Hysteretic Systems with Double Hysteretic Loops. Materials 2015, 8, 8414-8422. https://doi.org/10.3390/ma8125465
Pozo F, Zapateiro M. On the Passivity of Hysteretic Systems with Double Hysteretic Loops. Materials. 2015; 8(12):8414-8422. https://doi.org/10.3390/ma8125465
Chicago/Turabian StylePozo, Francesc, and Mauricio Zapateiro. 2015. "On the Passivity of Hysteretic Systems with Double Hysteretic Loops" Materials 8, no. 12: 8414-8422. https://doi.org/10.3390/ma8125465