Very High Cycle Fatigue Failure Analysis and Life Prediction of Cr-Ni-W Gear Steel Based on Crack Initiation and Growth Behaviors
Abstract
:1. Introduction
2. Experimental Procedure
2.1. Material and Specimen
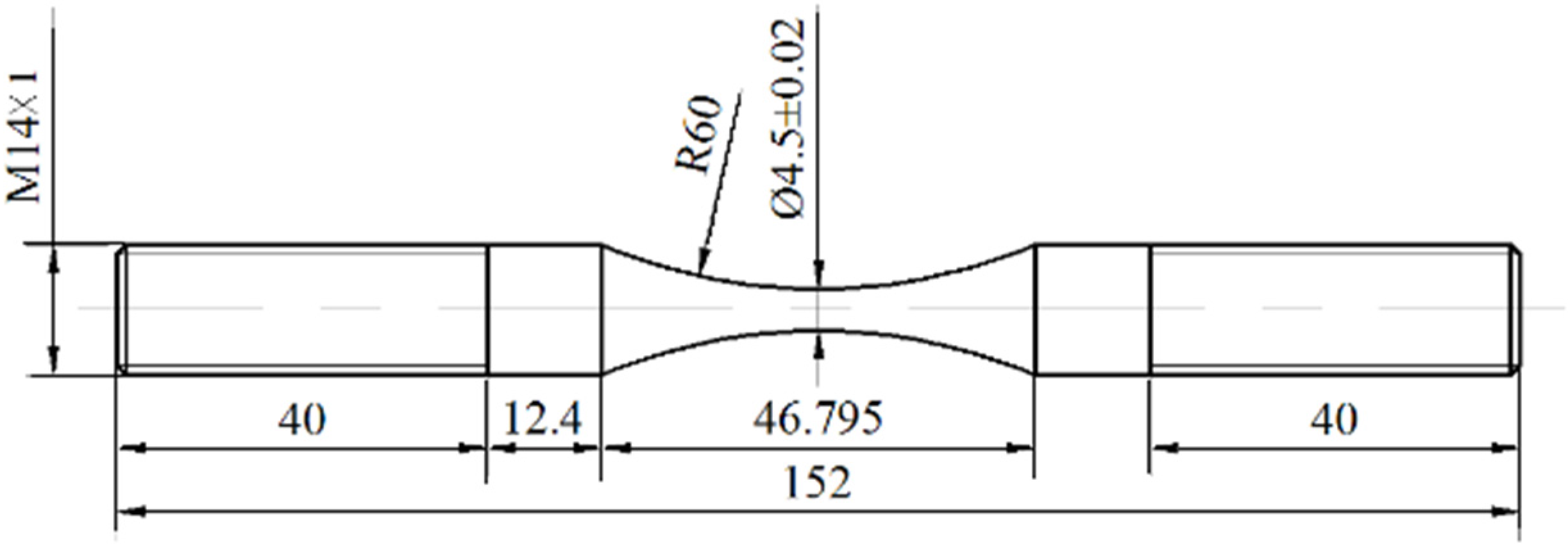

2.2. Experimental Method
3. Results and Discussion
3.1. S-N Property

3.2. Fatigue Failure Mechanism
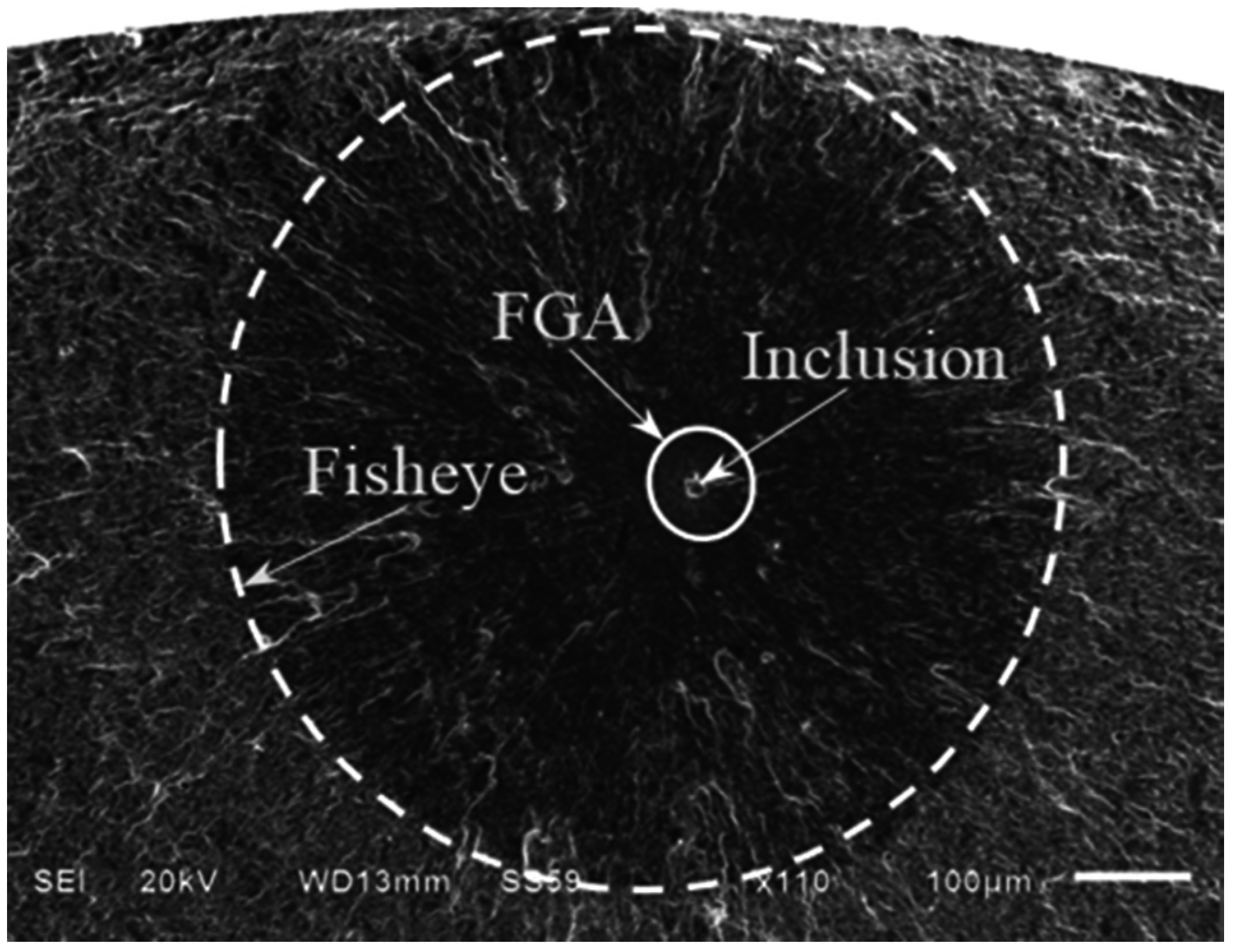
3.3. Crack Size Characteristics
| σa (MPa) | Rinc (μm) | RFGA (μm) | RFisheye (μm) |
|---|---|---|---|
| 700 | 10.89 | 23.34 | 334.23 |
| 675 | 8.05 | 24.68 | 65.86 |
| 650 | 11.85 | 27.89 | 229.75 |
| 625 | 8.12 | 31.45 | 260.57 |
| 625 | 7.12 | 30.61 | 271.83 |
| 600 | 7.86 | 32.42 | 366.04 |
| 600 | 10.13 | 33.49 | 132.43 |
| 575 | 6.16 | 36.32 | 299.69 |
| 550 | 8.56 | 40.62 | 421.14 |
| 525 | 8.14 | 47.48 | 514.76 |
3.4. Local Stress Distribution around Inclusion
3.4.1. RVE Model

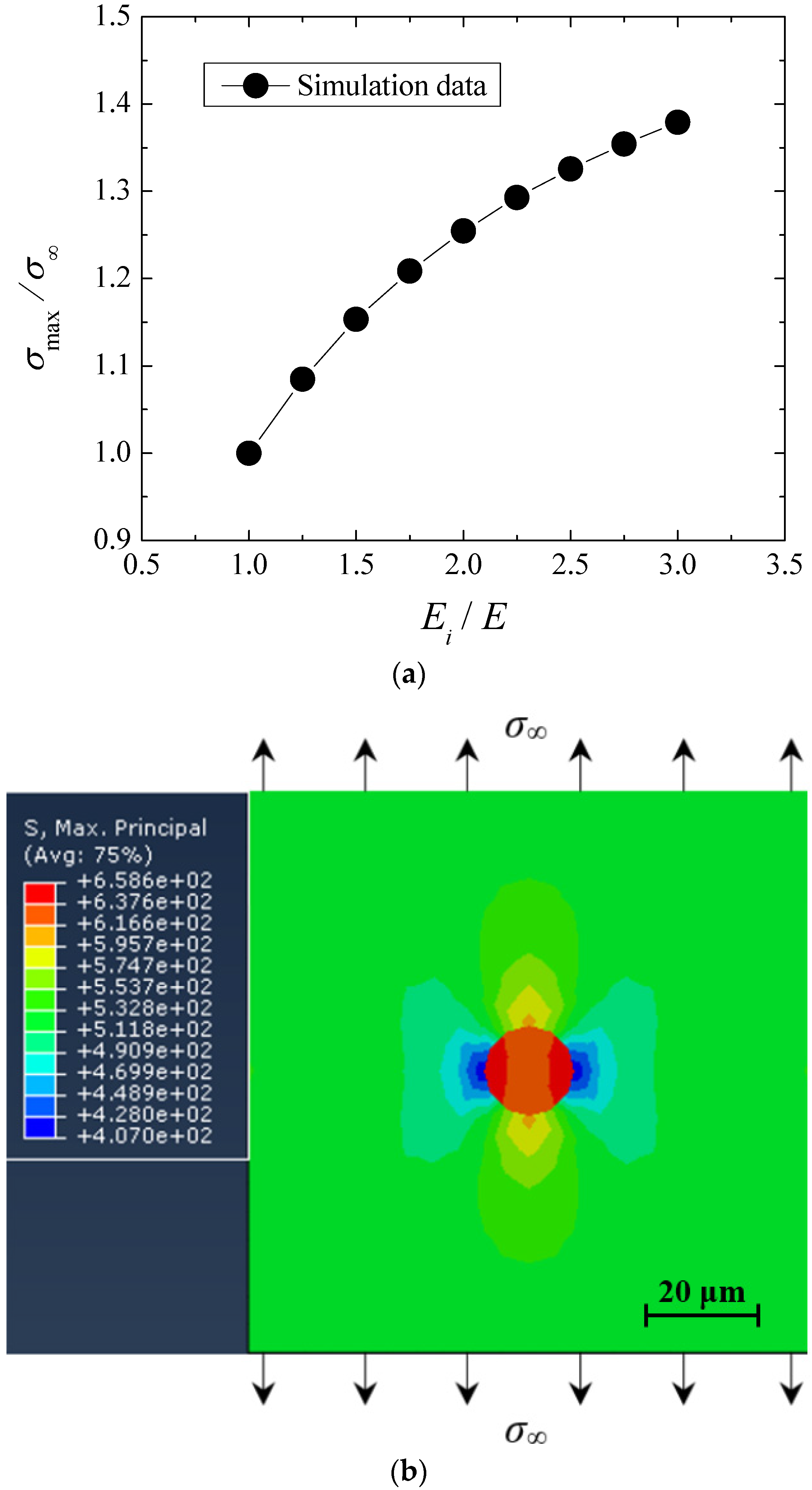
3.4.2. Effect of Inclusion Properties
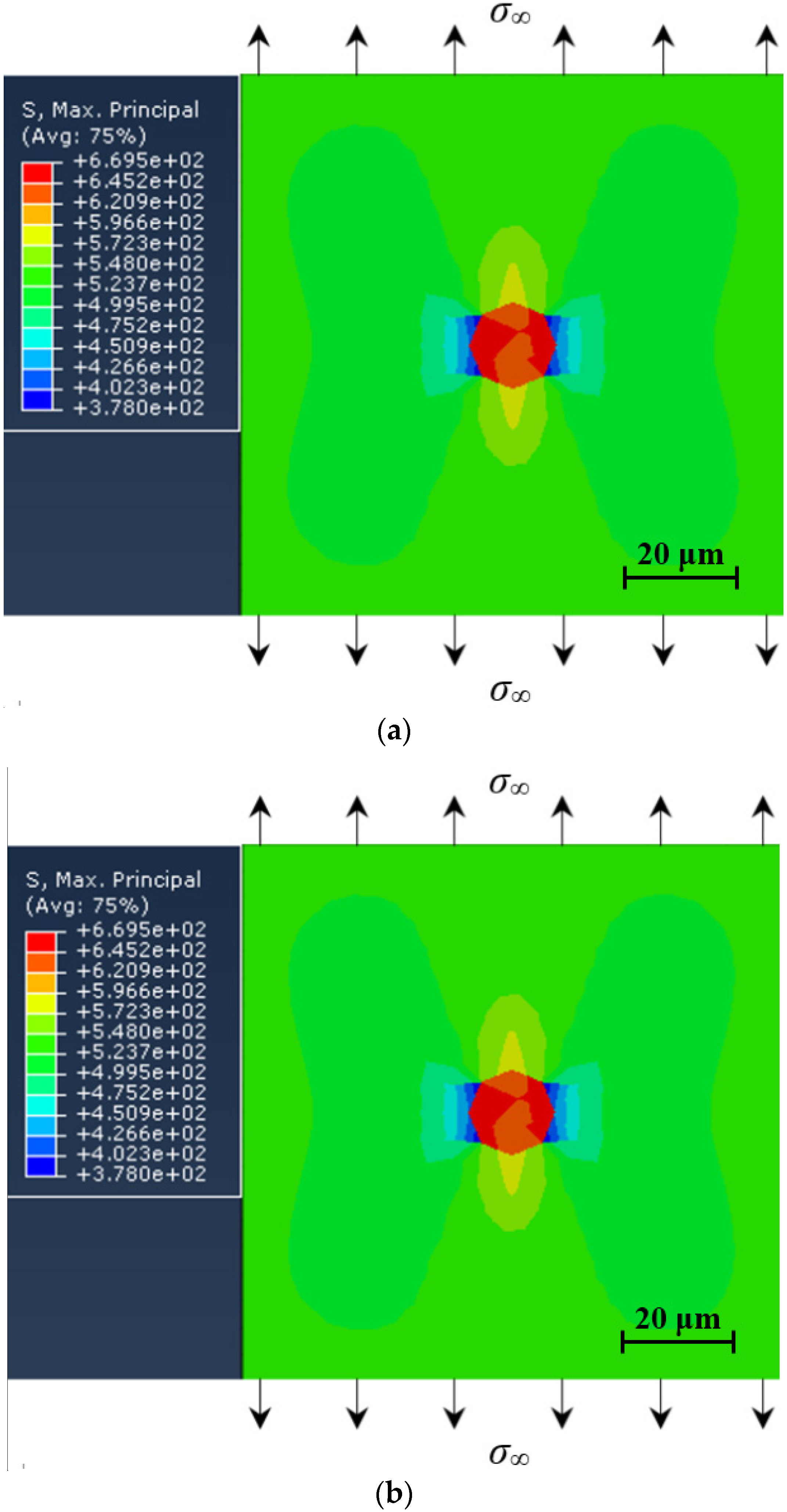
3.4.3. Effect of Cyclic Loading
3.4.4. Maximum Principal Stress Life Curve

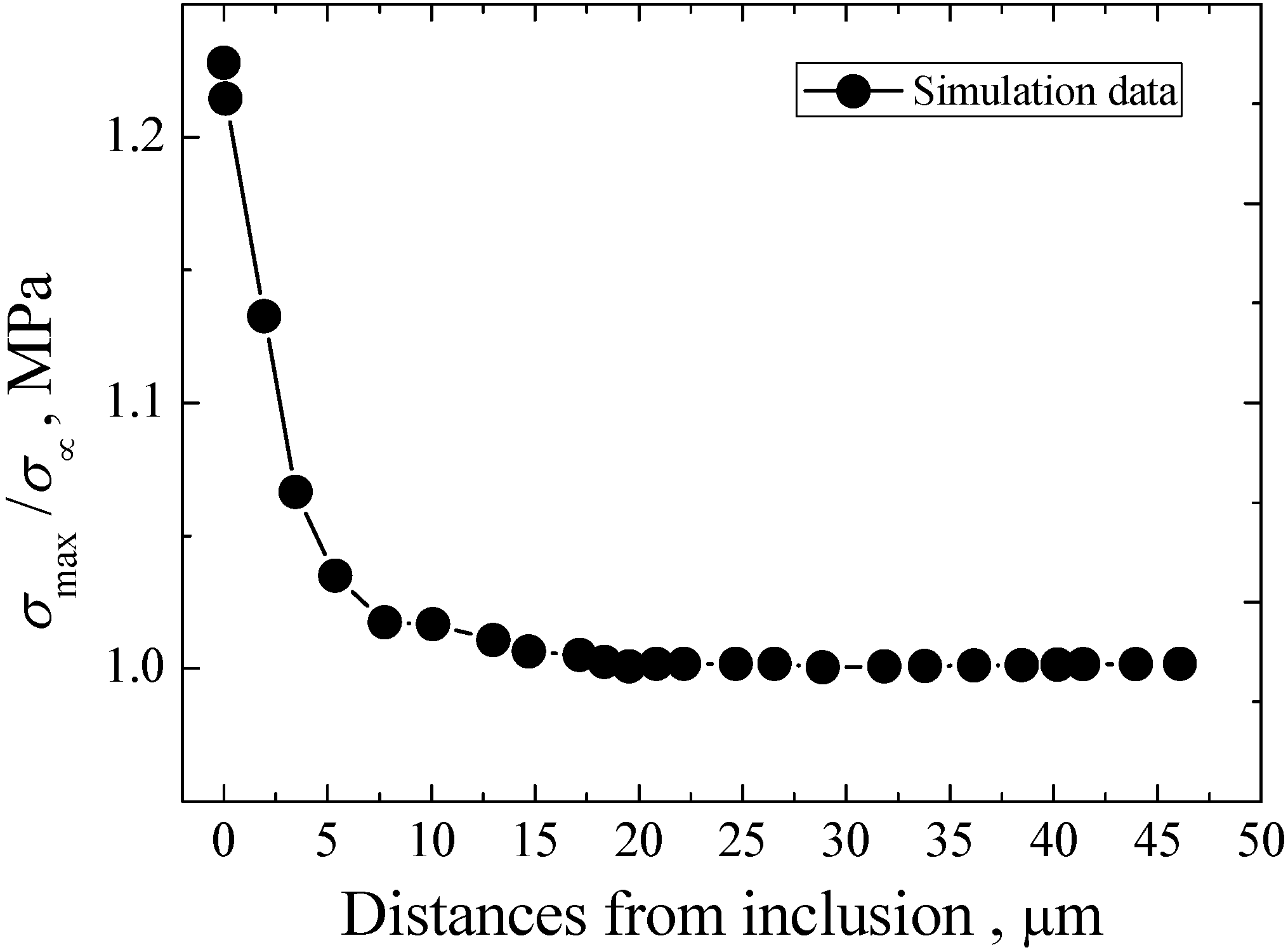
3.5. Crack Initiation Life
3.5.1. Local Stress-Life Model
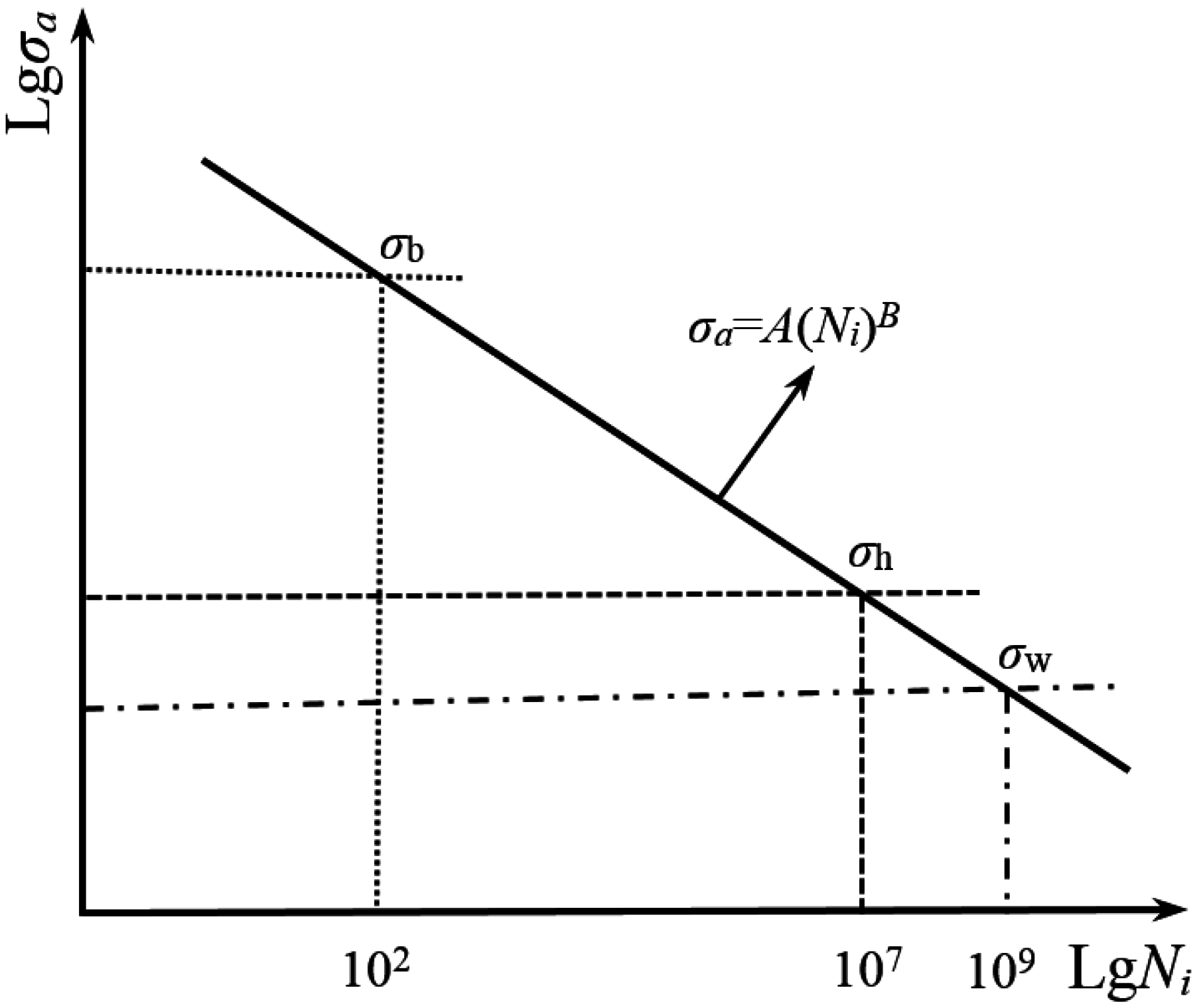
3.5.2. Tanaka-Mura Model
3.5.3. Modified Chan Model
3.5.4. Comparison of Model

3.6. Crack Growth Life

| σa (MPa) | σmax (MPa) | N1 (cycles) | N2 (cycles) | Np (cycles) |
|---|---|---|---|---|
| 700 | 842 | 7.36 × 103 | 3.15 × 105 | 3.23 × 105 |
| 675 | 837 | 1.01 × 104 | 1.40 × 105 | 1.51 × 105 |
| 650 | 781 | 9.40 × 103 | 3.10 × 105 | 3.19 × 105 |
| 625 | 783 | 1.32 × 104 | 2.40 × 105 | 2.54 × 105 |
| 625 | 792 | 1.36 × 104 | 2.27 × 105 | 2.41 × 105 |
| 600 | 761 | 1.44 × 104 | 2.65 × 105 | 2.80 × 105 |
| 600 | 725 | 1.41 × 104 | 2.31 × 105 | 2.45 × 105 |
| 575 | 714 | 1.90 × 104 | 2.34 × 105 | 2.53 × 105 |
| 550 | 672 | 1.97 × 104 | 3.11 × 105 | 3.31 × 105 |
| 525 | 645 | 2.33 × 104 | 3.08 × 105 | 3.31 × 105 |

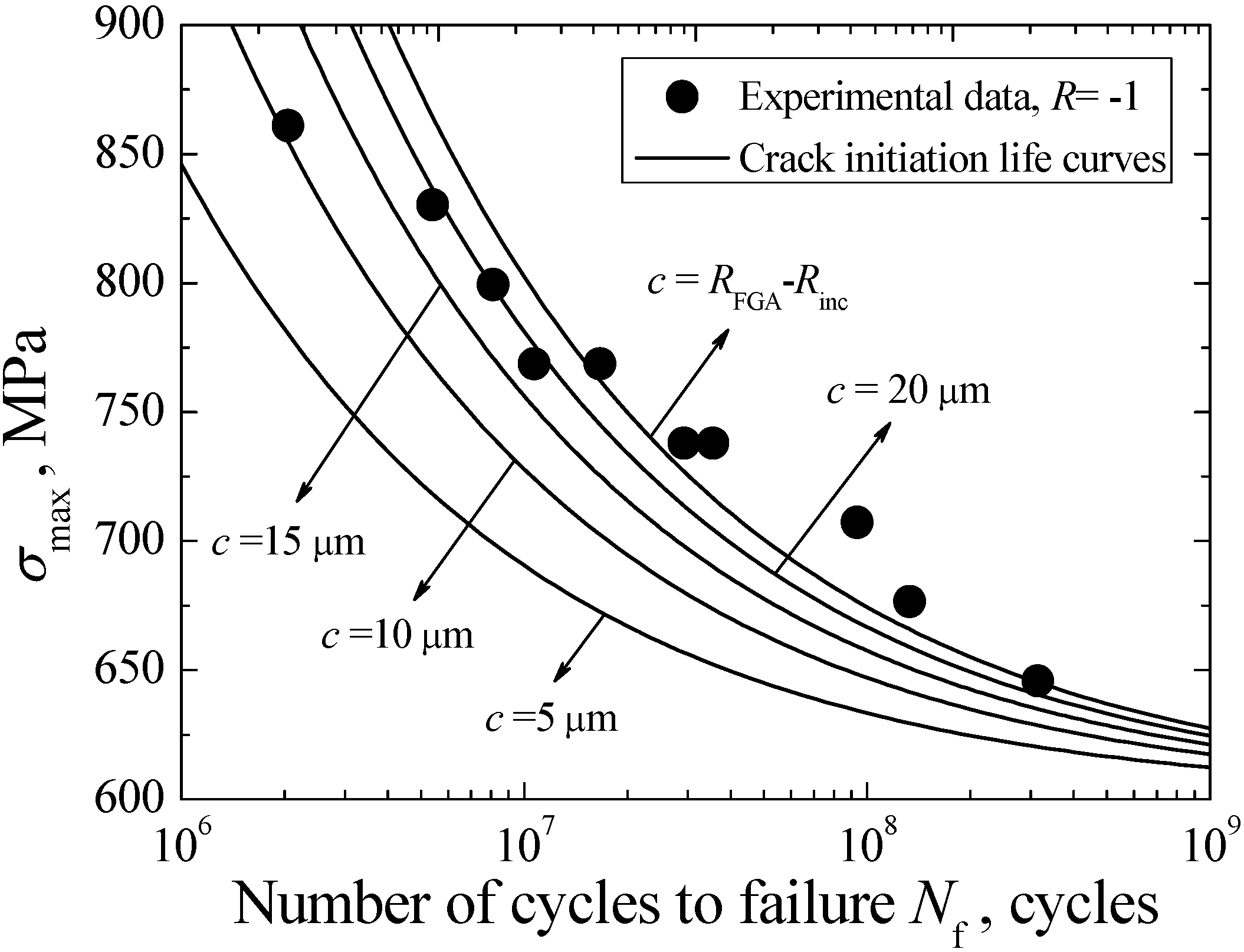
3.7. Total Fatigue Life Model
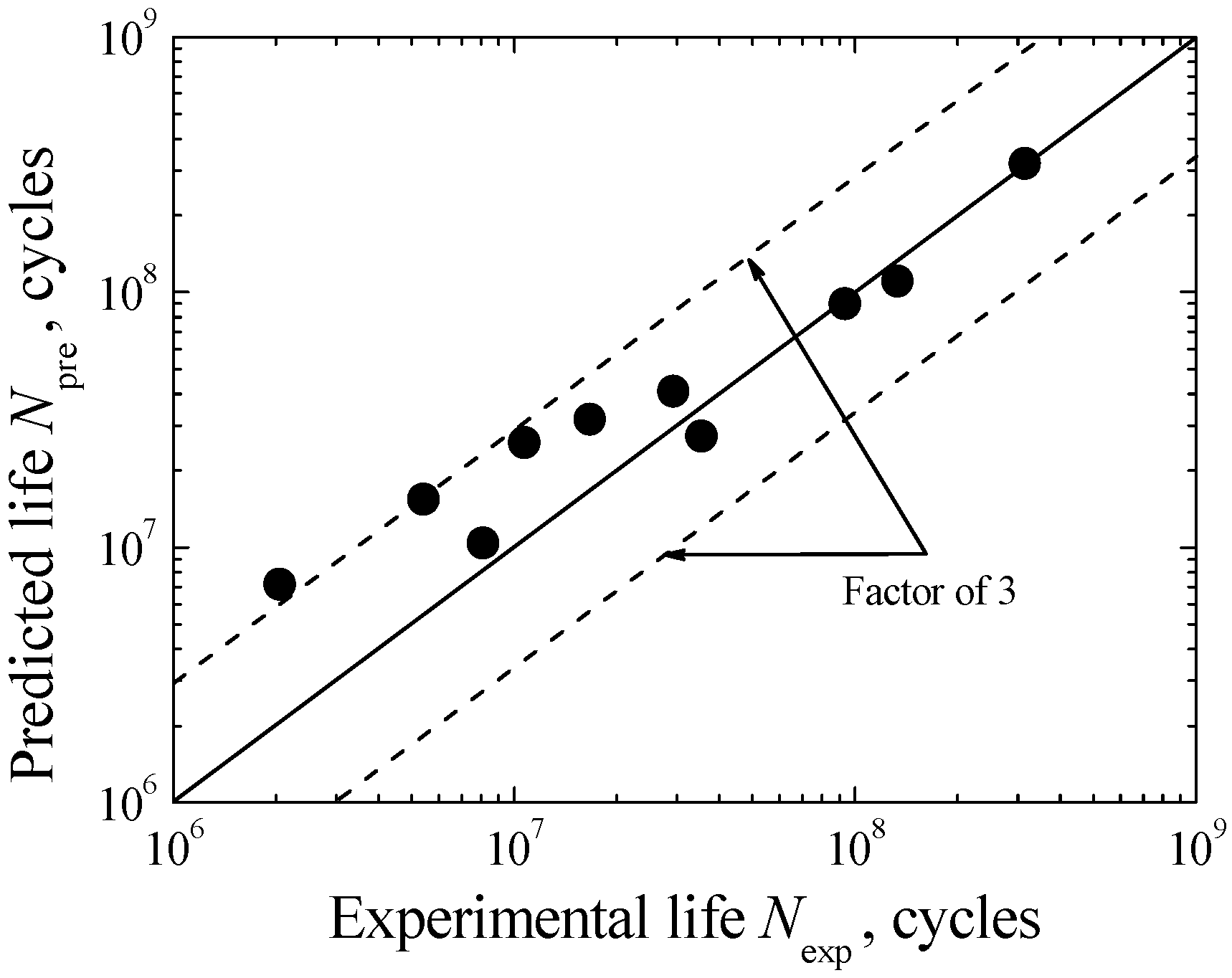
4. Conclusions
- (1)
- The Cr-Ni-W gear steel exhibits the constantly decreasing S-N property without traditional fatigue limit, and the fatigue strength corresponding to 109 cycles is around 485 MPa.
- (2)
- The inclusion-FGA-fisheye induced failure becomes the main failure mechanism of Cr-Ni-W gear steel in the VHCF regime.
- (3)
- By using the finite element analysis of representative volume element, the local stress around the inclusion tends to increase with the increase of elastic modulus difference between inclusion and matrix.
- (4)
- The local stress-life model, Tanaka-Mura model and modified Chan model were used to evaluate the crack initiation life, and the predicted results based on modified Chan model are better.
- (5)
- The predicted crack initiation life occupies the most majority of total fatigue life, while the predicted crack growth life is only accounts for a tiny fraction.
- (6)
- The established VHCF life prediction model involving crack initiation and growth for inclusion-FGA-fisheye induced failure is acceptable based on the good agreement between the predicted and experimental results.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Stanzl, S.; Tschegg, E.; Mayer, H. Lifetime measurements for random loading in the very high cycle fatigue range. Int. J. Fatigue 1986, 8, 195–200. [Google Scholar] [CrossRef]
- Ochi, Y.; Matsumura, T.; Masaki, K.; Yoshida, S. High-cycle rotating bending fatigue property in very long-life regime of high-strength steels. Fatigue Fract. Eng. Mater. Struct. 2002, 25, 823–823. [Google Scholar] [CrossRef]
- Sohar, C.R.; Betzwar-Kotas, A.; Gierl, C.; Weiss, B.; Danninger, H. Gigacycle fatigue behavior of a high chromium alloyed cold work tool steel. Int. J. Fatigue 2008, 30, 1137–1149. [Google Scholar] [CrossRef]
- Hong, Y.S.; Zhao, A.G.; Qian, G.A. Essential characteristics and influential factors for very-high cycle fatigue behavior of metallic materials. Acta Metall Sin. 2009, 45, 769–780. [Google Scholar]
- Murakami, Y.; Beretta, S. Small defects and inhomgenities in fatigue strength: Experiments, models and statistical implications. Extremes 1999, 2, 123–147. [Google Scholar] [CrossRef]
- Yang, Z.G.; Zhang, J.M.; Li, S.X.; Li, G.Y.; Wang, Q.Y.; Hui, W.J.; Weng, Y.Q. On the critical inclusion size of high strength steels under ultra-high cycle fatigue. Mater. Sci. Eng. A 2006, 427, 167–174. [Google Scholar] [CrossRef]
- Lai, J.; Lund, T.; Rydén, K.; Gabelli, A.; Strandell, I. The fatigue limit of bearing steels-Part I: A pragmatic approach to predict very high cycle fatigue strength. Int. J. Fatigue 2012, 37, 155–168. [Google Scholar] [CrossRef]
- Sakai, T.; Sato, Y.; Oguma, N. Characteristic S-N properties of high-carbon-chromium-bearing steel under axial loading in long-life fatigue. Fatigue Fract. Eng. Mater. Struct. 2002, 25, 765–773. [Google Scholar] [CrossRef]
- Li, W.; Deng, H.L.; Sun, Z.D.; Zhang, Z.Y.; Lu, L.T.; Sakai, T. Subsurface inclusion-induced crack nucleation and growth behaviors of high strength steels under very High cycle fatigue: Characterization and microstructure-based modeling. Mater. Sci. Eng. A 2015, 641, 10–20. [Google Scholar] [CrossRef]
- Shiozawa, K.; Lu, L.; Ishihara, S. S-N curve characteristics and subsurface crack initiation behaviour in ultra-long life fatigue of a high carbon-chromium bearing steel. Fatigue Fract. Eng. Mater. Struct. 2001, 24, 781–790. [Google Scholar] [CrossRef]
- Murakami, Y.; Yokoyama, N.N.; Nagata, J. Mechanism of fatigue failure in ultralong life regime. Fatigue Fract. Eng. Mater. Struct. 2002, 25, 735–746. [Google Scholar]
- Grad, P.; Reuscher, B.; Brodvanski, A.; Kopnarski, M.; Kerscher, E. Mechanism of fatigue crack initiation and propagation in the very high cycle fatigue regime of high-strength steels. Scr. Mater. 2012, 67, 838–841. [Google Scholar] [CrossRef]
- Nakamura, T.; Oguma, H.; Shinohara, Y. The effect of vacuum-like environment inside sub-surface fatigue crack on the formation of ODA fracture surface in high strength steel. Proc. Eng. 2010, 2, 2121–2129. [Google Scholar] [CrossRef]
- Mayer, H.; Haydn, W.; Schuller, R.; Issler, S.; Furtner, B.; Bacher-Hochst, B. Very high cycle fatigue properties of bainitic high carbonchromium steel. Int. J. Fatigue 2009, 31, 242–249. [Google Scholar] [CrossRef]
- Liu, Y.B.; Li, Y.D.; Li, S.X.; Yang, Z.G. Prediction of the S-N curves of high-strength steels in the very high cycle fatigue regime. Int. J. Fatigue 2010, 32, 1351–1357. [Google Scholar] [CrossRef]
- Sun, C.Q.; Lei, Z.Q.; Xie, J.J.; Zhao, A.; Hong, Y.S. Effects of inclusion size and stress ratio on fatigue strength for high-strength steels with fish-eye mode failure. Int. J. Fatigue 2013, 48, 19–27. [Google Scholar] [CrossRef]
- Chapetti, M.D.; Tagawa, T.; Miyata, T. Ultra-long cycle fatigue of high-strength carbon steels part II: Estimation of fatigue limit for failure from internal inclusions. Mater. Sci. Eng. A 2003, 356, 236–244. [Google Scholar] [CrossRef]
- Akiniwa, Y.; Miyamoto, N.; Tsuru, H.; Tanaka, K. Notch effect on fatigue strength reduction of bearing steel in very high cycle regime. Int. J. Fatigue 2006, 28, 1555–1565. [Google Scholar] [CrossRef]
- Sun, C.; Xie, J.; Zhao, A.; Lei, Z.; Hong, Y. A cumulative damage model for fatigue life estimation of high-strength steels in high-cycle and very-high-cycle fatigue regimes. Fatigue Fract. Eng. Mater. Struct. 2012, 35, 638–647. [Google Scholar] [CrossRef]
- Wang, Q.Y.; Bathias, C.; Kawagoishi, N.; Chen, Q. Effect of inclusion on subsurface crack initiation and gigacycle fatigue strength. Int. J. Fatigue 2002, 24, 1269–1274. [Google Scholar] [CrossRef]
- Murakami, Y. Stress Intensity Factor Handbook; Pergamon Press: Fukuoka, Japan, 1993; pp. 661–662. [Google Scholar]
- Cerullo, M. Sub-surface fatigue crack growth at alumina inclusions in AISI 52100 roller bearings. Proc. Eng. 2014, 74, 333–338. [Google Scholar] [CrossRef] [Green Version]
- Stephens, R.I.; Fatemi, A.; Stephens, R.R.; Henry, H.O. Metal Fatigue in Engineering; A Wiley Interscience Press: New York, NY, USA, 2001; pp. 84–84. [Google Scholar]
- Hill, R. Elastic properties of reinforced solids: Some theoretical principles. J. Mech. Phys. Solids 1963, 11, 357–372. [Google Scholar] [CrossRef]
- Hoeppner, D.W. Fatigue Testing of Weldments; American Society for Testing and Materials (ASTM) Press: Philadephia, PA, USA, 1978; pp. 134–158. [Google Scholar]
- Liu, C.R.; Choi, Y. Rolling contact fatigue life model incorporating residual stress scatter. Int. J. Mech. Sci. 2008, 50, 1572–1577. [Google Scholar] [CrossRef]
- Tanaka, K.; Mura, T. A Theory of Fatigue Crack Initiation at Inclusions. Metall. Mater. Trans. A 1982, 13, 117–123. [Google Scholar] [CrossRef]
- Anderson, T.L. Fracture Mechanics, Fundamental and Application; CRC Press: Boca Raton, FL, USA, 1991; pp. 80–83. [Google Scholar]
- Chan, K.S. A microstructure-based fatigue-crack-initiation model. Metall. Mater. Trans. A 2003, 34, 43–58. [Google Scholar] [CrossRef]
- Venkataraman, G.; Chung, Y.W.; Mura, T. Application of minimum energy formalism in a multiple slip band model for fatigue. I. Calculation of slip band spacing. Acta Metall. Mater. 1991, 9, 2631–2638. [Google Scholar] [CrossRef]
- Cheng, A.S.; Laird, C. A quick and simple method for orienting cubic single crystals from Laue back-reflection photographs. J. Appl. Crystallogr. 1982, 1, 137–137. [Google Scholar] [CrossRef]
- Paris, P.C.; Tada, H.; Donald, J.K. Service load fatigue damage-a historical perspective. Int. J. Fatigue 1999, 21, 35–46. [Google Scholar] [CrossRef]
- Hertzberg, R.W.; Pecorini, T.J. An examination of load shedding during fatigue fracture. Int. J. Fract. 1993, 15, 509–551. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, H.; Li, W.; Sakai, T.; Sun, Z. Very High Cycle Fatigue Failure Analysis and Life Prediction of Cr-Ni-W Gear Steel Based on Crack Initiation and Growth Behaviors. Materials 2015, 8, 8338-8354. https://doi.org/10.3390/ma8125459
Deng H, Li W, Sakai T, Sun Z. Very High Cycle Fatigue Failure Analysis and Life Prediction of Cr-Ni-W Gear Steel Based on Crack Initiation and Growth Behaviors. Materials. 2015; 8(12):8338-8354. https://doi.org/10.3390/ma8125459
Chicago/Turabian StyleDeng, Hailong, Wei Li, Tatsuo Sakai, and Zhenduo Sun. 2015. "Very High Cycle Fatigue Failure Analysis and Life Prediction of Cr-Ni-W Gear Steel Based on Crack Initiation and Growth Behaviors" Materials 8, no. 12: 8338-8354. https://doi.org/10.3390/ma8125459






