Ion-Induced Nanoscale Ripple Patterns on Si Surfaces: Theory and Experiment
Abstract
:1. Introduction
2. Continuum Theory of Ripple Formation During Low Energy Ion Sputtering
2.1. Sigmund’s theory of sputtering
2.2. The Bradley-Harper model
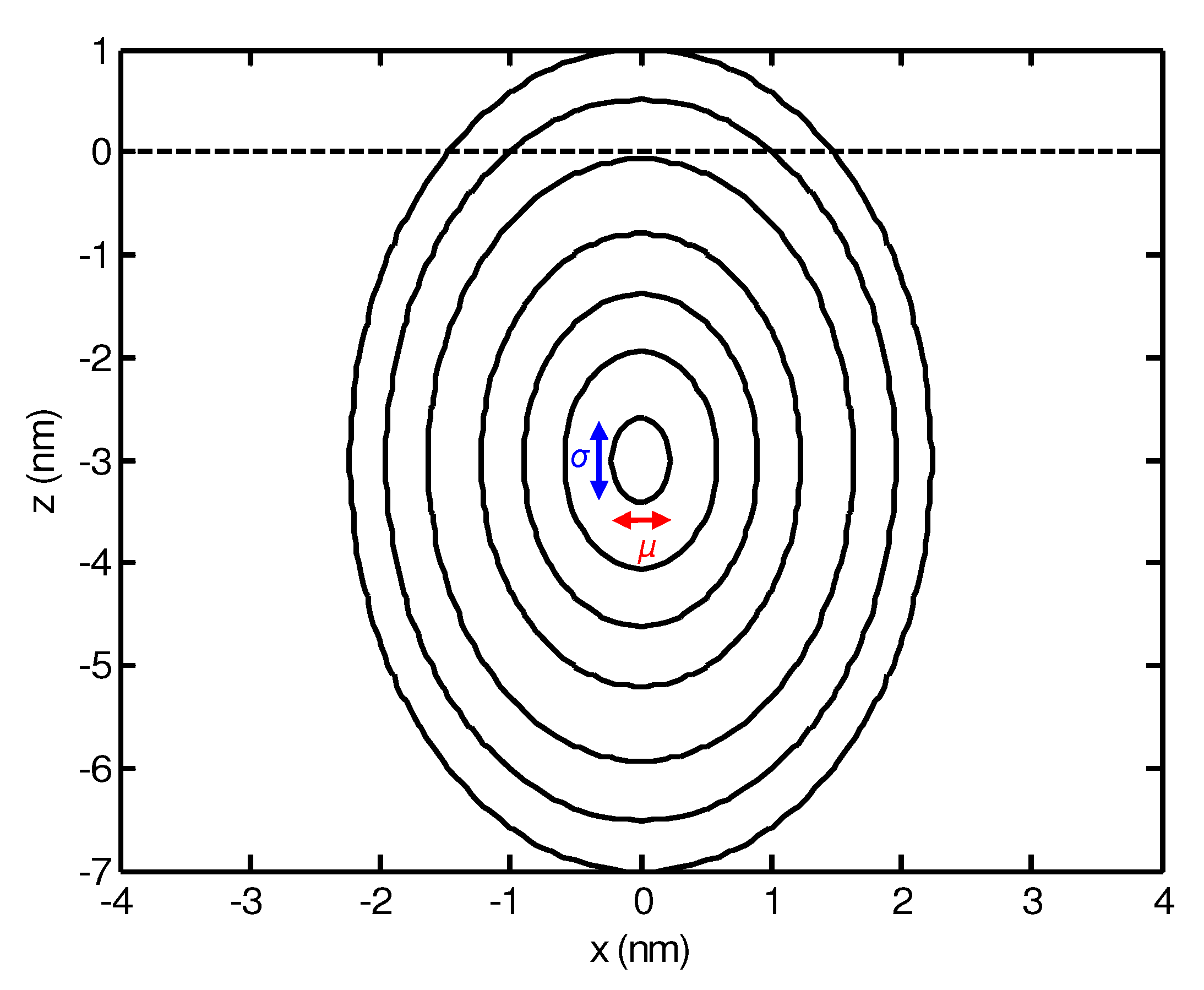

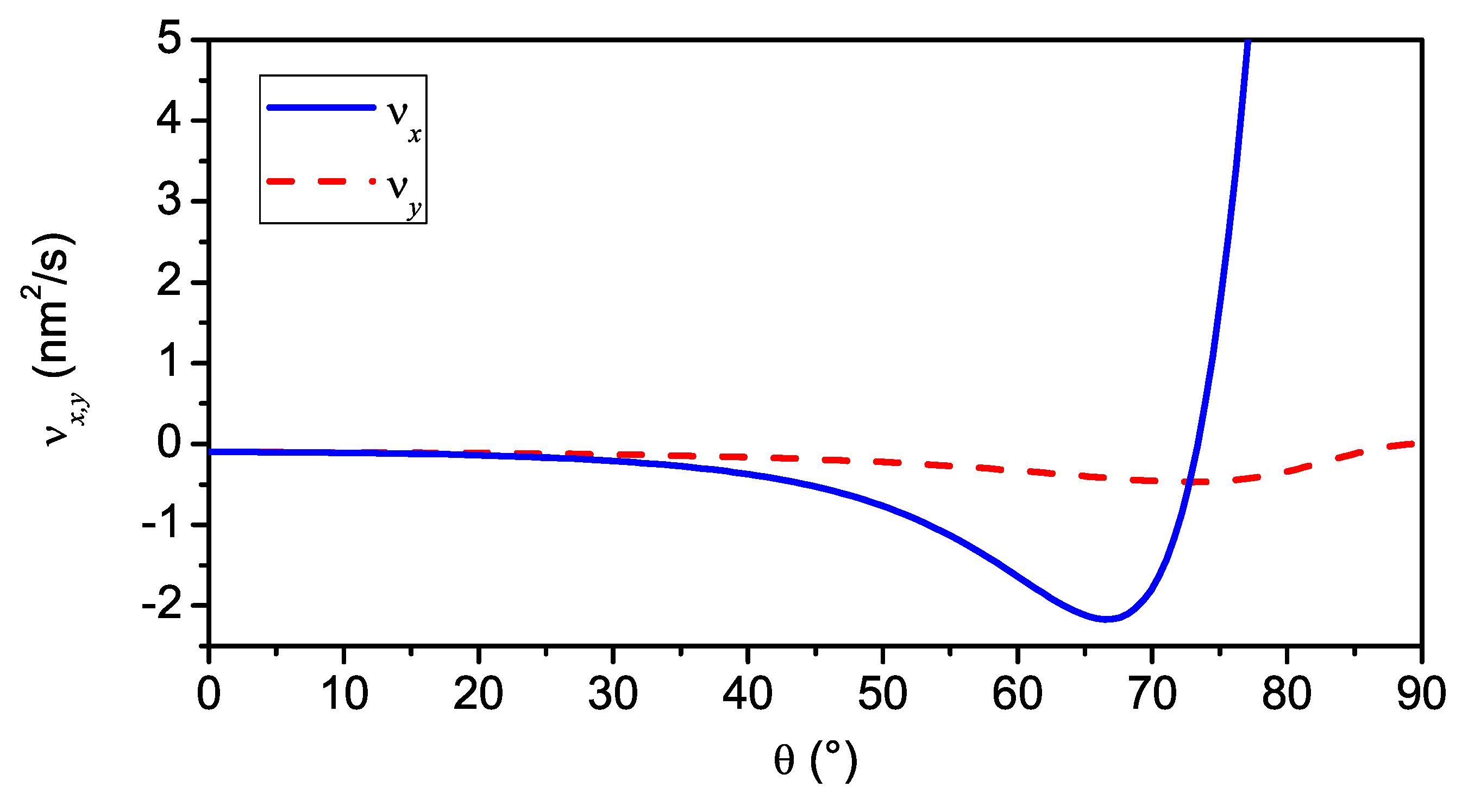
- Furthermore, from the same equations λ follows to be a function of the ion energy E and the penetration depth a, which again is a function of E. Therefore, one expects the ripple wavelength to decrease with the ion energy as with the negative exponent p [66]. However, this behavior is in general only observed at relatively high temperatures [67]. At low and moderate temperatures, several studies report the ripple wavelength to increase with energy [38,39,44,68,69].
- Equations (30) and (26) indicate a dependence of λ on the sample temperature. However, in the case of GaAs and InP, such a dependence of the wavelength was only observed at elevated temperatures whereas λ was found to be constant at room temperature and below [70]. Another study on SiO surfaces found λ to be relatively constant with temperature even up to about C [71].
2.3. Nonlinear continuum equations
2.3.1. Kuramoto-Sivashinsky equation
2.3.2. Damped Kuramoto-Sivashinsky equation
2.3.3. General continuum equation
2.3.4. Coupled two-field model
3. Morphology of Ion-sputtered Si Surfaces

3.1. The role of the incident angle: smoothing vs. roughening
3.2. Evolution of the surface morphology

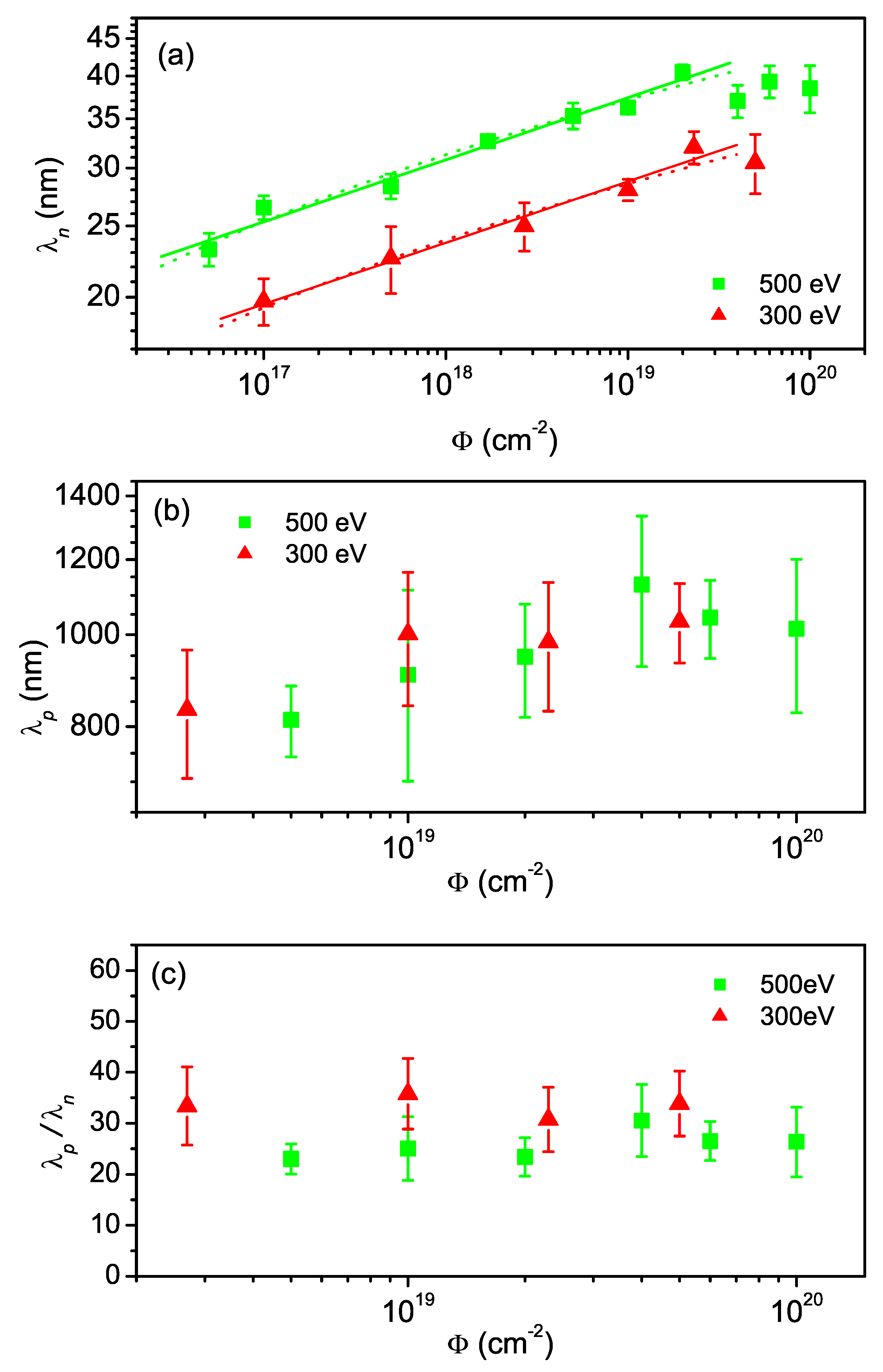
3.2.1. Formation of two ripple modes
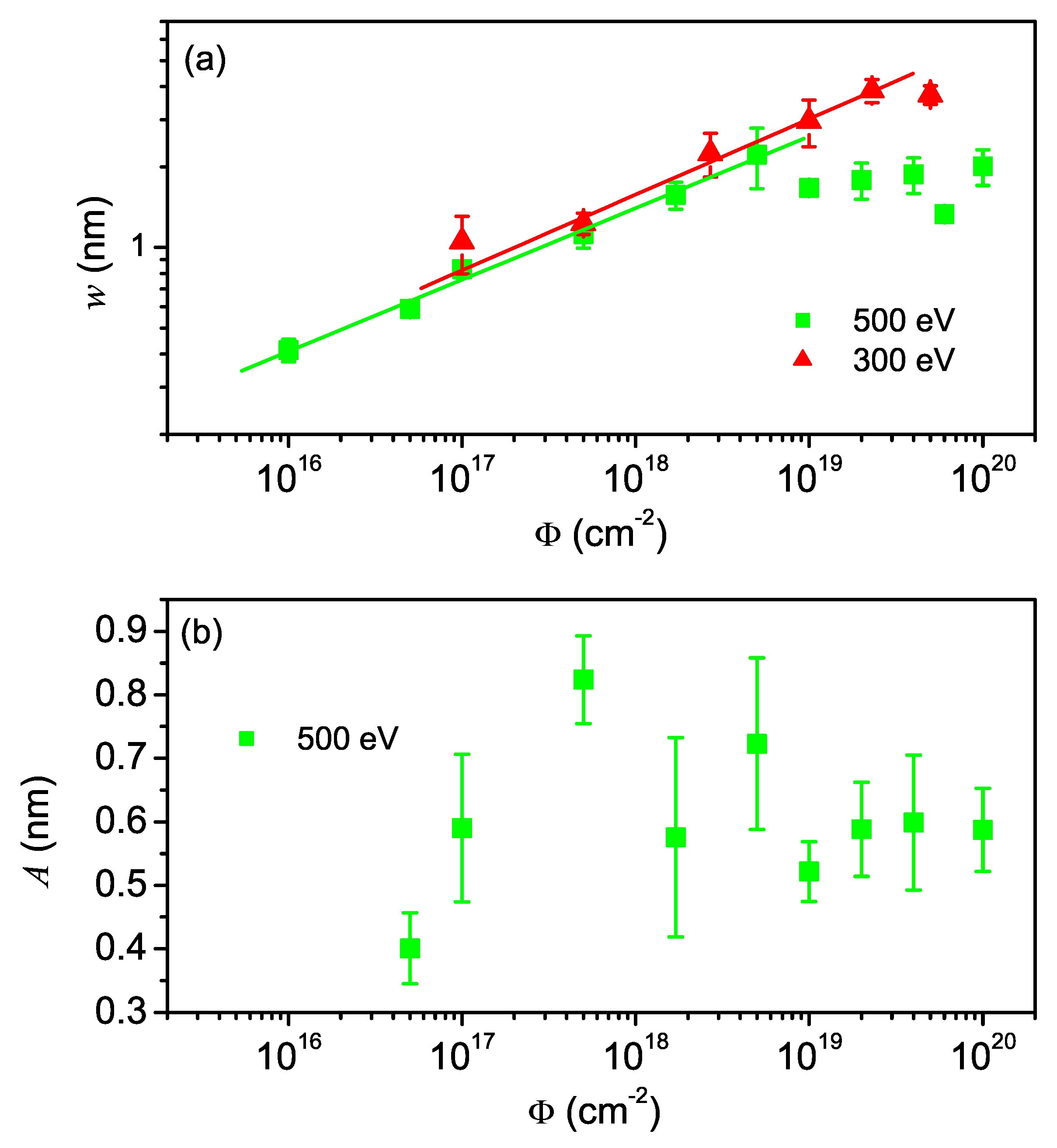
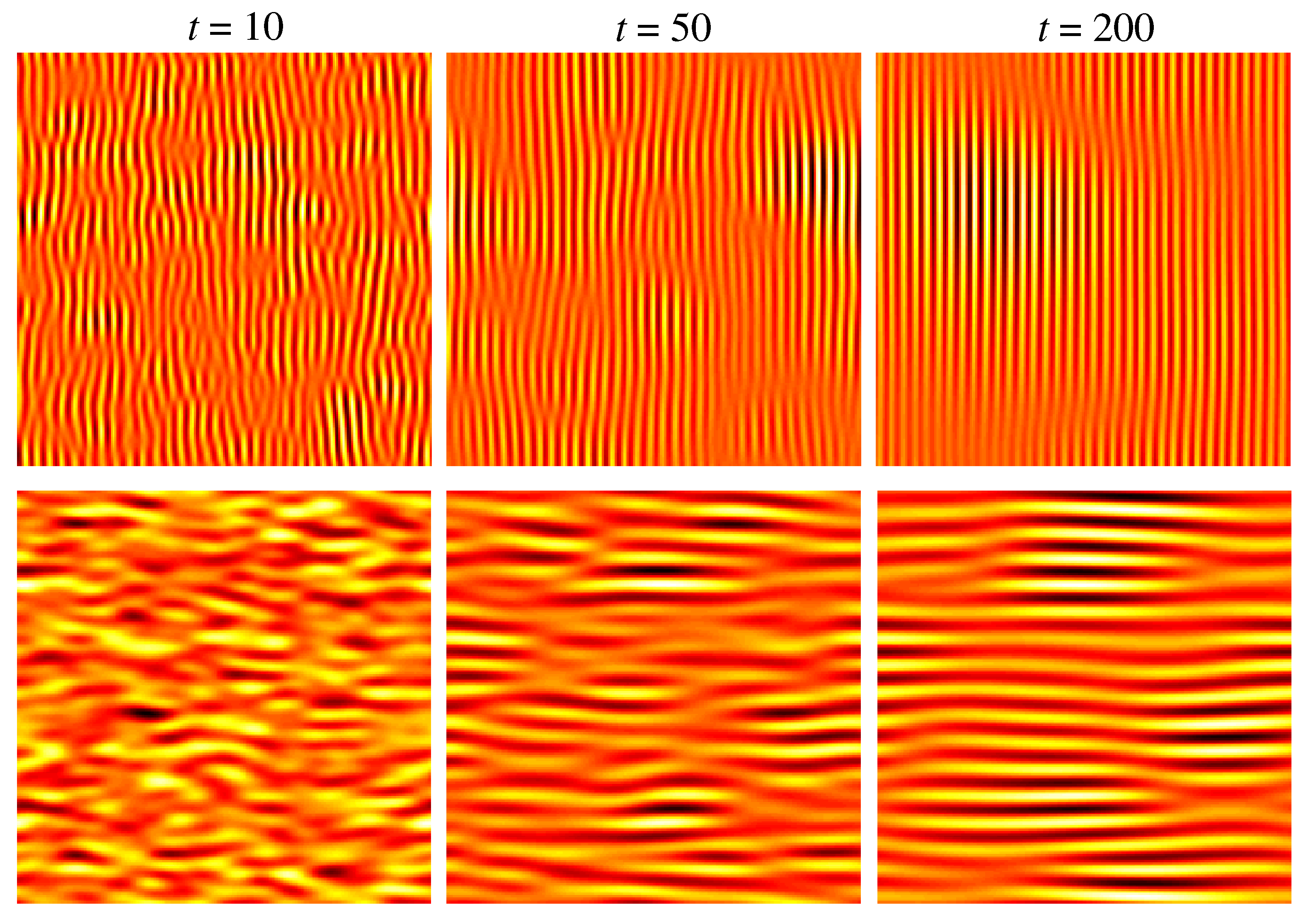
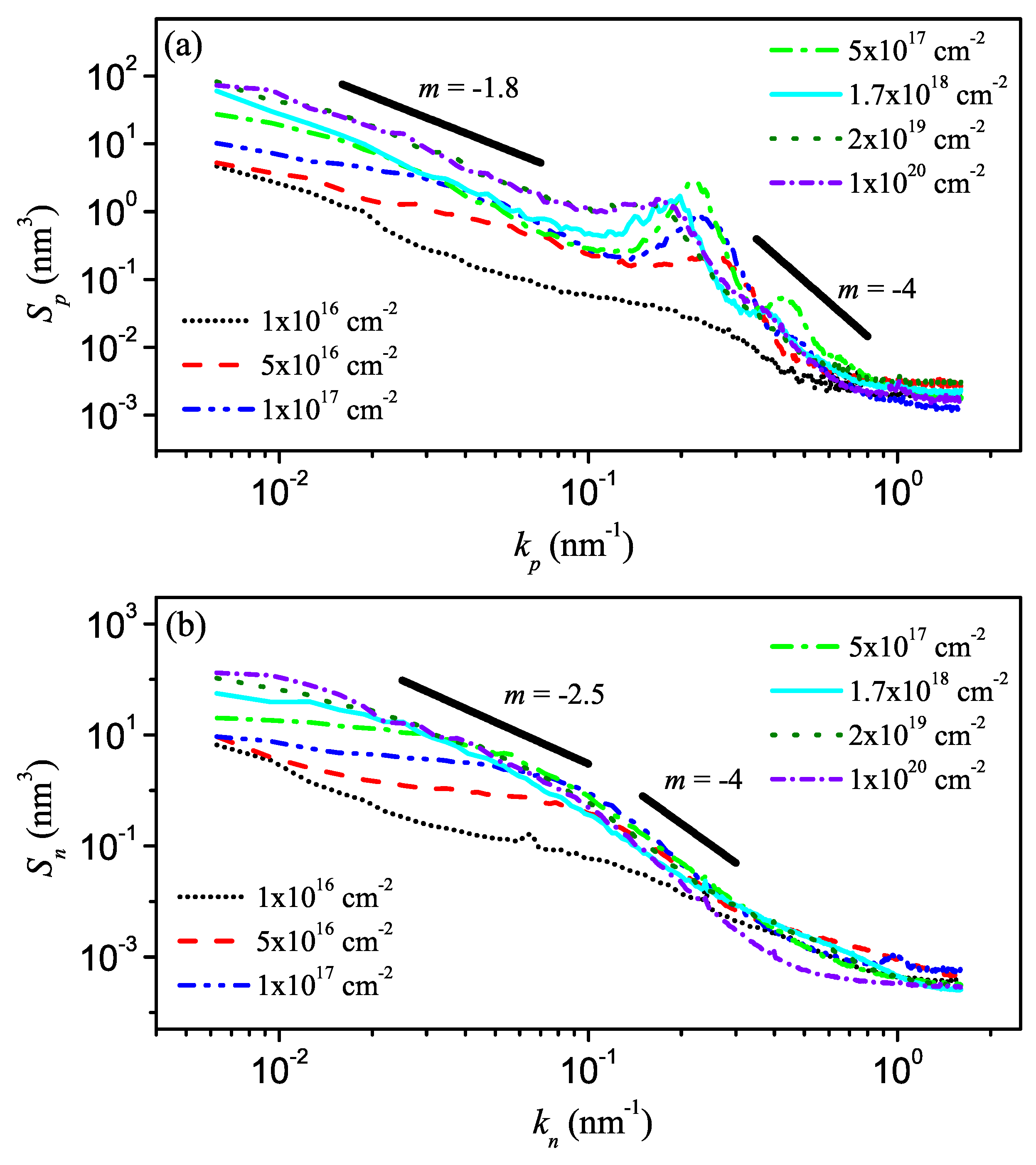
3.2.2. Dynamic scaling behavior
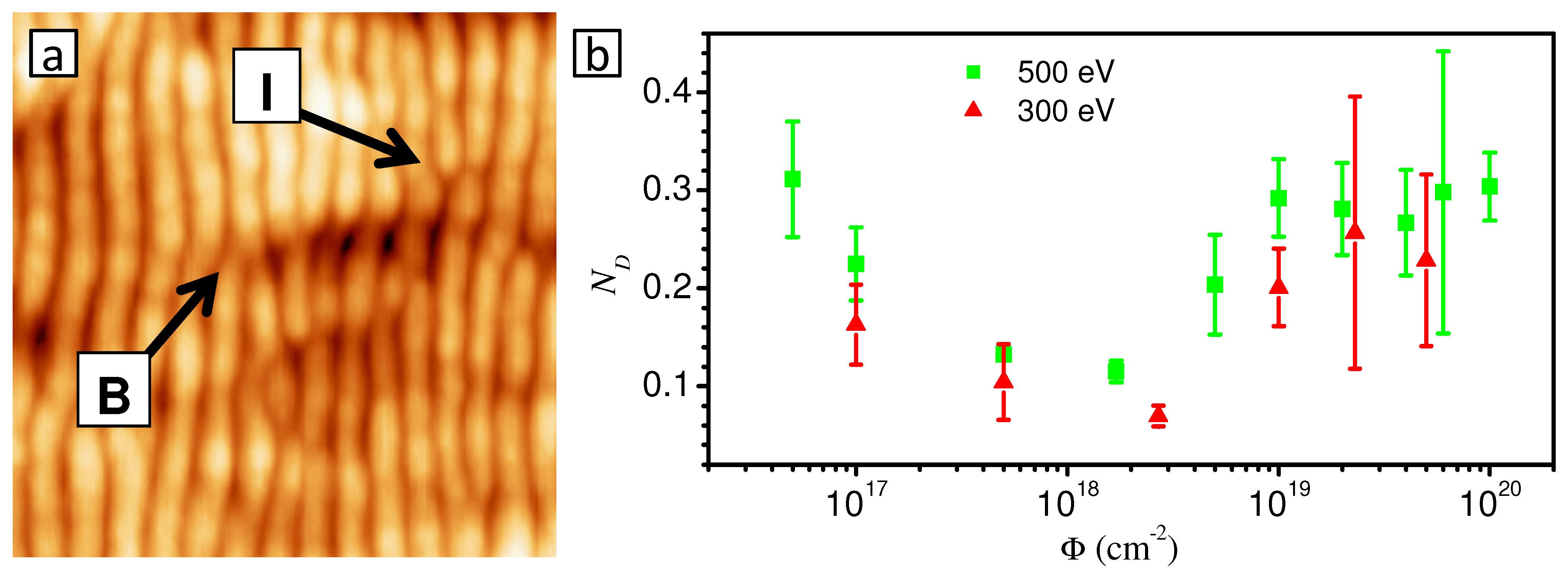
3.2.3. Dynamics of topological pattern defects

4. Summary
Acknowledgements
References
- Navez, M.; Sella, C.; Chaperot, D. Étude de l’attaque du verre par bombardement ionique. C. R. Acad. Sci. Paris 1962, 254, 240–248. [Google Scholar]
- Lewis, G.W.; Nobes, M.J.; Carter, G.; Whitton, J.L. The mechanisms of etch pit and ripple structure formation on ion bombarded Si and other amorphous solids. Nucl. Inst. Meth. Phys. Res. B 1980, 170, 363–369. [Google Scholar] [CrossRef]
- Carter, G.; Nobes, M.J.; Paton, F.; Williams, J.S.; Whitton, J.L. Ion bombardment induced ripple topography on amorphous solids. Radiat. Eff. Defects Solids 1977, 33, 65–73. [Google Scholar] [CrossRef]
- Vasiliu, F.; Teodorescu, I.A.; Glodeanu, F. SEM investigations of iron surface ion erosion as a function of specimen temperature and incidence angle. J. Mater. Sci. 1975, 10, 399–405. [Google Scholar] [CrossRef]
- Erlebacher, J.; Aziz, M.J.; Chason, E.; Sinclair, M.B.; Floro, J.A. Spontaneous Pattern Formation on Ion Bombarded Si(001). Phys. Rev. Lett. 1999, 82, 2330–2333. [Google Scholar] [CrossRef]
- Chason, E.; Mayer, T.M.; Kellerman, B.K.; McIlroy, D.T.; Howard, A.J. Roughening instability and evolution of the Ge(001) surface during ion sputtering. Phys. Rev. Lett. 1994, 72, 3040–3043. [Google Scholar] [CrossRef] [PubMed]
- Rusponi, S.; Costantini, G.; Boragno, C.; Valbusa, U. Ripple Wave Vector Rotation in Anisotropic Crystal Sputtering. Phys. Rev. Lett. 1998, 81, 2735–2738. [Google Scholar] [CrossRef]
- Mayer, T.M.; Chason, E.; Howard, A.J. Roughening instability and ion-induced viscous relaxation of SiO2 surfaces. J. Appl. Phys. 1994, 76, 1633–1643. [Google Scholar] [CrossRef]
- Carter, G.; Vishnyakov, V. Roughening and ripple instabilities on ion-bombarded Si. Phys. Rev. B 1996, 54, 17647–17653. [Google Scholar] [CrossRef]
- Facsko, S.; Dekorsy, T.; Koerdt, C.; Trappe, C.; Kurz, H.; Vogt, A.; Hartnagel, H. Formation of Ordered Nanoscale Semiconductor Dots by Ion Sputtering. Science 1999, 285, 1551–1553. [Google Scholar] [CrossRef] [PubMed]
- Gago, R.; Vázquez, L.; Cuerno, R.; Varela, M.; Ballesteros, C.; Albella, J.M. Production of ordered silicon nanocrystals by low-energy ion sputtering. Appl. Phys. Lett. 2001, 78, 3316–3318. [Google Scholar] [CrossRef]
- Frost, F.; Schindler, A.; Bigl, F. Roughness Evolution of Ion Sputtered Rotating InP Surfaces: Pattern Formation and Scaling Laws. Phys. Rev. Lett. 2000, 85, 4116–4119. [Google Scholar] [CrossRef] [PubMed]
- Ziberi, B.; Frost, F.; Rauschenbach, B. Pattern transitions on Ge surfaces during low-energy ion beam erosion. Appl. Phys. Lett. 2006, 88, 173115. [Google Scholar] [CrossRef]
- Smirnov, V.K.; Kibalov, D.S.; Orlov, O.M.; Graboshnikov, V.V. Technology for nanoperiodic doping of a metal-oxide-semiconductor field-effect transistor channel using a self-forming wave-ordered structure. Nanotechnology 2003, 14, 709–715. [Google Scholar] [CrossRef]
- Mussi, V.; Granone, F.; Boragno, C.; Buatier de Mongeot, F.; Valbusa, U.; Dodecaneso, V.; Marolo, T.; Montereali, R.M. Surface nanostructuring and optical activation of lithium fluoride crystals by ion beam irradiation. Appl. Phys. Lett. 2006, 88, 103116. [Google Scholar] [CrossRef]
- Mussi, V.; Montereali, R.M.; Nichelatti, E.; Boragno, C.; Buatier de Mongeot, F.; Valbusa, U. Broad band light-emitting nanostructured substrates by ion beam irradiation of lithium fluoride crystals. Surf. Sci. 2007, 601, 2746–2749. [Google Scholar] [CrossRef]
- Bobek, T.; Mikuszeit, N.; Camarero, J.; Kyrsta, S.; Yang, L.; Niño, M.A.; Hofer, C.; Gridneva, L.; Arvanitis, D.; Miranda, R.; de Miguel, J.J.; Teichert, C.; Kurz, H. Self-Organized Hexagonal Patterns of Independent Magnetic Nanodots. Adv. Mat. 2007, 19, 4375–4380. [Google Scholar] [CrossRef]
- Bobek, T.; Kurz, H. Fabrication of metallic nanomasks by transfer of self-organized nanodot patterns from semiconductor material into thin metallic layers. Nucl. Inst. Meth. Phys. Res. B 2007, 257, 771–776. [Google Scholar] [CrossRef]
- Bisio, F.; Moroni, R.; Buatier de Mongeot, F.; Canepa, M.; Mattera, L. Isolating the Step Contribution to the Uniaxial Magnetic Anisotropy in Nanostructured Fe/Ag(001) Films. Phys. Rev. Lett. 2006, 96, 057204. [Google Scholar] [CrossRef] [PubMed]
- Liedke, M.O.; Liedke, B.; Keller, A.; Hillebrands, B.; Mücklich, A.; Facsko, S.; Fassbender, J. Induced anisotropies in exchange-coupled systems on rippled substrates. Phys. Rev. B 2007, 75, 220407(R). [Google Scholar] [CrossRef]
- Fassbender, J.; Strache, T.; Liedke, M.O.; Markó, D.; Wintz, S.; Lenz, K.; Keller, A.; Facsko, S.; Mönch, I.; McCord, J. Introducing artificial length scales to tailor magnetic properties. New J. Phys. 2009, 11, 125002. [Google Scholar] [CrossRef]
- Körner, M.; Lenz, K.; Liedke, M.O.; Strache, T.; Mücklich, A.; Keller, A.; Facsko, S.; Fassbender, J. Interlayer exchange coupling of Fe/Cr/Fe thin films on rippled substrates. Phys. Rev. B 2009, 80, 214401. [Google Scholar] [CrossRef]
- Teichert, C.; de Miguel, J.J.; Bobek, T. Ion beam sputtered nanostructured semiconductor surfaces as templates for nanomagnet arrays. J. Phys.: Condens. Matter 2009, 21, 224025. [Google Scholar] [CrossRef] [PubMed]
- Oates, T.W.H.; Keller, A.; Facsko, S.; Mücklich, A. Aligned Silver Nanoparticles on Rippled Silicon Templates Exhibiting Anisotropic Plasmon Absorption. Plasmonics 2007, 2, 47–50. [Google Scholar] [CrossRef]
- Camelio, S.; Babonneau, D.; Lantiat, D.; Simonot, L.; Pailloux, F. Anisotropic optical properties of silver nanoparticle arrays on rippled dielectric surfaces produced by low-energy ion erosion. Phys. Rev. B 2009, 80, 155434. [Google Scholar] [CrossRef]
- Oates, T.W.H.; Keller, A.; Noda, S.; Facsko, S. Self-organized metallic nanoparticle and nanowire arrays from ion-sputtered silicon templates. Appl. Phys. Lett 2008, 93, 063106. [Google Scholar] [CrossRef]
- Toma, A.; Chiappe, D.; Massabó, D.; Boragno, C.; Buatier de Mongeot, F. Self-organized metal nanowire arrays with tunable optical anisotropy. Appl. Phys. Lett. 2008, 93, 163104. [Google Scholar] [CrossRef]
- Ranjan, M.; Oates, T.W.H.; Facsko, S.; Möller, W. Optical properties of silver nanowire arrays with 35 nm periodicity. Opt. Lett. 2010, 35, 2576–2578. [Google Scholar] [CrossRef] [PubMed]
- Bradley, R.M.; Harper, J.M.E. Theory of ripple topography induced by ion bombardment. J. Vac. Sci. Technol. A 1988, 6, 2390–2396. [Google Scholar] [CrossRef]
- Sigmund, P. A mechanism of surface micro-roughening by ion bombardment. J. Mater. Sci. 1973, 8, 1545–1553. [Google Scholar] [CrossRef]
- Kuramoto, Y.; Tsuzuki, T. Persistent Propagation of Concentration Waves in Dissipative Media Far from Thermal Equilibrium. Prog. Theor. Phys. 1976, 55, 356–369. [Google Scholar] [CrossRef]
- Sivashinsky, G.I. On self-turbulization of a laminar flame. Acta Astronaut. 1979, 6, 569–591. [Google Scholar] [CrossRef]
- Cuerno, R.; Barabási, A.L. Dynamic Scaling of Ion-Sputtered Surfaces. Phys. Rev. Lett. 1995, 74, 4746–4749. [Google Scholar] [CrossRef] [PubMed]
- Park, S.; Kahng, B.; Jeong, H.; Barabási, A.L. Dynamics of Ripple Formation in Sputter Erosion: Nonlinear Phenomena. Phys. Rev. Lett. 1999, 83, 3486–3489. [Google Scholar] [CrossRef]
- Cuerno, R.; Makse, H.A.; Tomassone, S.; Harrington, S.T.; Stanley, H.E. Stochastic Model for Surface Erosion via Ion Sputtering: Dynamical Evolution from Ripple Morphology to Rough Morphology. Phys. Rev. Lett. 1995, 75, 4464–4467. [Google Scholar] [CrossRef] [PubMed]
- Habenicht, S.; Bolse, W.; Lieb, K.P.; Reimann, K.; Geyer, U. Nanometer ripple formation and self-affine roughening of ion-beam-eroded graphite surfaces. Phys. Rev. B 1999, 60, R2200–R2203. [Google Scholar] [CrossRef]
- Bobek, T.; Facsko, S.; Kurz, H.; Dekorsy, T.; Xu, M.; Teichert, C. Temporal evolution of dot patterns during ion sputtering. Phys. Rev. B 2003, 68, 085324. [Google Scholar] [CrossRef]
- Ziberi, B.; Frost, F.; Höche, T.; Rauschenbach, B. Ripple pattern formation on silicon surfaces by low-energy ion-beam erosion: Experiment and theory. Phys. Rev. B 2005, 72, 235310. [Google Scholar] [CrossRef]
- Keller, A.; Roßbach, S.; Facsko, S.; Möller, W. Simultaneous formation of two ripple modes on ion sputtered silicon. Nanotechnology 2008, 19, 135303. [Google Scholar] [CrossRef] [PubMed]
- Rusponi, S.; Costantini, G.; Boragno, C.; Valbusa, U. Scaling Laws of the Ripple Morphology on Cu(110). Phys. Rev. Lett. 1998, 81, 4184–4187. [Google Scholar] [CrossRef]
- Alkemade, P.F.A.; Jiang, Z.X. Complex roughening of Si under oblique bombardment by low-energy oxygen ions. J. Vac. Sci. Technol. B 2001, 19, 1699–1705. [Google Scholar] [CrossRef]
- Datta, D.P.; Chini, T.K. Atomic force microscopy study of 60-keV Ar-ion-induced ripple patterns on Si(100). Phys. Rev. B 2004, 69, 235313. [Google Scholar] [CrossRef]
- Datta, D.P.; Chini, T.K. Coarsening of ion-beam-induced surface ripple in Si: Nonlinear effect vs. geometrical shadowing. Phys. Rev. B 2007, 76, 075323. [Google Scholar] [CrossRef]
- Keller, A.; Facsko, S.; Möller, W. The morphology of amorphous SiO2 surfaces during low energy ion sputtering. J. Phys.: Condens. Matter 2009, 21, 495305. [Google Scholar]
- Makeev, M.A.; Cuerno, R.; Barabási, A.L. Morphology of ion-sputtered surfaces. Nucl. Inst. Meth. Phys. Res. B 2002, 197, 185–227. [Google Scholar] [CrossRef]
- Facsko, S.; Bobek, T.; Stahl, A.; Kurz, H.; Dekorsy, T. Dissipative continuum model for self-organized pattern formation during ion-beam erosion. Phys. Rev. B 2004, 69, 153412. [Google Scholar] [CrossRef]
- Aste, T.; Valbusa, U. Ripples and ripples: from sandy deserts to ion-sputtered surfaces. New J. Phys. 2005, 7, 122. [Google Scholar] [CrossRef]
- Castro, M.; Cuerno, R.; Vázquez, L.; Gago, R. Self-Organized Ordering of Nanostructures Produced by Ion-Beam Sputtering. Phys. Rev. Lett. 2005, 94, 016102. [Google Scholar] [CrossRef] [PubMed]
- Muñoz-García, J.; Castro, M.; Cuerno, R. Nonlinear Ripple Dynamics on Amorphous Surfaces Patterned by Ion Beam Sputtering. Phys. Rev. Lett. 2006, 96, 086101. [Google Scholar] [CrossRef] [PubMed]
- Muñoz-García, J.; Vázquez, L.; Cuerno, R.; Sánchez-García, J.A.; Castro, M.; Gago, R. Self-organized surface nanopatterning by ion beam sputtering. In Toward Functional Nanomaterials; Wang, Z.M., Ed.; Springer: New York, NY, USA, 2009. [Google Scholar]
- Behrisch, R.; Anderson, H.H. (Eds.) Sputtering by Particle Bombardment I, Topics in Applied Physics; Springer: Berlin, Germany, 1981.
- Behrisch, R. (Ed.) Sputtering by Particle Bombardment II, Topics in Applied Physics; Springer: Berlin, Germany, 1983.
- Sigmund, P. Theory of Sputtering. I. Sputtering Yield of Amorphous and Polycrystalline Targets. Phys. Rev. 1969, 184, 383–416. [Google Scholar] [CrossRef]
- Gnaser, H. Low Energy Ion Irradiation of Solid Surfaces, 1st ed.; Springer-Verlag: New York, NY, USA, 1998. [Google Scholar]
- Neidhart, T.; Pichler, F.; Aumayr, F.; Winter, H.; Schmid, M.; Varga, P. Potential Sputtering of Lithium Fluoride by Slow Multicharged Ions. Phys. Rev. Lett. 1995, 74, 5280–5283. [Google Scholar] [CrossRef] [PubMed]
- Taoufik, A.; Chouiyakh, A.; Lang, B. Build-up and annealing of damage produced by low-energy argon ions at Si(111) surface. Radiat. Eff. Defects Solids 1987, 104, 117–125. [Google Scholar] [CrossRef]
- Mullins, W.W. Flattening of a Nearly Plane Solid Surface due to Capillarity. J. Appl. Phys. 1959, 30, 77–83. [Google Scholar] [CrossRef]
- Herring, C. Diffusional Viscosity of a Polycrystalline Solid. J. Appl. Phys. 1950, 21, 437–445. [Google Scholar] [CrossRef]
- Keller, A.; Facsko, S.; Cuerno, R. Numerical Integrator for Continuum Equations of Surface Growth and Erosion. In Computational Nanotechnology: Modelling and Applications with MATLAB; Musa, S.M., Ed.; CRC Press: Boca Raton, FL, USA, in press.
- Flamm, D.; Frost, F.; Hirsch, D. Evolution of surface topography of fused silica by ion beam sputtering. Appl. Surf. Sci. 2001, 179, 95–101. [Google Scholar] [CrossRef]
- Karmakar, P.; Ghose, D. Ion beam sputtering induced ripple formation in thin metal films. Surf. Sci. 2004, 554, L101–L106. [Google Scholar] [CrossRef]
- Toma, A.; Buatier de Mongeot, F.; Buzio, R.; Firpo, G.; Bhattacharyya, S.; Boragno, C.; Valbusa, U. Ion beam erosion of amorphous materials: evolution of surface morphology. Nucl. Inst. Meth. Phys. Res. B 2005, 230, 551–554. [Google Scholar] [CrossRef]
- Erlebacher, J.; Aziz, M.J.; Chason, E.; Sinclair, M.B.; Floro, J.A. Nonlinear amplitude evolution during spontaneous patterning of ion-bombarded Si(001). J. Vac. Sci. Technol. A 2000, 18, 115–120. [Google Scholar] [CrossRef]
- Chason, E.; Erlebacher, J.; Aziz, M.J.; Floro, J.A.; Sinclair, M.B. Dynamics of pattern formation during low-energy ion bombardment of Si(001). Nucl. Inst. Meth. Phys. Res. B 2001, 178, 55–61. [Google Scholar] [CrossRef]
- Ziberi, B.; Frost, F.; Rauschenbach, B. Formation of large-area nanostructures on Si and Ge surfaces during low energy ion beam erosion. J. Vac. Sci. Technol. A 2006, 24, 1344–1348. [Google Scholar] [CrossRef]
- Chan, W.L.; Chason, E. Making waves: Kinetic processes controlling surface evolution during low energy ion sputtering. J. Appl. Phys. 2007, 101, 121301. [Google Scholar] [CrossRef]
- Brown, A.D.; Erlebacher, J. Temperature and fluence effects on the evolution of regular surface morphologies on ion-sputtered Si(111). Phys. Rev. B 2005, 72, 075350. [Google Scholar] [CrossRef]
- Habenicht, S. Morphology of graphite surfaces after ion-beam erosion. Phys. Rev. B 2001, 63, 125419. [Google Scholar] [CrossRef]
- Chini, T.K.; Sanyal, M.K.; Bhattacharyya, S.R. Energy-dependent wavelength of the ion-induced nanoscale ripple. Phys. Rev. B 2002, 66, 153404. [Google Scholar] [CrossRef]
- MacLaren, S.W.; Baker, J.E.; Finnegan, N.L.; Loxton, C.M. Surface roughness development during sputtering of GaAs and InP: Evidence for the role of surface diffusion in ripple formation and sputter cone development. J. Vac. Sci. Technol. A 1992, 10, 468–476. [Google Scholar] [CrossRef]
- Umbach, C.C.; Headrick, R.L.; Chang, K.C. Spontaneous Nanoscale Corrugation of Ion-Eroded SiO2: The Role of Ion-Irradiation-Enhanced Viscous Flow. Phys. Rev. Lett. 2001, 87, 246104. [Google Scholar] [CrossRef] [PubMed]
- Brown, A.D.; Erlebacher, J.; Chan, W.L.; Chason, E. Transient Topographies of Ion Patterned Si(111). Phys. Rev. Lett 2005, 95, 056101. [Google Scholar] [CrossRef] [PubMed]
- Kardar, M.; Parisi, G.; Zhang, Y.C. Dynamic Scaling of Growing Interfaces. Phys. Rev. Lett. 1986, 56, 889–892. [Google Scholar] [CrossRef] [PubMed]
- Barabási, A.L.; Stanley, H.E. Fractal Concepts in Surface Growth; Cambridge University Press: New York, NY, USA, 1995. [Google Scholar]
- Paniconi, M.; Elder, K.R. Stationary, dynamical, and chaotic states of the two-dimensional damped Kuramoto-Sivashinsky equation. Phys. Rev. E 1997, 56, 2713–2721. [Google Scholar] [CrossRef]
- Buceta, J.; Pastor, J.; Rubio, M.A.; de la Rubia, F.J. Small scale properties of the stochastic stabilized Kuramoto-Sivashinsky equation. Physica D 1998, 113, 166–171. [Google Scholar] [CrossRef]
- Vogel, S.; Linz, S.J. Continuum modeling of sputter erosion under normal incidence: Interplay between nonlocality and nonlinearity. Phys. Rev. B 2005, 752, 035416. [Google Scholar] [CrossRef]
- Vogel, S.; Linz, S.J. How ripples turn into dots: Modeling ion-beam erosion under oblique incidence. Europhys. Lett. 2006, 76, 884–890. [Google Scholar] [CrossRef]
- Vogel, S.; Linz, S.J. Surface structuring by multiple ion beams. Phys. Rev. B 2007, 75, 085425. [Google Scholar] [CrossRef]
- Vogel, S.; Linz, S.J. Formation of structured islands by ion-beam erosion. Phys. Rev. B 2007, 75, 155417. [Google Scholar] [CrossRef]
- Makeev, M.A.; Barabási, A.L. Ion-induced effective surface diffusion in ion sputtering. Appl. Phys. Lett. 1997, 71, 2800–2802. [Google Scholar] [CrossRef]
- Muñoz-García, J.; Cuerno, R.; Castro, M. Coupling of morphology to surface transport in ion-beam irradiated surfaces: Oblique incidence. Phys. Rev. B 2008, 78, 205408. [Google Scholar] [CrossRef]
- Muñoz-García, J.; Cuerno, R.; Castro, M. Short-range stationary patterns and long-range disorder in an evolution equation for one-dimensional interfaces. Phys. Rev. E 2006, 74, 050103(R). [Google Scholar] [CrossRef] [PubMed]
- Muñoz-García, J.; Gago, R.; Vázquez, L.; Sánchez-García, J.A.; Cuerno, R. Observation and Modeling of Interrupted Pattern Coarsening: Surface Nanostructuring by Ion Erosion. Phys. Rev. Lett. 2010, 104, 026101. [Google Scholar] [CrossRef] [PubMed]
- Elst, K.; Vandervorst, J.; Alay, J.; Snauwaert, J.; Hellemans, L. Influence of oxygen on the formation of ripples on Si. J. Vac. Sci. Technol. B 1993, 11, 1968–1981. [Google Scholar] [CrossRef]
- Cuenat, A.; George, H.B.; Chang, K.C.; Blakely, J.M.; Aziz, M.J. Lateral Templating for Guided Self-Organization of Sputter Morphologies. Adv. Mater. 2005, 17, 2845–2849. [Google Scholar] [CrossRef]
- Chini, T.K.; Okuyama, F.; Tanemura, M.; Nordlund, K. Structural investigation of keV Ar-ion-induced surface ripples in Si by cross-sectional transmission electron microscopy. Phys. Rev. B 2003, 67, 205403. [Google Scholar] [CrossRef]
- Hazra, S.; Chini, T.K.; Sanyal, M.K.; Grenzer, J.; Pietsch, U. Ripple structure of crystalline layers in ion-beam-induced Si wafers. Phys. Rev. B 2004, 70, 121307(R). [Google Scholar] [CrossRef]
- Grigorian, S.; Pietsch, U.; Grenzer, J.; Datta, D.P.; Chini, T.K.; Hazra, S.; Sanyal, M.K. Microstructural anisotropy at the ion-induced rippled amorphous-crystalline interface of silicon. Appl. Phys. Lett. 2006, 89, 231915. [Google Scholar] [CrossRef]
- Habenicht, S.; Lieb, K.P.; Koch, J.; Wieck, A.D. Ripple propagation and velocity dispersion on ion-beam-eroded silicon surfaces. Phys. Rev. B 2002, 65, 115327. [Google Scholar] [CrossRef]
- Karmakar, P.; Mollick, S.A.; Ghose, D.; Chakrabarti, A. Role of initial surface roughness on ion induced surface morphology. Appl. Phys. Lett. 2008, 93, 103102. [Google Scholar] [CrossRef]
- Davidovitch, B.; Aziz, M.J.; Brenner, M.P. On the stabilization of ion sputtered surfaces. Phys. Rev. B 2007, 76, 205420. [Google Scholar] [CrossRef]
- Ziberi, B.; Frost, F.; Rauschenbach, B.; Höche, T. Highly ordered self-organized dot patterns on Si surfaces by low-energy ion-beam erosion. Appl. Phys. Lett. 2005, 87, 033113. [Google Scholar] [CrossRef]
- Ziberi, B.; Frost, F.; Tartz, M.; Neumann, H.; Rauschenbach, B. Ripple rotation, pattern transitions, and long range ordered dots on silicon by ion beam erosion. Appl. Phys. Lett. 2008, 92, 063102. [Google Scholar] [CrossRef]
- Sánchez-García, J.A.; Vázquez, L.; Gago, R.; Redondo-Cubero, A.; Albella, J.M.; Czigány, Z. Tuning the surface morphology in self-organized ion beam nanopatterning of Si(001) via metal incorporation: from holes to dots. Nanotechnology 2008, 19, 355306. [Google Scholar] [CrossRef] [PubMed]
- Ozaydin, G.; Özcan, A.S.; Wang, Y.; Ludwig, K.F.; Zhou, H.; Headrick, R.L.; Siddons, D.P. Real-time x-ray studies of Mo-seeded Si nanodot formation during ion bombardment. Appl. Phys. Lett. 2005, 87, 163104. [Google Scholar] [CrossRef]
- Macko, S.; Frost, F.; Ziberi, B.; Förster, D.F.; Michely, T. Is keV ion-induced pattern formation on Si(001) caused by metal impurities? Nanotechnology 2010, 21, 085301. [Google Scholar] [CrossRef] [PubMed]
- Shenoy, V.B.; Chan, W.L.; Chason, E. Compositionally Modulated Ripples Induced by Sputtering of Alloy Surfaces. Phys. Rev. Lett. 2007, 98, 256101. [Google Scholar] [CrossRef] [PubMed]
- Teichert, C.; Hofer, C.; Hlawacek, G. Self-organization of Nanostructures in Inorganic and Organic Semiconductor Systems. Adv. Eng. Mat. 2006, 8, 1065–1073. [Google Scholar] [CrossRef]
- Ozaydin, G.; Ludwig, K.F.; Zhou, H.; Headrick, R.L. Effects of Mo seeding on the formation of Si nanodots during low-energy ion bombardment. J. Vac. Sci. Technol. B 2008, 26, 551–558. [Google Scholar] [CrossRef]
- Zhang, K.; Rotter, F.; Uhrmacher, M.; Ronning, C.; Hofsäss, H.; Krauser, J. Pattern formation of Si surfaces by low-energy sputter erosion. Surf. Coat. Technol. 2007, 201, 8299–8302. [Google Scholar] [CrossRef]
- Madi, C.S.; George, H.B.; Aziz, M.J. Linear stability and instability patterns in ion-sputtered silicon. J. Phys.: Condens. Matter 2009, 21, 224010. [Google Scholar] [CrossRef] [PubMed]
- Mollick, S.A.; Ghose, D. Formation and characterization of perpendicular mode Si ripples by glancing angle sputtering at room temperature. J. Appl. Phys. 2009, 106, 044309. [Google Scholar] [CrossRef]
- Keller, A.; Cuerno, R.; Facsko, S.; Möller, W. Anisotropic scaling of ripple morphologies on high-fluence sputtered silicon. Phys. Rev. B 2009, 79, 115437. [Google Scholar] [CrossRef]
- Vicsek, T.; Family, F. Dynamic Scaling for Aggregation of Clusters. Phys. Rev. Lett. 1984, 52, 1669–1672. [Google Scholar] [CrossRef]
- Schmittmann, B.; Pruessner, G.; Janssen, H.K. Strongly anisotropic roughness in surfaces driven by an oblique particle flux. Phys. Rev. E 2006, 73, 051603. [Google Scholar] [CrossRef] [PubMed]
- Keller, A.; Facsko, S.; Möller, W. Minimization of topological defects in ion-induced ripple patterns on silicon. New J. Phys. 2008, 10, 063004. [Google Scholar] [CrossRef]
- Otsu, N. A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar]
- Hansen, H.; Redinger, A.; Messlinger, S.; Stoian, G.; Krug, J.; Michely, T. Rapid coarsening of ion beam ripple patterns by defect annihilation. Phys. Rev. Lett. 2009, 102, 146103. [Google Scholar] [CrossRef] [PubMed]
© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Keller, A.; Facsko, S. Ion-Induced Nanoscale Ripple Patterns on Si Surfaces: Theory and Experiment. Materials 2010, 3, 4811-4841. https://doi.org/10.3390/ma3104811
Keller A, Facsko S. Ion-Induced Nanoscale Ripple Patterns on Si Surfaces: Theory and Experiment. Materials. 2010; 3(10):4811-4841. https://doi.org/10.3390/ma3104811
Chicago/Turabian StyleKeller, Adrian, and Stefan Facsko. 2010. "Ion-Induced Nanoscale Ripple Patterns on Si Surfaces: Theory and Experiment" Materials 3, no. 10: 4811-4841. https://doi.org/10.3390/ma3104811



