Mechanical Modelling of the Plastic Flow Machining Process
Abstract
:1. Introduction
2. Fundamental Principles of PFM and Experiments
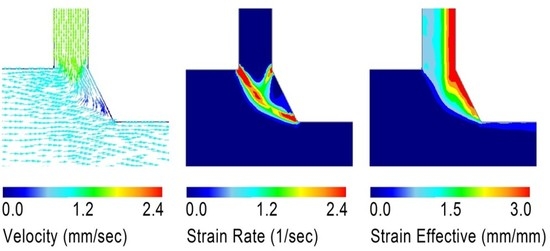
3. Numerical Simulation of the PFM Process
4. Analytical Modeling of the PFM Process
4.1. Model for the Lateral Extrusion Ratio
4.2. Model for the Strain Gradient
5. Discussion
5.1. The Lateral Extrusion Ratio
5.2. The Three Extrusion Modes
5.3. The Strain Gradient
6. Conclusions
- An analytical upper bound model was presented for modeling the lateral extrusion ratio of the PFM process. It was able to reproduce the effect of the applied back-pressure and produced results with excellent agreement with the experiment. With the help of this model, three extrusion modes were identified: Modes 1–3. The selection of the extrusion mode is determined by the applied back-pressure and one geometrical parameter, which is defined by the die geometry.
- Another analytical model was also established to describe the strain gradient found experimentally in the fin. The model was able to produce strain values in two zones, with values near to the experiment. The third, the very high deformation zone, was interpreted with the help of the friction between the metal flow and the die wall.
- Finite element modeling of the PFM process was carried out, where strain hardening and friction were considered. This modeling gave important information on the dead metal zone, and gave results that were generally in good agreement with the experimental observations.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Power Dissipation by Friction

Appendix B
Minimization of the Total Power for Obtaining the x Value
References
- Valiev, R.Z.; Estrin, Y.; Horita, Z.; Langdon, T.G.; Zehetbauer, M.J.; Zhu, Y. Producing bulk ultrafine-grained materials by severe plastic deformation: Ten years later. JOM 2016, 68, 1216–1226. [Google Scholar] [CrossRef]
- Estrin, Y.; Vinogradov, A. Extreme grain refinement by severe plastic deformation: A wealth of challenging science. Acta Mater. 2013, 61, 782–817. [Google Scholar] [CrossRef]
- Valiev, R.Z.; Estrin, Y.; Horita, Z.; Langdon, T.G.; Zechetbauer, M.J.; Zhu, Y.T. Producing bulk ultrafine-grained materials by severe plastic deformation. JOM 2006, 58, 33–39. [Google Scholar] [CrossRef] [Green Version]
- Saito, Y.; Utsunomiya, H.; Tsuji, N.; Sakai, T. Novel ultra-high straining process for bulk materials—Development of the accumulative roll-bonding (ARB) process. Acta Mater. 1999, 47, 579–583. [Google Scholar] [CrossRef]
- Cui, Q.; Ohori, K. Grain refinement of high purity aluminium by asymmetric rolling. Mater. Sci. Technol. 2000, 16, 1095–1101. [Google Scholar] [CrossRef]
- Lee, J.C.; Seok, H.K.; Suh, J.Y. Microstructural evolutions of the al strip prepared by cold rolling and continuous equal channel angular pressing. Acta Mater. 2002, 50, 4005–4019. [Google Scholar] [CrossRef]
- Saray, O.; Purcek, G.; Karaman, I. Principles of equal-channel angular sheet extrusion (ecase): Application to if-steel sheets. Rev. Adv. Mater. Sci. 2010, 25, 42–51. [Google Scholar]
- Saito, Y.; Utsunomiya, H.; Suzuki, H.; Sakai, T. Improvement in the r-value of aluminum strip by a continuous shear deformation process. Scr. Mater. 2000, 42, 1139–1144. [Google Scholar] [CrossRef]
- Huang, J.Y.; Zhu, Y.T.; Jiang, H.; Lowe, T.C. Microstructures and dislocation configurations in nanostructured cu processed by repetitive corrugation and straightening. Acta Mater. 2001, 49, 1497–1505. [Google Scholar] [CrossRef]
- Nam, C.Y.; Han, J.H.; Chung, Y.H.; Shin, M.C. Effect of precipitates on microstructural evolution of 7050 al alloy sheet during equal channel angular rolling. Mater. Sci. Eng. A 2003, 347, 253–257. [Google Scholar] [CrossRef]
- Moscoso, W.; Shankar, M.R.; Mann, J.B.; Compton, W.D.; Chandrasekar, S. Bulk nanostructured materials by large strain extrusion machining. J. Mater. Res. 2011, 22, 201–205. [Google Scholar] [CrossRef]
- Efe, M.; Moscoso, W.; Trumble, K.P.; Dale Compton, W.; Chandrasekar, S. Mechanics of large strain extrusion machining and application to deformation processing of magnesium alloys. Acta Mater. 2012, 60, 2031–2042. [Google Scholar] [CrossRef]
- Beygelzimer, Y.; Toth, L.S.; Fundenberger, J.-J. Procédé de Formation D’un Objet Plat Métallique à Grains Ultrafins. U.S. Patent WO2017017341, 2 February 2017. [Google Scholar]
- Vu, V.Q.; Beygelzimer, Y.; Toth, L.S.; Fundenberger, J.-J.; Kulagin, R.; Chen, C. The plastic flow machining: A new SPD process for producing metal sheets with gradient structures. Mater. Charact. 2018, 138, 208–214. [Google Scholar] [CrossRef]
- Hill, R. The Mathematical Theory of Plasticity; Oxford University Press: Oxford, UK, 1998. [Google Scholar]
- Hasani, A.; Tóth, L.S.; Beausir, B. Principles of nonequal channel angular pressing. J. Eng. Mater. Technol. 2010, 132, 31001–31009. [Google Scholar] [CrossRef]
- Tóth, L.S.; Lapovok, R.; Hasani, A.; Gu, C. Non-equal channel angular pressing of aluminum alloy. Scr. Mater. 2009, 61, 1121–1124. [Google Scholar] [CrossRef]
- Hollomon, J.H. Tensile Deformation. Trans. Metall. Soc. AIME 1945, 162, 268–290. [Google Scholar]
- Arzaghi, M.; Fundenberger, J.J.; Toth, L.S.; Arruffat, R.; Faure, L.; Beausir, B.; Sauvage, X. Microstructure, texture and mechanical properties of aluminum processed by high-pressure tube twisting. Acta Mater. 2012, 60, 4393–4408. [Google Scholar] [CrossRef]
- Alexander, P.Z.; Langdon, T.G. Reassessment of temperature increase and equivalent strain calculation during high-pressure torsion. IOP Conf. Ser. Mater. Sci. Eng. 2014, 63, 012052. [Google Scholar] [Green Version]
- Kachanov, L.M. Fundamentals of the Theory of Plasticity; North-Holland Publishing Company: Maastricht, The Netherlands, 1971. [Google Scholar]
- Johnson, W.; Mellor, P.B. Engineering Plasticity; Ellis Horwood Limited, Van Nostrand Reinhold Ltd.: Chichester, UK, 1983. [Google Scholar]
- Chen, C.; Beygelzimer, Y.; Toth, L.S.; Fundenberger, J.-J. Microstructure and strain in protrusions formed during severe plastic deformation of aluminum. Mater. Lett. 2015, 159, 253–256. [Google Scholar] [CrossRef]
- Prandtl, L. Anwendungsbeispiele zu einem Henckyschen Satz ueber das plastische Gleichgewicht. Zeits. Ang. Math. Mech. 1923, 3, 401. [Google Scholar] [CrossRef]









© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vu, V.Q.; Beygelzimer, Y.; Kulagin, R.; Toth, L.S. Mechanical Modelling of the Plastic Flow Machining Process. Materials 2018, 11, 1218. https://doi.org/10.3390/ma11071218
Vu VQ, Beygelzimer Y, Kulagin R, Toth LS. Mechanical Modelling of the Plastic Flow Machining Process. Materials. 2018; 11(7):1218. https://doi.org/10.3390/ma11071218
Chicago/Turabian StyleVu, Viet Q., Yan Beygelzimer, Roman Kulagin, and Laszlo S. Toth. 2018. "Mechanical Modelling of the Plastic Flow Machining Process" Materials 11, no. 7: 1218. https://doi.org/10.3390/ma11071218