Growth Description for Vessel Wall Adaptation: A Thick-Walled Mixture Model of Abdominal Aortic Aneurysm Evolution
Abstract
:1. Introduction
2. Methods
2.1. Mixture Theory
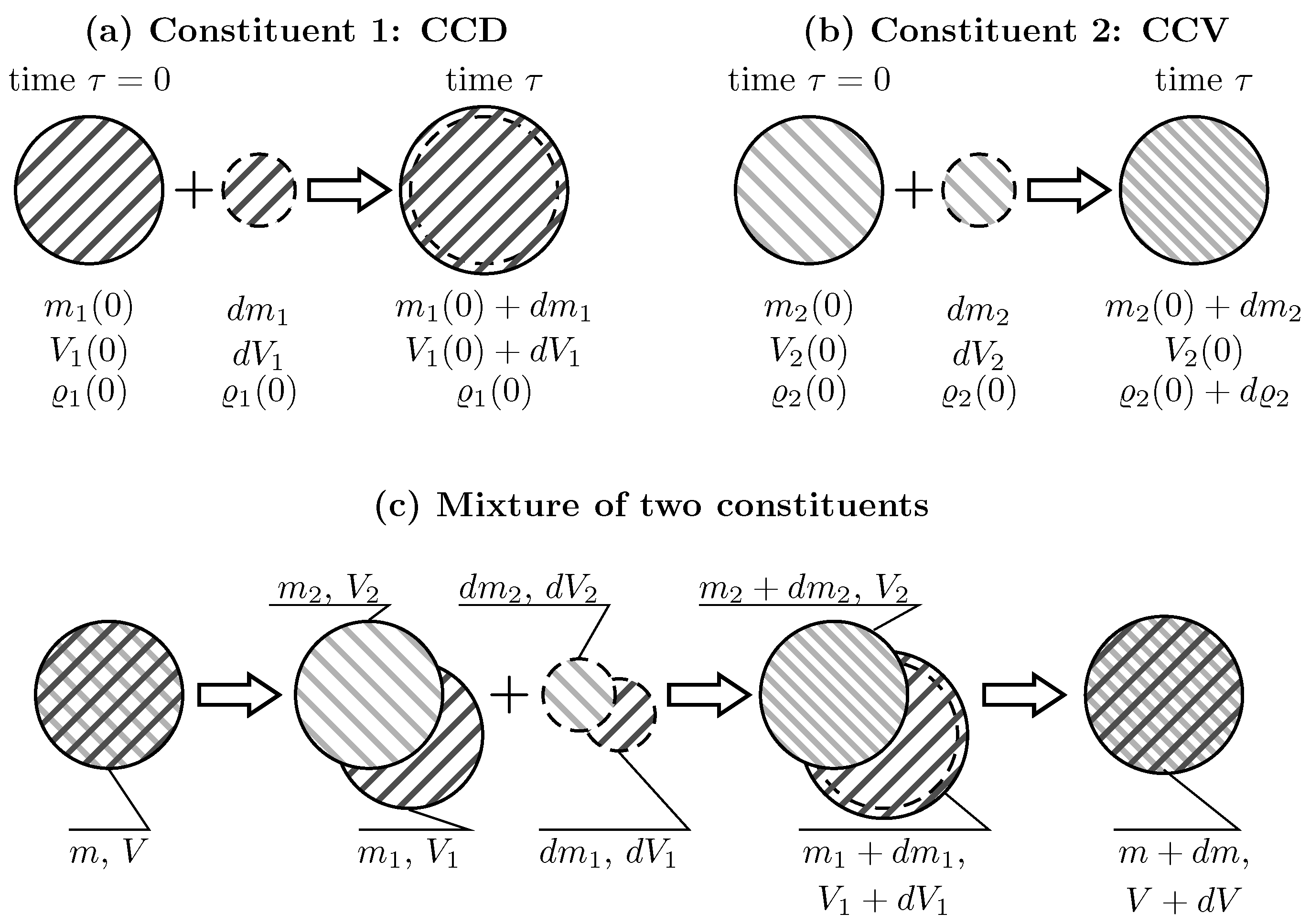
2.1.1. Deposition at Constant Constituent Density (CCD)
2.1.2. Deposition at Constant Constituent Volume (CCV)
2.1.3. Mixed Deposition
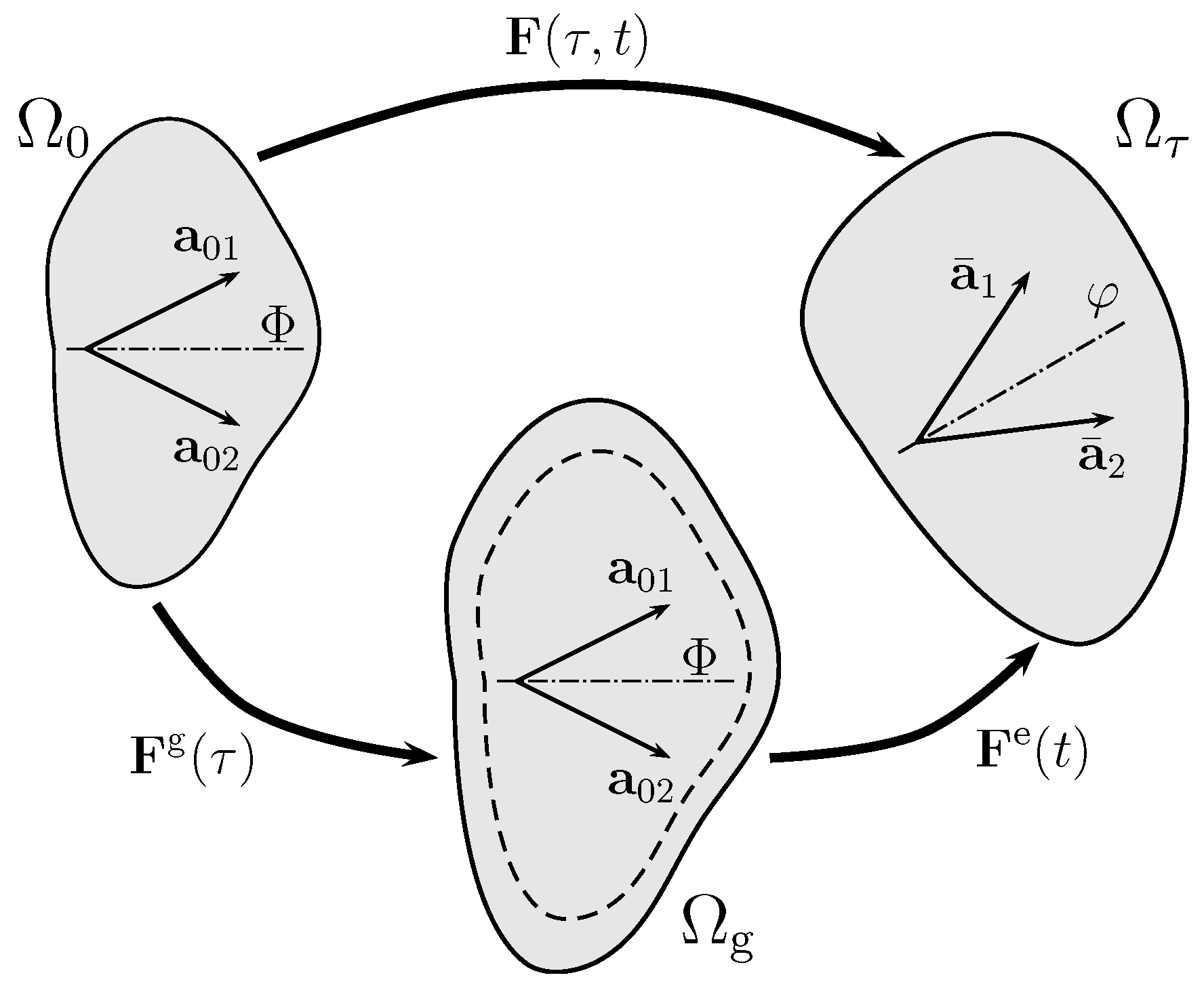
2.2. Kinematics
2.2.1. Quasi-Incompressible Elastic Response
2.2.2. Collagen Structure and Reference Configuration
2.2.3. Growth Tensor description
2.2.4. Implication of Growth Kinematics on the Equi-Biaxial Tissue Properties
2.3. Constitutive Modeling of Vascular Tissue
2.3.1. Elastic Properties
2.3.2. Collagen Turnover Modeling
2.3.3. Elastin Degradation
2.4. Axisymmetric Aorta Model
2.5. Parameter Study
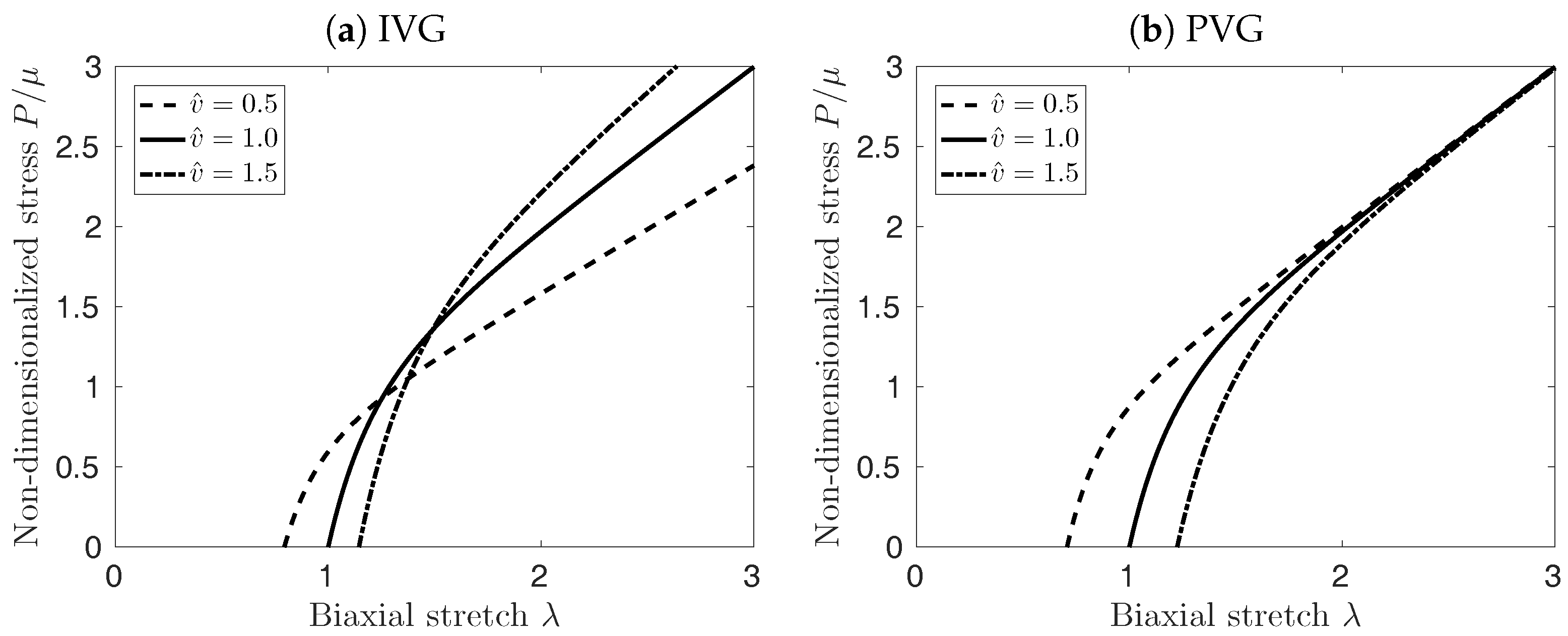
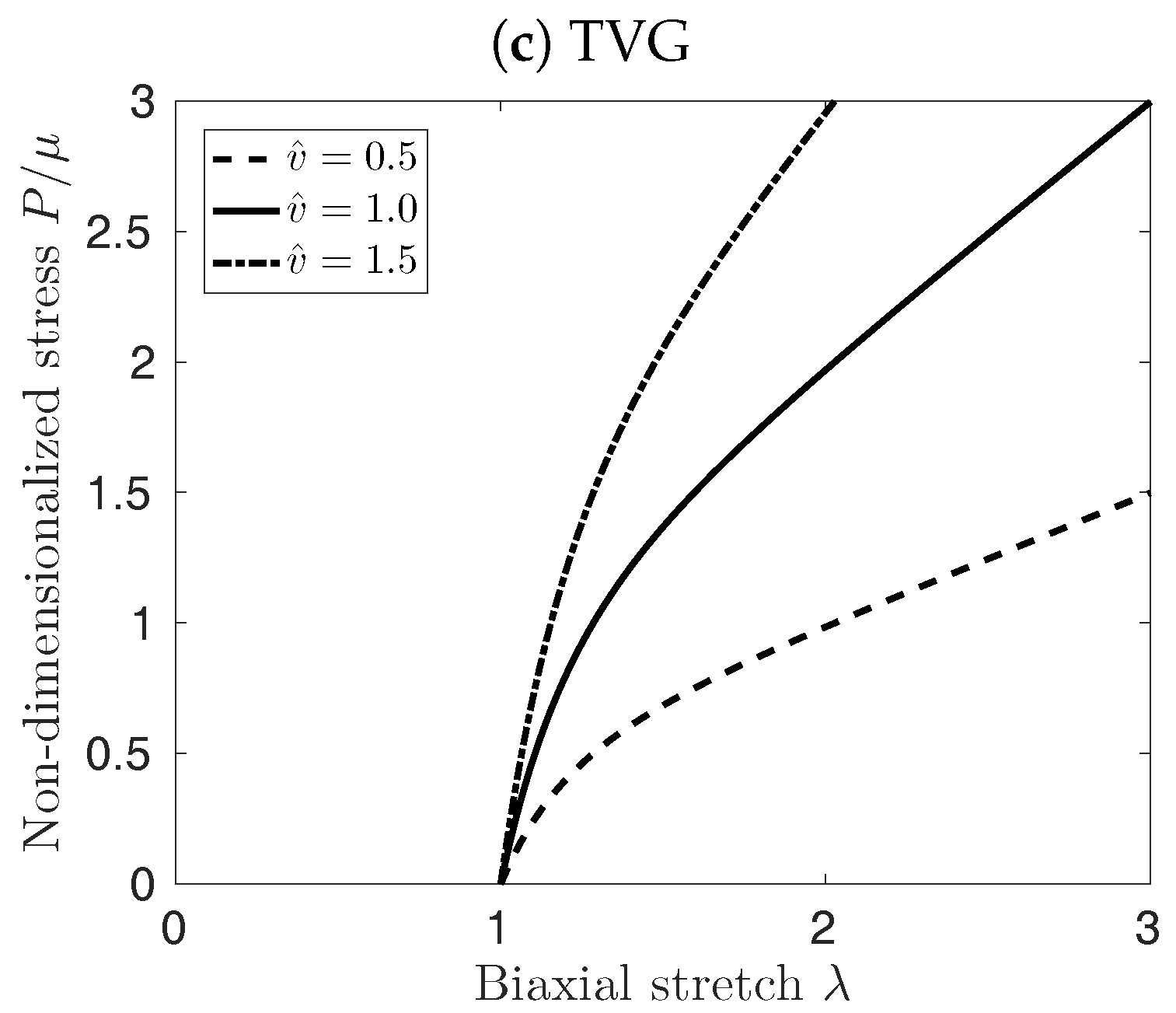
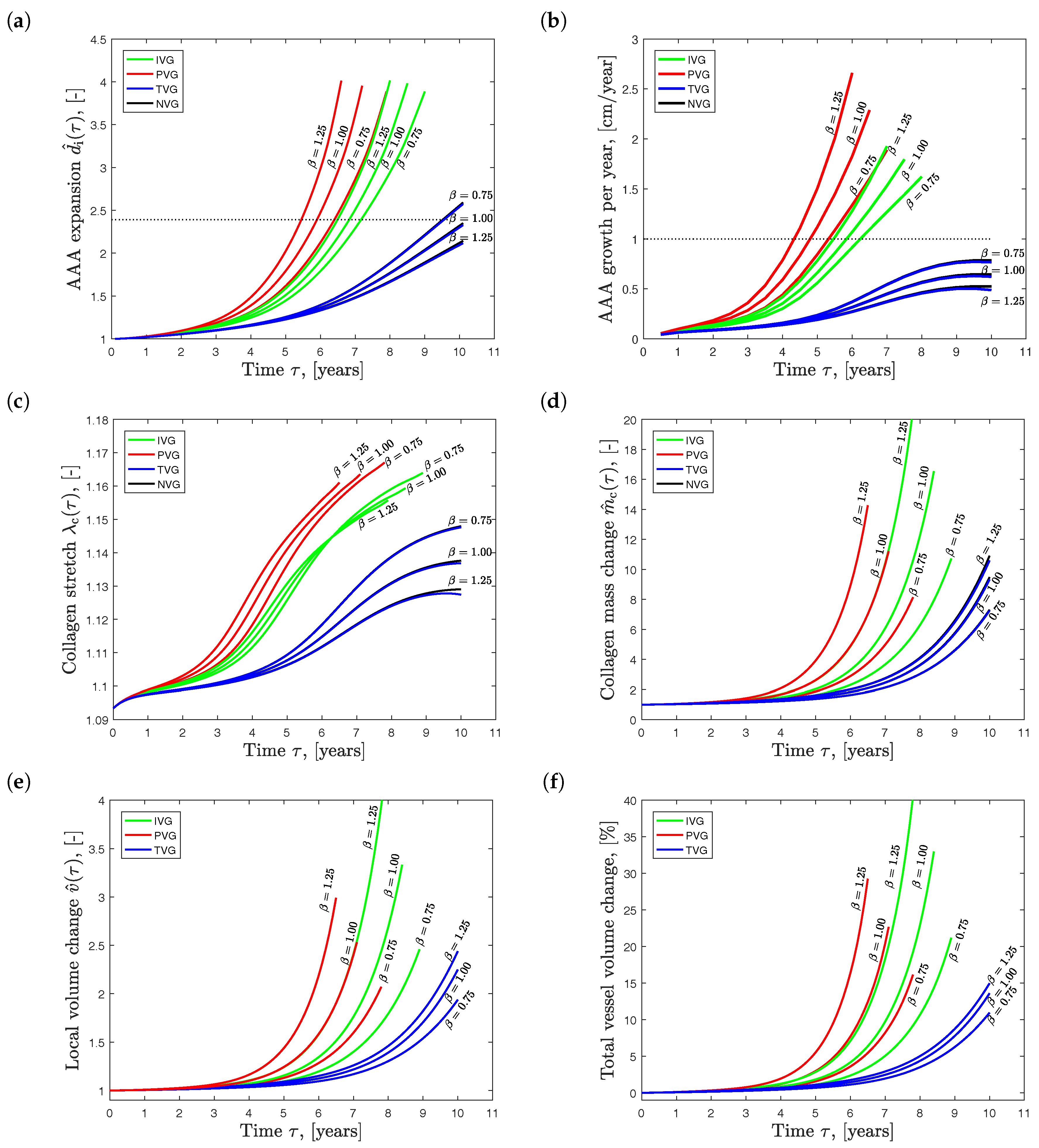
2.5.1. Study 1: Influence of Collagen Net Growth
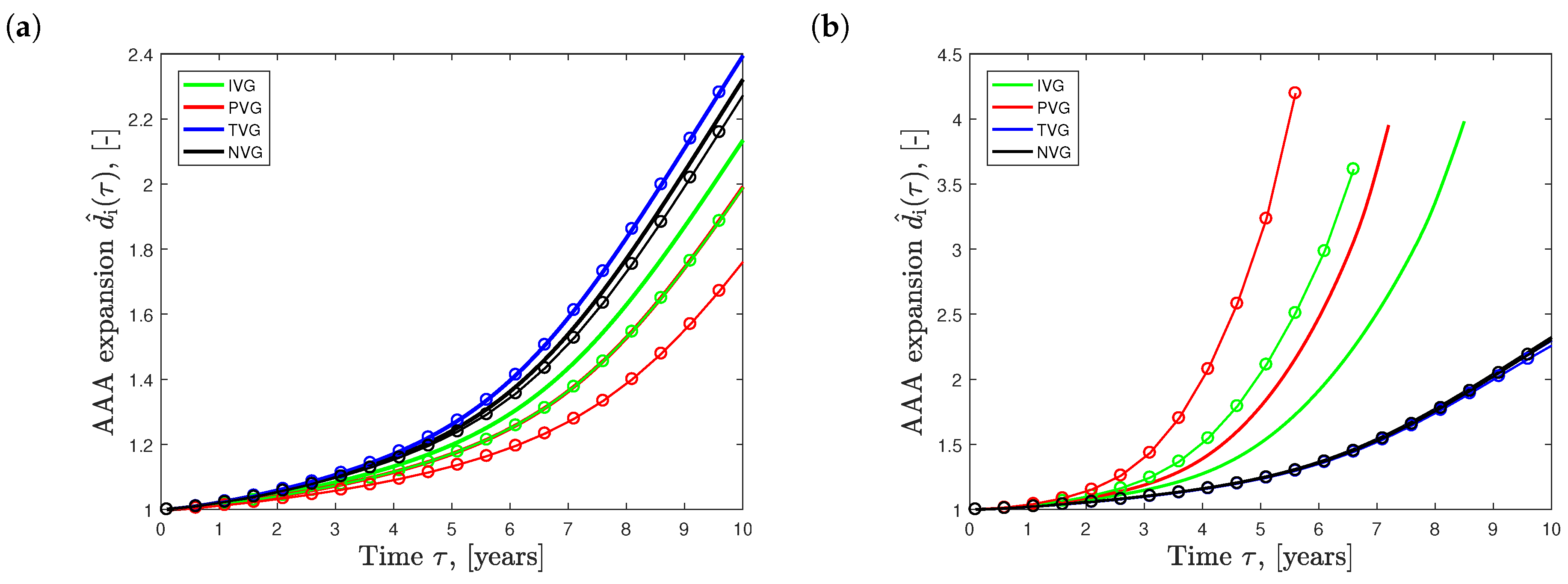
2.5.2. Study 2: Influence of Initial Volume Fractions
3. Results
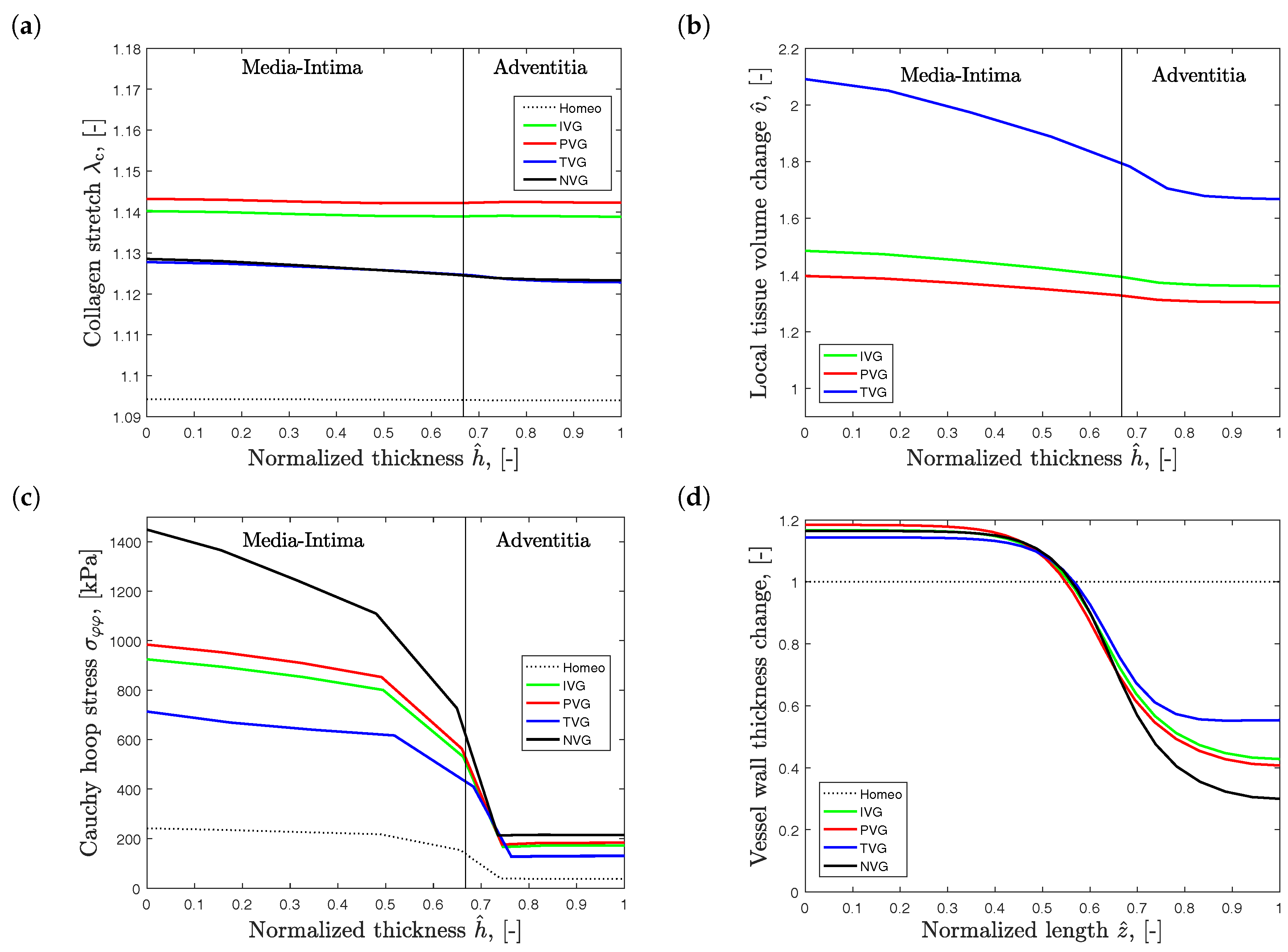
3.1. Study 1: Influence of Collagen Net Growth
3.2. Study 2: Influence of Initial Volume Fractions
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Humphrey, J.D. Cardiovascular Solid Mechanics. Cells, Tissues, and Organs; Springer: New York, NY, USA, 2002. [Google Scholar]
- Cowin, S.C. Tissue growth and remodeling. Ann. Rev. Biomed. Eng. 2004, 6, 77–107. [Google Scholar] [CrossRef] [PubMed]
- Kuhl, E.; Maas, R.; Himpel, G.; Menzel, A. Computational modeling of arterial wall growth. Biomech. Model. Mechanobiol. 2007, 6, 321–331. [Google Scholar] [CrossRef] [PubMed]
- Ambrosi, D.; Ateshian, G.; Arruda, E.; Cowin, S.; Dumais, J.; Goriely, A.; Holzapfel, G.; Humphrey, J.; Kemkemer, R.; Kuhl, E.; et al. Perspectives on biological growth and remodeling. J. Mech. Phys. Solids 2011, 59, 863–883. [Google Scholar] [CrossRef] [PubMed]
- Menzel, A.; Kuhl, E. Frontiers in growth and remodeling. Mech. Res. Commun. 2012, 42, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, J.; Dufresne, E.; Schwartz, M. Mechanotransduction and extracellular matrix homeostasis. Nat. Rev. Mol. Cell Biol. 2014, 15, 802–812. [Google Scholar] [CrossRef] [PubMed]
- Gasser, T.; Grytsan, A. Biomechanical modeling the adaptation of soft biological tissue. Curr. Opin. Biomed. Eng. 2017, 1, 71–77. [Google Scholar] [CrossRef]
- Nichols, W.W.; O’Rourke, M.F.; Vlachopoulos, C. McDonald’s Blood Flow in Arteries, Sixth Edition. Theoretical, Experimental and Clinical Principles, 6th ed.; Arnold: London, UK, 2011. [Google Scholar]
- Grote, K.; Flach, I.; Luchtefeld, M.; Akin, E.; Holland, S.; Drexler, H.; Schieffer, B. Mechanical stretch enhances mRNA expression and proenzyme release of matrix metalloproteinase-2 (MMP-2) via NAD(P)H oxidase-derived reactive oxygen species. Circ. Res. 2003, 92, e80–e86. [Google Scholar] [CrossRef] [PubMed]
- Bishop, J.E.; Lindahl, G. Regulation of cardiovascular collagen synthesis by mechanical load. Cardiovasc. Res. 1999, 42, 27–44. [Google Scholar] [CrossRef]
- Li, Q.; Muragaki, Y.; Hatamura, I.; Ueno, H.; Ooshima, A. Stretch-induced collagen synthesis in cultured smooth muscle cells from rabbit aortic media and a possible involvement of angiotensin II and transforming growth factor-beta. J. Vasc. Res. 1998, 35, 93–103. [Google Scholar] [CrossRef] [PubMed]
- Nabeshima, Y.; Grood, E.S.; Sakurai, A.; Herman, J.H. Uniaxial tension inhibits tendon collagen degradation by collagenase In Vitro. J. Orthop. Res. 1996, 14, 123–130. [Google Scholar] [CrossRef] [PubMed]
- Bhole, A.P.; Flynn, B.P.; Liles, M.; Saeidi, N.; Dimarzio, C.A.; Ruberti, J.W. Mechanical strain enhances survivability of collagen micronetworks in the presence of collagenase: Implications for loadbearing matrix growth and stability. Philos. Trans. R. Soc. A 2009, 367, 3339–3362. [Google Scholar] [CrossRef] [PubMed]
- Alberts, B.; Bray, D.; Lewis, J.; Raff, M.; Roberts, K.; Watson, J. Molecular Biology of the Cell; Garland Publishing: New York, NY, USA, 1994. [Google Scholar]
- Vrhovski, B.; Weiss, A. Biochemistry of tropoelastin. Eur. J. Biochem. 1998, 258, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Kröner, E. Allgemeine Kontinuumstheorie der Versetzungen und Eigenspannungen. Arch. Rat. Mech. Anal. 1960, 4, 273–334. [Google Scholar] [CrossRef]
- Skalak, R.; Zargaryan, S.; Jain, R.K.; Netti, P.A.; Hoger, A. Compatibility and the genesis of residual stress by volumetric growth. J. Math. Biol. 1996, 34, 889–914. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez, E.K.; Hoger, A.; McCulloch, A.D. Stress-dependent finite growth in soft elastic tissues. J. Biomech. 1994, 27, 455–467. [Google Scholar] [CrossRef]
- Taber, L.A.; Eggers, D.W. Theoretical study of stress-modulated growth in the aorta. J. Theor. Biol. 1996, 180, 343–357. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez, J.; Goicolea, J.M.; Gabaldon, F. A volumetric model for growth of arterial walls with arbitrary geometry and loads. J. Biomech. 2007, 40, 961–971. [Google Scholar] [CrossRef] [PubMed]
- Tsamis, A.; Cheng, A.; Nguyen, T.; Langer, F.; Miller, D.; Kuhl, E. Kinematics of cardiac growth: In Vivo characterization of growth tensors and strains. J. Mech. Behav. Biomed. Mater. 2012, 8, 165–177. [Google Scholar] [CrossRef] [PubMed]
- Gleason, R.L.; Humphrey, J.D. A mixture model of arterial growth and remodeling in hypertension: Altered muscle tone and tissue turnover. J. Vasc. Res. 2004, 41, 352–363. [Google Scholar] [CrossRef] [PubMed]
- Baek, S.; Rajagopal, K.R.; Humphrey, J.D. A theoretical model of enlarging intracranial fusiform aneurysms. J. Biomech. Eng. 2006, 128, 142–149. [Google Scholar] [CrossRef] [PubMed]
- Kroon, M.; Holzapfel, G. A theoretical model for fibroblast-controlled growth of saccular cerebral aneurysms. J. Theor. Biol. 2009, 257, 73–83. [Google Scholar] [CrossRef] [PubMed]
- Alford, P.W.; Humphrey, J.D.; Taber, L.A. Growth and remodeling in a thick-walled artery model: Effects of spatial variations in wall constituents. Biomech. Model. Mechanobiol. 2008, 7, 245–262. [Google Scholar] [CrossRef] [PubMed]
- Machyshyn, I.M.; Bovendeerd, P.H.M.; van de Ven, A.A.F.; Rongen, P.M.J.; van de Vosse, F.N. A model for arterial adaptation combining microstructural collagen remodeling and 3D tissue growth. Biomech. Model. Mechanobiol. 2010, 9, 671–687. [Google Scholar] [CrossRef] [PubMed]
- Cyron, C.J.; Aydin, R.C.; Humphrey, J.D. A homogenized constrained mixture (and mechanical analog) model for growth and remodeling of soft tissue. Biomech. Model. Mechanobiol. 2016, 15, 1389–1403. [Google Scholar] [CrossRef] [PubMed]
- Schmid, H.; Pauli, L.; Paulus, A.; Kuhl, E.; Itskov, M. Consistent formulation of the growth process at the kinematic and constitutive level for soft tissues composed of multiple constituents. Comput. Methods Biomech. Biomed. Eng. 2012, 15, 547–561. [Google Scholar] [CrossRef] [PubMed]
- Valentin, A.; Humphrey, J.D.; Holzapfel, G.A. A finite element-based constrained mixture implementation for arterial growth, remodeling, and adaptation: Theory and numerical verification. Int. J. Numer. Method. Eng. 2013, 29, 822–849. [Google Scholar] [CrossRef] [PubMed]
- Eriksson, T.S.E.; Watton, P.N.; Luo, X.Y.; Ventikos, Y. Modelling volumetric growth in a thick walled fibre reinforced artery. J. Mech. Phys. Solids 2014, 73, 134–150. [Google Scholar] [CrossRef]
- Finlay, H.M.; McCullough, L.; Canham, P.B. Three-dimensional collagen organization of human brain arteries at different transmural pressures. J. Vasc. Res. 1995, 32, 301–312. [Google Scholar] [CrossRef] [PubMed]
- Schriefl, A.; Zeindlinger, G.; Pierce, D.; Regitnig, P.; Holzapfel, G. Determination of the layer-specific distributed collagen fiber orientations in human thoracic and abdominal aortas and common iliac arteries. J. R. Soc. Interface 2012, 7, 1275–1286. [Google Scholar] [CrossRef] [PubMed]
- Polzer, S.; Gasser, T.; Novak, K.; Man, V.; Tichy, M.; Skacel, P.; Bursa, J. Structure-based constitutive model can accurately predict planar biaxial properties of aortic wall tissue. Acta Biomater. 2015, 14, 133–145. [Google Scholar] [CrossRef] [PubMed]
- Thunes, J.R.; Pal, S.; Fortunato, R.N.; Phillippi, J.A.; Gleason, G.; Vorp, D.A.; Maiti, S. A structural finite element model for lamellar unit of aortic media indicates heterogeneous stress field after collagen recruitment. J. Biomech. 2016, 49, 1562–1569. [Google Scholar] [CrossRef] [PubMed]
- Gasser, T.C.; Gallinetti, S.; Xing, X.; Forsell, C.; Swedenborg, J.; Roy, J. Spatial orientation of collagen fibers in the Abdominal Aortic Aneurysm wall and its relation to wall mechanics. Acta Biomater. 2012, 8, 3091–3103. [Google Scholar] [CrossRef] [PubMed]
- Baek, S.; Wells, P.B.; Rajagopal, K.R.; Humphrey, J.D. Heat-induced changes in the finite strain viscoelastic behavior of a collagenous tissue. J. Biomech. Eng. 2005, 127, 580–586. [Google Scholar] [CrossRef] [PubMed]
- Menzel, A. A Fibre reorientation model for ortbotropic multiplicative growth—Configurational driving stresses, kinematics-based reorientation, and algorithmic aspects. Biomech. Model. Mechanobiol. 2007, 6, 303–320. [Google Scholar] [CrossRef] [PubMed]
- Wan, W.; Hansen, L.; Gleason, R.L., Jr. A 3-D constrained mixture model for mechanically mediated vascular growth and remodeling. Biomech. Model. Mechanobiol. 2010, 9, 403–419. [Google Scholar] [CrossRef] [PubMed]
- Braeu, F.A.; Seitz, A.; Aydin, R.C.; Cyron, C.J. Homogenized constrained mixture models for anisotropic volumetric growth and remodeling. Biomech. Model. Mechanobiol. 2016, 16, 9889–9906. [Google Scholar] [CrossRef] [PubMed]
- Kurvers, H.; Veith, F.; Lipsitz, E.; Ohki, T.; Gargiulo, N.; Cayne, N.; Suggs, W.; Timaran, C.; Kwon, G.; Rhee, S.; et al. Discontinuous, staccato growth of abdominal aortic aneurysms. J. Am. Coll. Surg. 2004, 199, 709–715. [Google Scholar] [CrossRef] [PubMed]
- Martufi, G.; Roy, J.; Swedenborg, J.; Sakalihasan, N.; Panuccio, G.; Gasser, T.C. Multidimensional growth measurements of Abdominal Aortic Aneurysms. J. Vasc. Surg. 2013, 58, 748–755. [Google Scholar] [CrossRef] [PubMed]
- Martufi, G.; Liljeqvist, M.L.; Sakalihasan, N.; Panuccio, G.; Hultgren, R.; Roy, J.; Gasser, T. Local Diameter, Wall Stress and Thrombus Thickness Influence the Local Growth of Abdominal Aortic Aneurysms. J. Endovas. Ther. 2016, 23, 957–966. [Google Scholar] [CrossRef] [PubMed]
- Lindquist, M.L.; Hultgren, R.; Gasser, T.; Roy, J. Volume growth of abdominal aortic aneurysms correlates with baseline volume and increasing finite element analysis-derived rupture risk. J. Vasc. Surg. 2016, 63, 1434–1442. [Google Scholar] [CrossRef] [PubMed]
- Liljeqvist, M.L.; Hultgren, R.; Gasser, T.; Roy, J. Gender, smoking, body size and aneurysm geometry influence the biomechanical rupture risk of abdominal aortic aneurysms as estimated by finite element analysis. J. Vasc. Surg. 2017, 65, 1014–1021. [Google Scholar] [CrossRef] [PubMed]
- Grytsan, A.; Watton, P.; Holzapfel, G. A Thick-Walled Fluid-Solid-Growth Model of Abdominal Aortic Aneurysm Evolution: Application to a Patient-Specific Geometry. J. Biomed. Eng. 2015, 137, 031008. [Google Scholar] [CrossRef] [PubMed]
- Watton, P.N.; Hill, N.A.; Heil, M. A mathematical model for the growth of the Abdominal Aortic Aneurysm. Biomech. Model. Mechanobiol. 2004, 3, 98–113. [Google Scholar] [CrossRef] [PubMed]
- Holzapfel, G.A.; Gasser, T.C.; Ogden, R.W. A new constitutive framework for arterial wall mechanics and a comparative study of material models. J. Elast. 2000, 61, 1–48. [Google Scholar] [CrossRef]
- Rizzo, R.; McCarthy, W.; Dixit, S.; Lilly, M.; Shively, V.; Flinn, W.; Yao, J. Collagen types and matrix protein content in human abdominal aortic aneurysms. J. Vasc. Surg. 1989, 10, 365–373. [Google Scholar] [CrossRef]
- Hans, S.S.; Jareunpoon, O.; Balasubramaniam, M.; Zelenock, G.B. Size and location of thrombus in intact and ruptured Abdominal Aortic Aneurysms. J. Vasc. Surg. 2005, 41, 584–588. [Google Scholar] [CrossRef] [PubMed]
- The UK Small Aneurysm Trial Participants. Mortality results for randomised controlled trial of early elective surgery or ultrasonographic surveillance for small abdominal aortic aneurysms. Lancet 1998, 352, 1649–1655. [Google Scholar]
- RM, R.G.; Powell, J. Endovascular repair of abdominal aortic aneurysm. N. Engl. J. Med. 2008, 358, 494–501. [Google Scholar]
- Watton, P.N.; Hill, N.A. Evolving mechanical properties of a model of Abdominal Aortic Aneurysm. Biomech. Model. Mechanobiol. 2009, 8, 25–42. [Google Scholar] [CrossRef] [PubMed]
- Sonesson, B.; Hansen, F.; Stale, H.; Länne, T. Compliance and diameter in the huma abdomial aorta—The influence of age and sex. Eur. J. Vasc. Surg. 1993, 7, 690–697. [Google Scholar] [CrossRef]
- O’Leary, S.; Doyle, B.; McGloughlin, T. Comparison of methods used to measure the thickness of soft tissues and their influence on the evaluation of tensile stress. J. Biomech. 2013, 46, 1955–1960. [Google Scholar] [CrossRef] [PubMed]
- Rosero, E.B.; Peshock, R.M.; Khera, A.; Clagett, G.P.; Lo, H.; Timaran, C. Agreement Between Methods of Measurement of Mean Aortic Wall Thickness by MRI. J. Magn. Reson. Imaging 2009, 29, 576–582. [Google Scholar] [CrossRef] [PubMed]
- Slobodin, G.; Nakhleh, A.; Rimar, D.; Wolfson, V.; Rosner, I.; Odeh, M. Increased aortic wall thickness for the diagnosis of aortitis: A computed tomography-based study. Int. J. Rheum. Dis. 1998, 19, 82–86. [Google Scholar] [CrossRef] [PubMed]
- Gasser, T.C. Biomechanical Rupture Risk Assessment: A Consistent and Objective Decision-Making Tool for Abdominal Aortic Aneurysm Patients. AORTA 2016, 4, 42–60. [Google Scholar] [PubMed]
- Raghavan, M.L.; Ma, B.; Fillinger, M.F. Non-invasive determination of zero-pressure geometry of arterial aneurysms. Ann. Biomed. Eng. 2006, 34, 1414–1419. [Google Scholar] [CrossRef] [PubMed]
- Martufi, G.; Gasser, T.C. Turnover of fibrillar collagen in soft biological tissue with application to the expansion of abdominal aortic aneurysms. J. R. Soc. Interface 2012, 9, 3366–3377. [Google Scholar] [CrossRef] [PubMed]
- Aparicio, P.; Thompson, M.; Watton, P.N. A novel chemo-mechano-biological model of arterial tissue growth and remodelling. J. Biomech. 2016, 49, 2321–2330. [Google Scholar] [CrossRef] [PubMed]
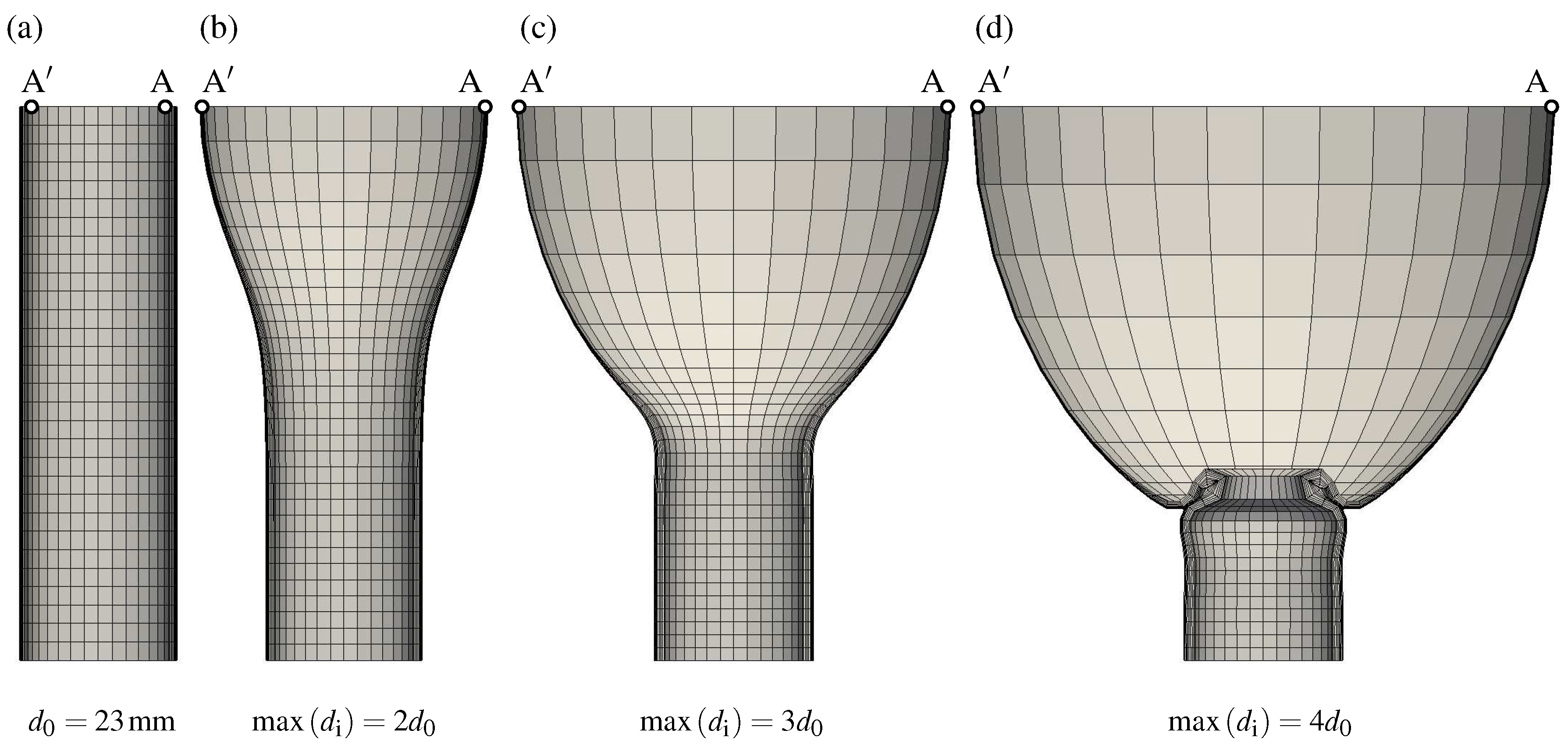
| Reference Geometry and Loading | Value | ||
| Inner radius | 8.4 (mm) | ||
| Artery length | L | 147.4 (mm) | |
| Media-intima thickness | 1.18 (mm) | ||
| Adventitia thickness | 0.59 (mm) | ||
| Inner pressure | 16 (kPa) | ||
| Axial pre-stretch | 1.2 | ||
| Material Model | Media | Adventitia | |
| Elastin shear modulus | 133.81 (kPa) | 0 (kPa) | |
| Elastin initial volume fraction | 0.12 | 0 | |
| Ground matrix shear modulus | 33.45 (kPa) | 33.45 (kPa) | |
| Ground matrix initial volume fraction | 0.73 | 0.86 | |
| Collagen parameter | 3.52 (kPa) | 3.52 (kPa) | |
| Collagen parameter | 40 | 40 | |
| Collagen family initial volume fraction | 0.075 | 0.075 | |
| Fictitious bulk modulus | 100 (kPa) | 100 (kPa) | |
| Aneurysm growth | Equation | Value | |
| Collagen remodeling rate | Equation (18) | 0.6 (year−1) | |
| Collagen net growth rate | Equation (18) | 1.0 (year−1) | |
| Collagen attachment stretch | Equation (17) | 1.093 | |
| Initial value collagen recruitment stretch | Equation (18) | 1.13 | |
| Target amount of elastin | Equation (19) | 0.6 | |
| Degradation time | T | Equation (19) | 10 (years) |
| Shape parameter | Equation (19) | 20 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grytsan, A.; Eriksson, T.S.E.; Watton, P.N.; Gasser, T.C. Growth Description for Vessel Wall Adaptation: A Thick-Walled Mixture Model of Abdominal Aortic Aneurysm Evolution. Materials 2017, 10, 994. https://doi.org/10.3390/ma10090994
Grytsan A, Eriksson TSE, Watton PN, Gasser TC. Growth Description for Vessel Wall Adaptation: A Thick-Walled Mixture Model of Abdominal Aortic Aneurysm Evolution. Materials. 2017; 10(9):994. https://doi.org/10.3390/ma10090994
Chicago/Turabian StyleGrytsan, Andrii, Thomas S. E. Eriksson, Paul N. Watton, and T. Christian Gasser. 2017. "Growth Description for Vessel Wall Adaptation: A Thick-Walled Mixture Model of Abdominal Aortic Aneurysm Evolution" Materials 10, no. 9: 994. https://doi.org/10.3390/ma10090994





