Largest Magnetic Moments in the Half-Heusler Alloys XCrZ (X = Li, K, Rb, Cs; Z = S, Se, Te): A First-Principles Study
Abstract
:1. Introduction
2. Computational Details
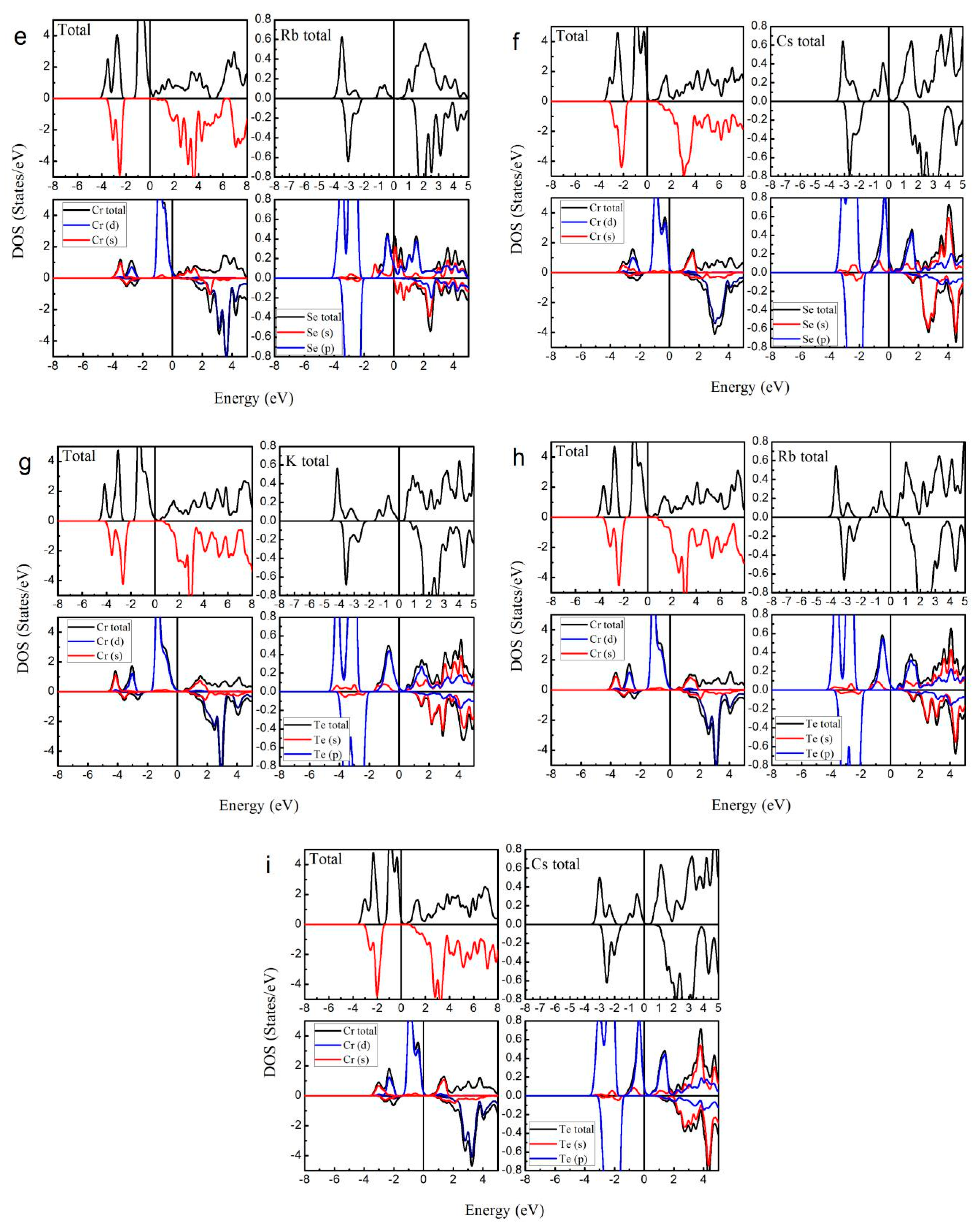
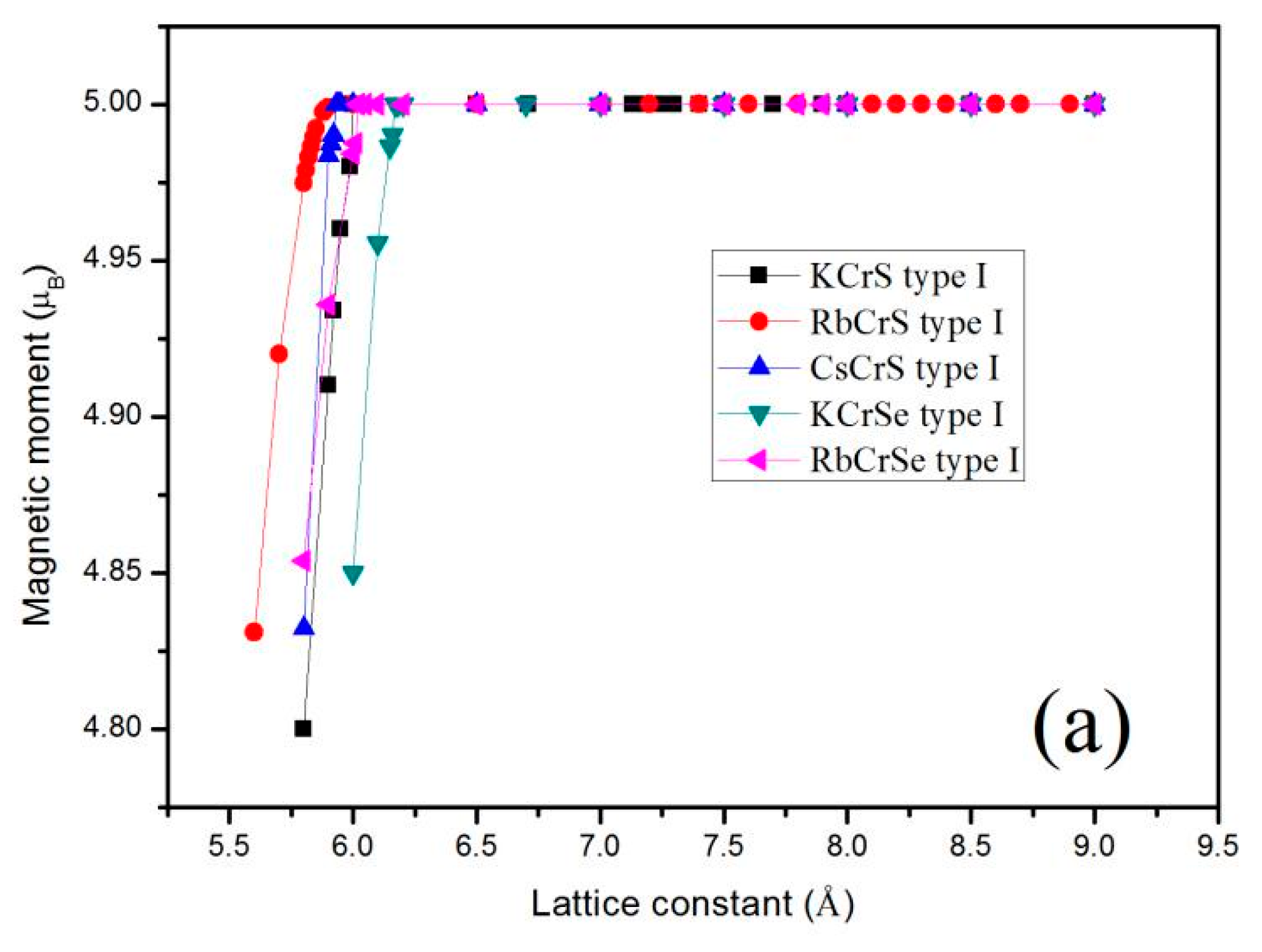
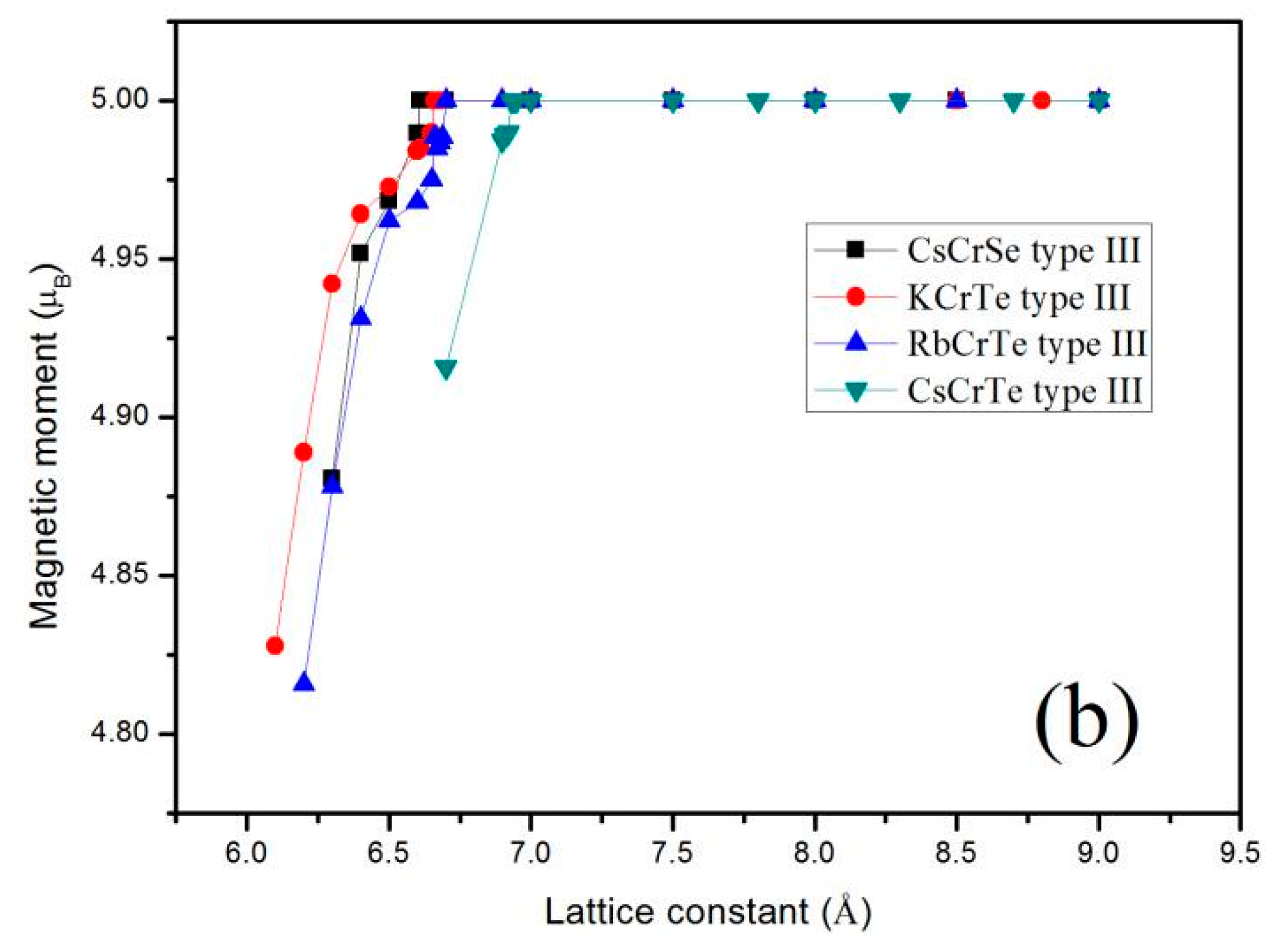
3. Results and Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Žutić, I.; Fabian, J.; Sarma, S.D. Spintronics: Fundamentals and applications. Rev. Mod. Phys. 2004, 76, 323–410. [Google Scholar] [CrossRef]
- Park, J.H.; Vescovo, E.; Kim, H.; Kwon, C. Direct evidence for a half-metallic ferromagnet. Nature 1998, 392, 794–796. [Google Scholar] [CrossRef]
- Wang, Y.Y.; Wu, M.W. Schottky-barrier-induced spin relaxation in spin injection. Phys. Rev. B 2005, 72, 153301. [Google Scholar] [CrossRef]
- Hashemifar, S.J.; Kratzer, P.; Scheffler, M. Preserving the half-metallicity at the Heusler alloy Co2MnSi (001) surface: A density functional theory study. Phys. Rev. Lett. 2005, 94, 096402. [Google Scholar] [CrossRef] [PubMed]
- Lin, H.; Wray, L.A.; Xia, Y.; Xu, S.; Jia, S.; Cava, R.J.; Hasan, M.Z. Half-Heusler ternary compounds as new multifunctional experimental platforms for topological quantum phenomena. Nat. Mater. 2010, 9, 546–549. [Google Scholar] [CrossRef] [PubMed]
- De Groot, R.A.; Mueller, F.M.; Van Engen, P.G.; Buschow, K.H.J. New class of materials: Half-metallic ferromagnets. Phys. Rev. Lett. 1983, 50, 2024. [Google Scholar] [CrossRef]
- Khalaf Alzyadi, J.M.; Jolan, M.H.; Yao, K.L. Surface half-metallicity of half-Heusler compound FeCrSe and interface half-metallicity of FeCrSe/Gap. J. Magn. Magn. Mater. 2016, 403, 8–13. [Google Scholar] [CrossRef]
- Lakdja, A.; Rozale, H.; Chahed, A.; Benhelal, O. Ferromagnetism in the half-heusler XCsBa compounds from first-principles calculations (X = C, Si, and Ge). J. Alloys Compd. 2013, 564, 8–12. [Google Scholar] [CrossRef]
- Lakdja, A.; Rozale, H.; Sayede, A.; Chahed, A. Origin of ferromagnetism in the half-Heusler XRbCs compounds (X = N, P and As). J. Magn. Magn. Mater. 2014, 354, 235–238. [Google Scholar] [CrossRef]
- Sedeek, K.; Hantour, H.; Makram, N.; Said, S.A. Observation of strong ferromagnetism in the half-heusler compound cotisb system. J. Magn. Magn. Mater. 2016, 407, 218–223. [Google Scholar] [CrossRef]
- Rozale, H.; Amar, A.; Lakdja, A.; Moukadem, A.; Chahed, A. Half-metallicity in the half-Heusler RbSrC, RbSrSi and RbSrGe compounds. J. Magn. Magn. Mater. 2013, 336, 83–87. [Google Scholar] [CrossRef]
- Białek, B.; Lee, J.I.; Kim, M. The surface electronic properties of newly designed half-metallic ferromagnets: GeKCa and SnKCa. Comput. Mater. Sci. 2014, 81, 510–516. [Google Scholar] [CrossRef]
- Umamaheswari, R.; Vijayalakshmi, D.; Kalpana, G. First-principles calculation of structural, electronic and magnetic properties of half-Heusler LiCaC and NaCaC compounds. Phys. B Condens. Matter 2014, 448, 256–259. [Google Scholar] [CrossRef]
- Chen, J.; Gao, G.Y.; Yao, K.L.; Song, M.H. Half-metallic ferromagnetism in the half-Heusler compounds GeKCa and SnKCa from first-principles calculations. J. Alloys Compd. 2011, 509, 10172–10178. [Google Scholar] [CrossRef]
- Ahmad, M.; Murtaza, G.; Khenata, R.; Omran, S.B.; Bouhemadou, A. Structural, elastic, electronic, magnetic and optical properties of RbSrX (X = C, Si, Ge) half-Heusler compounds. J. Magn. Magn. Mater. 2015, 377, 204–210. [Google Scholar] [CrossRef]
- Damewood, L.; Busemeyer, B.; Shaughnessy, M.; Fong, C.Y.; Yang, L.H.; Felser, C. Stabilizing and increasing the magnetic moment of half-metals: The role of Li in half-Heusler LiMnZ (Z = N, P, Si). Phys. Rev. B 2015, 91, 064409. [Google Scholar] [CrossRef]
- Zhang, X.M.; Xu, G.Z.; Du, Y.; Liu, E.K.; Liu, Z.Y.; Liu, G.D.; Wu, G.H. Phase stability, magnetism and generalized electron-filling rule of vanadium-based inverse Heusler compounds. Europhys. Lett. 2013, 104, 27012. [Google Scholar] [CrossRef]
- Fecher, G.H.; Kandpal, H.C.; Wurmehl, S.; Felser, C.; Schönhense, G. Slater-pauling rule and curie temperature of Co2-based Heusler compounds. J. Appl. Phys. 2006, 99, 08J106. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, X.; Cheng, Z. Electronic, magnetic, mechanical, half-metallic and highly dispersive zero-gap half-metallic properties of rare-earth-element-based quaternary Heusler compounds. J. Alloys Compd. 2017, 718, 63–74. [Google Scholar] [CrossRef]
- Gao, G.Y.; Hu, L.; Yao, K.L.; Luo, B.; Liu, N. Large half-metallic gaps in the quaternary Heusler alloys CoFeCrZ (Z = Al, Si, Ga, Ge): A first-principles study. J. Alloys Compd. 2013, 551, 539–543. [Google Scholar] [CrossRef]
- Payne, M.C.; Teter, M.P.; Allan, D.C.; Arias, T.A.; Joannopoulos, J.D. Iterative minimization techniques for ab initio total-energy calculations: Molecular dynamics and conjugate gradients. Rev. Mod. Phys. 1992, 64, 1045. [Google Scholar] [CrossRef]
- Segall, M.D.; Lindan, P.J.; Probert, M.A.; Pickard, C.J.; Hasnip, P.J.; Clark, S.J.; Payne, M.C. First-principles simulation: Ideas, illustrations and the CASTEP code. J. Phys. Condens. Matter 2002, 14, 2717–2744. [Google Scholar] [CrossRef]
- Vanderbilt, D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B 1990, 41, 7892–7895. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D.; Edgecombe, K.E.A. Simple measure of electron localization in atomic and molecular systems. J. Chem. Phys. 1990, 92, 5397–5403. [Google Scholar] [CrossRef]
- Silvi, B.; Savin, A. Classification of chemical bonds based on topological analysis of electron localization functions. Nature 1994, 371, 683–686. [Google Scholar] [CrossRef]
- Wang, X.; Cheng, Z.; Wang, J.; Wang, L.; Yu, Z.; Fang, C.; Liu, G. Origin of the half-metallic band-gap in newly designed quaternary Heusler compounds ZrVTiZ (Z = Al, Ga). RSC Adv. 2016, 6, 57041–57047. [Google Scholar] [CrossRef]
- Birsan, A. Small interfacial distortions lead to significant changes of the half-metallic and magnetic properties in Heusler alloys: The case of the new CoFeZrSi compound. J. Alloys Compd. 2017, 710, 393–398. [Google Scholar] [CrossRef]
- Wei, X.P.; Zhang, Y.L.; Wang, T.; Sun, X.W.; Song, T.; Guo, P.; Deng, J.B. Stability, electronic and magnetic properties investigations on Zr2YZ (Y = Co, Cr, V and Z = Al, Ga, In, Pb, Sn, Tl) compounds. Mater. Res. Bull. 2017, 86, 139–145. [Google Scholar] [CrossRef]
- Wang, X.T.; Cui, Y.T.; Liu, X.F.; Liu, G.D. Electronic structures and magnetism in the Li2AgSb-type Heusler alloys, Zr2CoZ (Z = Al, Ga, In, Si, Ge, Sn, Pb, Sb): A first-principles study. J. Magn. Magn. Mater. 2015, 394, 50–59. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Liu, Z.H.; Liu, G.D.; Ma, X.Q. Half-metallic fully compensated ferrimagnetism in C1b-type half heusler compounds Mn2Si1−xGex. J. Magn. Magn. Mater. 2015, 387, 67–71. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Liu, Z.H.; Liu, E.K.; Liu, G.D.; Ma, Q.X.; Wu, G.H. Towards fully compensated ferrimagnetic spin gapless semiconductors for spintronic applications. Europhys. Lett. 2015, 111, 37009. [Google Scholar] [CrossRef]
- Kieven, D.; Klenk, R.; Naghavi, S.; Felser, C.; Gruhn, T. I-II-V half-Heusler compounds for optoelectronics: Ab initio calculations. Phys. Rev. B 2010, 81, 075208. [Google Scholar] [CrossRef]
- Jungwirth, T.; Novák, V.; Martí, X.; Cukr, M.; Máca, F.; Shick, A.B.; Zemek, J. Demonstration of molecular beam epitaxy and a semiconducting band structure for I-Mn-V compounds. Phys. Rev. B 2011, 83, 035321. [Google Scholar] [CrossRef]
- Zhang, X.M.; Xu, G.Z.; Liu, E.K.; Liu, Z.Y.; Wang, W.H.; Wu, G.H. On the influence of tetrahedral covalent-hybridization on electronic band structure of topological insulators from first principles. J. Appl. Phys. 2015, 117, 045706. [Google Scholar] [CrossRef]
- Luo, H.; Xin, Y.; Liu, B.; Meng, F.; Liu, H.; Liu, E.; Wu, G. Competition of L2 1 and XA structural ordering in Heusler alloys X2CuAl (X = Sc, Ti, V, Cr, Mn, Fe, Co, Ni). J. Alloys Compd. 2016, 665, 180–185. [Google Scholar] [CrossRef]
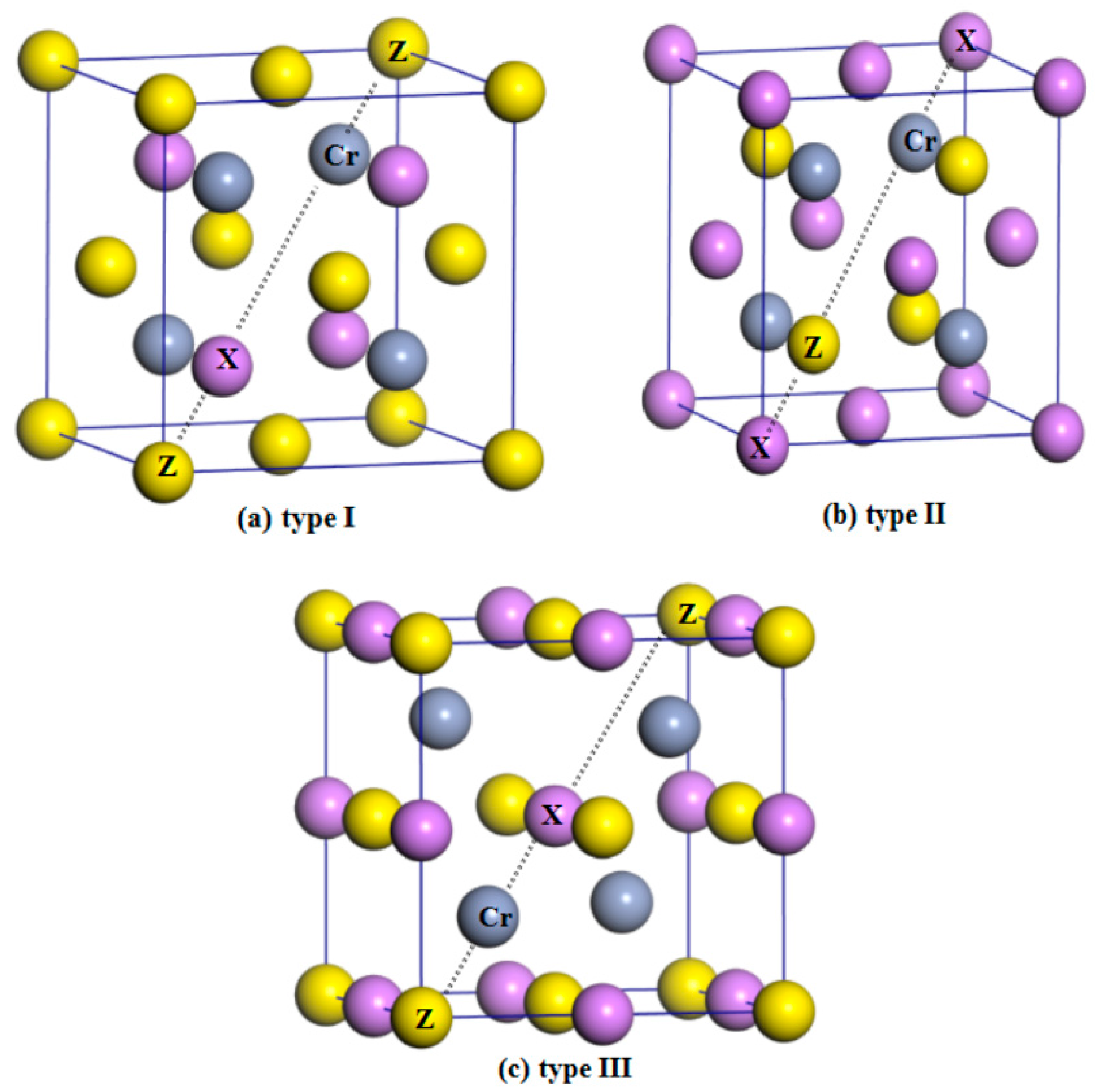
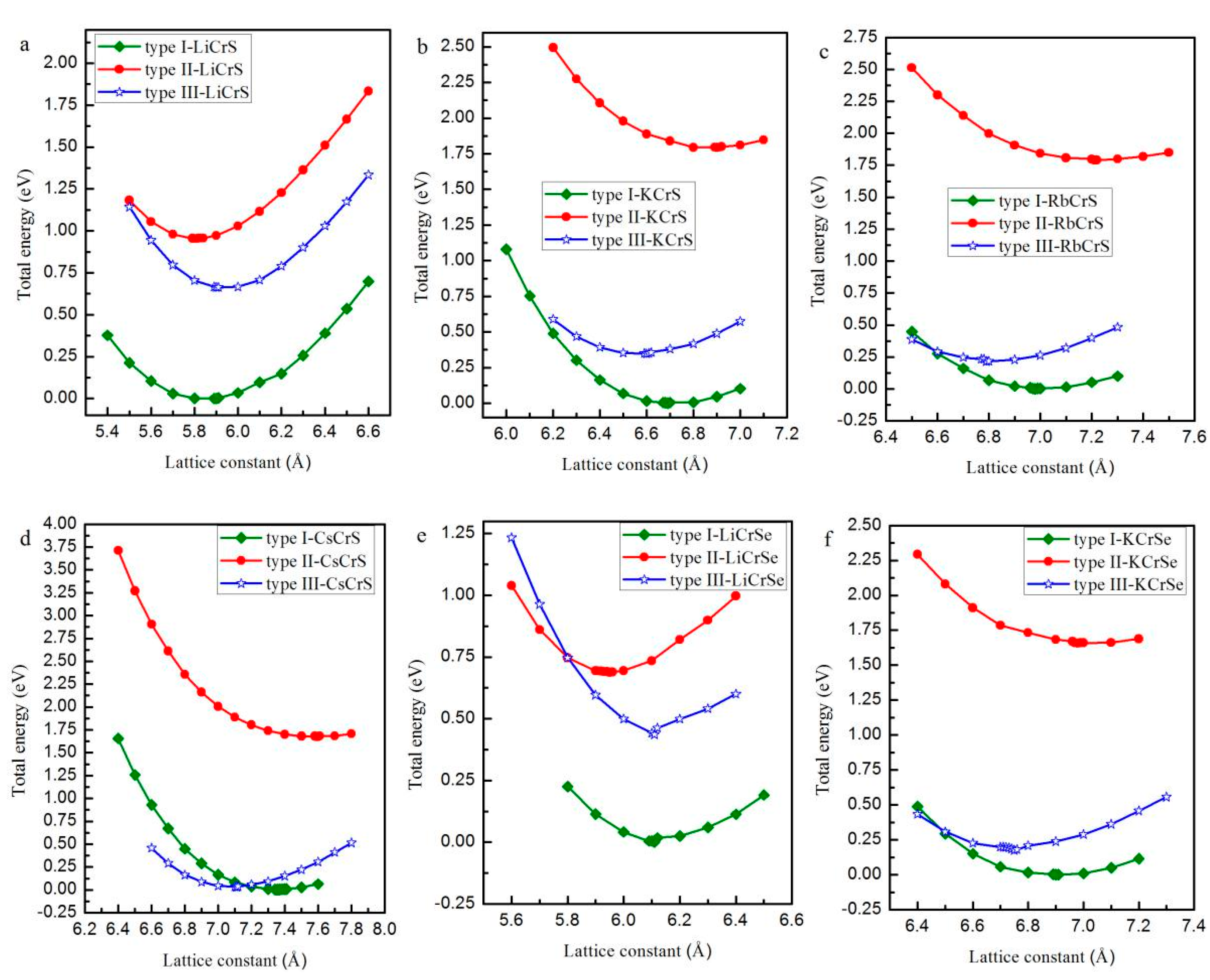
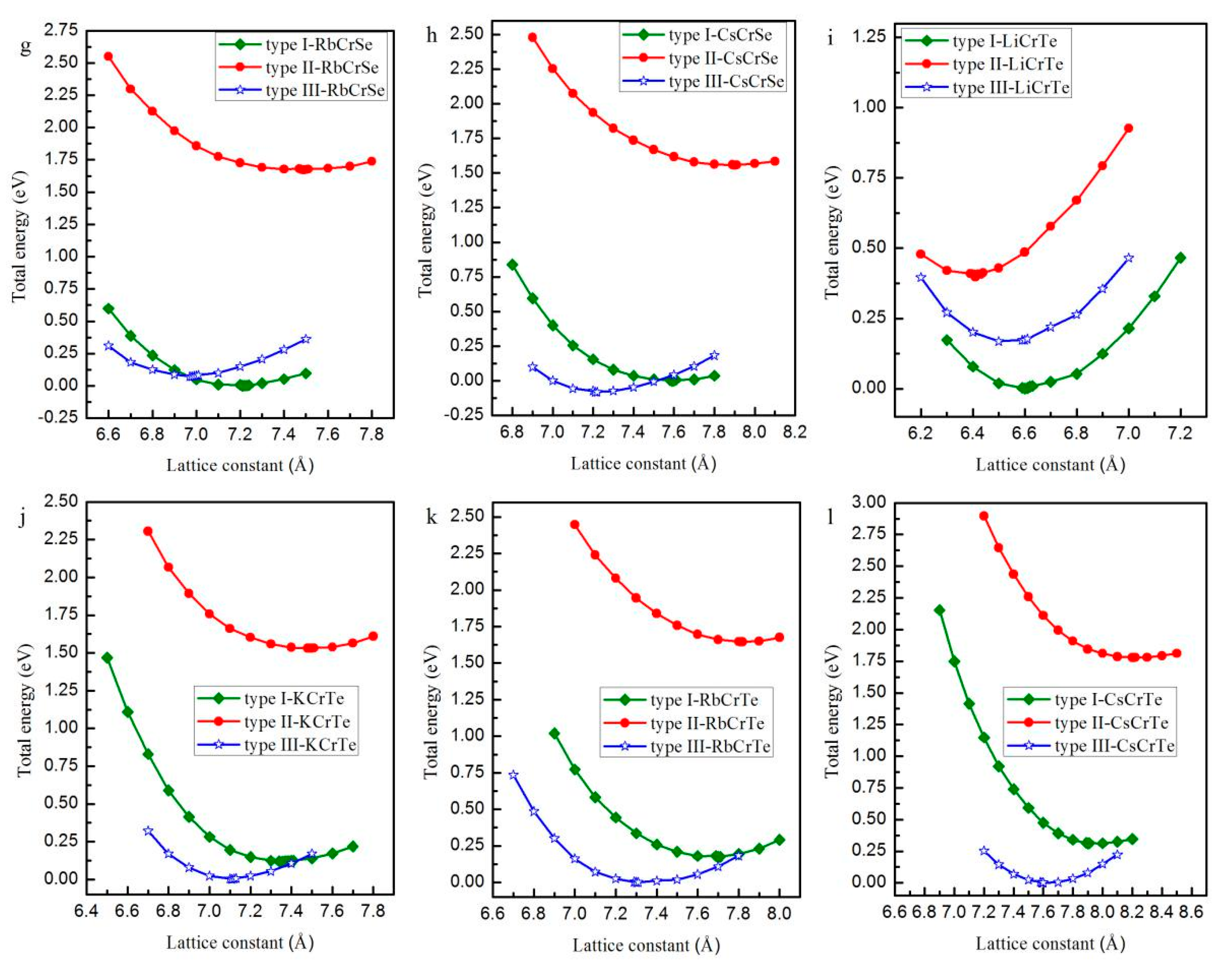
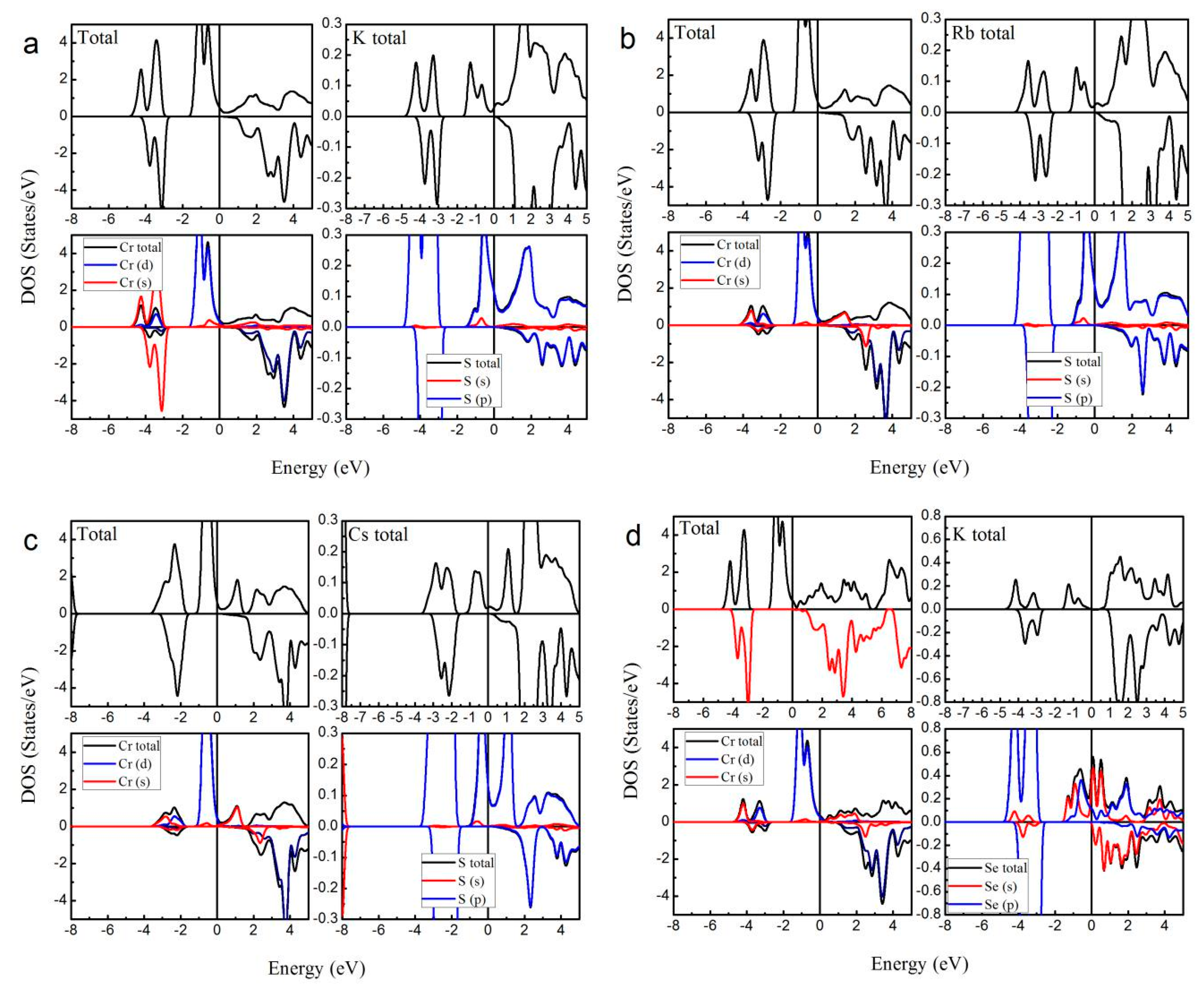

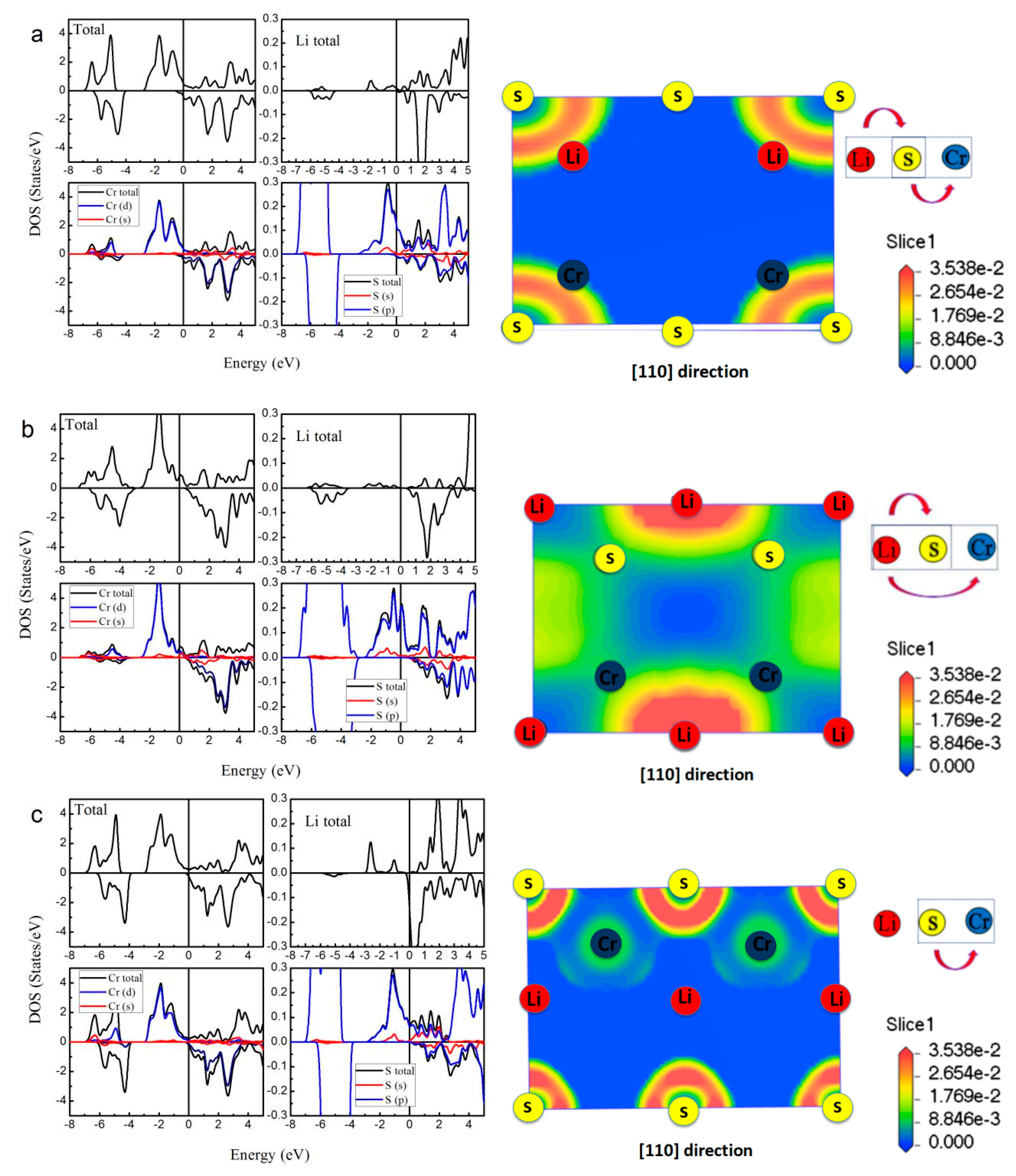
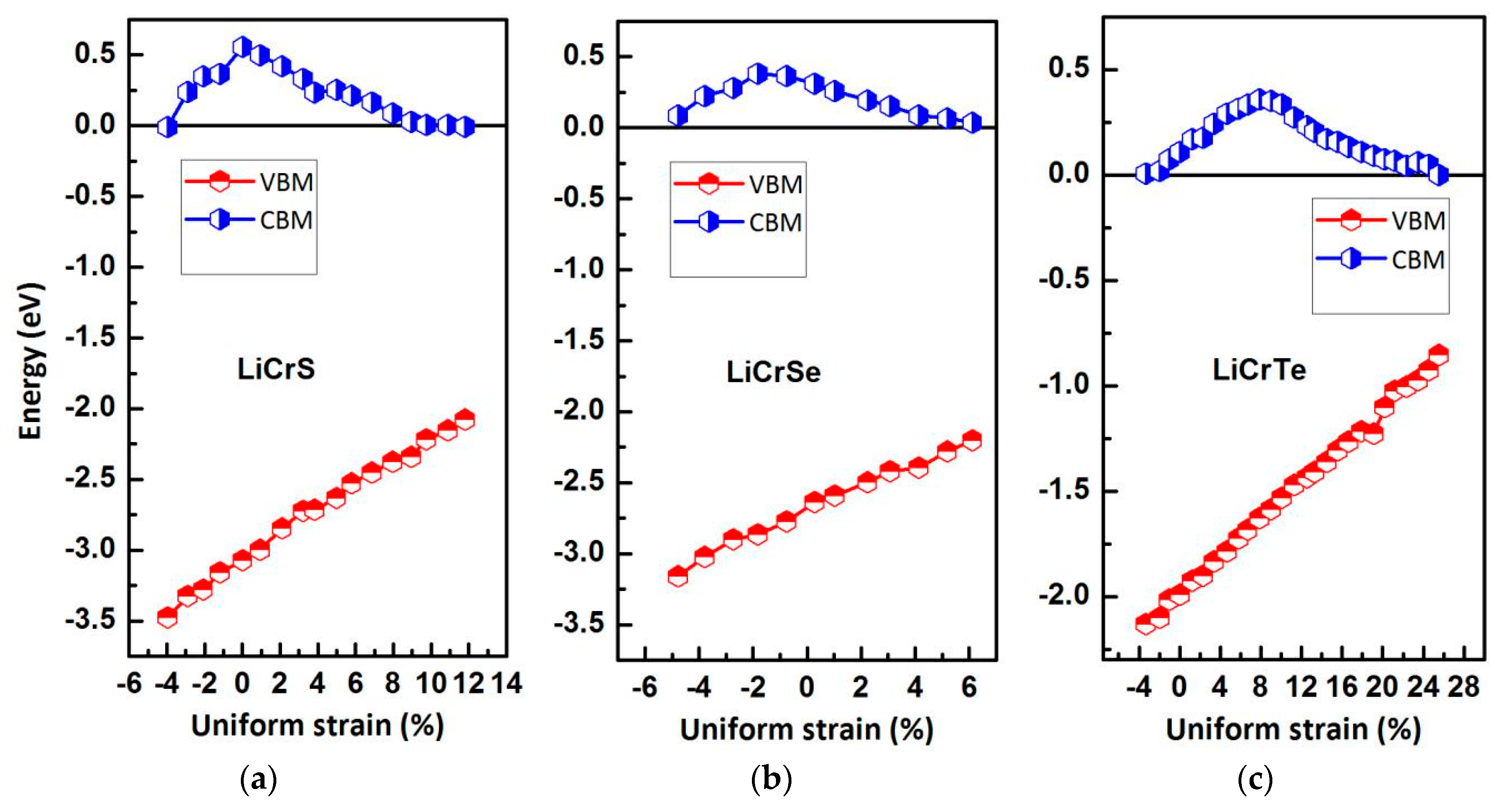
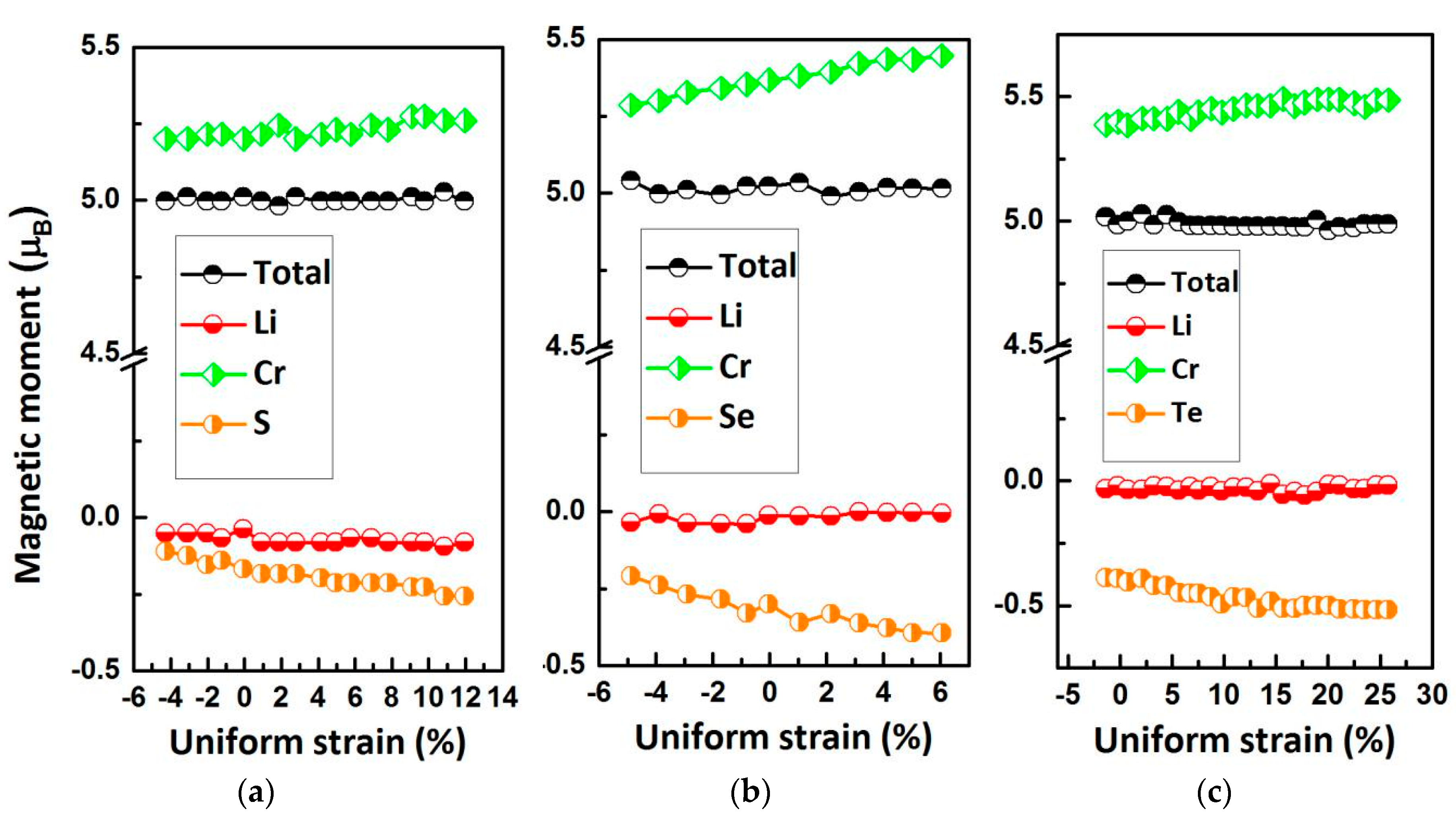
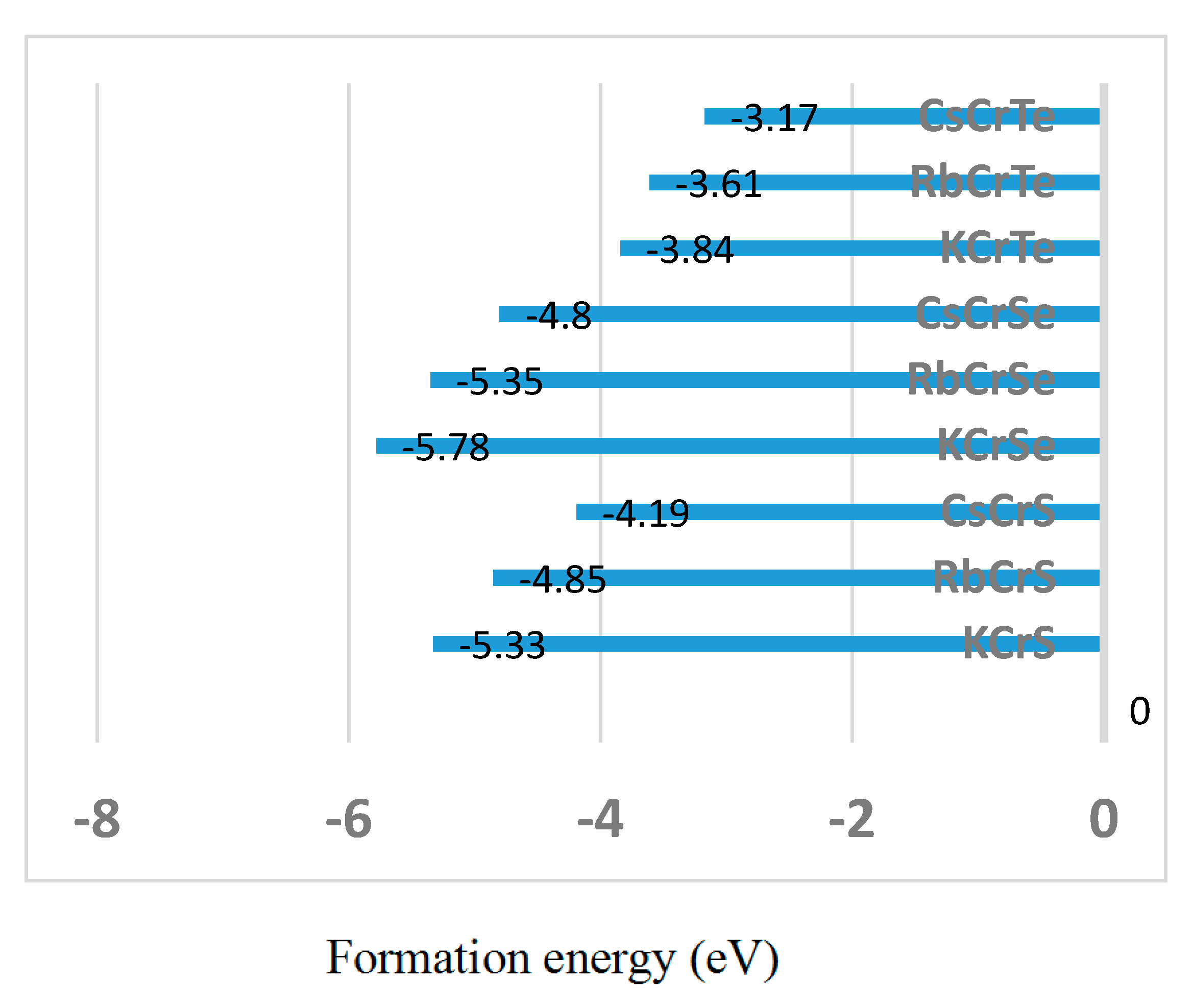
| Alloy | Type | a (Å) | Mtot (μB) | MX | MCr | MZ | Gap (eV) | HM Behavior |
|---|---|---|---|---|---|---|---|---|
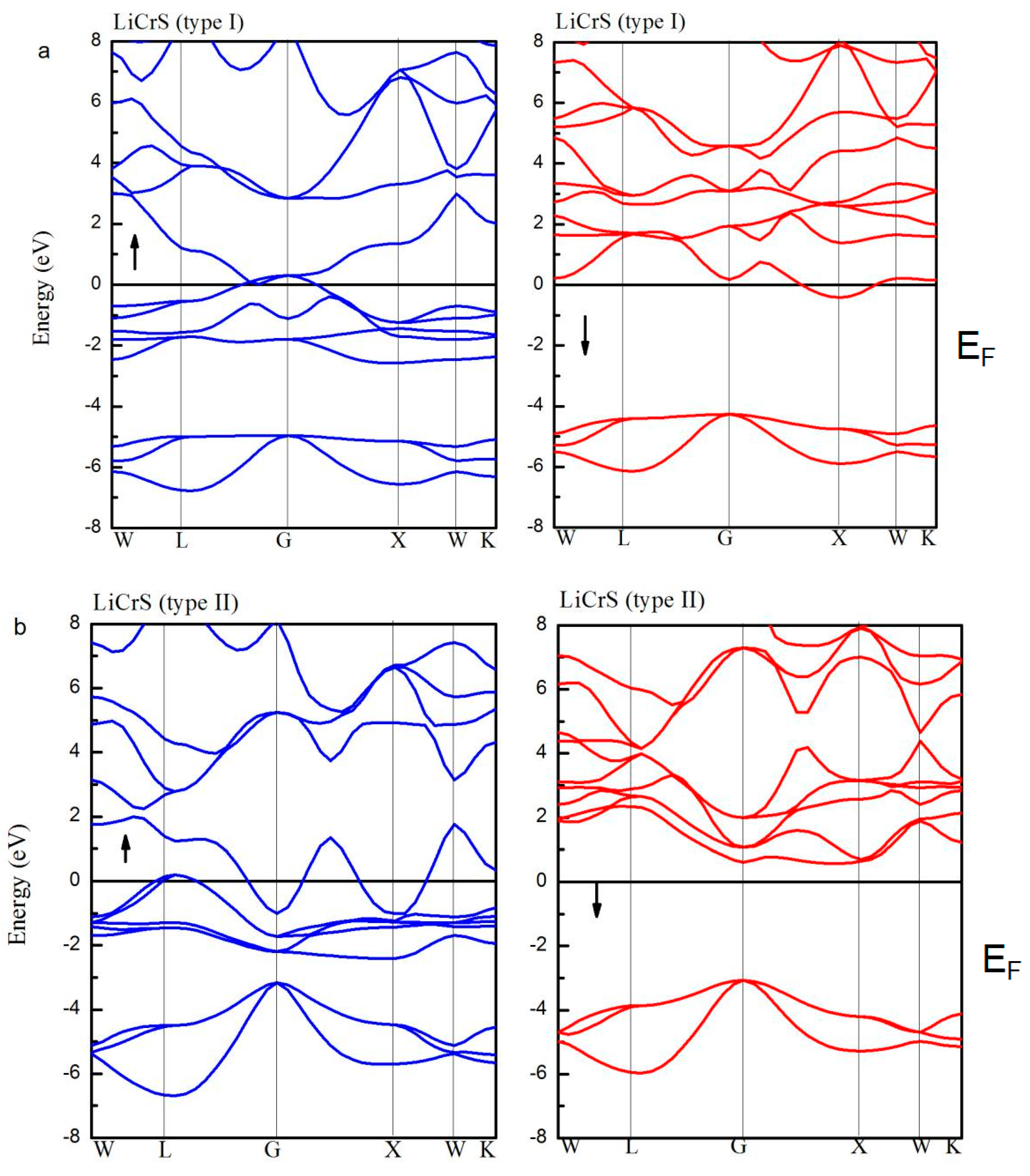
| LiCrS | Type I | 5.89 | 4.82 | −0.08 | 5.04 | −0.14 | - | No |
| Type II | 5.82 | 5.00 | −0.08 | 5.22 | −0.12 | 3.62 | Yes | |
| Type III | 5.90 | 4.97 | −0.02 | 5.18 | −0.20 | - | No | |
| LiCrSe | Type I | 6.19 | 4.92 | −0.08 | 5.16 | −0.16 | - | No |
| Type II | 6.00 | 5.00 | −0.04 | 5.36 | −0.32 | 3.15 | Yes | |
| Type III | 6.11 | 4.97 | 0.04 | 5.30 | −0.36 | - | No | |
| LiCrTe | Type I | 6.60 | 4.95 | −0.02 | 5.30 | −0.32 | - | No |
| Type II | 6.37 | 5.00 | −0.02 | 5.42 | −0.40 | 2.10 | Yes | |
| Type III | 6.60 | 4.94 | 0.02 | 5.40 | −0.48 | - | No | |
| KCrS | Type I | 6.71 | 5.00 | −0.12 | 5.34 | −0.22 | 3.15 | Yes |
| Type II | 6.90 | 5.00 | −0.32 | 5.54 | −0.24 | 2.14 | Yes | |
| Type III | 6.60 | 5.00 | −0.24 | 5.40 | −0.18 | 3.41 | Yes | |
| KCrSe | Type I | 6.91 | 5.00 | −0.26 | 5.38 | −0.12 | 2.85 | Yes |
| Type II | 6.98 | 5.00 | −0.12 | 5.58 | −0.46 | 2.09 | Yes | |
| Type III | 6.75 | 5.00 | −0.14 | 5.46 | −0.34 | 3.07 | Yes | |
| KCrTe | Type I | 7.35 | 5.00 | −0.06 | 5.46 | −0.42 | 2.87 | Yes |
| Type II | 7.41 | 5.00 | −0.08 | 5.66 | −0.58 | 1.87 | Yes | |
| Type III | 7.11 | 5.00 | −0.10 | 5.54 | −0.46 | 2.92 | Yes | |
| RbCrS | Type I | 7.01 | 5.00 | −0.14 | 5.38 | −0.24 | 2.65 | Yes |
| Type II | 7.21 | 5.00 | −0.30 | 5.56 | −0.26 | 1.69 | Yes | |
| Type III | 6.79 | 5.00 | −0.24 | 5.40 | −0.18 | 3.19 | Yes | |
| RbCrSe | Type I | 7.21 | 5.00 | −0.12 | 5.42 | −0.30 | 2.33 | Yes |
| Type II | 7.49 | 5.00 | −0.08 | 5.64 | −0.56 | 1.49 | Yes | |
| Type III | 6.98 | 5.00 | −0.16 | 5.46 | −0.30 | 2.72 | Yes | |
| RbCrTe | Type I | 7.63 | 5.00 | −0.04 | 5.50 | −0.46 | 2.40 | Yes |
| Type II | 7.81 | 5.00 | −0.06 | 5.68 | −0.62 | 1.54 | Yes | |
| Type III | 7.30 | 5.00 | −0.12 | 5.54 | −0.42 | 2.71 | Yes | |
| CsCrS | Type I | 7.35 | 5.00 | −0.14 | 5.42 | −0.28 | 2.09 | Yes |
| Type II | 7.59 | 5.00 | −0.26 | 5.58 | −0.30 | 1.41 | Yes | |
| Type III | 7.11 | 5.00 | −0.22 | 5.40 | −0.18 | 2.83 | Yes | |
| CsCrSe | Type I | 7.54 | 5.00 | −0.02 | 5.48 | −0.46 | 2.01 | Yes |
| Type II | 7.90 | 5.00 | −0.04 | 5.68 | −0.64 | 1.31 | Yes | |
| Type III | 7.21 | 5.00 | −0.14 | 5.42 | −0.28 | 2.61 | Yes | |
| CsCrTe | Type I | 7.98 | 5.00 | −0.02 | 5.52 | −0.50 | 2.09 | Yes |
| Type II | 8.21 | 5.00 | −0.02 | 5.72 | −0.70 | 1.31 | Yes | |
| Type III | 7.59 | 5.00 | −0.12 | 5.54 | −0.42 | 2.29 | Yes |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Cheng, Z.; Liu, G. Largest Magnetic Moments in the Half-Heusler Alloys XCrZ (X = Li, K, Rb, Cs; Z = S, Se, Te): A First-Principles Study. Materials 2017, 10, 1078. https://doi.org/10.3390/ma10091078
Wang X, Cheng Z, Liu G. Largest Magnetic Moments in the Half-Heusler Alloys XCrZ (X = Li, K, Rb, Cs; Z = S, Se, Te): A First-Principles Study. Materials. 2017; 10(9):1078. https://doi.org/10.3390/ma10091078
Chicago/Turabian StyleWang, Xiaotian, Zhenxiang Cheng, and Guodong Liu. 2017. "Largest Magnetic Moments in the Half-Heusler Alloys XCrZ (X = Li, K, Rb, Cs; Z = S, Se, Te): A First-Principles Study" Materials 10, no. 9: 1078. https://doi.org/10.3390/ma10091078





