Crack Extension and Possibility of Debonding in Encapsulation-Based Self-Healing Materials
Abstract
:1. Introduction
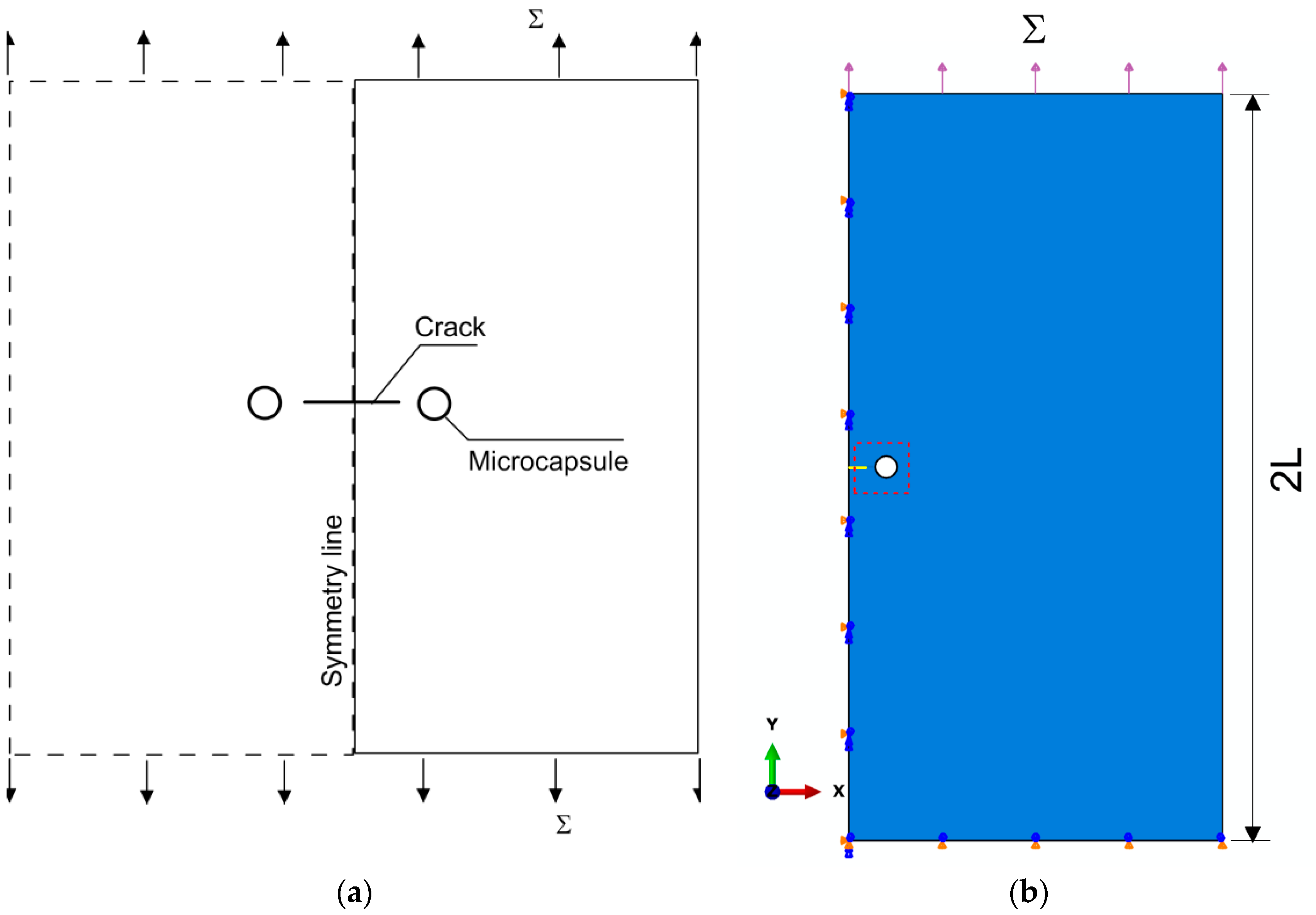
2. Numerical Setup
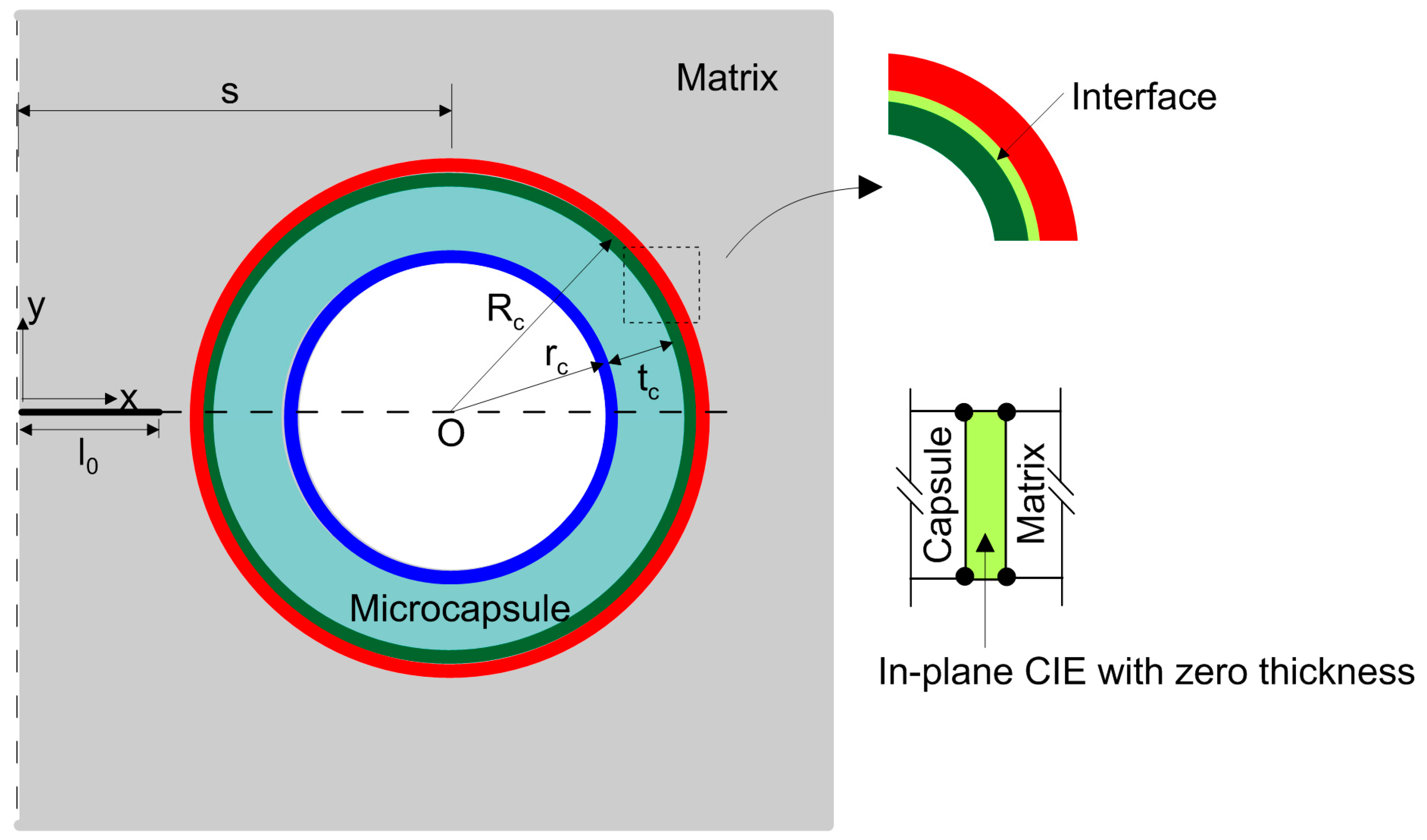
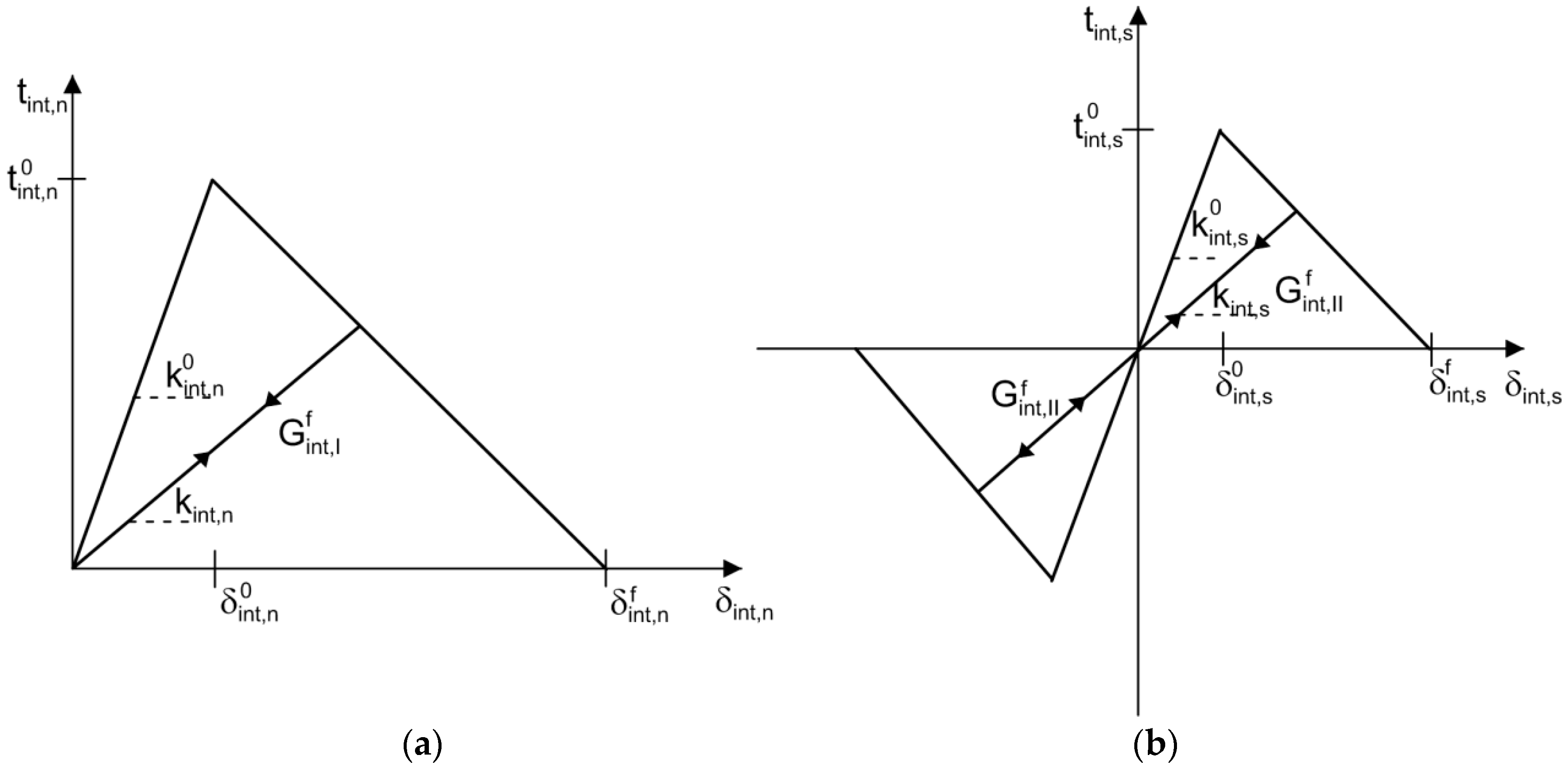
2.1. Cohesive Crack Model for Capsule-Matrix Interaction
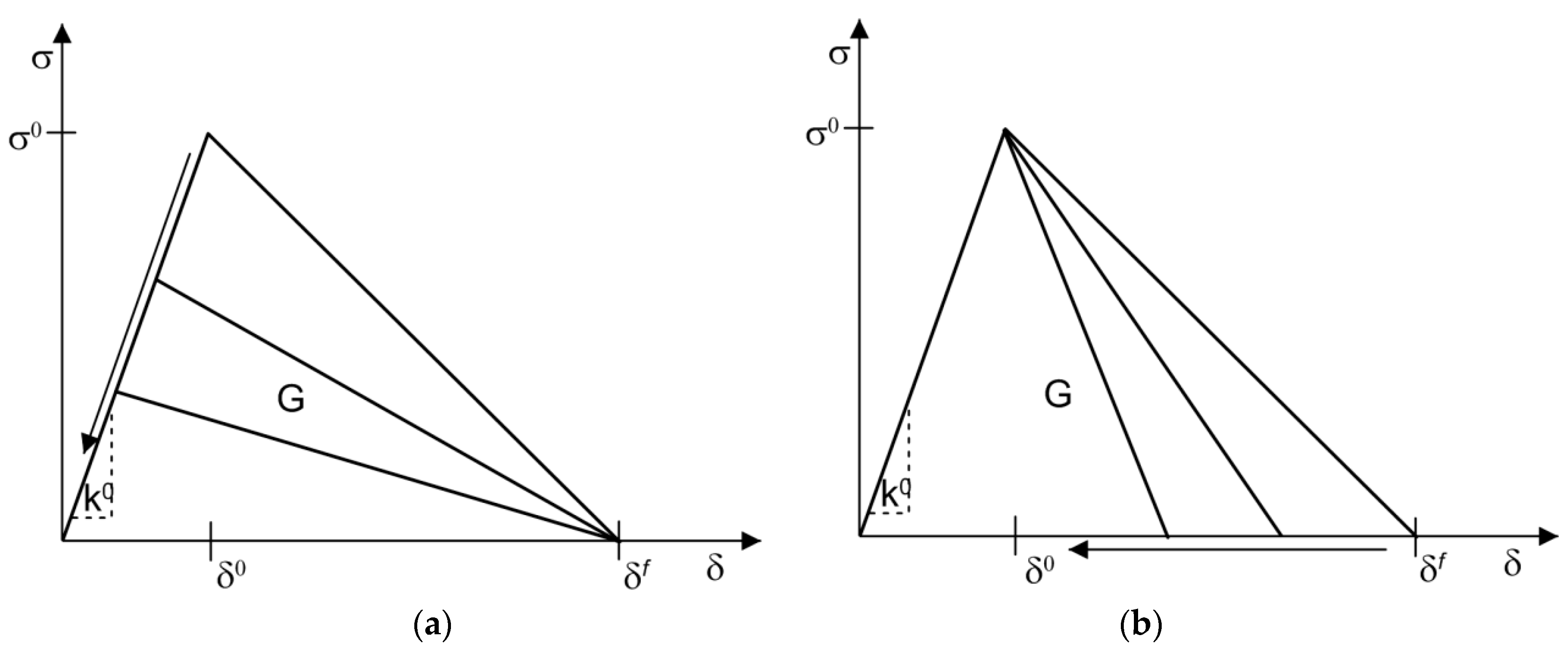
2.2. XFEM-Based Cohesive Behavior for Crack Propagation in Matrix
2.3. Input Parameters for Material Properties
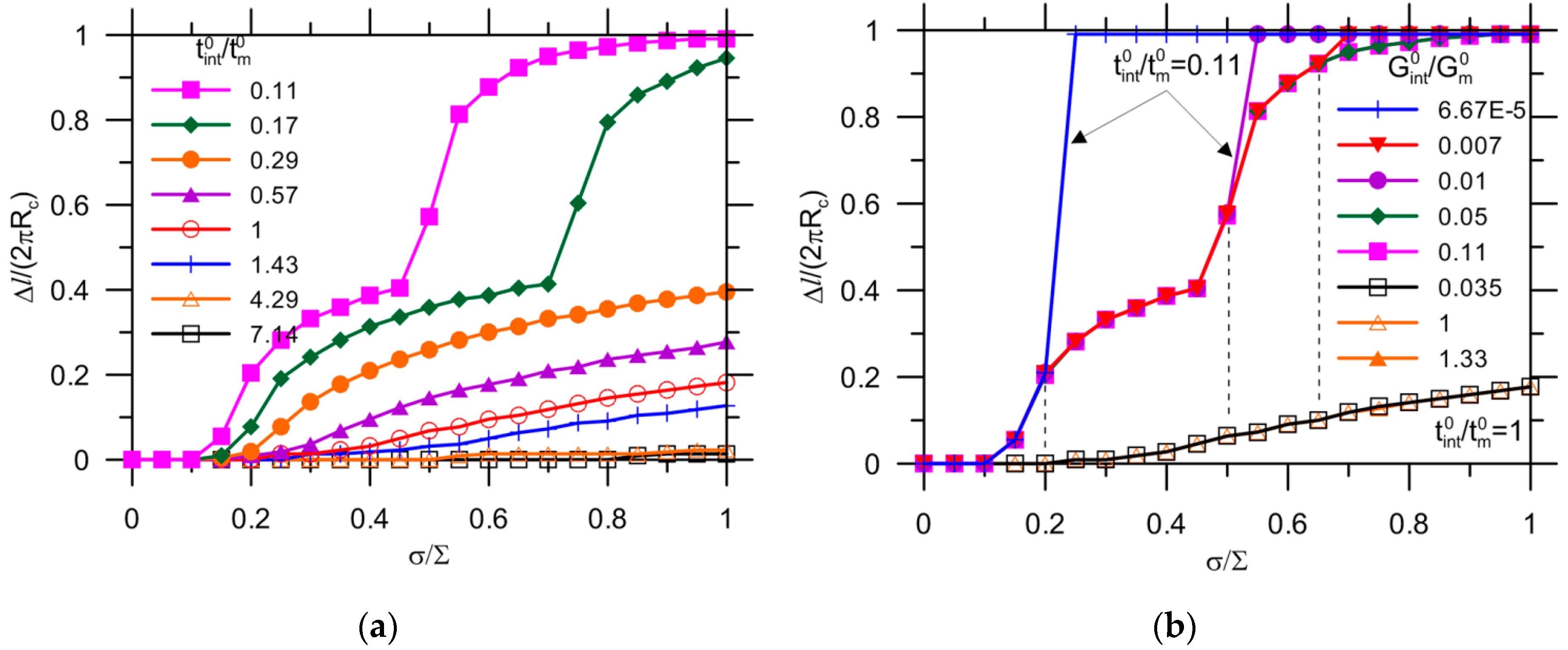
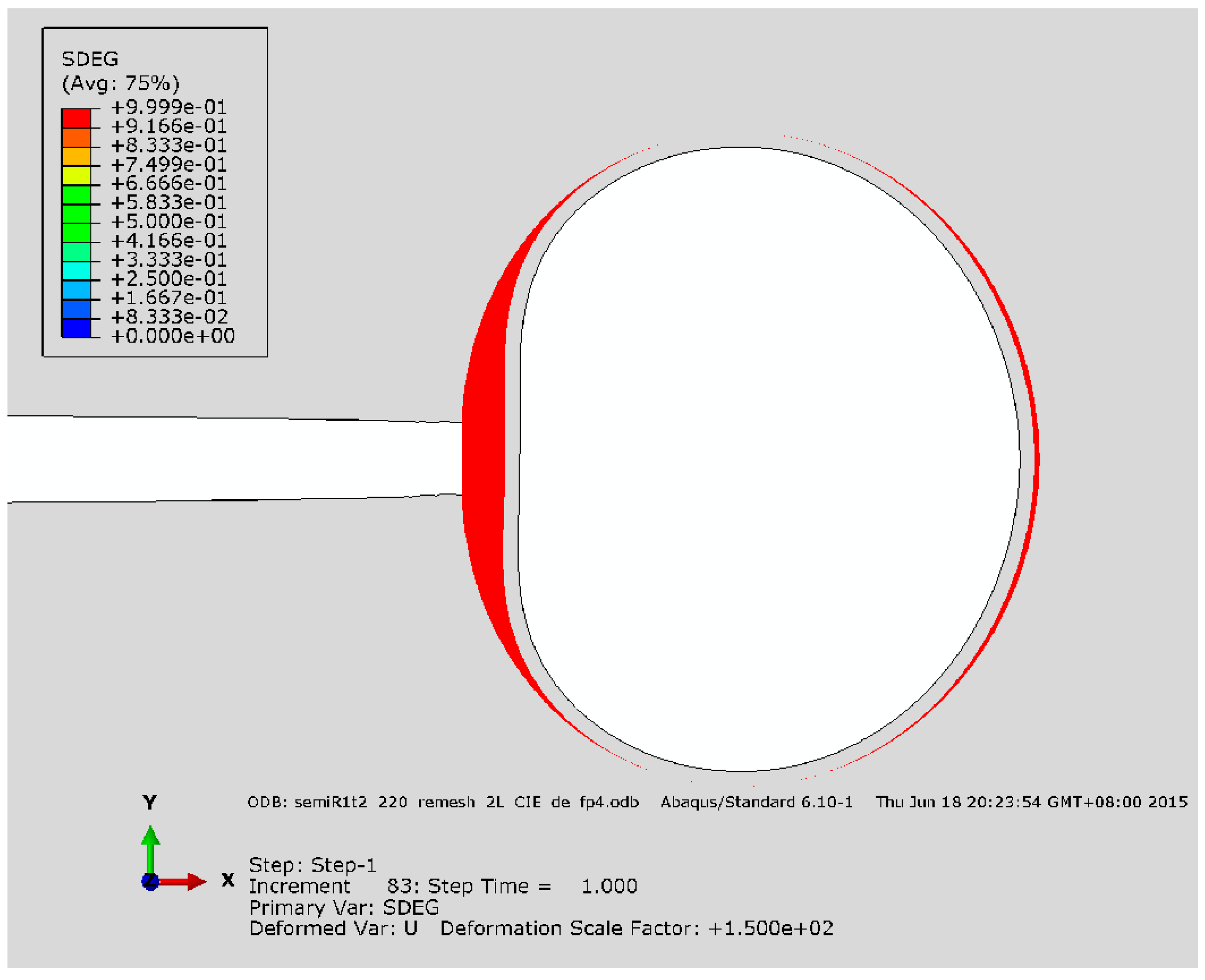
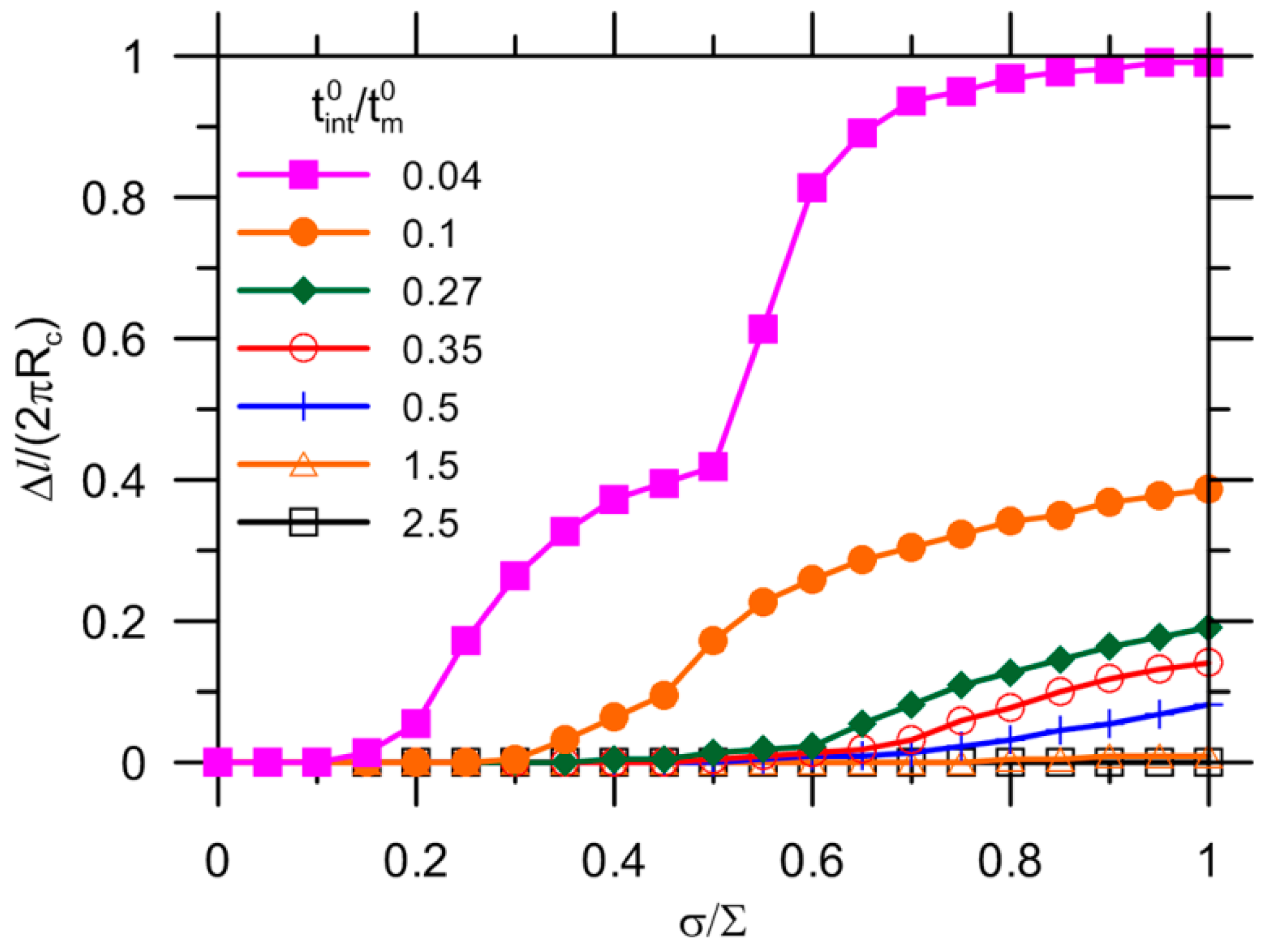
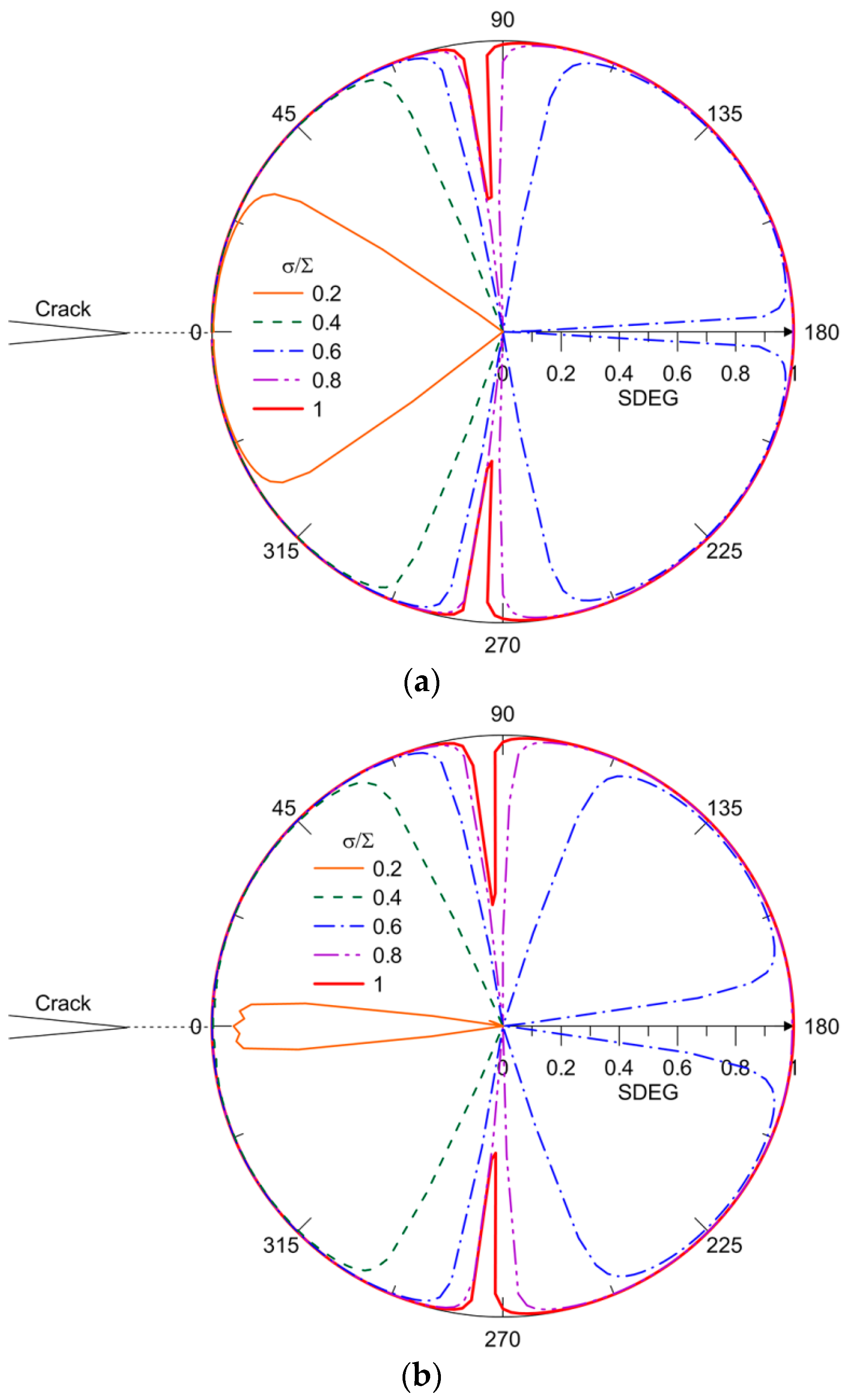
3. Results and Discussion
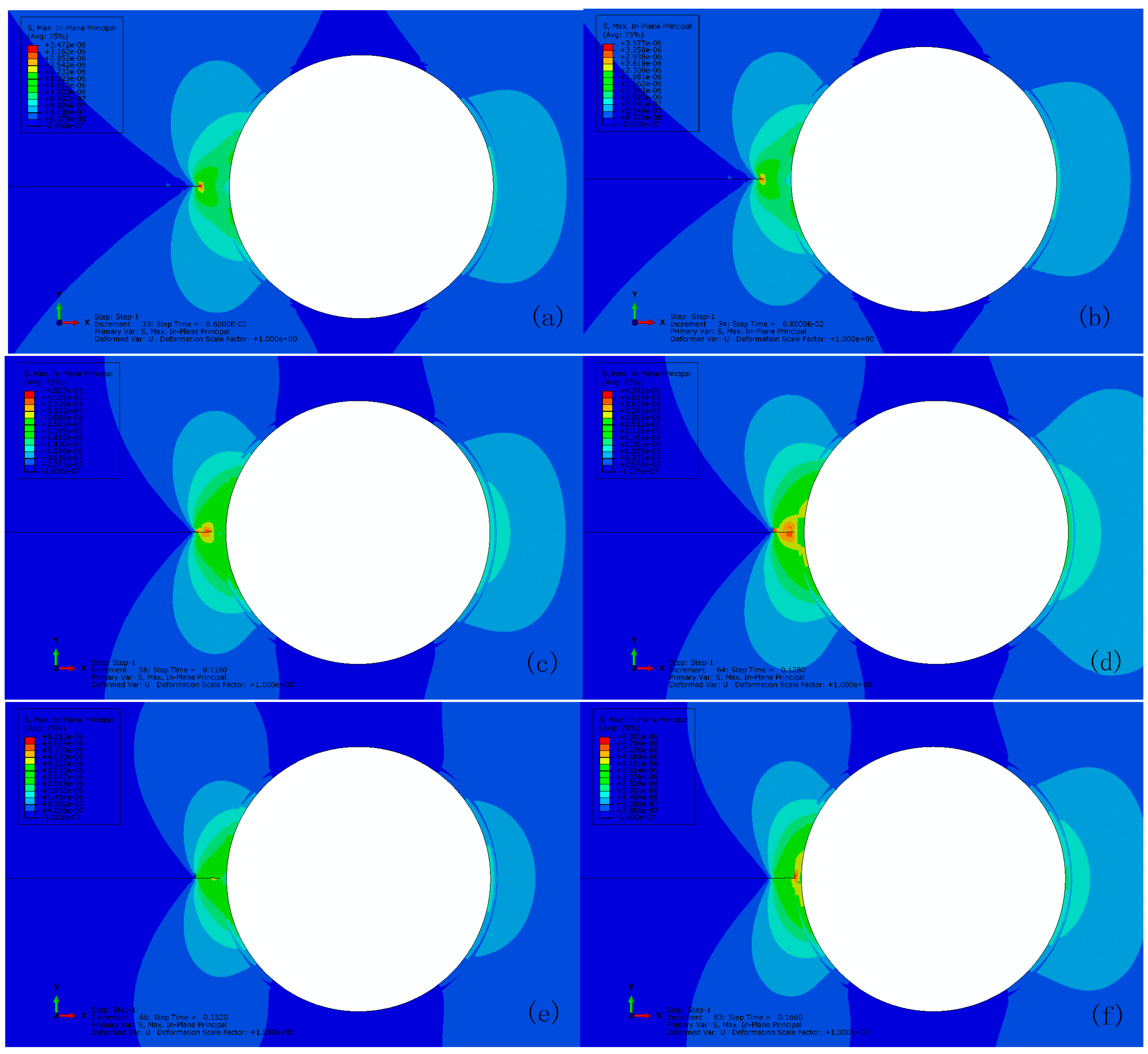
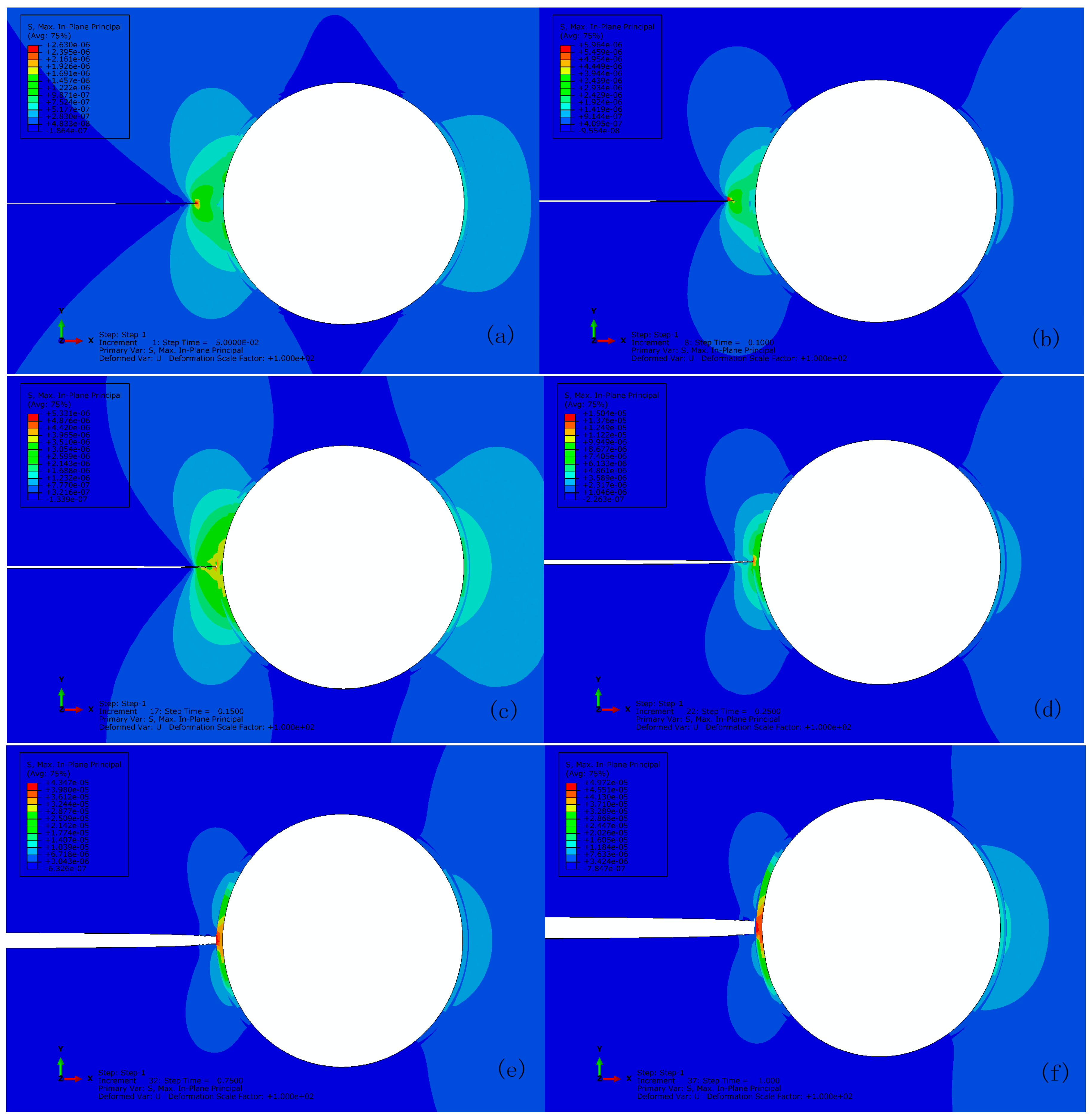
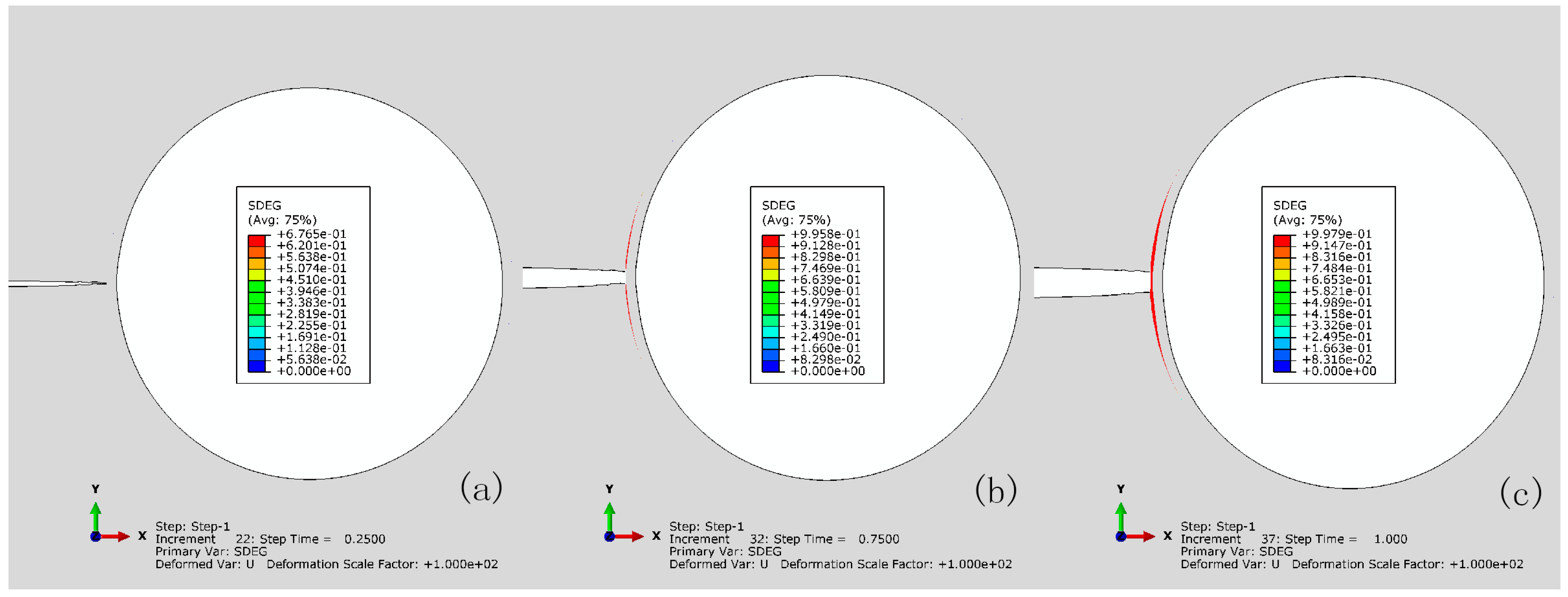
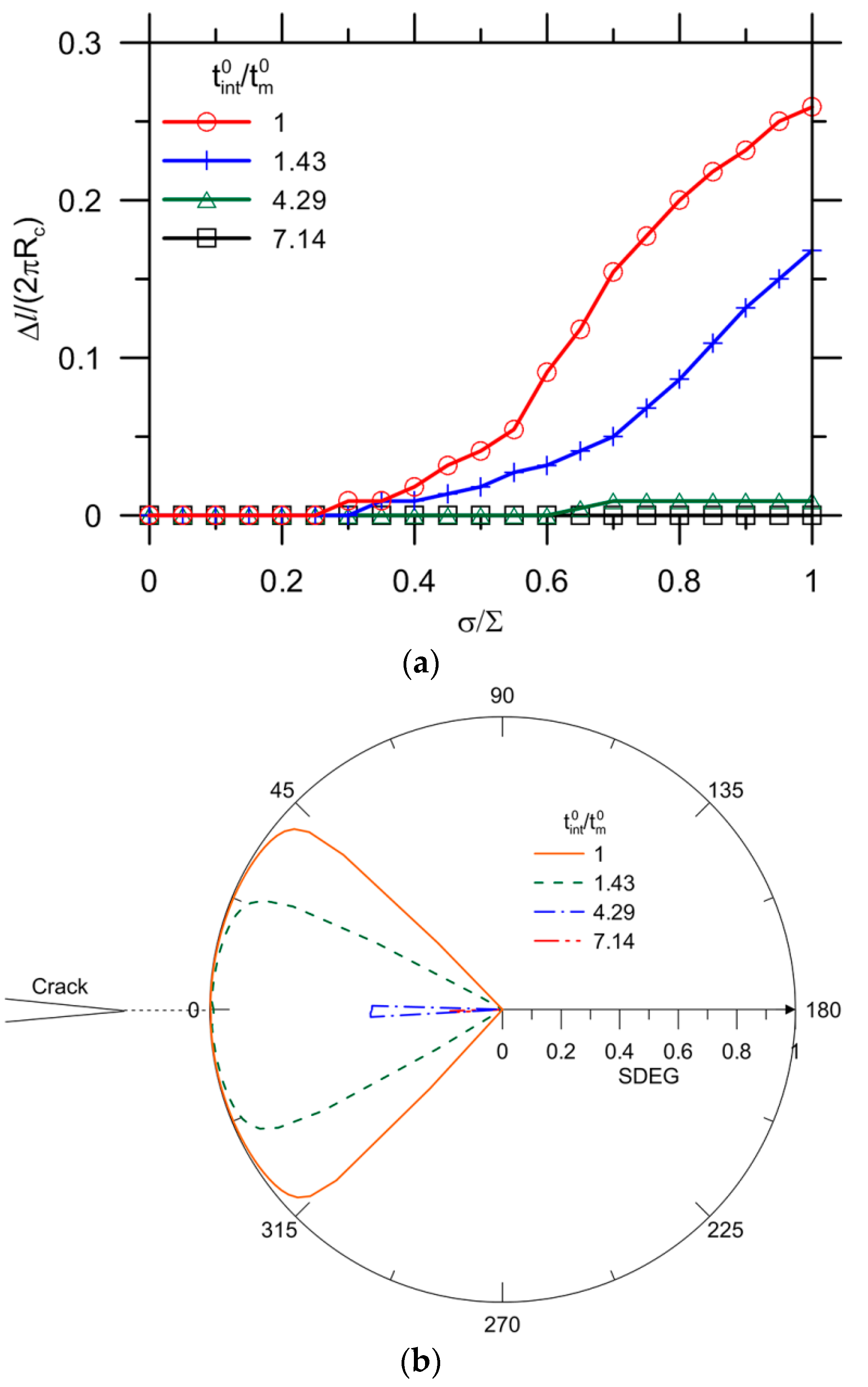
3.1. Crack Extension in Matrix for Perfect Bonding
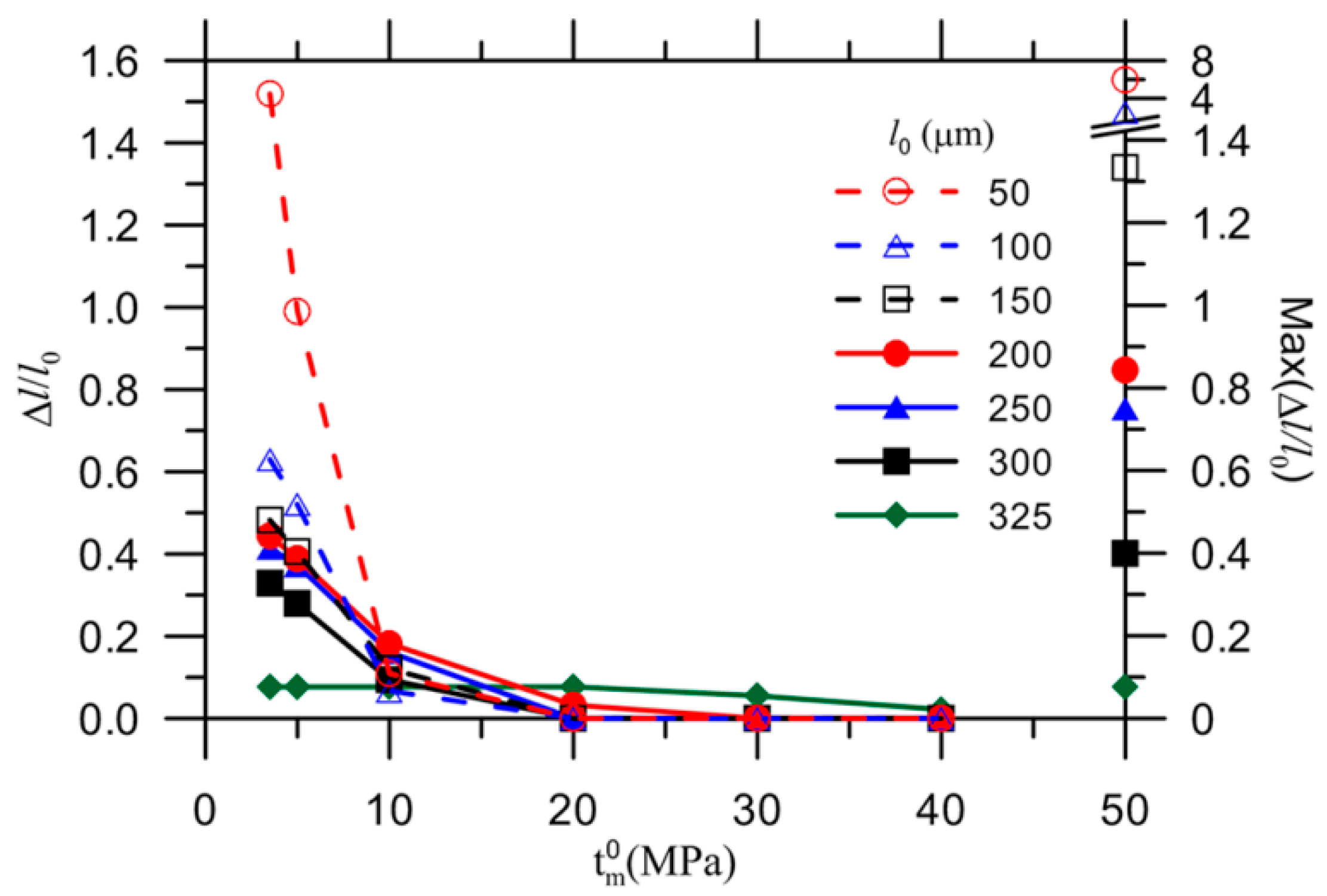
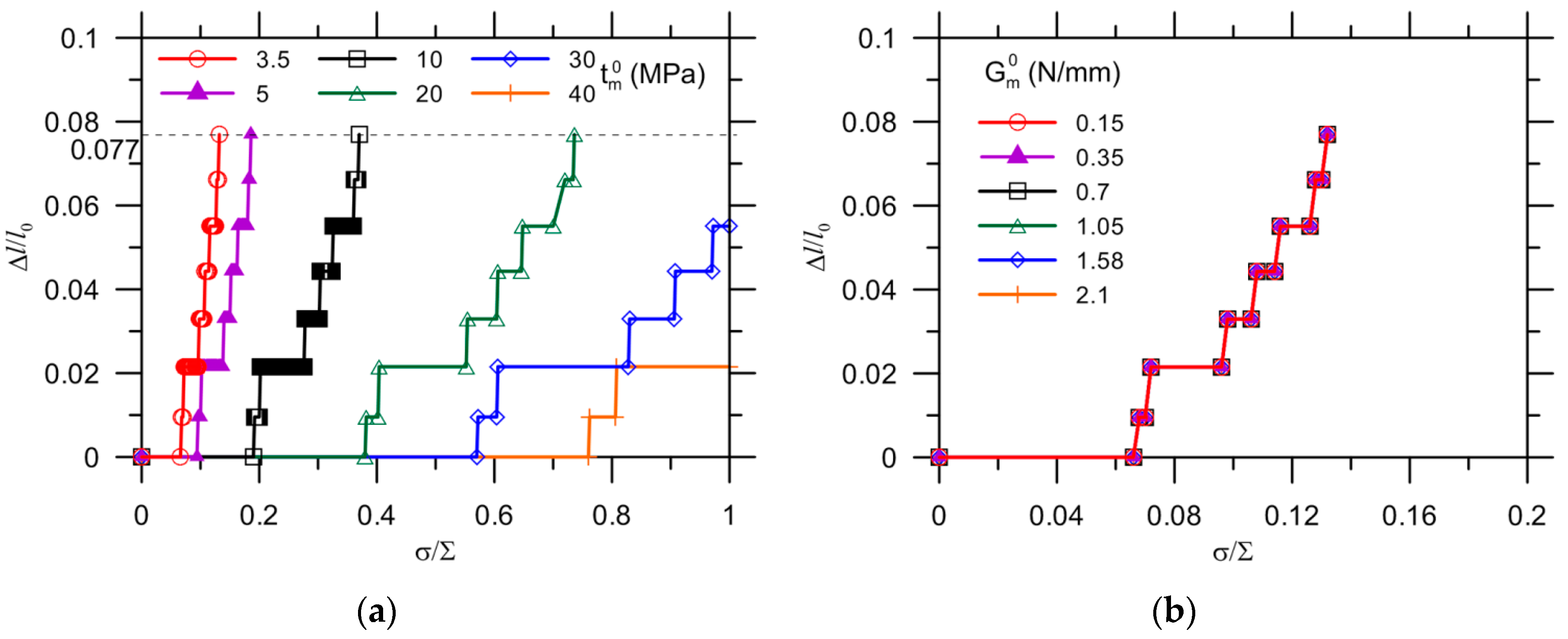
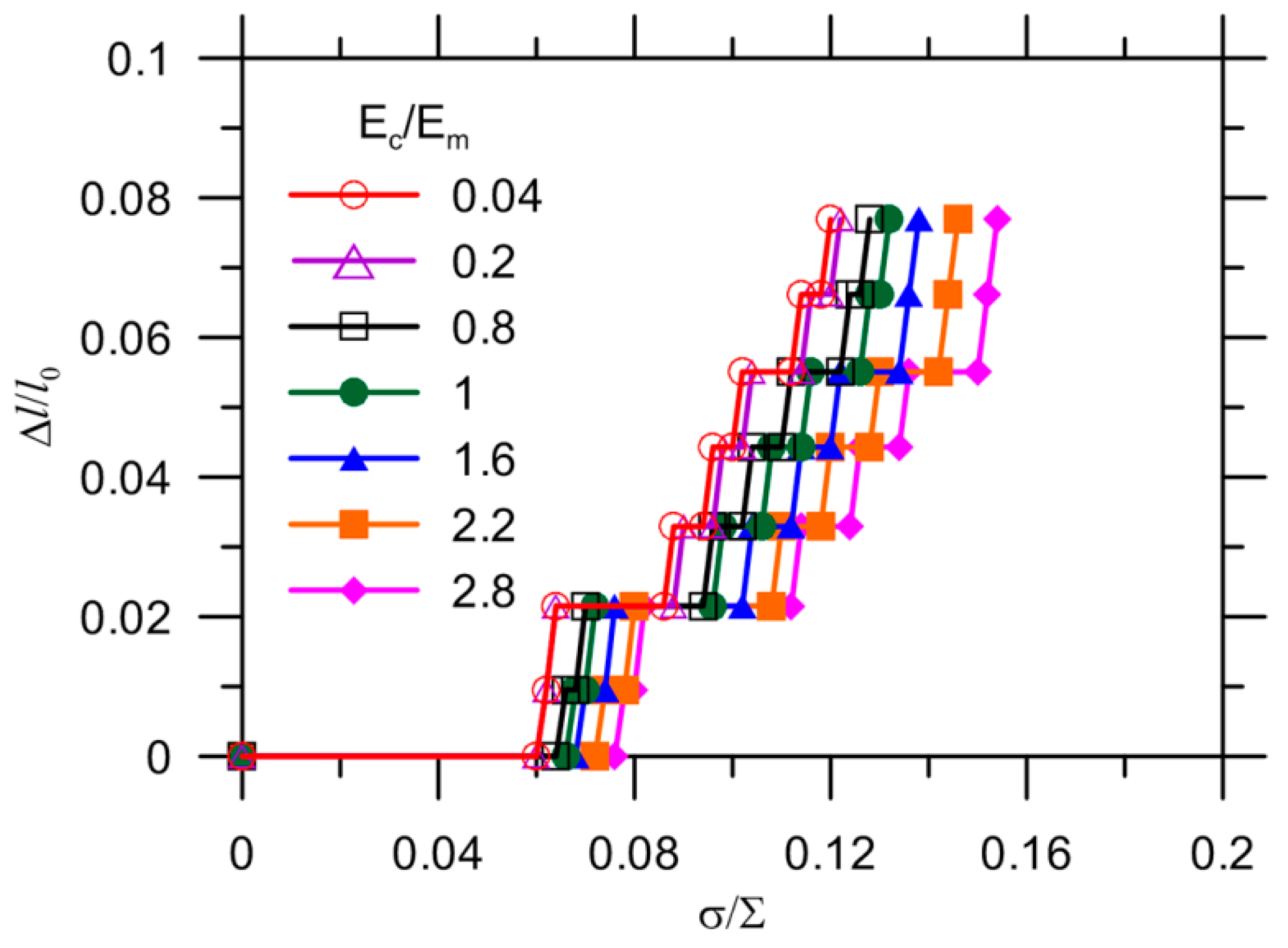
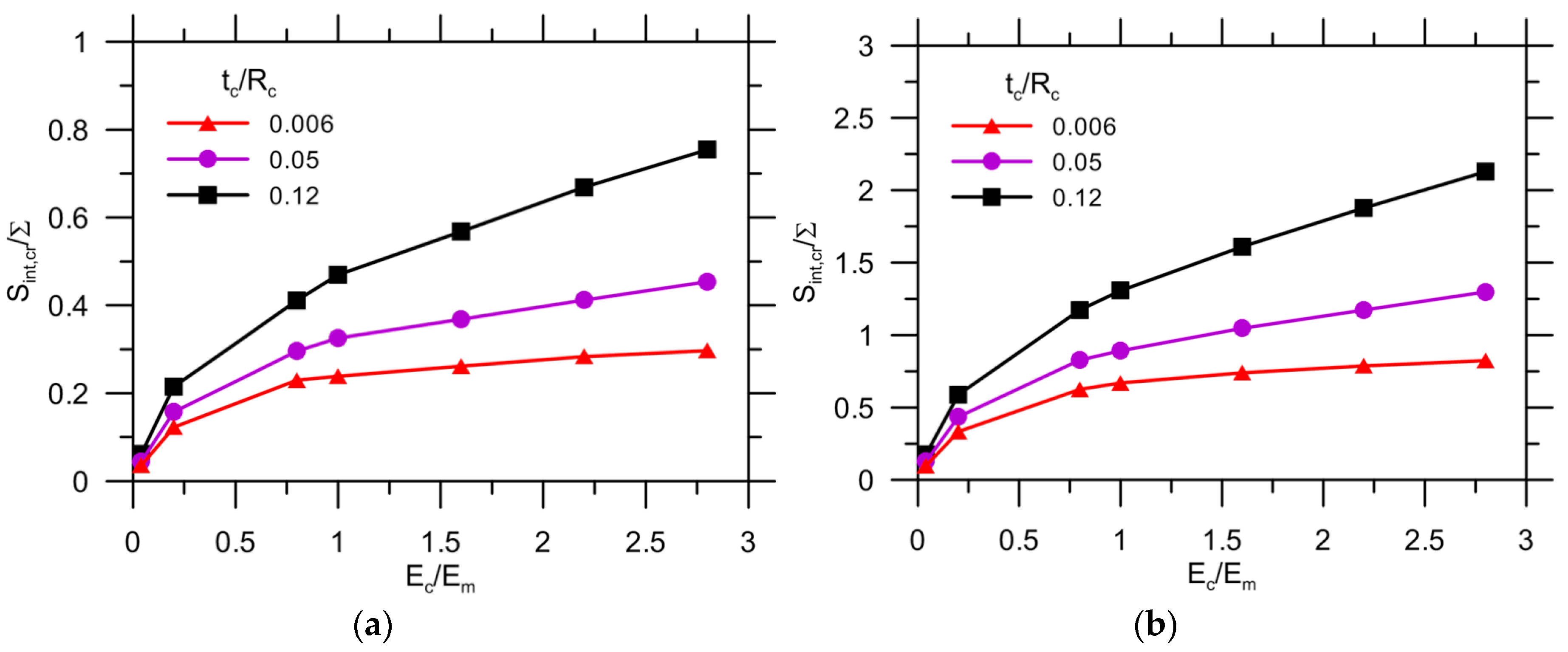
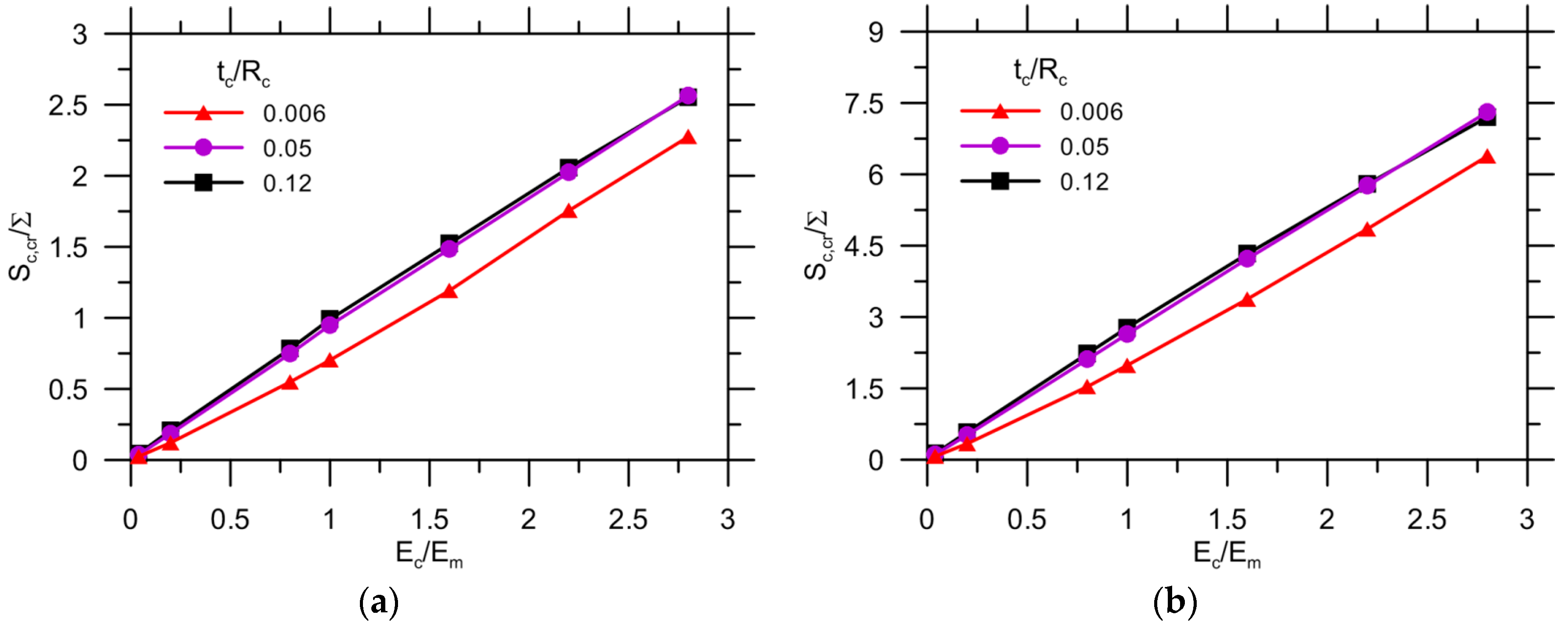
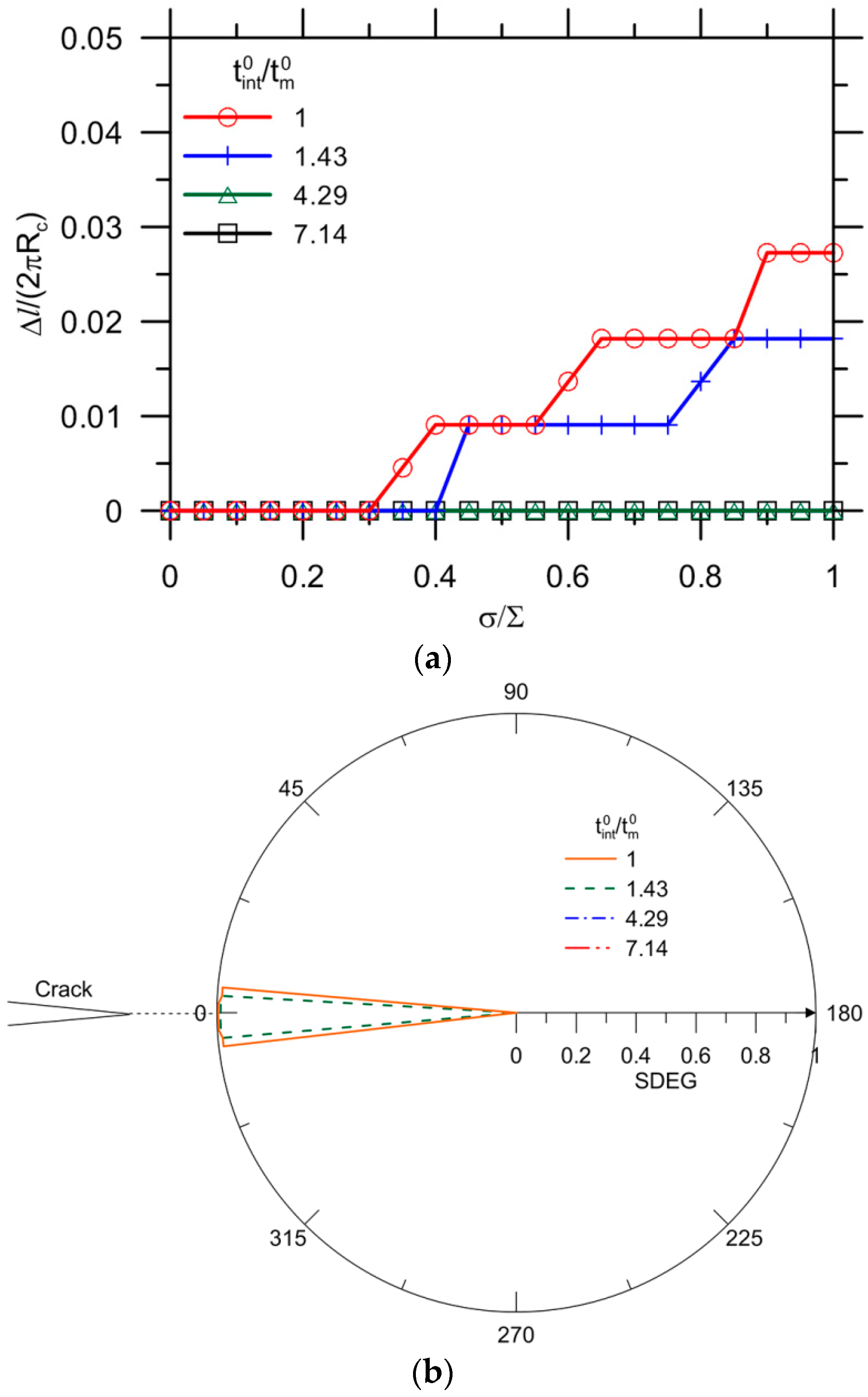
3.2. Debonding Due to Capsule-Matrix Interaction
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Dry, C. Procedure developed for self-repair of polymer matrix composite materials. Compos. Struct. 1996, 35, 263–269. [Google Scholar] [CrossRef]
- Bleay, S.M.; Loader, C.B.; Hawyes, V.J.; Humberstone, L.; Curtis, P.T. A smart repair system for polymer matrix composites. Compos. A Appl. Sci. Manuf. 2001, 32, 1767–1776. [Google Scholar] [CrossRef]
- Pang, J.W.C.; Bond, I.P. ‘Bleeding composites’—Damage detection and self-repair using a biomimetic approach. Compos. A Appl. Sci. Manuf. 2005, 36, 183–188. [Google Scholar] [CrossRef]
- Pang, J.W.C.; Bond, I.P. A hollow fibre reinforced polymer composite encompassing self-healing and enhanced damage visibility. Compos. Sci. Technol. 2005, 65, 1791–1799. [Google Scholar] [CrossRef]
- Ghosh, S.K. (Ed.) Functional coatings and microencapsulation: A general perspective. In Functional Coatings; Wiley: Hoboken, NJ, USA, 2006. [Google Scholar]
- White, S.R.; Sottos, N.R.; Geubelle, P.H.; Moore, J.S.; Kessler, M.R.; Sriram, S.R.; Brown, E.N.; Viswanathan, S. Autonomic healing of polymer composites. Nature 2001, 409, 794. [Google Scholar] [CrossRef] [PubMed]
- Boh, B.; Šumiga, B. Microencapsulation technology and its applications in building construction materials. Mater. Geoenviron. 2008, 55, 329–344. [Google Scholar]
- Nishiwaki, T. Fundamental Study on Development of Intelligent Concrete with Self-Healing Capability. Master’s Thesis, Department of Architecture and Building Science, Graduate School of Engineering, Tohoku University, Sendai, Japan, 1997. [Google Scholar]
- Ahn, T.H. Development of Self-Healing Concrete Incorporating Geo-Materials: A Study on Its Mechanism and Behavior in Cracked Concrete. Ph.D. Thesis, The University of Tokyo, Tokyo, Japan, 2008. [Google Scholar]
- Jonkers, H.M.; Thijssen, A.; Muyzer, G.; Copuroglu, O.; Schlangen, E. Application of Bacteria as Self-Healing Agent for the Development of Sustainable Concrete. In Proceedings of the 1st International Conference on Biogeocivil Engineering, Delft, The Netherlands, 23–25 June 2008. [Google Scholar]
- Tittelboom, K.V.; Belie, N.D.; Muynck, W.D.; Verstraete, W. Use of bacteria to repair cracks in concrete. Cem. Concr. Res. 2010, 40, 157–166. [Google Scholar] [CrossRef]
- Van der Zwaag, S. Routes and mechanisms towards self-healing behavior in engineering materials. Bull. Pol. Acad. Sci. 2010, 58, 227–236. [Google Scholar]
- Breugel, K.V. Is there a market for self-healing cement-based materials? In Proceedings of the 1st International Conference on Self-Healing Materials, Noordwijk, The Netherlands, 18–20 April 2007. [Google Scholar]
- Neville, A. Autogenous healing—A concrete miracle? Concr. Int. 2002, 24, 76–82. [Google Scholar]
- Igarashi, S.; Kunieda, M.; Nishiwaki, T. Technical Committee on Autogenous Healing in Cementitious Materials; Technical Committee Report; JCI.TC075B; JCI: St. Louis, MO, USA, 1 July 2009. (In Japanese) [Google Scholar]
- Richard, P.W. Self-healing materials: A review. Soft Matter 2008, 4, 400–418. [Google Scholar]
- Wu, M.; Johannesson, B.; Geiker, M. A review: Self-healing in cementitious materials and engineered cementitious composite as a self-healing material. Constr. Build. Mater. 2012, 28, 571–583. [Google Scholar] [CrossRef]
- Rattner, E. Cost-Effective Self-Healing Concrete. Available online: http://thefutureofthings.com/4361-cost-effective-self-healing-concrete/ (accessed on 9 August 2010).
- Joseph, C.; Gardner, D.; Jefferson, T.; Isaacs, B.; Lark, B. Self-healing cementitious materials: A review of recent work. Proc. Inst. Civ. Eng. Constr. Mater. 2011, 164, 29–41. [Google Scholar] [CrossRef]
- Ghosh, S.K. (Ed.) Self-Healing Materials: Fundamentals, Design Strategies, and Applications; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2009; Volume 1–3, pp. 141–178. [Google Scholar]
- Yan, X.; Miao, C. A numerical method for a void–crack interaction under cyclic loads. Acta Mech. 2012, 223, 1015–1029. [Google Scholar] [CrossRef]
- Cheng, Y. Effect of a hole near a crack tip on the stress intensity factor. Int. J. Fract. 1987, 32, R39–R42. [Google Scholar]
- Hasebe, N.; Wang, X.; Kondo, M. Interaction between crack and arbitrarily shaped hole with stress and displacement boundaries. Int. J. Fract. 2003, 119, 83–102. [Google Scholar] [CrossRef]
- Tamate, O. The effect of a circular inclusion on the stresses around a line crack in a sheet under tension. Int. J. Fract. Mech. 1968, 4, 257–266. [Google Scholar] [CrossRef]
- Gilabert, F.A.; Garoz, D.; Van Paepegem, W. Stress concentrations and bonding strength in encapsulation-based self-healing materials. Mater. Des. 2015, 67, 28–41. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, H.; Dong, X. Simulation Research of Self-healing Mechanism for Microcapsule Composite. In Proceedings of the 20th International Conference on Structural Mechanics in Reactor Technology (SMiRT 20), Espoo, Finland, 9–14 August 2009; p. 2054. [Google Scholar]
- Wang, H.; Wang, J.; Chen, J. Micromechanical analysis of asphalt mixture fracture with adhesive and cohesive failure. Eng. Fract. Mech. 2014, 132, 104–119. [Google Scholar] [CrossRef]
- Zhang, M. A Study on Microcapsule Based Self-Healing Method and Mechanism for Cementitious Composites. Ph.D. Thesis, Central South University, Changsha, China, May 2013. [Google Scholar]
- Keller, M.W.; Sottos, N.R. Mechanical properties of microcapsules used in a self-healing polymer. Exp. Mech. 2006, 46, 725–733. [Google Scholar] [CrossRef]
- Van Tittelboom, K. Self-Healing Concrete through Incorporation of Encapsulated Bacteria- or Polymer-Based Healing Agents. Ph.D. Thesis, Ghent University, Ghent, Belgium, 2012. [Google Scholar]
- Barenblatt, G.I. The formation of equilibrium cracks during brittle fracture: General ideas and hypothesis, axially symmetric cracks. Appl. Math. Mech. 1959, 23, 622–636. [Google Scholar] [CrossRef]
- Hillerborg, A.; Modeer, M.; Petersson, P. Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements. Cem. Concr. Res. 1976, 6, 773–782. [Google Scholar] [CrossRef]
- Dugdale, D.S. Yielding of steel sheets containing slits. J. Mech. Phys. Solids 1960, 8, 100–104. [Google Scholar] [CrossRef]
- Belytschko, T.; Black, T. Elastic Crack Growth in Finite Elements with Minimal Remeshing. Int. J. Numer. Methods Eng. 1999, 45, 601–620. [Google Scholar] [CrossRef]
- Melenk, J.; Babuska, I. The Partition of Unity Finite Element Method: Basic Theory and Applications. Comput. Methods Appl. Mech. Eng. 1996, 39, 289–314. [Google Scholar] [CrossRef]
- ABAQUS. ABAQUS Analysis User’s Manual, version 6.10; Habbit, Karlsson & Sorenson Inc.: Pawtucket, RI, USA, 2010. [Google Scholar]
- Yang, Z.J.; Su, X.T.; Chen, J.F.; Liu, G.H. Monte Carlo simulation of complex cohesive fracture in random heterogeneous quasi-brittle materials. Int. J. Solids Struct. 2009, 46, 3222–3234. [Google Scholar] [CrossRef]
- Brown, E.N.; White, S.R.; Sottos, N.R. Microcapsule induced toughening in a self-healing polymer composite. J. Mater. Sci. 2004, 39, 1703–1710. [Google Scholar] [CrossRef]
- Enfedaque, A.; Gálvez, J.C.; Suárez, F. Analysis of fracture tests of glass fibre reinforced cement (GRC) using digital image correlation. Constr. Build. Mater. 2015, 75, 472–487. [Google Scholar] [CrossRef]
- Mark, J. Physical Properties of Polymers Handbook; Springer: Heidelberg, Germany, 2007; ISBN 9780387690025. [Google Scholar]
- Shackelford, J.; Doremus, R. Ceramic and Glass Materials: Structure, Properties and Processing; Springer: Berlin/Heidelberg, Germany, 2008; ISBN 9781441944603. [Google Scholar]
- Parmigiani, J.P.; Thouless, M.D. The role of toughness and cohesive strength on crack deflection at interfaces. J. Mech. Phys. Solids 2006, 54, 266–287. [Google Scholar] [CrossRef]
- He, M.Y.; Hutchinson, J.W. Crack deflection at an interface between dissimilar elastic materials. Int. J. Solids Struct. 1989, 25, 1053–1067. [Google Scholar]
- He, M.Y.; Evans, A.G.; Hutchinson, J.W. Crack deflection at an interface between dissimilar elastic materials: Role of residual stresses. Int. J. Solids Struct. 1994, 31, 3443–3455. [Google Scholar] [CrossRef]
- Martinez, D.; Gupta, V. Energy criterion for crack deflection at an interface between two orthotropic media. II. Results and experimental verification. J. Mech. Phys. Solids 1993, 42, 1247–1271. [Google Scholar] [CrossRef]



| Solid | Young’s Modulus (GPa) | Strength (MPa) | Fracture Energy (N/mm) |
|---|---|---|---|
| Matrix | = 25 | = 3.5, 5, 10, 20, 30, 40 | |
| capsule | - | - | |
| Interface | = 25 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, W.; Jiang, Z.; Yang, Z. Crack Extension and Possibility of Debonding in Encapsulation-Based Self-Healing Materials. Materials 2017, 10, 589. https://doi.org/10.3390/ma10060589
Li W, Jiang Z, Yang Z. Crack Extension and Possibility of Debonding in Encapsulation-Based Self-Healing Materials. Materials. 2017; 10(6):589. https://doi.org/10.3390/ma10060589
Chicago/Turabian StyleLi, Wenting, Zhengwu Jiang, and Zhenghong Yang. 2017. "Crack Extension and Possibility of Debonding in Encapsulation-Based Self-Healing Materials" Materials 10, no. 6: 589. https://doi.org/10.3390/ma10060589





