A New Energy-Critical Plane Damage Parameter for Multiaxial Fatigue Life Prediction of Turbine Blades
Abstract
:1. Introduction
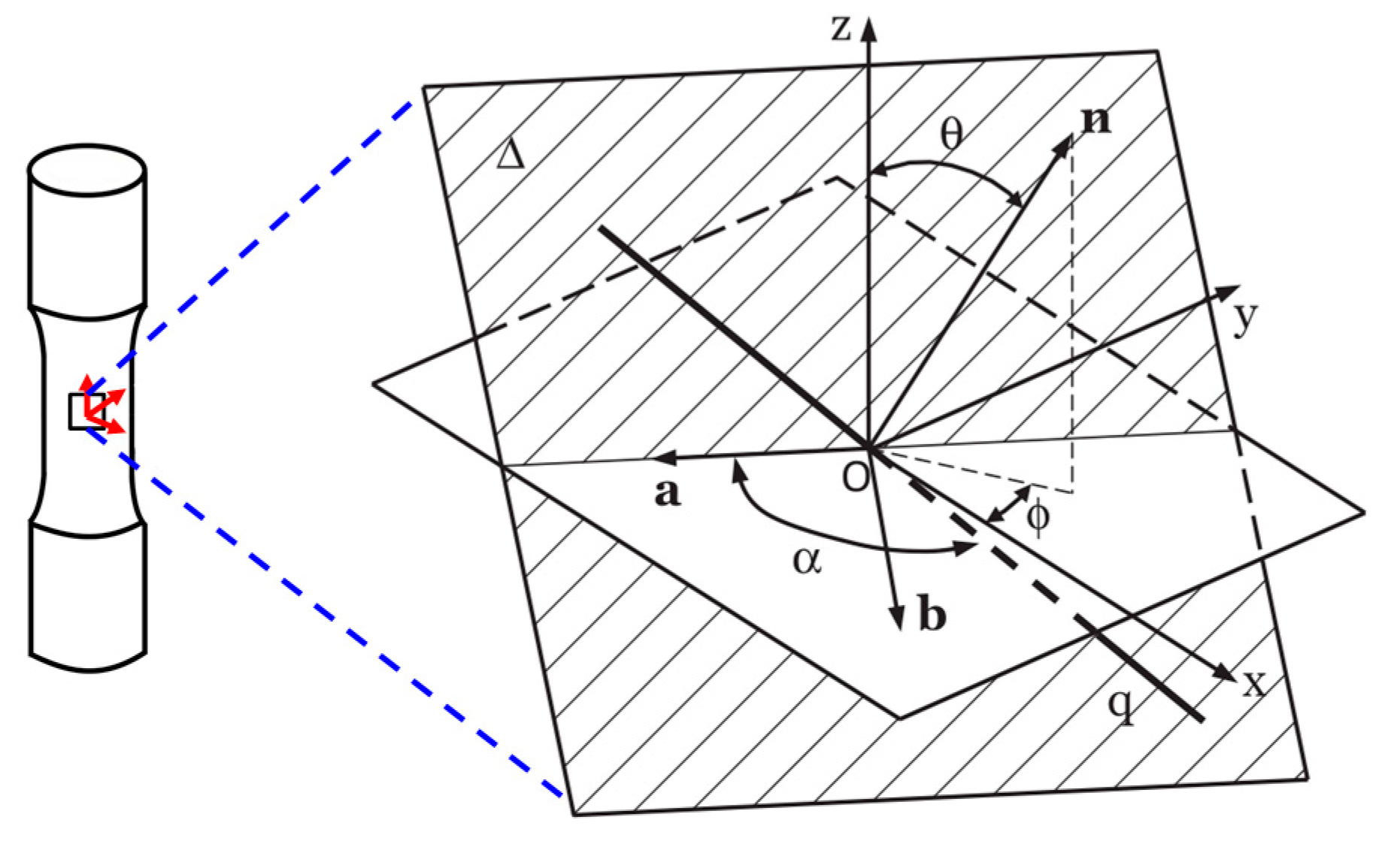
2. Critical Plane Approach for Multiaxial Fatigue Analysis
- (1)
- Conduct an elastic-plastic FE analysis for the component under given loading conditions to determine the time-variable stress and strain tensors at the critical region;
- (2)
- Using stress and strain tensors to express the states of stress and strain and three direction vectors, , and at the internal reference point of element where there is a plane with maximum shear strain in the whole critical locations to determine the candidate material planes through every 5° to change the directions of and , , ;
- (3)
- Since the shear strain directly calculated from Equation (8) is a time consuming process by involving three cycles of angle calculation, then shear strains and can be obtained respectively along the direction and similar to Equation (8). The shear strain amplitude acting on the th candidate material plane can be determined by:where is the number of subdivisions per cycle (each cycle is divided into p subdivisions).
- (4)
- Find critical plane through comparing the value of shear strain amplitude of each candidate material planes to determinate the location of the maximum one;
- (5)
- The normal strain ranges acting on the critical plane can be calculated by:where can be calculated using Equation (6).
- (6)
- Calculate normal stress of each candidate plane according to Equation (5). The maximum normal stress of critical plane is calculated by:
3. Proposed Energy-Critical Plane Damage Parameter for Multiaxial Fatigue Analysis
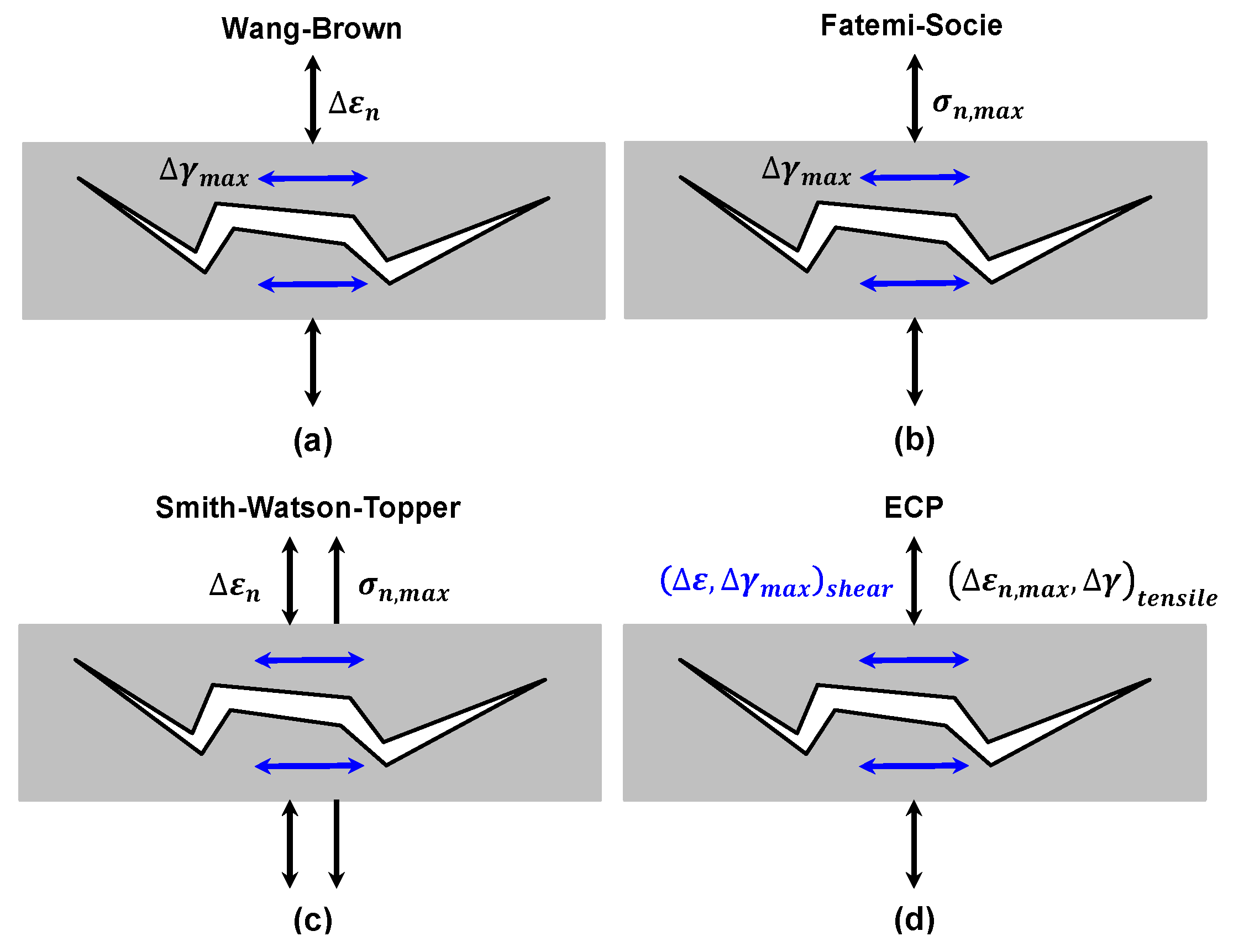
3.1. Wang-Brown Model with Maximum Damage Parameter
3.2. Fatemi-Socie Model with Maximum Damage Parameter
3.3. Smith-Watson-Topper Model with Maximum Damage Parameter
3.4. New Energy-Critical Plane Damage Parameter
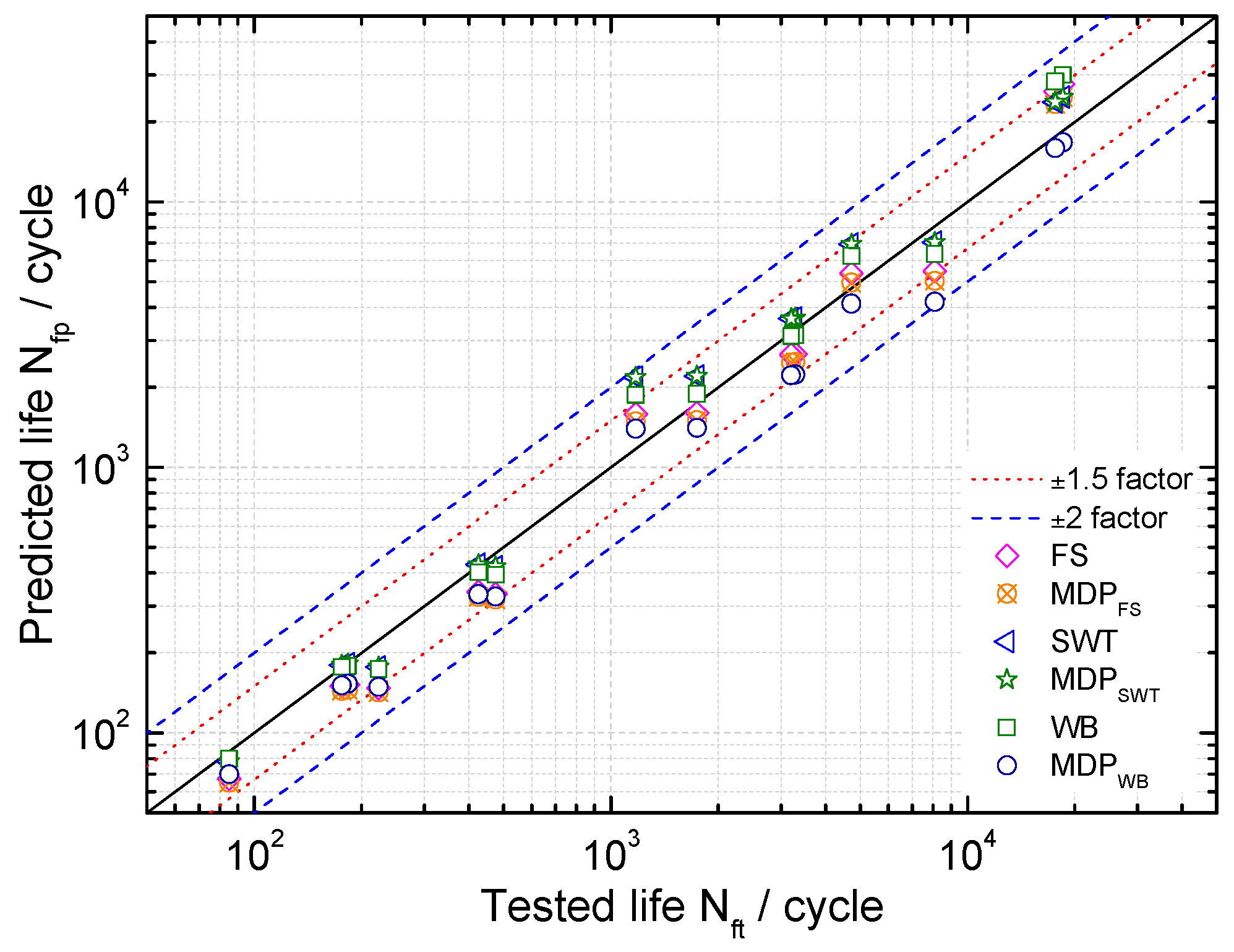
4. Experimental Validation
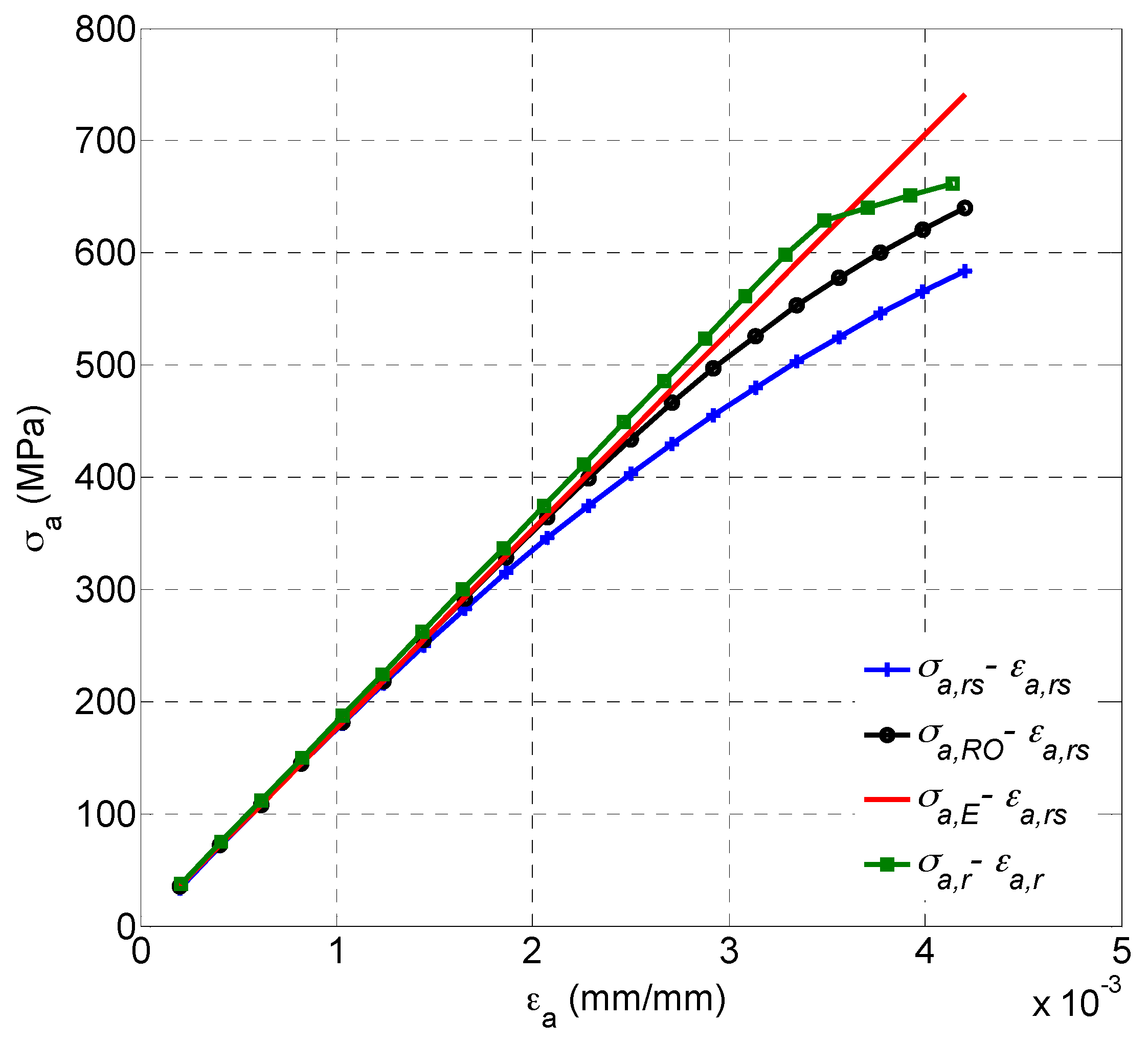
4.1. Model Vvalidation to Turbine Blade Alloy GH4169
4.2. Model Validation to a Turbine Disk-Blade Contact System
5. Conclusions
- (1)
- Based on the SWT parameter, and considering different failure types, a new energy-critical plane damage parameter is proposed for multiaxial fatigue life prediction, and no extra fitted material constants will be needed for both of the tensile and shear failure types.
- (2)
- Three multiaxial models with maximum damage parameters on the critical plane are evaluated under tension-compression and tension-torsion loadings.
- (3)
- For GH4169 alloy, note that the proposed damage parameter provides more accurate multiaxial fatigue life predictions than the SWT model. The WB and FS models with maximum damage parameters have shown satisfactory uniaxial and multiaxial fatigue life predictions.
- (4)
- For the turbine blade, both of the proposed damage parameters and the SWT model show reasonably acceptable correlations with its field number of flight cycles. However, the definition of the critical plane of the maximum damage parameter is inappropriate for the WB model, but desirable for FS and SWT models. In general, the predicted lives of these models with maximum damage parameters as a critical plane are relatively conservative, except for the WB model. Therefore, it is not recommended to apply the maximum damage parameter to the WB model for multiaxial fatigue analysis.
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| Generic material plane | |
| Shear modulus | |
| Normal stress components | |
| Normal strain components | |
| Shear stress components | |
| Shear strain components | |
| Three axial vector of the second reference coordinate | |
| Generic direction on candidate material planes | |
| Euler angles | |
| Stress normal to plane | |
| Strain normal to plane | |
| Shear stress along the direction | |
| Shear strain ranges on the ith candidate plane | |
| Number of subdivisions in one cycle | |
| Normal strain ranges acting on the critical plane | |
| Maximum normal stress normal to critical plane | |
| Maximum shear strain amplitude on the critical plane | |
| , | Material constants |
| , | Elastic and plastic Poisson’s ratio |
| Effective Poisson’s ratio | |
| Fatigue strength coefficient | |
| Fatigue ductility coefficient | |
| Fatigue strength exponent | |
| FS | Fatemi-Socie |
| WB | Wang-Brown |
| MDP | Maximum damage parameter |
| E | Young modulus |
| Model predicted life | |
| Number of cycles to failure | |
| Normal mean stress normal to critical plane | |
| Axial strain in uniaxial fatigue tests | |
| Axial mean stress in uniaxial fatigue tests | |
| Shear fatigue strength coefficient | |
| Shear fatigue ductility coefficient | |
| Shear fatigue strength exponent | |
| Shear fatigue ductility exponent | |
| Yield strength | |
| Shear strain along the direction | |
| Cyclic strength coefficient | |
| Cyclic strain hardening exponent | |
| Real normal stress amplitude on plane with shear behavior | |
| Real normal strain amplitude on plane with shear behavior | |
| Real normal stress amplitude on plane without shear behavior | |
| Real normal strain amplitude on plane without shear behavior | |
| Normal stress calculated by Ramberg-Osgood equation | |
| Normal stress calculated by Young modulus | |
| Experimental life | |
| Model prediction error | |
| Fatigue ductility exponent | |
| SWT | Smith-Watson-Topper |
| ECP | Energy-critical plane |
References
- Hou, J.; Wicks, B.J.; Antonious, R.A. An investigation of fatigue failures of turbine blades in a gas turbine engine by mechanical analysis. Eng. Fail. Anal. 2002, 9, 201–211. [Google Scholar] [CrossRef]
- Silveira, E.; Atxaga, G.; Irisarri, A.M. Failure analysis of two sets of aircraft blades. Eng. Fail. Anal. 2010, 17, 641–647. [Google Scholar] [CrossRef]
- Wang, R.Z.; Zhang, X.C.; Gong, J.G. Creep-fatigue life prediction and interaction diagram in nickel-based GH4169 superalloy at 650 °C based on cycle-by-cycle concept. Int. J. Fatigue 2017, 97, 114–123. [Google Scholar] [CrossRef]
- Wang, R.Z.; Zhang, X.C.; Tu, S.T. The effects of inhomogeneous microstructure and loading waveform on creep-fatigue behaviour in a forged and precipitation hardened nickel-based superalloy. Int. J. Fatigue 2017, 97, 190–201. [Google Scholar] [CrossRef]
- Zhu, S.P.; Yang, Y.J.; Huang, H.Z. A unified criterion for fatigue-creep life prediction of high temperature components. Proc. Inst. Mech. Eng. Part G 2017, 231, 677–688. [Google Scholar] [CrossRef]
- Hu, D.; Wang, R. Combined fatigue experiments on full scale turbine components. Airc. Eng. Aerosp. Technol. 2013, 85, 4–9. [Google Scholar] [CrossRef]
- Hu, D.; Meng, F.; Liu, H. Experimental investigation of fatigue crack growth behavior of GH2036 under combined high and low cycle fatigue. Int. J. Fatigue 2016, 85, 1–10. [Google Scholar] [CrossRef]
- Sinclair, G.B.; Cormier, N.G. Contact stresses in dovetail attachments: Finite element modeling. In Proceedings of the ASME 1999 International Gas Turbine and Aeroengine Congress and Exhibition, Indianapolis, IN, USA, 7–10 June 1999. [Google Scholar]
- Tao, C.; Zhong, P.; Li, R.Z. Failure Analysis and Prevention for Rotor in Aero-Engine; National Defence Industry Press: Beijing, China, 2000; pp. 102–163. [Google Scholar]
- Zhu, S.P.; Huang, H.Z.; Peng, W.; Wang, H.K.; Mahadevan, S. Probabilistic physics of failure-based framework for fatigue life prediction of aircraft gas turbine discs under uncertainty. Reliab. Eng. Syst. Saf. 2016, 146, 1–12. [Google Scholar] [CrossRef]
- Zhu, S.P.; Huang, H.Z.; He, L. A generalized energy-based fatigue-creep damage parameter for life prediction of turbine disk alloys. Eng. Fract. Mech. 2012, 90, 89–100. [Google Scholar] [CrossRef]
- Kermanpur, A.; Sepehri Amin, H.; Ziaei-Rad, S. Failure analysis of Ti6Al4V gas turbine compressor blades. Eng. Fail. Anal. 2008, 15, 1052–1064. [Google Scholar] [CrossRef]
- Golden, P.J.; Calcaterra, J.R. A fracture mechanics life prediction methodology applied to dovetail fretting. Tribol. Int. 2006, 39, 1172–1180. [Google Scholar] [CrossRef]
- Chen, L.; Liu, Y.; Xie, L. Power-exponent function model for low-cycle fatigue life prediction and its applications–Part II: Life prediction of turbine blades under creep-fatigue interaction. Int. J. Fatigue 2007, 29, 10–19. [Google Scholar] [CrossRef]
- Fatemi, A.; Socie, D.F. A Critical plane to multiaxial fatigue damage including out-of-phase loading. Fatigue Fract. Eng. Mater. Struct. 1988, 11, 149–165. [Google Scholar] [CrossRef]
- Wang, C.H.; Brown, M.W. A path-independent parameter for fatigue under proportional and non-proportional loading. Fatigue Fract. Eng. Mater. Struct. 1993, 16, 1285–1298. [Google Scholar] [CrossRef]
- Wang, C.H.; Brown, M.W. Multiaxial random load fatigue: Life prediction techniques and experiments. In Multiaxial Fatigue and Design, ESIS 21; Pineau, A., Cailletaud, G., Lindley, T.C., Eds.; Mechanical Engineering: London, UK, 1996; pp. 513–527. [Google Scholar]
- Smith, R.N.; Watson, P.; Topper, T.H. A stress-strain function for the fatigue of metals. J. Mater. 1970, 5, 767–778. [Google Scholar]
- Brown, M.W.; Miller, K.J. A theory for fatigue under multiaxial stress-strain conditions. Proc. Inst. Mech. Eng. 1973, 187, 745–756. [Google Scholar]
- Wu, Z.R.; Hu, X.T.; Song, Y.D. Multiaxial fatigue life prediction for titanium alloy TC4 under proportional and nonproportional loading. Int. J. Fatigue 2014, 59, 170–175. [Google Scholar] [CrossRef]
- Wang, L.; Shi, S.; Fu, S. Evaluation of multiaxial fatigue life prediction criteria for PEEK. Theor. Appl. Fract. Mech. 2014, 73, 128–135. [Google Scholar] [CrossRef]
- Albinmousa, J.; Jahed, H. Multiaxial effects on LCF behaviour and fatigue failure of AZ31B magnesium extrusion. Int. J. Fatigue 2014, 67, 103–116. [Google Scholar] [CrossRef]
- Babaei, S.; Ghasemi-Ghalebahman, A.; Hajighorbani, R. A fatigue model for sensitive materials to non-proportional loadings. Int. J. Fatigue 2015, 80, 266–277. [Google Scholar] [CrossRef]
- Jiang, Y.; Sehitoglu, H. Fatigue and Stress Analysis of Rolling Contact; College of Engineering, University of Illinois at Urbana-Champaign: Champaign, IL, USA, 1992. [Google Scholar]
- Zhao, T.; Jiang, Y. Fatigue of 7075-T651 aluminum alloy. Int. J. Fatigue 2008, 30, 834–849. [Google Scholar] [CrossRef]
- Ince, A. A mean stress correction model for tensile and compressive mean stress fatigue loadings. Fatigue Fract. Eng. Mater. Struct. 2017, in press. [Google Scholar] [CrossRef]
- Zhu, S.P.; Lei, Q.; Wang, Q.Y. Mean stress and ratcheting corrections in fatigue life prediction of metals. Fatigue Fract. Eng. Mater. Struct. 2017, in press. [Google Scholar] [CrossRef]
- Zhu, S.P.; Lei, Q.; Huang, H.Z. Mean stress effect correction in strain energy-based fatigue life prediction of metals. Int. J. Damage Mech. 2016, in press. [Google Scholar] [CrossRef]
- Ince, A.; Glinka, G. A generalized fatigue damage parameter for multiaxial fatigue life prediction under proportional and non-proportional loadings. Int. J. Fatigue 2014, 62, 34–41. [Google Scholar] [CrossRef]
- Calvo, S.; Canales, M.; Gómez, C. Probabilistic formulation of the multiaxial fatigue damage of Liu. Int. J. Fatigue 2011, 33, 460–465. [Google Scholar] [CrossRef]
- Correia, J.; Apetre, N.; Arcari, A. Generalized probabilistic model allowing for various fatigue damage variables. Int. J. Fatigue 2017, 100, 187–194. [Google Scholar] [CrossRef]
- Blasón, S.; Correia, J.A.F.O.; De Jesus, A.M.P. A probabilistic analysis of Miner’s law for different loading conditions. Struct. Eng. Mech. 2016, 60, 71–90. [Google Scholar] [CrossRef]
- Castillo, E.; Alfonso, F.-C. A Unified Statistical Methodology for Modeling Fatigue Damage; Springer Science & Business Media: Dordrecht, The Netherlands, 2009. [Google Scholar]
- Zhu, S.P.; Huang, H.Z.; Li, Y. Probabilistic modeling of damage accumulation for time-dependent fatigue reliability analysis of railway axle steels. Proc. Inst. Mech. Eng. Part F 2015, 229, 23–33. [Google Scholar] [CrossRef]
- Koutiri, I.; Bellett, D.; Morel, F. A probabilistic model for the high cycle fatigue behaviour of cast aluminium alloys subject to complex loads. Int. J. Fatigue 2013, 47, 137–147. [Google Scholar] [CrossRef]
- Bonnand, V.; Chaboche, J.L.; Cherouali, H. Investigation of multiaxial fatigue in the prospect of turbine disc applications: Part II-Fatigue criteria analysis and formulation of a new combined one. In Proceedings of the ICMFF9, Parma, Italy, 7–9 June 2010. [Google Scholar]
- Shamsael, N.; Fatemi, A. Effect of hardness on multiaxial fatigue behaviour and some simple approximations for steels. Fatigue Fract. Eng. Mater. Struct. 2009, 32, 631–646. [Google Scholar] [CrossRef]
- Bannantine, J.A.; Socie, D.F. A variable amplitude multiaxial fatigue life prediction method. In Proceedings of the Third International Conference on Biaxial/Multiaxial Fatigue, Stuttgart, Germany, 3–6 April 1989. [Google Scholar]
- Banvillet, A.; Łagoda, T.; Macha, E. Fatigue life under non-Gaussian random loading from various models. Int. J. Fatigue 2000, 26, 349–363. [Google Scholar] [CrossRef]
- Wei, H.; Liu, Y. A critical plane-energy model for multiaxial fatigue life prediction. Fatigue Fract. Eng. Mater. Struct. 2017, in press. [Google Scholar] [CrossRef]
- Kandil, F.A.; Brown, M.W.; Miller, K.J. Biaxial low-cycle fatigue failure of 316 stainless steel at elevated temperatures. In Mechanical Behaviour and Nuclear Applications of Stainless Steel at Elevated Temperatures; Maney Pub.: London, UK, 1982. [Google Scholar]
- Liu, K.C. A method based on virtual strain-energy parameters for multiaxial fatigue life prediction. In Advances in Multiaxial Fatigue; ASTM International: West Conshohocken, PA, USA, 1993. [Google Scholar]
- Glinka, G.; Shen, G.; Plumtree, A. A multiaxial fatigue strain energy density parameter related to the critical fracture plane. Fatigue Fract. Eng. Mater. Struct. 1995, 18, 37–46. [Google Scholar] [CrossRef]
- Glinka, G.; Wang, G.; Plumtree, A. Mean stress effects in multiaxial fatigue. Fatigue Fract. Eng. Mater. Struct. 1995, 18, 755–764. [Google Scholar] [CrossRef]
- Chu, C.C.; Conle, F.A.; Bonnen, J.J.F. Multiaxial stress-strain modeling and fatigue life prediction of SAE axle shafts. In Advances in Multiaxial Fatigue; ASTM International: West Conshohocken, PA, USA, 1993. [Google Scholar]
- Ramberg, W.; Osgood, W.R. Description of Stress-Strain Curves by Three Parameters; Technical Note No. 902; National Advisory Committee for Aeronautics: Washington, DC, USA, 1943.
- Chaboche, J.L. Constitutive equations for cyclic plasticity and cyclic viscoplasticity. Int. J. Plast. 1989, 5, 247–302. [Google Scholar] [CrossRef]
- Zhao, G.P.; Zhao, B.K. China Aeronautical Materials Handbook; China Standard Press: Beijing, China, 2002.
- Sun, G.Q.; Shang, D.G.; Bao, M. Multiaxial fatigue damage parameter and life prediction under low cycle loading for GH4169 alloy and other structural materials. Int. J. Fatigue 2010, 32, 1108–1115. [Google Scholar] [CrossRef]
- Maktouf, W.; Ammar, K.; Naceur, I.B. Multiaxial high-cycle fatigue criteria and life prediction: Application to gas turbine blade. Int. J. Fatigue 2016, 92, 25–35. [Google Scholar] [CrossRef]
- Li, J.; Zhang, Z.; Sun, Q. Multiaxial fatigue life prediction for various metallic materials based on the critical plane approach. Int. J. Fatigue 2011, 33, 90–101. [Google Scholar] [CrossRef]
- Wang, Y.; Susmel, L. The Modified Manson-Coffin Curve Method to estimate fatigue lifetime under complex constant and variable amplitude multiaxial fatigue loading. Int. J. Fatigue 2016, 83, 135–149. [Google Scholar] [CrossRef]
- Castro, F.; Jiang, Y. Fatigue of extruded AZ31B magnesium alloy under stress-and strain-controlled conditions including step loading. Mech. Mater. 2017, in press. [Google Scholar] [CrossRef]
- Szolwinski, M.P.; Harish, G.; Farris, T.N. Comparison of fretting fatigue crack nucleation experiments to multiaxial fatigue theory life predictions. Anal. Des. Issues Mod. Aerosp. Veh. 1997, 55, 449–457. [Google Scholar]
- Nitta, A.; Ogata, T.; Kuwabara, K. Fracture mechanisms and life assessment under high strain-biaxial cyclic loading of type 304 stainless steel. Fatigue Fract. Eng. Mater. Struct. 1989, 12, 77–92. [Google Scholar] [CrossRef]
- Socie, D.; Marquis, G. Multiaxial Fatigue; Society of Automotive Engineers: Warrendale, PA, USA, 1999. [Google Scholar]



| T (°C) | E (GPa) | (MPa) | (MPa) | b | c | (MPa) | ||
|---|---|---|---|---|---|---|---|---|
| 650 | 182 | 626.4 | 1476 | 0.162 | −0.086 | −0.58 | 1933 | 0.1483 |
| No. | (°) | (%) | (%) | (MPa) | (MPa) | (cycles) |
|---|---|---|---|---|---|---|
| 1 | 45 | 0.354 | 0.420 | 601 | 347 | 4420 |
| 2 | 90 | 0.397 | 0.479 | 679 | 434 | 5665 |
| 3 | 0 | 0.408 | 0.592 | 503 | 295 | 1544 |
| 4 | 45 | 0.524 | 0.745 | 658 | 560 | 722 |
| 5 | 45 | 0.553 | 0.813 | 691 | 436 | 295 |
| 6 | 90 | 0.548 | 0.833 | 762 | 475 | 436 |
| 7 | 90 | 0.586 | 0.838 | 801 | 506 | 563 |
| 8 | 0 | 0.546 | 0.884 | 584 | 301 | 458 |
| 9 | 45 | 0.704 | 1.090 | 793 | 477 | 171 |
| 10 | 45 | 0.701 | 1.160 | 757 | 492 | 260 |
| 11 | 90 | 0.783 | 1.330 | 899 | 607 | 121 |
| 12 * | 0 | 0.54 | 0.896 | 745 | 317 | 338 |
| 13 * | 0 | 0.536 | 0.945 | 642 | 401 | 161 |
| 14 * | 0 | 0.427 | 0.633 | 637 | 268 | 1108 |
| 15 * | 0 | 0.448 | 0.709 | 556 | 370 | 1370 |
| 16 * | 45 | 0.478 | 0.749 | 655 | 426 | 1048 |
| 17 * | 45 | 0.625 | 1.000 | 648 | 435 | 222 |
| 18 * | 90 | 0.613 | 1.010 | 838 | 527 | 529 |
| Model | Evaluated Life (cycles) | ||
|---|---|---|---|
| 0-450r/s-0 | 230r/s-450r/s-230r/s | 431r/s-450r/s-431r/s | |
| WB | 993346 | 59560715 | > |
| MDPWB | 13481520 | 113213394 | > |
| FS | 360185 | 63404561 | > |
| MDPFS | 253996 | 53007514 | > |
| SWT | 71540 | 676766 | > |
| MDPSWT | 71540 | 676766 | > |
| ECP | 85932 | 936842 | > |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, Z.-Y.; Zhu, S.-P.; Liu, Q.; Liu, Y. A New Energy-Critical Plane Damage Parameter for Multiaxial Fatigue Life Prediction of Turbine Blades. Materials 2017, 10, 513. https://doi.org/10.3390/ma10050513
Yu Z-Y, Zhu S-P, Liu Q, Liu Y. A New Energy-Critical Plane Damage Parameter for Multiaxial Fatigue Life Prediction of Turbine Blades. Materials. 2017; 10(5):513. https://doi.org/10.3390/ma10050513
Chicago/Turabian StyleYu, Zheng-Yong, Shun-Peng Zhu, Qiang Liu, and Yunhan Liu. 2017. "A New Energy-Critical Plane Damage Parameter for Multiaxial Fatigue Life Prediction of Turbine Blades" Materials 10, no. 5: 513. https://doi.org/10.3390/ma10050513






