Predictive Simulation of Process Windows for Powder Bed Fusion Additive Manufacturing: Influence of the Powder Bulk Density
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Setup
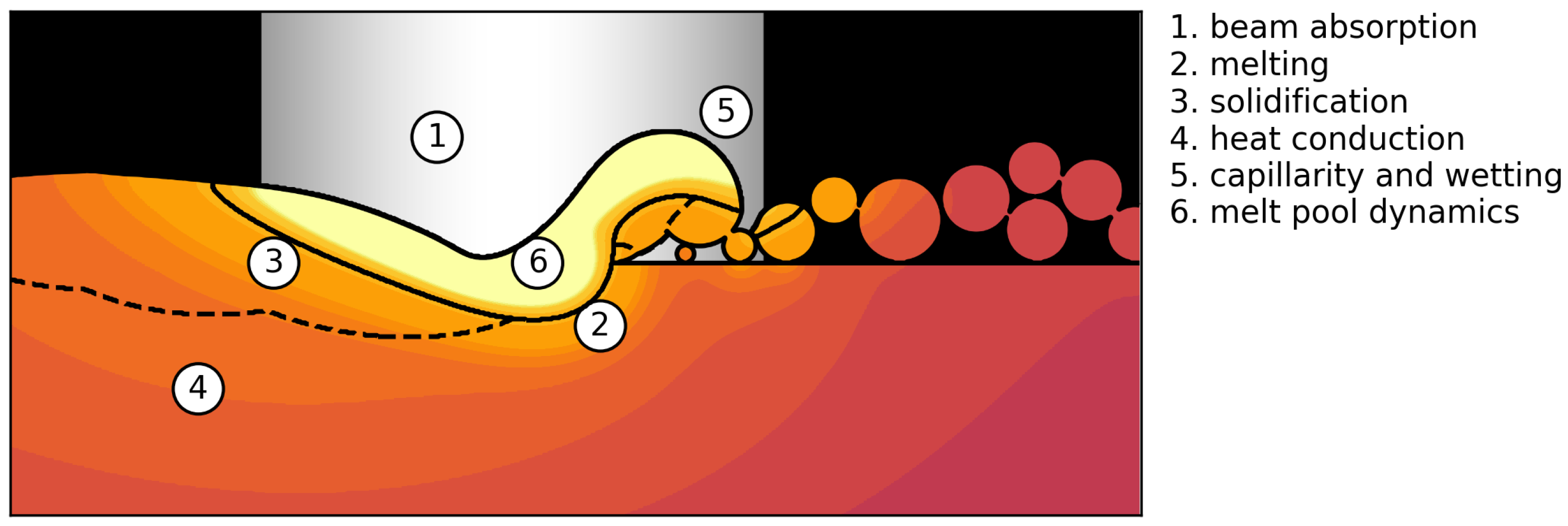
2.2. Numerical Setup
3. Results and Discussion
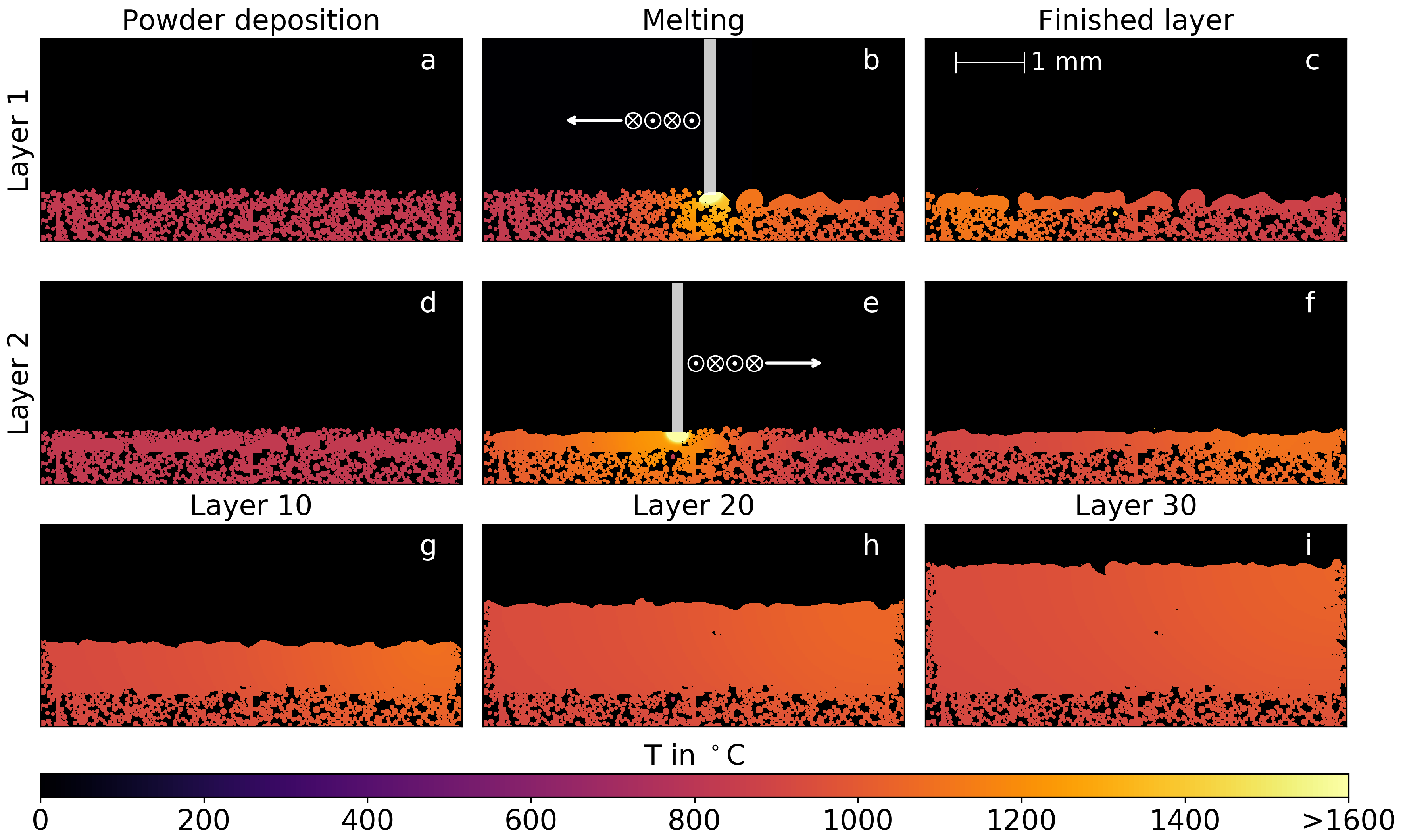
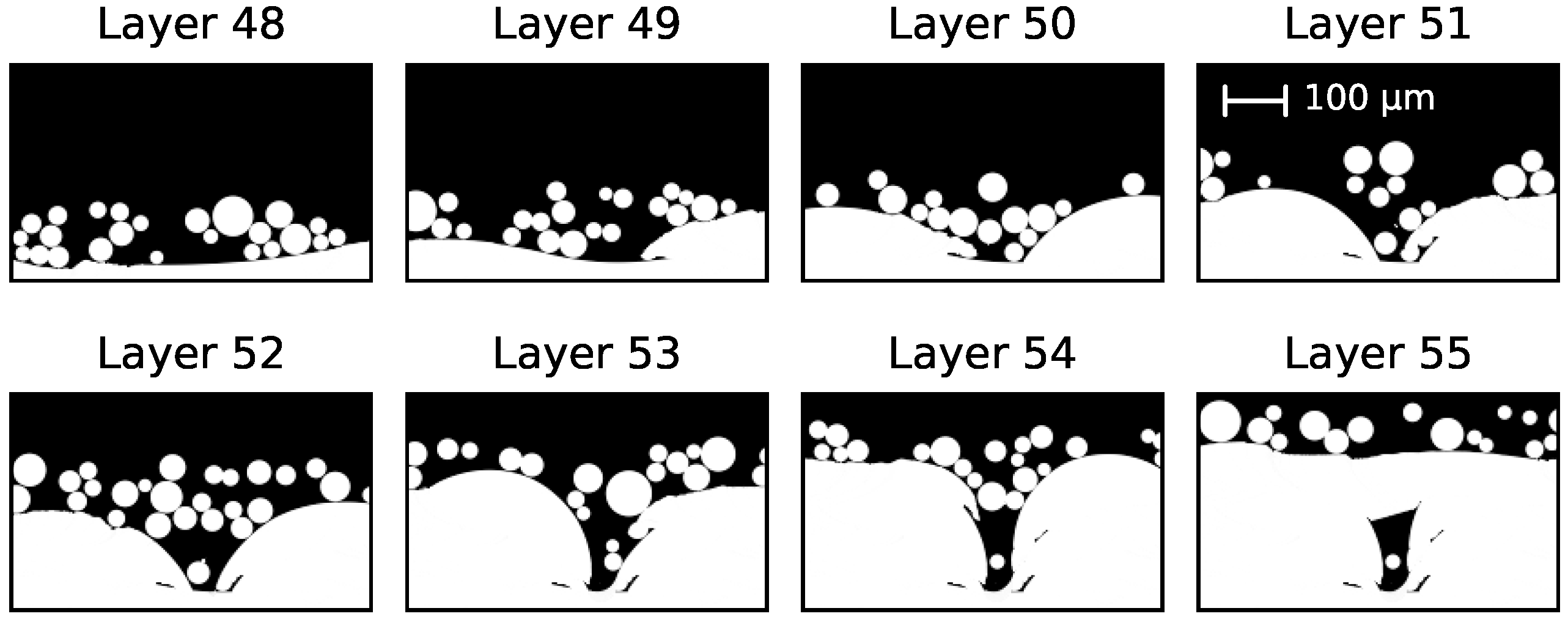
3.1. Temporal Evolution of Multi-Layer Manufacturing
3.2. Comparison between Experiment and Simulation
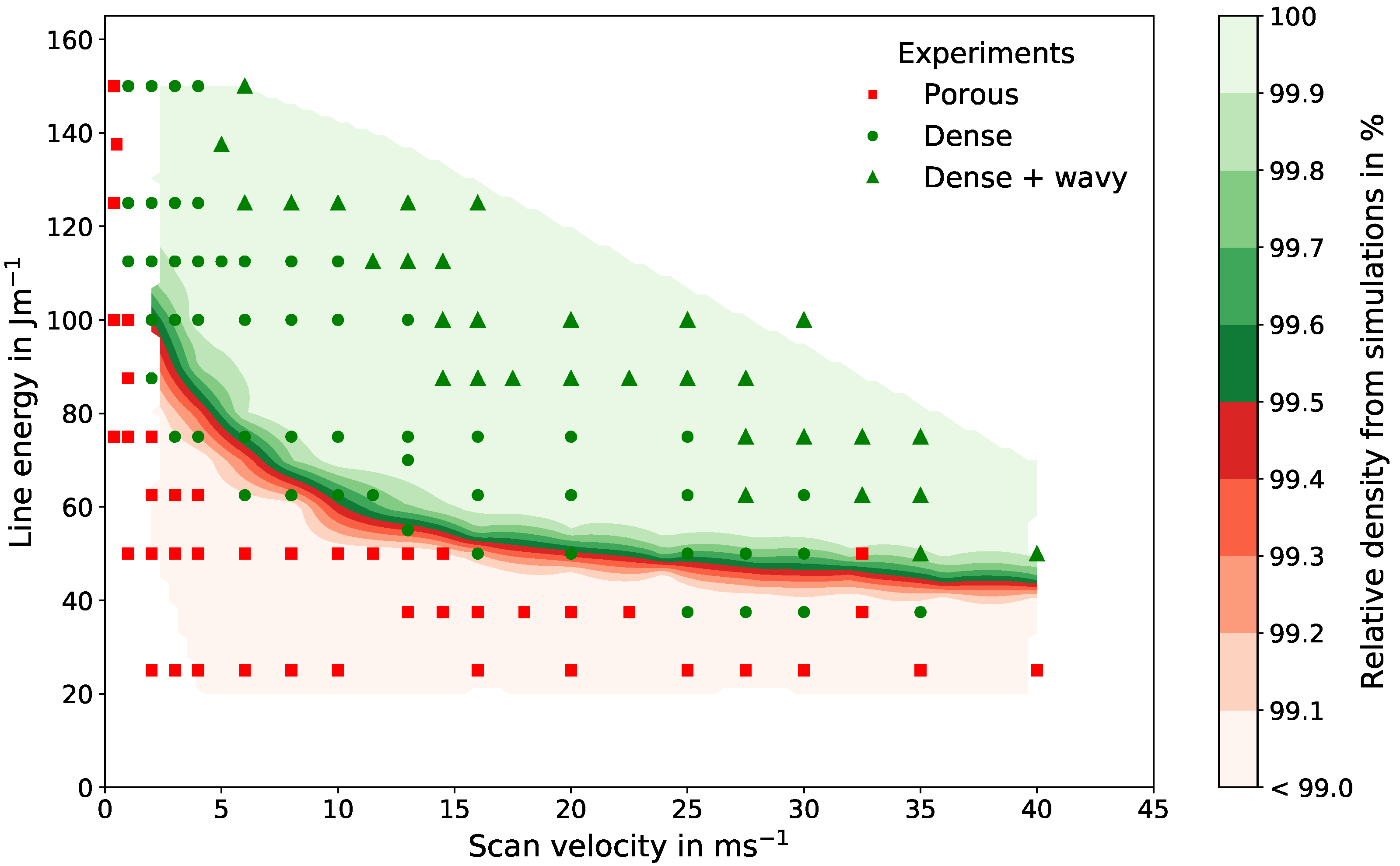
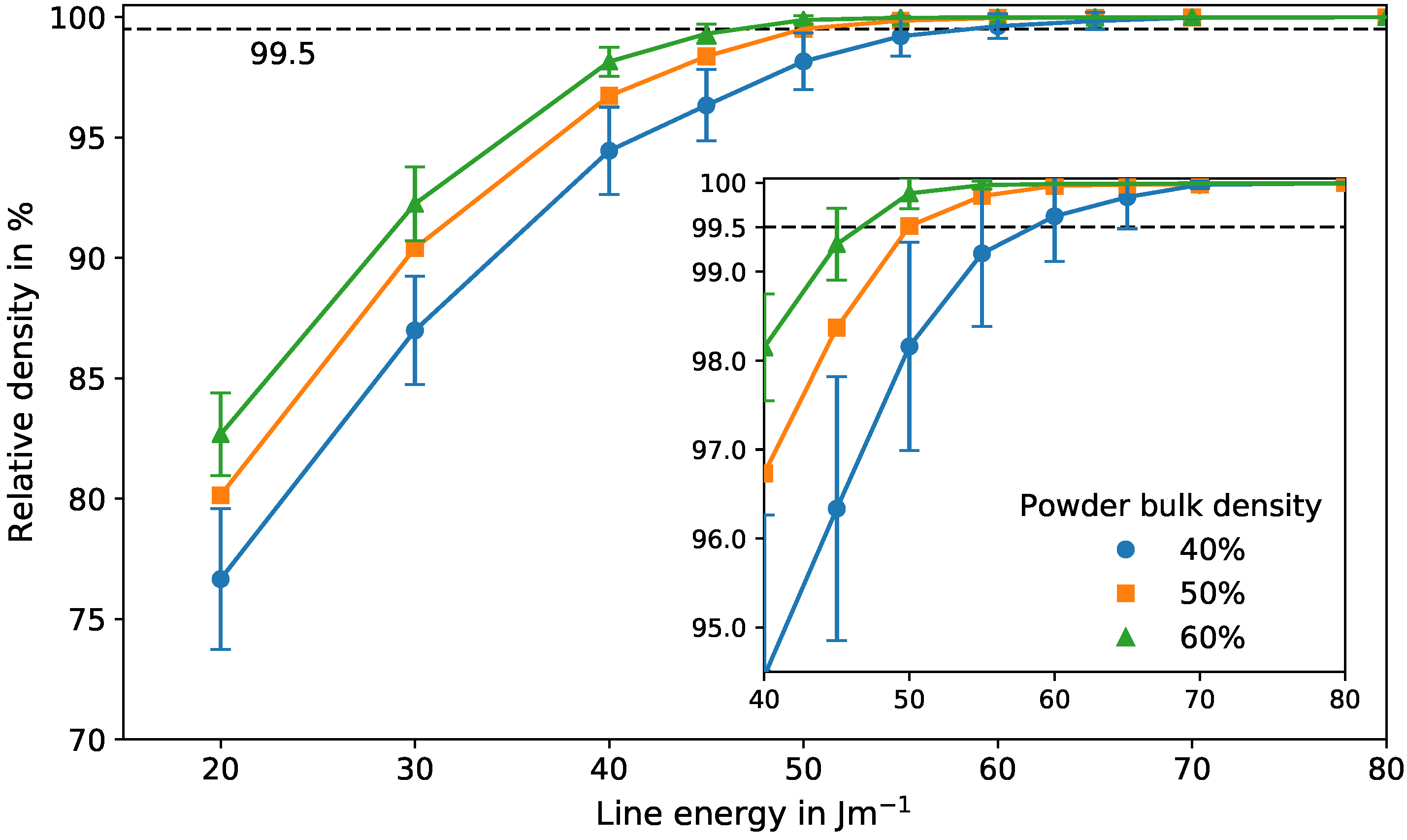
3.3. Experimental and Numerical Process Window
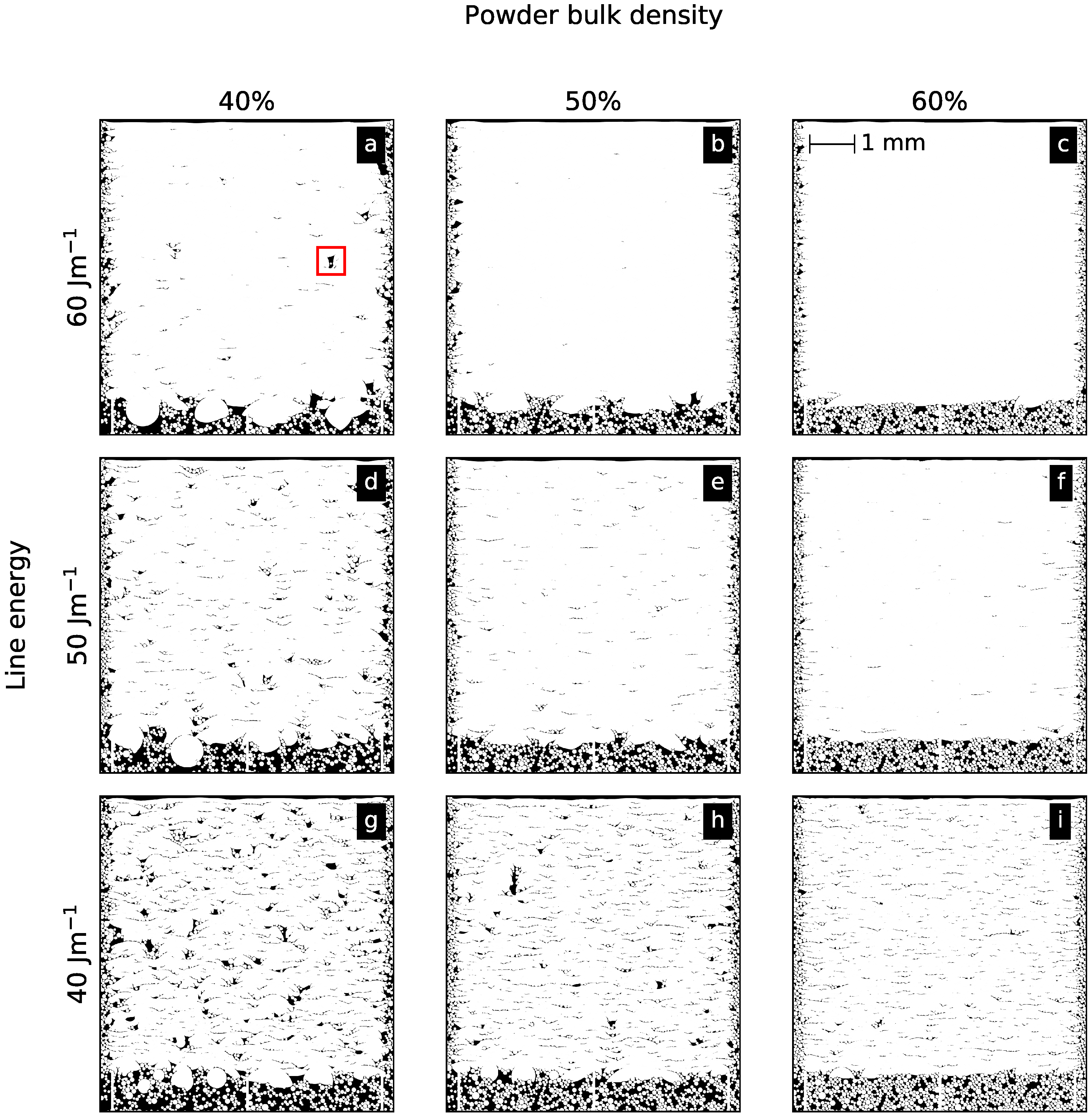
3.4. Influence of the Powder Bulk Density on Defect Evolution
3.5. Influence of the Powder Bulk Density on the Process Window
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Levy, G.N.; Schindel, R.; Kruth, J. Rapid Manufacturing and Rapid Tooling with Layer Manufacturing (LM) Technologies, State of the Art and Future Perspectives. CIRP Ann. Manuf. Technol. 2003, 52, 589–609. [Google Scholar] [CrossRef]
- Murr, L.E.; Gaytan, S.M.; Ramirez, D.A.; Martinez, E.; Hernandez, J.; Amato, K.N.; Shindo, P.W.; Medina, F.R.; Wicker, R.B. Metal Fabrication by Additive Manufacturing Using Laser and Electron Beam Melting Technologies. J. Mater. Sci. Technol. 2012, 28, 1–14. [Google Scholar] [CrossRef]
- Körner, C.; Bauereiß, A.; Attar, E. Fundamental consolidation mechanisms during selective beam melting. Model. Simul. Mater. Sci. Eng. 2013, 21, 085011. [Google Scholar] [CrossRef]
- Juechter, V.; Scharowsky, T.; Singer, R.; Körner, C. Processing window and evaporation phenomena for Ti-6Al-4V produced by selective electron beam melting. Acta Mater. 2014, 76, 252–258. [Google Scholar] [CrossRef]
- Juechter, V.; Körner, C. Influence of Scanning Strategy on Properties of Titanium Aluminides Produced by Selective Electron Beam Melting. In Proceedings of the Fraunhofer Direct Digital Manufacturing Conference, Berlin, Germany, 16–17 March 2016. [Google Scholar]
- Kirchner, A.; Klöden, B.; Luft, J.; Weißgärber, T.; Kieback, B. Process window for electron beam melting of Ti-6Al-4V. Powder Metall. 2015, 58, 246–249. [Google Scholar] [CrossRef]
- Scharowsky, T.; Bauereiß, A.; Körner, C. Influence of the hatching strategy on consolidation during selective electron beam melting of Ti-6Al-4V. Int. J. Adv. Manuf. Technol. 2017, 92, 2809–2818. [Google Scholar] [CrossRef]
- Scharowsky, T.; Juechter, V.; Singer, R.F.; Körner, C. Influence of the Scanning Strategy on the Microstructure and Mechanical Properties in Selective Electron Beam Melting of Ti-6Al-4V. Adv. Eng. Mater. 2015, 17, 1573–1578. [Google Scholar] [CrossRef]
- Osmanlic, F.; Klassen, A.; Scharowsky, T.; Körner, C. Numerical investigation of the influence of electron beam acceleration voltage in powder based additive manufacturing processes. In Proceedings of the International Conference on Electron Beam Technologies, Varna, Bulgaria, 13–18 June 2016. [Google Scholar]
- Helmer, H.E.; Körner, C.; Singer, R.F. Additive manufacturing of nickel-based superalloy Inconel 718 by selective electron beam melting: Processing window and microstructure. J. Mater. Res. 2014, 29, 1987–1996. [Google Scholar] [CrossRef]
- Montgomery, C.; Beuth, J.; Sheridan, L.; Klingbeil, N. Process Mapping of Inconel 625 in Laser Powder Bed Additive Manufacturing. In Proceedings of the Annual International Solid Freeform Fabrication Symposium, Austin, TX, USA, 10–12 August 2015; pp. 1195–1204. [Google Scholar]
- Hauser, C.; Childs, T.; Badrossamay, M. Further developments in process mapping and modelling in direct metal selective laser melting. In Proceedings of the Annual International Solid Freeform Fabrication Symposium, Austin, TX, USA, 2–4 August 2004; pp. 2–4. [Google Scholar]
- Li, C.; Guo, Y.; Zhao, J. Interfacial phenomena and characteristics between the deposited material and substrate in selective laser melting Inconel 625. J. Mater. Process. Technol. 2017, 243, 269–281. [Google Scholar] [CrossRef]
- Childs, T.H.C.; Hauser, C.; Badrossamay, M. Selective laser sintering (melting) of stainless and tool steel powders: Experiments and modelling. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2005, 219, 339–357. [Google Scholar] [CrossRef]
- Körner, C.; Attar, E.; Heinl, P. Mesoscopic simulation of selective beam melting processes. J. Mater. Process. Technol. 2011, 211, 978–987. [Google Scholar] [CrossRef]
- Seifi, M.; Christiansen, D.; Beuth, J.; Harrysson, O.; Lewandowski, J.J. Process mapping, fracture and fatigue behavior of Ti-6Al-4V produced by EBM additive manufacturing. In Proceedings of the World Conference on Titanium, San Diego, CA, USA, 16–20 August 2015; pp. 1373–1377. [Google Scholar]
- Gockel, J.; Beuth, J. Understanding Ti-6Al-4V microstructure control in additive manufacturing via process maps. In Proceedings of the Annual International Solid Freeform Fabrication Symposium, Austin, TX, USA, 12–14 August 2013; pp. 666–674. [Google Scholar]
- Zäh, M.F.; Lutzmann, S. Modelling and simulation of electron beam melting. Prod. Eng. 2010, 4, 15–23. [Google Scholar] [CrossRef]
- Guo, C.; Ge, W.; Lin, F. Effects of scanning parameters on material deposition during Electron Beam Selective Melting of Ti-6Al-4V powder. J. Mater. Process. Technol. 2015, 217, 148–157. [Google Scholar] [CrossRef]
- Markl, M.; Ammer, R.; Rüde, U.; Körner, C. Numerical investigations on hatching process strategies for powder-bed-based additive manufacturing using an electron beam. Int. J. Adv. Manuf. Technol. 2015, 78, 239–247. [Google Scholar] [CrossRef]
- Ammer, R.; Markl, M.; Jüchter, V.; Körner, C.; Rüde, U. Validation Experiments for LBM Simulations of Electron Beam Melting. Int. J. Mod. Phys. C 2014, 25, 1441009. [Google Scholar] [CrossRef]
- Markl, M.; Körner, C. Multiscale Modeling of Powder Bed–Based Additive Manufacturing. Ann. Rev. Mater. Res. 2016, 46, 93–123. [Google Scholar] [CrossRef]
- Zielinski, J.; Vervoort, S.; Mindt, H.W.; Megahed, M. Influence of Powder Bed Characteristics on Material Quality in Additive Manufacturing. BHM Berg Hüttenmännische Monatshefte 2017, 162, 192–198. [Google Scholar] [CrossRef]
- Gürtler, F.J.; Karg, M.; Dobler, M.; Kohl, S.; Tzivilsky, I.; Schmidt, M. Influence of powder distribution on process stability in laser beam melting: Analysis of melt pool dynamics by numerical simulations. In Proceedings of the Annual International Solid Freeform Fabrication Symposium, Austin, TX, USA, 4–6 August 2014; pp. 1099–1117. [Google Scholar]
- Spierings, A.; Herres, N.; Levy, G. Influence of the particle size distribution on surface quality and mechanical properties in AM steel parts. Rapid Prototyp. J. 2011, 17, 195–202. [Google Scholar] [CrossRef]
- Spierings, A.; Levy, G. Comparison of density of stainless steel 316L parts produced with selective laser melting using different powder grades. In Proceedings of the Annual International Solid Freeform Fabrication Symposium, Austin, TX, USA, 3–5 August 2009; pp. 342–353. [Google Scholar]
- Liu, B.; Wildman, R.; Tuck, C.; Ashcroft, I.; Hague, R. Investigation the effect of particle size distribution on processing parameters optimisation in selective laser melting process. In Proceedings of the Annual International Solid Freeform Fabrication Symposium, Austin, TX, USA, 8–10 August 2011; pp. 227–238. [Google Scholar]
- Moser, D.; Cullinan, M.; Murthy, J. Particle-Scale Melt Modeling of the Selective Laser Melting Process. In Proceedings of the Annual International Solid Freeform Fabrication Symposium, Austin, TX, USA, 8–10 August 2016; pp. 247–256. [Google Scholar]
- Matthews, M.J.; Guss, G.; Khairallah, S.A.; Rubenchik, A.M.; Depond, P.J.; King, W.E. Denudation of metal powder layers in laser powder bed fusion processes. Acta Mater. 2016, 114, 33–42. [Google Scholar] [CrossRef]
- Panwisawas, C.; Qiu, C.; Anderson, M.J.; Sovani, Y.; Turner, R.P.; Attallah, M.M.; Brooks, J.W.; Basoalto, H.C. Mesoscale modelling of selective laser melting: Thermal fluid dynamics and microstructural evolution. Comput. Mater. Sci. 2017, 126, 479–490. [Google Scholar] [CrossRef]
- Khairallah, S.A.; Anderson, A. Mesoscopic simulation model of selective laser melting of stainless steel powder. J. Mater. Process. Technol. 2014, 214, 2627–2636. [Google Scholar] [CrossRef]
- Kovaleva, I.; Kovalev, O.; Smurov, I. Model of Heat and Mass Transfer in Random Packing Layer of Powder Particles in Selective Laser Melting. Phys. Procedia 2014, 56, 400–410. [Google Scholar] [CrossRef]
- Lee, Y.; Zhang, W. Mesoscopic simulation of heat transfer and fluid flow in laser powder bed additive manufacturing. In Proceedings of the Annual International Solid Freeform Fabrication Symposium, Austin, TX, USA, 10–12 August 2015; pp. 1154–1165. [Google Scholar]
- Bauereiß, A.; Scharowsky, T.; Körner, C. Defect generation and propagation mechanism during additive manufacturing by selective beam melting. J. Mater. Process. Technol. 2014, 214, 2522–2528. [Google Scholar] [CrossRef]
- DIN German Institute for Standardization. DIN EN ISO 3923-1—Metallic Powders—Determination of Apparent Density—Part 1: Funnel Method; DIN German Institute for Standardization: Berlin, Germany, 2010. [Google Scholar]
- Klassen, A.; Bauereiß, A.; Körner, C. Modelling of electron beam absorption in complex geometries. J. Phys. D Appl. Phys. 2014, 47, 065307. [Google Scholar] [CrossRef]
- Attar, E.; Körner, C. Lattice Boltzmann method for dynamic wetting problems. J. Colloid Interface Sci. 2009, 335, 84–93. [Google Scholar] [CrossRef] [PubMed]
- Klassen, A.; Scharowsky, T.; Körner, C. Evaporation model for beam based additive manufacturing using free surface lattice Boltzmann methods. J. Phys. D Appl. Phys. 2014, 47, 275303. [Google Scholar] [CrossRef]
- Klassen, A.; Forster, V.E.; Körner, C. A multi-component evaporation model for beam melting processes. Model. Simul. Mater. Sci. Eng. 2017, 25, 025003. [Google Scholar] [CrossRef]
- Rai, A.; Markl, M.; Körner, C. A coupled Cellular Automaton-Lattice Boltzmann model for grain structure simulation during additive manufacturing. Comput. Mater. Sci. 2016, 124, 37–48. [Google Scholar] [CrossRef]
- Körner, C.; Thies, M.; Hofmann, T.; Thürey, N.; Rüde, U. Lattice Boltzmann Model for Free Surface Flow for Modeling Foaming. J. Stat. Phys. 2005, 121, 179–196. [Google Scholar] [CrossRef]
- Zhang, R.; Fan, H.; Chen, H. A lattice Boltzmann approach for solving scalar transport equations. Philos. Trans. R. Soc. Lond. A Math. Phys. Eng. Sci. 2011, 369, 2264–2273. [Google Scholar] [CrossRef] [PubMed]
- Bauereiß, A. Mesoskopische Simulation des Selektiven Strahlschmelzens Mittels einer Lattice Boltzmann Methode mit Dynamischer Adaptiver Gitteranpassung. Ph.D. Thesis, Friedrich-Alexander-Universität Erlangen-Nürnberg (FAU), Erlangen, Germany, 2017. submitted. [Google Scholar]
- Boivineau, M.; Cagran, C.; Doytier, D.; Eyraud, V.; Nadal, M.H.; Wilthan, B.; Pottlacher, G. Thermophysical Properties of Solid and Liquid Ti-6Al-4V (TA6V) Alloy. Int. J. Thermophys. 2006, 27, 507–529. [Google Scholar] [CrossRef]
- Li, J.J.Z.; Johnson, W.L.; Rhim, W.K. Thermal expansion of liquid Ti-6Al-4V measured by electrostatic levitation. Appl. Phys. Lett. 2006, 89, 111913. [Google Scholar] [CrossRef]
- Boyer, R.; Welsch, G.; Collings, E. Materials Properties Handbook: Titanium Alloys; ASM International: Materials Park, OH, USA, 1998. [Google Scholar]
- Rai, R.; Burgardt, P.; Milewski, J.O.; Lienert, T.J.; DebRoy, T. Heat transfer and fluid flow during electron beam welding of 21Cr-6Ni-9Mn steel and Ti-6Al-4V alloy. J. Phys. D Appl. Phys. 2009, 42, 025503. [Google Scholar] [CrossRef]
- Wunderlich, R.K. Surface Tension and Viscosity of Industrial Ti-Alloys measured by the Oscillating Drop Method on Board Parabolic Flights. High Temp. Mater. Process. 2008, 27, 401–412. [Google Scholar] [CrossRef]
- Iida, T.; Guthrie, R. The Physical Properties of Liquid Metals; Clarendon Press: Oxford, UK, 1988. [Google Scholar]
- Meakin, P.; Jullien, R. Restructuring effects in the rain model for random deposition. J. Phys. Fr. 1987, 48, 1651–1662. [Google Scholar] [CrossRef]
- Qiu, C.; Panwisawas, C.; Ward, M.; Basoalto, H.C.; Brooks, J.W.; Attallah, M.M. On the role of melt flow into the surface structure and porosity development during selective laser melting. Acta Mater. 2015, 96, 72–79. [Google Scholar] [CrossRef]
- Karapatis, N.; Egger, G.; Gygax, P.; Glardon, R. Optimization of powder layer density in selective laser sintering. In Proceedings of the Annual International Solid Freeform Fabrication Symposium, Austin, TX, USA, 9–11 August 1999; pp. 255–263. [Google Scholar]
- German, R.M. Prediction of sintered density for bimodal powder mixtures. Metall. Trans. A 1992, 23, 1455–1465. [Google Scholar] [CrossRef]
- Nasato, D.S.; Pöschel, T.; Parteli, E.J.R. Effect of vibrations applied to the transport roller in the quality of the powder bed during additive manufacturing. In Proceedings of the International Conference on Additive Technologies, Nürnberg, Germany, 29–30 November 2016; pp. 260–265. [Google Scholar]

| Parameter | Value | Reference |
|---|---|---|
| Density | 4122 | [45] |
| Solidus temperature | 1878 | [46] |
| Liquidus temperature | 1928 | [46] |
| Boiling temperature | 3315 | [47] |
| Dynamic viscosity | 4.76 | [48] |
| Surface tension | 1.52 | [48] |
| Specific heat (liquid) | 670 | [44] |
| Specific heat (solid) | 1126 | [44] |
| Thermal conductivity (solid) at 1200 | 17.2 | [44] |
| Thermal conductivity (solid) at 1900 | 27.4 | [44] |
| Thermal conductivity (liquid) at 2100 | 31.8 | [44] |
| Thermal conductivity (liquid) at 2600 | 40.9 | [44] |
| Latent heat of fusion | 290 | [44] |
| Latent heat of vaporization | 9820 | [49] |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rausch, A.M.; Küng, V.E.; Pobel, C.; Markl, M.; Körner, C. Predictive Simulation of Process Windows for Powder Bed Fusion Additive Manufacturing: Influence of the Powder Bulk Density. Materials 2017, 10, 1117. https://doi.org/10.3390/ma10101117
Rausch AM, Küng VE, Pobel C, Markl M, Körner C. Predictive Simulation of Process Windows for Powder Bed Fusion Additive Manufacturing: Influence of the Powder Bulk Density. Materials. 2017; 10(10):1117. https://doi.org/10.3390/ma10101117
Chicago/Turabian StyleRausch, Alexander M., Vera E. Küng, Christoph Pobel, Matthias Markl, and Carolin Körner. 2017. "Predictive Simulation of Process Windows for Powder Bed Fusion Additive Manufacturing: Influence of the Powder Bulk Density" Materials 10, no. 10: 1117. https://doi.org/10.3390/ma10101117






