Ferrocene Molecular Architectures Grafted on Si(111): A Theoretical Calculation of the Standard Oxidation Potentials and Electron Transfer Rate Constant
Abstract
:1. Introduction
2. Computational Details
3. Charge Transfer Dynamics
4. Results and Discussion
4.1. Standard Oxidation Potential Calculation
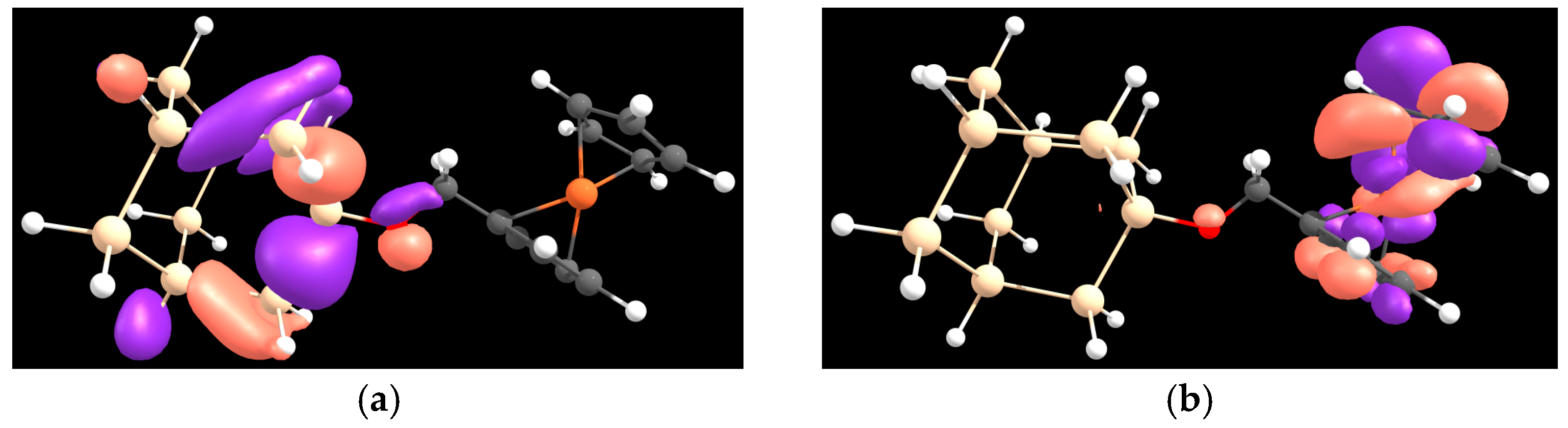
4.2. Dynamics
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Nalwa, H.S. Preface. In Silicon-Based Material and Devices; Academic Press: Burlington, UK, 2001; ISBN 978-0-12-513909-0. [Google Scholar]
- Shimura, F. Semiconductor Silicon Crystal Technology; Academic Press: Burlington, UK, 1989; ISBN 978-0-12-640045-8. [Google Scholar]
- Korotcenkov, G. Porous Silicon from Formation to Application: Formation and Properties; CRC Press: Boca Raton, FL, USA, 2015; Volume 1, ISBN 978-1-4822-6454-8. [Google Scholar]
- Chrostowski, L.; Hochberg, M. Silicon Photonics Design Devices Systems|Electronic, Optoelectronic Devices, and Nanotechnology; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Rizal, C.; Niraula, B. Nanoscale Silicon Waveguide Based Thermo-Optic Sensor Using a Compact Mach-Zehnder Interferometer. Preprints 2016. [Google Scholar] [CrossRef]
- Rizal, C.; Niraula, B. A Compact, fast, and low loss MZI-based thermo-optical switch on SOI platform. Opt. Commun. 2017. in printing. [Google Scholar]
- Lopinski, G.P.; Fortier, T.M.; Moffatt, D.J.; Wolkow, R.A. Multiple bonding geometries and binding state conversion of benzene/Si(100). J. Vac. Sci. Technol. A 1998, 16, 1037–1042. [Google Scholar] [CrossRef]
- Hamers, R.J.; Hovis, J.S.; Lee, S.; Liu, H.; Shan, J. Formation of Ordered, Anisotropic Organic Monolayers on the Si(001) Surface. J. Phys. Chem. B 1997, 101, 1489–1492. [Google Scholar] [CrossRef]
- Lopinski, G.P.; Moffatt, D.J.; Wayner, D.D.M.; Wolkow, R.A. Determination of the absolute chirality of individual adsorbed molecules using the scanning tunnelling microscope. Nature 1998, 392, 909–911. [Google Scholar] [CrossRef]
- Buriak, J.M. Organometallic Chemistry on Silicon and Germanium Surfaces. Chem. Rev. 2002, 102, 1271–1308. [Google Scholar] [CrossRef] [PubMed]
- Ciampi, S.; Harper, J.B.; Gooding, J.J. Wet chemical routes to the assembly of organic monolayers on silicon surfaces via the formation of Si–C bonds: Surface preparation, passivation and functionalization. Chem. Soc. Rev. 2010, 39, 2158–2183. [Google Scholar] [CrossRef] [PubMed]
- Allongue, P.; de Villeneuve, C.H.; Pinson, J.; Ozanam, F.; Chazalviel, J.N.; Wallart, X. Organic monolayers on Si(111) by electrochemical method. Electrochim. Acta 1998, 43, 2791–2798. [Google Scholar] [CrossRef]
- Hartig, P.; Rappich, J.; Dittrich, T. Engineering of Si surfaces by electrochemical grafting of p-nitrobenzene molecules. Appl. Phys. Lett. 2002, 80, 67–69. [Google Scholar] [CrossRef]
- Finklea, H.O. Self-Assembled Monolayers on Electrodes. In Encyclopedia of Analytical Chemistry; John Wiley & Sons, Ltd.: New York, NY, USA, 2006; ISBN 978-0-470-02731-8. [Google Scholar]
- Tsierkezos, N.G. Cyclic Voltammetric Studies of Ferrocene in Nonaqueous Solvents in the Temperature Range from 248.15 to 298.15 K. J. Solut. Chem. 2007, 36, 289–302. [Google Scholar] [CrossRef]
- Slinker, J.D.; Muren, N.B.; Renfrew, S.E.; Barton, J.K. DNA Charge Transport over 34 nm. Nat. Chem. 2011, 3, 230–235. [Google Scholar] [CrossRef] [PubMed]
- Chidsey, C.E.D.; Bertozzi, C.R.; Putvinski, T.M.; Mujsce, A.M. Coadsorption of ferrocene-terminated and unsubstituted alkanethiols on gold: Electroactive self-assembled monolayers. J. Am. Chem. Soc. 1990, 112, 4301–4306. [Google Scholar] [CrossRef]
- Wayner, D.D.M.; Wolkow, R.A. Organic modification of hydrogen terminated silicon surfaces 1. J. Chem. Soc. Perkin Trans. 2002, 2, 23–34. [Google Scholar] [CrossRef]
- Roth, K.M.; Yasseri, A.A.; Liu, Z.; Dabke, R.B.; Malinovskii, V.; Schweikart, K.-H.; Yu, L.; Tiznado, H.; Zaera, F.; Lindsey, J.S.; et al. Measurements of Electron-Transfer Rates of Charge-Storage Molecular Monolayers on Si(100). Toward Hybrid Molecular/Semiconductor Information Storage Devices. J. Am. Chem. Soc. 2003, 125, 505–517. [Google Scholar] [CrossRef] [PubMed]
- Fabre, B.; Hauquier, F. Single-Component and Mixed Ferrocene-Terminated Alkyl Monolayers Covalently Bound to Si(111) Surfaces. J. Phys. Chem. B 2006, 110, 6848–6855. [Google Scholar] [CrossRef] [PubMed]
- Hauquier, F.; Ghilane, J.; Fabre, B.; Hapiot, P. Conducting Ferrocene Monolayers on Nonconducting Surfaces. J. Am. Chem. Soc. 2008, 130, 2748–2749. [Google Scholar] [CrossRef] [PubMed]
- Calborean, A.; Buimaga-Iarinca, L.; Graur, F. DFT charge transfer of hybrid molecular ferrocene/Si structures. Phys. Scr. 2015, 90, 055803. [Google Scholar] [CrossRef]
- Nitzan, A. Chemical Dynamics in Condensed Phases Relaxation, Transfer and Reactions in Condensed Molecular Systems; Oxford University Press: Oxford, NY, USA, 2006; ISBN 978-0-19-152387-8. [Google Scholar]
- Paul, A.; Watson, R.M.; Wierzbinski, E.; Davis, K.L.; Sha, A.; Achim, C.; Waldeck, D.H. Distance Dependence of the Charge Transfer Rate for Peptide Nucleic Acid Monolayers. J. Phys. Chem. B 2010, 114, 14140–14148. [Google Scholar] [CrossRef] [PubMed]
- Bard, A.J.; Faulkner, L.R. Electrochemical Methods: Fundamentals and Applications, 2nd ed.; Wiley: New York, NY, USA, 2001; ISBN 978-0-471-04372-0. [Google Scholar]
- Fontanesi, C.; Tassinari, F.; Parenti, F.; Cohen, H.; Mondal, P.C.; Kiran, V.; Giglia, A.; Pasquali, L.; Naaman, R. New One-Step Thiol Functionalization Procedure for Ni by Self-Assembled Monolayers. Langmuir 2015. [Google Scholar] [CrossRef] [PubMed]
- Vanossi, D.; Benassi, R.; Parenti, F.; Tassinari, F.; Giovanardi, R.; Florini, N.; De Renzi, V.; Arnaud, G.; Fontanesi, C. Functionalization of glassy carbon surface by means of aliphatic and aromatic amino acids. An experimental and theoretical integrated approach. Electrochim. Acta 2012, 75, 49–55. [Google Scholar] [CrossRef]
- Tassinari, F.; Vanossi, D.; Mucci, A.; Parenti, F.; Fontanesi, C. Regiochemistry in the electrochemical assisted grafting of glassy carbon. With focus on sterical hindrance of lateral chains in the electroreduction process of multi-functionalized bithiophene. J. Electroanal. Chem. 2013. [Google Scholar] [CrossRef]
- Fontanesi, C.; Bortolotti, C.A.; Vanossi, D.; Marcaccio, M. Dissociation Dynamics of Asymmetric Alkynyl(Aryl)Iodonium Radicals: An ab Initio DRC Approach to Predict the Surface Functionalization Selectivity. J. Phys. Chem. A 2011, 115, 11715–11722. [Google Scholar] [CrossRef] [PubMed]
- Marcus, R.A.; Sumi, H. Solvent dynamics and vibrational effects in electron transfer reactions. J. Electroanal. Chem. Interfac. Electrochem. 1986, 204, 59–67. [Google Scholar] [CrossRef]
- Marcus, R.A. Electron transfer reactions in chemistry. Theory and experiment. Rev. Mod. Phys. 1993, 65, 599–610. [Google Scholar] [CrossRef]
- Wu, Q.; Van Voorhis, T. Direct optimization method to study constrained systems within density-functional theory. Phys. Rev. A 2005, 72, 024502. [Google Scholar] [CrossRef]
- Wu, Q.; Van Voorhis, T. Direct Calculation of Electron Transfer Parameters through Constrained Density Functional Theory. J. Phys. Chem. A 2006, 110, 9212–9218. [Google Scholar] [CrossRef] [PubMed]
- Dalchiele, E.A.; Aurora, A.; Bernardini, G.; Cattaruzza, F.; Flamini, A.; Pallavicini, P.; Zanoni, R.; Decker, F. XPS and electrochemical studies of ferrocene derivatives anchored on n- and p-Si(100) by Si–O or Si–C bonds. J. Electroanal. Chem. 2005, 579, 133–142. [Google Scholar] [CrossRef]
- Decker, F.; Cattaruzza, F.; Coluzza, C.; Flamini, A.; Marrani, A.G.; Zanoni, R.; Dalchiele, E.A. Electrochemical Reversibility of Vinylferrocene Monolayers Covalently Attached on H-Terminated p-Si(100). J. Phys. Chem. B 2006, 110, 7374–7379. [Google Scholar] [CrossRef] [PubMed]
- Lu, M.; He, T.; Tour, J.M. Surface Grafting of Ferrocene-Containing Triazene Derivatives on Si(100). Chem. Mater. 2008, 20, 7352–7355. [Google Scholar] [CrossRef]
- Marrani, A.G.; Dalchiele, E.A.; Zanoni, R.; Decker, F.; Cattaruzza, F.; Bonifazi, D.; Prato, M. Functionalization of Si(100) with ferrocene derivatives via “click” chemistry. Electrochim. Acta 2008, 53, 3903–3909. [Google Scholar] [CrossRef]
- Zigah, D.; Herrier, C.; Scheres, L.; Giesbers, M.; Fabre, B.; Hapiot, P.; Zuilhof, H. Tuning the Electronic Communication between Redox Centers Bound to Insulating Surfaces. Angew. Chem. Int. Ed. 2010, 49, 3157–3160. [Google Scholar] [CrossRef] [PubMed]
- Riveros, G.; González, G.; Chornik, B. Modification of silicon surface with redox molecules derived from ferrocene. J. Braz. Chem. Soc. 2010, 21, 25–32. [Google Scholar] [CrossRef]
- Kondov, I.; Cizek, M.; Benesch, C.; Wang, H.; Thoss, M. Quantum Dynamics of Photoinduced Electron-Transfer Reactions in Dye-Semiconductor Systems: First-Principles Description and Application to Coumarin 343-TiO2. J. Phys. Chem. C 2007, 111, 11970–11981. [Google Scholar] [CrossRef]
- Li, J.; Kondov, I.; Wang, H.; Thoss, M. Theoretical Study of Photoinduced Electron-Transfer Processes in the Dye-Semiconductor System Alizarin-TiO2. J. Phys. Chem. C 2010, 114, 18481–18493. [Google Scholar] [CrossRef]
- May, V.; Kuhn, O. Charge and Energy Transfer Dynamics in Molecular Systems, 3rd ed.; May, V., Kuhn, O., Eds.; Wiley: New York, NY, USA, 2011. [Google Scholar]
- Aliev, A.E.; Shin, H.W. Nanostructured materials for electrochromic devices. Solid State Ion. 2002, 154, 425–431. [Google Scholar] [CrossRef]
- Rakshit, T.; Liang, G.-C.; Ghosh, A.W.; Datta, S. Silicon-based Molecular Electronics. Nano Lett. 2004, 4, 1803–1807. [Google Scholar] [CrossRef]
- Shim, G.H.; Han, M.G.; Sharp-Norton, J.C.; Creager, S.E.; Foulger, S.H. Inkjet-printed electrochromic devices utilizing polyaniline–silica and poly(3,4-ethylenedioxythiophene)–silica colloidal composite particles. J. Mater. Chem. 2008, 18, 594–601. [Google Scholar] [CrossRef]
- Ribeiro, T.; Baleizão, C.; Farinha, J.P.S. Functional Films from Silica/Polymer Nanoparticles. Materials 2014, 7, 3881–3900. [Google Scholar] [CrossRef] [PubMed]
- Valiev, M.; Bylaska, E.J.; Govind, N.; Kowalski, K.; Straatsma, T.P.; Van Dam, H.J.J.; Wang, D.; Nieplocha, J.; Apra, E.; Windus, T.L.; et al. NWChem: A comprehensive and scalable open-source solution for large scale molecular simulations. Comput. Phys. Commun. 2010, 181, 1477–1489. [Google Scholar] [CrossRef]
- Granovsky, A.A. Firefly Version 8.0.0. Available online: http://classic.chem.msu.su/gran/firefly/index.html (accessed on 21 October 2016).
- Schmidt, M.W.; Baldridge, K.K.; Boatz, J.A.; Elbert, S.T.; Gordon, M.S.; Jensen, J.H.; Koseki, S.; Matsunaga, N.; Nguyen, K.A.; Su, S.; et al. General atomic and molecular electronic structure system. J. Comput. Chem. 1993, 14, 1347–1363. [Google Scholar] [CrossRef]
- Winget, P.; Weber, E.J.; Cramer, C.J.; Truhlar, D.G. Computational electrochemistry: Aqueous one-electron oxidation potentials for substituted anilines. Phys. Chem. Chem. Phys. 2000, 2, 1231–1239. [Google Scholar] [CrossRef]
- Winget, P.; Cramer, C.J.; Truhlar, D.G. Computation of equilibrium oxidation and reduction potentials for reversible and dissociative electron-transfer reactions in solution. Theor. Chem. Acc. 2004, 112. [Google Scholar] [CrossRef]
- Cramer, C.J. Essentials of Computational Chemistry: Theories and Models; John Wiley & Sons: Singapore, 2005; ISBN 978-0-470-09183-8. [Google Scholar]
- Barone, V.; Cossi, M. Quantum Calculation of Molecular Energies and Energy Gradients in Solution by a Conductor Solvent Model. J. Phys. Chem. A 1998, 102, 1995–2001. [Google Scholar] [CrossRef]
- Bruno, C.; Benassi, R.; Passalacqua, A.; Paolucci, F.; Fontanesi, C.; Marcaccio, M.; Jackson, E.A.; Scott, L.T. Electrochemical and Theoretical Investigation of Corannulene Reduction Processes. J. Phys. Chem. B 2009, 113, 1954–1962. [Google Scholar] [CrossRef] [PubMed]
- Bruno, C.; Paolucci, F.; Marcaccio, M.; Benassi, R.; Fontanesi, C.; Mucci, A.; Parenti, F.; Preti, L.; Schenetti, L.; Vanossi, D. Experimental and Theoretical Study of the p- and n-Doped States of Alkylsulfanyl Octithiophenes. J. Phys. Chem. B 2010, 114, 8585–8592. [Google Scholar] [CrossRef] [PubMed]
- Cigarini, L.; Vanossi, D.; Bondioli, F.; Fontanesi, C. A novel synthetic strategy for magnetite-type compounds. A combined experimental and DFT-computational study. Phys. Chem. Chem. Phys. 2015, 17, 20522–20529. [Google Scholar] [CrossRef] [PubMed]
- Farazdel, A.; Dupuis, M.; Clementi, E.; Aviram, A. Electric-field induced intramolecular electron transfer in spiro .pi.-electron systems and their suitability as molecular electronic devices. A theoretical study. J. Am. Chem. Soc. 1990, 112, 4206–4214. [Google Scholar] [CrossRef]
- Ma, S.-H.; Zhang, X.-D.; Xu, H.; Shen, L.-L.; Zhang, X.-K.; Zhang, Q.-Y. Theoretical studies on the self-exchange electron-transfer reaction between 2,3-dicyano-5,6-dichloro-p-benzoquinone (DDQ) and its radical anion DDQ−. J. Photochem. Photobiol. Chem. 2001, 139, 97–104. [Google Scholar] [CrossRef]
- Vanossi, D.; Pigani, L.; Seeber, R.; Ferrarini, P.; Baraldi, P.; Fontanesi, C. Electropolymerization of ortho-phenylenediamine. Structural characterisation of the resulting polymer film and its interfacial capacitive behaviour. J. Electroanal. Chem. 2013. [Google Scholar] [CrossRef]
- Noviandri, I.; Brown, K.N.; Fleming, D.S.; Gulyas, P.T.; Lay, P.A.; Masters, A.F.; Phillips, L. The Decamethylferrocenium/Decamethylferrocene Redox Couple: A Superior Redox Standard to the Ferrocenium/Ferrocene Redox Couple for Studying Solvent Effects on the Thermodynamics of Electron Transfer. J. Phys. Chem. B 1999, 103, 6713–6722. [Google Scholar] [CrossRef]
- Trasatti, S. The “absolute” electrode potential—The end of the story. Electrochim. Acta 1990, 35, 269–271. [Google Scholar] [CrossRef]
- Tissandier, M.D.; Cowen, K.A.; Feng, W.Y.; Gundlach, E.; Cohen, M.H.; Earhart, A.D.; Coe, J.V.; Tuttle, T.R. The Proton’s Absolute Aqueous Enthalpy and Gibbs Free Energy of Solvation from Cluster-Ion Solvation Data. J. Phys. Chem. A 1998, 102, 7787–7794. [Google Scholar] [CrossRef]
- Tripkovic, V.; Björketun, M.E.; Skúlason, E.; Rossmeisl, J. Standard hydrogen electrode and potential of zero charge in density functional calculations. Phys. Rev. B 2011, 84, 115452. [Google Scholar] [CrossRef]
- Mishra, D.; Markus, T.Z.; Naaman, R.; Kettner, M.; Gohler, B.; Zacharias, H.; Friedman, N.; Sheves, M.; Fontanesi, C. Spin-dependent electron transmission through bacteriorhodopsin embedded in purple membrane. Proc. Natl. Acad. Sci. USA 2013, 110, 14872–14876. [Google Scholar] [CrossRef] [PubMed]
- Kettner, M.; Göhler, B.; Zacharias, H.; Mishra, D.; Kiran, V.; Naaman, R.; Fontanesi, C.; Waldeck, D.H.; Sęk, S.; Pawłowski, J.; et al. Spin Filtering in Electron Transport Through Chiral Oligopeptides. J. Phys. Chem. C 2014. [Google Scholar] [CrossRef]
- Li, F.; Basile, V.M.; Rose, M.J. Electron Transfer through Surface-Grown, Ferrocene-Capped Oligophenylene Molecular Wires (5–50 Å) on n-Si(111) Photoelectrodes. Langmuir 2015, 31, 7712–7716. [Google Scholar] [CrossRef] [PubMed]
- Sek, S.; Palys, B.; Bilewicz, R. Contribution of Intermolecular Interactions to Electron Transfer through Monolayers of Alkanethiols Containing Amide Groups. J. Phys. Chem. B 2002, 106, 5907–5914. [Google Scholar] [CrossRef]
- Sek, S.; Swiatek, K.; Misicka, A. Electrical Behavior of Molecular Junctions Incorporating α-Helical Peptide. J. Phys. Chem. B 2005, 109, 23121–23124. [Google Scholar] [CrossRef] [PubMed]
- Bui, P.T.; Nishino, T. Electron transfer through coordination bond interaction between single molecules: conductance switching by a metal ion. Phys. Chem. Chem. Phys. 2014, 16, 5490–5494. [Google Scholar] [CrossRef] [PubMed]
- Fontanesi, C.; Camurri, G.; Tassinari, F. On the co-adsorption process of sodium dodecyl sulfate and sodium dodecylbenzenesulfonate on a 1-decanethiol-functionalized Au electrode, as a corrosion inhibiting mimic process. J. Appl. Electrochem. 2012, 43, 101–106. [Google Scholar] [CrossRef]
- Rose, D.A.; Benjamin, I. Molecular dynamics of adiabatic and nonadiabatic electron transfer at the metal-water interface. J. Chem. Phys. 1994, 100, 3545–3555. [Google Scholar] [CrossRef]
- Launay, J.-P.; Verdaguer, M. Electrons in Molecules: From Basic Principles to Molecular Electronics; Oxford University Press: Oxford, NY, USA, 2013; ISBN 978-0-19-929778-8. [Google Scholar]
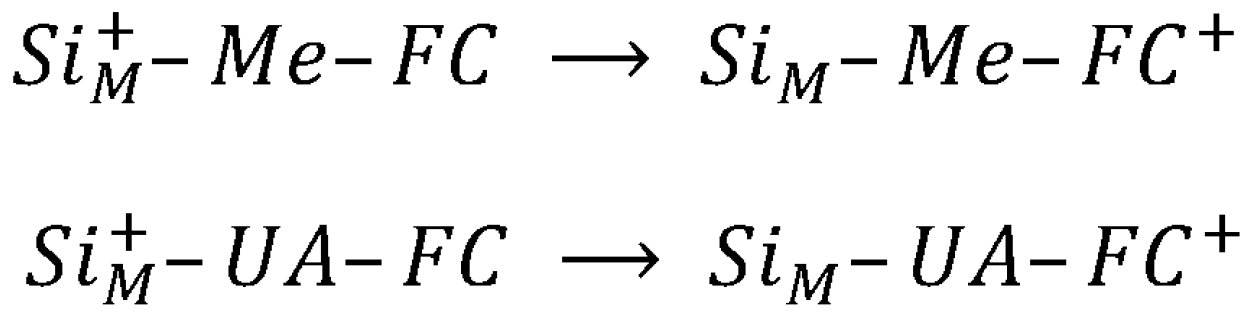
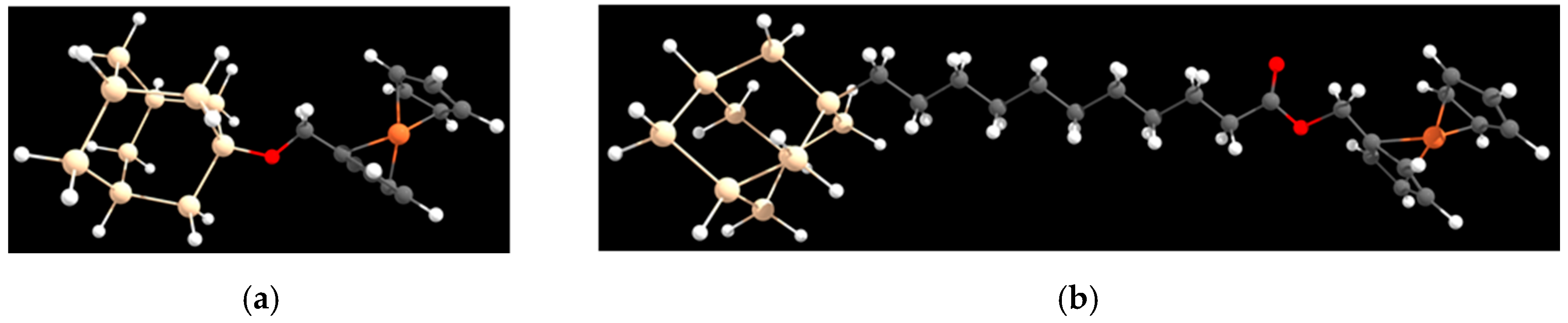

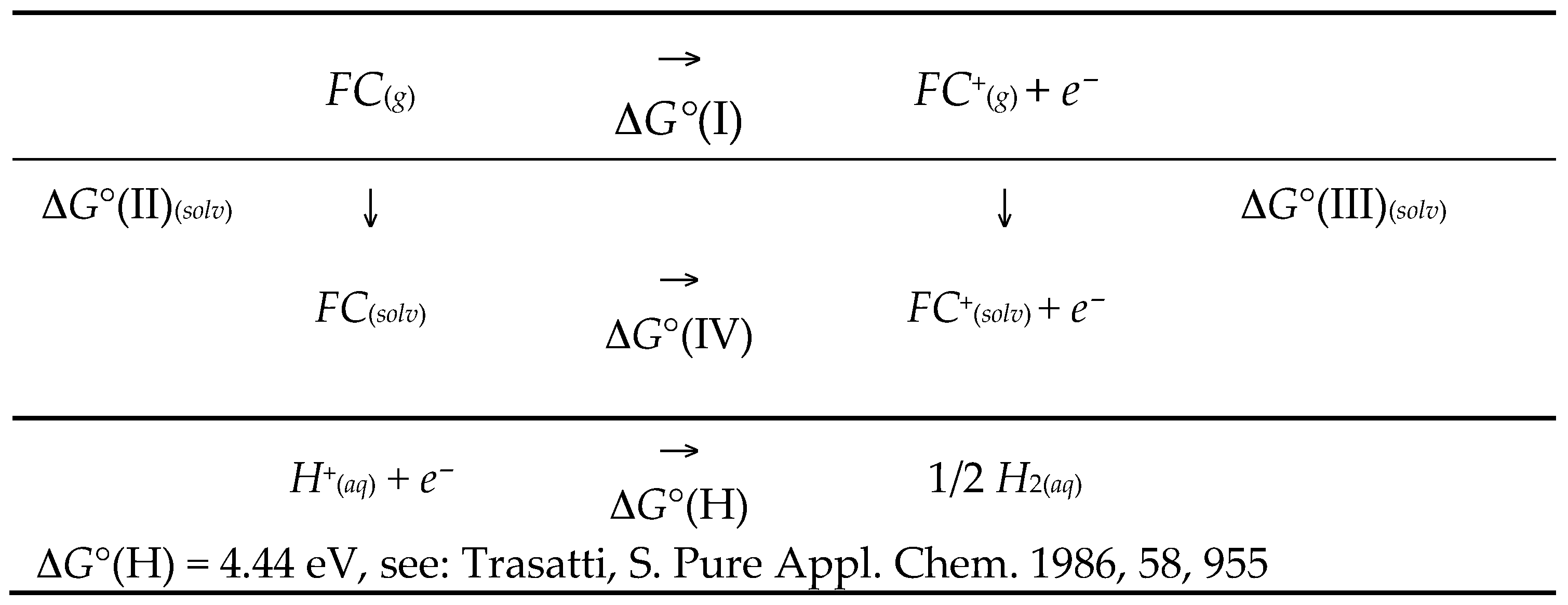
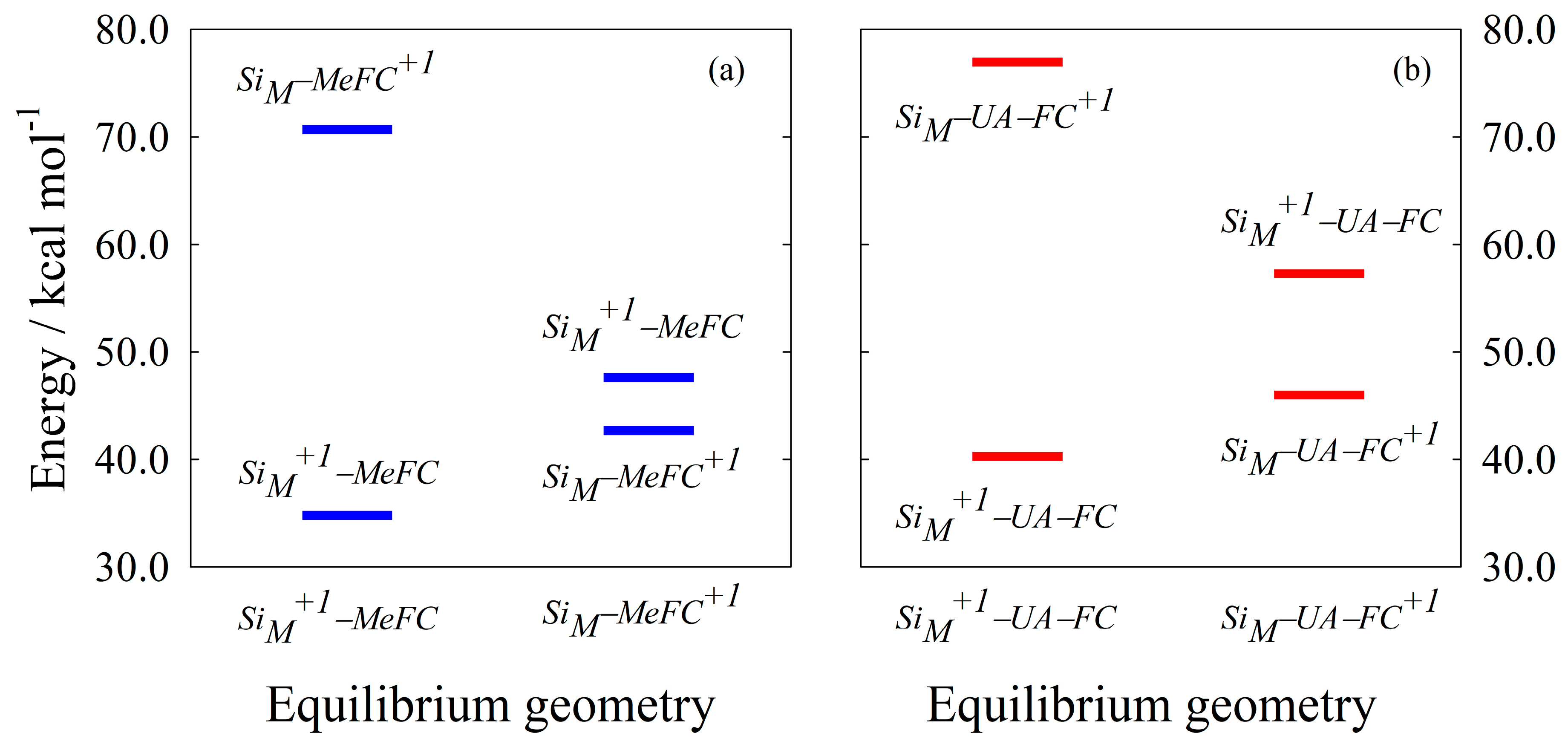
| Redox System | Energy Ox Species, (a.u.) | ∆G°(III)(solv), (kcal mol−1) | Energy Red Species, (a.u.) | ∆G°(II)(solv), (kcal mol−1) | ||
|---|---|---|---|---|---|---|
| Total | Elec. (a) | Total | Elec. (a) | |||
| −5172.168587 | −5.78 | −47.14 | −5172.41199 | 35.55 | −5.81 | |
| −4666.305597 | −5.65 | −42.34 | −4666.544377 | 33.21 | −3.48 | |
| −1649.745848 | −40.38 | −44.53 | −1649.986325 | 1.43 | −2.66 | |
| Redox System | (a), () | (b), () | (a), () | , () |
|---|---|---|---|---|
| SiM–Me–FC | 28.9 | 22.0 | 7.93 | 0.019 |
| SiM–UA–FC | 30.9 | 40.1 | 5.71 | 10−6 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fontanesi, C.; Innocenti, M.; Vanossi, D.; Da Como, E. Ferrocene Molecular Architectures Grafted on Si(111): A Theoretical Calculation of the Standard Oxidation Potentials and Electron Transfer Rate Constant. Materials 2017, 10, 1109. https://doi.org/10.3390/ma10101109
Fontanesi C, Innocenti M, Vanossi D, Da Como E. Ferrocene Molecular Architectures Grafted on Si(111): A Theoretical Calculation of the Standard Oxidation Potentials and Electron Transfer Rate Constant. Materials. 2017; 10(10):1109. https://doi.org/10.3390/ma10101109
Chicago/Turabian StyleFontanesi, Claudio, Massimo Innocenti, Davide Vanossi, and Enrico Da Como. 2017. "Ferrocene Molecular Architectures Grafted on Si(111): A Theoretical Calculation of the Standard Oxidation Potentials and Electron Transfer Rate Constant" Materials 10, no. 10: 1109. https://doi.org/10.3390/ma10101109





