Analytical Calculation of D- and Q-axis Inductance for Interior Permanent Magnet Motors Based on Winding Function Theory
Abstract
:1. Introduction
2. Analytical Method
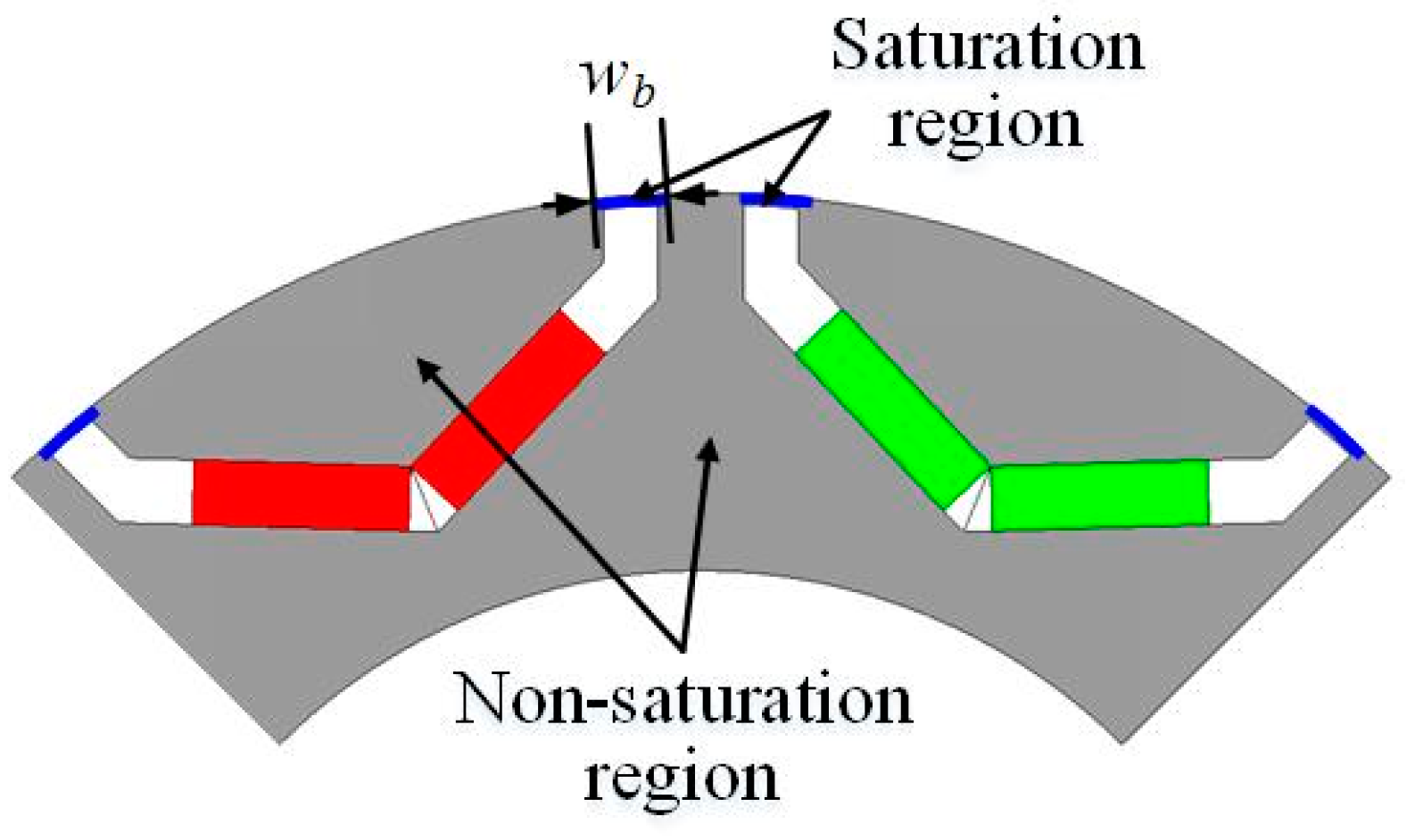
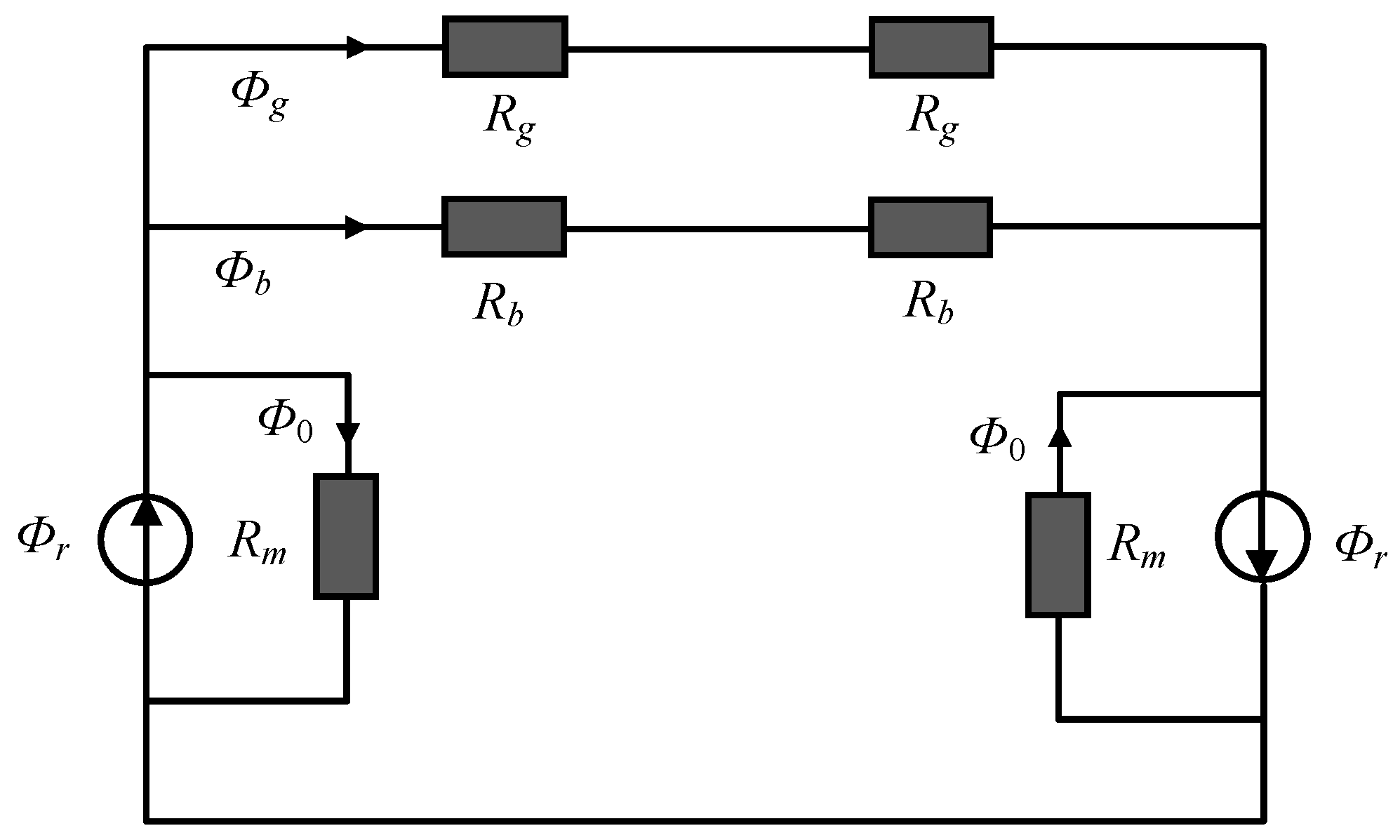
2.1. Saturation Calculation
- Firstly, the initial flux density of bridge is supposed as Bb.
- Secondly, calculate all the reluctances and fluxes according to the material B–H profile and the law of magnetic flux continuity.
- Thirdly, compare the obtained flux density of bridge Bb1 with Bb.
- Finally, adjust Bb and repeat this process until the error is satisfied.
2.2. Inductance Calculation
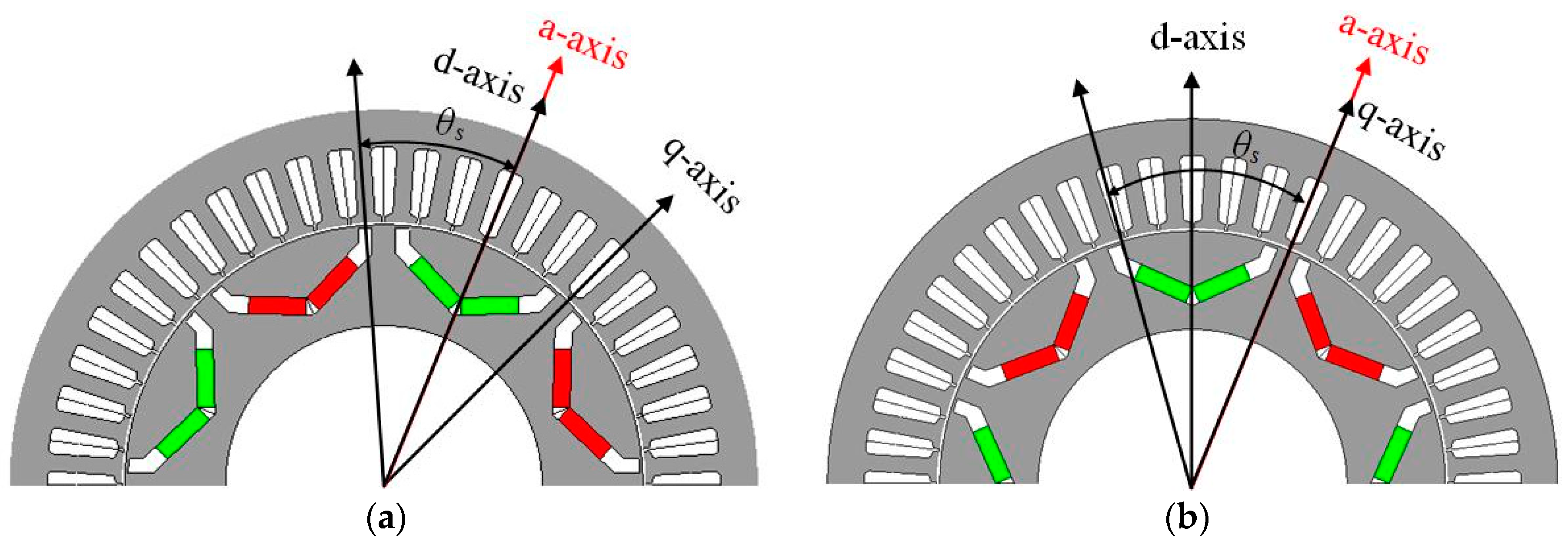
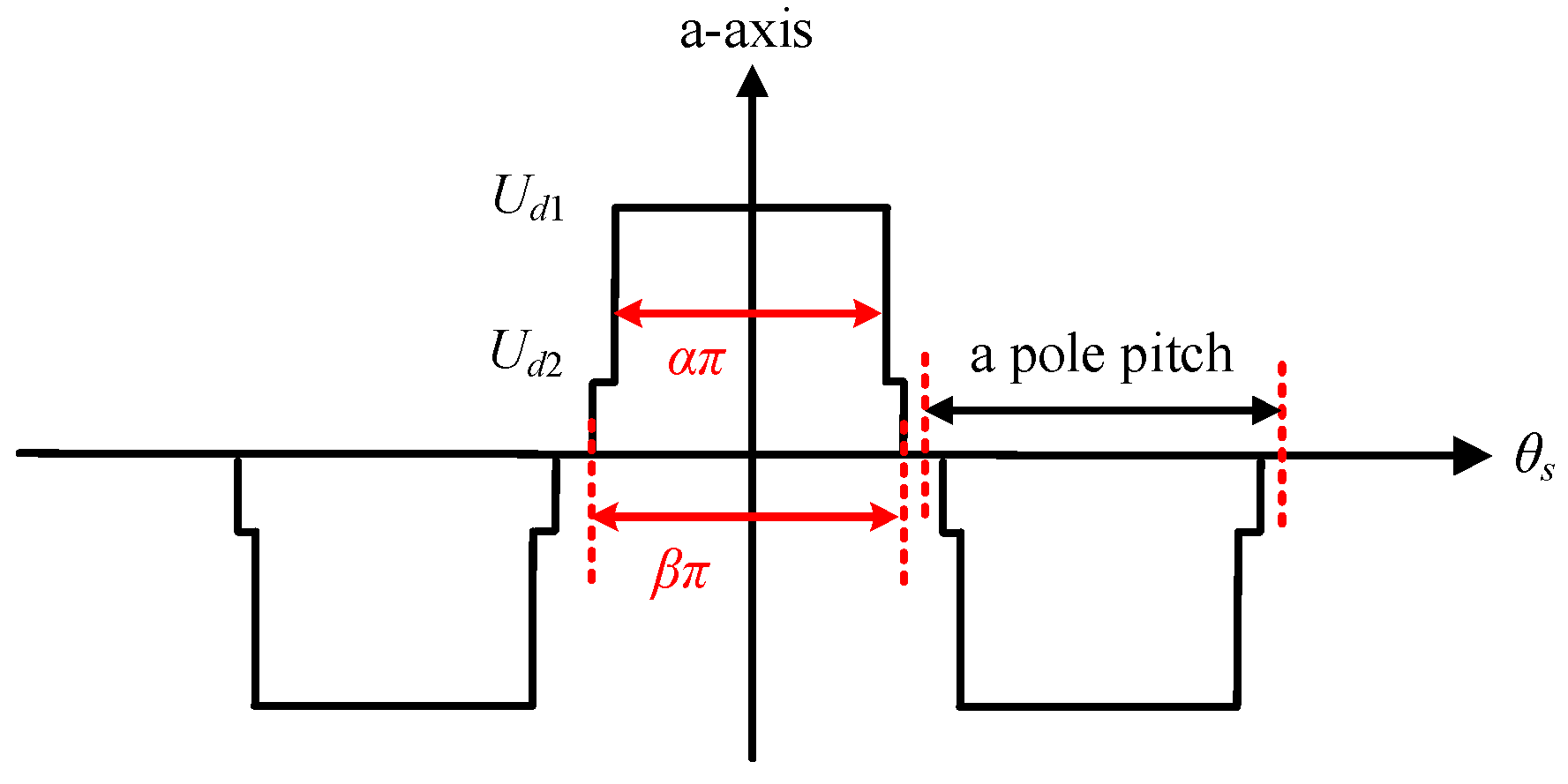
2.2.1. D-Axis Magnetic Potential
2.2.2. Q-Axis Magnetic Potential
2.2.3. D-and Q-Axis Inductances
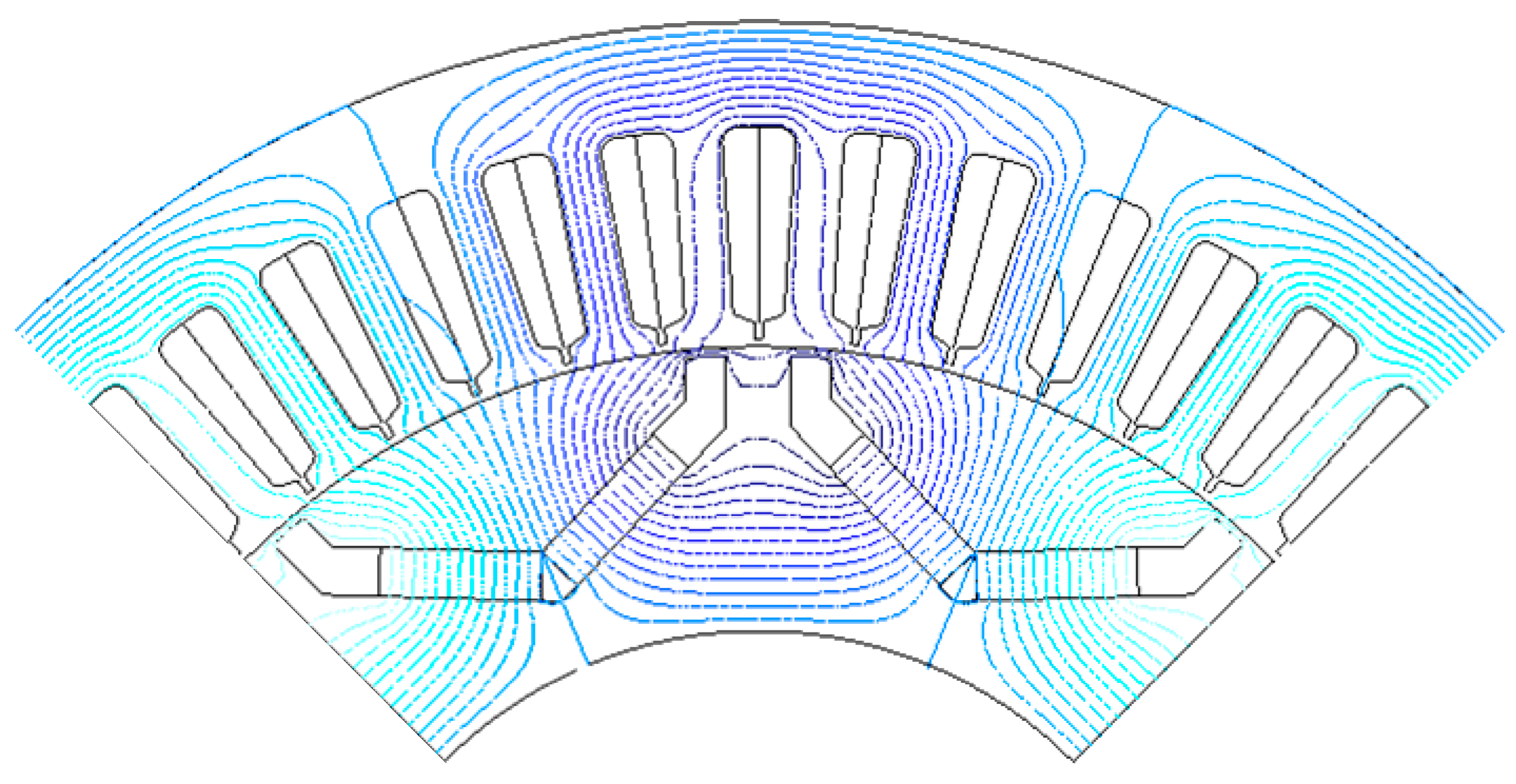
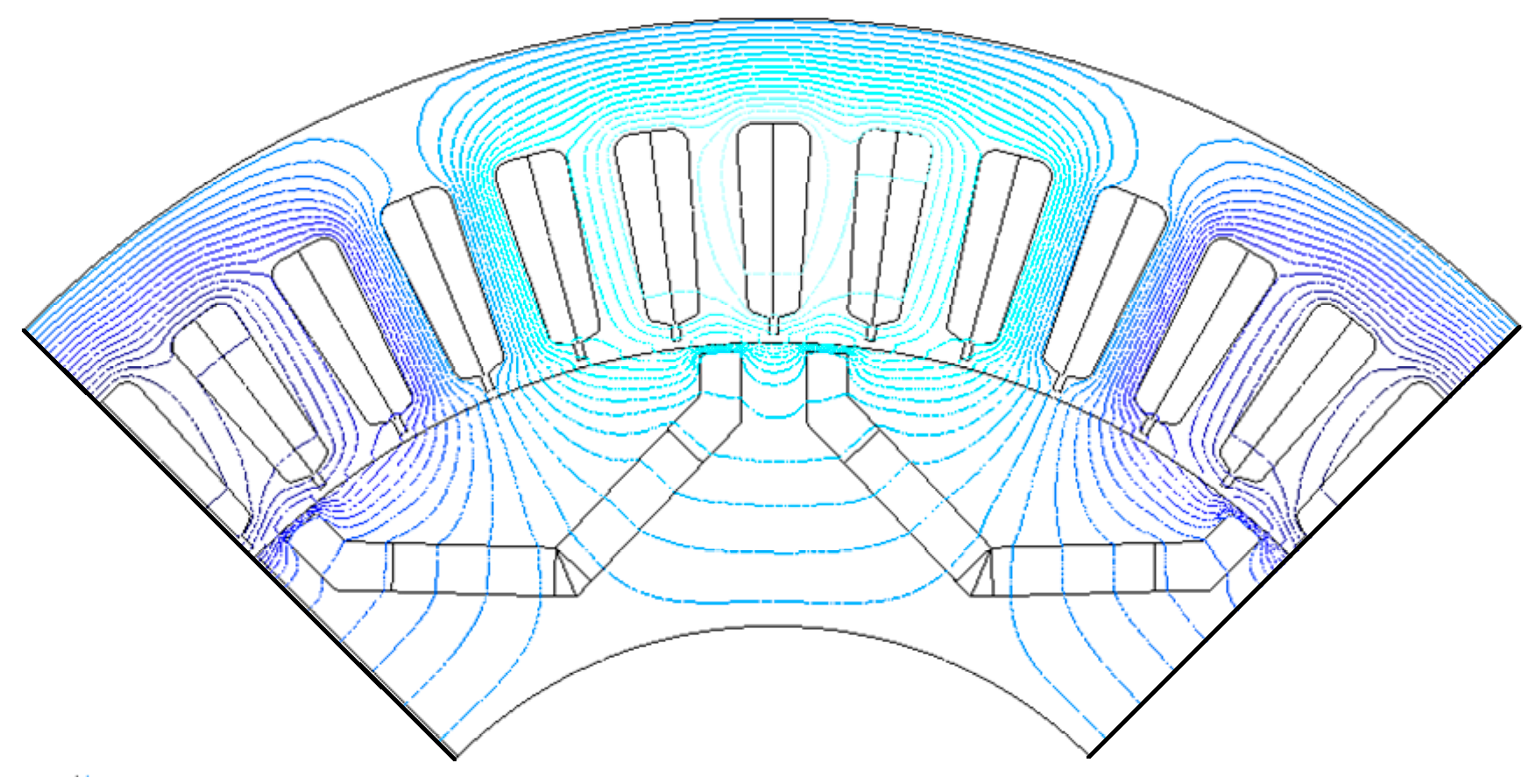
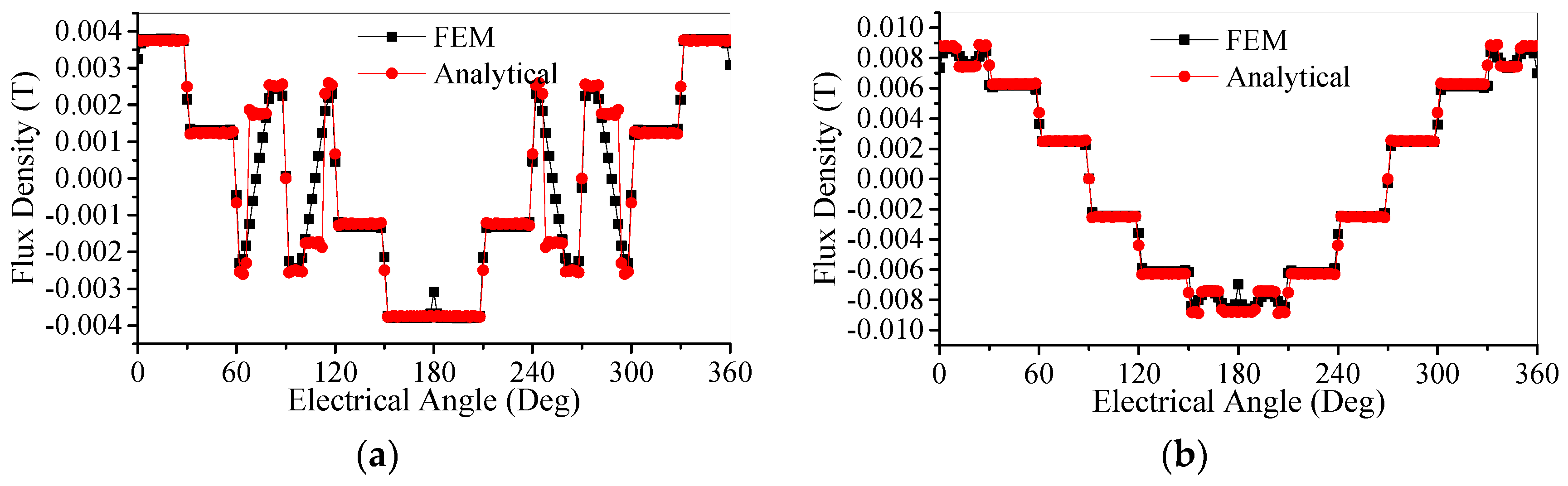
3. Results and Analysis
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wang, Y.; Niu, S.; Fu, W. Electromagnetic Performance Analysis of Novel Flux-Regulatable Permanent Magnet Machines for Wide Constant-Power Speed Range Operation. Energies 2015, 8, 13971–13984. [Google Scholar]
- Wang, K.; Zhu, Z.Q.; Ombach, G. Torque Enhancement of Surface-Mounted Permanent Magnet Machine Using Third-Order Harmonic. IEEE Trans. Magn. 2014, 50, 104–113. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, J.; Chen, Z.; Liu, X. Investigation of a Five-Phase Dual-Rotor Permanent Magnet Synchronous Motor Used for Electric Vehicles. Energies 2014, 7, 3955–3984. [Google Scholar]
- Zheng, P.; Wu, F.; Lei, Y.; Sui, Y.; Yu, B. Investigation of a Novel 24-Slot/14-Pole Six-Phase Fault-Tolerant Modular Permanent-Magnet In-Wheel Motor for Electric Vehicles. Energies 2013, 6, 4980–5002. [Google Scholar]
- Zhao, J.; Li, B.; Gu, Z. Research on an Axial Flux PMSM with Radially Sliding Permanent Magnets. Energies 2015, 8, 1663–1684. [Google Scholar]
- Wu, X.; Wang, H.; Huang, S.; Huang, K.; Wang, L. Sensorless Speed Control with Initial Rotor Position Estimation for Surface Mounted Permanent Magnet Synchronous Motor Drive in Electric Vehicles. Energies 2015, 8, 11030–11046. [Google Scholar]
- Chai, F.; Liang, P.; Pei, Y.; Cheng, S. Analytical Method for Iron Losses Reduction in Interior Permanent Magnet Synchronous Motor. IEEE Trans. Magn. 2015, 51, 1–4. [Google Scholar]
- Sun, T.; Wang, J. Extension of Virtual-Signal-Injection-Based MTPA Control for Interior Permanent-Magnet Synchronous Machine Drives Into the Field-Weakening Region. IEEE Trans. Ind. Electron. 2015, 62, 6809–6817. [Google Scholar]
- Li, Q.; Fan, T.; Wen, X.; Ning, P. An Analytical Approach to Magnet Eddy-Current Losses for Interior Permanent-Magnet Synchronous Machines during Flux Weakening. IEEE Trans. Magn. 2015, 51, 1–9. [Google Scholar]
- Gu, W.; Zhu, X.; Quan, L.; Du, Y. Design and Optimization of Permanent Magnet Brushless Machines for Electric Vehicle Applications. Energies 2015, 8, 13996–14008. [Google Scholar]
- Zhao, J.; Liu, W.; Li, B.; Liu, X.; Gao, C.; Gu, Z. Investigation of Electromagnetic, Thermal and Mechanical Characteristics of a Five-Phase Dual-Rotor Permanent-Magnet Synchronous Motor. Energies 2015, 8, 9688–9718. [Google Scholar]
- Zhang, G.; Hua, W.; Cheng, M. Steady-State Characteristics Analysis of Hybrid-Excited Flux-Switching Machines with Identical Iron Laminations. Energies 2015, 8, 12898–12916. [Google Scholar]
- Ni, R.; Wang, G.; Gui, X.; Xu, D. Investigation of d- and q-Axis Inductances Influenced by Slot-Pole Combinations Based on Axial Flux Permanent-Magnet Machines. IEEE Trans. Ind. Electron. 2014, 61, 4539–4551. [Google Scholar]
- Kallio, S.; Karttunen, J.; Peltoniemi, P.; Silventoinen, P.; Pyrhonen, O. Determination of the inductance parameters for the decoupled d-q model of double-star permanentmagnet synchronous machines. IET Electr. Power Appl. 2014, 8, 39–49. [Google Scholar]
- Soualmi, A.; Dubas, F.; Depernet, D.; Randria, A.; Espanet, C. Inductances estimation in the d-q axis for an interior permanent-magnet synchronous machines with distributed windings. In Proceeding of the 2012 2nd International Conference on Electrical Machines (ICEM), Marseille, France, 2–5 September 2012; pp. 308–314.
- Li, Q.; Shang, J. Experimental Measurement and FEM Calculations of the Inductance Parameters in SRM. In Proceeding of the 2010 First International Conference on Pervasive Computing Signal Processing and Applications (PCSPA), Harbin, China, 17–19 September 2010; pp. 1273–1276.
- Chen, X.; Wu, J. Calculation of inductances with 3-D FEM for SRM with segmental rotors and fully-picthed windings. In Proceeding of the 2014 17th International Conference on Electrical Machines and Systems (ICEMS), Hangzhou, China, 22–25 Octerber 2014; pp. 1822–1824.
- Ma, M.; Li, L.; Zhang, J.; Yu, J.; Zhang, H. Investigation of Cross-Coupling Inductances for Long-Stator PM Linear Motor Arranged in Multiple Segments. IEEE Trans. Magn. 2015, 51, 8205304. [Google Scholar]
- Kim, W.H.; Kim, M.J.; Lee, K.D.; Lee, J.J.; Han, J.H.; Jeong, T.C.; Cho, S.Y.; Lee, J. Inductance Calculation in IPMSM Considering Magnetic Saturation. IEEE Trans. Magn. 2014, 50, 4001304. [Google Scholar] [CrossRef]
- Lee, K.D.; Lee, J.; Lee, H.W. Inductance Calculation of Flux Concentrating Permanent Magnet Motor through Nonlinear Magnetic Equivalent Circuit. IEEE Trans. Magn. 2015, 51, 8204304. [Google Scholar]
- Yue, L.; Yulong, P.; Yanjun, Y.; Yanwen, S.; Feng, C. Increasing the saliency ratio of fractional slot concentrated winding interior permanent magnet synchronous motors. IET Electr. Power Appl. 2015, 9, 439–448. [Google Scholar]
- Qi, L.; Tao, F.; Xuhui, W. Armature-Reaction Magnetic Field Analysis for Interior Permanent Magnet Motor Based on Winding Function Theory. IEEE Trans. Magn. 2013, 49, 1193–1201. [Google Scholar]
- Hong, C.; Dawei, L.; Ronghai, Q.; Zhe, Z.; Jian, L. An Improved Analytical Model for Inductance Calculation of Interior Permanent Magnet Machines. IEEE Trans. Magn. 2014, 50, 7027108. [Google Scholar]
- Ponomarev, P.; Alexandrova, Y.; Petrov, I.; Lindh, P.; Lomonova, E.; Pyrh, J. Inductance Calculation of Tooth-Coil Permanent-Magnet Synchronous Machines. IEEE Trans. Ind. Electron. 2014, 61, 5966–5973. [Google Scholar] [Green Version]
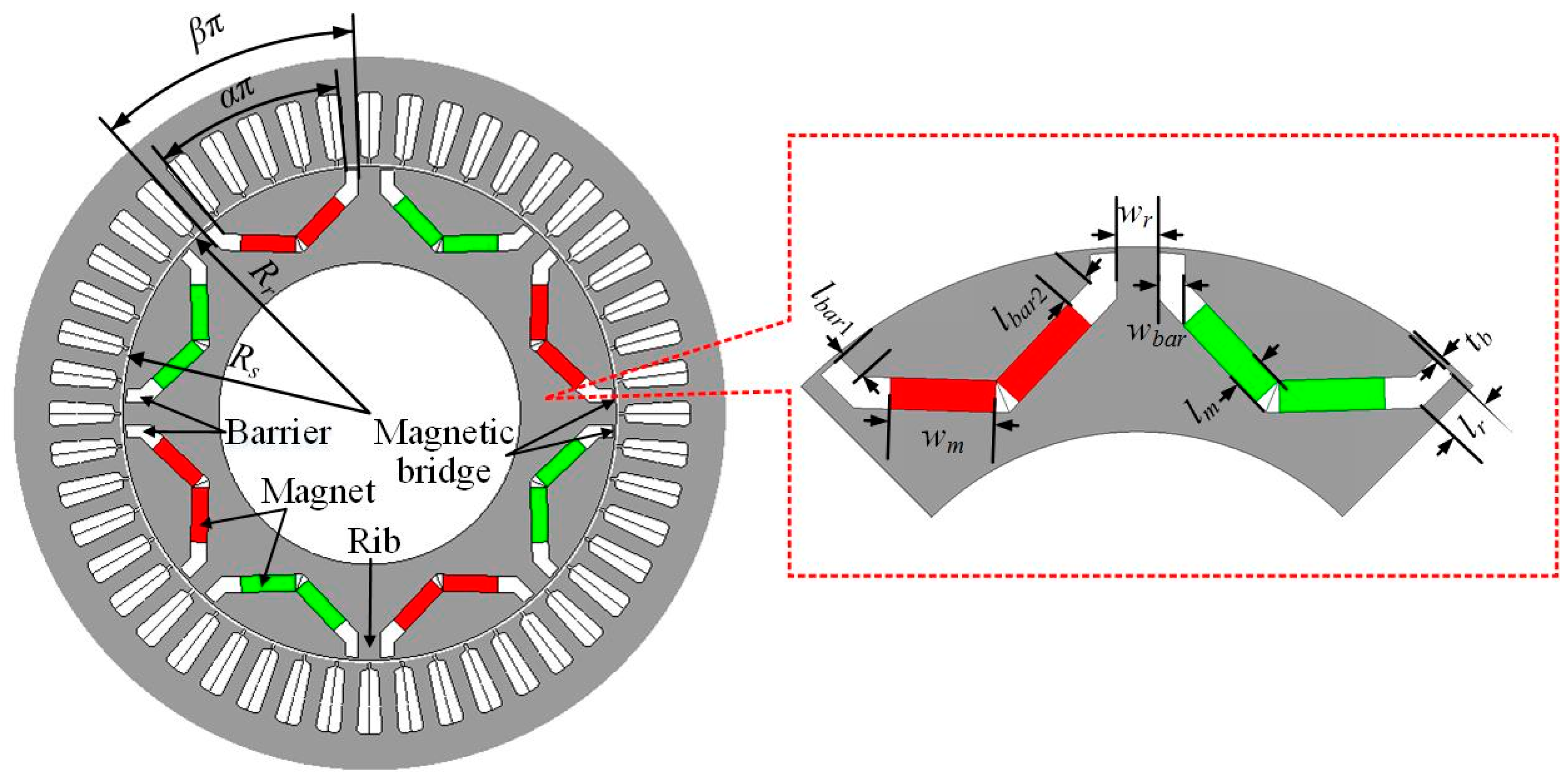

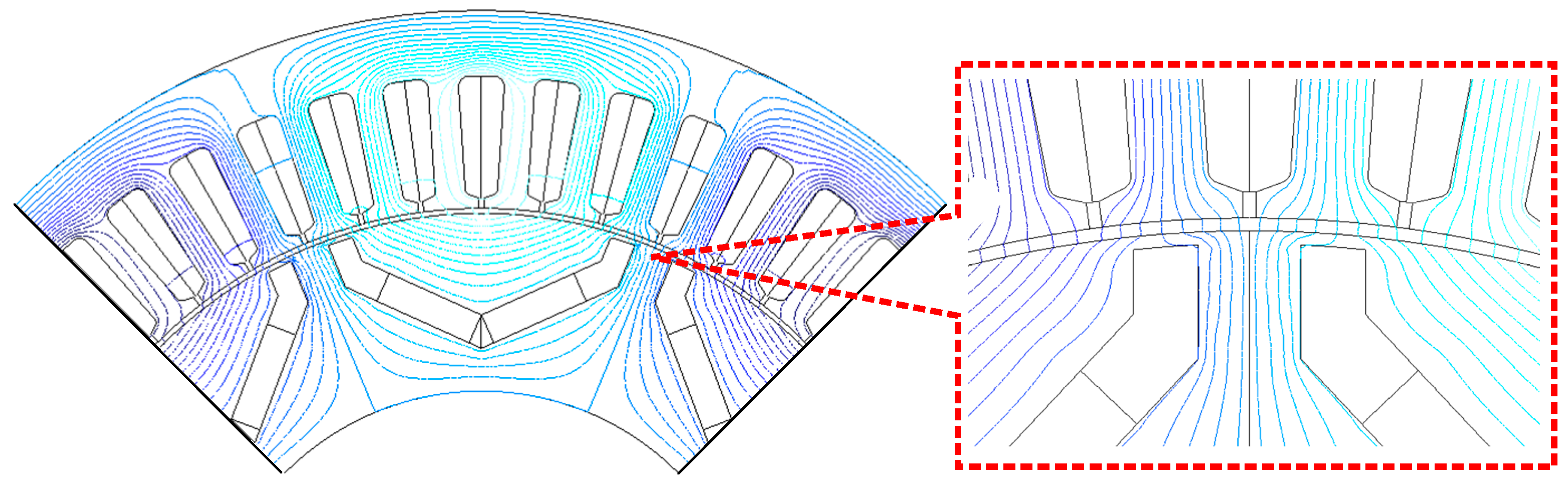

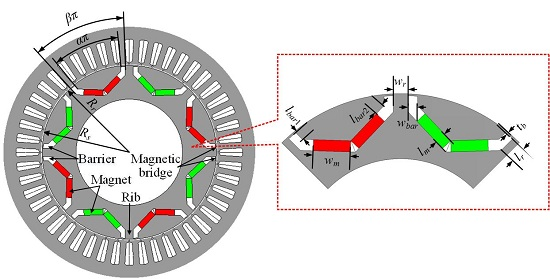
| Symbol | Parameter | Results and Unit |
|---|---|---|
| p | Number of pole pairs | 4 |
| Q | Number of slots | 48 |
| I | Amplitude of phase current | 1A |
| N | Amount of winding turns in series of stator phase | 32 |
| Br | Remanence of magnet | 1.25 |
| μr | Relative permeability of magnet | 1.024 |
| α | Magnet pole-arc to pole-pitch ratio | 0.742 |
| β | Barrier arc to pole-pitch ratio | 0.886 |
| Rs | Stator bore radius | 91 mm |
| Rr | Rotor outer radius | 90 mm |
| tb | Bridge thickness | 1 mm |
| wbar | Barrier width | 5 mm |
| lbar1 | Barrier 1 length | 5 mm |
| lbar2 | Barrier 2 length | 5.9 mm |
| wm | PM width | 20 mm |
| lm | PM length in magnetization direction | 6 mm |
| wr | Rib width | 8 mm |
| lr | Rib length | 8.8 mm |
| Method | Value | Unit |
|---|---|---|
| Proposed method | 4.40 × 10−5 | H/m |
| Finite element method (FEM) | 4.52 × 10−5 | H/m |
| Item | Proposed Method | FEM | Unit |
|---|---|---|---|
| D-axis inductance | 0.524 | 0.513 | mH |
| Q-axis inductance | 1.267 | 1.271 | mH |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, P.; Pei, Y.; Chai, F.; Zhao, K. Analytical Calculation of D- and Q-axis Inductance for Interior Permanent Magnet Motors Based on Winding Function Theory. Energies 2016, 9, 580. https://doi.org/10.3390/en9080580
Liang P, Pei Y, Chai F, Zhao K. Analytical Calculation of D- and Q-axis Inductance for Interior Permanent Magnet Motors Based on Winding Function Theory. Energies. 2016; 9(8):580. https://doi.org/10.3390/en9080580
Chicago/Turabian StyleLiang, Peixin, Yulong Pei, Feng Chai, and Kui Zhao. 2016. "Analytical Calculation of D- and Q-axis Inductance for Interior Permanent Magnet Motors Based on Winding Function Theory" Energies 9, no. 8: 580. https://doi.org/10.3390/en9080580