A Novel Method to Magnetic Flux Linkage Optimization of Direct-Driven Surface-Mounted Permanent Magnet Synchronous Generator Based on Nonlinear Dynamic Analysis
Abstract
:1. Introduction
2. System Modelling
2.1. Conventional Direct-Driven Surface-Mounted Permanent Magnet Synchronous Generator (D-SPMSG) for Wind Power
- Voltage equationswhere .
- Magnetic flux linkage equations
- Torque equation
- Motion equation
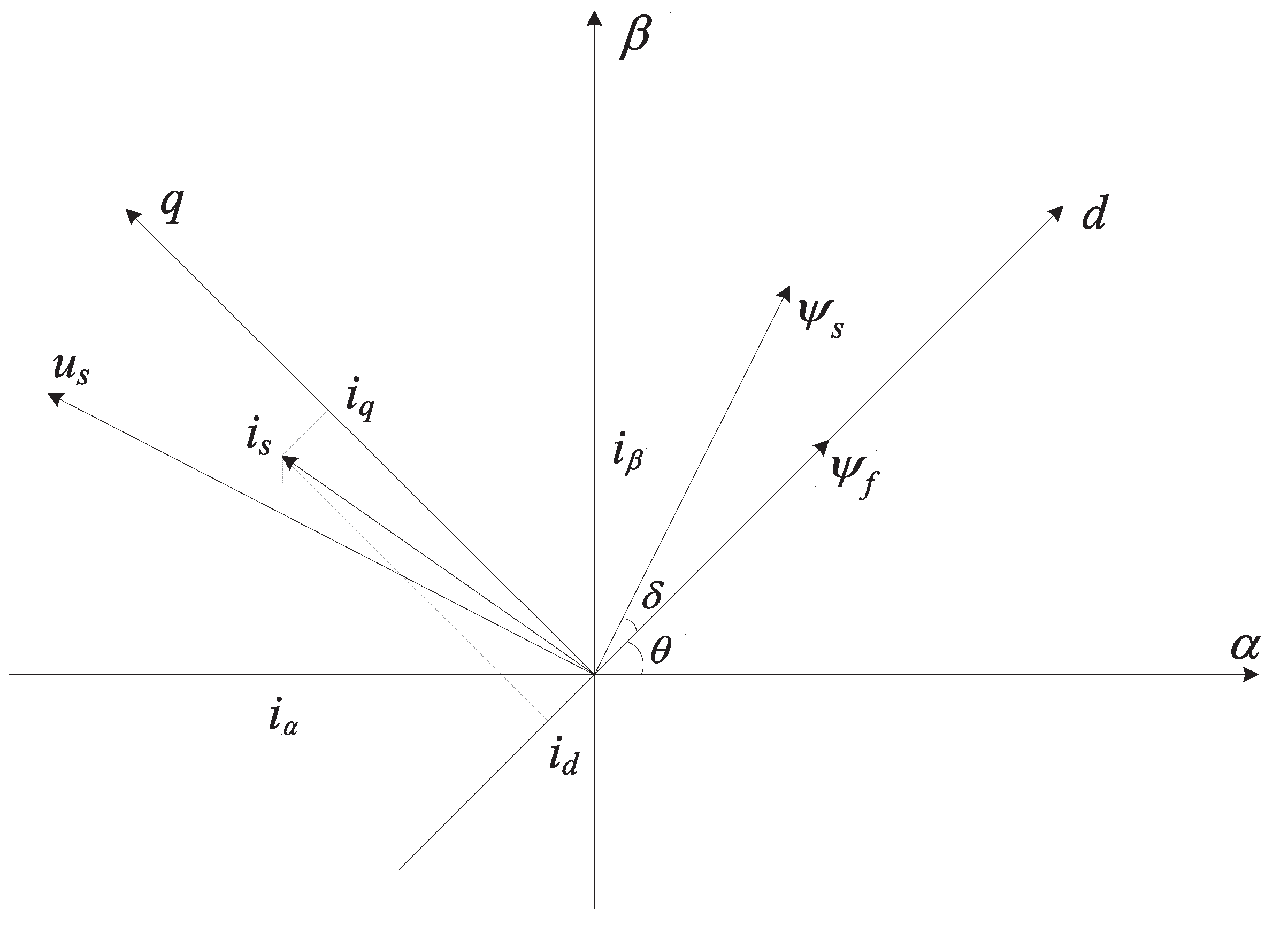
2.2. Transformation to the Compact Representation
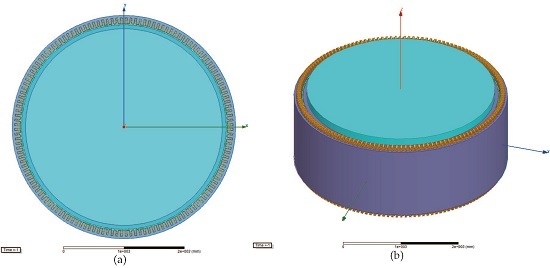
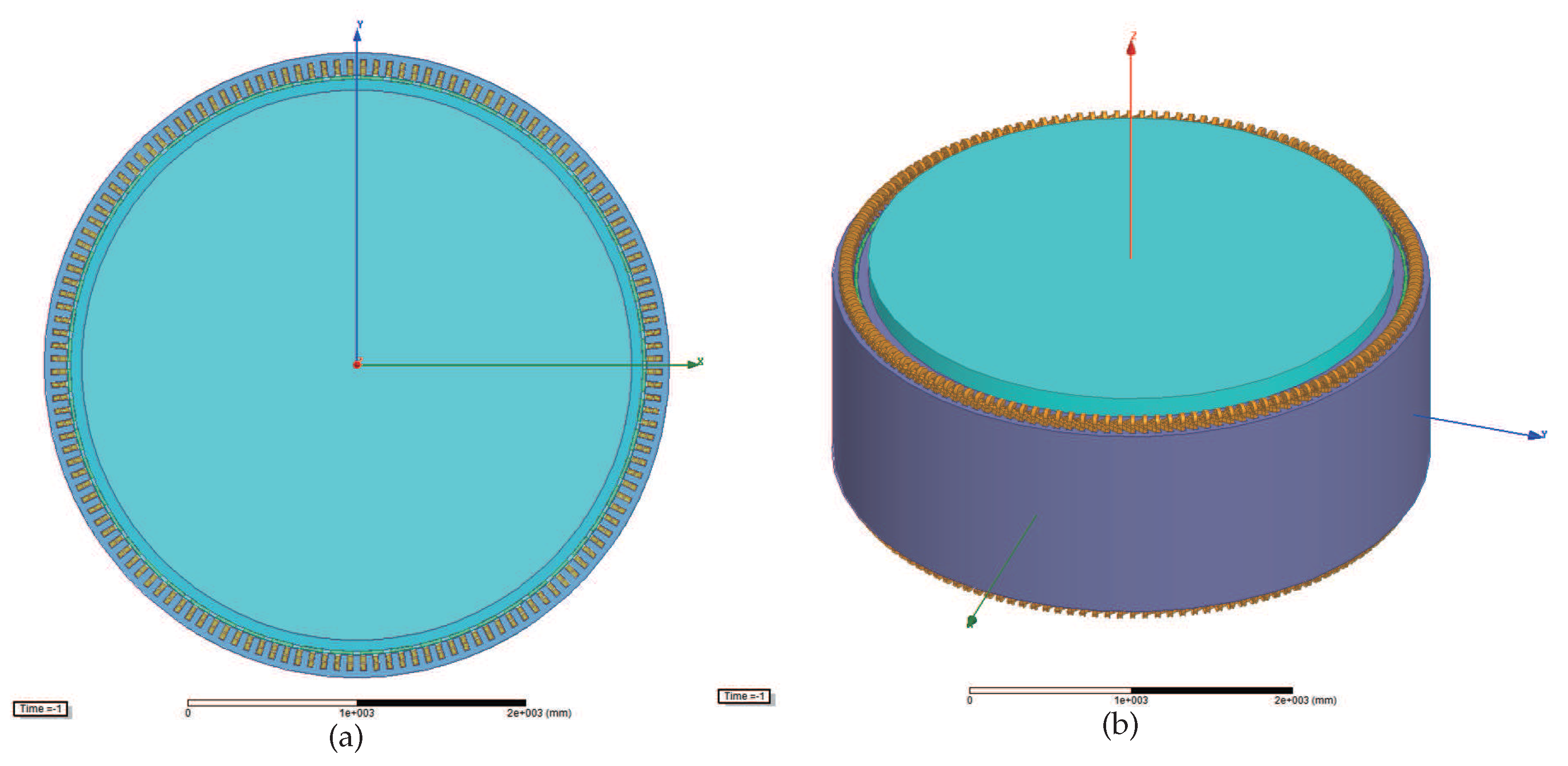
3. Design of 2MW D-SPMSG
4. Basic Dynamic Behavior Analysis
4.1. Dissipativity and Attractor Existence
4.2. Equilibrium and Stability
- For equilibrium point , the characteristic equation isIf the system is stable at the equilibrium point , then the real parts of all the roots must be negative. According to the Routh–Hurwitz criterion, system (24) must satisfy the following conditions:Then, we can getThus, .
- For equilibrium points and , the characteristic equation isIf the system is stable at the equilibrium points and , then the real parts of all the roots must be negative. According to the Routh–Hurwitz criterion, system (24) must satisfy the following conditions:Then, we can get
- If ,Thus, .
- If ,Thus, .
4.3. Lyapunov Exponent Spectrums by Varying Parameters
- When , we can obtain , and . For instance, Figure 4 shows phase orbits, Poincaré map, time waveform and power spectrum with , and the Lyapunov exponents are , and . The system is stable with respect to the equilibrium point , thus , and tends to be a constant. Furthermore, there are some linear points in the Poincaré map. A regular circle appeared in the phase orbit. Therefore, all of these results indicate that the system can better cope with disturbances and keep steady at this range of the magnetic flux linkage .
- When , we can obtain , and . For instance, the system dynamical behaviors at are shown in Figure 5, , and . The motion regularities of , and are periodical. A limit cycle appeared in the phase orbit and only some isolated points turn up in the Poincaré map. All of these results indicate that the D-SPMSG system exhibits a periodic vibration and further reveal that the system cannot tend to be stable.
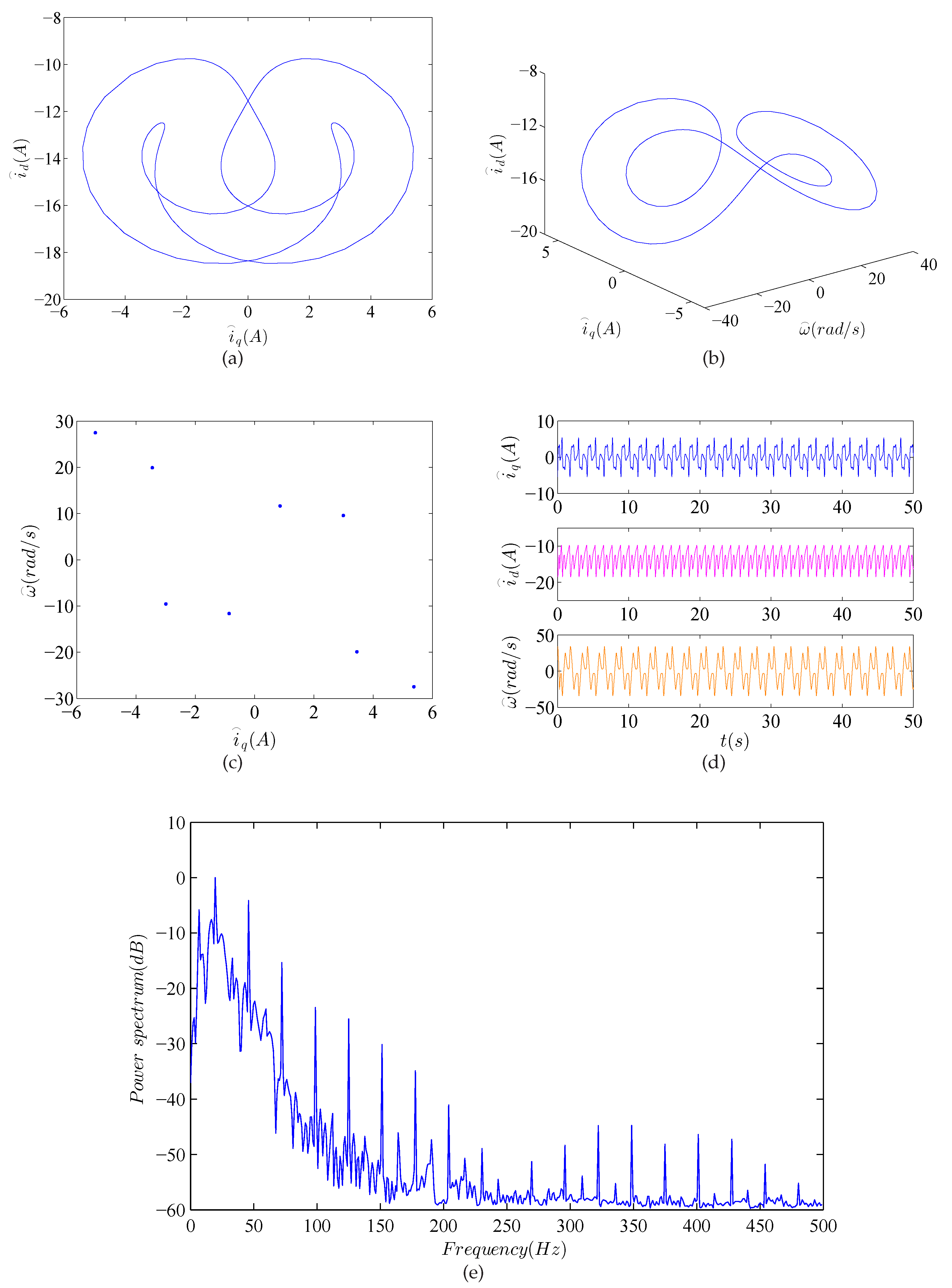
- When , we can obtain , and . For instance, the phase orbits, Poincaré map, time waveform and power spectrum of the system (24) with are depicted in Figure 6, , and . From Figure 6e, the frequency distribution is not as regular as . The system exhibits quasi-periodic motion and results in the two-dimensional torus.
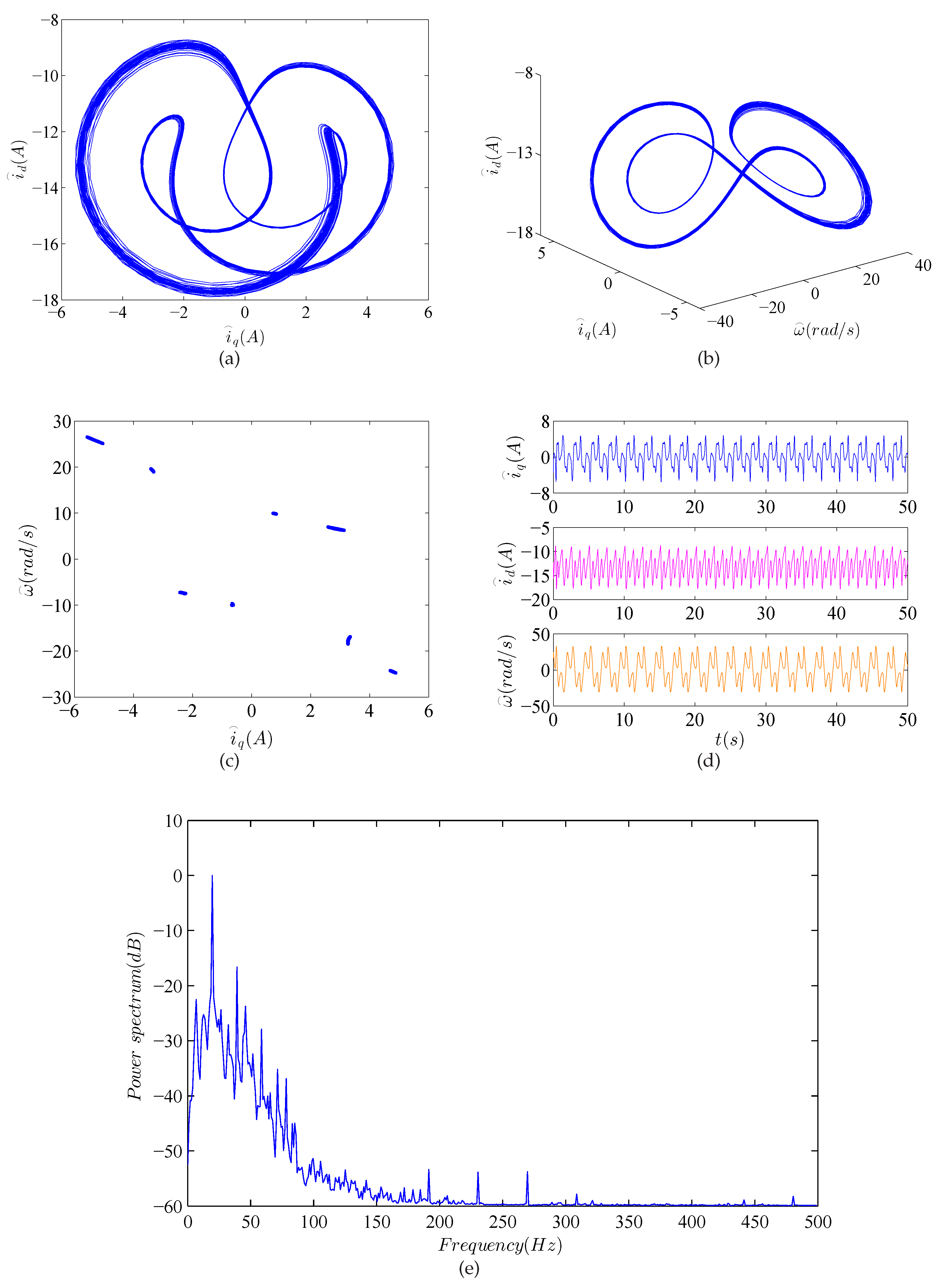
- When , we can obtain , and . For instance, the system dynamical behaviors for of the system (24) are depicted in Figure 7, , and . The Poincaré map shows patches of dense points, there is a hierarchy dense point, and it has a hierarchical structure. Figure 7e shows a broadband noise-like power spectrum. Therefore, all these results indicate that the system exhibits chaotic motion and results in the chaotic attractor.
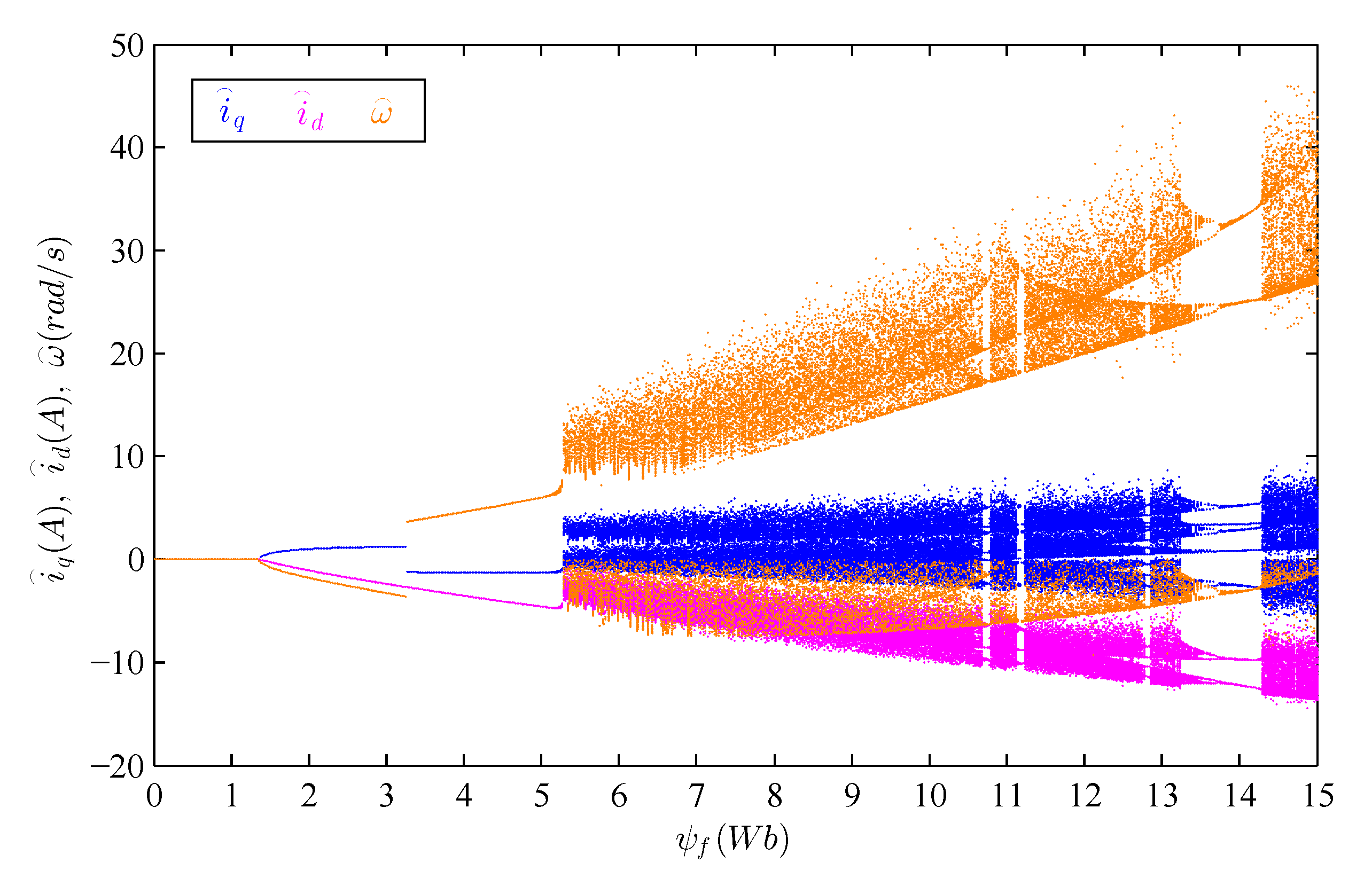
4.4. Bifurcation Diagram by Varying Parameters
5. Finite Element Analysis of D-SPMSG
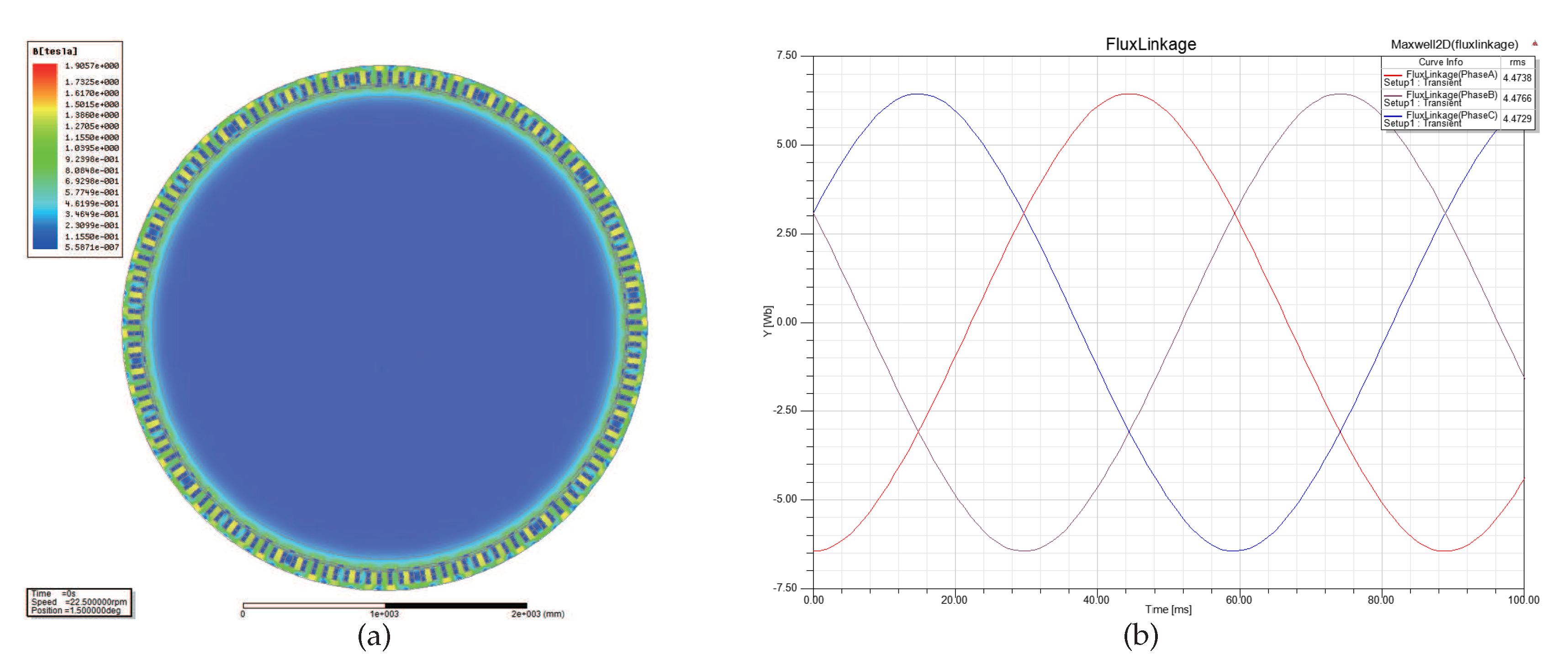
- Case 1 and Case 2: Figure 9 and Figure 10 show the nephogram of magnetic flux density and the corresponding waveform of magnetic flux linkage with Wb and Wb, respectively. We can observe the magnetic flux density 1.2 T in Figure 9 and T in Figure 10. Thus, this indicates that the performance of D-SPMSG is improving, as is increasing. However, low utilization ratio of generator material in these two cases results in a waste of permanent magnet material.
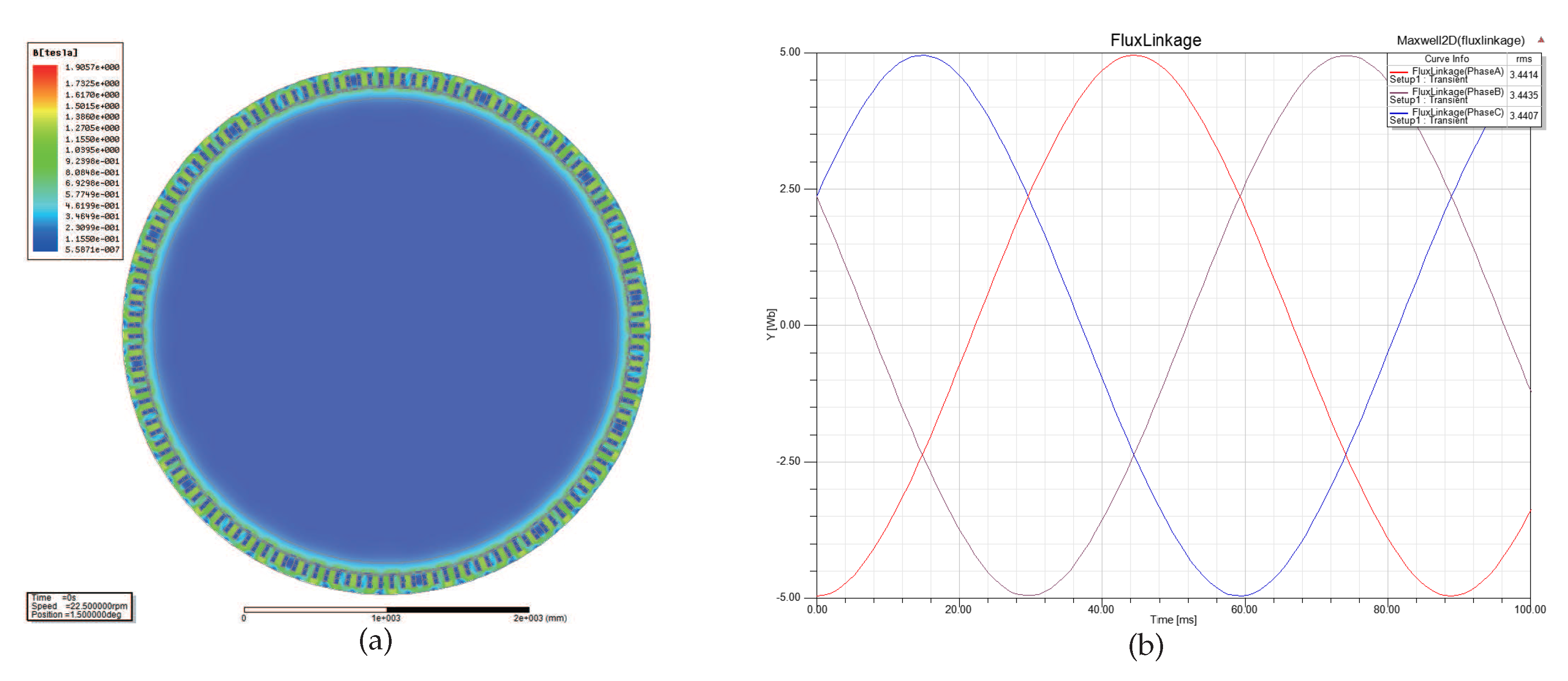
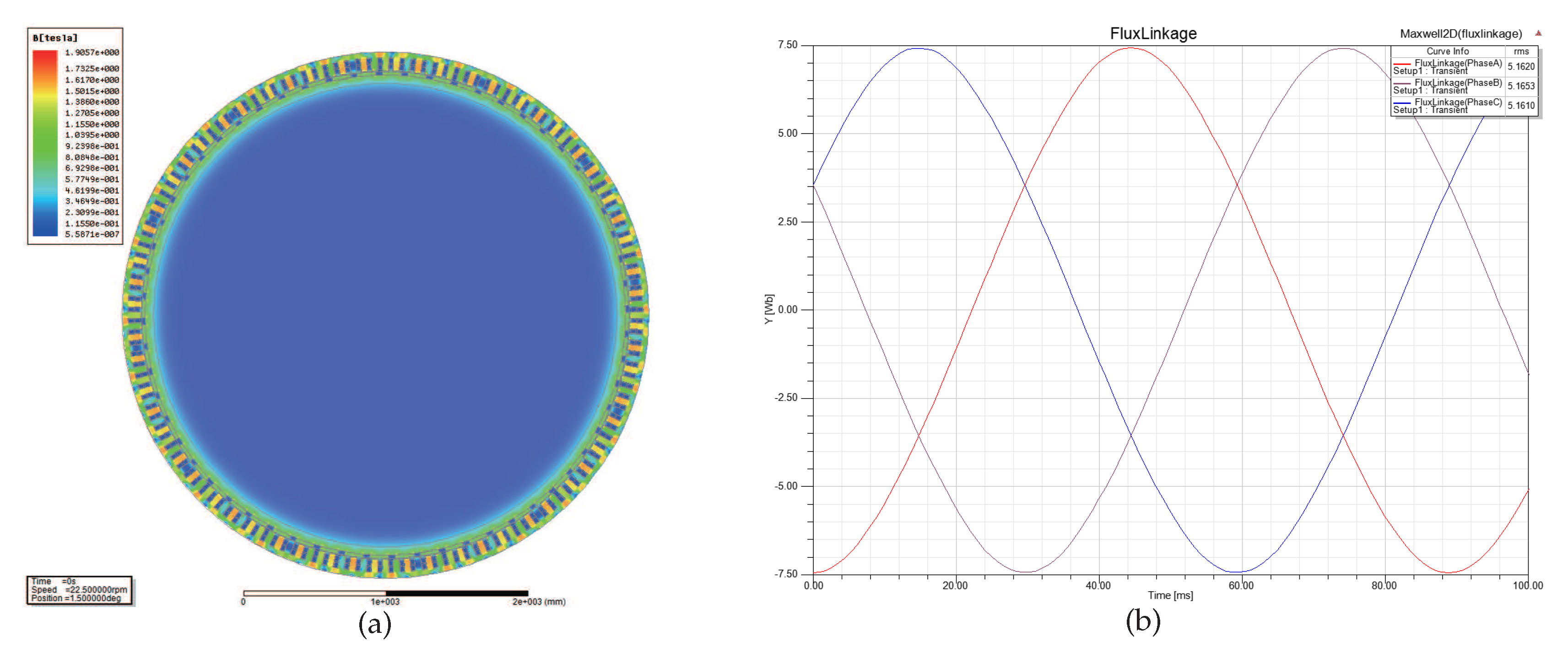
- Case 3: The nephogram of magnetic flux density and the waveform of magnetic flux linkage at Wb are shown in Figure 11. It is obviously 1.6 T; in other words, the magnetic flux density is nearing saturation. In this case, the saturation point of magnetic flux density at each stator-teeth and stator-yoke are discontinuous, that is to say, permanent magnets work at the optimal operating point, thus maximizing the utilization ratio of generator material and optimizing the performances.
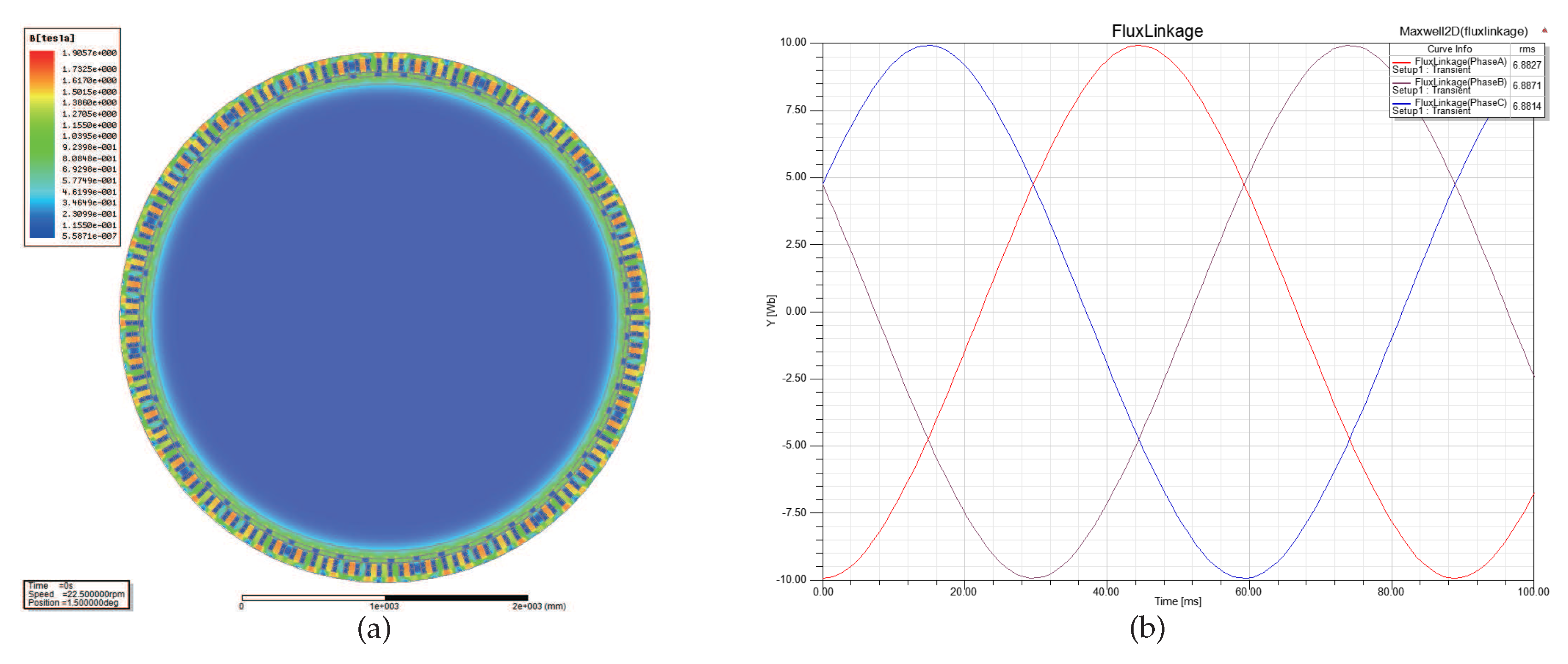
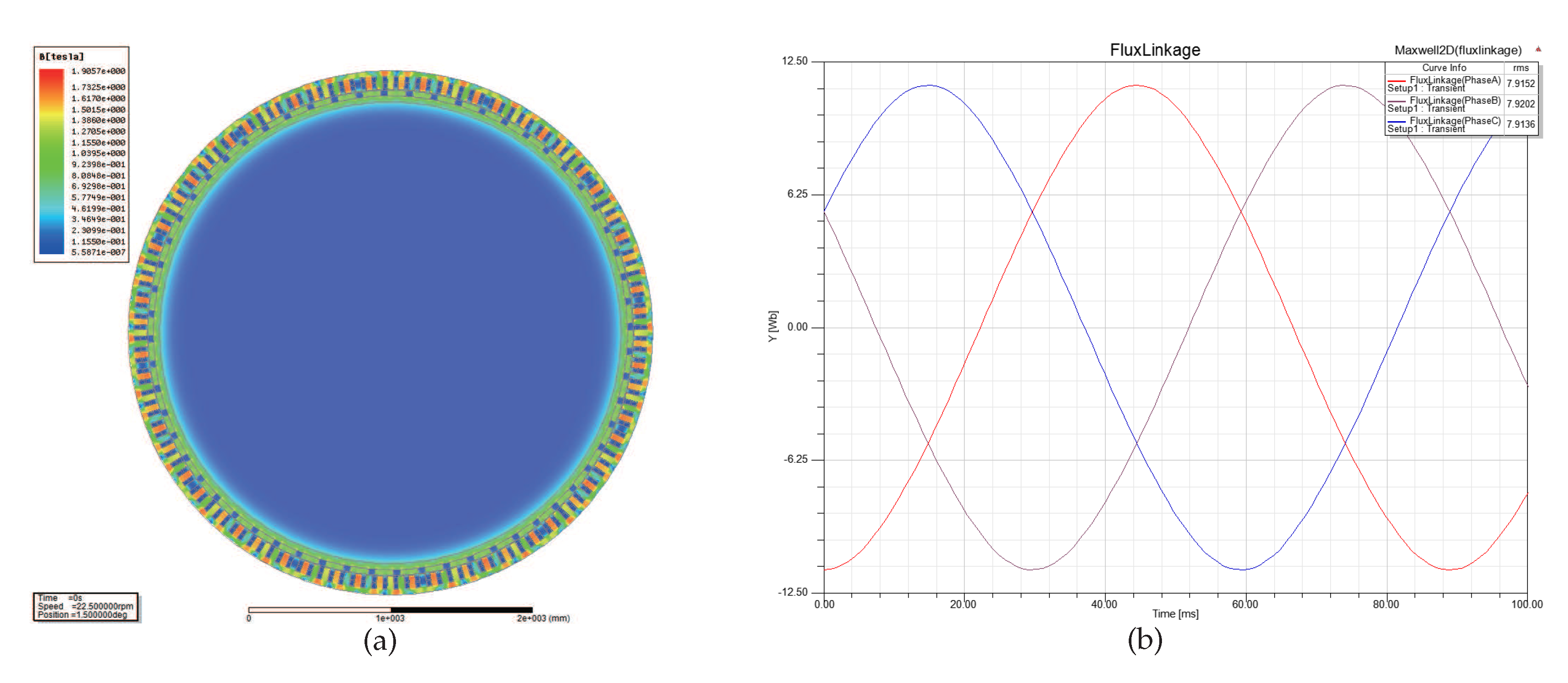
- Case 4 and Case 5: For 6.88 Wb and 7.92 Wb, the nephogram of magnetic flux density and the corresponding waveform of magnetic flux linkage are shown in Figure 12 and Figure 13. Hence, the magnetic flux density 1.75 T and 1.9 T are obtained in Figure 12 and Figure 13 respectively. It is obvious that the saturation points of magnetic flux density at each stator-teeth and stator-yoke are continuous. Therefore, this implies that the D-SPMSG is increasingly unstable as is increasing. In these two cases, the excessive magnetic flux density will cause the generator to have unstable operation, overheating , unit vibration, speed fluctuation, output voltage instability and other problems.
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Haque, M.E.; Negnevitsky, M.; Muttaqi, K.M. A Novel Control Strategy for a Variable-Speed Wind Turbine with a Permanent-Magnet Synchronous Generator. IEEE Trans. Ind. Appl. 2010, 46, 331–339. [Google Scholar] [CrossRef]
- Yun-Su, K.; Il-Yop, C.; Seung-Il, M. Tuning of the PI Controller Parameters of a PMSG Wind Turbine to Improve Control Performance under Various Wind Speeds. Energies 2015, 8, 1406–1425. [Google Scholar]
- Bhende, C.N.; Mishra, S.; Malla, S.G. Permanent Magnet Synchronous Generator-Based Standalone Wind Energy Supply System. IEEE Trans. Sustain. Energy 2011, 2, 361–373. [Google Scholar] [CrossRef]
- Hui, H.; Chengxiong, M.; Jiming, L.; Dan, W. Electronic Power Transformer Control Strategy in Wind Energy Conversion Systems for Low Voltage Ride-through Capability Enhancement of Directly Driven Wind Turbines with Permanent Magnet Synchronous Generators (D-PMSGs). Energies 2014, 7, 7330–7347. [Google Scholar]
- Liu, K.; Zhu, Z.Q. Online Estimation of the Rotor Flux Linkage and Voltage-Source Inverter Nonlinearity in Permanent Magnet Synchronous Machine Drives. IEEE Trans. Power Electron. 2014, 29, 418–427. [Google Scholar] [CrossRef]
- Zaijun, W.; Xiaobo, D.; Jiawei, C.; Minqiang, H. Operation and Control of a Direct-Driven PMSG-Based Wind Turbine System with an Auxiliary Parallel Grid-Side Converter. Energies 2013, 6, 3405–3421. [Google Scholar]
- Arumugam, P.; Hamiti, T.; Brunson, C.; Gerada, C. Analysis of Vertical Strip Wound Fault-Tolerant Permanent Magnet Synchronous Machines. IEEE Trans. Ind. Electron. 2014, 61, 1158–1168. [Google Scholar] [CrossRef]
- Tang, Y.; Xing, X.; Karimi, H.R.; Kocarev, L.; Kurths, J. Tracking Control of Networked Multi-Agent Systems Under New Characterizations of Impulses and Its Applications in Robotic Systems. IEEE Trans. Ind. Electron. 2016, 63, 1299–1307. [Google Scholar] [CrossRef]
- Coria, L.N.; Starkov, K.E. Bounding a domain containing all compact invariant sets of the permanent-magnet motor system. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 3879–3888. [Google Scholar] [CrossRef]
- Tang, Y.; Gao, H.J.; Zhang, W.B.; Kurths, J. Leader-following consensus of a class of stochastic delayed multi-agent systems with partial mixed impulses. Automatica 2015, 53, 346–354. [Google Scholar] [CrossRef]
- Yu, J.P.; Yu, H.S.; Chen, B.; Gao, J.W.; Qin, Y. Direct adaptive neural control of chaos in the permanent magnet synchronous motor. Nonlinear Dyn. 2012, 70, 1879–1887. [Google Scholar] [CrossRef]
- Xie, Q.; Si, G.Q.; Zhang, Y.B.; Yuan, Y.W.; Yao, R. Finite-time synchronization and identification of complex delayed networks with Markovian jumping parameters and stochastic perturbations. Chaos Solitons Fractals 2016, 86, 35–49. [Google Scholar] [CrossRef]
- Rasoolzadeh, A.; Tavazoei, M.S. Prediction of chaos in non-salient permanent-magnet synchronous machines. Phys. Lett. A 2012, 377, 73–79. [Google Scholar] [CrossRef]
- Wu, X.T.; Tang, Y.; Zhang, W.B. Input-to-state stability of impulsive stochastic delayed systems under linear assumptions. Automatica 2016, 66, 195–204. [Google Scholar] [CrossRef]
- Jing, Z.J.; Yu, C.; Chen, G.R. Complex dynamics in a permanent-magnet synchronous motor model. Chaos Solitons Fractals 2004, 22, 831–848. [Google Scholar] [CrossRef]
- Tang, Y.; Wang, Z.D.; Gao, H.J.; Qiao, H.; Kurths, J. On Controllability of Neuronal Networks with Constraints on the Average of Control Gains. IEEE Trans. Cybern. 2014, 44, 2670–2681. [Google Scholar] [CrossRef] [PubMed]
- Lu, P.L.; Yang, Y.; Huang, L. Global Dynamic Properties of a Synchronous Machine Model. Int. J. Bifurc. Chaos 2008, 18, 3113–3128. [Google Scholar] [CrossRef]
- Li, Z.; Park, J.B.; Joo, Y.H.; Zhang, B.; Chen, G.R. Bifurcations and chaos in a permanent-magnet synchronous motor. IEEE Trans. Circuits Syst. I-Fundam. Theory Appl. 2002, 49, 383–387. [Google Scholar]
- Hemati, N. Strange Attractors in Brushless DC Motors. IEEE Trans. Circuits Syst. I-Fundam. Theory Appl. 1994, 41, 40–45. [Google Scholar] [CrossRef]
- Chen, D.Y.; Liu, S.; Ma, X.Y. Modeling, nonlinear dynamical analysis of a novel power system with random wind power and it’s control. Energy 2013, 53, 139–146. [Google Scholar] [CrossRef]
- Slemon, G.R. On the Design of High-Performance Surface-Mounted PM Motors. IEEE Trans. Ind. Appl. 1994, 30, 134–140. [Google Scholar] [CrossRef]
- Gao, Y.; Chau, K.T. Design of permanent magnets to avoid chaos in doubly salient PM machines. IEEE Trans. Magn. 2004, 40, 3048–3050. [Google Scholar] [CrossRef]
- Romeral, L.; Urresty, J.C.; Ruiz, J.R.R.; Espinosa, A.G. Modeling of Surface-Mounted Permanent Magnet Synchronous Motors with Stator Winding Interturn Faults. IEEE Trans. Ind. Electron. 2011, 58, 1576–1585. [Google Scholar] [CrossRef]
- Silva, R.; Salimi, A.; Li, M.; Freitas, A.R.R.; Guimaraes, F.G.; Lowther, D.A. Visualization and Analysis of Tradeoffs in Many-Objective Optimization: A Case Study on the Interior Permanent Magnet Motor Design. IEEE Trans. Magn. 2016, 52. [Google Scholar] [CrossRef]
- Yang, L.; Ho, S.L.; Fu, W.N.; Li, W. Design Optimization of a Permanent Magnet Motor Derived from a General Magnetization Pattern. IEEE Trans. Magn. 2015, 51. [Google Scholar] [CrossRef]
- Virtic, P.; Vrazic, M.; Papa, G. Design of an Axial Flux Permanent Magnet Synchronous Machine Using Analytical Method and Evolutionary Optimization. IEEE Trans. Energy Convers. 2016, 31, 150–158. [Google Scholar] [CrossRef]

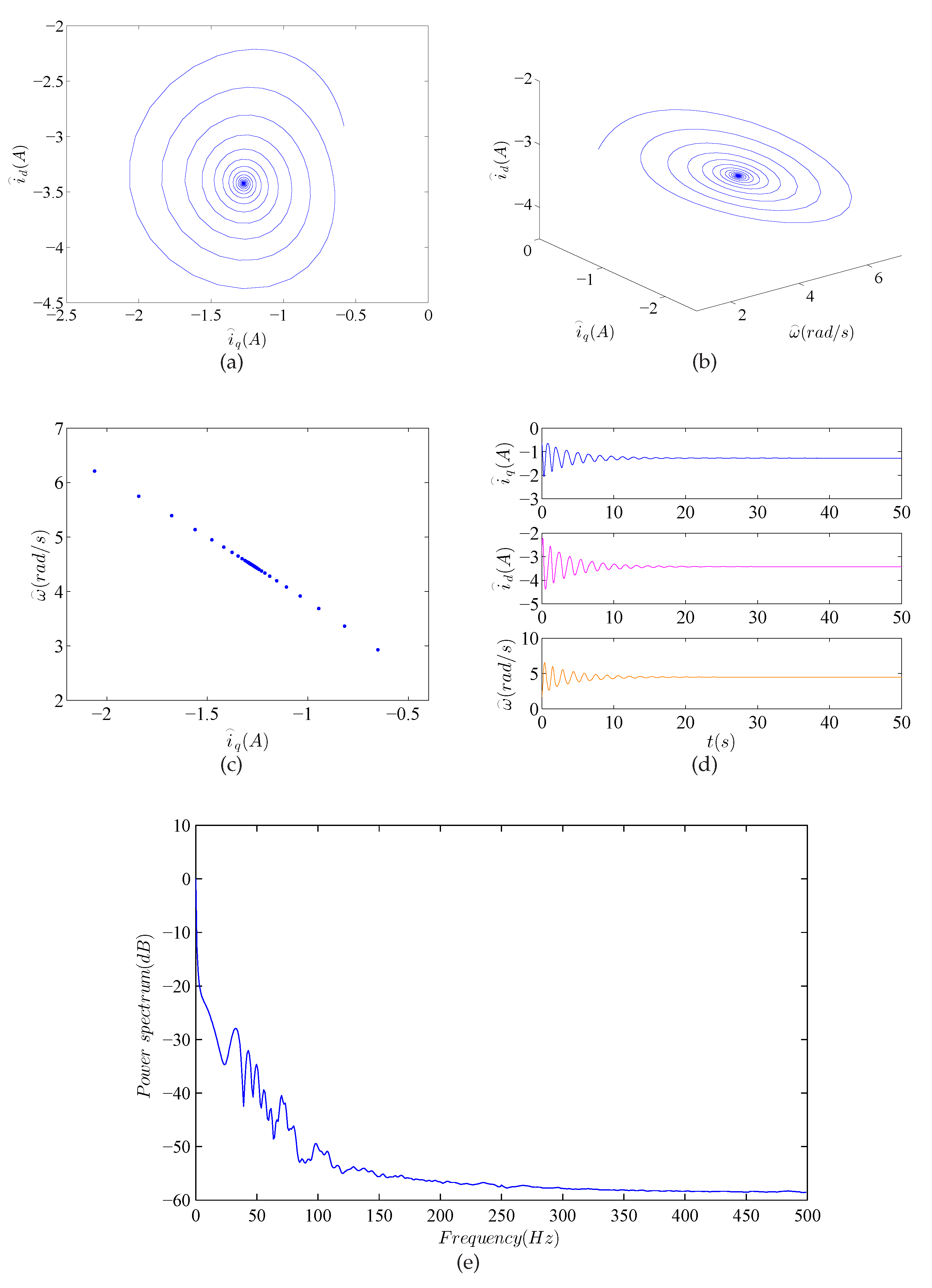

| Parameters | Descriptions | Unit |
|---|---|---|
| R | Stator winding resistance | Ω |
| q-axis stator inductance | H | |
| d-axis stator inductance | H | |
| q-axis stator voltage | V | |
| d-axis stator voltage | V | |
| q-axis stator current | A | |
| d-axis stator current | A | |
| q-axis stator flux | Wb | |
| d-axis stator flux | Wb | |
| Flux of permanent magnet | Wb | |
| Mechanical torque | N·m | |
| Electromagnetic torque | N·m | |
| Number of pole pairs | - | |
| ω | Rotor angular speed | rad/s |
| Electrical angular frequency | rad/s | |
| b | Friction coefficient | N·m |
| J | Moment of inertia | kg |
| Parameters | Descriptions | Values |
|---|---|---|
| m | Number of stator phase | 3 |
| Type of circuit | Y | |
| Rated voltage | 660 V | |
| Rated torque | ||
| Rated speed | 22.5 rpm | |
| Rated power factor | 0.98 | |
| Number of pole pairs | 30 | |
| Q | Number of stator slots | 144 |
| f | Rated frequency | 11.25 Hz |
| Rated output power | 2000 KW | |
| Rated efficiency | 95% | |
| Outer diameter of stator | 3750 mm | |
| Inner diameter of stator | 3480 mm | |
| δ | Air gap | 5 mm |
| Outer diameter of rotor | 3470 mm | |
| Inner diameter of rotor | 3300 mm | |
| l | Length of rotor | 1300 mm |
| Parameters | Values |
|---|---|
| R | Ω |
| 30 | |
| b | |
| J |
| Parameters | Values |
|---|---|
| Residual flux density | 1.3223 T |
| Coercive force | 915 kA/m |
| Maximum energy density | 302.475 |
| Relative recoil permeability | 1.15003 |
| Mechanical pole embrace | 0.72 |
| Length of magnet | 1300 mm |
| Outer diameter of magnet | 3470 mm |
| Inner diameter of magnet | 3431.6 mm |
| Thickness of magnet | 19.2 mm |
| Width of magnet | 130.092 mm |
| Parameters | Values |
|---|---|
| Winding type | The 3-phase, 2-layer winding |
| Coil pitch | 2 |
| Number of wires per conductor | 2 |
| Wire diameter | 5.971 mm |
| Wire wrap thickness | 0.1 mm |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, Q.; Zhang, Y.; Yu, Y.; Si, G.; Yang, N.; Luo, L. A Novel Method to Magnetic Flux Linkage Optimization of Direct-Driven Surface-Mounted Permanent Magnet Synchronous Generator Based on Nonlinear Dynamic Analysis. Energies 2016, 9, 557. https://doi.org/10.3390/en9070557
Xie Q, Zhang Y, Yu Y, Si G, Yang N, Luo L. A Novel Method to Magnetic Flux Linkage Optimization of Direct-Driven Surface-Mounted Permanent Magnet Synchronous Generator Based on Nonlinear Dynamic Analysis. Energies. 2016; 9(7):557. https://doi.org/10.3390/en9070557
Chicago/Turabian StyleXie, Qian, Yanbin Zhang, Yanan Yu, Gangquan Si, Ningning Yang, and Longfei Luo. 2016. "A Novel Method to Magnetic Flux Linkage Optimization of Direct-Driven Surface-Mounted Permanent Magnet Synchronous Generator Based on Nonlinear Dynamic Analysis" Energies 9, no. 7: 557. https://doi.org/10.3390/en9070557