Nonlinear Coupled Dynamics of a Rod Fastening Rotor under Rub-Impact and Initial Permanent Deflection
Abstract
:1. Introduction
2. Modeling of a Rub-Impact Rod Fastening Rotor System
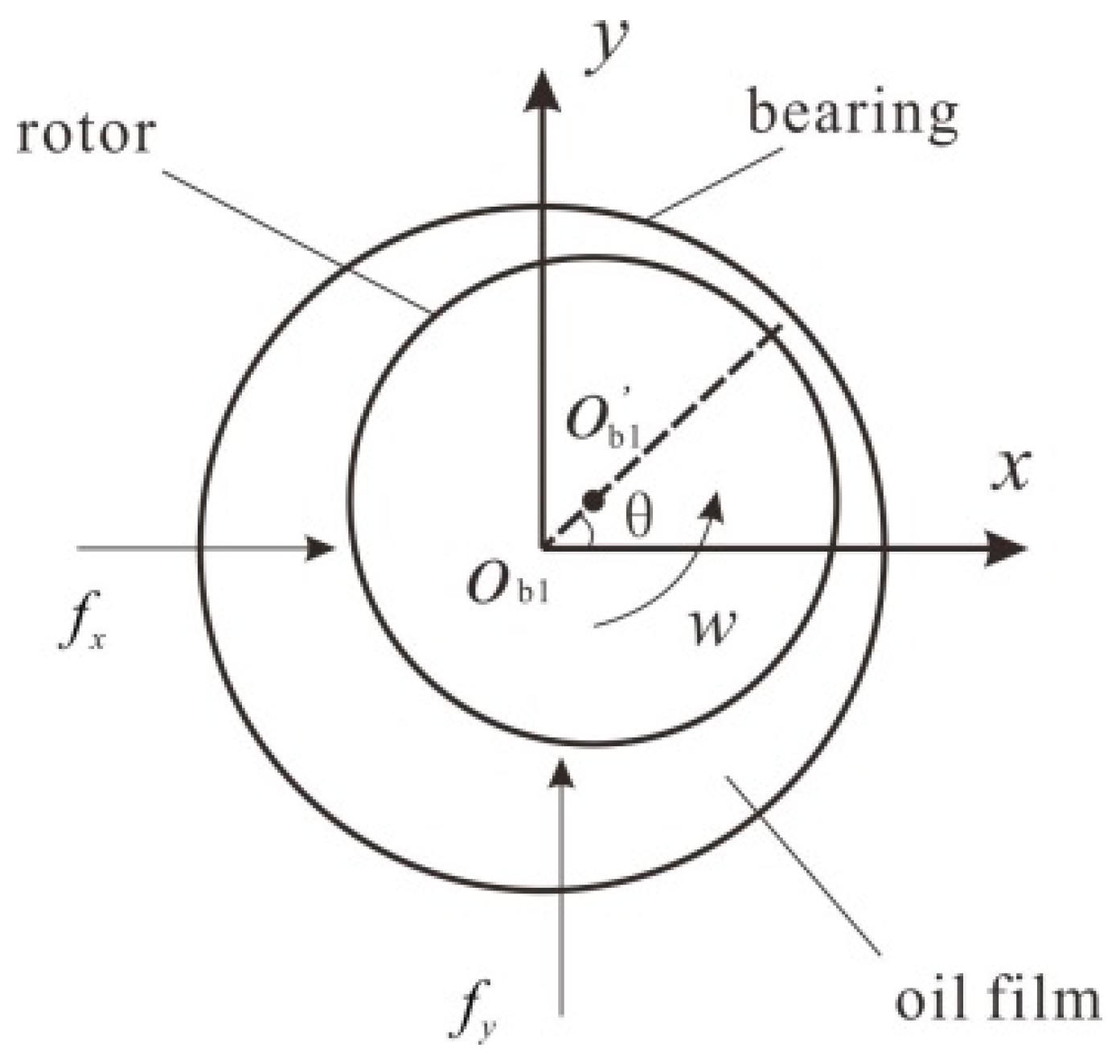
2.1. Rub-Impact Force
2.2. Nonlinear Oil-Film Force
2.3. The Governing Equations of Motion
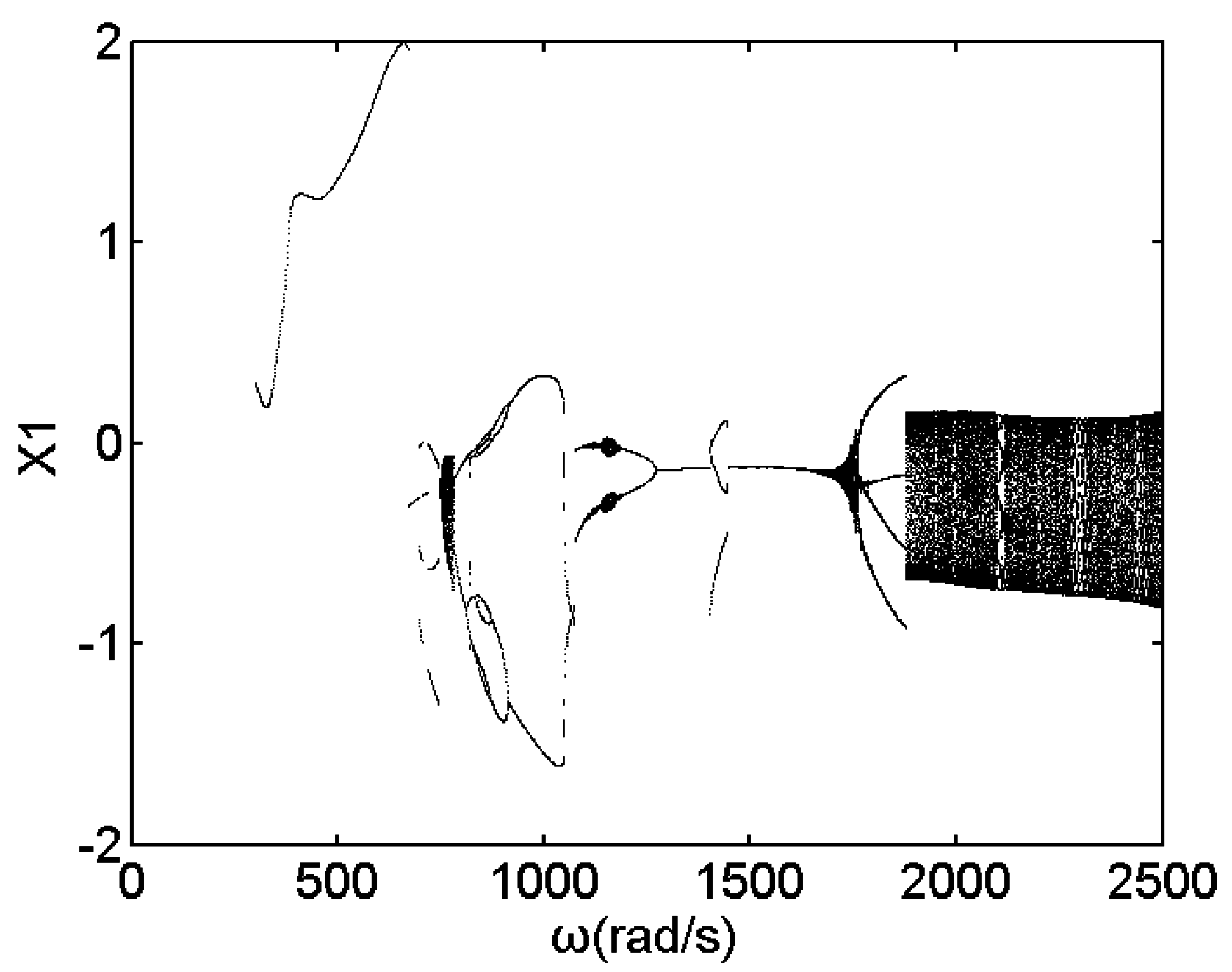
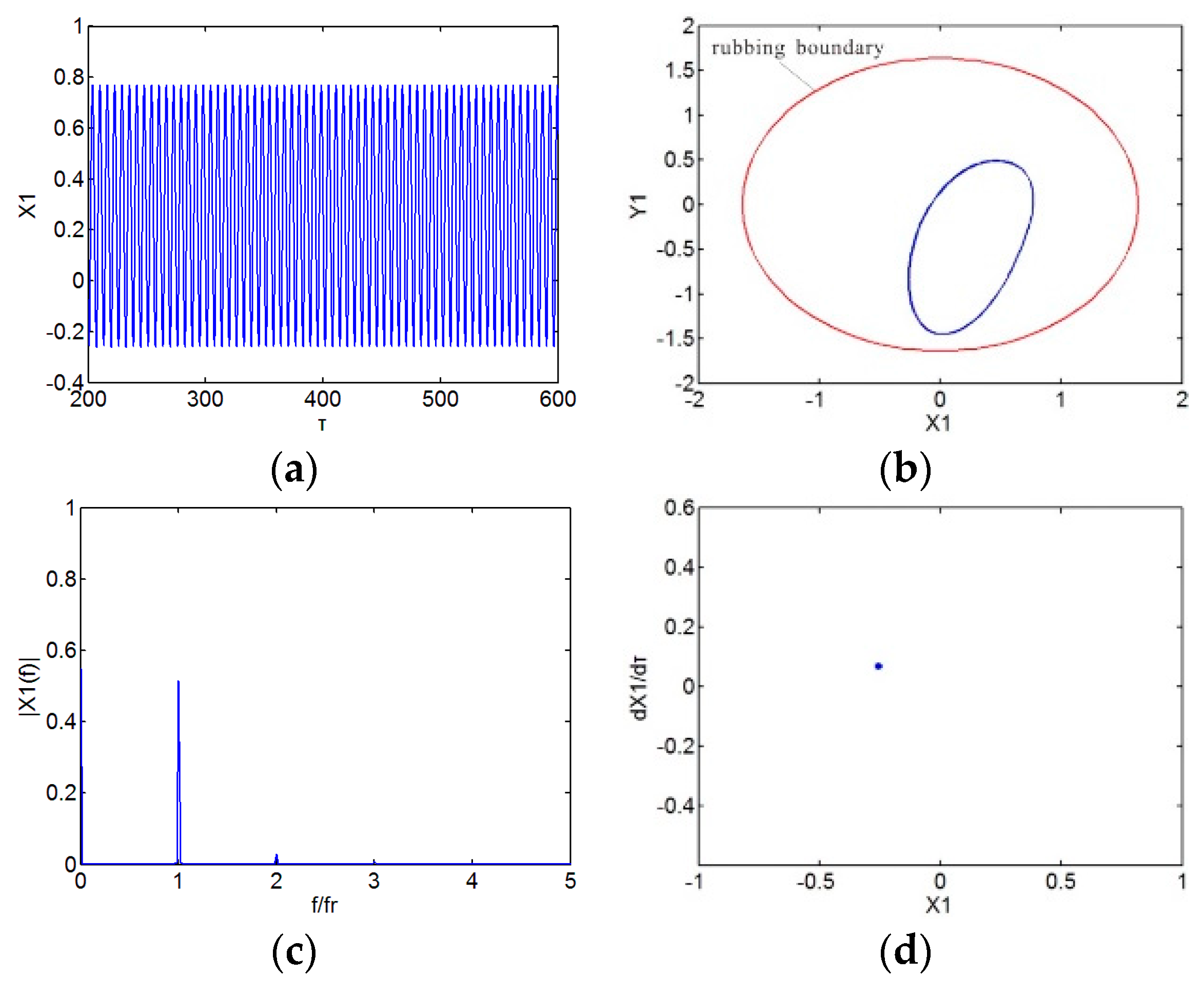
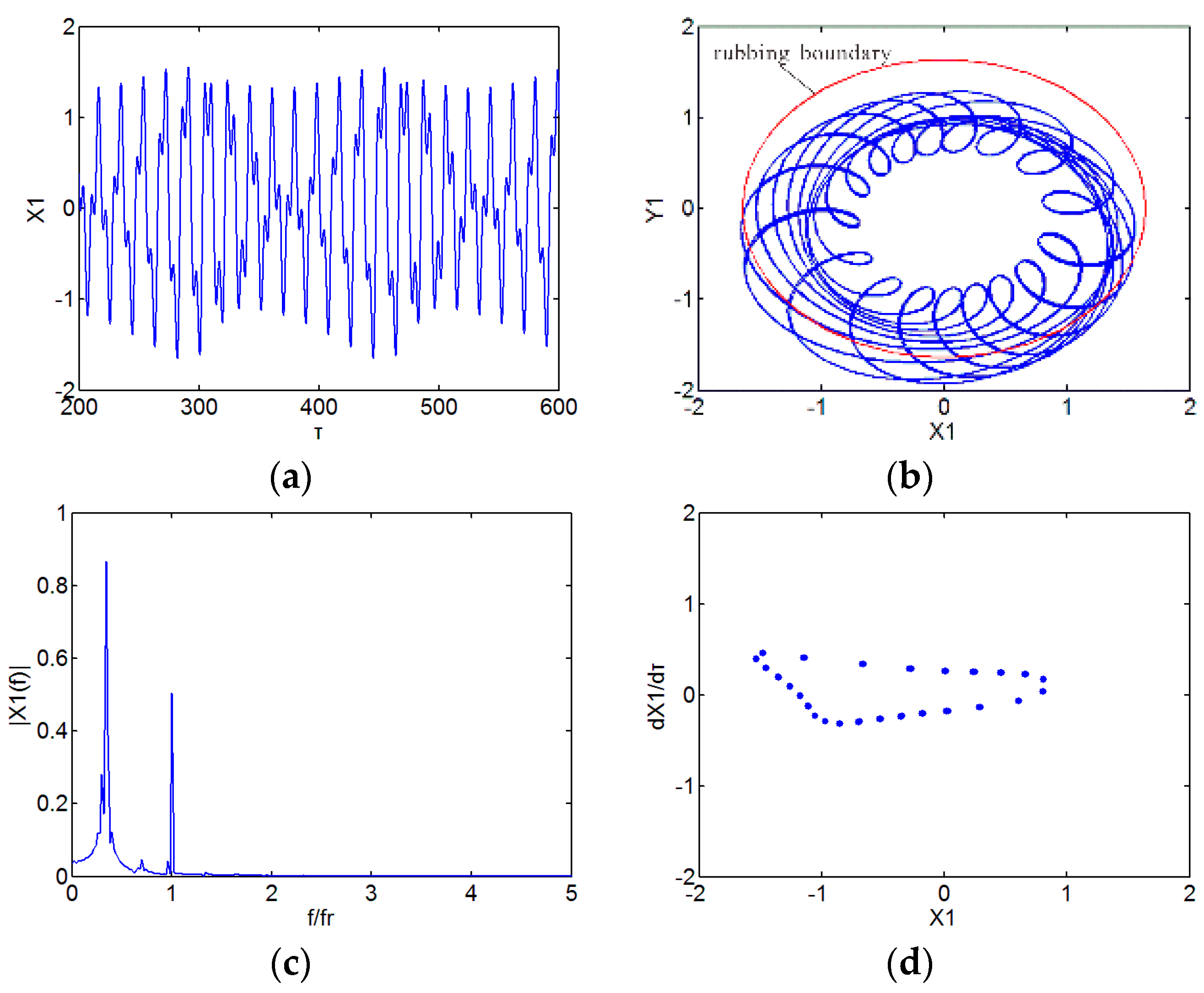
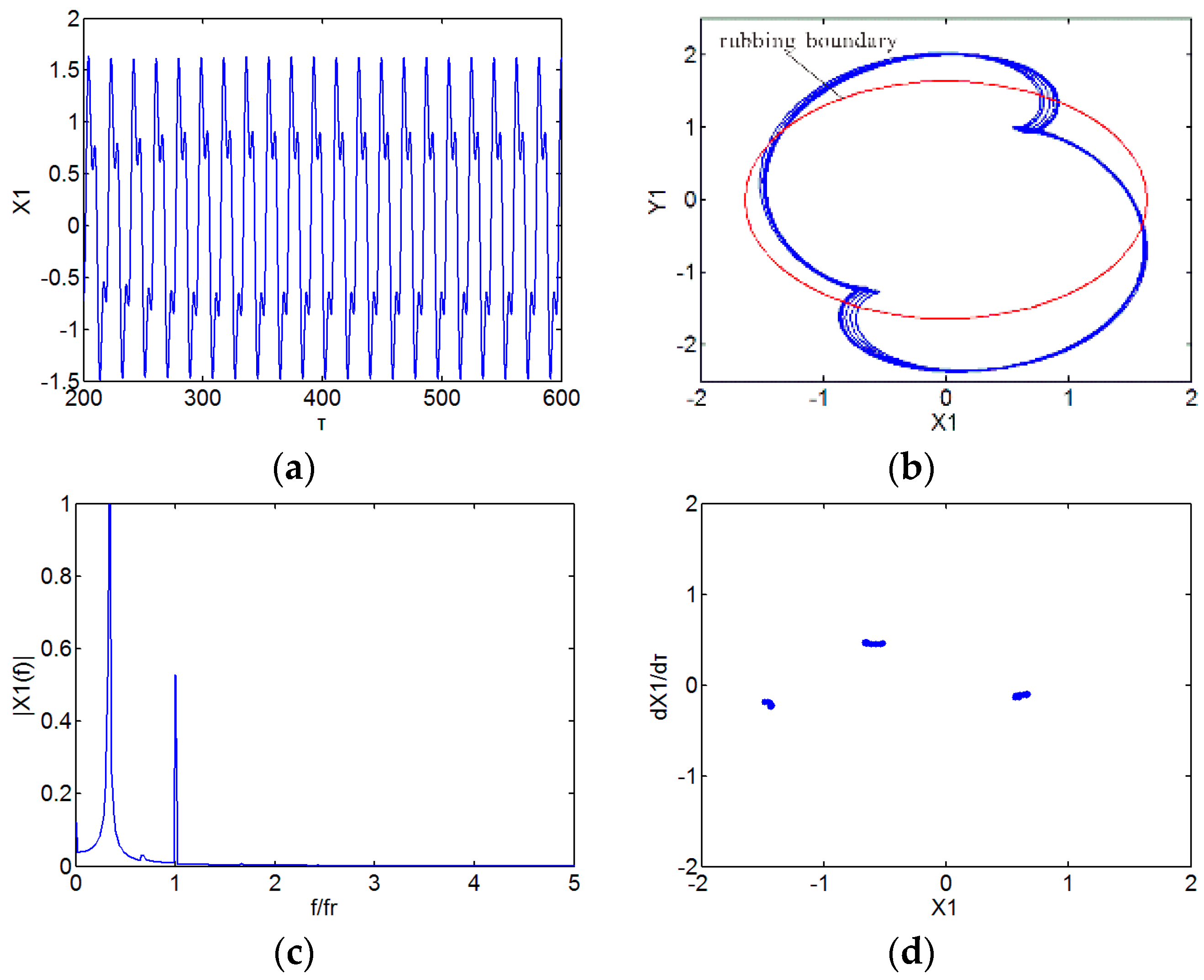
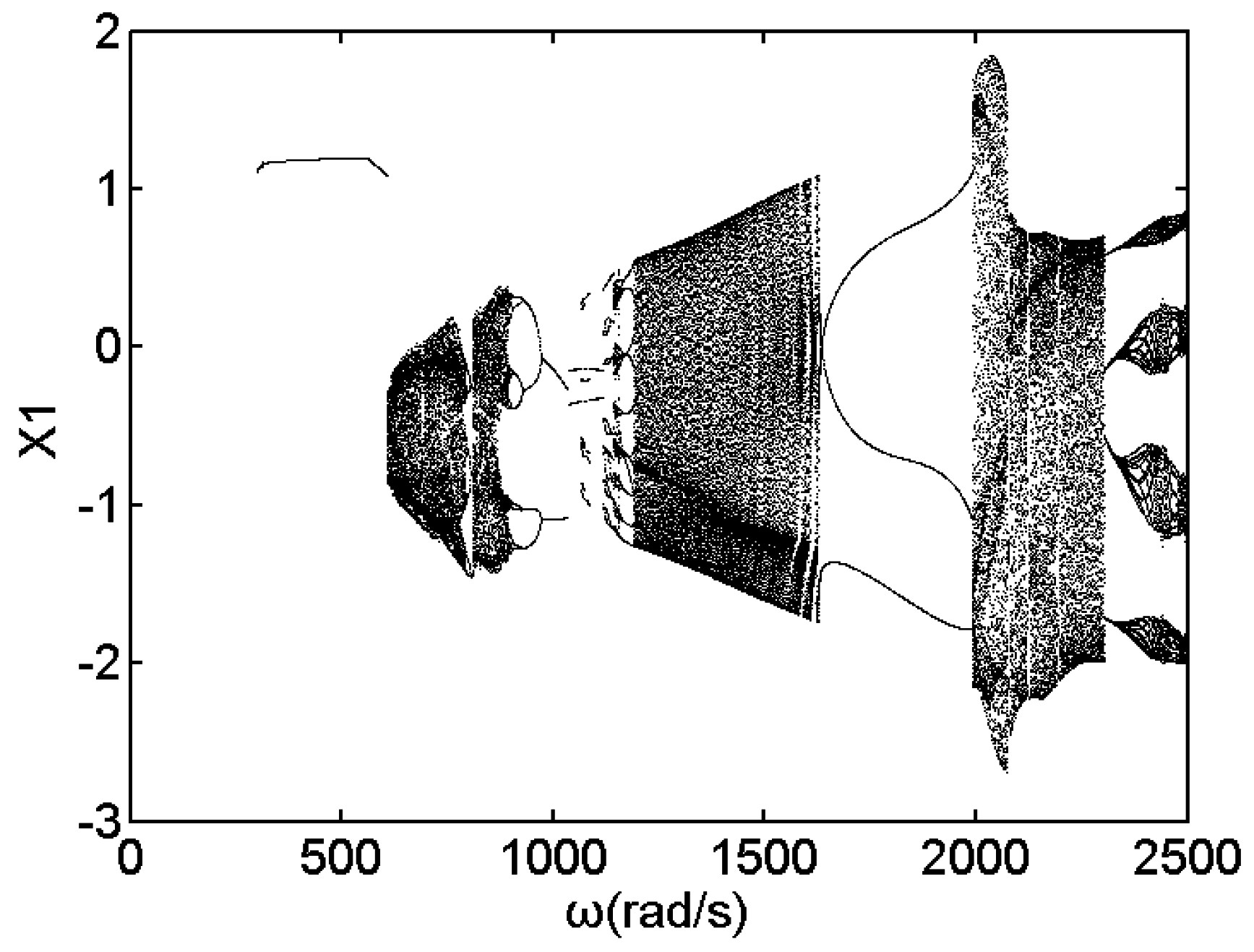
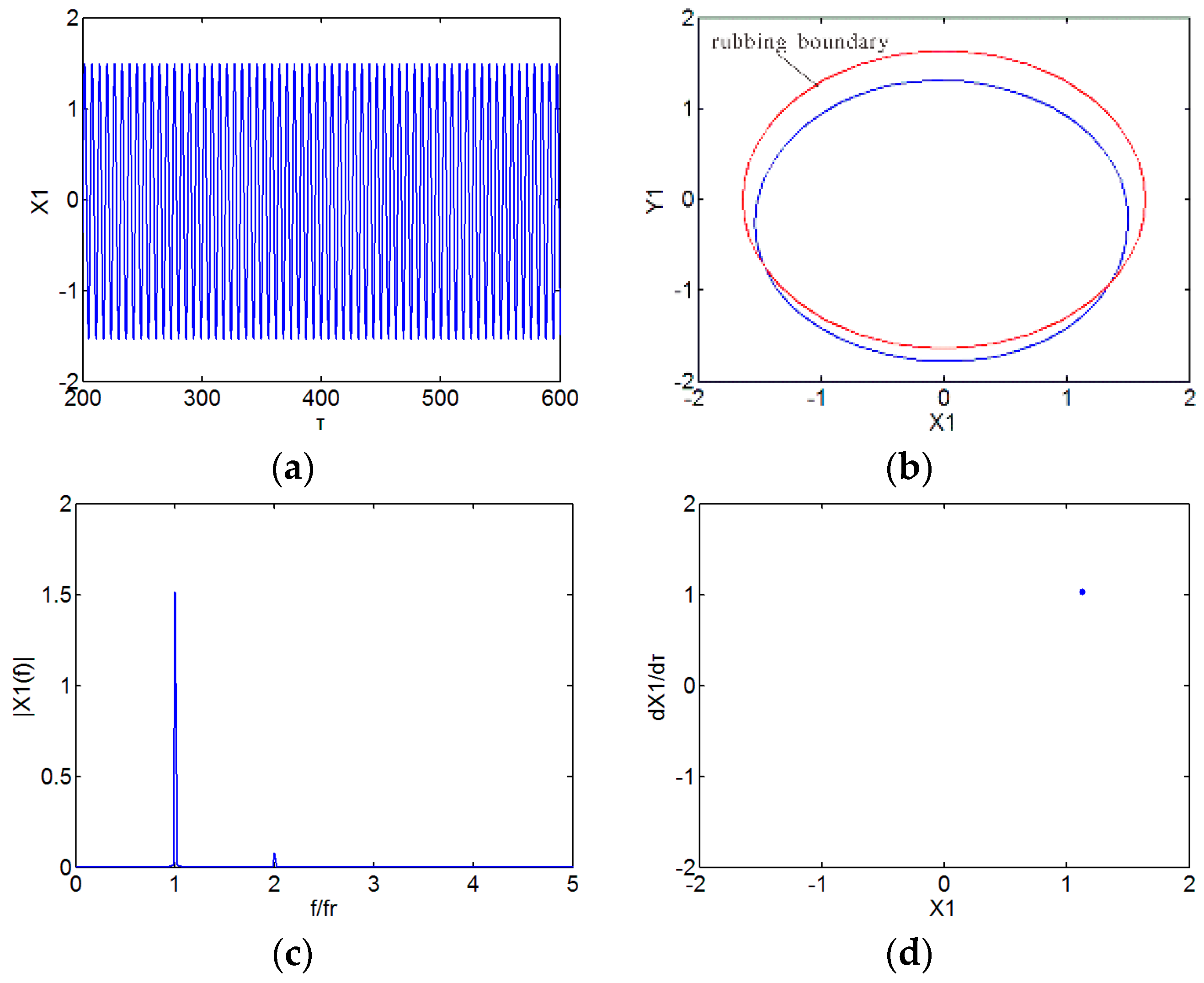
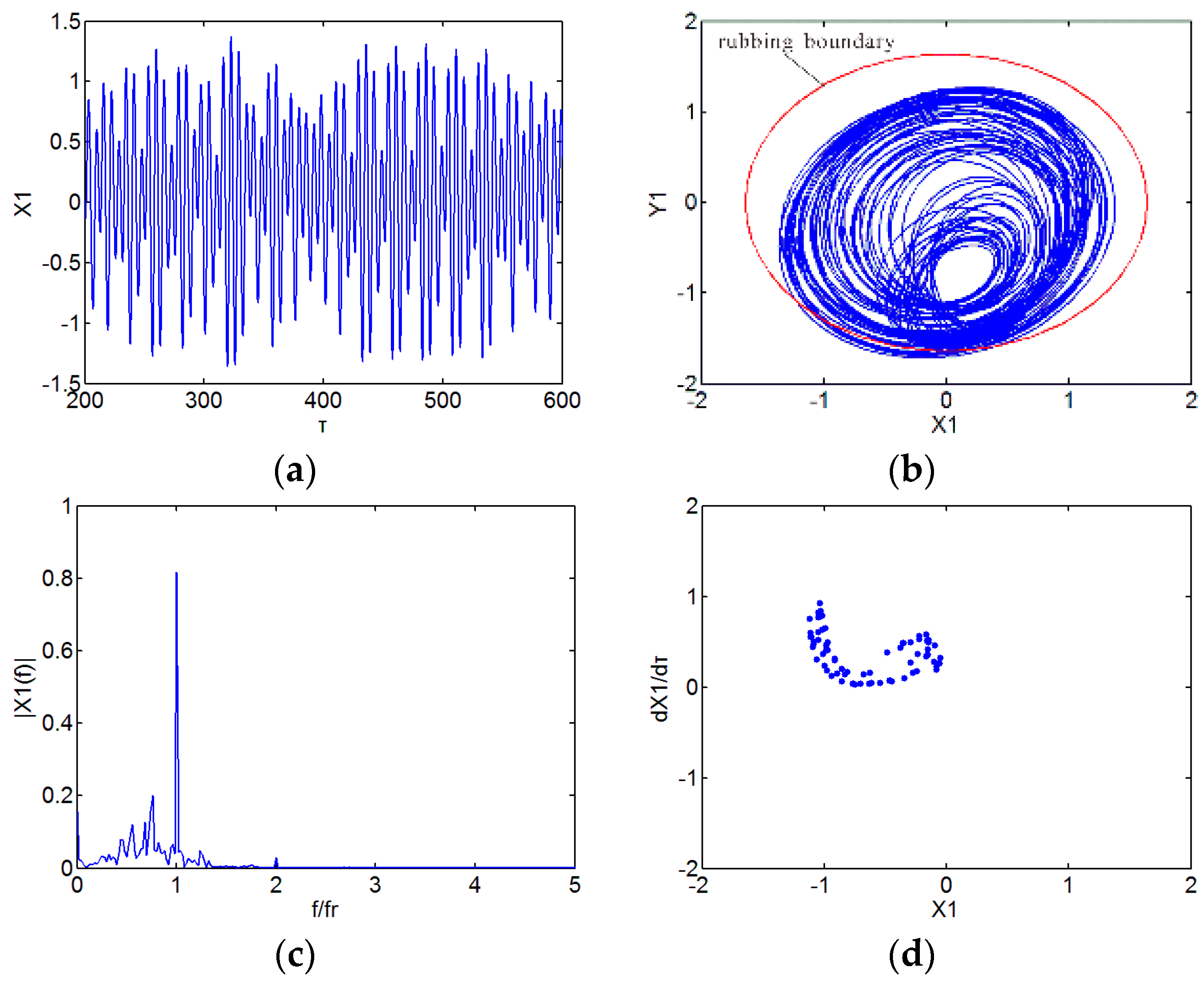
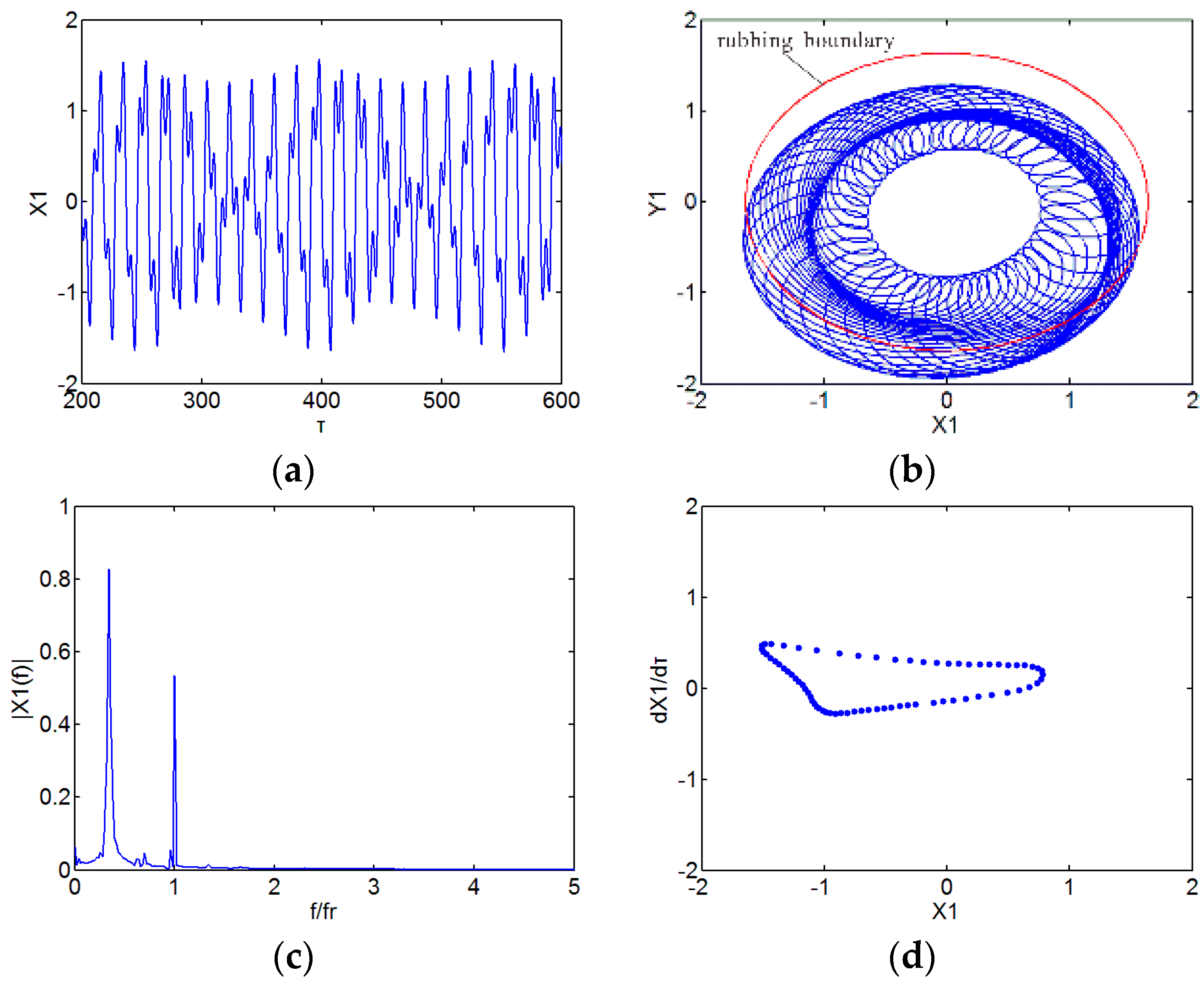
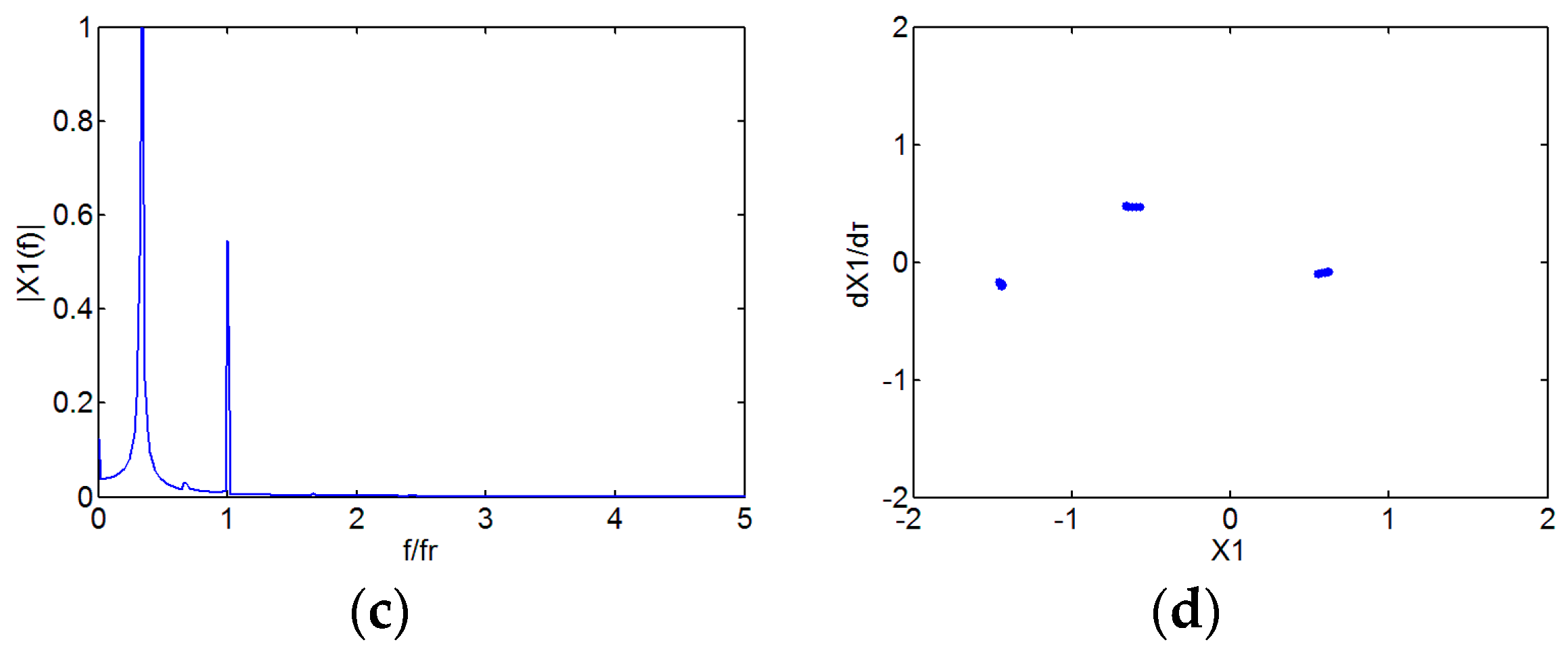
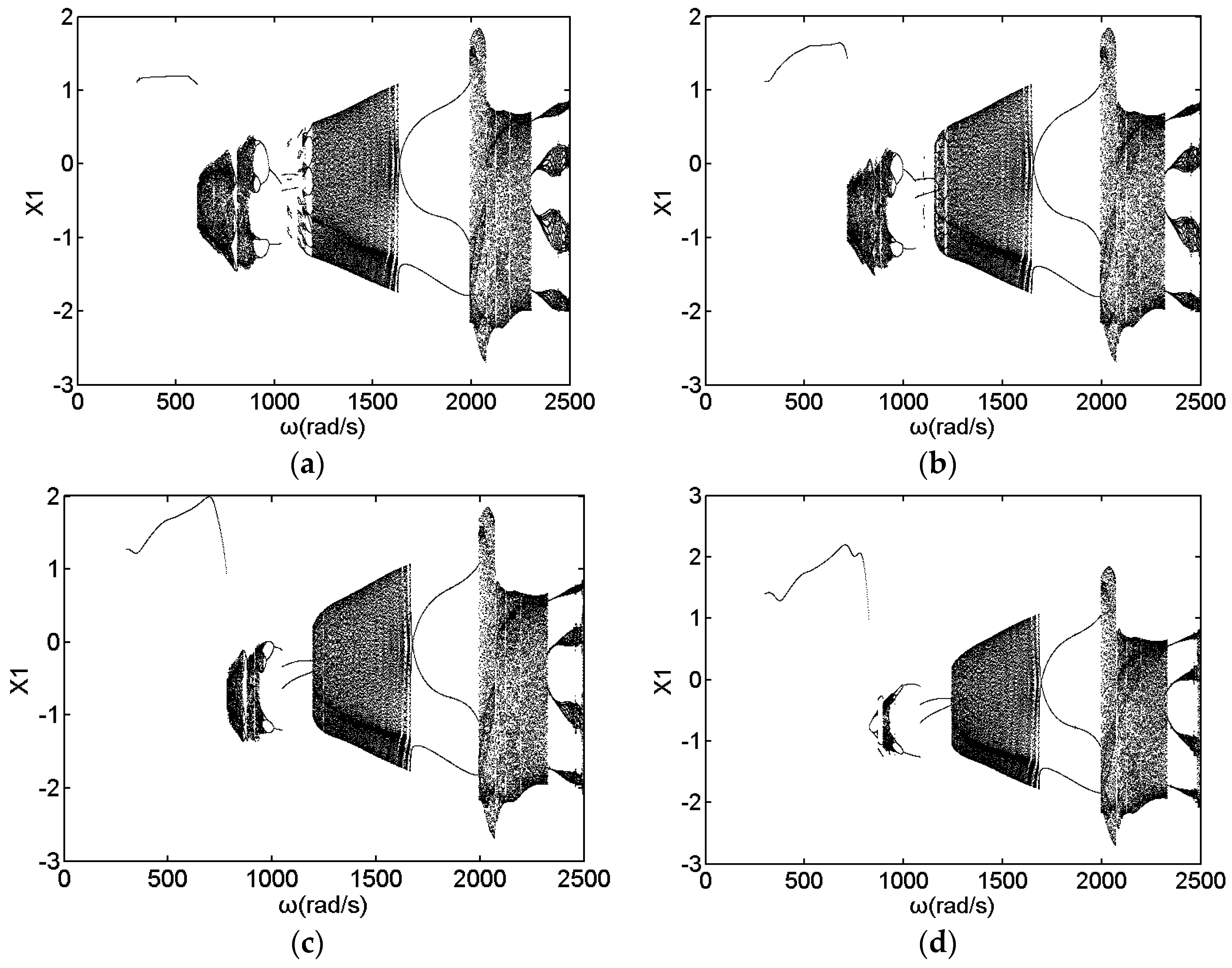
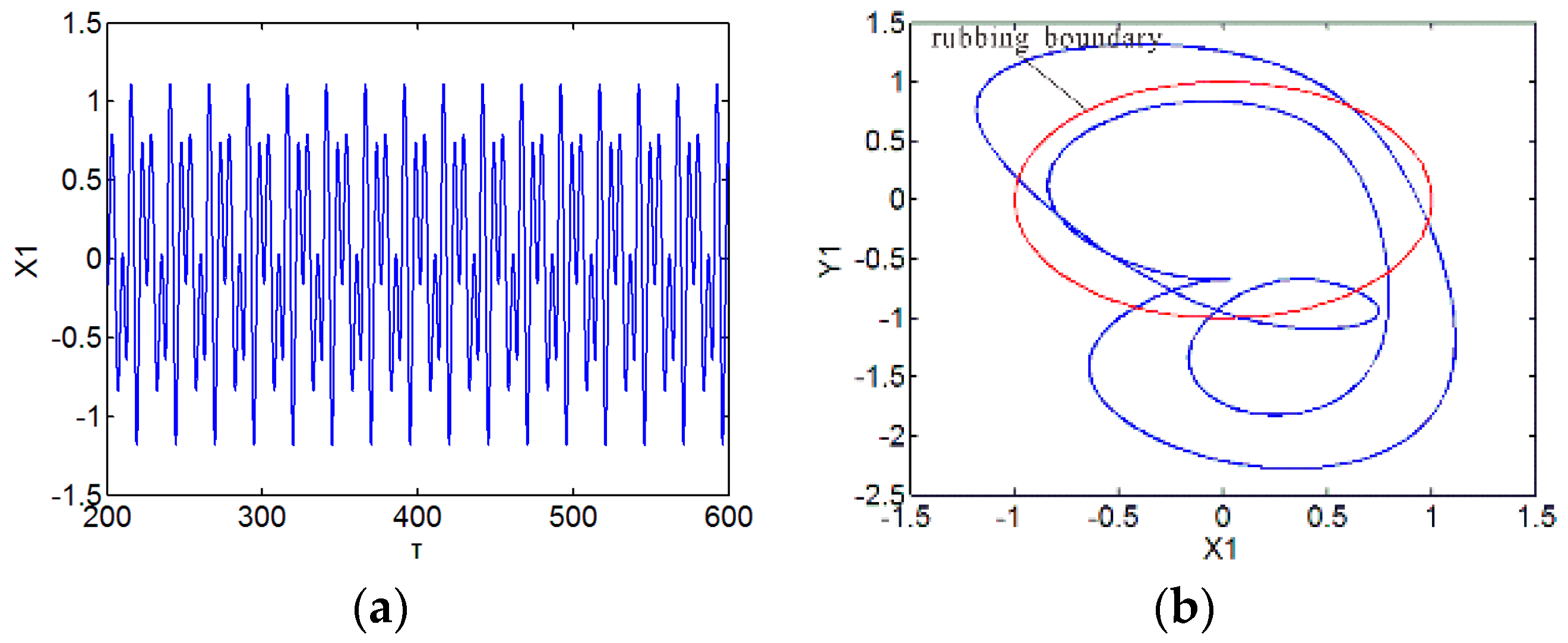
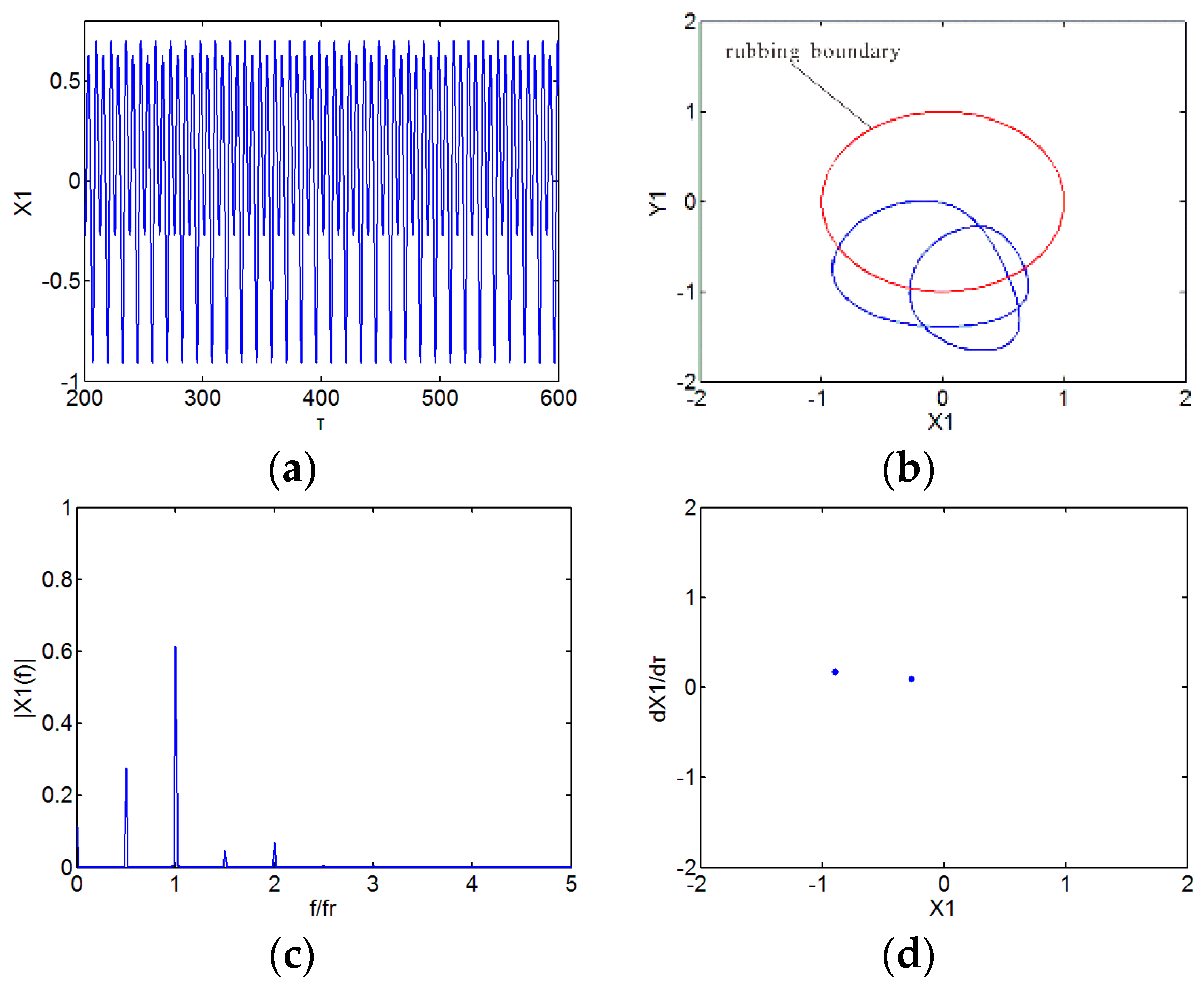
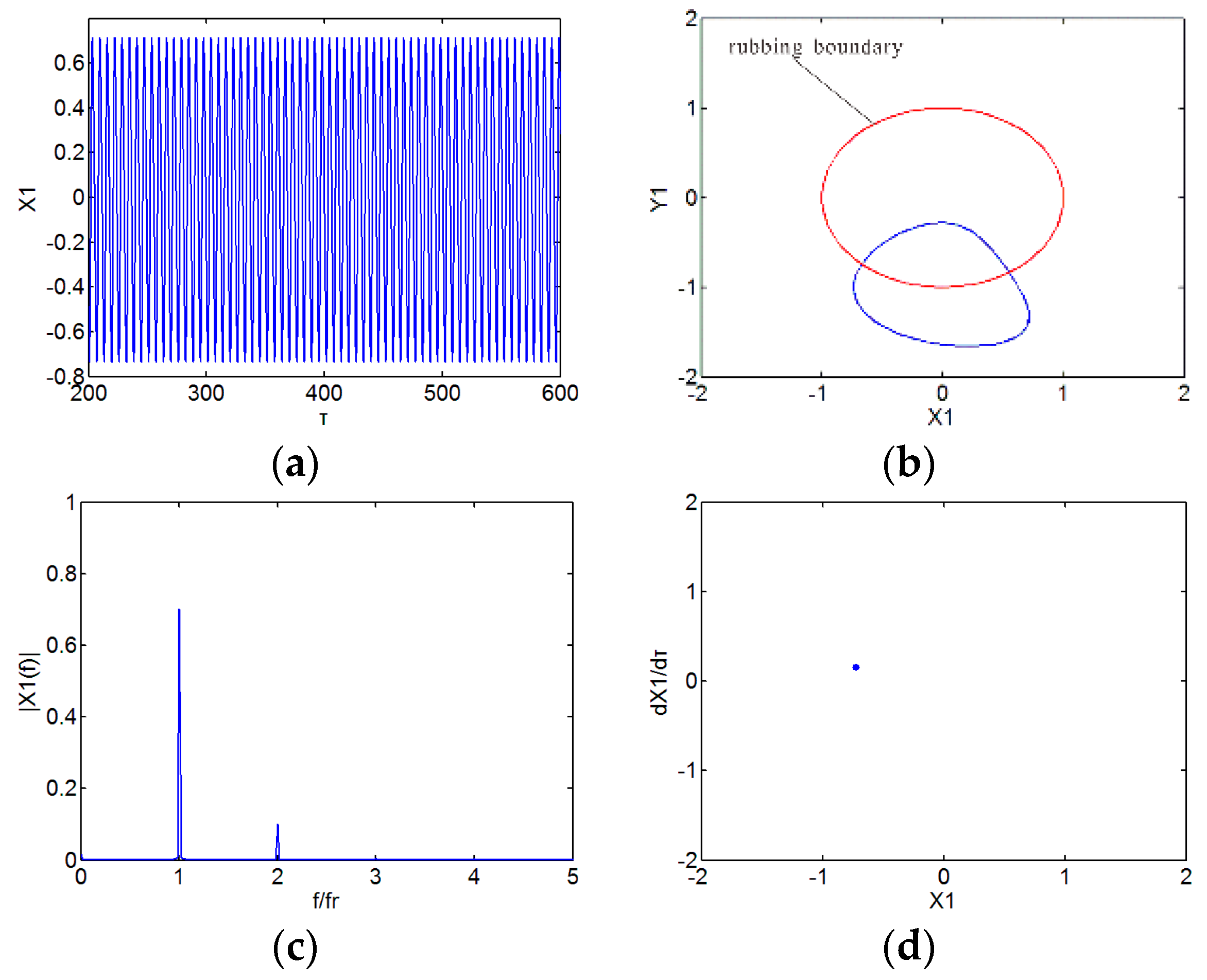
3. Numerical Results and Discussion
3.1. Effect of Speed
3.2. Effect of Initial Permanent Deflection
3.3. Effect of Radial Stiffness of the Stator
4. Conclusions
- The dynamic responses of the rod fastening rotor bearing system under rub-impact and initial permanent deflection exhibit a rich nonlinear dynamic diversity, synchronous periodic-1 motion, multi-periodic motion, chaotic motion and quasi-periodic motion can be observed through the analysis.
- Initial permanent deflection length has a great effect on the dynamic response of the system in the low-speed regions. With the increase of initial permanent deflection length, the instability speed of the system gradually rises, and the chaotic motion region becomes smaller and smaller.
- With the increase of radial stiffness of the stator, the system response becomes simpler under certain conditions. Meanwhile, the oil whirl is weaker or even disappears at a certain rotating speed.
- It is unsuitable to take the rod fastening rotor as an integral rotor in analyzing the coupled nonlinear dynamic responses of the system under rub-impact and initial permanent deflection.
Acknowledgments
Author Contributions
Conflicts of Interest
Symbols
| c | Radial clearance of bearing |
| μ | Oil viscosity |
| L | Bearing length |
| R | Bearing radius |
| δ | Sommerfeld correction coefficient |
| h | Thickness of oil-film |
| p | Dimensionless pressure of oil-film |
| Fx, Fy | Nonlinear oil-film force in x-direction and y-direction |
| fx, fy | Dimensionless nonlinear film force in x-direction and y-direction |
| PT, PN | Rub-impact force in radial and tangential direction |
| Px, Py | Rub-impact in x-direction and y-direction |
| η | Friction coefficient |
| r0 | Initial clearance |
| δ0 | Initial permanent deflection |
| kc | Radial stiffness of the stator |
| Fcx, Fcy | Restoring force of contact layer in x-direction and y-direction |
| mb1, mb2 | Lumped mass of bearings |
| m1, m2 | Lumped mass of disks |
| e1, e2 | Eccentric distance of disks |
| φ | Angle between mass eccentricity of the two disks |
| β | Angle between mass eccentricity and initial permanent deflection |
| k | Shaft stiffness |
| k1 | Linear contact stiffness |
| k1′ | Nonlinear contact stiffness |
| c1 | Damping of bearing |
| c2 | Damping of disk |
| c3 | Damping of contact layer |
| xi, yi (i = 1, 2) | Displacements of disks in x-direction and y-direction |
| xbi, ybi (i = 1, 2) | Displacements of bearings in x-direction and y-direction |
| Xi, Yi (i = 1, 2) | Dimensionless displacements of disks in x-direction and y-direction |
| Xbi, Ybi (i = 1, 2) | Dimensionless displacements of bearings in x-direction and y-direction |
| ω | Rotating speed |
| g | Gravitational acceleration |
References
- Muszynska, A. Rotor-to-stationary element rub-related vibration phenomenon in rotating machinery—Literature survey. Shock Vib. Dig. 1989, 21, 3–11. [Google Scholar] [CrossRef]
- Ma, H.; Zhao, Q.B.; Zhao, X.Y.; Han, Q.K.; Wen, B.C. Dynamic characteristics analysis of a rotor-stator system under different rubbing forms. Appl. Math. Model. 2015, 39, 2392–2408. [Google Scholar] [CrossRef]
- Ma, H.; Yin, F.L.; Wu, Z.Y.; Tai, X.Y.; Wen, B.C. Nonlinear vibration response analysis of a rotor-blade system with blade-tip rubbing. Nonlinear Dyn. 2015, 84, 1225–1258. [Google Scholar] [CrossRef]
- Ma, H.; Yu, T.; Han, Q.K.; Zhang, Y.M.; Wen, B.C.; Chen, X.L. Time-frequency features of two types of coupled rub-impact faults in rotor systems. J. Sound Vib. 2009, 321, 1109–1128. [Google Scholar] [CrossRef]
- Weaver, B.K.; Zhang, Y.; Clarens, A.F.; Untaroiu, A. Nonlinear Analysis of Rub Impact in a Three-Disk Rotor and Correction Via Bearing and Lubricant Adjustment. J. Eng. Gas Turbines Power 2015, 137, 092504. [Google Scholar] [CrossRef]
- Goldman, P.; Muszynska, A. Chaotic behavior of rotor-stator systems with rubs. J. Eng. Gas Turbines Power 1994, 116, 692–701. [Google Scholar] [CrossRef]
- Xiang, L.; Hu, A.J.; Hou, L.L.; Xiong, Y.P.; Xing, J.T. Nonlinear coupled dynamics of an asymmetric double-disc rotor-bearing system under rub-impact and oil-film forces. Appl. Math. Model. 2016, 40, 4505–4523. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, D.Y.; Ma, Y.H.; Liang, Z.C.; Hong, J. Theoretical and experimental investigation on the sudden unbalance and rub-impact in rotor system caused by blade off. Mech. Syst. Signal Process. 2016, 76, 111–135. [Google Scholar] [CrossRef]
- Varney, P.; Green, I. Nonlinear phenomena, bifurcations, and routes to chaos in an asymmetrically supported rotor–stator contact system. J. Sound Vib. 2015, 336, 207–226. [Google Scholar] [CrossRef]
- Tai, X.Y.; Ma, H.; Liu, F.H.; Liu, Y.; Wen, B.C. Stability and steady-state response analysis of a single rub-impact rotor system. Arch. Appl. Mech. 2014, 85, 133–148. [Google Scholar] [CrossRef]
- Nembhard, A.D.; Sinha, J.K.; Yunusa-Kaltungo, A. Experimental observations in the shaft orbits of relatively flexible machines with different rotor related faults. Measurement 2015, 75, 320–337. [Google Scholar] [CrossRef]
- Yunusa-Kaltungo, A.; Nembhard, A.D.; Sinha, J.K. Experimental Observations of Rotor Orbit Analysis in Rotating Machines; Springer: Berlin, Germany, 2015; Volume 21, pp. 1551–1560. [Google Scholar]
- Edwards, S.; Lees, A.W.; Friswell, M.I. The influence of torsion on rotor-stator contact in rotating machinery. J. Sound Vib. 1999, 225, 767–778. [Google Scholar] [CrossRef]
- Sun, Z.C.; Xu, J.X.; Zhou, T.; Tan, N. Study on influence of bending-torsion coupling in an impacting-rub rotor system. Appl. Math. Mech. 2003, 24, 1316–1323. [Google Scholar]
- Khanlo, H.M.; Ghayour, M.; Ziaei-Rad, S. The effects of lateral-torsional coupling on the nonlinear dynamic behavior of a rotating continuous flexible shaft-disk system with rub-impact. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 1524–1538. [Google Scholar] [CrossRef]
- Patel, T.H.; Darpe, A.K. Coupled bending-torsional vibration analysis of rotor with rub and crack. J. Sound Vib. 2009, 326, 740–752. [Google Scholar] [CrossRef]
- Yuan, Z.W.; Chu, F.L.; Hao, R.J. Simulation of rotor’s axial rub-impact in full degrees of freedom. Mech. Mach. Theory 2007, 42, 763–775. [Google Scholar] [CrossRef]
- Nicholas, J.C.; Gunter, E.J.; Allaire, P.E. Effect of residual shaft bow on unbalance response and balancing of a single mass flexible rotor. J. Eng. Power-Trans. ASME 1976, 98, 171–189. [Google Scholar] [CrossRef]
- Song, G.F.; Yang, Z.J.; Ji, C.; Wang, F.P. Theoretical-experimental study on a rotor with a residual shaft bow. Mech. Mach. Theory 2013, 63, 50–58. [Google Scholar] [CrossRef]
- Darpe, A.K.; Gupta, K.; Chawla, A. Dynamics of a bowed rotor with a transverse surface crack. J. Sound Vib. 2006, 296, 888–907. [Google Scholar] [CrossRef]
- Flack, R.D.; Rooke, J.H. A theoretical-experimental comparison of the synchronous response of a bowed rotor in five different sets of fluid film bearings. J. Sound Vib. 1980, 73, 507–517. [Google Scholar] [CrossRef]
- He, P.; Liu, Z.H.; Huang, F.L.; Liu, Z.X. Experimental Study of the Variation of Tie-bolt Fastened Rotor Critical Speeds with Tighten Force. J. Sound Vib. Meas. Diagn. 2014, 34, 644–649. (In Chinese) [Google Scholar]
- Yuan, Q.; Gao, J.; Li, P. Nonlinear Dynamics of the Rod-Fastened Jeffcott Rotor. J. Vib. Acoust. 2014, 136, 1–10. [Google Scholar] [CrossRef]
- Mat Isa, A.A.; Penny, J.E.T.; Garvey, S.D. Dynamics of bolted and laminated rotors. In Proceedings of the 18th IMAC Conference on Computational Challenges in Structural Dynamics, San Antonio, TX, USA, 7–10 February 2000.
- Hei, D.; Lu, Y.J.; Zhang, Y.F.; Liu, F.X.; Zhou, C.; Müller, N. Nonlinear dynamic behaviors of rod fastening rotor-hydrodynamic journal bearing system. Arch. Appl. Mech. 2015, 85, 855–875. [Google Scholar] [CrossRef]
- Hei, D.; Lu, Y.J.; Zhang, Y.F.; Lu, Z.Y.; Gupta, P.; Müller, N. Nonlinear dynamic behaviors of a rod fastening rotor supported by fixed–tilting pad journal bearings. Chaos Solitons Fractals 2014, 69, 129–150. [Google Scholar] [CrossRef]
- Cheng, L.; Qian, Z.W.; Chen, W.; Fan, J.D. Influence of Structural Parameters on the Bistable Response of a Disk-Rod-Fastening Rotor. J. Sound Vib. Meas. Diagn. 2012, 32, 767–772. (In Chinese) [Google Scholar]
- Qian, Z.W.; Cheng, L.; Chen, W.; Li, Y.H. Analysis on bistable response of a disk-rod-fastening rotor. J. Aerosp. Power. 2011, 26, 1563–1568. (In Chinese) [Google Scholar]
- Capone, G. Analytical Description of Fluid-dynamic Force Field in Cylindrical Journal Bearing. L'Energia Elettr. 1991, 3, 105–110. [Google Scholar]
- Adiletta, G.; Guido, A.R.; Rossi, C. Chaotic Motions of a Rigid Rotor in Short Journal Bearings. Nonlinear Dyn. 1996, 10, 251–269. [Google Scholar] [CrossRef]








© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, L.; Liu, Y.; Teng, W.; Zhou, C. Nonlinear Coupled Dynamics of a Rod Fastening Rotor under Rub-Impact and Initial Permanent Deflection. Energies 2016, 9, 883. https://doi.org/10.3390/en9110883
Hu L, Liu Y, Teng W, Zhou C. Nonlinear Coupled Dynamics of a Rod Fastening Rotor under Rub-Impact and Initial Permanent Deflection. Energies. 2016; 9(11):883. https://doi.org/10.3390/en9110883
Chicago/Turabian StyleHu, Liang, Yibing Liu, Wei Teng, and Chao Zhou. 2016. "Nonlinear Coupled Dynamics of a Rod Fastening Rotor under Rub-Impact and Initial Permanent Deflection" Energies 9, no. 11: 883. https://doi.org/10.3390/en9110883




