1. Introduction
The future trend of energy production is moving towards a higher share of renewable energy sources driven by global warming issues and the desire to reduce dependence on fossil fuels. Wind power generation is one of the most attractive of the renewable energy sources due to its availability in different areas and the economic benefits of generating large-scale power. So, the dependency on large-scale wind turbines or wind farms is increasing day by day for power generation [
1]. A doubly fed induction generator (DFIG) is one of the most widely used generators in wind turbines due to its variable speed operation, power control, improving power quality, smaller converter capacity, and grid tie feasibility. The DFIG is able to control its active and reactive power outputs as required by system operators. Although the active power depends on the energy transferred from the wind, it can be controlled in a transient manner by resorting to the mechanical system kinetic energy. This will allow more renewable energy resources with DFIG as a combined system to be connected to the grid. When two or more renewable energy resources generate maximum power by controlling the active power of DFIG, the total system power can be controlled to fulfill the grid requirement. In the case of a weak grid, where the voltage may fluctuate, the DFIG may be ordered to produce or absorb an amount of reactive power to or from the grid, with the purpose of voltage control. Therefore, the control technologies and the dynamic characteristics of the variable-speed constant-frequency (VSCF) doubly fed induction generator are important topics in wind energy research [
2].
In doubly-fed configuration, two back-to-back connected converters provide the required magnetization current at rotor windings. In fact, three phase power supply or grid connection to a three phase converter provides a stable DC-link voltage. This converter is usually called grid side converter (GSC). The DC-link voltage can be used as the voltage source for the other three phase converters, which are directly connected to the rotor winding terminals and called rotor side converters (RSC).
Although the main task of GSC is to keep the DC-link voltage constant, it may also be used to compensate for the reactive power or in some cases to remove the reactive power pulsation during unbalanced conditions [
3]. The RSC would provide the required magnetization current waveforms in rotor windings to generate the required active and reactive power at stator terminals.
According to a survey done by O. Carlson
et al. [
4], the energy production can be increased by 2%–6% for a variable-speed wind turbine in comparison to a fixed-speed wind turbine, while D.S. Zinger
et al. [
5] stated that the increase in energy can be 39%. German brochure
et al. [
6] shows that the gain in energy generation of the variable-speed wind turbine compared to the most simple fixed-speed wind turbine can vary between 3%–28% depending on the site conditions and design parameters. Calculations of the energy efficiency of the doubly-fed induction generator system have been presented in several papers [
7,
8,
9]. A comparison to other electrical systems for wind turbines is, however, harder to find. R. Datta
et al. [
10] have made a comparison of the energy capture for different schemes of the electrical configuration,
i.e., a fixed-speed wind turbine using an induction generator, full variable-speed wind turbine using an inverter-fed induction generator, and a variable-speed wind turbine using a doubly-fed induction generator. The energy capture can be significantly enhanced by using a doubly-fed induction machine as a generator and the increased energy capture of a doubly-fed induction generator by over 20% with respect to a variable-speed system using a cage rotor induction machine and by over 60% in comparison to a fixed-speed system [
10]. Aspects such as the wind distribution and electrical and mechanical losses in the systems were neglected in that study. When the doubly fed generation method was introduced and implemented for reluctance machines [
11], the idea led to early attempts to use wound rotor induction machines for such applications. The first implementation of DFIG is recorded by R. Pena
et al. [
12], where the control strategy is based on PI controllers in conjunction with a sinusoidal PWM that ends up with a constant switching frequency. This work was followed by more research in control method. The detailed model-based studies on DFIG are presented by R. Pena, where the rotor position would be found through current and voltage models [
13]. Another important modeling study is reported by A. Peterson
et al. [
14], namely the grid integration of the DFIG and its operation under voltage sag. Further studies on transient analysis of doubly fed induction generator followed in P. Ledesma
et al [
15]. Implementation of the current controlled method on DFIG using hysteresis controller to achieve better dynamics was reported by Chowdhury
et al. [
16]. To study the DFIG, RSC and GSC might be studied separately. In practice, as long as a stable DC-link voltage is provided by GSC, the RSC can operate in total isolation from the GSC. M. Mesbah
et al. [
17] provides a GSC that is able to control the DC-link voltage even in unbalanced grid voltage source condition. However, the solution lacks the reactive power compensation. Also, in most methods, RSC operates in total isolation from the GSC and a separate controller would handle the operation of each converter. On the other hand, to deal with the active power pulsations in an unbalanced grid voltage, there is a control method reported in L. Xu
et al. [
3], where both converters are considered in one control loop. Thus, the set points of GSC would be derived out of the RSC set points and the turbine generator operating condition. A feedback linearization based nonlinear voltage and slip controller are proposed by A. Balogun
et al. [
18] for a DFIG connected to an infinite bus. A direct active and reactive power controller based on stator flux estimation is discussed by B. Singh
et al. [
19]. The paper uses a basic hysteresis controller. M.E. Zarei
et al. [
20] proposed the well-known vector control and direct power control to regulate the active and reactive power generated by DFIG. A DFIG control strategy that is very similar to the conventional AVR/PSS for synchronous generator is proposed by R.Dev Shukla
et al. [
21] to support the power grid voltage and frequency.
Several researchers are still investigating the best control strategies to improve the performance of DFIG [
22], which is a key concern for DFIG. The main drawback of these works is their inability to cope with large changes in grid parameters. Furthermore, in B. Singh
et al. [
19], the rotor position is estimated using stator voltage-current and rotor current, where the rotor is connected to a battery bank with a fixed DC-link voltage producing a fixed rotor current, which is not economical and applicable in large-scale wind farms as the rotor is connected to the grid through a DC-link converter and its voltage needs to be regulated to overcome the variations in the system, and in [
23], the vector control and direct power controller for the rotor side converter is applied without any control for the DC-link voltage, which is an important issue for the practical operation of DFIG based Wind Energy Conversion System (WECS). Even though practical results from the previous studies have offered some useful hints for hardware setup, there is not enough detailed design available in the literature. For this reason, the study of DFIG through a practical implementation would help to justify various methods and ideas that will be investigated in this work.
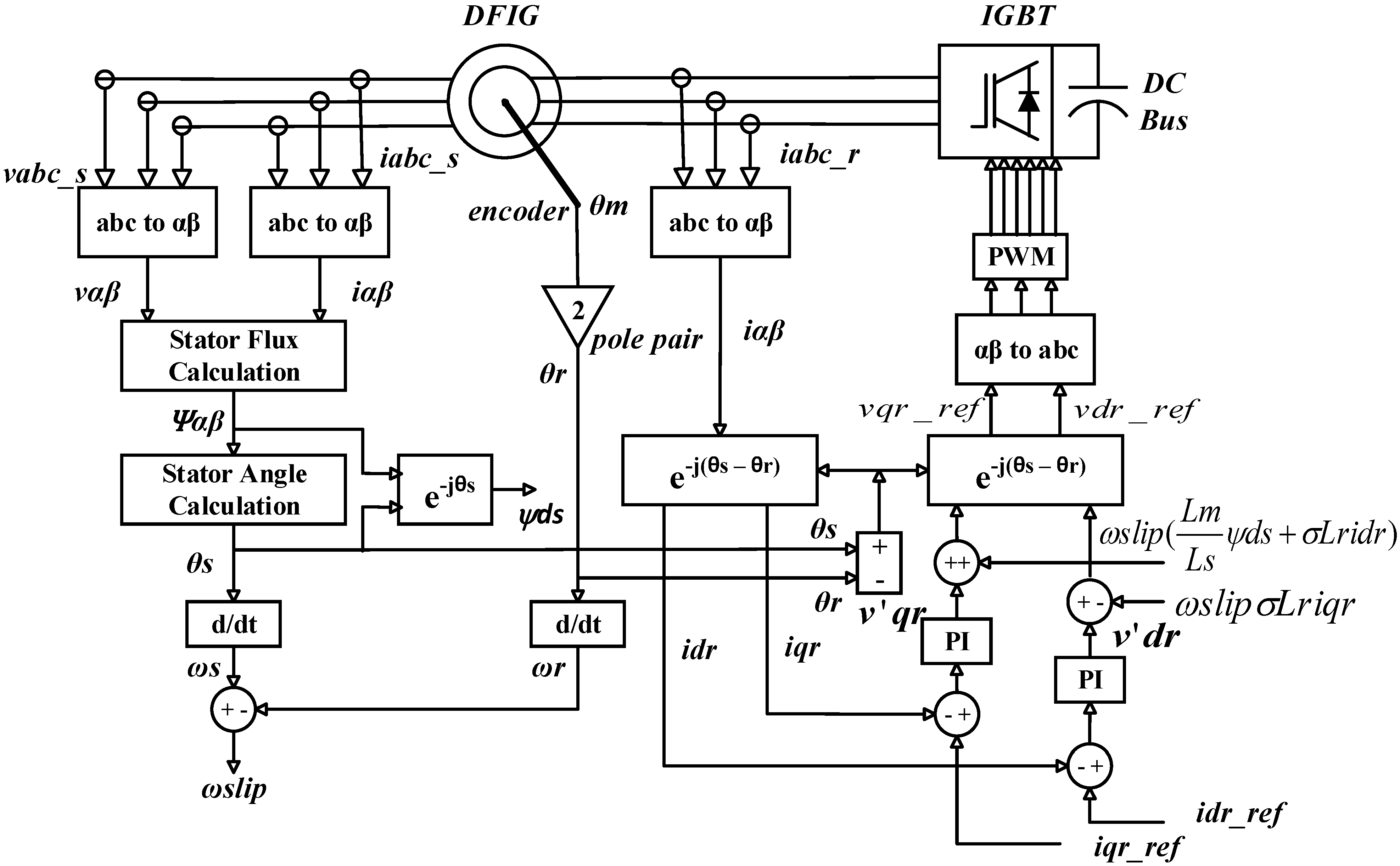
This paper proposes a theoretical and physical implementation of a control scheme for the Double Fed Induction Generator based Wind Turbine (DFIG-WT). The control design uses the field-oriented control (FOC) theory to regulate the rotor side converter (RSC) and the hysteresis control approach to regulate the grid side converter (GSC). The most challenging task in DFIG operation is to keep the DC-link voltage constant. In this paper, a hysteresis controller is developed for the voltage side controller, which has a fast dynamic response. The traditional current control strategies are mostly proportional-integral (PI) based on a linearized model; they are difficult to obtain and may not give satisfactory performance under parameter variations, load disturbances, and a large-scale wind changes. The RSC control scheme leads to an independent control of the DFIG active and reactive power by controlling the rotor currents. For its implementation, this type of control heavily relies on the electrical parameters of the machine and multiple reference frame transformations of the electrical signals (voltages and currents). However, the FOC approach delivers a great control performance in terms of robustness, transitory and steady state response, and instrumentation specifications. The grid side converter (GSC) facilitates the power exchange through the rotor converter, and also provides additional reactive power support. GSC is controlled by a hysteresis current controller in such a way as to guarantee a smooth DC-link voltage and ensure sinusoidal current in the grid side. This paper investigates DFIG power generation and converter control characteristics through a dynamic steady-state approach, which provides better and effective understanding of DFIG in wind energy applications under different control conditions in a broader spectrum.
In order to show the performance of the control scheme, an experimental platform has been designed and used. It consists of the LabVolt 2 kW DFIG system with OPAL-RT’s OP5600/8660 Real-Time HIL Controller and Data Acquisition System. The control algorithms are carried out by the Opal-RT’s powerful real-time target simulator equipped with 3.3-GHz processor core and implemented in Matlab/Simulink and RT-LAB software.
4. Experimental Results
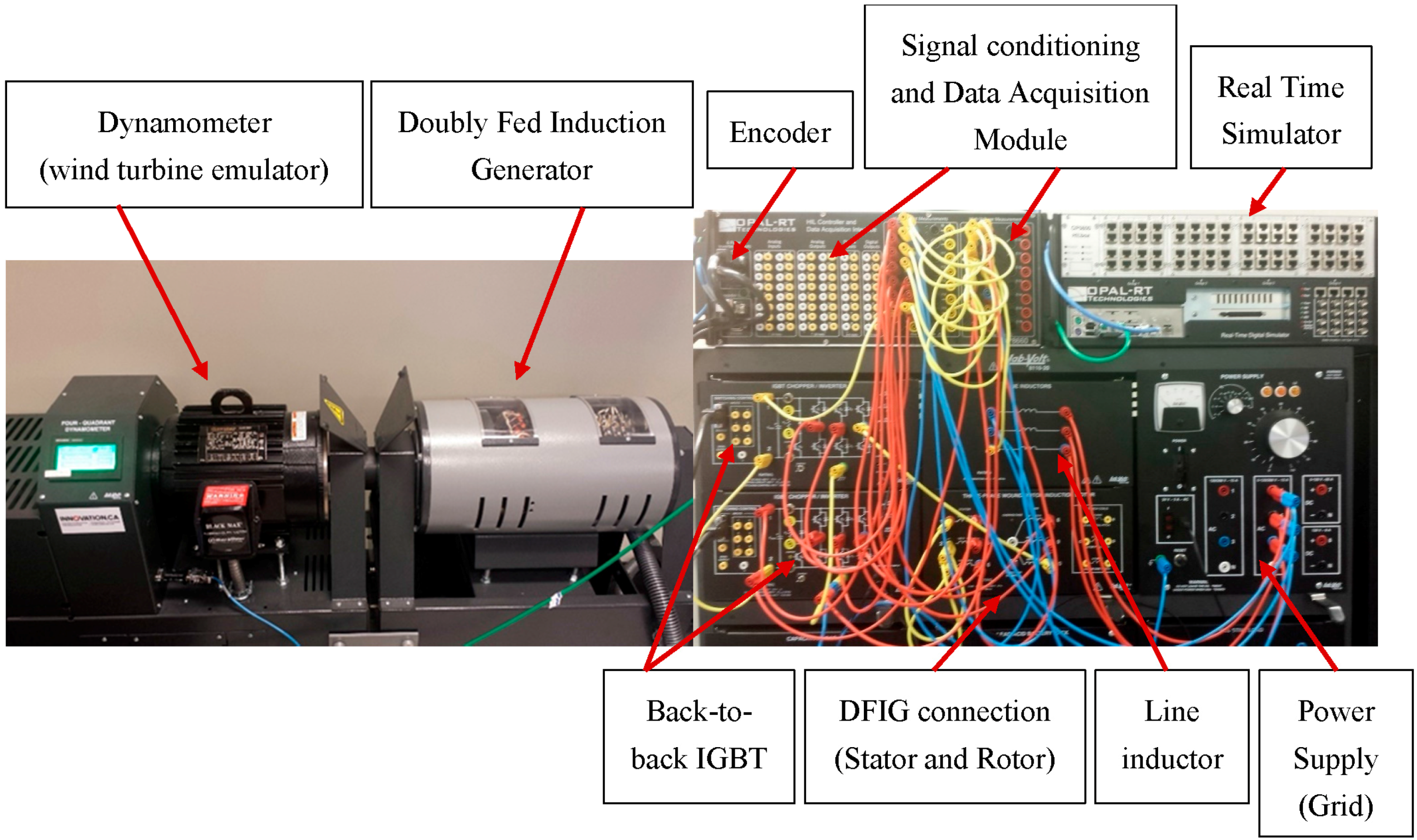
The experimental system shown in
Figure 3 consists of a doubly fed induction generator, dynamometer, IGBT inverters, line inductors, power supply, Opal RT’s data acquisition system OP8600, and real-time digital simulator OP5600, which is a powerful tool for rapid control prototyping with a processor Intel Xeon Quad Core 2.4 GHz. The system parameters are listed in
Table A1 (see the
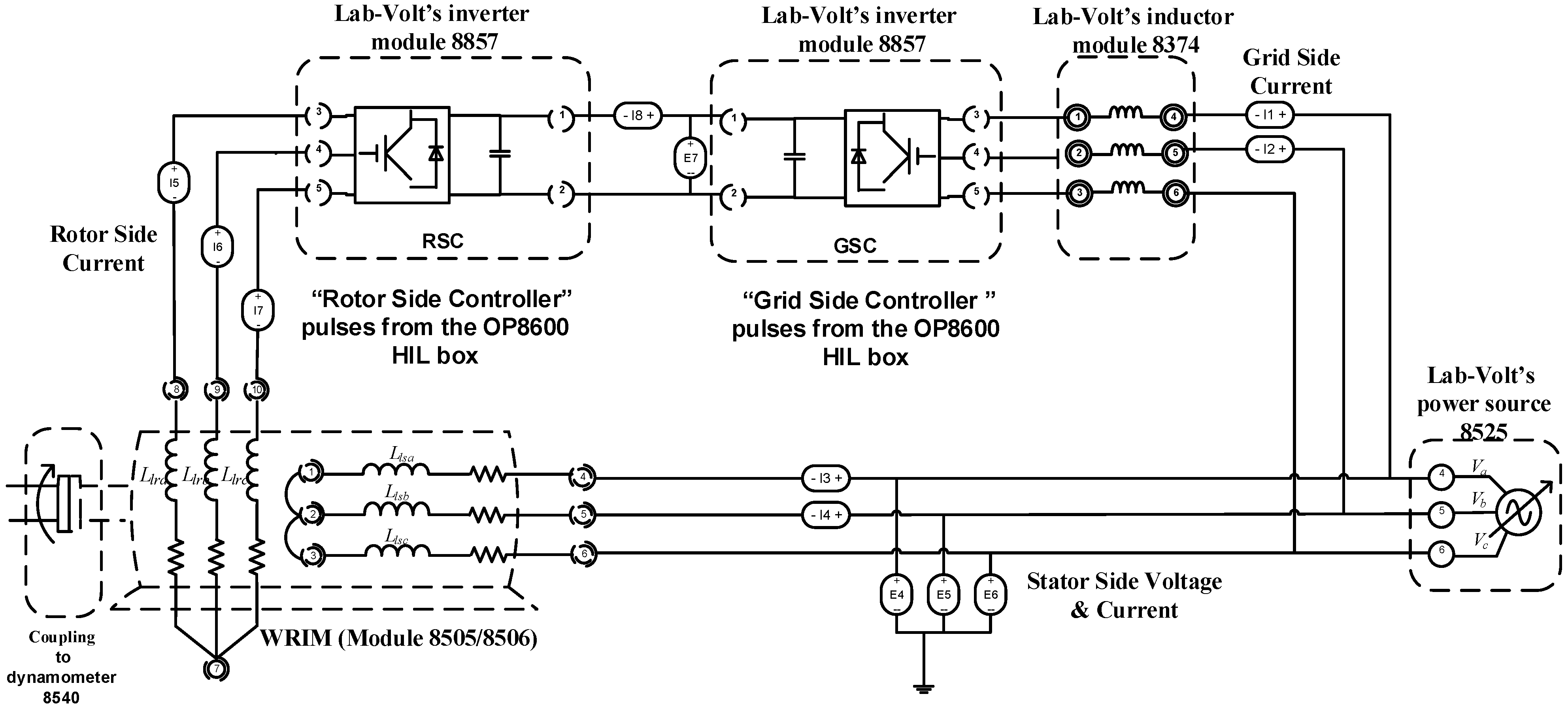
appendix). The schematic of all connected modules is shown in
Figure 4.
Figure 3.
Experimental setup to emulate WECS.
Figure 3.
Experimental setup to emulate WECS.
Figure 4.
Schematic of the connected experimental setup to emulate WECS.
Figure 4.
Schematic of the connected experimental setup to emulate WECS.
The four-quadrant dynamometer, a type of squirrel cage induction motor, works as a real wind turbine emulator by running at a variable speed to generate the effect of wind on the bladed rotor of a wind turbine.
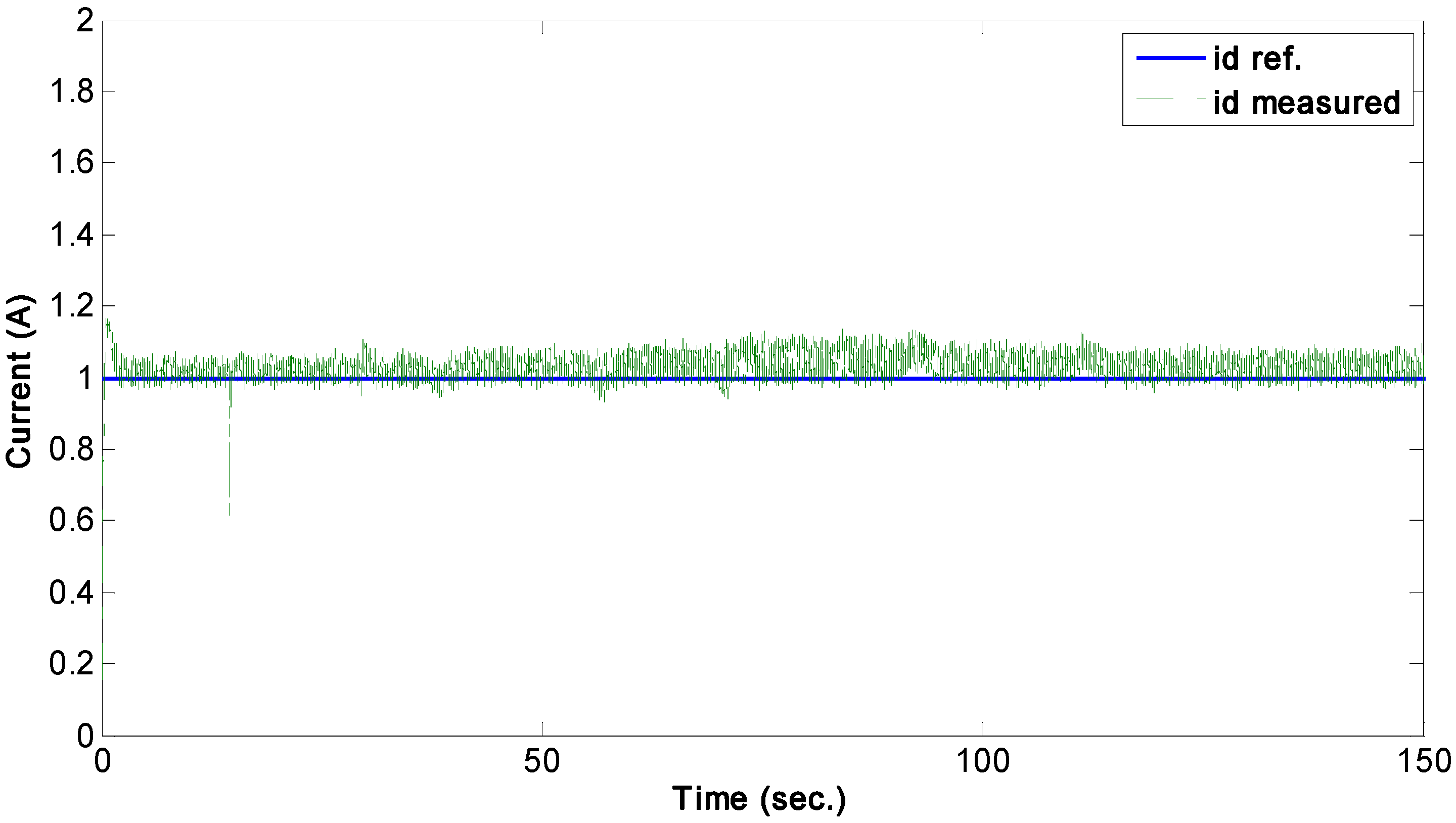
Following Equations (10) and (11), the active and reactive powers can be manipulated by controlling the rotor currents through the machine side controller. Furthermore, a proper power transfer can be ensured by regulating the DC-link voltage using the grid side controller. Several experiments are carried out in order to demonstrate the capabilities of the control system to operate the wind energy conversion under different scenarios of power extraction and transfer.
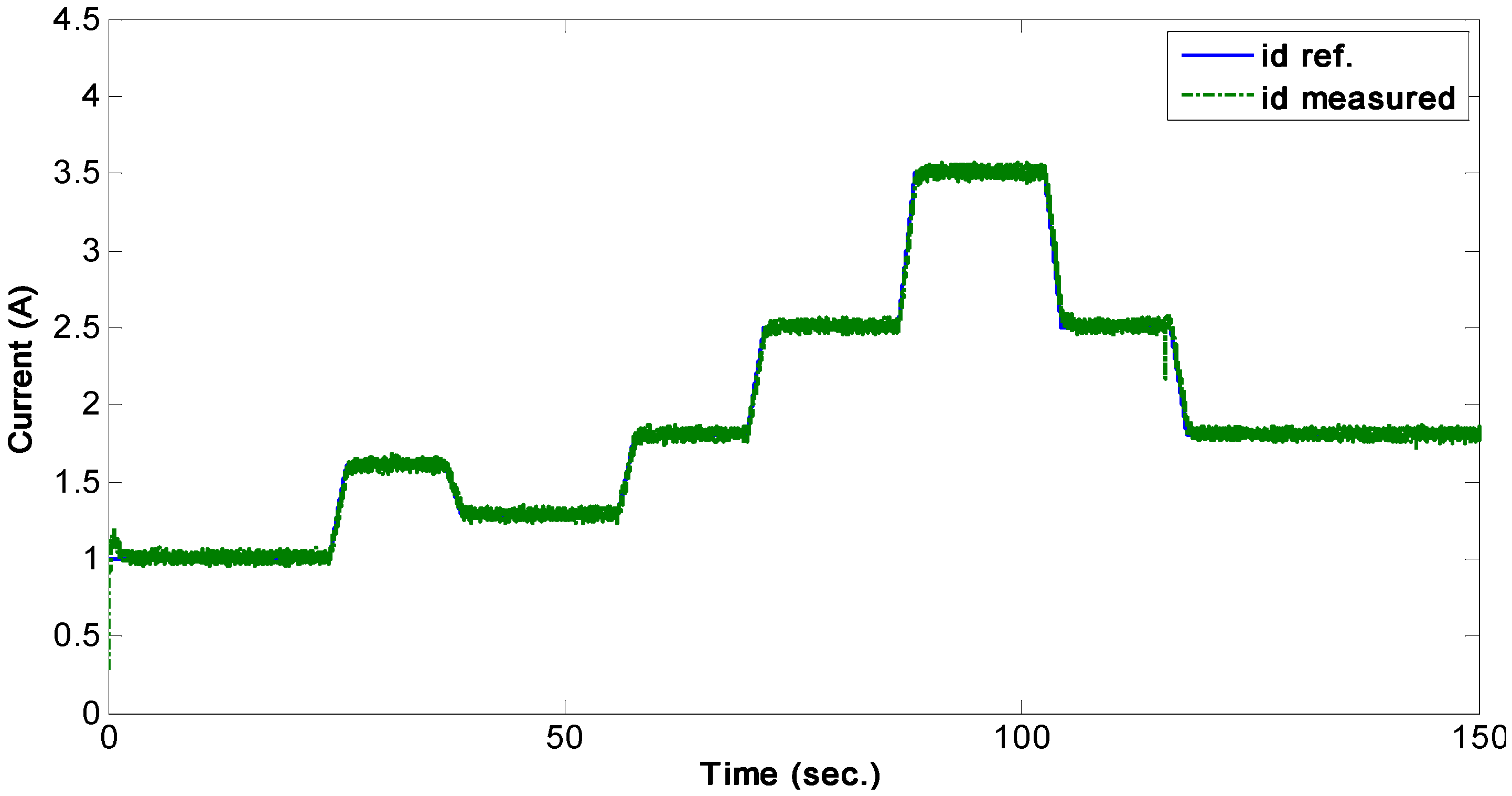
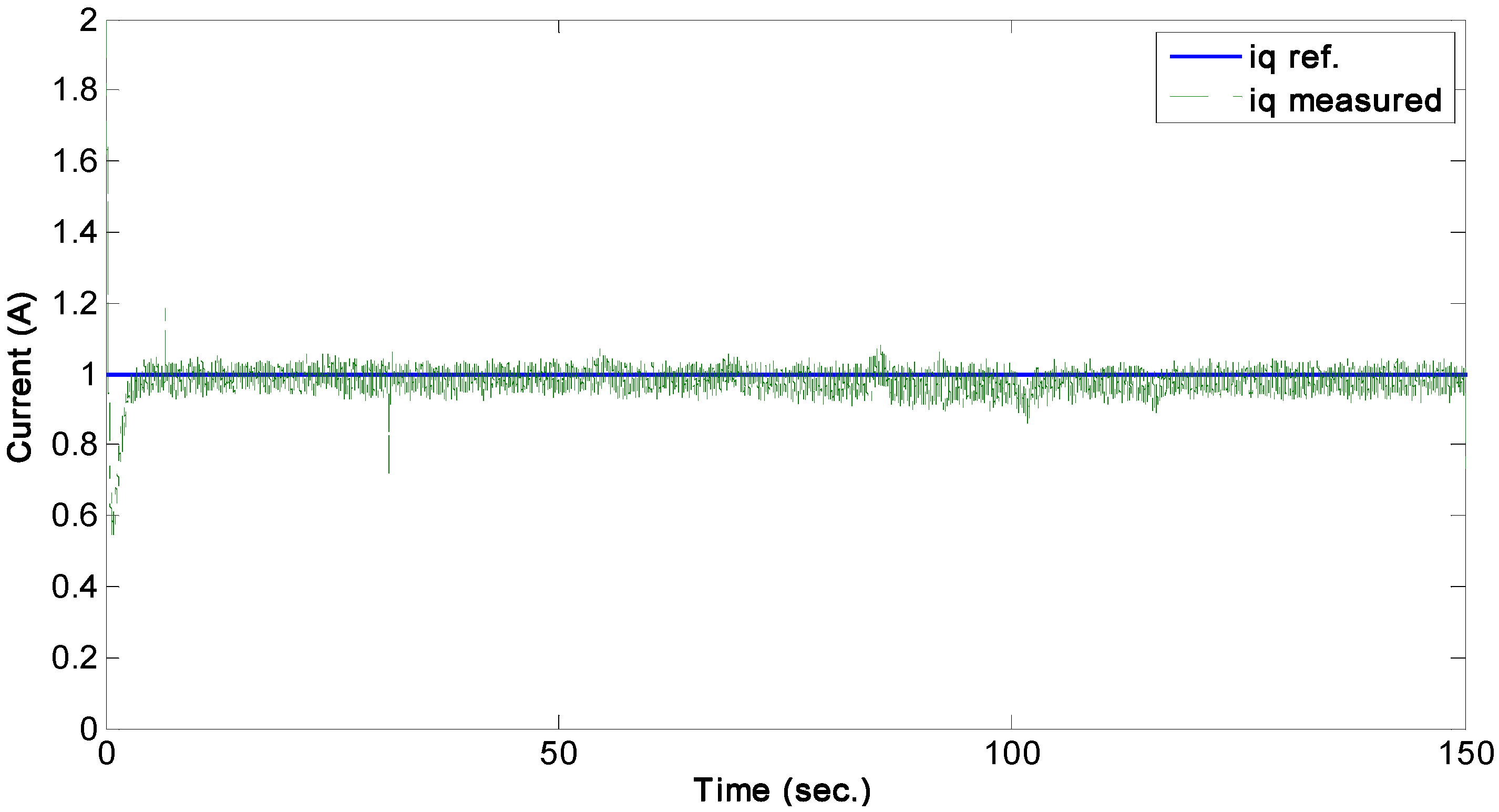
4.1. Power Control by Rotor D-Current
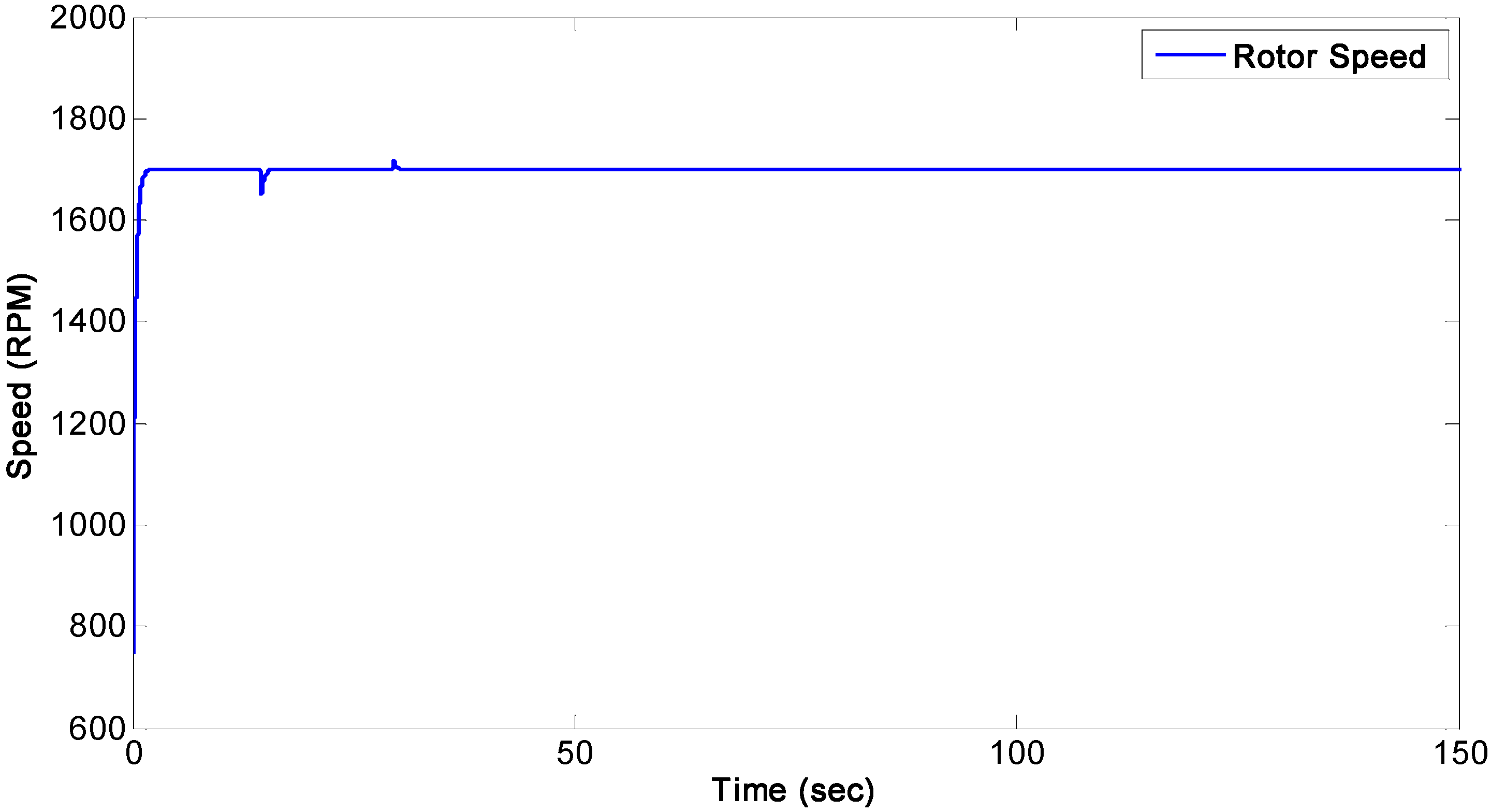
In this test, the dynamometer (wind turbine emulator) is running at constant speed, as shown in
Figure 5, and the active and reactive power can be controlled by controlling the rotor
d-current
to follow a reference
, while regulating the rotor
q-current
to be constant at
Responses of the controlled rotor
d- and
q-currents are illustrated in
Figure 6 and
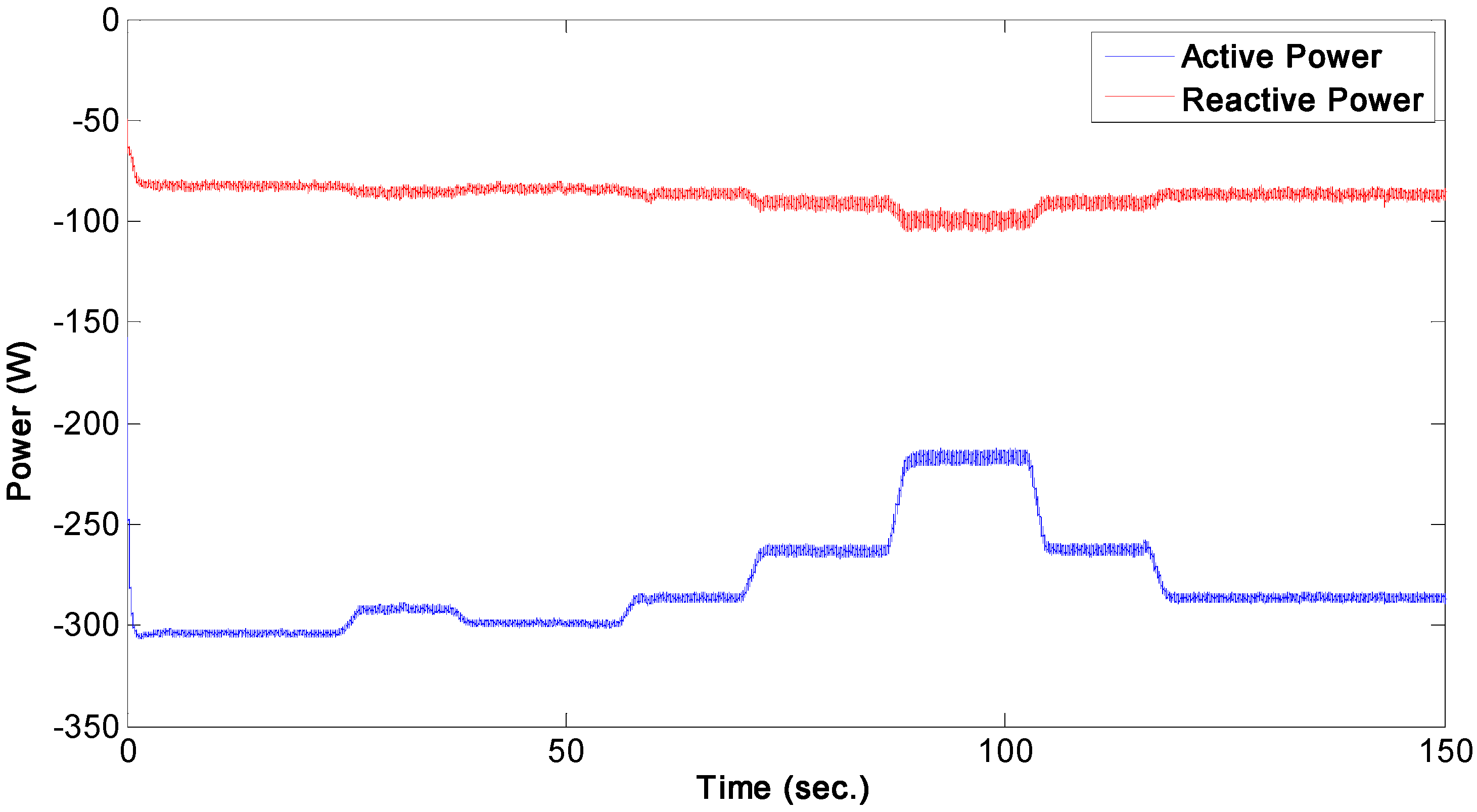
Figure 7, respectively, and it can be seen that the current tracking for both currents is successfully achieved. From the power response, shown in
Figure 8, it can be observed that the active and reactive power can be controlled by varying the rotor
d-current
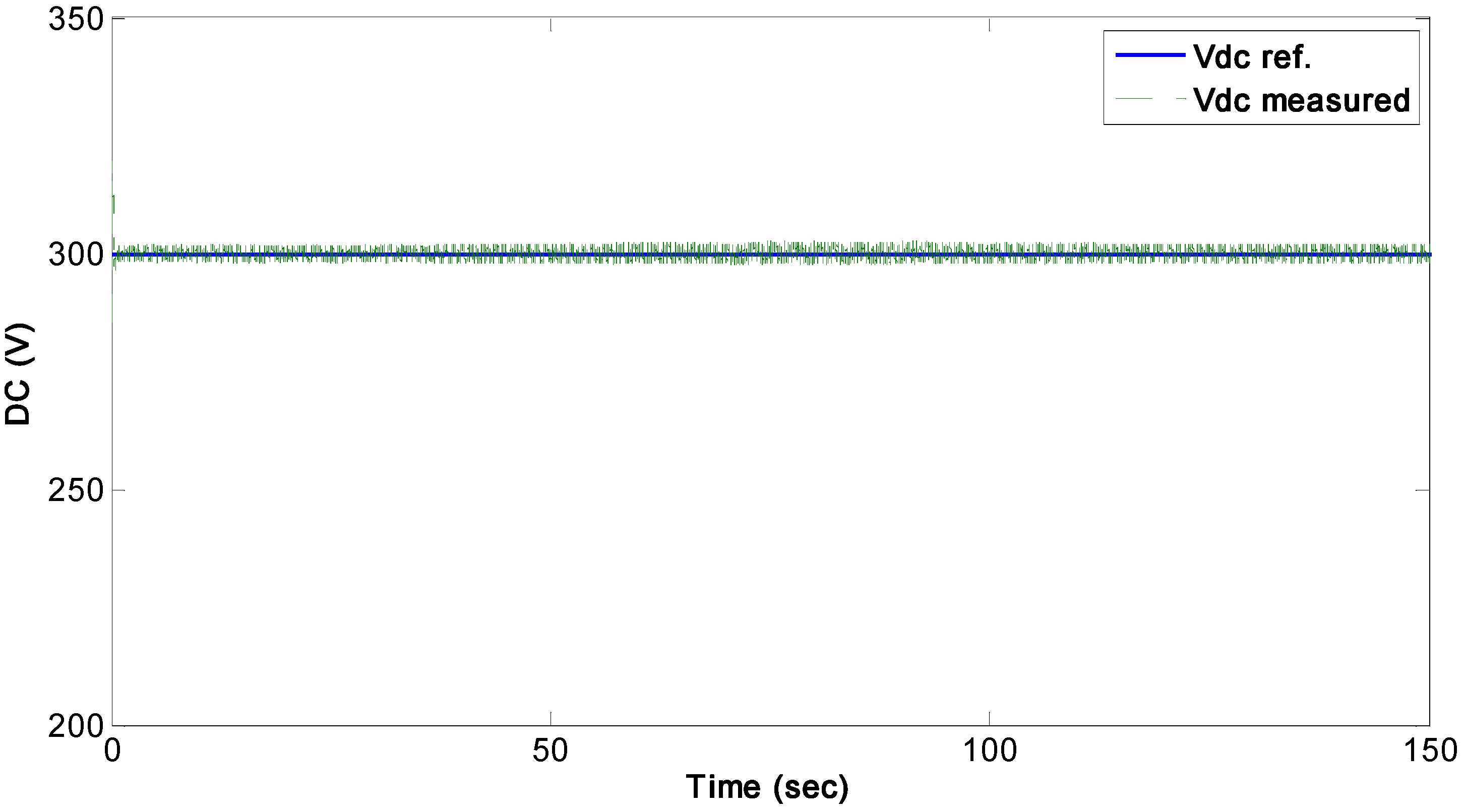
. The reactive power increases while the active power decreases to balance the total power. This is a practical controller that supports the reactive power to the grid to improve the power factor. Furthermore, the DC-link voltage is successfully regulated to follow a constant reference, as shown in
Figure 9, by the grid side controller despite the variation of the rotor
d-current at the machine side.
Figure 5.
Rotor speed of DFIG.
Figure 5.
Rotor speed of DFIG.
Figure 6.
Response of the controlled rotor d-current.
Figure 6.
Response of the controlled rotor d-current.
Figure 7.
Response of the controlled rotor q-current.
Figure 7.
Response of the controlled rotor q-current.
Figure 8.
Power response by varying the rotor d-current.
Figure 8.
Power response by varying the rotor d-current.
Figure 9.
DC-link voltage regulation.
Figure 9.
DC-link voltage regulation.
4.2. Power Control by Rotor Q-Current
Now, the active and reactive powers can be controlled by controlling the rotor
q-current
to follow a reference
, while regulating the rotor
d-current
to be constant at
as shown in
Figure 10 and
Figure 11, respectively. It can be observed that the current tracking performance is good. From the power response, shown in
Figure 12, it can be observed that the active power can be varied by controlling the rotor
q-current to follow a reference
equivalent to the desired active power, while the reactive power increases to balance the power with the grid.
Figure 10.
Response of the controlled rotor q-current.
Figure 10.
Response of the controlled rotor q-current.
Figure 11.
Response of the controlled rotor d-current.
Figure 11.
Response of the controlled rotor d-current.
Figure 12.
Power response by varying the rotor q-current.
Figure 12.
Power response by varying the rotor q-current.
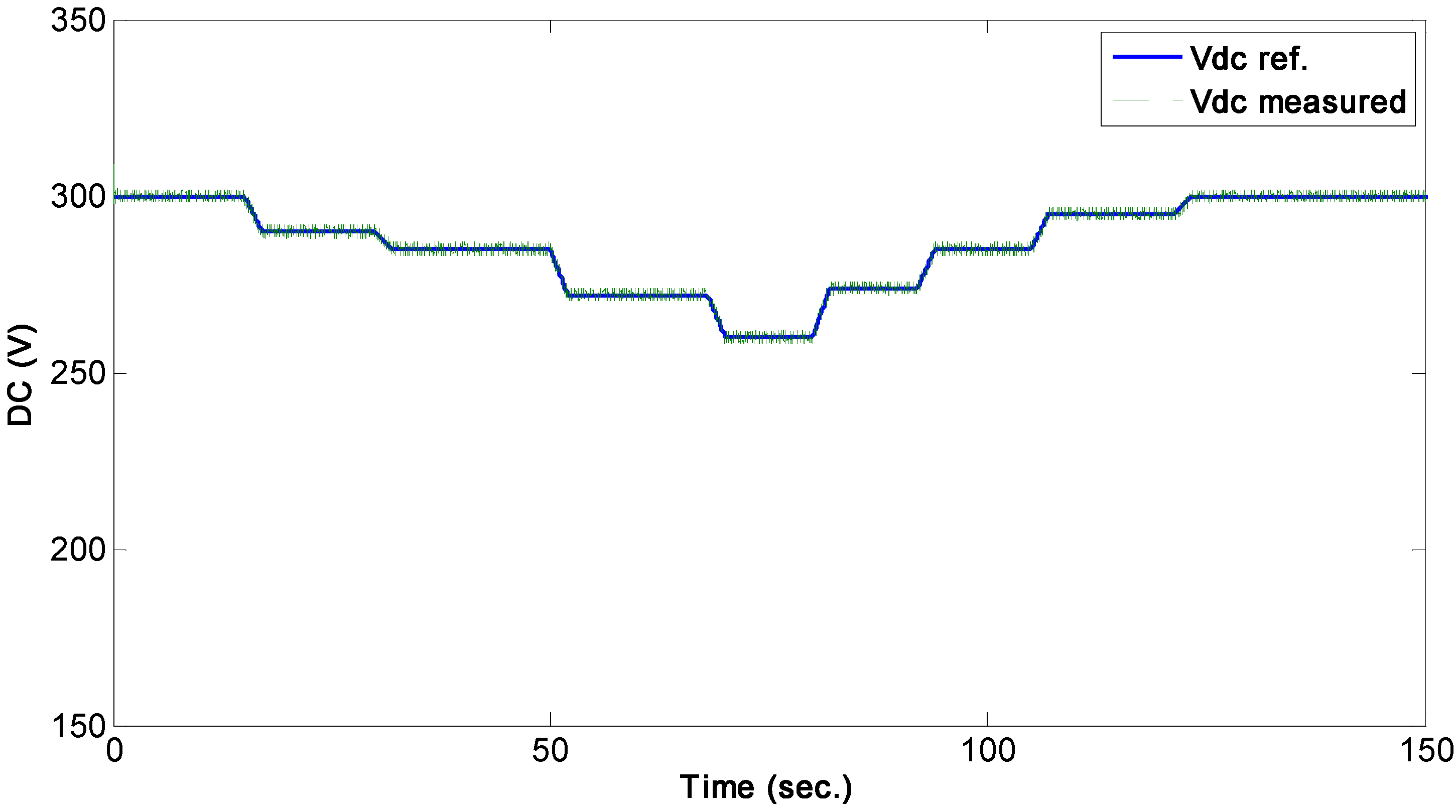
4.3. Effect of the DC-Link Voltage Variation on the Rotor Current Control
In this section, the effect of a variable DC-link voltage on the performance of the RSC current controllers is tested. The DC-link voltage is controlled to follow a varying reference, as shown in
Figure 13, at the grid side, while the
d-q currents are controlled to track the desired references, as shown in
Figure 14 and
Figure 15, at the machine side simultaneously. It can be observed that the current tracking performance is well established despite the variation of the DC-link voltage, which ensures the high tracking performance of the overall control system at the grid and machine sides.
Figure 13.
Response of the DC-link voltage controller.
Figure 13.
Response of the DC-link voltage controller.
Figure 14.
Response of the controlled rotor d-current.
Figure 14.
Response of the controlled rotor d-current.
Figure 15.
Response of the controlled rotor q-current.
Figure 15.
Response of the controlled rotor q-current.
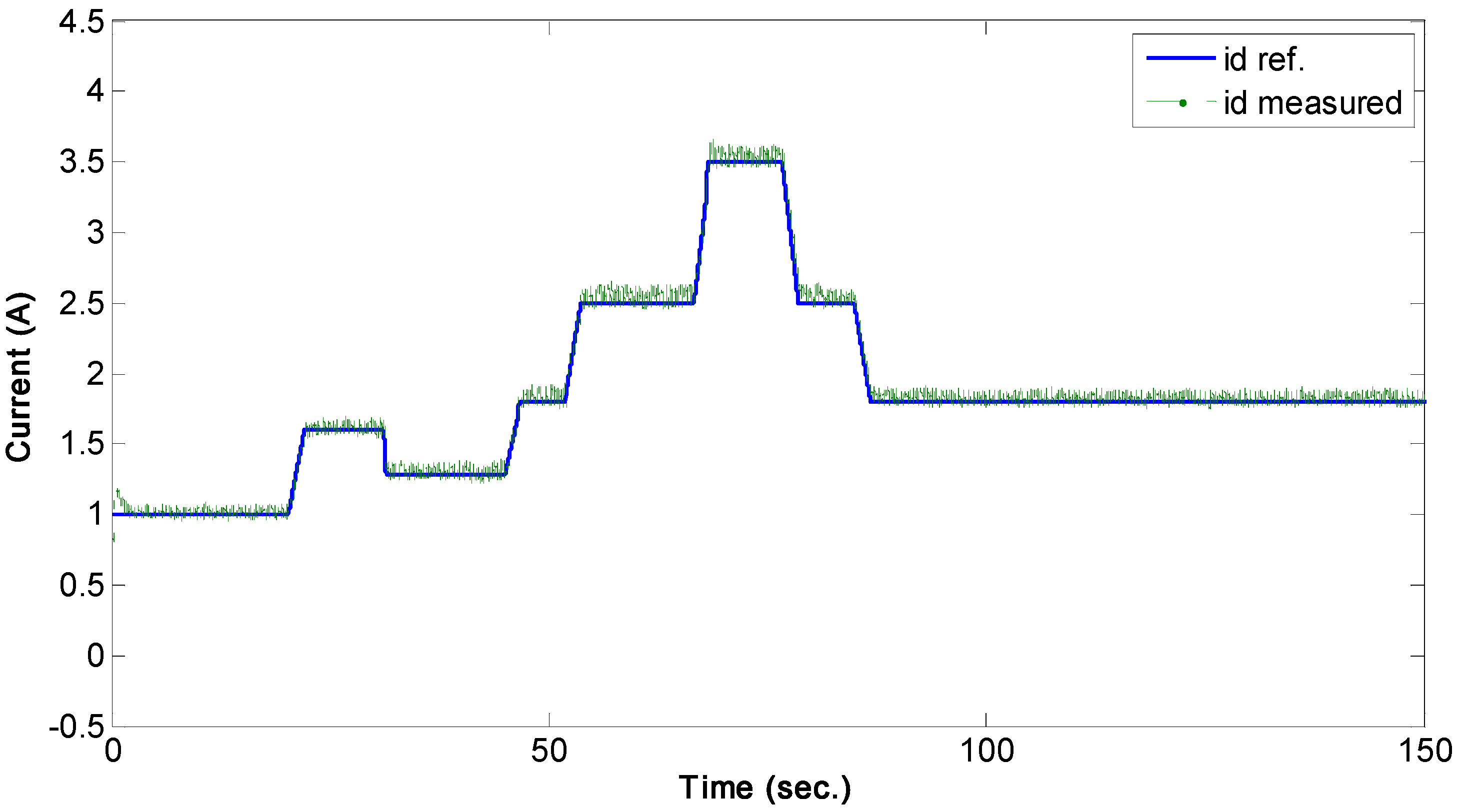
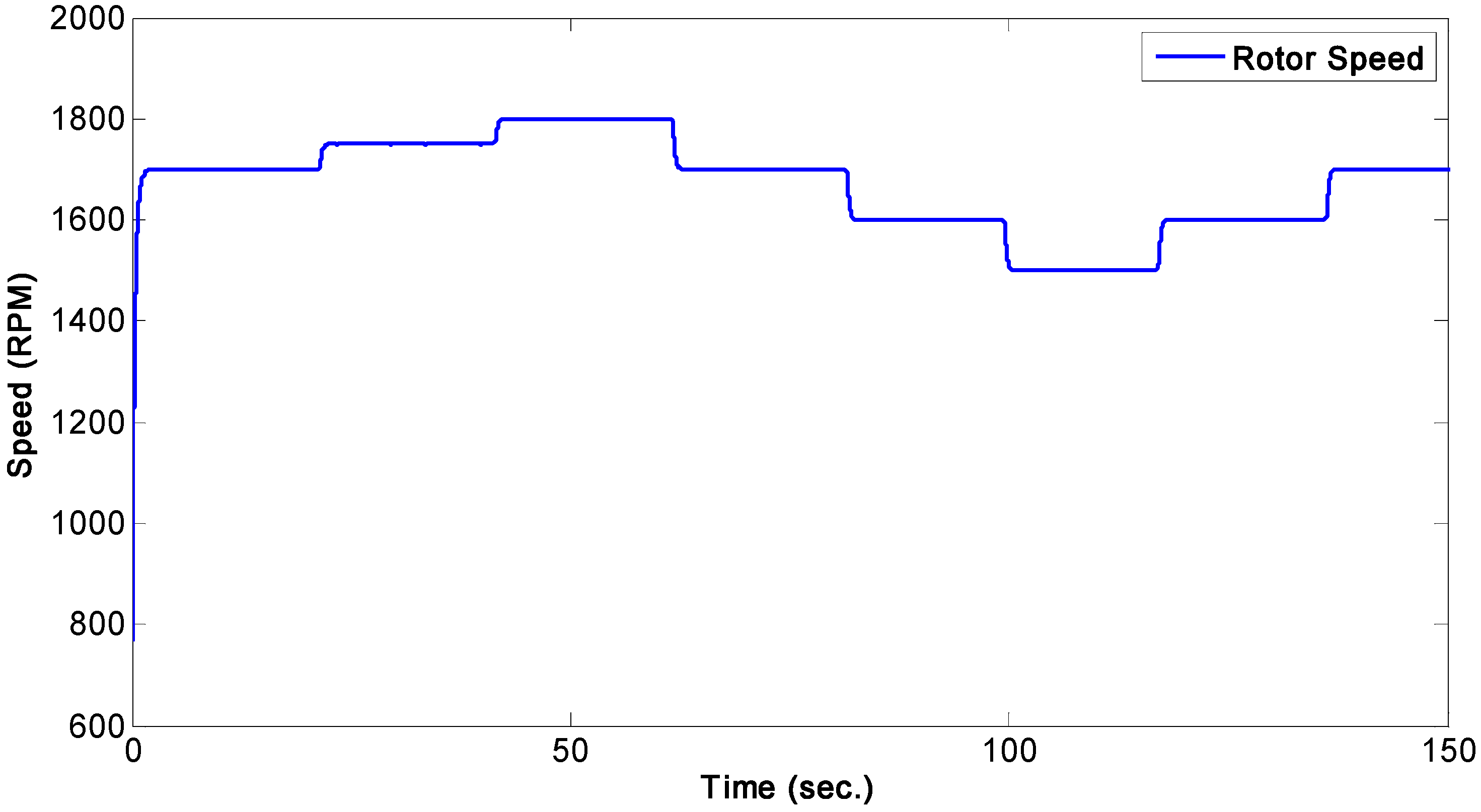
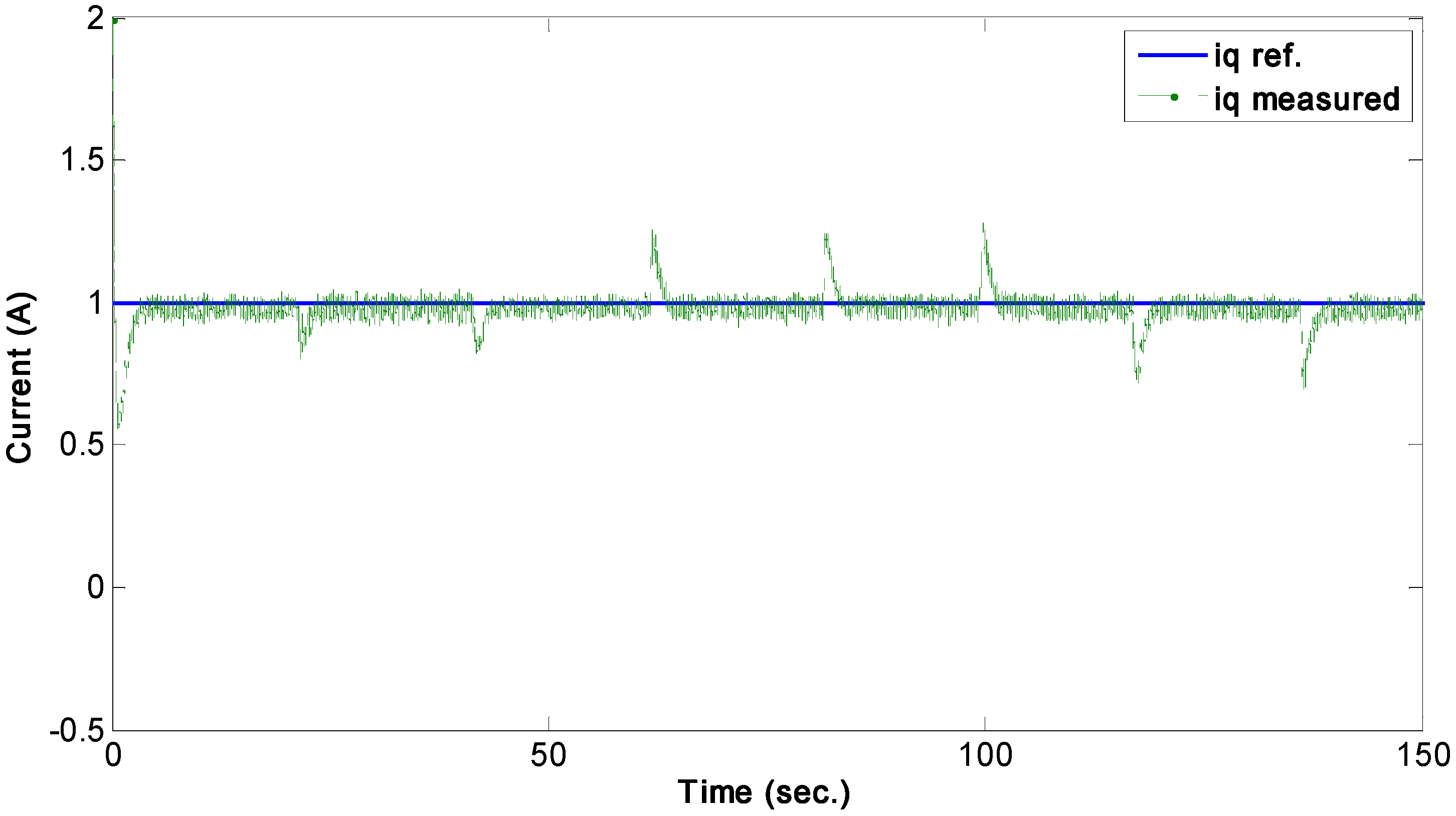
4.4. Effects of Variable Rotor Speed on the Rotor Current Control
Finally, the effect of wind speed variation, emulated by varying the rotor speed through the dynamometer, on the rotor
d-q currents is tested by regulating the currents to follow constant references while changing the rotor speed as shown in
Figure 16. It can be observed from the
d-q current responses, shown in
Figure 17 and
Figure 18, that the
d-current component is well regulated with no effects from the rotor speed variation and the
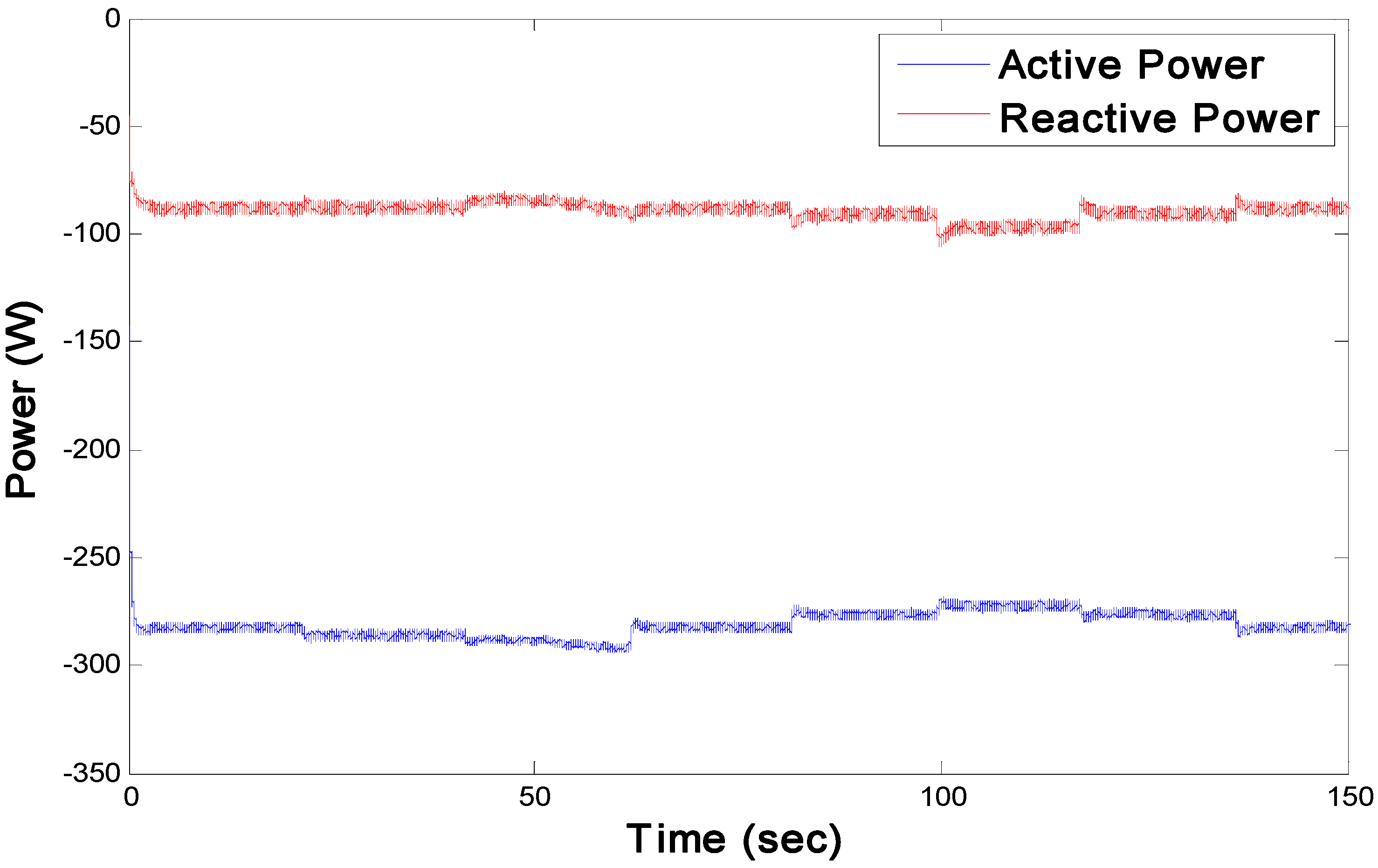
q-current component is affected by the rotor speed; however a zero-steady state tracking error is quickly established, which ensures the robustness of the control system. The response for active and reactive power is shown in
Figure 19 and it can be observed that they follow the controlled
d-q rotor currents. Therefore, the rotor side controller can be used to regulate the power by tracking appropriate rotor currents. This experiment demonstrates that the power can be controlled to track a desired reference despite the variation of the rotor speed during variable wind speeds.
Figure 16.
Variable rotor speed of DFIG.
Figure 16.
Variable rotor speed of DFIG.
Figure 17.
Response of the controlled rotor d-current.
Figure 17.
Response of the controlled rotor d-current.
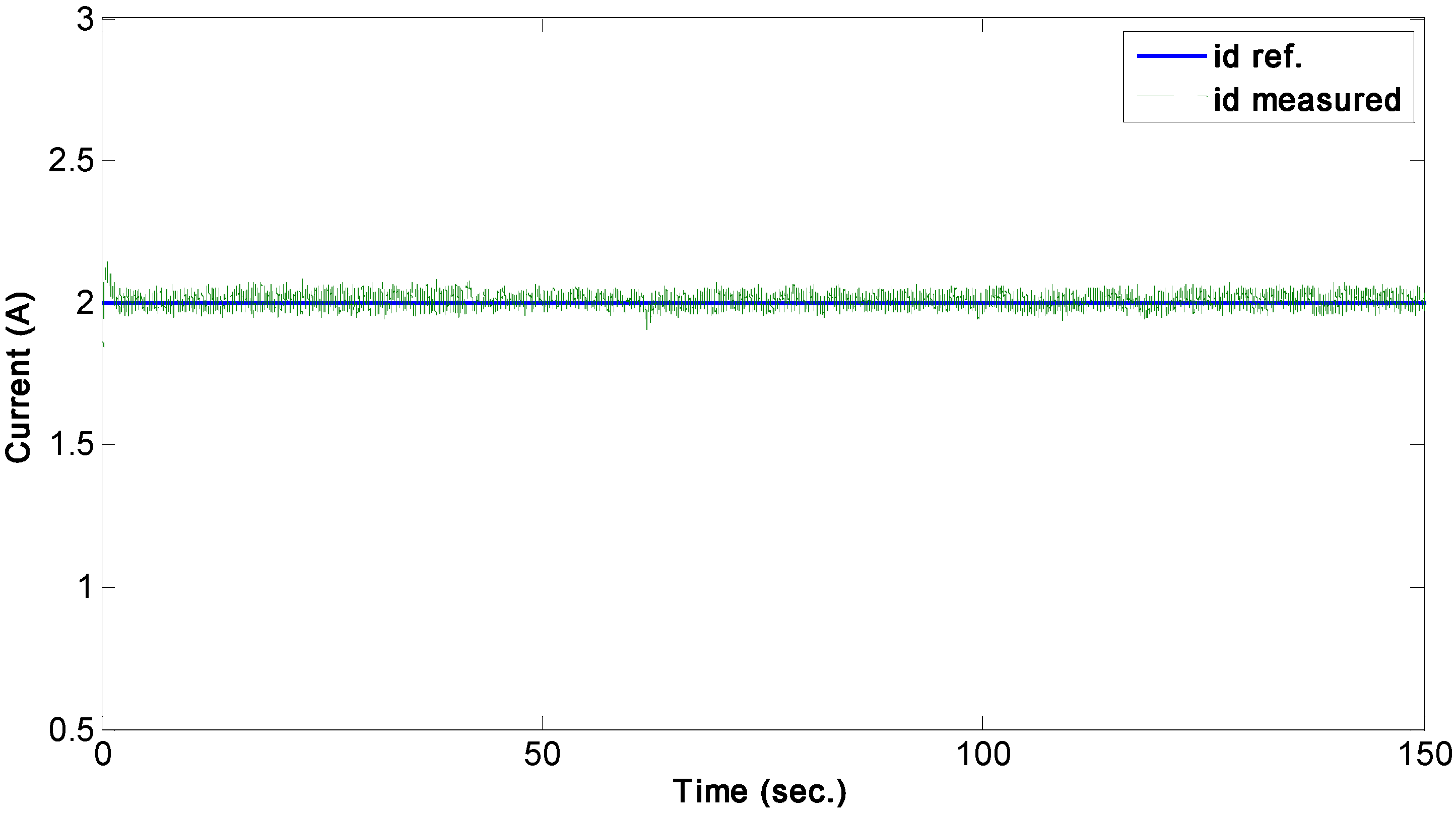
Figure 18.
Response of the controlled rotor q-current.
Figure 18.
Response of the controlled rotor q-current.
Figure 19.
Power response for rotor speed variation.
Figure 19.
Power response for rotor speed variation.