1. Introduction
This is a follow-up paper of a series on closed loop control systems for power system transient stability. The previous work proposed a real-time approach to detect transient instability with high accuracy and wide applicability, while this paper mainly focuses on how and where to control the system after the instability is detected.
In China, transient stability control systems acquire some characteristic variables according to a large number of offline calculations and identify the stability by the combination of these characteristic variables. For unstable situations, the control quantity of different situations is obtained by repeated simulations to develop a cure table. When disturbances occur, protection devices operate on the basis of the cure table [
1,
2].
The samples consist of different situations, including power flow, grid topology and fault conditions making it hard to ensure an effective cure table. In order to decrease the number of samples and improve the utility of the cure table, a simulation which is helpful to detect transient instability and form control law adopts measurement results to update the online power flow with a refresh cycle of 3–5 min [
3,
4,
5,
6]. Corresponding approaches has been introduced in [
5,
6], including preplanned remedial action and system integrity protection schemes, software processes and hardware requirements. To speed up the simulation, the transient energy function method, the equal area criterion, topological energy function or quasi-real-time online transient analysis are employed in the time domain simulation, which can greatly improve the efficiency [
7,
8,
9,
10,
11,
12].
In any case these methods need repeated simulations to calculate control laws by taking into account the changes in operating conditions or parameter variations. The validity of the cure table depends on the similarity between the anticipated faults and actual faults and the accuracy of the model parameters. However, a practical operating model (especially a model of the load) or the system parameters are hard to acquire. Meanwhile, the rapid development and the operation variations lead to a large number of calculation samples.
With the development of computer science and communication technology, especially the application of phase measurement unit (PMU) based on global positioning system (GPS) in power systems, wider-area measurement systems (WAMS) offer an opportunity to develop real-time protection and control systems [
13]. As a result, recently there has been a focus on online instability control, out-of-step protection and their corresponding theories.
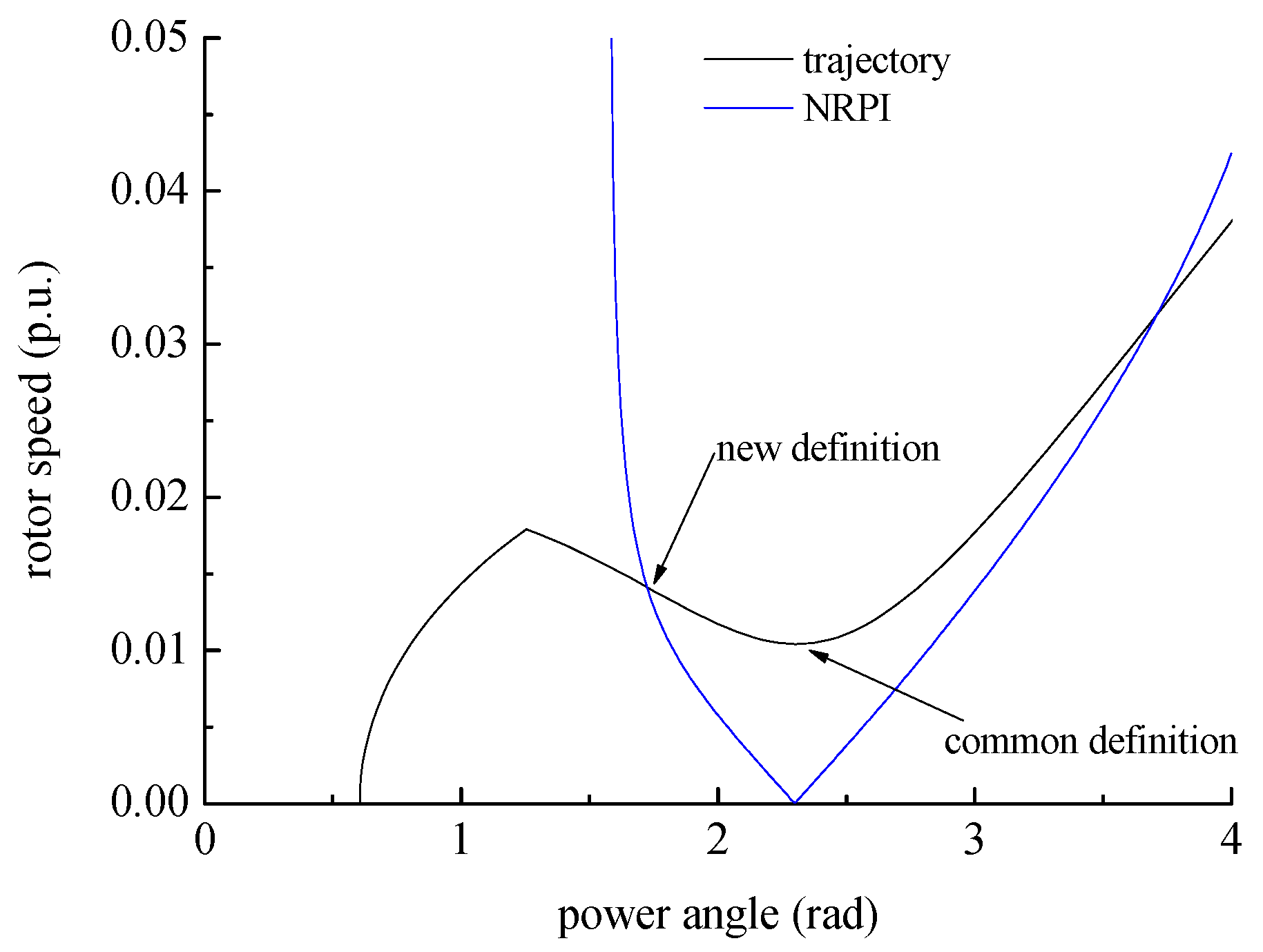
It has been reported that the geometric characteristics of the system trajectory can be employed to detect the system instability [
14]. Depending on the nature of the stability studied, Girgis has found that the characteristic shape (concave or convex) of a surface, on which a post-fault transient trajectory lies, can be used as an index for online instability detection [
15]. The assumption is proved in a phase portrait, and an instability detection method is presented, which is independent of the network structure, system parameters and model because it only uses observation data. During the process of proof, a damping coefficient is considered in the system model to keep it more reasonable [
16,
17,
18]. However, the discrete expression of the detection method in [
18] requires differential calculations. The curve of the index looks ragged. For a stable situation after disturbances, it may cause some erroneous judgments.
This paper aims to introduce a real-time transient stability control system which employs the generator speed, power angle and unbalanced power to detect the system instability and develop a control strategy. In this paper, the system instability is detected by the characteristics concave or convex shape of the trajectory. Then, the control law is achieved based on the slope of the state plane trajectory, when the power system is unstable. Because the expected variables can be obtained from the trajectory information and the calculations are very simple, the control system can be realized in real time. The simulation indicates that the mentioned transient stability control system is fast, efficient, and realizable.
3. Control Method
There are many transient stability control measures, including generator shedding and load shedding [
19,
20]. In North America, generator shedding has been proved to be one of the most effective discrete supplementary control means for maintaining stability [
21]. In this paper, generator shedding is mainly discussed too.
3.1. The Slope of the State-Plane Trajectory
According to Equation (2), the expression of the slope is related to the unbalanced power which can be changed by generator shedding. It is supposed that the system returns to a stable state by generator shedding. If the value of the slope at control time is obtained, the corresponding generator shedding can be calculated by Equation (2). To obtain the value of the slope at control time, the characteristic of the slope is analyzed below. A single machine infinite bus system is shown in
Figure 3.
Figure 3.
The topology network of the SMIB system.
Figure 3.
The topology network of the SMIB system.
Under normal conditions, the system operates at a stable equilibrium point (SEP). The initial state of the generator is 0.812 rad, 0 rad/s. A three-phase grounding fault occurs on one of the two transmission lines, and the fault is cleared by switching off the line. The clearing time is 0.18 s (critical clearing time) and 0.22 s. When the system is unstable, different control quantities are taken. The trajectory of the state-plane and the slope of the trajectory are shown in
Figure 4 and
Figure 5.
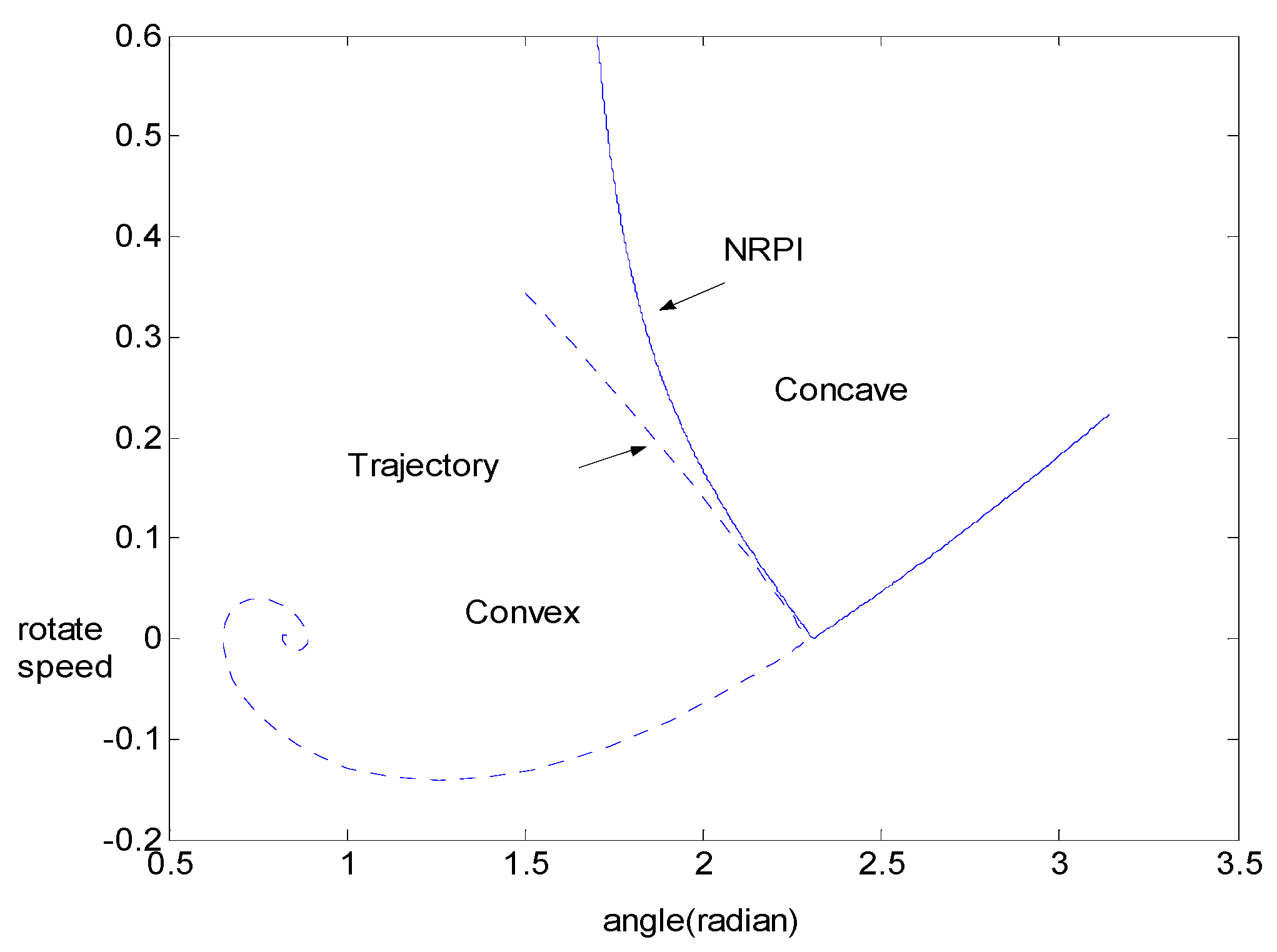
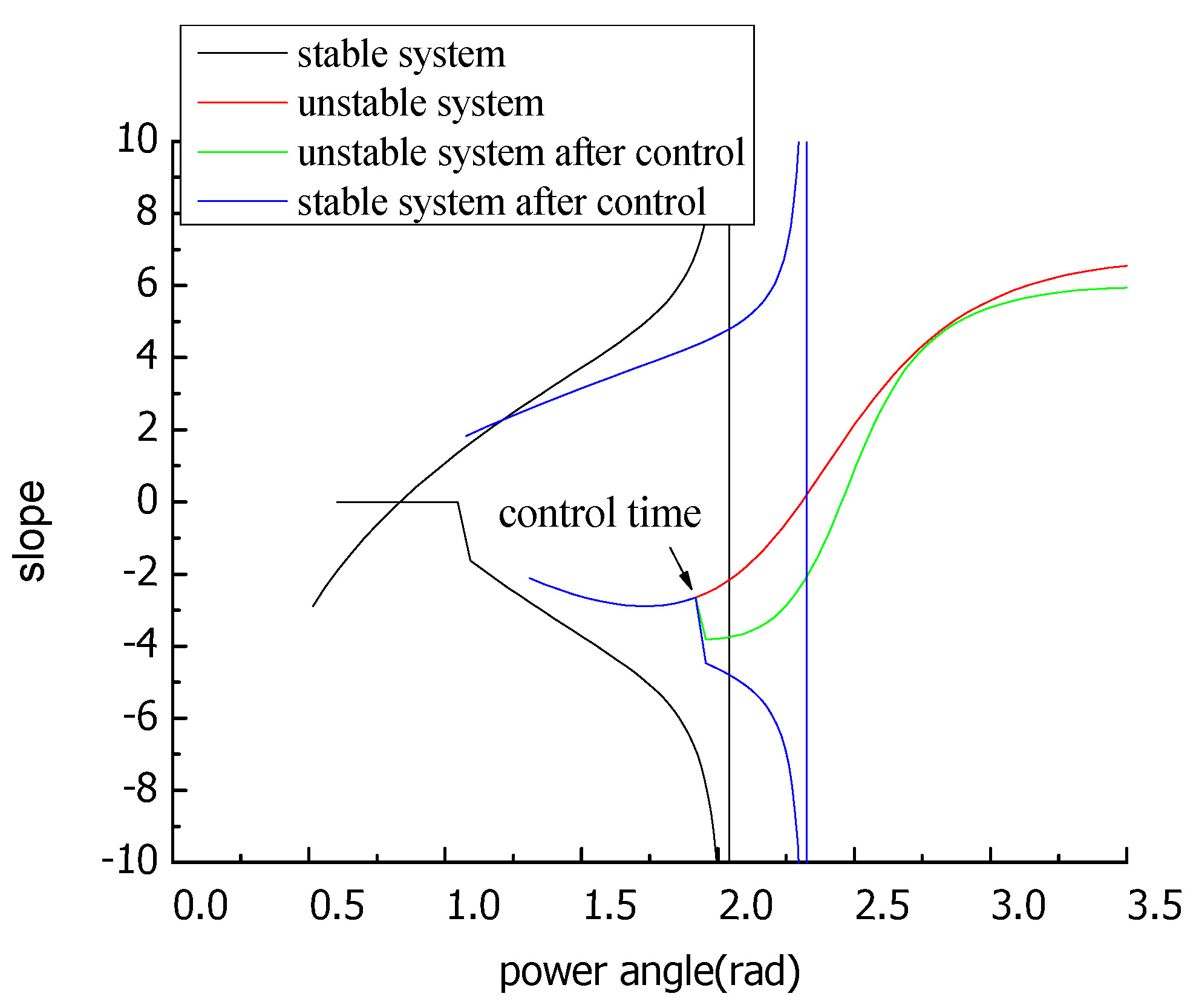
For the black curve, the system is stable without control. The trajectory swings back at the far end point (FEP) which exists only in a stable system. The slope of the trajectory keeps decreasing with the mutation at the FEP.
For the red curve, the system is unstable without control. The slope begins to increase after the inflexion point and grows to zero at the dynamic saddle point (DSP).
For the green curve, the system is unstable with insufficient control. A sudden change of the slope is caused by the control at the control time. The larger the control quantity is, the greater the change of the slope at the control time is. However, the slope begins to increase at another inflexion point after control.
For the blue curve, the system is stable with enough control. The control causes a sudden reduction of the slope at the control time, and the slope keeps decreasing after the control with the mutation at the FEP. Apparently, the trajectory of the state-plane turns back at the unstable equilibrium point (UEP) by the minimum control quantity.
Figure 4.
State-plane representation of speed and angle.
Figure 4.
State-plane representation of speed and angle.
Figure 5.
The slope over power angle.
Figure 5.
The slope over power angle.
The derivative of Equation (2) with respect to
t is given by:
A similar equation can be found in the detection algorithm mentioned in the previous article. Obviously the decrease of the slope indicates that the trajectory runs in the concave area, and the trajectory runs in the convex area after the slope begins to increase. If the control is appropriate, the system will return to a stable state and the slope of the trajectory will keep decreasing until it reaches FEP.
3.2. Calculation of Control Quantity for SMIB
To find the relationship between the slope and angular speed, integrating both sides of Equation (2) gives:
where
and
are the bounds of the integration;
and
are the angular speed corresponding to
and
. Let
be the power angle at the control time
; and then
is the angular speed at
. For stable state,
is zero when
is the FEP. For unstable state, if
can be zero by the control, the system will return from
to a stable state and
will be the FEP. Therefore Equation (13) can be written as:
Therefore, the value of the slope at control time can be calculated by Equation (14), and the corresponding control quantity can be calculated by Equation (2). There are two unknowns and in Equation (14). is related to the unbalanced power on the basis of Equation (2). can be preset as the FEP as needed, but it must be no more than the UEP, so when is acquired, can be calculated. If is just the UEP, the corresponding control quantity is the minimum.
3.3. Approximation Method to Calculate Control Quantity
As can be seen from the trajectories in
Figure 3,
is nonlinear and changes corresponding to different control quantities at
. Because of the nonlinear nature of
, the value of
at
could not be acquired exactly. Therefore, an approximation method is presented to acquire the value of
at
. Employing a constant
instead of
in Equation (14):
Obviously, the angular speed and power angle at control time and the power angle at FEP are necessary to calculate . Above all must be preset less than or equal to UEP, then the system can be stable after control. Therefore, will keep decreasing after the control and the trajectory will return at . Because that will keep decreasing after the control, is surely less than the value of at control time. Hence, the control quantity calculated by is a little bigger than actually needed.
For a SMIB system, suppose the ratio of generator shedding is
, the relation of
and
after control is as follows:
where
is the generator output electrical power at
. When
is obtained by Equation (16), the generator shedding ratio of SMIB system can be calculated by Equation (18).
3.4. Seeking for FEP
The parameters needed in calculation can be collected by WAMS except for FEP. Two methods to acquire the FEP are provided in this paper:
Method 1: In order to obtain the minimum control quantity, it is intended to slow down the angular speed to zero at UEP by the control. It can be supposed that the power equilibrium point of the system after control is the UEP. Generator electrical power can be written as Equation (19), and mechanical power is considered as a constant in a short time period. It is assumed that generator shedding has a corresponding change on mechanical power:
where
are parameters to be identified at
instant.
are considered as constant in a short time when no other operations occur. At
instant,
are calculated by the least square method, and then the electrical power can be acquired.
In order to seek for the UEP after the control, the control should be known at first. Therefore an iterative method can be employed as follows:
- (1)
Obtain the prediction curve of the electrical power;
- (2)
Preset zero to the generator shedding ratio and UPE: , ;
- (3)
Mechanical power decreases at the same ratio:
- (4)
Search for the power equilibrium point as ;
- (5)
Acquire the according to the ;
- (6)
If , complete the iterator; or return to step 3.
where
is the convergence conditions;
is the number of the iterator.
Method 2: Preset a FEP as needed. On the basis of the operating requirement, the FEP, which must be less than or equal to the power equilibrium point, can be preset within the limits as needed.
Two control objectives are provided according to the way of acquiring the FEP: scheme one is the minimal cost to help restore the system to a stable state; scheme two is the minimal cost to limit the maximum angle.
3.5. Control Method for Multi-Machine System
Using the assumption made by [
22] that the disturbed multi-machine system separates into two groups, leading group S and lagging group A, the partial center of angles, angular speed, mechanical power and electrical power of the two-machine power system are shown as follows:
Further, the two-machine power system can be equivalent to the SMIB system:
where
According to the calculation method applied to SMIB equivalent system, the expected slope
of SMIB equivalent system can be acquired. Transform the expected slope to control quantity:
where
is the original slope before control.