Asymptotic Solutions of Serial Radial Fuel Shuffling
Abstract
:1. Introduction
2. Formulation and Modeling
2.1. Diffusion Model Coupled by Burn-Up Equations
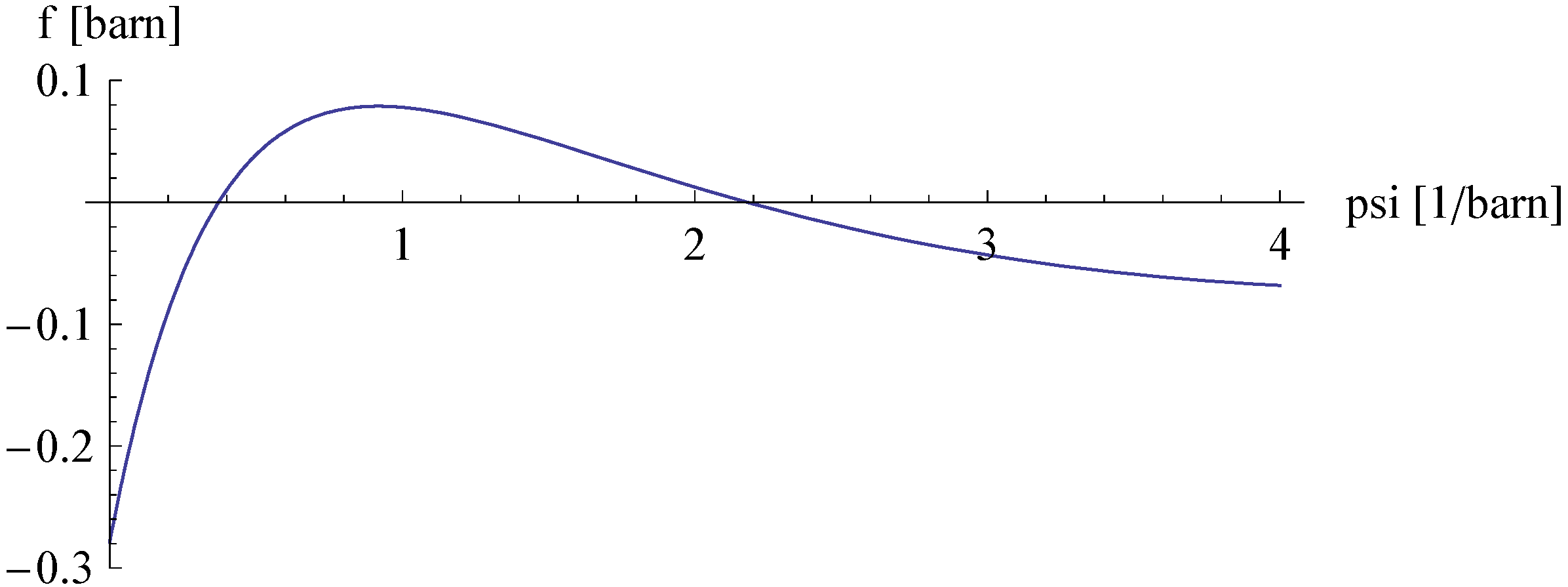
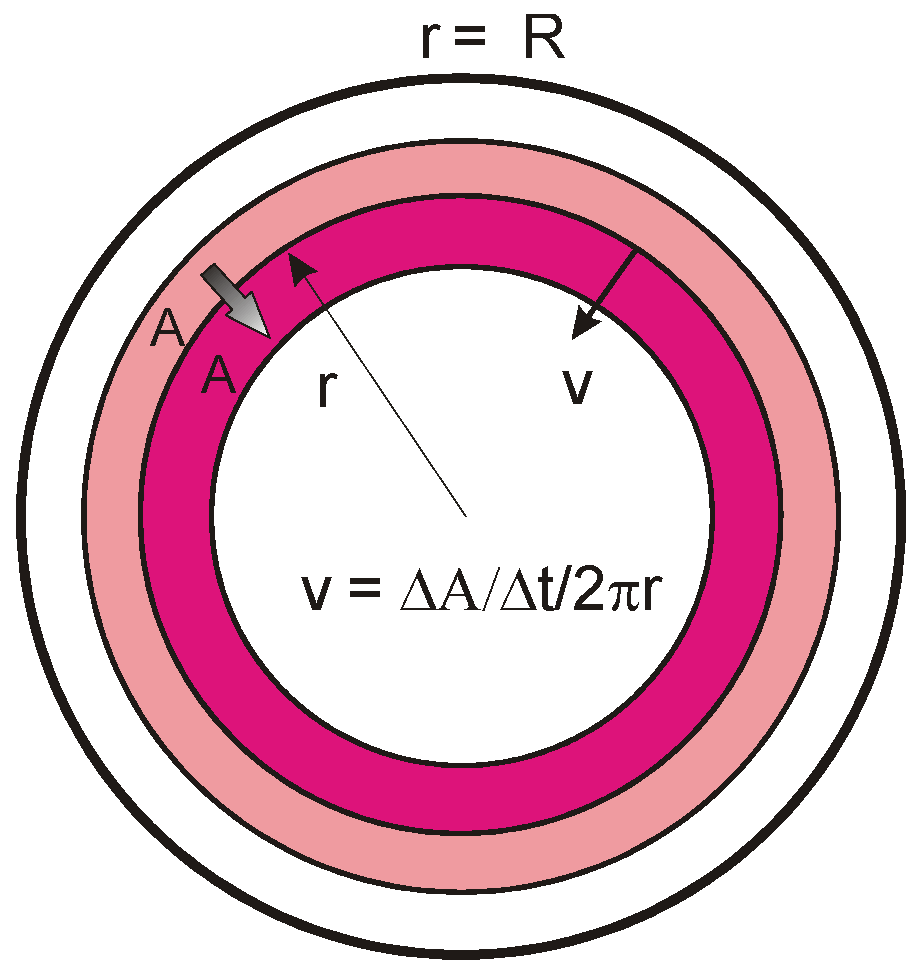
2.2. Radial Fuel Drifting
2.3. Boundary Conditions and Nonlinear Eigenvalue Problem
3. 1-D Integration and Solutions
3.1. Integration
3.2. Dimensionalization and Dimensionless Characterizing Number
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| R | 150 cm | d | 2.52 cm |
| r0 | 0 cm | NHM,0 | 1.221 × 1022 cm−3 |
| D | 1.260 cm | ϕmax | 3 × 1015 cm−2·s−1 |
3.3. Solution of Inward Fuel Drifting
| Variable | Case 1 | Case 2 * | Case 3 | Case 4 |
|---|---|---|---|---|
| (barn cm) | 443.2 | 886.4 | 2659.2 | 8864 |
| (barn cm) | 22.76 | 28.58 | 40.23 | 63.56 |
| (barn cm) | 15.00 | 16.37 | 14.28 | 12.54 |
| keff | 0.96685 | 1.00376 | 1.03119 | 1.01414 |
| Flux peaking factor | 1.517 | 1.746 | 2.804 | 5.069 |
| Boundary factor | 19.48 | 31.01 | 66.43 | 139.5 |
| Power peaking factor | - | 1.91 | - | |
| Burn-up (at%) | - | 55.3 | - |
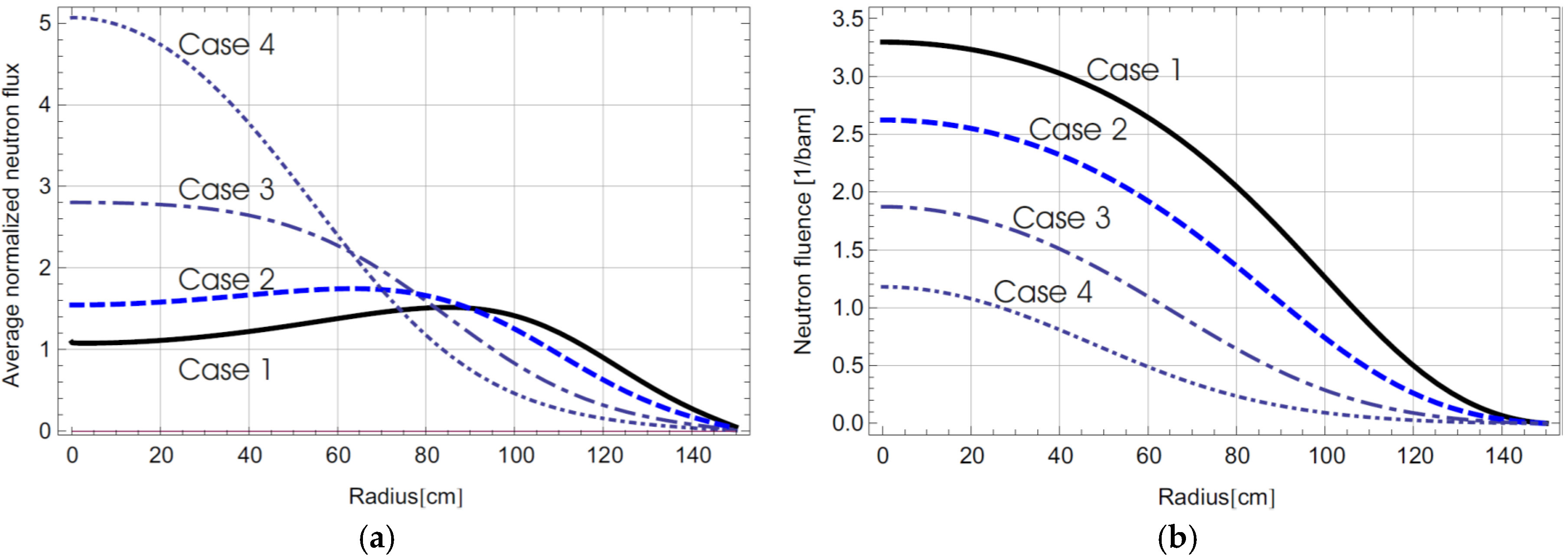
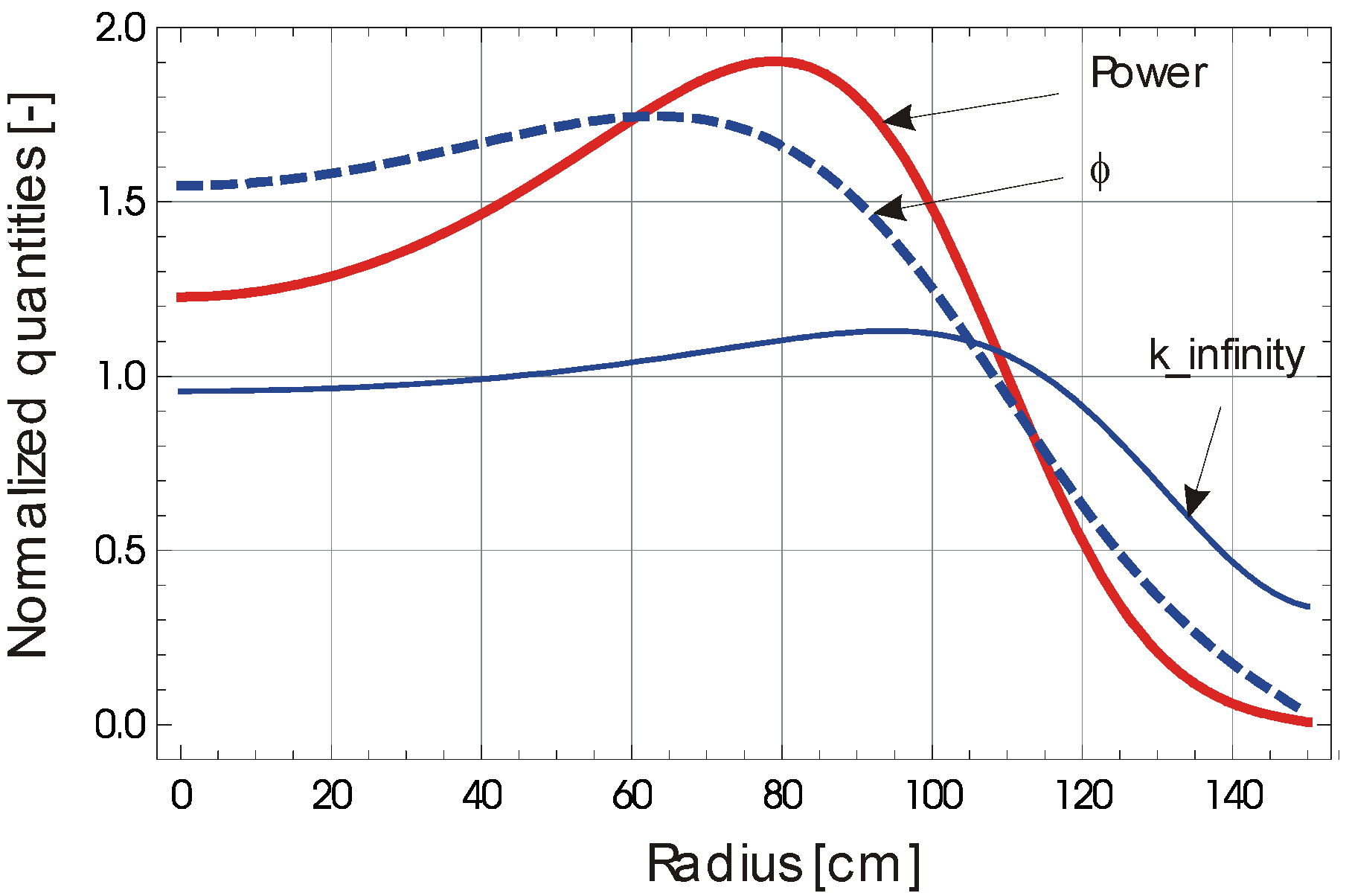
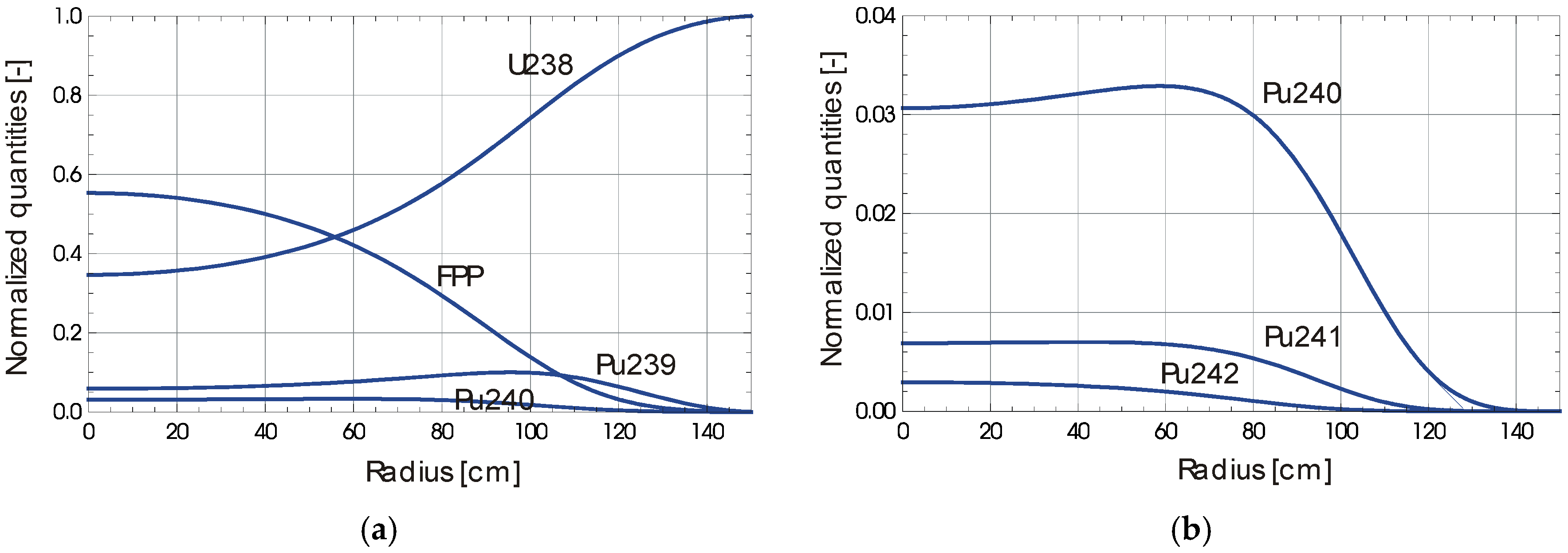
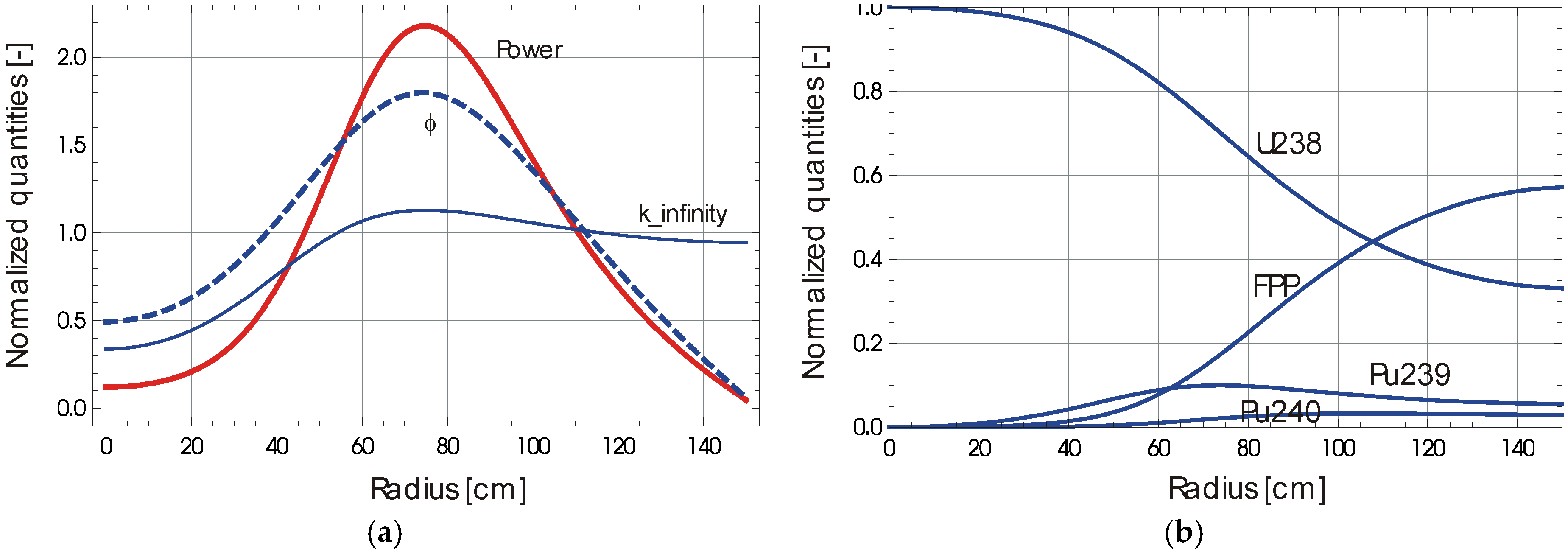
3.4. Solution of Outward Fuel Drifting
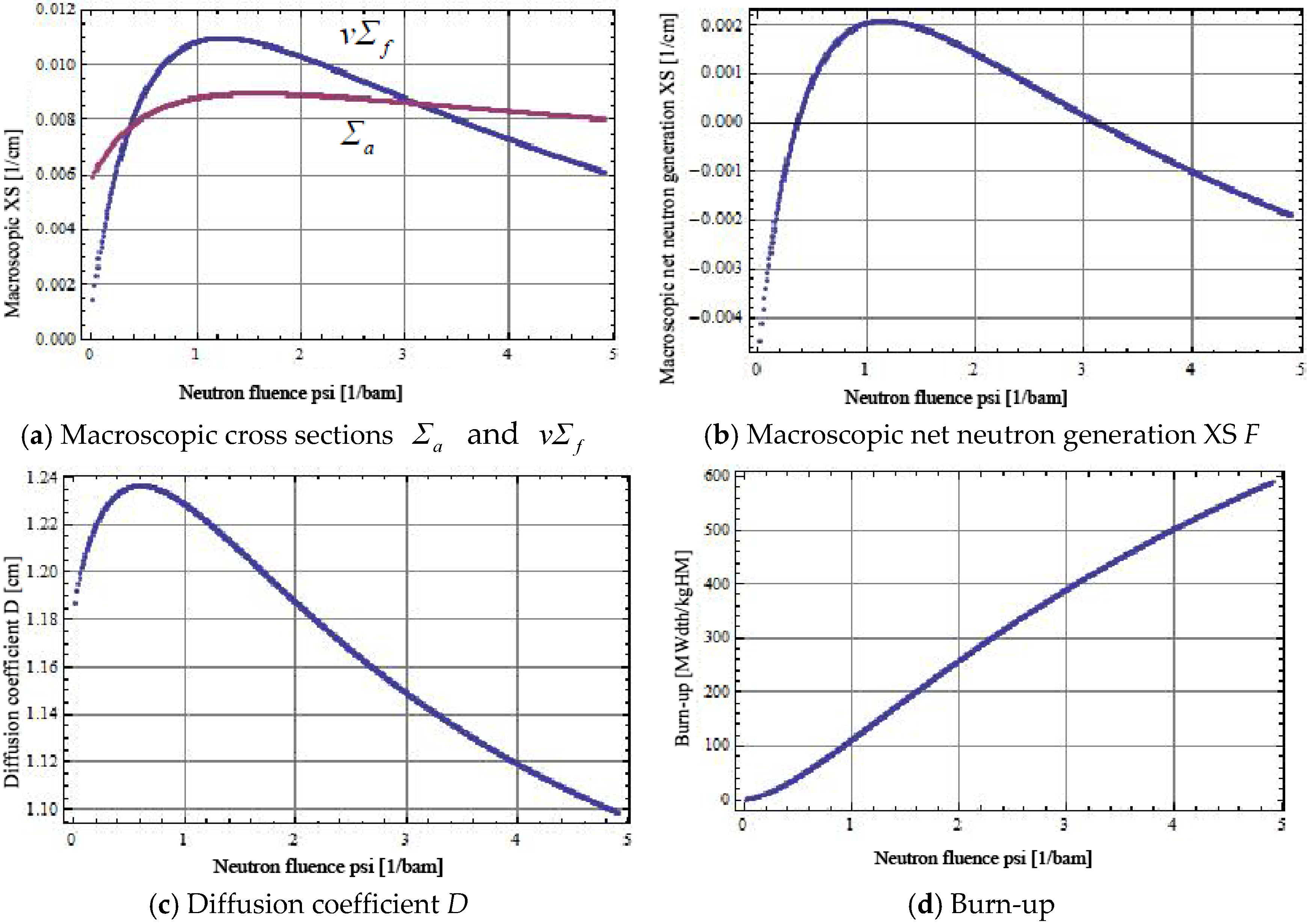
4. 2-D Numerical Solution
4.1. Data Preparation
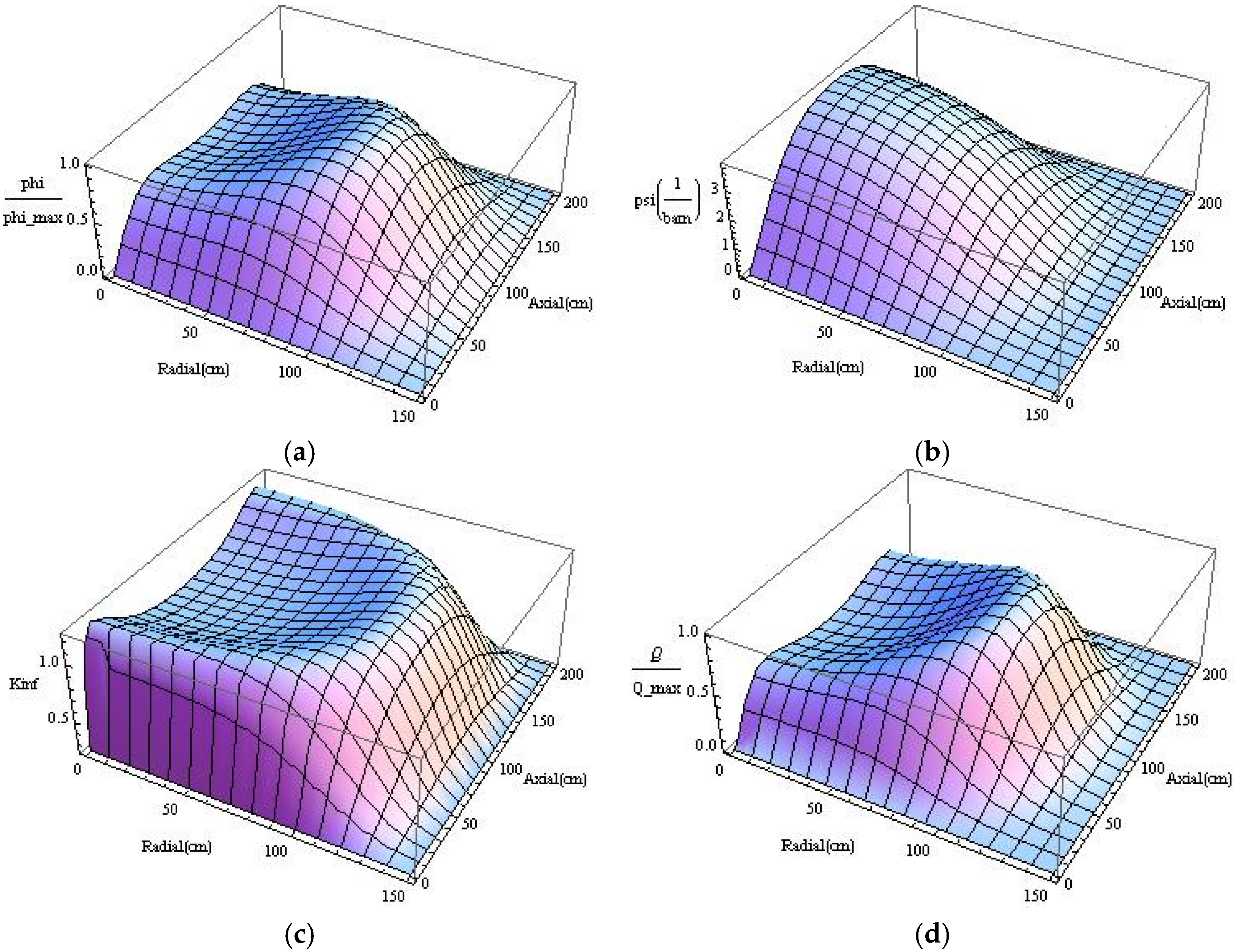
4.2. Unsteady Problem Formulation
4.3. Normalization and Time Stepping Iteration
4.4. Numerical Results
| Variable | Case 1 | Case 2 | Case 3 |
|---|---|---|---|
| in (barn cm) | 11.695 | 10.455 | 6.796 |
| in (barn cm) | 28.34 | 41.18 | 70.34 |
| keff | 1.02230 | 1.06208 | 1.04664 |
| in (1/barn) | 3.8576 | 2.9857 | 2.0912 |
| in (1/barn) | 2.6466 | 1.8211 | 1.0664 |
| Flux peaking factor | 2.423 | 3.939 | 10.35 |
| Flux peak position | 0.581 | 0.303 | 0 |
| Power peaking factor | 2.745 | 4.345 | 12.20 |
| Power peak position | 0.665 | 0.385 | 0 |
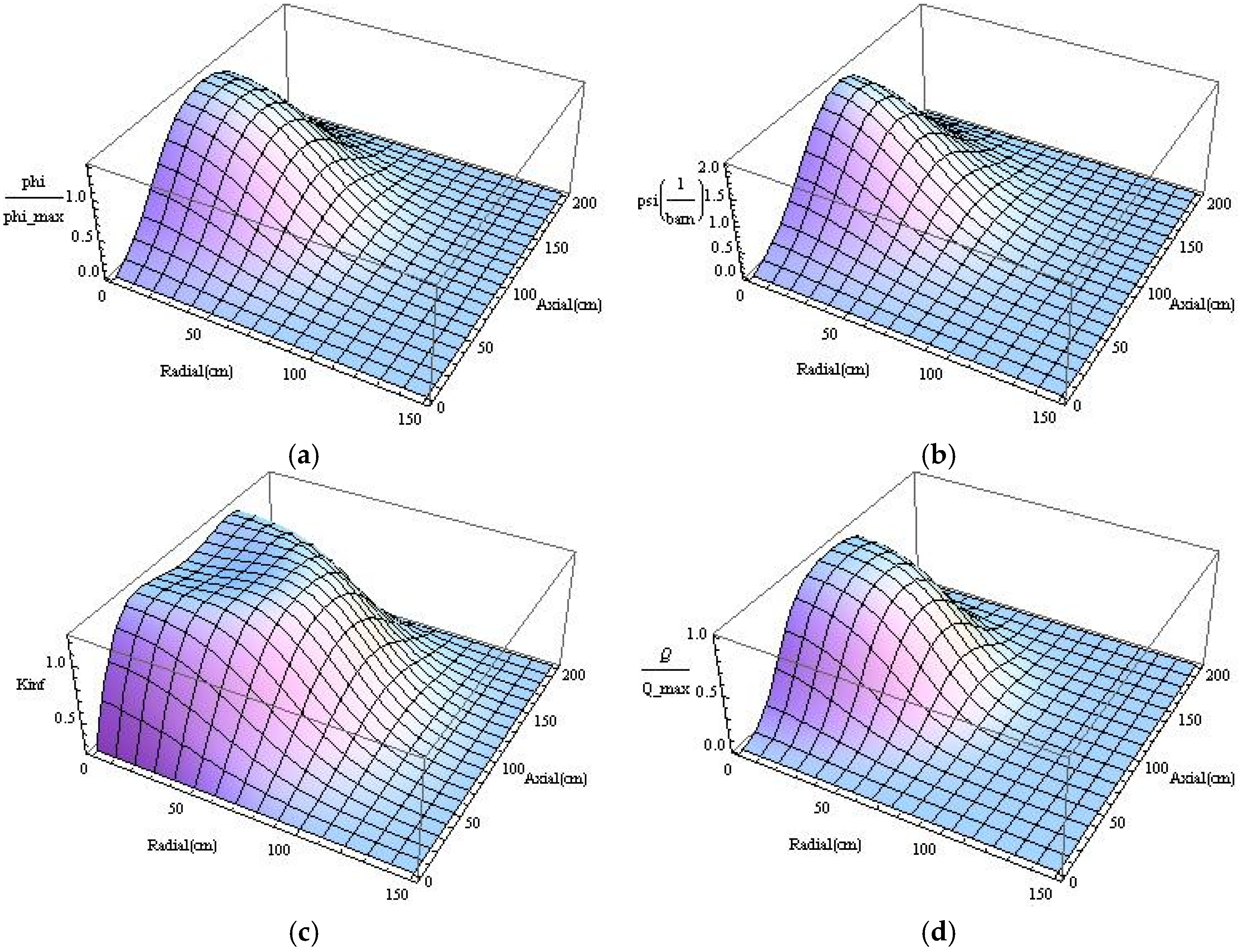
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hejzlar, P.; Petroski, R.; Cheatham, J.; Touran, N.; Cohen, M.; Truong, B.; Latta, R.; Werner, M.; Burke, T.; Tandy, J.; et al. TerraPower, LLC Traveling wave reactor development program overview. Nucl. Eng. Technol. 2013, 45, 731–744. [Google Scholar] [CrossRef]
- Traveling Wave Reactor. Available online: http://en.wikipedia.org/wiki/Traveling_wave_reactor (accessed on 30 November 2015).
- Weaver, K.D.; Ahlfeld, C.; Gilleland, J.; Whitmer, C.; Zimmerman, G. Extending the nuclear fuel cycle with traveling-wave reactors. In Proceedings of the Global 2009, Paris, France, 6–10 September 2009.
- Ellis, T.; Petroski, R.; Hejzlar, P.; Zimmerman, G.; McAlees, D.; Whitmer, C.; Touran, N.; Hejzlar, J.; Weaver, K.; Walter, J.C.; et al. Traveling-Wave Reactors: A truly sustainable and full-scale resource for global energy needs. In Proceedings of the ICAPP’10, San Diego, CA, USA, 13–17 June 2010.
- Gilleland, J. The History of TerraPower and Traveling Wave Reactor Development, 2006 to Present. In Proceedings of the INES-3, Tokyo, Japan, 31 October–3 November 2010.
- Feoktistov, L.P. Neutron-fissioning wave. Rep. Acad. Sci. USSR 1989, 309, 864–867. [Google Scholar]
- Teller, E.; Ishikawa, M.; Wood, L. Completely automated nuclear reactors for long-term operation, Part I. In Proceedings of the Frontiers in Physics Symposium, American Physical Society and the American Association of Physics Teachers Texas Meeting, Lubbock, TX, USA, 26–28 October 1995.
- Teller, E.; Ishikawa, M.; Wood, L.; Hyde, R.; Nuckolls, J. Completely automated nuclear reactors for long-term operation, Part II. Toward a concept-level point-design of a high-temperature, gas-cooled central power station system. In Proceedings of the ICENES’96, Obninsk, Russia, 24–28 June 1996; pp. 151–158.
- Van Dam, H. Self-stabilizing criticality waves. Ann. Nucl. Energy 2000, 27, 1505–1521. [Google Scholar] [CrossRef]
- Seifritz, W. Solitary burn-up waves in a multiplying medium. Kerntechnik 2000, 65, 261–264. [Google Scholar]
- Sekimoto, H.; Ryu, K.; Yoshimura, Y. CANDLE: The new burnup strategy. Nucl. Sci. Technol. 2001, 139, 306–317. [Google Scholar] [CrossRef]
- Chen, X.-N.; Kiefhaber, E.; Maschek, W. Fundamental burn-up mode in a pebble-bed type reactor. Prog. Nucl. Energy 2008, 50, 219–224. [Google Scholar] [CrossRef]
- Chen, X.-N.; Kiefhaber, E.; Zhang, D.; Maschek, W. Fundamental solution of nuclear solitary wave. Energy Convers. Manag. 2012, 59, 40–49. [Google Scholar] [CrossRef]
- Chen, X.-N.; Zhang, D.; Maschek, W.; Schulenberg, T. Solitary breeding/burning waves in a supercritical water cooled fast reactor. Energy Convers. Manag. 2010, 51, 1792–1798. [Google Scholar] [CrossRef]
- Zhang, D.; Chen, X.-N.; Gabrielli, F.; Rineiski, A.; Maschek, W.; Schulenberg, T. Numerical studies of nuclear traveling waves in a supercritical water cooled fast reactor. Prog. Nucl. Energy 2011, 53, 806–813. [Google Scholar] [CrossRef]
- Osborne, A.G.; Deinert, M.R. Comparison of neutron diffusion and Monte Carlo simulations of a fission wave. Ann. Nucl. Energy 2013, 62, 269–273. [Google Scholar] [CrossRef]
- Chen, X.-N.; Zhang, D.; Maschek, W. Theoretical modeling of radial standing wave reactor. Trans. Fusion Sci. Technol. 2012, 61, 275–280. [Google Scholar]
- Zhang, D.; Chen, X.-N.; Flad, M.; Rineiski, A.; Maschek, W. Theoretical and numerical studies of TWR based on ESFR core design. Energy Convers. Manag. 2013, 72, 12–18. [Google Scholar] [CrossRef]
- Seifritz, W. A standing wave reactor by continuous radial fuel shuffling. Kerntechnik 2012, 77, 68–71. [Google Scholar]
- Chen, X.-N.; Maschek, W. Transverse buckling effects on solitary burnup waves. Ann. Nucl. Energy 2005, 32, 1377–1390. [Google Scholar] [CrossRef]
- Fomin, S.P.; Mel’nik, Yu.P.; Pilipenko, V.V.; Shul’ga, N.F. Initiation and propagation of nuclear burning wave in fast reactor. Prog. Nucl. Energy 2008, 50, 163–169. [Google Scholar] [CrossRef]
- Rusov, V.D.; Linnik, E.P.; Tarasov, V.A.; Zelentsova, T.N.; Sharph, I.V.; Vashchenko, V.N.; Kosenko, S.I.; Beglaryan, M.E.; Chernezhenko, S.A.; Molchinkolov, P.A.; et al. Traveling wave reactor and condition of existence of nuclear burning soliton-like wave in neutron-multiplying media. Energies 2011, 4, 1337–1361. [Google Scholar] [CrossRef]
- Rusov, V.D.; Tarasov, V.; Sharph, I.V.; Vashchenko, V.N.; Linnik, E.P.; Zelentsova, T.N. On some fundamental peculiarities of the traveling wave reactor. Sci. Technol. Nucl. Install. 2015, 2015. [Google Scholar] [CrossRef]
- Zheng, M.; Tian, W.; Chu, X.; Zhang, D.; Qiu, S.; Su, G. Preliminary design study of a board type radial fuel shuffling sodium cooled breed and burn reactor core. Nucl. Eng. Des. 2014, 278, 679–685. [Google Scholar] [CrossRef]
- Glasstone, S.; Edlund, M.C. The Elements of Nuclear Reactor Theory; D. Van Nostrand Company, Inc.: Princeton, NJ, USA; London, UK, 1952. [Google Scholar]
- Rimpault, G.; Plisson, D.; Tommasi, J.; Jacqmin, R.; Rieunier, J.M.; Verrier, D.; Biron, D. The ERANOS code and data system for fast reactor neutronic analyses. In Proceedings of the PHYSOR 2002, Seoul, Korea, 7–10 October 2002.
- Pahl, R.G.; Porter, D.L.; Lahm, C.E.; Hofman, G.L. Experimental studies of U-Pu-Zr fast reactor fuel pins in the experimental breeder reactor-II. Metall. Mater. Trans. A 1990, 21, 1863–1870. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.-N.; Kiefhaber, E. Asymptotic Solutions of Serial Radial Fuel Shuffling. Energies 2015, 8, 13829-13845. https://doi.org/10.3390/en81212398
Chen X-N, Kiefhaber E. Asymptotic Solutions of Serial Radial Fuel Shuffling. Energies. 2015; 8(12):13829-13845. https://doi.org/10.3390/en81212398
Chicago/Turabian StyleChen, Xue-Nong, and Edgar Kiefhaber. 2015. "Asymptotic Solutions of Serial Radial Fuel Shuffling" Energies 8, no. 12: 13829-13845. https://doi.org/10.3390/en81212398





