Investigation of a Five-Phase Dual-Rotor Permanent Magnet Synchronous Motor Used for Electric Vehicles
Abstract
: This paper presents a novel five-phase permanent magnet synchronous motor (PMSM), which contains dual rotors and a single stator, equivalent to two five-phase motors working together. Thus, this kind of motor has the potential of good fault tolerant capability and high torque density, which makes it appropriate for use in electric vehicles. In view of the different connection types, the inside and outside stator windings can be driven in series or parallel, which results in the different performances of the magnetomotive force (MMF) and torque under open-circuit fault conditions. By decomposing the MMF, the reason that torque ripple increases after open-circuit faults is explained, and the relationship between MMF and torque is revealed. Then, the current control strategy is applied to adjust the open-circuit faults, and the electromagnetic analysis and MMF harmonics analysis are performed to interpret the phenomenon that the torque ripple is still larger than in the normal situation. The investigations are verified by finite element analysis results.1. Introduction
With the requirements of energy conservation and emissions reduction around the world, electric vehicles (EVs) have been seen as an ideal alternative of transportation, and thus, have got more and more attention from researchers and governments [1]. Compared with the traditional induction machine, the permanent magnet synchronous motor (PMSM) is an attractive candidate for EVs, due to its advantages of high power density and high efficiency [2,3]. In addition, good reliability is also necessary for a motor to be used for EVs, so that the EVs continue to run smoothly under fault conditions. Due to the fact additional degrees of freedom can be used to improve the fault tolerant capability, as compared with the conventional three-phase motor, multiphase motors (generally at least four phases) have been used in the fields where high reliability is needed [4–9], especially in EVs. Among a variety of faults which may occur in the machine or drive unit, open-circuit faults are the most common type. Therefore, many fault tolerant control methods have been proposed to remedy this kind of fault [10–16]. In [10], an optimal torque control method is put forward for fault tolerant permanent magnet brushless machines, which enables ripple-free torque operation and minimum copper loss to be obtained in open-circuit fault situations, and the voltage and current constraints are considered at the same time. In [11], the authors proposed a current control strategy, with the third-order harmonic current injection, to reduce the torque ripple of five phase permanent magnet motor under open-circuit faults conditions, but the solutions are not optimized. Similarly, the fault tolerant control technique proposed in [12] also considers the third time-harmonic current, which is used for five phase permanent magnet (PM) motor with trapezoidal back electromotive force (EMF). By introducing some proper constraints, such as the balanced fundamental current components and relaxation of the sixth-harmonic pulsating torque component, the optimum current solutions are obtained, which can ensure the motor to acquire a higher torque as compared with the solutions in [11].
The magnetomotive force (MMF) distribution is mainly affected by the winding structure and current waveform. In turn, it influences the motor performances. Thus, much attention has been paid to researching the MMF [14–20]. Under open-circuit fault conditions, a novel current control strategy is proposed in [14–16], which aims to obtain an undisturbed MMF by regulating the remaining healthy phase currents of a multiphase machine. By means of MMF harmonics analysis, the different winding structures are compared and one suitable winding distribution is selected for the high speed spindle motor in [17]. In [18–20], the rotor losses induced by the MMF harmonics are investigated for fractional-slot PM machines, and the different design parameters, such as winding layer [19], combination of poles and slots [18–20] and phase number [20] are discussed.
The flux-MMF diagram technique, differing from the analytical method used to study the cogging torque in [21,22], is researched and applied to predicate the cogging torque of the PM machine in [23], which makes it easier to understand the generating mechanism of cogging torque by the graphical interpretation. In addition, based on the flux-MMF diagram, the torque comparison between several kinds of motor is accomplished in [24].
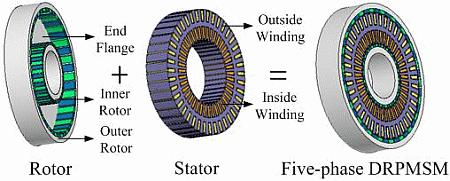
Nowadays, most multiphase PM motors have a single stator and a single rotor, whose structure limits the power density from further increasing. In order to increase the power density, many compound-structure PMSMs integrated by two machines have been proposed [25–29], but they are three-phase PM motors, which lack fault-tolerant capability. To combine the advantages of multiphase PM motors and compound-structure PM motors, a novel five-phase dual-rotor PMSM (DRPMSM) is proposed in this paper, which contains two rotors and one stator, as shown in Figure 1. Due to the different connection types of inside and outside stator windings, the five-phase DRPMSM can be driven in series or parallel, which will lead to different MMF and torque performances under open-circuit fault conditions, so they are investigated in this paper. By introducing the equivalent current, the main reason that the torque ripple increases after open-circuit faults is explained and the relationship between MMF and torque is proved. Then, based on the idea of disturbance-free rotating MMF, the current control strategy is applied to adjust the open-circuit faults to improve the torque performance. In this paper, Ansoft Maxwell software is employed for the finite element analysis (FEA) results.
2. Description of Motor Model
According to the drive mode, the topologies for four-wheel-drive EVs can be classified into high-speed drive incorporating an additional gear box and low-speed direct drive. Table 1 lists some design parameters of the electric drive systems, i.e., the commercial Prius [30] and five-phase DRPMSM proposed in this paper.
It can be known from Table 1 that the 2010 Prius uses a high speed PMSM, so an additional gear box is needed. Due to the cantilevered mechanical structure of the outer rotor and stator, the five-phase DRPMSM is not suitable for running at high speed. Therefore, it is more appropriate to use it in the direct-drive structure. Besides, the torque density of Prius is higher than that of the five-phase DRPMSM, but its current density is larger as well, which make it need a good cooling system.
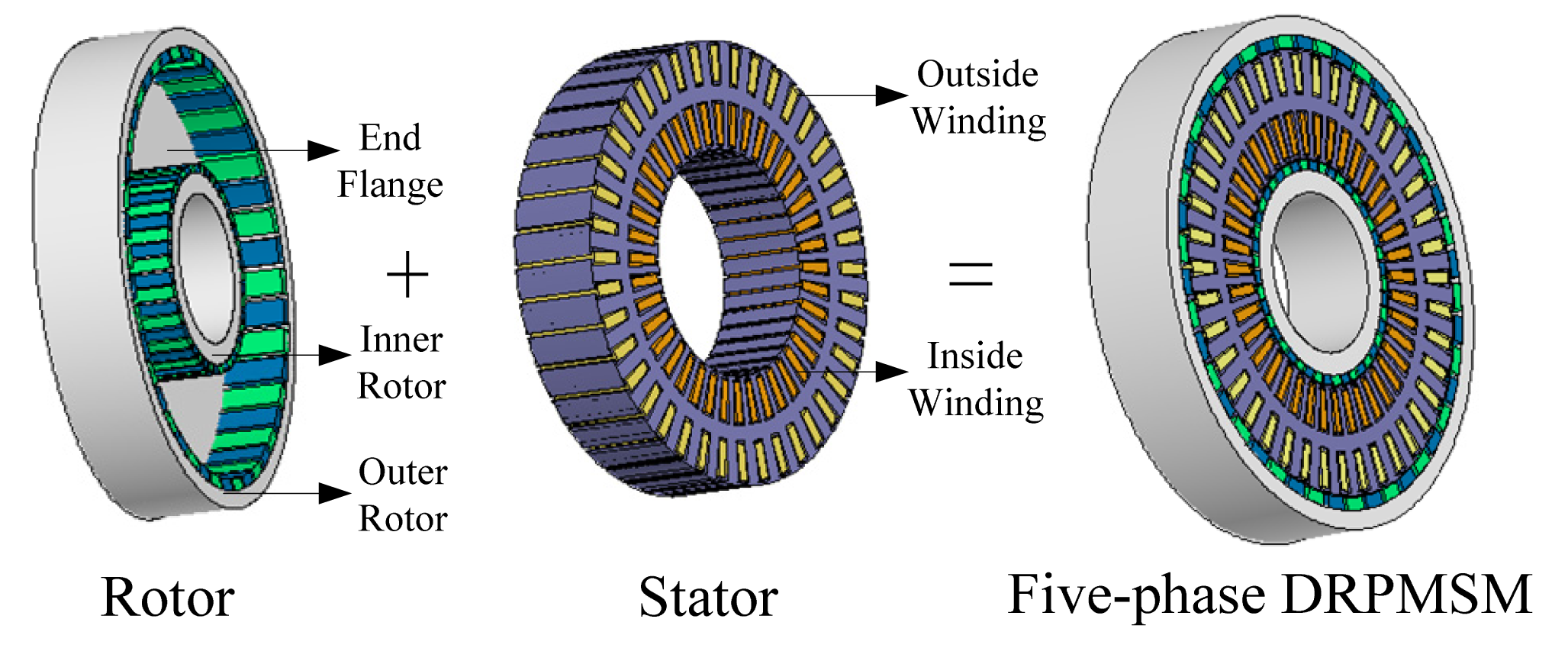
To ensure the coaxial output, the inner and outer rotors are connected by the end flange, as shown in Figure 1, which can be used as the fan to dissipate the heat. The PMs of inner and outer rotors are surface-mounted and they are polarized in the radial direction consistently, as shown in Figure 2.
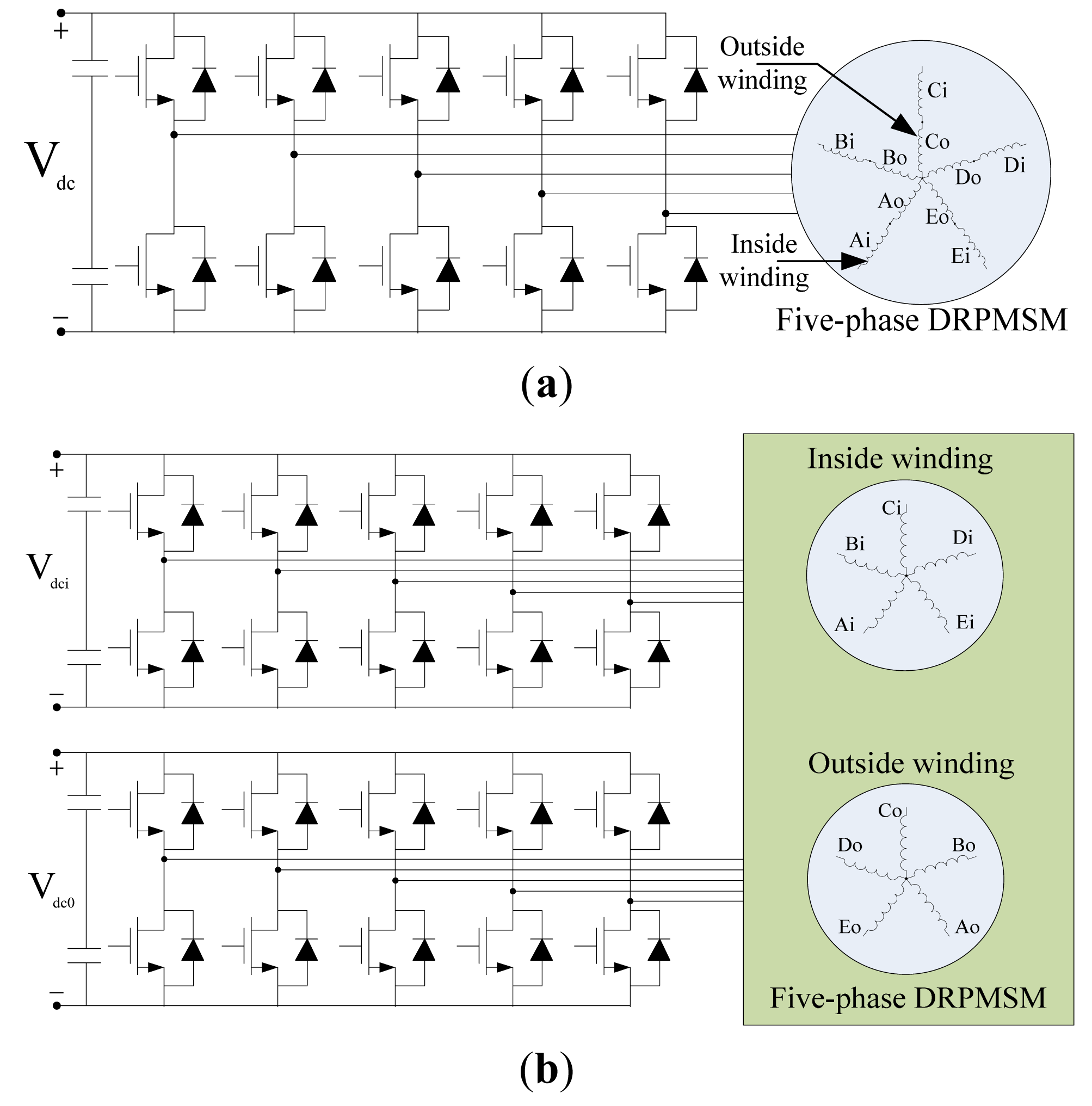
As there are slots on the inside and outside surfaces of stator iron, two sets of windings (inside winding and outside winding) can be installed, which can be used to improve the fault tolerant ability. In addition, there are two working air-gaps, so the five-phase DRPMSM has a higher torque density, which makes it very suitable for use for EVs. Here, the inner rotor and inside stator winding operates as one motor called inner motor, and the outer rotor and outside stator winding operates as another one called outer motor. Due to the different connections, inside and outside windings can be driven in parallel or series, as shown in Figure 3.
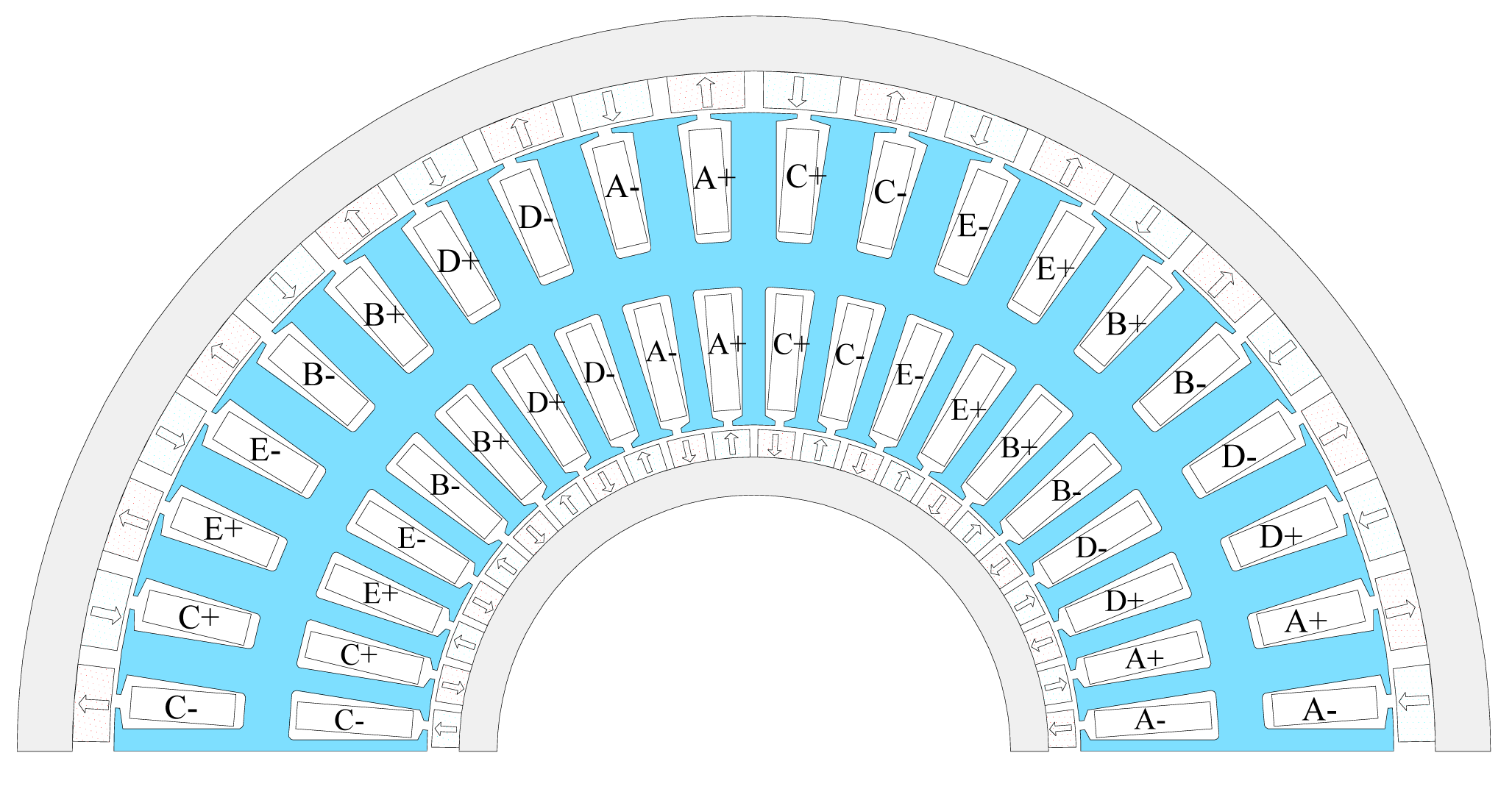
In order to achieve the physical separation and magnetic decoupling between the fault phases and other healthy phases, the armature coils are wound around the alternate stator teeth [31], as depicted in Figure 2, which means that the fractional slot combination has to be selected. From the perspective of maximizing the torque density and reducing the noise, the combination of 2P = Q ± 2 (where P is the number of pole pairs, Q is the number of slot) is a good choice [32]. Although the low pole choice (2P = Q − 2) has a lower rotor loss [33], the high pole choice (2P = Q + 2) can make full use of the iron to improve the torque density in a limit space and increase the diameter of outer air-gap, which is helpful to heat dissipation. Therefore, the unit motor model of 22-pole/20-slot is selected. Considering the big out diameter of the five-phase DRPMSM, the combination of 44-poles/40-slots is selected ultimately to make best use of the core space. For convenience, the unit motor model is used to analyse the MMF harmonics in this paper.
3. Analysis under Normal Conditions
It is assumed that the lengths of inside and outside air gaps along the armature surfaces are uniform. Originating from the winding axis, the winding function of phase “a” can be described by Figure 4.
The Fourier series of the phase “a” winding function can be expressed as:
Therefore, the resulting MMF of inner and outer motor is obtained:
It can be concluded from Equation (3) that only the harmonics of 10υ±1 order (υ is integer) exist, wherein, the space harmonics of 10υ+1 order travel forward, whereas the space harmonics of 10υ −1 order travel backward. For the PM motor, constant torque can be generated, only if the number of poles of the armature field produced by the stator space MMF harmonics is equal to that of rotor PMs, and their rotating speeds are simultaneously the same. Therefore, the 11th stator MMF harmonic is the working MMF. As for other MMF space harmonics of order lower and higher than 11, they do not generate torque, but they will induce eddy losses in the rotor when interacting with the rotor field. The subject has been researched widely [18–20], so it is not discussed in this paper. If only considering the 11th space MMF harmonic, the resulting MMF can be represented as:
If defined ϕ=11ψ, Equation (4) can be written as:
Ideally, the output torque of five-phase DRPMSM is the sum of that of inner and outer motors. Applying the instantaneous power balance theory, the electromagnetic torque of five-phase DRPMSM can be computed by:
According to Equation (6), one constant, which stands for the contributing rate of inner or outer motor to the total torque of five-phase DRPMSM, can be defined as:
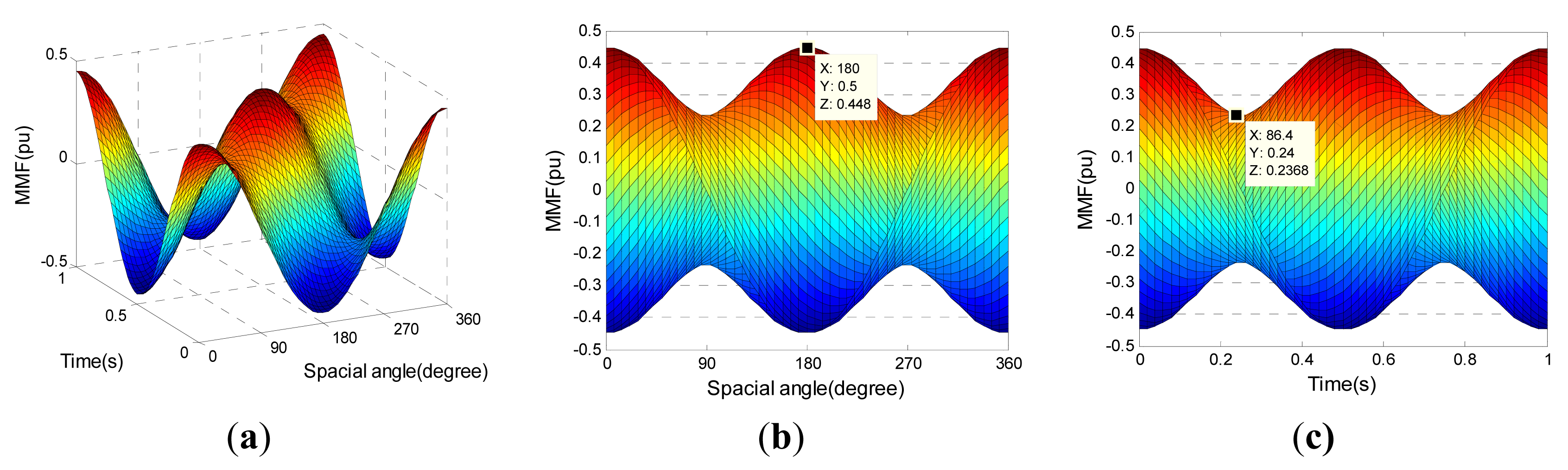
Let , the MMF distribution is shown in Figure 5. It can be seen that with time passes by, the resultant MMF wave keeps its sinusoidal amplitude and form but rotates progressively around the air-gap.
Furthermore, the net result (black line shown in Figure 5c) can be seen as an MMF wave of constant amplitude rotating at a uniform angular velocity. Wherein, the amplitude is 0.449 pu, denoted by Fn.
Using the AC standstill test [34], the self and mutual inductances of inside and outside windings are acquired based on the FEA, as reported in Table 2, where, the capital letters in the subscript stand for the outside winding, and the lowercase letter in the subscript stand for the inside winding. Lii(i = a, A) is the self-inductance, Mij (i = A, a; j = B, C, b, c) is the mutual inductance. It can be found that the mutual inductances between the adjacent windings on both sides are very small, as compared with the self inductance, as well as the adjacent windings on the same side. Therefore, the magnetic coupling between inner and outer motors is quite weak, they can be controlled independently.
Let the phase current be in phase with the phase EMF, namely, employing the vector control strategy that direct-axis current is equal to zero, the torques are obtained under different working situations, as informed in Table 3.
It can be found from Table 3 that the torque difference between the inner and outer motors working together and the linear addition of inner and outer motors working alone is very small, meanwhile the influences of outer PMs on the inner motor and inner PMs on the outer motor are also very small. This demonstrates that the inner and outer motors are decoupled from another aspect. Furthermore, it can be obtained that ki = 0.297, ko = 0.703, which are similar to the results obtained by analyzing the EMF. Under the case of inner and outer motors working together, the average torque of five-phase DRPMSM is listed in Table 3, which is denoted by Tn, and the torque ripple is 1.49%.
4. Analysis under Open-Circuit Faults without Adjustment
In this section, the following open-circuit faults are discussed: one phase open-circuit fault, two adjacent phases open-circuit fault and two non-adjacent phases open-circuit fault.
4.1. One Phase Open Circuit Fault without Adjustment
It is assumed that phase “a” is open circuited. For the star connection without neutral line, the constraint that current vector sum is equal to zero has to be satisfied. By regulating the phase angle, the remaining four phase currents can be depicted as:
From the constraint of star connection, it can be obtained that:
In order to maximize the average torque, basing on Equation (6), it can be obtained that:
To eliminate the two degrees of freedom existing in Equation (11), it is helpful to suppose that:
Then, Equation (11) can be written as:
Taking Equation (12) as the objective function and Equation (14) as the constraint condition, the Lagrange equation can be established. By solving, we can get:
According to the instantaneous power balance theory, one can learn that the fault winding can output about 76.1% of the torque acquired when the winding working under normal conditions. For the series drive, as shown in Figure 3a, one phase of inside or outside winding occurring in open-circuit fault will lead the other side to the same failure. However, for the parallel drive, as shown in Figure 3b, the fault may occur in the inside winding or outside winding. Therefore, one phase open-circuit fault can be divided into the following three cases:
- Case a:
phase “a” of the inner motor is open circuited in the parallel drive, so the resulting stator MMF of five-phase DRPMSM can be expressed as:
- Case b:
phase “a” of the outer motor is open circuited in the parallel drive, so the resulting stator MMF of five-phase DRPMSM can be expressed as:
- Case c:
phase “a” is open circuited in the series drive, so the total stator MMF can be expressed as:
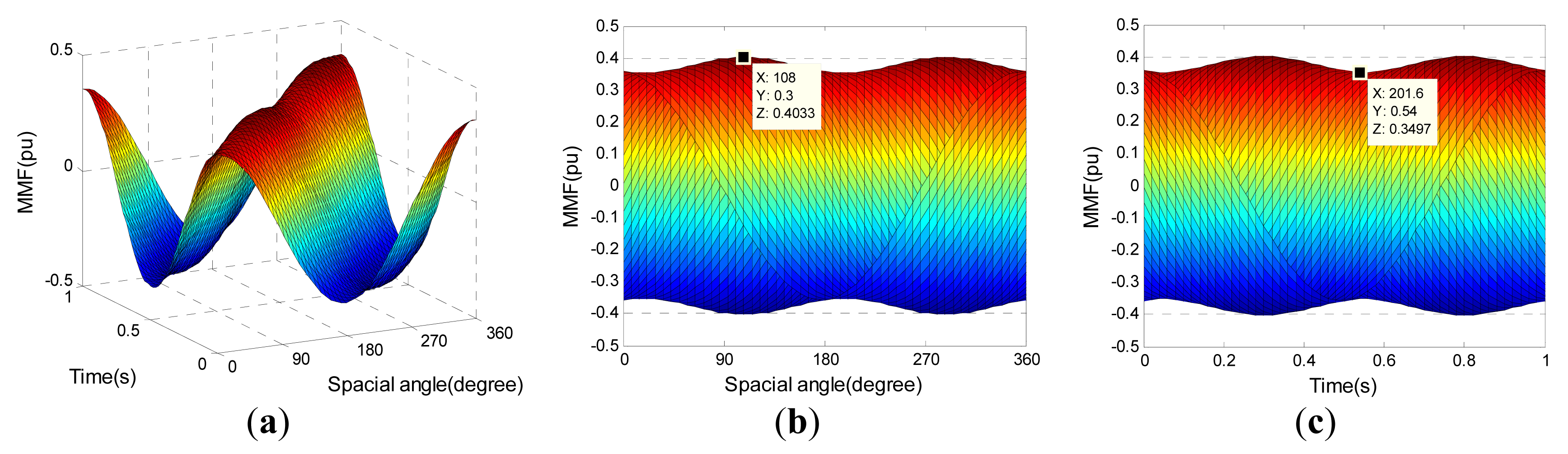
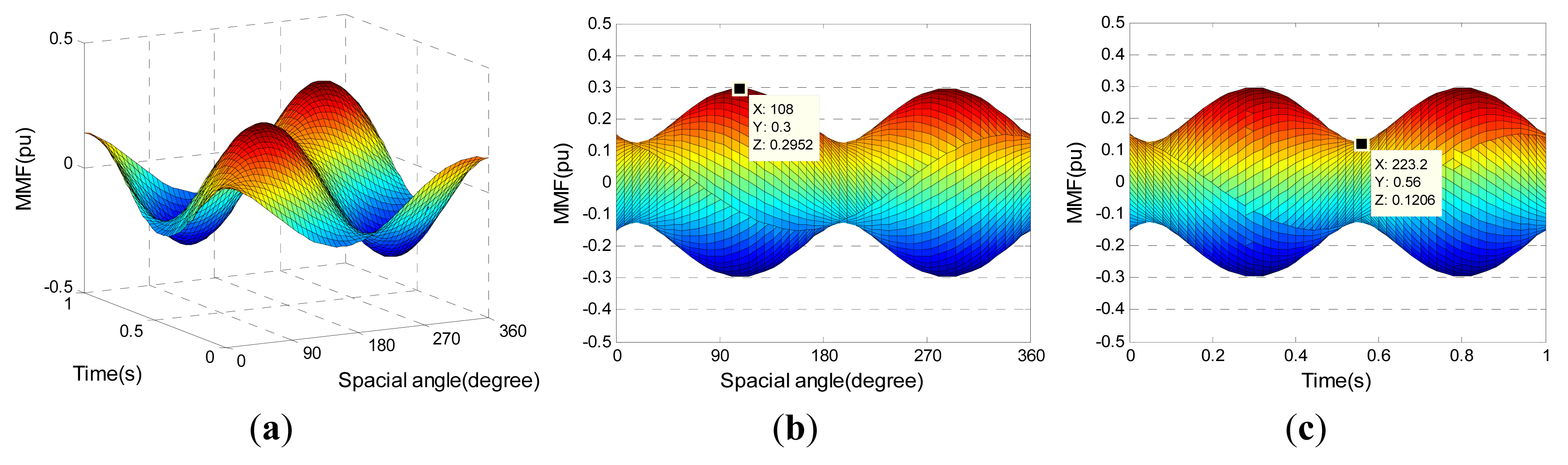
The MMF distributions under these three fault cases are shown in Figures 6, 7 – 8, respectively. Comparing with Figure 5, it can be found that there is fluctuation on the edge of MMF amplitude, and the fluctuation frequency is twice of that of net result. The averages of the MMF amplitude edge under three fault cases are shown in Table 4. Here, the ripple is defined as the ratio between half of the peak-to-peak (Pk-Pk) value and the average value.
It can be seen from Table 4 that the average of the MMF amplitude edge is greater in the parallel drive, and its ripple is smaller at the same time, as compared with the series drive. Comparing with Equation (9), one can find that there is one negative-rotating component in the fault MMF, as shown in the Part II of Equation (18). In order to evaluate the impact of MMF changes on torque, the equivalent currents are introduced to generate the fault MMF, i.e., each component of the fault MMF is produced by one group of five-phase balanced current. Then, these groups of current are superimposed to get a series of equivalent torque characteristics. Take the fault case c for example, the generating currents of the MMF as described in the Part I and Part II of Equation (18) can be expressed respectively as:
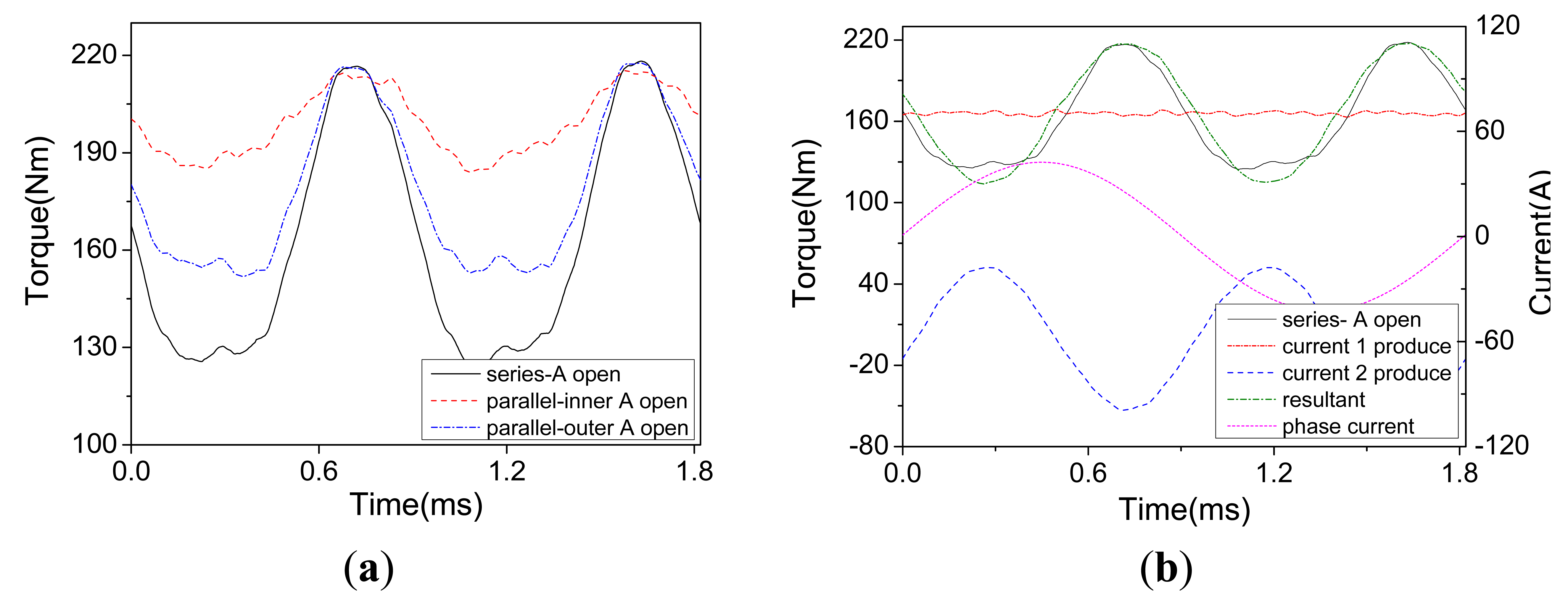
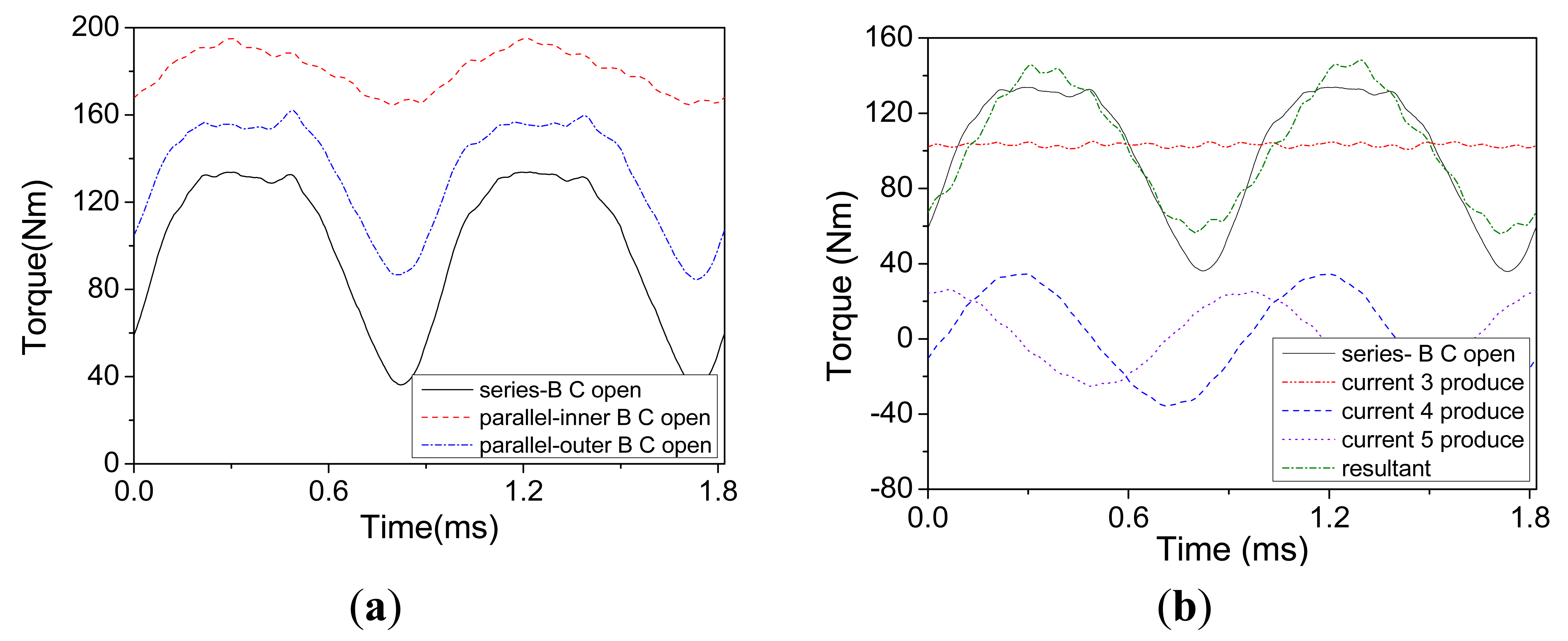
Under these three open-circuit fault cases, the torques are acquired, as shown in Figure 9a. Similarly, the torques produced by current 1 and 2 are obtained, and their resultant torque is obtained by linear superposition, as shown in Figure 9b.
It can be observed from Table 5 that the motor is able to exhibit better torque performances in the parallel drive, whose average torque is higher about 7%–17% of Tn, and torque ripple is lower about 36%–73% than the series drive. Furthermore, the performances of resultant torque are similar to that of the direct output torque under fault case c, i.e., average torque and ripple, and its average torque is mainly produced by current 1. However, the ripple of torque produced by current 1 is much smaller than the resultant torque, which is about 1.73%. Therefore, the ripple of resultant torque is mainly caused by the torque produced by current 2, and its fluctuation frequency is twice of the current frequency, as shown in Figure 9b.
4.2. Two Adjacent Phases Open Circuit Fault without Adjustment
It is supposed that phase “b” and “c” occur in an open-circuit fault simultaneously. To satisfy the constraint of star connection, the remaining three normal phase currents are regulated, but their amplitudes are kept unchanged, as follows:
From the condition that current vector sum is equal to zero, it can be obtained that:
For the sake of obtaining the maximum average torque, it can be known from Equation (6) that:
By solving Equation (22) and (23), the optimal solution can be acquired:
Hence, one can learn that the fault winding can output about 46.8% of the normal torque, which is obtained under the case of five phase currents are in healthy state.
In this paper, it is assumed that the fault only happens in one side winding at the same time, thus the fault cases can be described as:
- Case a:
the inner motor encounters open-circuit fault in the parallel drive, so the resulting MMF of five-phase DRPMSM changes into:
- Case b:
the outer motor encounters open-circuit fault in the parallel drive, so the resulting MMF of five-phase DRPMSM changes into:
- Case c:
the open-circuit fault occurs in the series drive, so the total stator MMF changes into:
Under open-circuit faults, the MMF distributions are shown in Figures 10, 11 – 12. Comparing with Figure 5, one can find that the areas projecting into the space and time domain all reduce by about 54% under fault case c, but under the other two fault cases, the areas decrease by about 38.4% at most. This means that the five-phase DRPMSM can output more torque in the parallel drive than the series drive. Furthermore, there is vibration on the edge of MMF amplitude under all of these three fault cases. The performances of MMF amplitude edge are shown in Table 6.
From Table 6, one can conclude that the parallel drive has better MMF performances than the series drive, wherein, its average is higher about15% of Fn, and its ripple is smaller about 19% at least. In contrast with Equation (9), it can be discovered that there are two other types of MMF except the positive-rotating component in Equation (27), as described in the Part II and Part III. Similar with the fault of one phase open-circuit, the generating currents of the MMF depicted in the Part I, Part II, and Part III of Equation (27) can be expressed respectively as:
Under the three fault cases, the output torques of five-phase DRPMSM are shown in Figure 13a. By means of the FEA, the torques produced by current 3–5 are also obtained, and their resultant torque is acquired by linear addition, as shown in Figure 13b.
It can be seen from Table 7 that the average torque is higher about 16%–38% of Tn and the ripple is lower about 20%–40% in the parallel drive, as compared with the series drive. In addition, the characteristics of resultant torque are similar to that of the torque direct output under fault case c, i.e., average torque and ripple. Although the average torque produced by current 3 is nearly equal to the resultant torque, its ripple is very small (about 2.07%) as compared with the ripple of resultant torque (about 45.2%). Thus, the ripple torque of resultant torque is mainly produced by currents 4 and 5.
4.3. Two Non-Adjacent Phases Open Circuit without Adjustment
Supposing that phase “a” and “d” are open circuited. To satisfy the constraint of star connection, the phase angles of remaining normal phases are regulated, whereas their current amplitudes are kept unchanged, as follows:
Accordingly, it can be got that:
In order to maximize the average torque produced by fault winding, based on Equation (6), it can be obtained that:
By solving Equations (32) and (33), the optimal solution can be obtained that:
Thus, it can be known that the fault winding can output about 56.5% of normal torque, which is higher than the case of two adjacent phases open-circuit fault. If only considering the fault occurring in one side winding, two non-adjacent phases open-circuit fault can be classified into the following three cases:
- Case a:
the fault occurs in the inner motor in the parallel drive, so the resulting MMF of five-phase DRPMSM becomes:
- Case b:
the fault occurs in the outer motor in the parallel drive, so the resulting MMF of five-phase DRPMSM becomes:
- Case c:
the fault occurs in the series drive, so the total MMF becomes:
The MMF distributions under these three fault cases are shown in Figures 14, 15–16. It can be seen the net result still remains a sinusoidal form, but there is fluctuation on the fringe of MMF amplitude. As compared with Figure 5, one can find that the areas projecting into the space- and time domain all reduce by about 13%–43%, which leads the average torque to decrease under open-circuit faults. The performances of MMF amplitude edge are informed in Table 8.
By comparing Figures 14, 15–16, it can be concluded that the areas projecting into the space- and time domain decrease by a smaller proportion in the parallel drive than the series drive. At the same time, the average of MMF amplitude edge is greater but the ripple is smaller in the parallel drive than the series drive, as shown in Table 8. Similarly to the former open-circuit faults, the generating currents of the MMF depicted in the Part I, Part II and Part III of Equation (37) can be expressed respectively as:
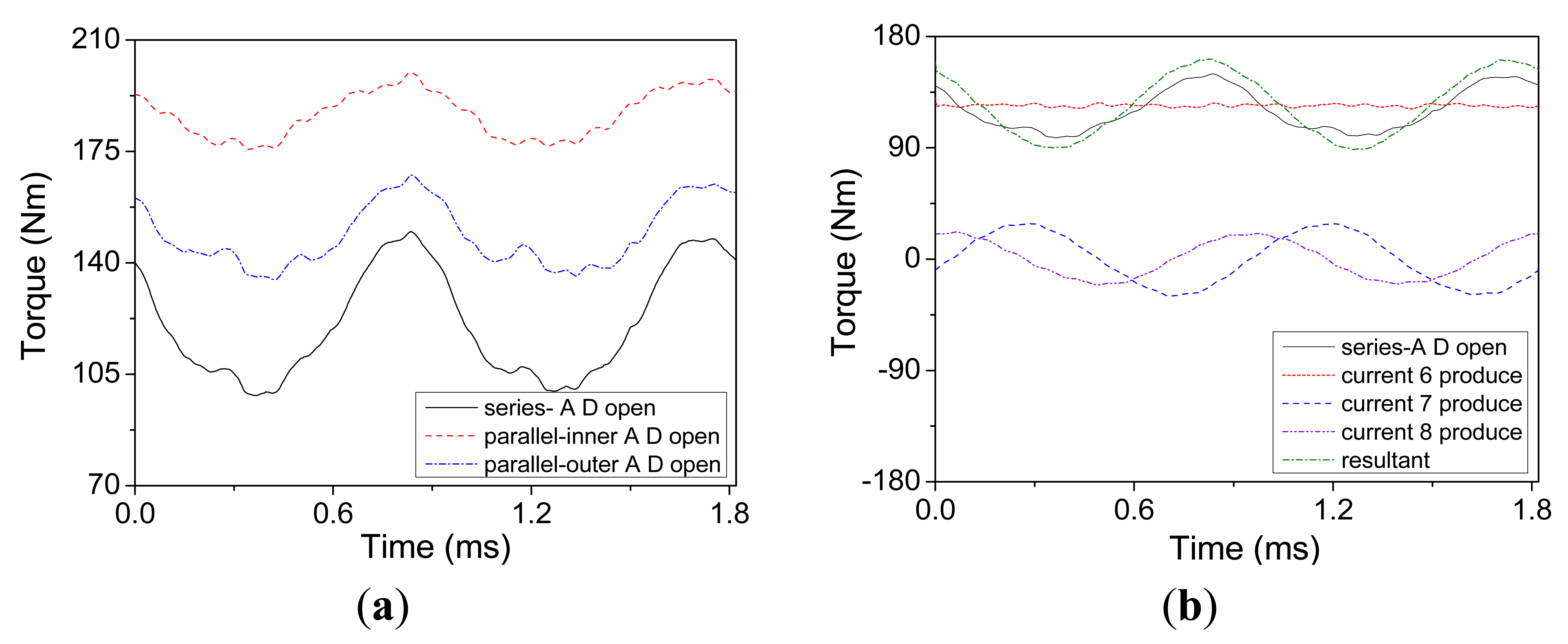
Under the three open-circuit fault cases, the torques are obtained by the FEA, as shown in Figure 17a. Similarly, the torques produced by current 6–8 are obtained, as shown in Figure 17b, and their resultant torque is obtained by linear superposition at the same time.
It can be learned from Table 9 that the average of the resultant torque is similar to that of direct output torque under fault case c, as well as the torque ripple. Comparing with the torque produced by current 6, the ripple of resultant torque is relatively larger, about 29.5%, but their averages are almost the same. Therefore, the ripple torque of resultant torque is mainly produced by current 7 and 8. In addition, it can be known that the motor driven in parallel can output a larger average torque with a smaller ripple than in series.
4.4. Comparison and Analysis
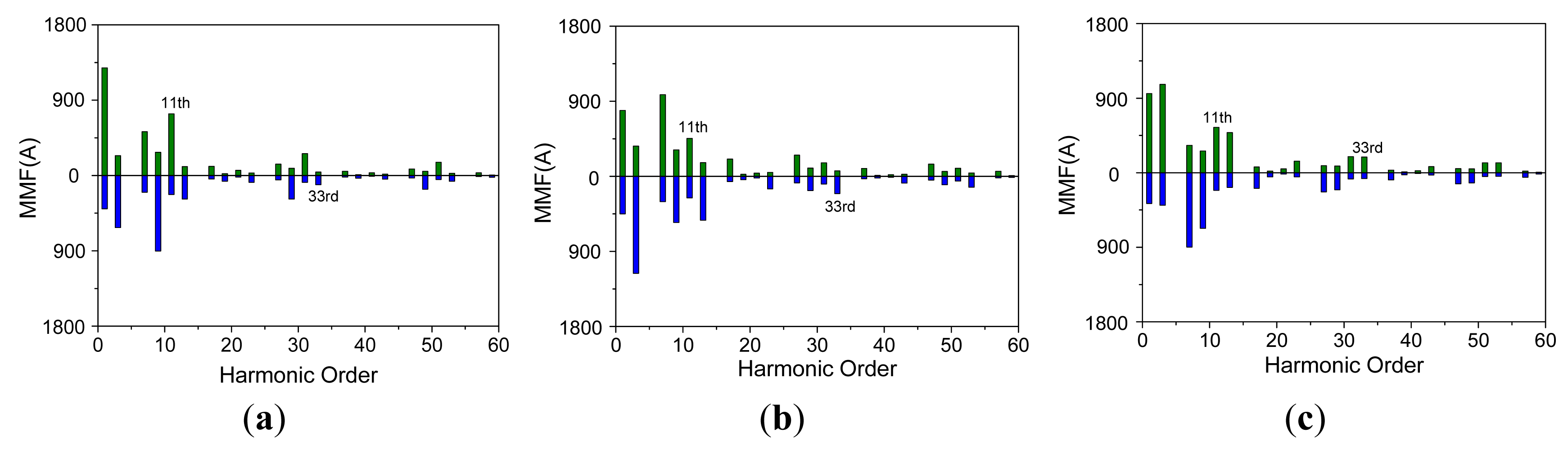
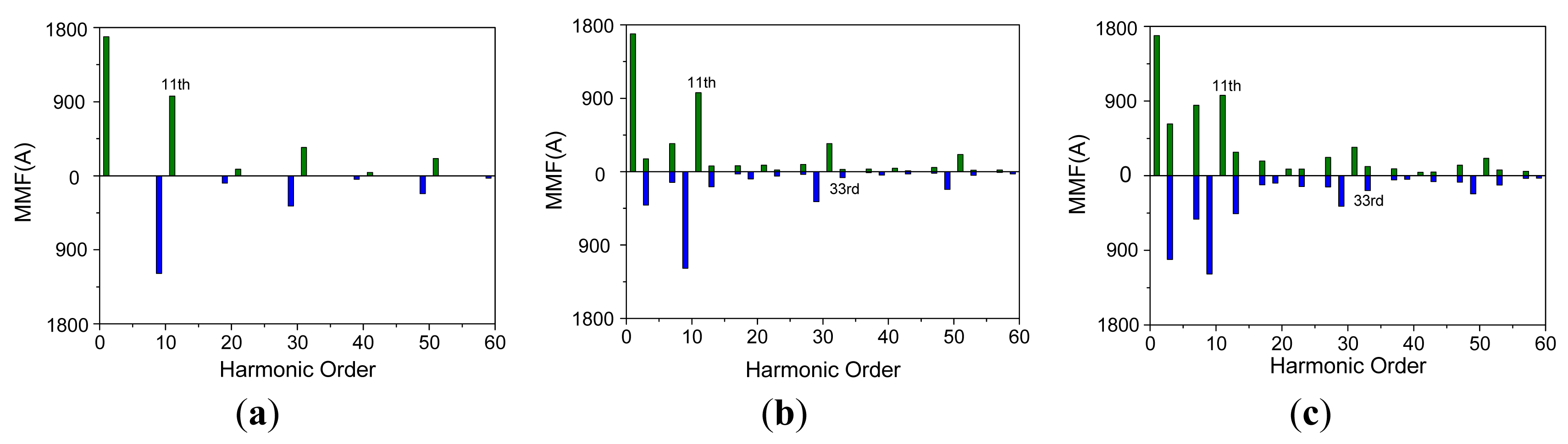
By comparing the simulation results, it can be concluded that the performances of torque and MMF are similar, i.e., average ratio and ripple, even though there are some small differences between them. To explain this phenomenon, the MMF harmonics analysis is performed based on the winding function, as shown in Figure 18, where, the green columns stand for the MMF harmonics traveling forward and the blue columns stand for the MMF harmonics traveling backward.
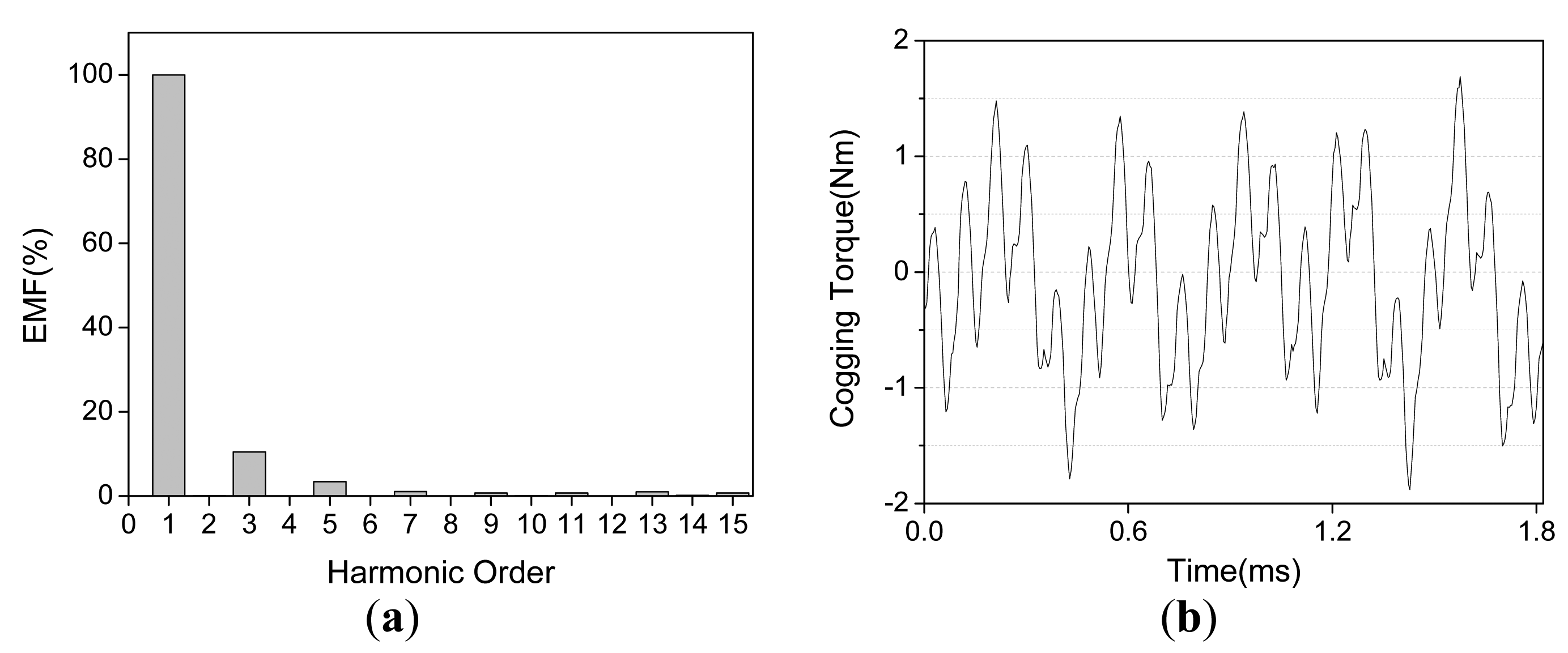
It can be found from Figure 18 that the space harmonics of 10υ±3 order appear after open-circuit fault, apart from the negative rotating component of 11th harmonic. Due to the different rotating speed, the ripple torques of second and fourth order will be generated, when the 33rd stator MMF harmonic interacting with the 33rd rotor MMF harmonic, i.e., the third order harmonic of back-EMF, as shown in Figure 19a. Furthermore, the cogging torque is also the main contributor of torque ripple, which is obtained by the FEA, as shown in Figure 19b. These two factors are all ignored in the MMF analysis, thus the differences are generated between the performances of MMF and torque.
In order to make clear the relationship between torque and MMF, the following derivation is given. For the vector control that direct-axis current is equal to zero, the electromagnetic torque of five-phase DRPMSM can be computed by:
Where ψf is the total PM flux linkage produced by inner and outer rotors.
When the stator windings encounter open-circuit faults, the PM flux-linkage is not affected at all. Hence, the variation of average torque keeps synchronous with the change of current amplitude, which can be seen from Equation (41). What is more, the current amplitude is proportional to the MMF amplitude. Taking the open-circuit faults occurring in the series drive as an example, simulating the change of MMF amplitude fringe, a kind of equivalent current amplitude function is constructed. In the time domain, the current amplitude function can be expressed as:
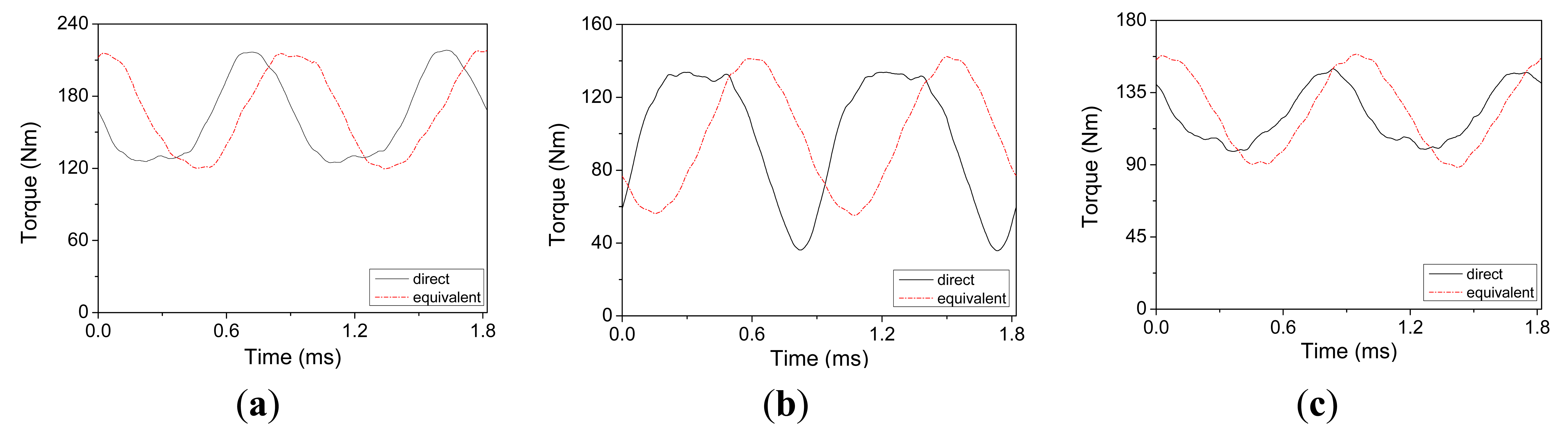
The torques generated by the equivalent currents are shown in Figure 20. It can be observed that the waveforms of torque produced by the equivalent currents are similar to that of the direct output under open-circuit faults, except for the phase angle. The reason may be that the space factor is ignored in the process of constructing the equivalent current. In addition, one can find from Table 11 that the torque characteristics of equivalent output are close to that of direct output under fault cases, which proves the relationship between MMF and torque from another aspect.
5. Analysis under Open Circuit Fault with Adjustment
It can be known from Section 4 that the torque ripple is mainly caused by other types of MMF except for the positive rotating component in the 11th MMF harmonic, under open-circuit fault conditions. Therefore, the current control strategy is employed to obtain a disturbance-free MMF (11th harmonic MMF) in this section and the total stator MMF of five-phase DRPMSM is kept constant in pre- and post fault situations.
5.1. One Phase Open Circuit with Adjustment
It is assumed that phase “a” is open circuited. From Section 4.1, one can learn that the ripple current, as depicted in Equation (20), can generate a negative rotating MMF. For the five-phase DRPMSM, the total MMF is the sum of inner and outer motors, whereas the inner motor and outer motor can be controlled independently in the parallel drive. Thus, the same ripple current is injected into the normal working winding to cancel out the negative rotating MMF, so that the disturbance free MMF can be obtained. Then, the phase currents of the normal working winding can be depicted as:
As for the fault winding, its currents expression are kept unchanged, as depicted in Equation (10), but the amplitude has to increase about 31.3% so as to improve the average torque to the normal level.
For the fault occurring in the series drive, the remaining healthy phase currents are adjusted by applying the current control strategy proposed in [15]. After adjustment, the remaining normal phase currents become:
Under the new current excitations, the torques for the three fault cases (as depicted in Section 4.1) are obtained, as shown in Figure 21 and Table 12. One can find that the average torque can increase to about 96%–98% of Tn in the series drive and parallel drive. However, the torque ripple is smaller in the parallel drive than series drive.
5.2. Two Adjacent Phase Open Circuit with Adjustment
It is assumed that phase “b” and “c” are open circuited. Similar to one phase open-circuit, the ripple currents, as depicted in Equation (29) and (30), are injected into the normal winding in the parallel drive, but the fault winding current expressions are remained unchanged. By adjusting, the phase currents of normal winding can be expressed as:
If the average torque is kept unchanged in pre- and post fault situations for the fault winding, its current amplitude has to become into 2.14 times of Im. For the fault happening in the series drive, the rest of normal phase currents after adjustment can be depicted as:
Under the condition of faults with adjustment, the torques for the three cases (as depicted in Section 4.2) are obtained, as shown in Table 13. It can be discovered that the motor can output more than 91% of Tn in both of the parallel drive and series drive, but the torque ripple is relatively smaller in the parallel drive.
5.3. Two Non-Adjacent Phase Open Circuit with Adjustment
It is assumed that phase “a” and “d” are open circuited. When the five-phase DRPMSM is driven in parallel, the current expressions of fault windings are kept unchanged, and the ripple currents (as depicted in Equation (39) and (40)) are injected into the normal winding to obtain an undisturbed rotating MMF. Thus, the phase currents of normal winding change to:
Supposing that the average torque remains unchanged before and after the fault, the current amplitude of fault winding must increase by about 77%. For the series drive, after the fault with adjustment, the remaining normal phase currents can be described as:
Under the three fault cases (as depicted in Section 4.3) with adjustment, the torques are obtained, as shown in Table 14. It can be found that the average torques increase by about 8%–38% of Tn, and the torque ripples decrease by more than 50%, as compared with the fault without adjustment. In addition, the average torque is larger, but the ripple is relatively smaller in the parallel drive than series drive.
5.4. Comparison and Discussion
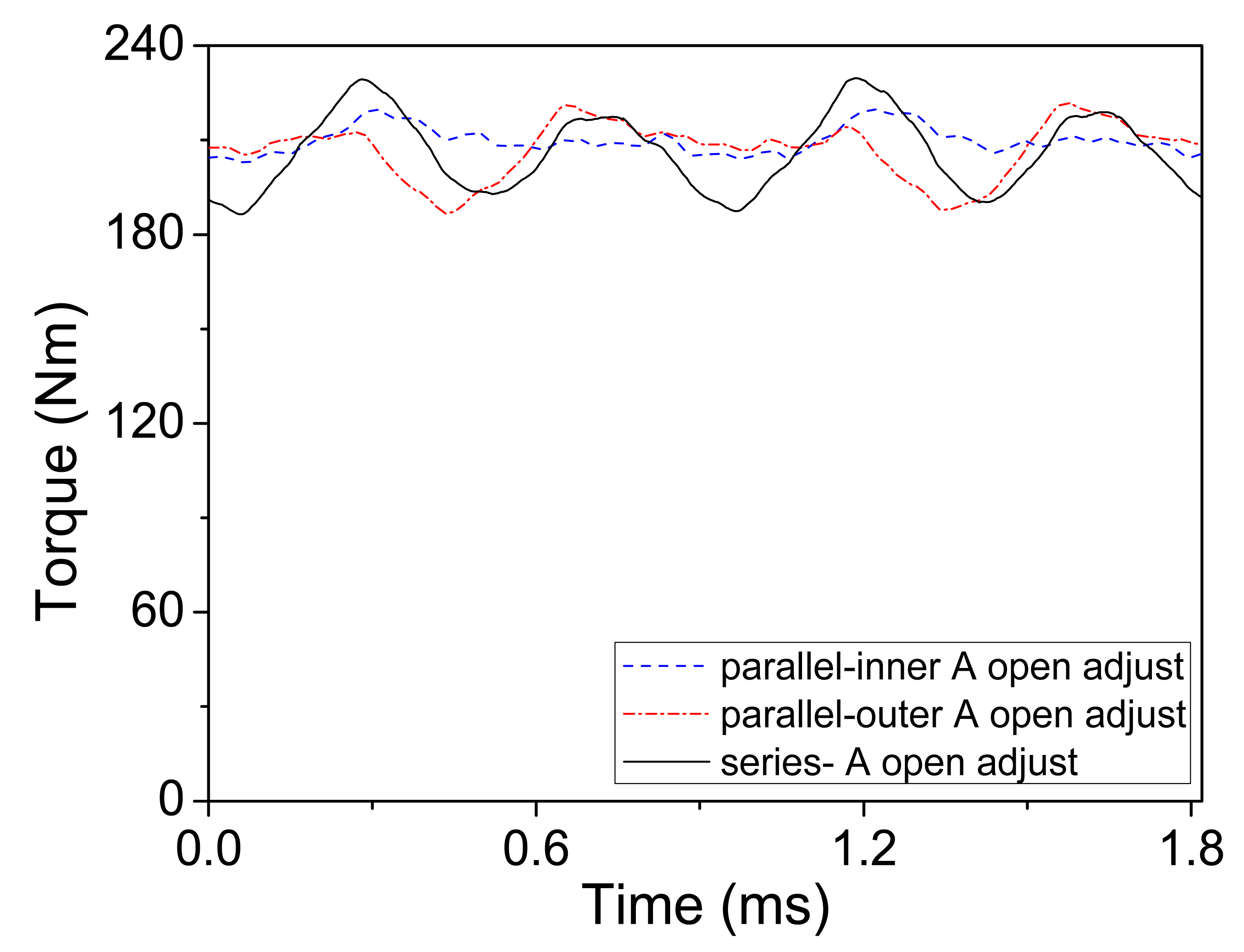
From the above results, one can learn that the average torque increases to about 91%–98% of normal value, after the open-circuit faults with adjustment. Nevertheless, the torque ripple is still lager than under normal conditions. Taking a one phase open-circuit fault happening in the series drive as an example, this phenomenon is explained as follows: based on the winding function, the MMF harmonics analysis are performed under normal and open-circuit faults with adjustment, as shown in Figure 22. It can be seen that the negative rotating MMF component of 11th harmonic is removed, and the harmonics amplitudes of 10υ±1 order are improved to the normal value, as depicted in Figure 22a. However, the harmonics of 10υ±3 order still exist, and their amplitudes increase a lot, as compared with the fault without adjustment. Due to the asynchronous speed, the ripple torque of second and fourth order will be generated, when the 33rd stator MMF harmonic interacting with the 33rd rotor MMF harmonic. This influences the torque ripple in some extent. What is more, one can find that the harmonics amplitudes of 10υ±3 order are smaller in the parallel drive than series drive, thus the rotor losses induced by MMF harmonics are less in the parallel drive.
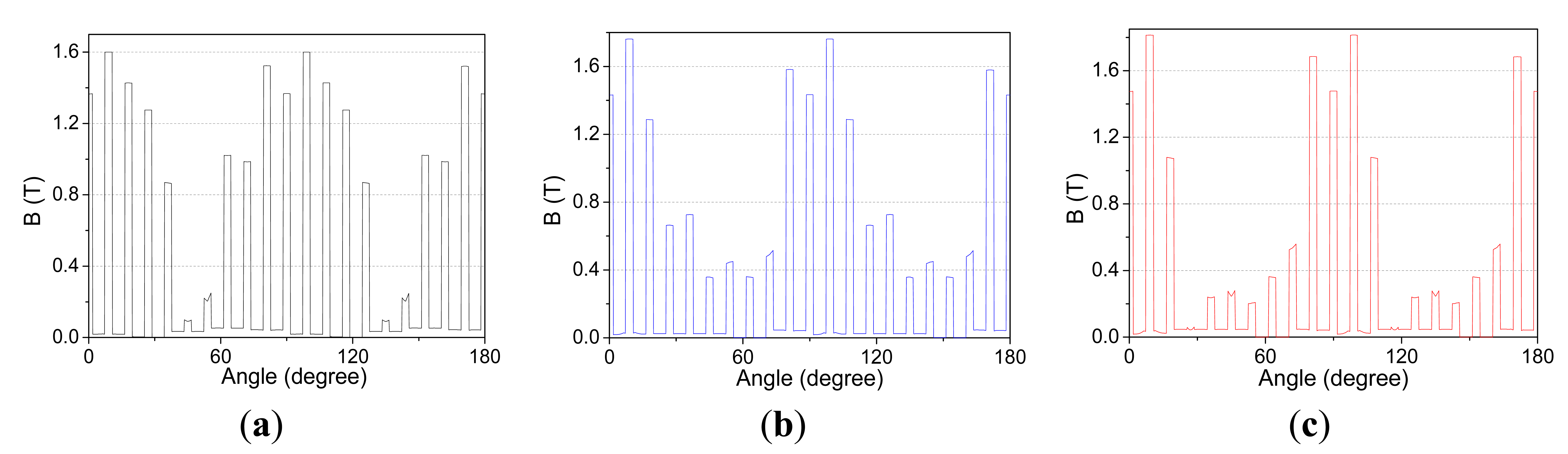
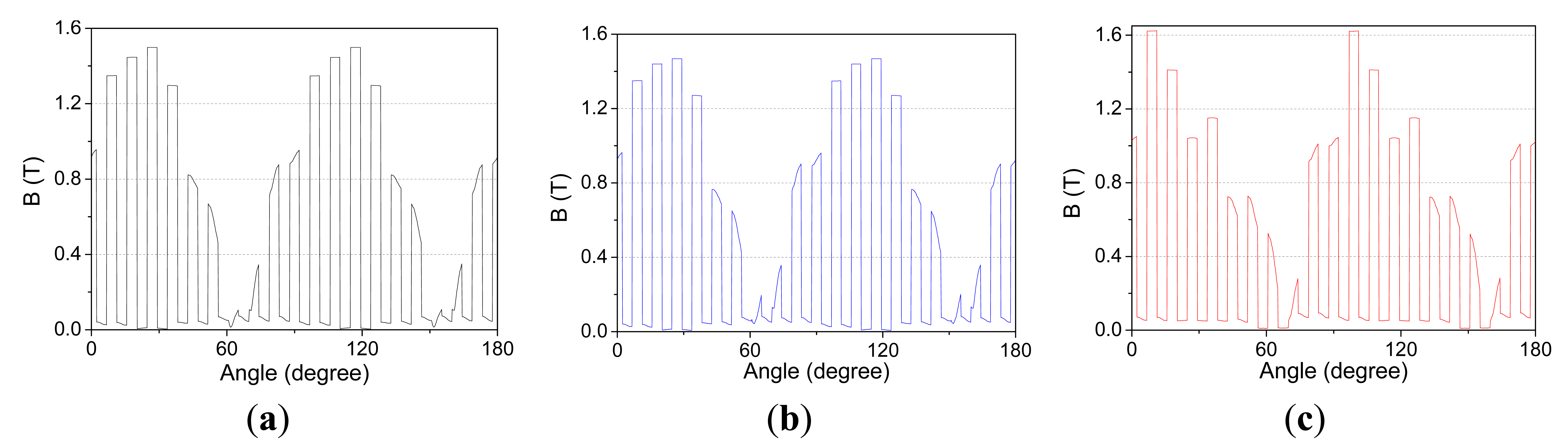
In addition, it can be known from Section 5.1 that the current amplitudes of fault winding increase by about 31%–38% of Im, which results in the flux density in the stator teeth on the fault side becoming saturation(B > 1.6T), as shown in Figures 23 and 24. Thus, the actual back-EMF waveforms are distorted, which leads to larger torque ripple [35].
6. Conclusions
In this paper, the MMF and torque performances of a novel five-phase DRPMSM, with both advantages of good fault tolerant capability and high torque density, have been investigated. Due to the different connection types, the inside windings and outside windings can be driven in series or parallel. Through analysis, it can be concluded that the inner motor and outer motor are magnetic decoupling, so they can be controlled independently in the parallel drive. Comparing with the series drive, the motor is able to exhibit better MMF and torque performances in the parallel drive, i.e., higher average and smaller ripple, when facing the same fault conditions.
Under the condition of open-circuit faults without adjustment, the remaining normal phase currents of the faulty winding are regulated to meet the constraint of star-connection and the maximum average torque is obtained. By comparison, it is found that the characteristics of torque and MMF magnitude edge are similar, i.e., average ratio and ripple, even though there are some differences between them. This may be caused by the existence of cogging torque and ripple torques of second and fourth order, which are generated by the interaction between 33rd order stator MMF space harmonic and 33rd rotor MMF harmonic, because of the different rotating speed. Furthermore, it can be known that the other types of MMF are present in the fault MMF, which leads to the torque ripple becoming larger.
Then, the open-circuit faults are adjusted to obtain an undisturbed rotating MMF. For the parallel drive, this objective is achieved by injecting the ripple currents into the normal working winding, whereas the fault winding currents expression are kept unchanged except increasing the amplitude; for the series drive, this objective is achieved by keeping the total MMF unchanged in pre- and post fault situations. After adjustment, one can discover that the average torque can increase to about 91%–98% of normal torque, but the torque ripple is still larger than in a normal situation. One reason is that the current amplitudes of the faulty winding improve a lot, as compared with the normal situation, which causes the local magnetic saturation, thus results in larger torque ripple. Another reason is that the 33rd order stator MMF space harmonic still exists and its amplitude increases. Due to the asynchronous velocity, the ripple torques of second and fourth order are generated, when it interacting with the 33rd rotor MMF harmonic.
Acknowledgments
This work was supported in part by the National Natural Science Foundation of China under Project 51307008 and 11372034, in part by Ph.D. Programs Foundation of Ministry of Education of China under Project 20121101120024, in part by Basic Research Foundation of Beijing Institute of Technology under Grant 20110642015 and 20120642013, and in part by Excellent Young Scholars Research Fund of Beijing Institute of Technology.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chan, C.C. An overview of electric vehicle technology. Proc. IEEE 1993, 81, 1202–1213. [Google Scholar]
- Zhu, Z.Q.; Howe, D. Electrical machines and drives for electric, hybrid, and fuel cell vehicles. Proc. IEEE 2007, 95, 746–765. [Google Scholar]
- Pellegrino, G.; Vagati, A.; Boazzo, B.; Guglielmi, P. Comparison of induction and PM synchronous motor drives for EV application including design examples. IEEE Trans. Ind. Appl. 2012, 48, 2322–2332. [Google Scholar]
- Mecrow, B.C.; Jack, A.G.; Atkinson, D.J.; Green, S.R.; Atkinson, G.J.; King, A.; Green, B. Design and testing of a four-phase fault tolerant permanent-magnet machine for an engine fuel pump. IEEE Trans. Energy Convers. 2004, 19, 671–678. [Google Scholar]
- Villani, M.; Tursini, M.; Fabri, G.; Castellini, L. High reliability permanent magnet brushless motor drive for aircraft application. IEEE Trans. Ind. Electron. 2012, 59, 2073–2081. [Google Scholar]
- Parsa, L.; Toliyat, H.A. Fault-tolerant interior-permanent-magnet machines for hybrid electric vehicle applications. IEEE Trans. Veh. Technol. 2007, 56, 1546–1552. [Google Scholar]
- Chen, Q.; Liu, G.; Gong, W.; Zhao, W. A new fault-tolerant permanent magnet machines for electric vehicle applications. IEEE Trans. Magn. 2011, 47, 4183–4186. [Google Scholar]
- Simoes, M.G.; Vieira, P., Jr. A high-torque low-speed multiphase brushless machine-A perspective application for electric vehicles. IEEE Trans. Ind. Electron. 2002, 49, 1154–1164. [Google Scholar]
- Liu, G.; Gong, W.; Chen, Q.; Jian, L.; Shen, Y. Design and analysis of new fault-tolerant permanent magnet motors for four-wheel-driving electric vehicles. J. Appl. Phys. 2012, 111. [Google Scholar] [CrossRef]
- Wang, J.; Atallah, K.; Howe, D. Optimal torque control of fault-tolerant permanent magnet brushless machines. IEEE Trans. Magn. 2003, 39, 2962–2964. [Google Scholar]
- Bianchi, N.; Bolognani, S.; Pre, M.D. Strategies for the fault-tolerant current control of a five-phase permanent-magnet motor. IEEE Trans. Ind. Appl. 2007, 43, 960–970. [Google Scholar]
- Dwari, S.; Parsa, L. Fault-tolerant control of five-phase permanent-magnet motors with trapezoidal back EMF. IEEE Trans. Ind. Electron. 2011, 58, 476–485. [Google Scholar]
- Tani, A.; Mengoni, M.; Zarri, L.; Serra, G.; Casadei, D. Control of multi-phase induction motors with an odd number of phases under open circuit faults. IEEE Trans. Power Electron. 2012, 27, 565–577. [Google Scholar]
- Fu, J.R.; Lipo, T.A. Disturbance-free operation of a multiphase current-regulated motor drive with an opened phase. IEEE Trans. Ind. Appl. 1994, 30, 1267–1274. [Google Scholar]
- Toliyat, H.A. Analysis and simulation of five-phase variable-speed induction motor drives under asymmetrical connections. IEEE Trans. Power Electron. 1998, 13, 748–756. [Google Scholar]
- Xu, H.; Toliyat, H.A.; Petersen, L.J. Resilient current control of five-phase induction motor under asymmetrical fault conditions. Proceedings of Applied Power Electronics Conference and Exposition (APEC), Dallas, TX, USA, 10–14 March 2002; pp. 64–71.
- Phyu, H.N.; Aung, N.L.H.; Bi, C. Influence of winding structure and the effect of MMF harmonics to the spindle motor performance for ultrahigh TPI HDD. IEEE Trans. Magn. 2013, 49, 2779–2781. [Google Scholar]
- Li, J.; Choi, D.W.; Son, D.H.; Cho, Y.H. Effects of MMF harmonics on rotor eddy-current losses for inner-rotor fractional slot axial flux permanent magnet synchronous machines. IEEE Trans. Magn. 2012, 48, 839–842. [Google Scholar]
- Bianchi, N.; Bolognani, S.; Fornasiero, E. An overview of rotor losses determination in three-phase fractional-slot PM machines. IEEE Trans. Ind. Appl. 2010, 46, 2338–2345. [Google Scholar]
- Fornasiero, E.; Bianchi, N.; Bolognani, S. Slot harmonic impact on rotor losses in fractional-slot permanent-magnet machines. IEEE Trans. Ind. Electron. 2012, 59, 2557–2564. [Google Scholar]
- Zhu, Z.Q.; Howe, D. Analytical prediction of the cogging torque in radial-field permanent magnet brushless motors. IEEE Trans. Magn. 1992, 28, 1080–1083. [Google Scholar]
- Lin, D.; Ho, S.L.; Fu, W.N. Analytical prediction of cogging torque in surface-mounted permanent-magnet motors. IEEE Trans. Magn. 2009, 45, 3296–3302. [Google Scholar]
- Deodhar, R.P.; Staton, D.A.; Jahns, T.M.; Miller, T.J.E. Prediction of cogging torque using the flux-MMF diagram technique. IEEE Trans. Ind. Appl. 1996, 32, 569–576. [Google Scholar]
- Staton, D.A.; Deodhar, R.P.; Soong, W.L.; Miller, T.J.E. Torque prediction using the flux-MMF diagram in ac, dc, and reluctance motors. IEEE Trans. Ind. Appl. 1996, 32, 180–188. [Google Scholar]
- Qu, R.; Lipo, T.A. Design and parameter effect analysis of dual-rotor, radial-flux, toroidally wound, permanent-magnet machines. IEEE Trans. Ind. Appl. 2004, 40, 771–779. [Google Scholar]
- Praveen, R.P.; Ravichandran, M.H.; Achari, V.T.S.; Raj, V.P.J.; Madhu, G.; Bindu, G.R. A novel slotless Halbach-array permanent-magnet brushless dc motor for spacecraft applications. IEEE Trans. Ind. Electron. 2012, 59, 3553–3560. [Google Scholar]
- Hamadou, G.B.; Masmoudi, A.; Abdennadher, I. Design of a single-stator dual-rotor permanent-magnet machine. IEEE Trans. Magn. 2009, 45, 127–132. [Google Scholar]
- Chai, F.; Xia, J.; Guo, B.; Cheng, S.; Zhang, J. Double-stator permanent magnet synchronous in-wheel motor for hybrid electric drive system. IEEE Trans. Magn. 2009, 45, 278–281. [Google Scholar]
- Wang, Y.; Cheng, M.; Chen, M.; Du, Y.; Chau, K.T. Design of high-torque-density double-stator permanent magnet brushless motors. IET. Electr. Power Appl. 2011, 5, 317–323. [Google Scholar]
- Burress, T.A.; Campbell, S.L.; Coomer, C.L.; Ayers, C.W.; Wereszczak, A.A.; Cunningham, J.P.; Marlino, L.D.; Seiber, L.E.; Lin, H.T. Evaluation of the 2010 Toyota Prius Hybrid Synergy Drive System; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 2011. [Google Scholar]
- Mitcham, A.J.; Antonopoulos, G.; Cullen, J.J.A. Favourable slot and pole number combinations for fault-tolerant PM machines. IEE Proc. Electr. Power Appl. 2004, 151, 520–525. [Google Scholar]
- Ishak, D.; Zhu, Z.Q.; Howe, D. Permanent-magnet brushless machines with unequal tooth widths and similar slot and pole numbers. IEEE Trans. Ind. Appl. 2005, 41, 584–590. [Google Scholar]
- Aslan, B.; Semail, E.; Legranger, J. General analytical model of magnet average eddy-current volume losses for comparison of multiphase PM machines with concentrated winding. IEEE Trans. Energy Convers. 2014, 29, 72–83. [Google Scholar]
- Cheng, S.K.; Yu, Y.J.; Chai, F.; Gao, H.W.; Liu, W. Analysis of the inductances of interior permanent magnet synchronous motor. Proc. CSEE 2009, 29, 94–99. [Google Scholar]
- Azar, Z.; Zhu, Z.Q.; Ombach, G. Influence of electric loading and magnetic saturation on cogging torque, back-EMF and torque ripple of PM machines. IEEE Trans. Magn. 2012, 48, 2650–2658. [Google Scholar]








| Parameter | 2010 Prius | Five-phase DRPMSM |
|---|---|---|
| Peak power (kw) | 60 | 18@750 rpm |
| Maximum speed (rpm) | 13,500 | 1500 |
| Peak torque (nm) | 207 | 210 |
| Outer rotor out diameter (mm) | - | 320 |
| Outer rotor in diameter (mm) | - | 300 |
| Stator outer diameter (mm) | 264 | 298 |
| Stator inner diameter (mm) | 161.9 | 130 |
| Inner rotor out diameter (mm) | 160.4 | 128 |
| Inner rotor inner diameter (mm) | 51 | 100 |
| Rotor stack length (mm) | 50.165 | 60 |
| Stator stack length (mm) | 50.8 | 60 |
| Air gap (mm) | 0.73 | 1 |
| Number of stator slots | 48 | 40 |
| Number of rotor poles | 8 | 44 |
| Current density (A/mm2) | 40.1 | 20 |
| Torque density (kNm/m3) | 74.15 | 43.52 |
| Case | Inductance | Case | Inductance | Case | Inductance |
|---|---|---|---|---|---|
| LAA | 750 μH | MAa | 0.888 μH | Laa | 775 μH |
| MAB | 1.157 μH | MAb | 0.1 μH | Mab | 0.076 μH |
| MAC | 3.765 μH | MAc | 0.286 μH | Mac | 1.177 μH |
| Case | Average torque (Tav, Nm) | Linear addition (Nm) |
|---|---|---|
| Inside winding-inner rotor | 63.8 | 214.6 |
| Outside winding-outer rotor | 150.8 | |
| Inside winding-inner and outer rotors | 64 | 214.7 |
| Outside winding-inner and outer rotors | 150.7 | |
| Inside and outside windings-inner and outer rotors | 214.7 | - |
| Case | Average of MMF amplitude edge (Fav,pu) | Fav / Fn (%) | Ripple (%) |
|---|---|---|---|
| Case a | 0.4156 | 92.6 | 7.98 |
| Case b | 0.3741 | 83.3 | 19.9 |
| Case c | 0.3424 | 76.3 | 30.8 |
| Case | Tav (Nm) | Pk-Pk value of fluctuation (Nm) | Torque ripple (%) | Tav / Tn (%) |
|---|---|---|---|---|
| Case a | 199.2 | 31.4 | 7.87 | 92.8 |
| Case b | 178 | 65.7 | 18.4 | 82.9 |
| Case c | 162.7 | 93.6 | 28.8 | 75.8 |
| Current 1 | 165.8 | 5.74 | 1.73 | 77.2 |
| Current 2 | 0 | 105.3 | - | - |
| Resultant | 166 | 103.9 | 31.2 | 77.3 |
| Case | Fav (pu) | Fav / Fn (%) | Ripple (%) |
|---|---|---|---|
| Case a | 0.3765 | 83.9 | 7.12 |
| Case b | 0.2768 | 61.6 | 23.2 |
| Case c | 0.2079 | 46.3 | 42 |
| Case | Tav (Nm) | Pk-Pk value of fluctuation (Nm) | Torque ripple (%) | Tav / Tn (%) |
|---|---|---|---|---|
| Case a | 180.3 | 30.4 | 8.44 | 84 |
| Case b | 133.4 | 77.5 | 29 | 62.1 |
| Case c | 98.8 | 98.1 | 49.5 | 46 |
| Current 3 | 100.1 | 4.27 | 2.07 | 46.6 |
| Current 4 | 0 | 70.2 | - | 0 |
| Current 5 | 0 | 51.4 | - | 0 |
| Resultant | 100 | 92.4 | 45.2 | 46.6 |
| Case | Fav (pu) | Fav / Fn (%) | Ripple (%) |
|---|---|---|---|
| Case a | 0.3896 | 86.8 | 5.76 |
| Case b | 0.3117 | 69.4 | 15.9 |
| Case c | 0.2538 | 56.5 | 27.8 |
| Case | Tav (Nm) | Pk-Pk value of fluctuation (Nm) | Torque ripple (%) | Tav / Tn (%) |
|---|---|---|---|---|
| Case a | 186.7 | 24.5 | 6.55 | 87 |
| Case b | 148.7 | 32.9 | 11.1 | 69.3 |
| Case c | 120.7 | 51.6 | 21.3 | 56.2 |
| Current 6 | 124.1 | 8.98 | 3.6 | 57.8 |
| Current 7 | 0 | 58.4 | - | 0 |
| Current 8 | 0 | 42.8 | - | 0 |
| Resultant | 124 | 73.8 | 29.5 | 57.8 |
| Type of open-circuit | λ | η | θ (degree) |
|---|---|---|---|
| One phase | 0.763 | 0.235 | 90 |
| Two adjacent phases | 0.463 | 0.1944 | 210 |
| Two non-adjacent phases | 0.565 | 0.157 | 73 |
| Type of open-circuit | Tav (Nm) | Torque ripple (%) | |
|---|---|---|---|
| One phase | direct | 162.7 | 28.8 |
| equivalent | 167.9 | 29.4 | |
| Two adjacent phases | direct | 99 | 49.5 |
| equivalent | 98.5 | 43 | |
| Two non-adjacent phases | direct | 120.7 | 21.3 |
| equivalent | 124.2 | 28.4 | |
| Fault case | Tav (Nm) | Torque ripple (%) | Tav/ Tn (%) |
|---|---|---|---|
| Case a | 209.9 | 4 | 97.8 |
| Case b | 206.9 | 8.49 | 96.4 |
| Case c | 206.5 | 10.4 | 96.2 |
| Fault case | Tav (Nm) | Torque ripple (%) | Tav/Tn (%) |
|---|---|---|---|
| Case a | 203.3 | 4.9 | 94.7 |
| Case b | 200.8 | 10.6 | 93.5 |
| Case c | 195.7 | 15.4 | 91.1 |
| Fault case | Tav (Nm) | Torque ripple (%) | Tav / Tn (%) |
|---|---|---|---|
| Case a | 207.3 | 3 | 96.5 |
| Case b | 205.4 | 4.85 | 95.7 |
| Case c | 202 | 8.2 | 94.1 |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Li, Y.; Zhao, J.; Chen, Z.; Liu, X. Investigation of a Five-Phase Dual-Rotor Permanent Magnet Synchronous Motor Used for Electric Vehicles. Energies 2014, 7, 3955-3984. https://doi.org/10.3390/en7063955
Li Y, Zhao J, Chen Z, Liu X. Investigation of a Five-Phase Dual-Rotor Permanent Magnet Synchronous Motor Used for Electric Vehicles. Energies. 2014; 7(6):3955-3984. https://doi.org/10.3390/en7063955
Chicago/Turabian StyleLi, Yumeng, Jing Zhao, Zhen Chen, and Xiangdong Liu. 2014. "Investigation of a Five-Phase Dual-Rotor Permanent Magnet Synchronous Motor Used for Electric Vehicles" Energies 7, no. 6: 3955-3984. https://doi.org/10.3390/en7063955