A Systematic Method for Designing a PR Controller and Active Damping of the LCL Filter for Single-Phase Grid-Connected PV Inverters
Abstract
: The Proportional Resonant (PR) current controller provides gains at a certain frequency (resonant frequency) and eliminates steady state errors. Therefore, the PR controller can be successfully applied to single grid-connected PV inverter current control. On the contrary, a PI controller has steady-state errors and limited disturbance rejection capability. Compared with the L- and LC filters, the LCL filter has excellent harmonic suppression capability, but the inherent resonant peak of the LCL filter may introduce instability in the whole system. Therefore, damping must be introduced to improve the control of the system. Considering the controller and the LCL filter active damping as a whole system makes the controller design method more complex. In fact, their frequency responses may affect each other. The traditional trial-and-error procedure is too time-consuming and the design process is inefficient. This paper provides a detailed analysis of the frequency response influence between the PR controller and the LCL filter regarded as a whole system. In addition, the paper presents a systematic method for designing controller parameters and the capacitor current feedback coefficient factor of LCL filter active-damping. The new method relies on meeting the stable margins of the system. Moreover, the paper also clarifies the impact of the grid on the inverter output current. Numerical simulation and a 3 kW laboratory setup assessed the feasibility and effectiveness of the proposed method.1. Introduction
The rapid increase in global energy consumption has accelerated the need for greener energy sources. Nowadays, renewable, highly sustainable energies derived from inexhaustible sources such as wind, photovoltaic, or tides have attracted much more attention [1]. Distributed power generation systems (DPGS) are attractive both for the market and for researchers, and the most important part of a DPGS, the grid-connected inverter, is a research hotspot.
The filter is an essential component that suppresses the harmonics introduced through the Pulse-Width Modulation (PWM) technique used in grid-connected inverters. Thanks to the excellent harmonic suppression ability an LCL filter topology is much more attractive than L and LC filters. However, the LCL filter generates significant resonance peaks that worsen the system stability, and the control scheme design of grid-connected inverters take into consideration this behavior. Damping the filter resonance overcomes LCL filter oscillations and stabilizes the system [2,3]. Simple passive damping with a resistor connected in series or parallel to the LCL filter capacitor, results in additional power loss and decreases the LCL filter performance [4]. Papers in the literature present different active damping methods. The so-called ‘active damping by well-designed control algorithm' method is usually preferred because it has no additional power losses [4,5]. Among the active damping methods, the capacitor current feedback control algorithm is important because it is simple to manipulate and is stable [6].
The quality of the injected grid current is important in grid-connected inverter control. Because of the infinite gain of the PR controller at the selected resonant frequency, the zero steady-state error can be achieved [7,8]. Papers in the literature do not discuss in detail the analysis of the frequency response influence between the PR controller and LCL filter. Moreover, the design methods of PR controllers and active damping of the LCL filter have not been well clarified. In most cases, many trial-and-error procedures have been carried out to obtain a set of parameters.
Considering the controller and the LCL filter active damping as a whole system enhances the complexity of controller design method. Their frequency responses may influence each other and affect the system stability. The design of the PI controller and the LCL filter active damping has been thoroughly investigated in [6]. However, a systematic study of the design procedures of the PR controller and the LCL filter active damping is missing. This paper discusses in detail such a design method. When adopting the PR controller instead of PI controller, the grid may produce a different impact on the inverter output current. The paper also deals with the grid impact and proposes a method to eliminate the grid effect on the output currents of the inverter.
2. System Overview and Numerical Modeling
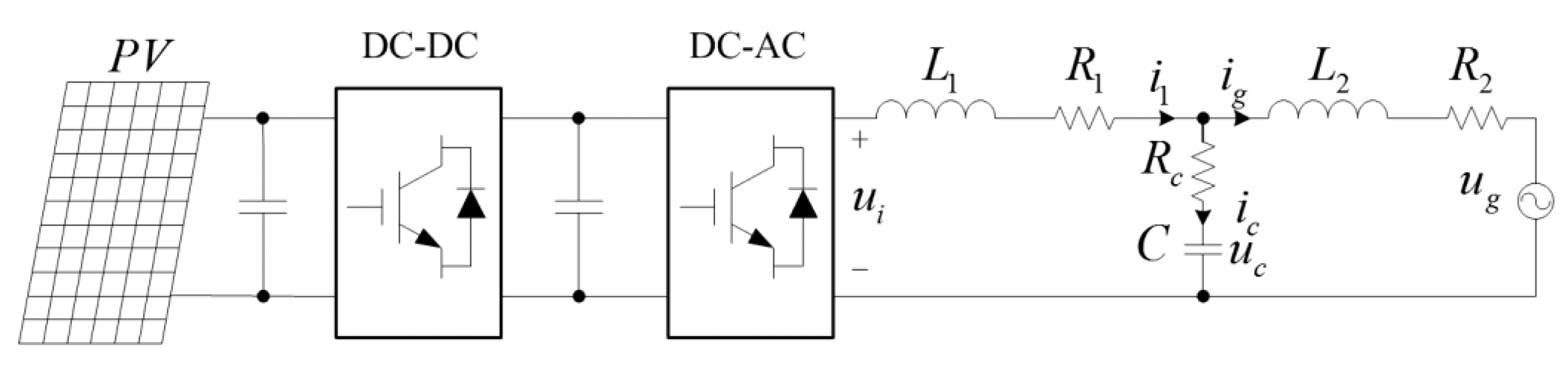
Figure 1 shows the typical topology of a two-stage single-phase grid-connected photovoltaic (PV) system.
The series connected L1 + R1, L2 + R2 and C + Rc that compose the LCL-type filter attenuate the harmonic injected into the grid generated from the inverter with the PWM technique. The boost DC-DC converter connected to the photovoltaic panel step up the voltage of the DC bus to a proper level for the DC-AC inverter. The H-bridge DC-AC inverter produces proper sinusoidal current in the grid with unity power factor based on the Maximum Power Point Tracking (MPPT) and Phase Locked Loop (PLL) algorithms. According to Figure 1, the mathematical model of the grid-connected inverter and the LCL filter is:
3. Control Scheme
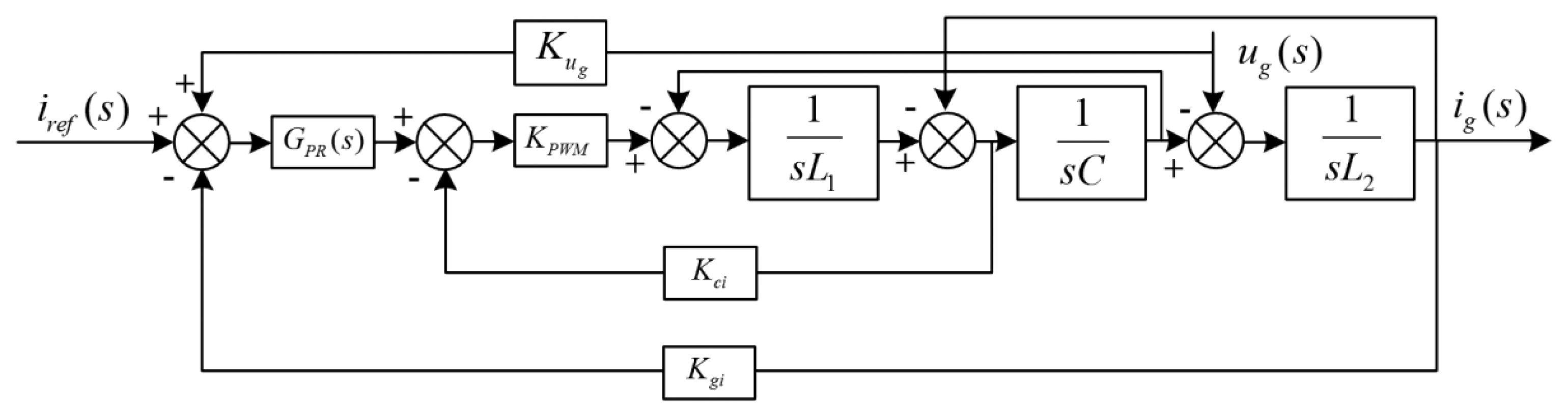
Figure 2 shows the PV system control scheme. By sampling the PV panel current and the voltage a proper MPPT algorithm can be ran. Papers in the literature present different MPPT algorithms [9–12]. The DC bus voltage control algorithm gives the injected current reference. Moreover, a PLL algorithm synchronizes the injected current with the grid voltage. Wide discussions on PLL algorithms for single-phase inverters can be found in various papers in the literature [13,14].
The current reference is sinusoidal: since a PI controller is unable to track a sinusoidal reference without steady-state errors, the PR controller has been adopted. The PR controller tracks the current introducing an infinite gain at a certain frequency (resonant frequency) [8,15]. Sampling the LCL filter capacitor current modifies the control algorithm to perform an active damping; the active damping is mostly used to smooth the resonance peak of the LCL filter. The feedforward of grid voltage is essential and the following sections of the paper will focus on it.
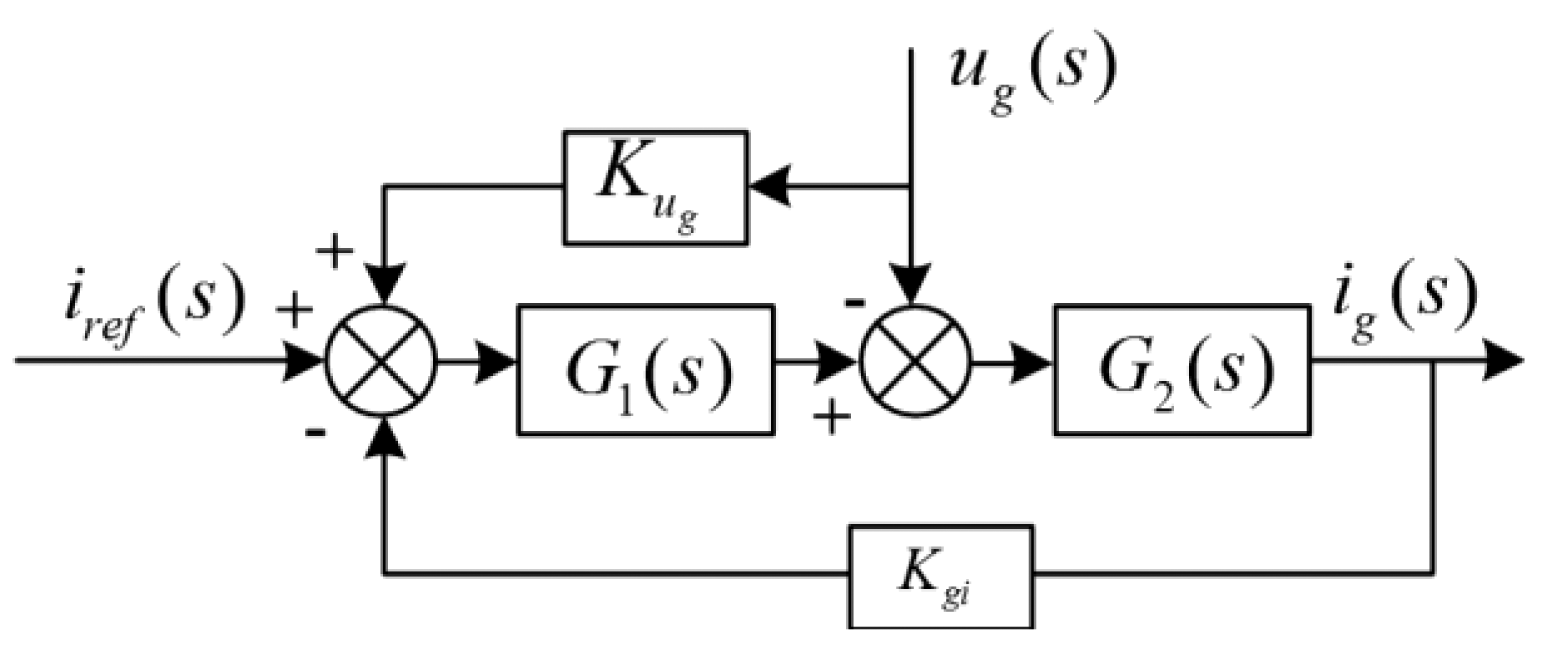
According to Equation (1) and Figure 2, Figure 3 shows the control diagram of injected current. To simplify the analysis, resistors R1, R2, and Rc have been omitted: this corresponds to the worst LCL filter working condition. Figure 4 shows the equivalent control block diagram.
where:
3.1. PR Controller
The Laplace transform of the ideal PR controller is:
Equation (4) shows the PR controller improved form; the integral term has been approximated using a high-gain low-pass filter [8]:
3.2. LCL Filter
LCL filter is a high order system; the Laplace transfer function is given by following Equation (R1, R2, and Rc have been omitted):
The LCL filter resonant frequency is:
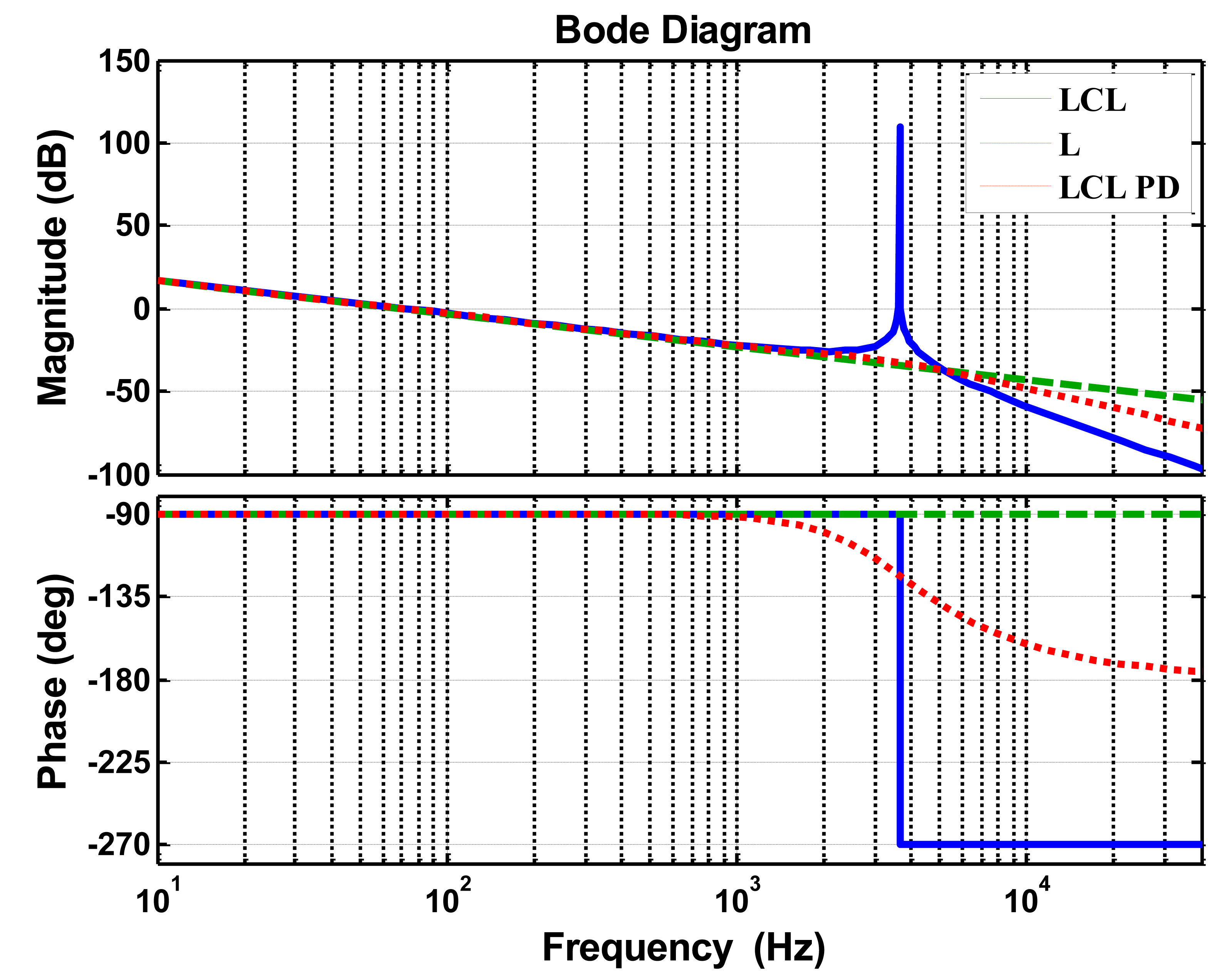
The LCL-filter provides outstanding performance attenuating the switching frequency current harmonics, better than the L- and LC-filters. Figure 7 compares the Bode diagram of the LCL and L filters. The red curve LCL PD (passive damping) represents the characteristic of the LCL-filter with a resistor connected in series with the capacitor. At low frequencies range, LCL and L filters show similar dynamic behaviors. At the high frequency range, LCL filter has stronger attenuation ability than the L-filter; this feature applies to medium and large power applications, since the very low switch frequency. As a drawbacks, the LCL filter presents resonance peaks around the resonant frequency and the phase-frequency curve across −π. As a result, systems become highly sensitive to disturbances and unstable, and the control algorithm design must consider the presence of an effective damping method.
The red curve LCL PD shows that the damping smooths the resonance peak, but worsens the LCL filter performance at the high frequency range, and generates additional power losses. Thus, an active damping method that modifies the control algorithm is preferable. This study adopts the active damping method based on the capacitor current feedback; the detailed design process is discussed later in the paper.
3.3. Grid Impact and Feedforward Control
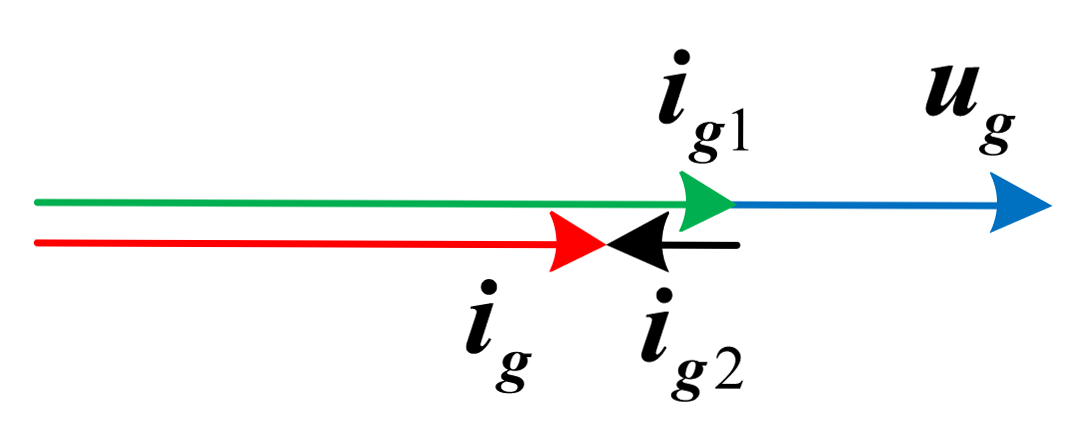
With reference to Figure 4, the current injected into the grid can be written as:
Defining the ratio between ig2(s) and ig1(s) as:
The grid can be treated as a disturb; omitting the feedforward from the grid the Equation (6) becomes:
Taking the grid fundamental frequency as subject, the capacitor in LCL filter can be omitted since the resonant frequency of LCL filter is far greater than the fundamental frequency [6]. Thus, Equation (4) can be written as Equation (8):
Substituting Equations (7) and (8) into Equation (6), gives:
Therefore, the feedforward of the grid is required; setting ig2 to zero, the feedforward factor becomes:
If the feedforward control lies behind the PR controller, the feedforward factor has a very simple form:
4. PR Controller and Active-Damping of LCL Filter Design
4.1. PR Controller Design
4.1.1. Proportional Gain Kp
Assuming that the fundamental frequency of the grid varies in the range ±1 Hz, ωPRc is:
Following Equation describes the control diagram open-loop transfer function:
The relationship between the cutoff frequency fc, the sampling frequency fs, and the resonant frequency fres is [6,16]:
The cutoff frequency fc of the system is usually designed to be far lower than the sampling frequency fs, and much smaller than the resonant frequency fres of LCL filter. Therefore, considering the frequency response of the system lower than the cutoff frequency, the capacitor of LCL filter can be omitted [6], and Equation (13) can be rewritten as Equation (14):
The cutoff frequency fc is higher than the fundamental frequency f1. As a result, according to Figure 6 the PR controller expression simplifies. At cutoff frequency, the magnitude frequency response of the system is zero, and Equation (15) is obtained:
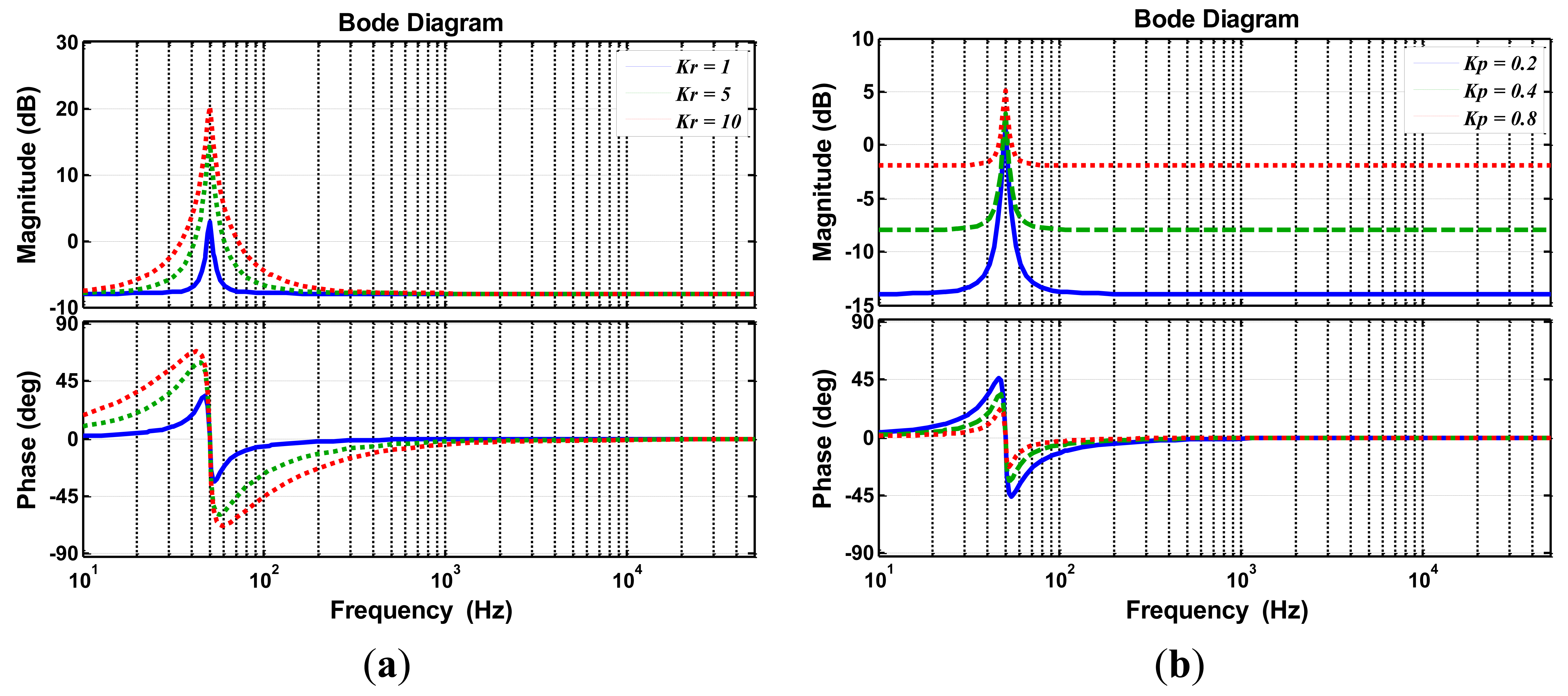
By successive approximations of Equation (15), the gain Kp is:
4.1.2. Fundamental Frequency Gain Kr
The tracking steady-state error of the grid current ig can be calculated as:
Assuming the adoption of grid feedforward control, Equation (17) can be simplified as:
Considering the fundamental frequency f1, and supposing the steady-state error of ig is η, following Equation gives the minimum of the magnitude-frequency response of open-loop transfer function at the fundamental frequency f1:
That is:
Taking Equation (16) into Equation (19), the lower threshold of Kr is deduced as:
The phase-frequency response of PR controller can be written as:
As the improved PR controller Bode plot shows (Figure 6), the larger K, the larger gain at the fundamental frequency is. It is beneficial to the quick response speed, but it emphasizes an extra drawback. The phase response of the controller tends to as Kr increases, which would affect the phase margins of the whole PV system. Therefore, a compromise between the response speed and the stability is required. Assuming the phase-frequency response of PR controller at cutoff frequency not exceeds −ϕ, and that the phase response of the other components at cutoff frequency must not exceed (PM − π + ϕ), following Equation (22) describes the phase:
Taking Equation (16) into Equation (22), the upper threshold of Kr is:
According to Equations (20) and (23), the range of Kr is defined through Equation (24):
4.2. Active-Damping of LCL Filter
Figure 9 shows the Bode diagram of the PV system with no PR controller. A high value of Kci shows better resonance peak damping capability, but phase margins become smaller. The reciprocal of magnitude-response at the LCL filter resonant frequency corresponds to the grid-connected system magnitude margins (GM). Thus, Equation (25) can be written as:
Since the resonant frequency is far from the fundamental frequency, the PR controller can be considered as a proportional component. Taking Equation (16) into Equation (25), the lower threshold of Kci is:
The phase margins (PM) of the whole system can be written as:
Thus:
The superior threshold of Kci can be written as Equation (28):
According to Equations (26) and (28) the range of the Kci is given by Equation (29):
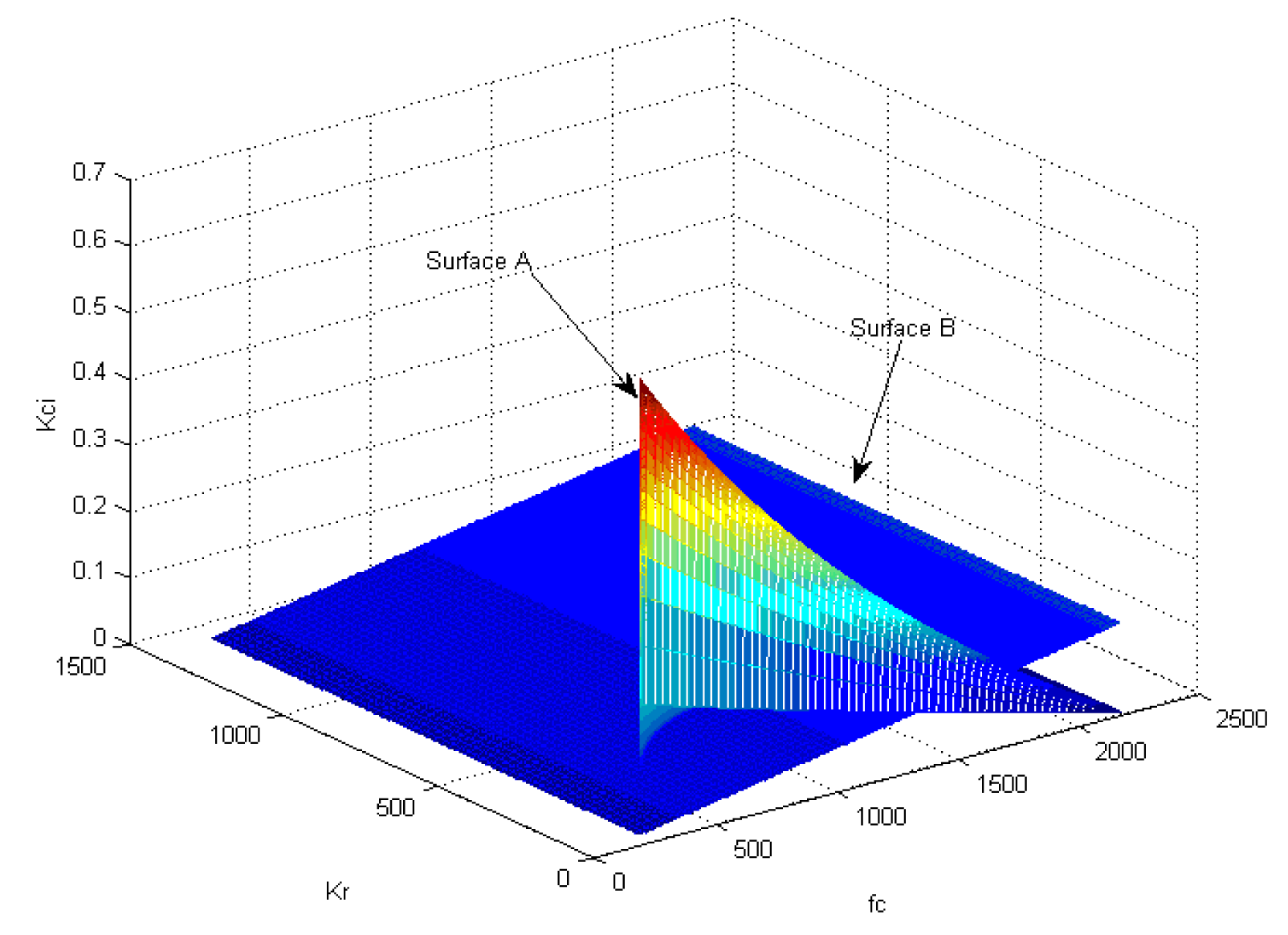
According to Equations (24) and (29) the relationship between fc, Kr and Kci can be represented in a 3-D plot. Figure 10 shows the relationship between the three above-mentioned parameters; the space surrounded by Surface A and Surface B indicates the satisfactory range of the Kr and Kci at a specific fc:
5. Numerical Simulation and Experimental Results
Following Table 1 summarizes simulation and experimental parameters.
This section describes a practical example using parameters of Table 1. According to parameters, the calculated resonant frequency of LCL filter is 3.65 kHz. The cutoff frequency is defined as , and the selected value of fc is 900 Hz.
- (1)
The calculated proportional gain Kp (Equation (16)) is:
- (2)
The resonant factor Kr range has been calculated (Equation (24)):
Supposing the steady-state tracking error of ig is 1%, the minimum of the magnitude-frequency response of open-loop transfer function at the fundamental frequency f1 equals 99. Assuming the minimum phase-frequency response of PR controller at the cutting frequency −ϕ is −10°. Therefore, resonance factor Kr range is:
where Krmin = 3.717, and Krmax = 41.075.- (3)
The active-damping factor Kci range has been calculated through Equation (29):
Supposing the magnitude margin of the system equals 3 dB, and the phase margin 45°, thus:
where Kcimin = 0.039, Kcimax = 0.364.
Considering the previous three steps, a set of proper parameters can be defined:
Moreover, the calculated feedforward factor of the grid voltage Kug equals 0.44.
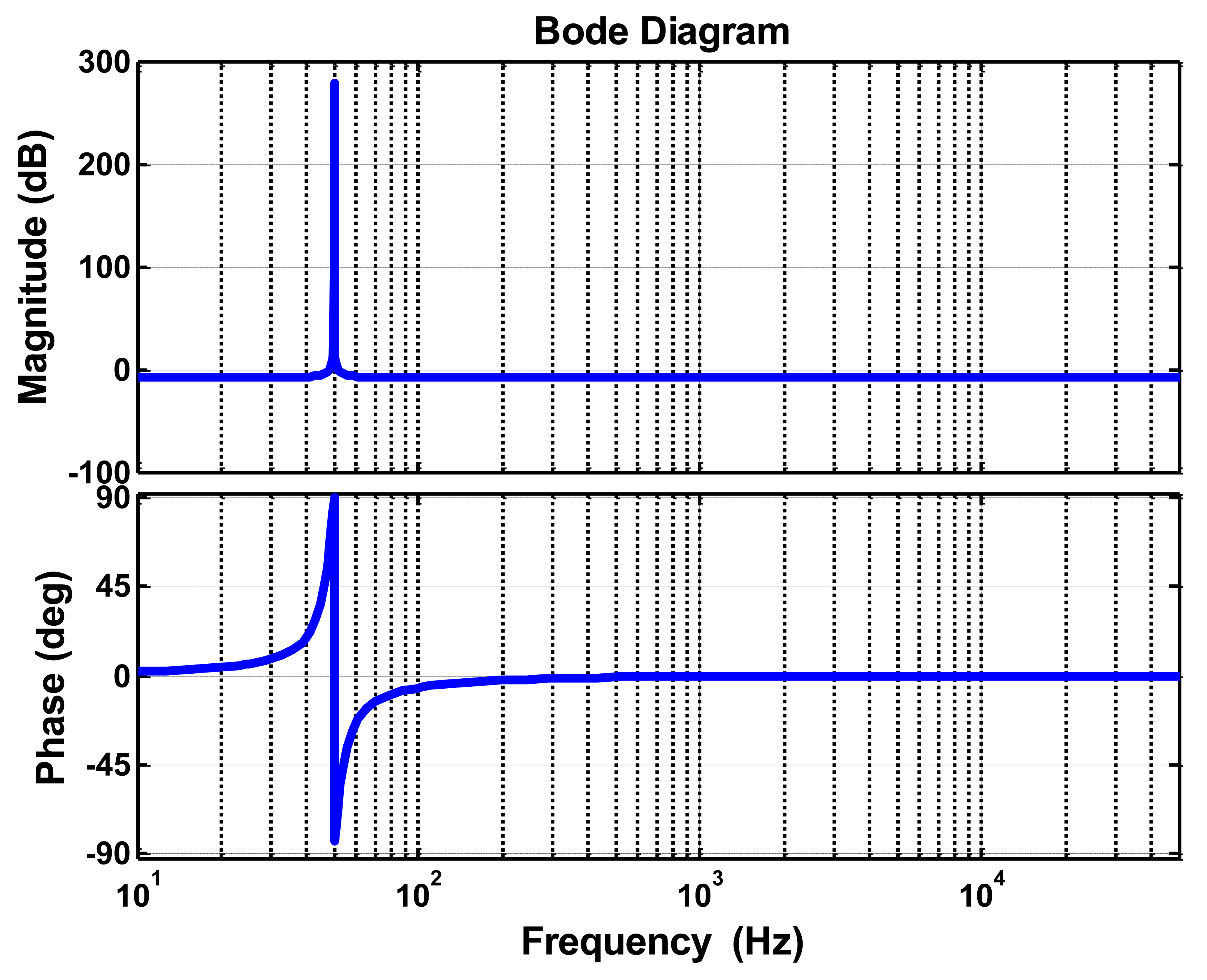
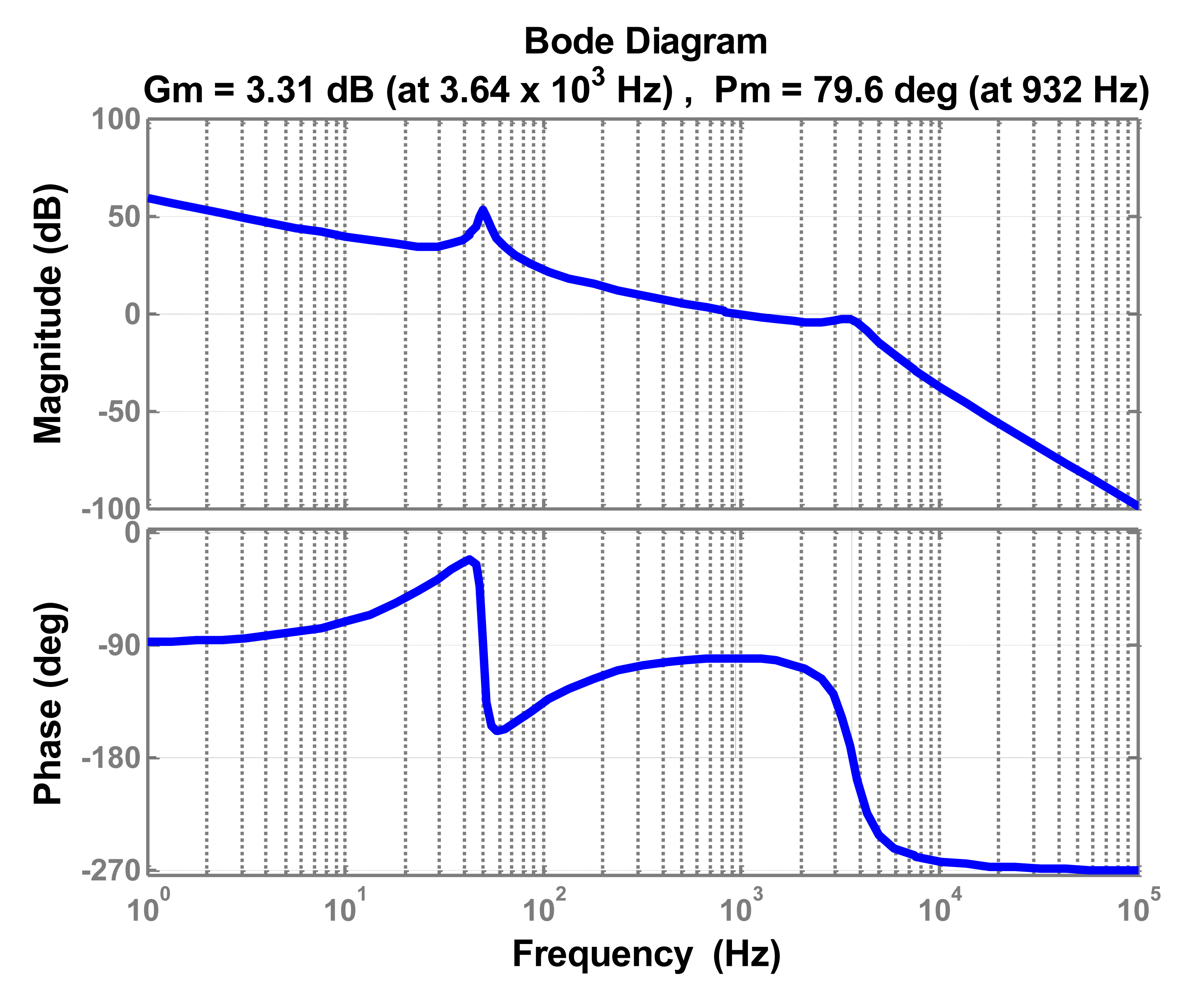
MATLAB/Simulink toolbox helps verifying the feasibility of design parameters method. Figure 11 shows the system Bode diagram, based on the above-mentioned parameters. The magnitude margin (3.31 dB) and the phase margin (79.6 degrees), both confirm the stability of the system.
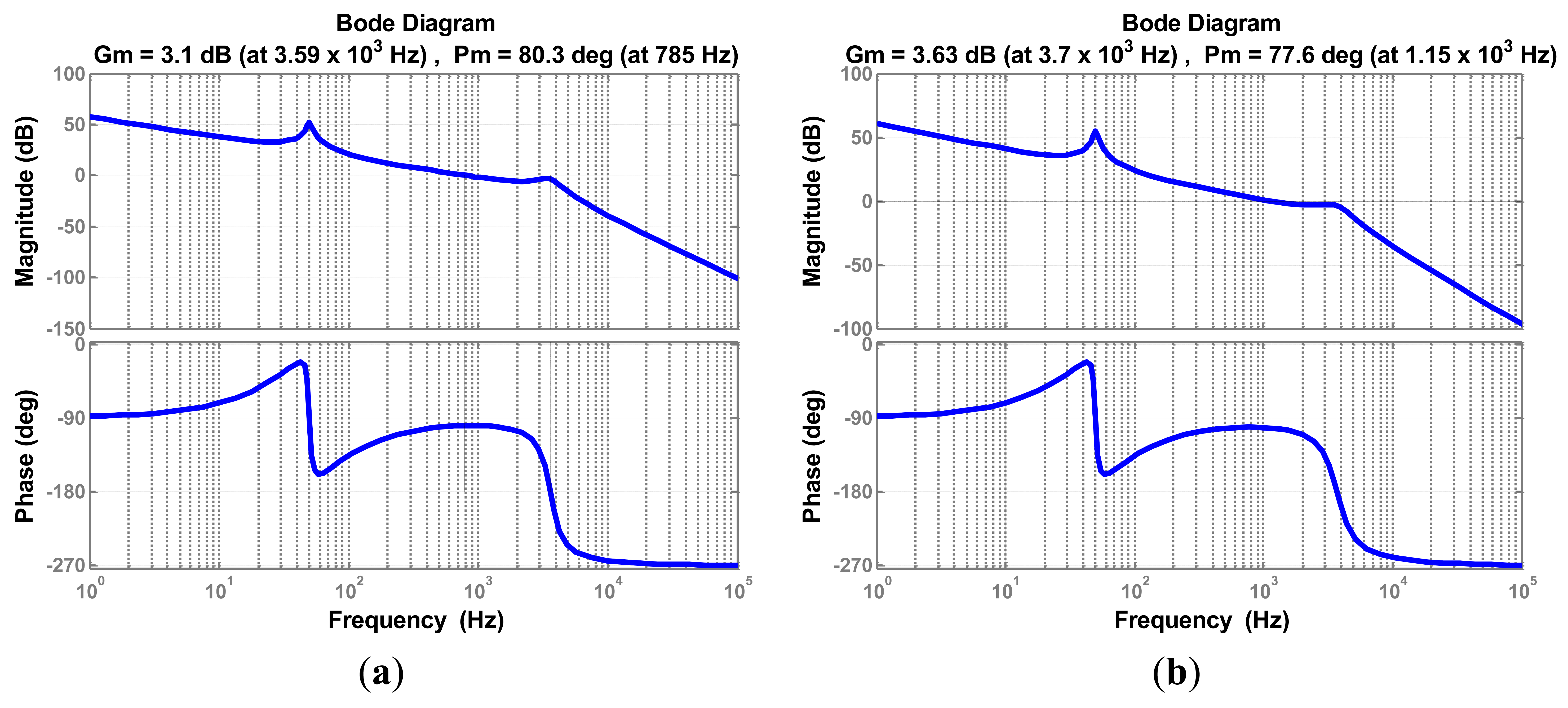
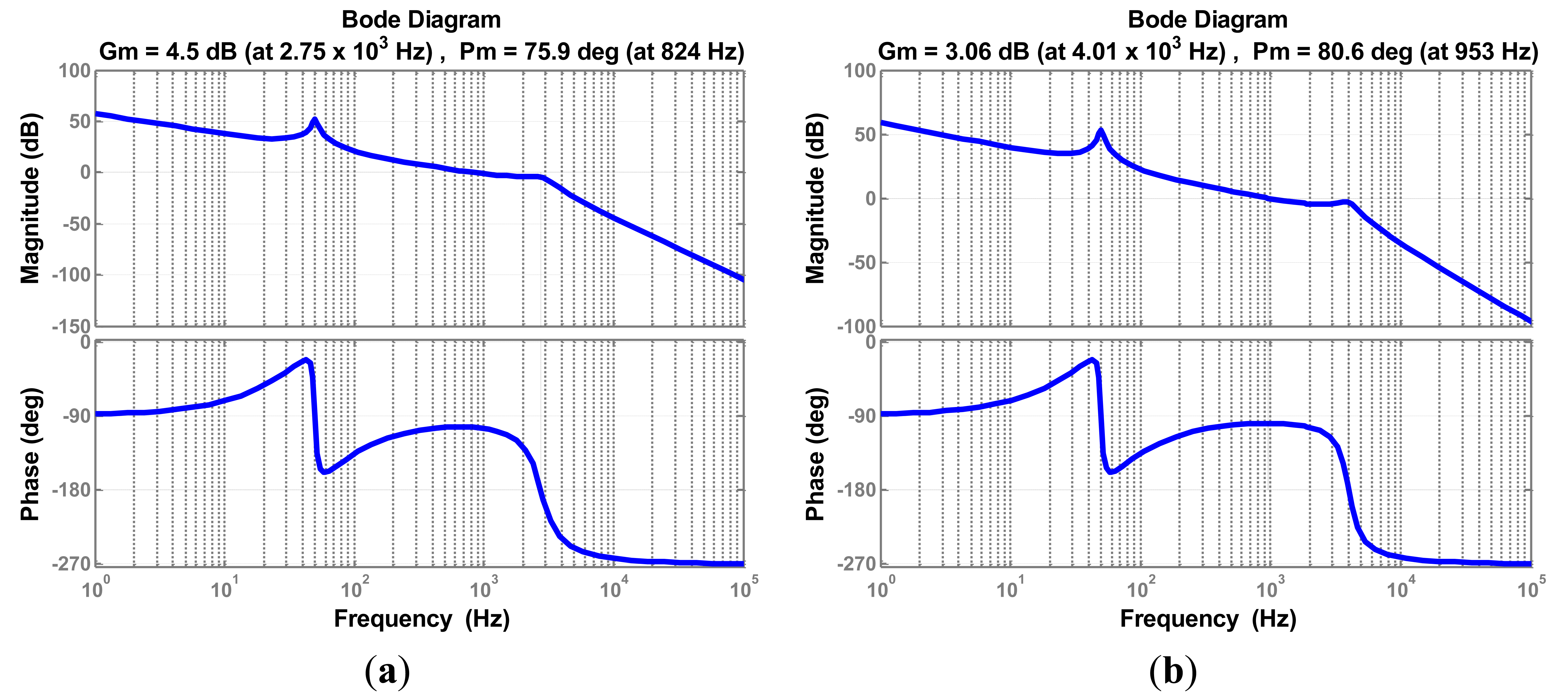
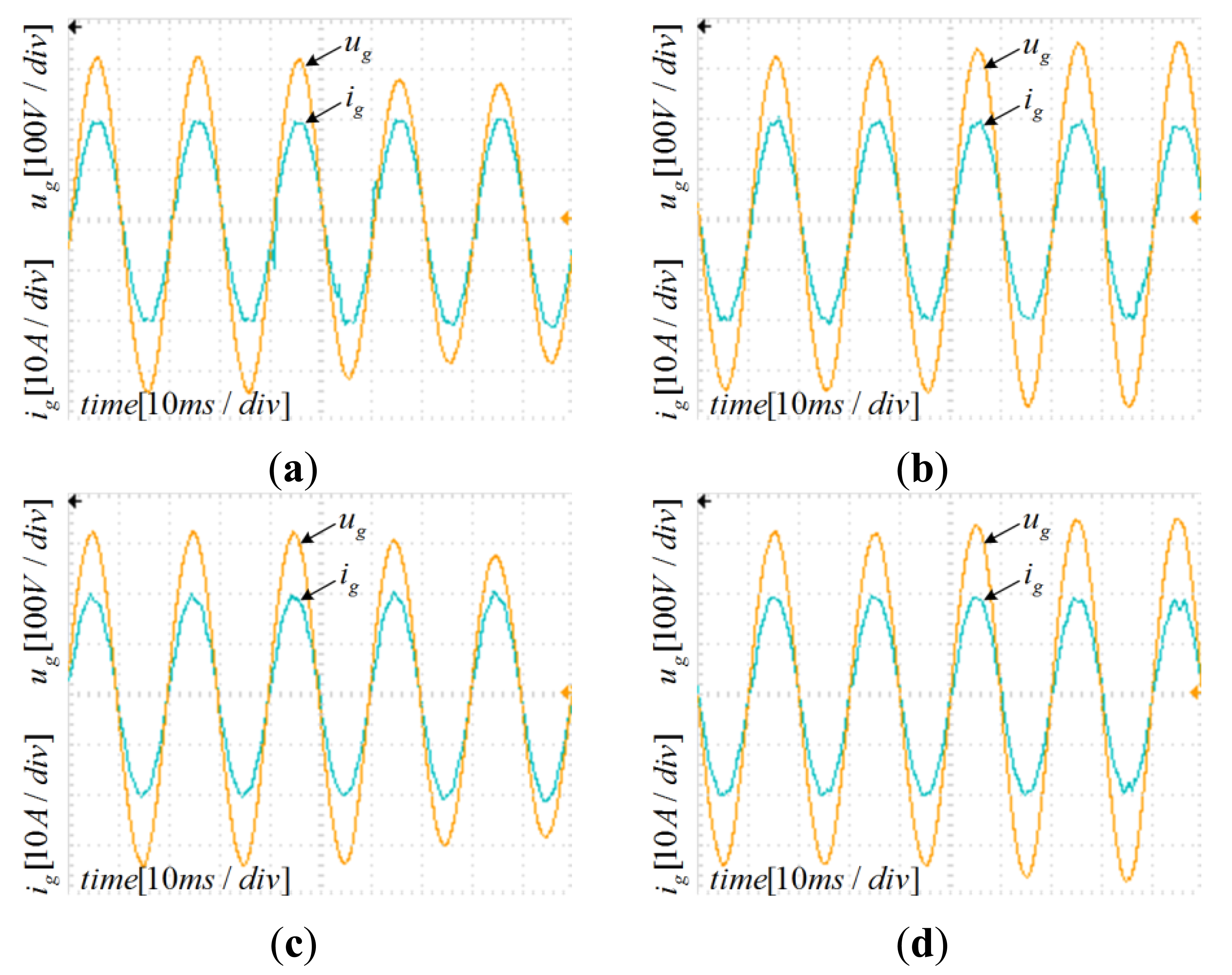
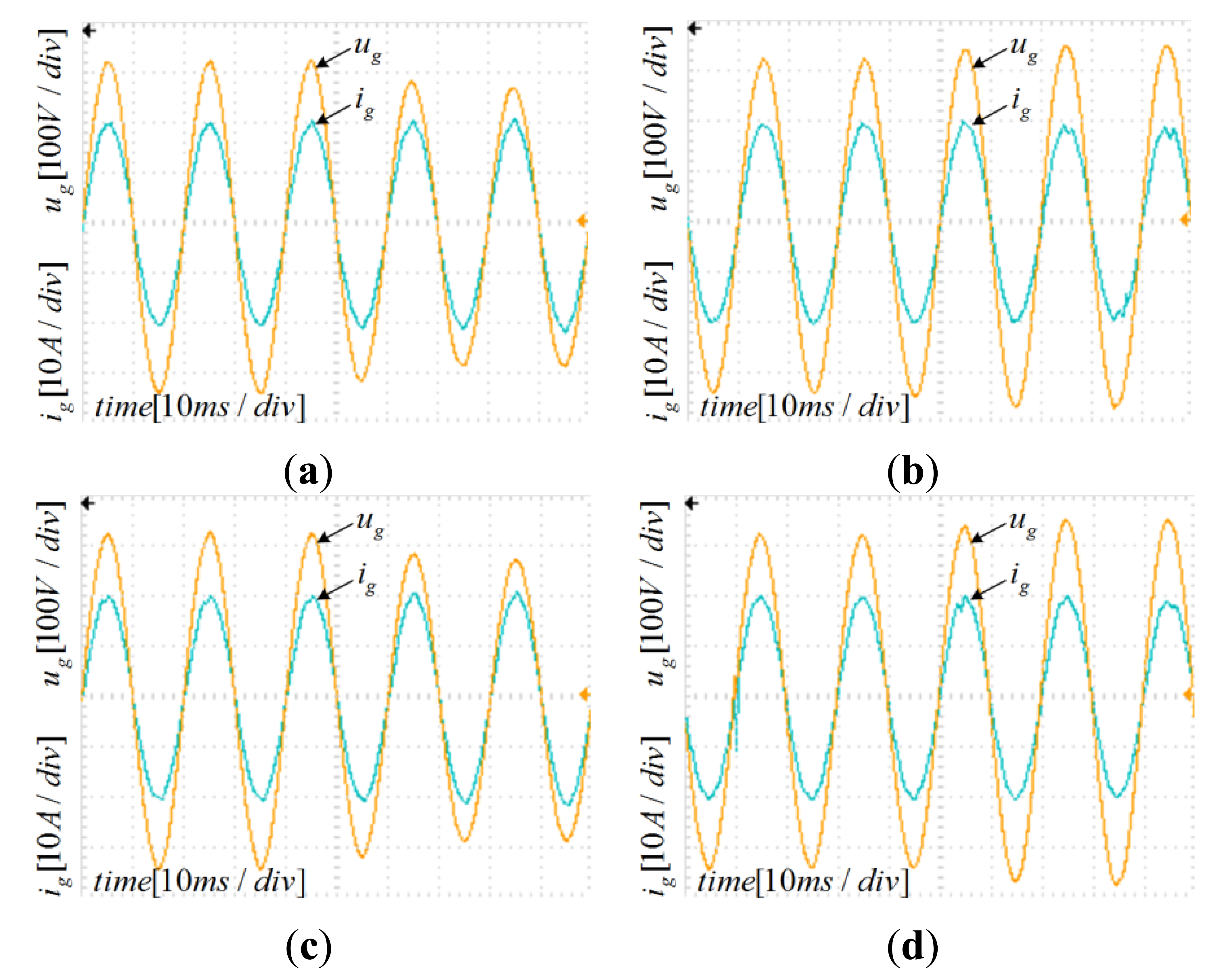
However, it is impossible to manufacture a filter whose parameters completely match the initial design. Moreover, parameters change while filter operates; the grid impedance must be considered, since inductive impedance of long cables and low power transformers. Therefore, the current controller parameters must be enough robust against the parameters variation. Since the inductor L2 is connected in series to the grid, the grid impedance variation can be merged with L2 variation. Figures 12, 13–14 depict the Bode plots of the system. Current controller has been designed using the aforementioned method under different parameter variations.
Table 2 summarizes the results shown in previous Figures 12, 13–14. Since the controller design considered well the system stability margin requirements, the system is stable even with important changes in parameters, in the range −20% to 20% (in case of inductor L2 the range extends from −20% to 250%). The minimum system magnitude margin is higher than 3 dB and the minimum phase margin is higher than 75 degrees. Therefore, the current controller parameters obtained by applying the proposed method enhance robustness against system parameters variation.
5.1. Numerical Simulation Results
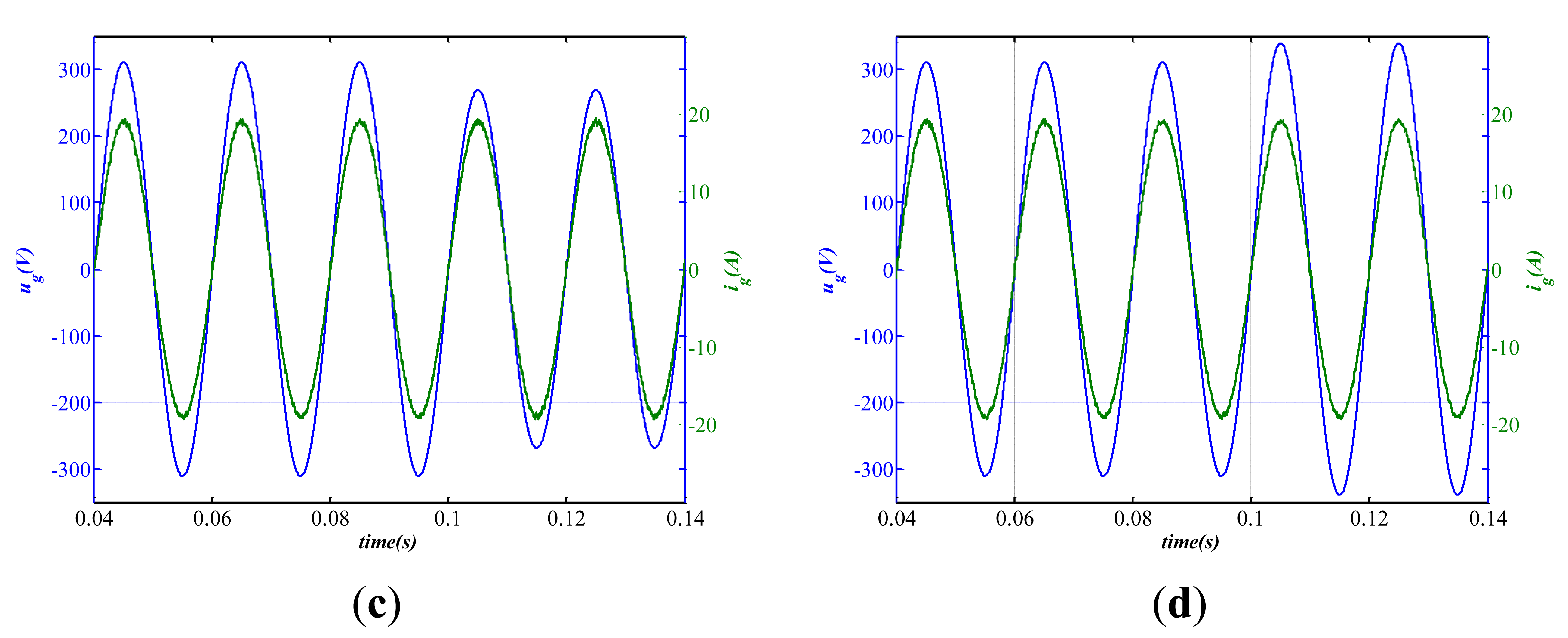
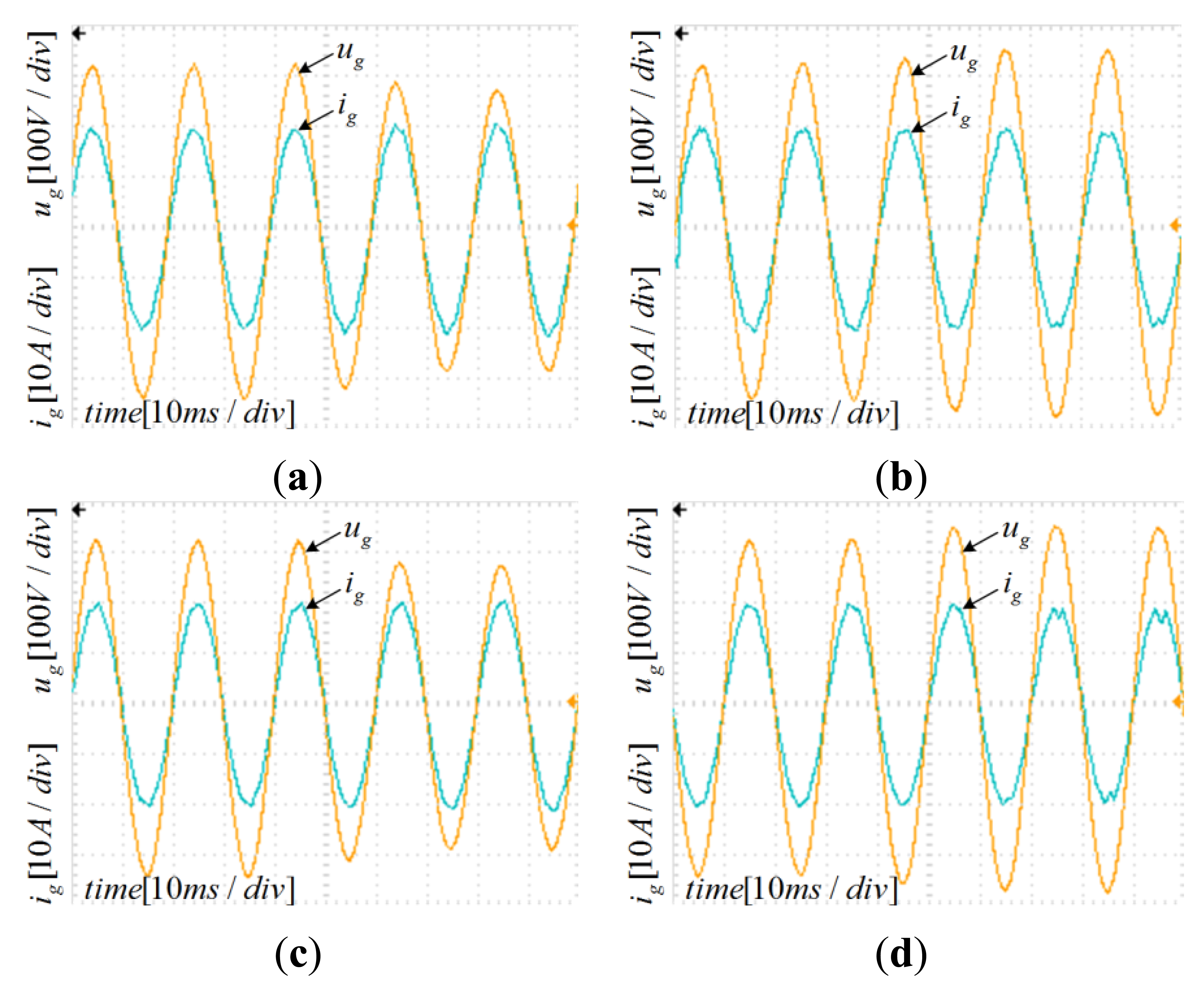
Besides the filter parameters and grid impedance variation, the grid voltage is not always stable. Therefore, we must test the robustness of the grid-connected system against grid voltage fluctuations. The application of the proposed method gives the current controller parameters. Figures 15, 16, 17–18 below show the simulation results of grid voltage fluctuation and injected current at full load under different parameter variation conditions. All simulations give the grid voltage sag equals about 42 V and voltage swell equals about 30 V. Figure 15 shows that with the nominal LCL-filter the injected current remains stable during the grid voltage sag or voltage swell. The grid fluctuation does not affect the system stability. According to the Bode diagrams shown in Figures 12, 13–14 the stable margins of the system are enough even with important changes in parameters. Figures 16, 17–18 show that the injected current is stable under nominal grid voltage with filter parameters variation. Moreover, even when the grid fluctuates, the system remains stable, as a confirmation of the effectiveness of the controller against filter parameters variation and grid fluctuations. If the inverter is connected to a weak grid (a very common situation in rural areas), the grid impedance is inductive and it can be regarded as equivalent to the increasing of inductor L2. In this study, L2 increases by 150% its value to simulate a weak grid situation. Even if the grid is weak and fluctuates, the overall system remains stable as Figure 17a,b shows.
5.2. Experimental Results
The design parameters have been verified through a 3-kW experimental setup. Inductors, capacitors, and other parameters have been set as in the corresponding simulations described in previous sections. All of the PV system algorithms have been implemented on a digital signal processor TMS320F2808 (Texas Instruments, Dallas, TX, USA). The PR controller has been discretized using the Tustin method with frequency pre-warping [17] for poles and zeroes, that yields a better matching frequency response. The adoption of the unipolar modulation SPWM regulated the injected grid current and a PV simulator replaced the PV panel. The DC source of DC-AC inverter has been given through the Boost DC-DC converter by applying the P&O MPPT method that guarantees simplicity and effectiveness [9–12]. To simulate the grid voltage fluctuation, a Programmable AC Power Source replaced the grid, while the voltage sag and swell values have been set equals to numerical simulation. Figures 19, 20, 21–22 show the experimental waveforms at full load under different parameters variations; the simulation results and the experimental data have been plot into one-to-one correspondence. Although the experimental results are worse than the numerical simulation ones because of the parasitic parameters of the inductors and capacitor, they are still very satisfactory. The experimental data well match numerical simulations.
6. Conclusions
The stability analysis of the system composed by a PR controller and an LCL filter together is not easy: the frequency responses may affect each other and the PR controller design becomes complex. The traditional method based on trial-and-error procedures, is too time-consuming, and the design process is inefficient. This paper provides a detailed analysis of the frequency response influence between the PR controller and the LCL filter. In addition, the paper presents a systematic design method for the PR controller parameters and the capacitor current feedback coefficient, used in the active damping of the LCL filter. Using the new parameters, a numerical simulation shows that the system meets the requirements of stable margins and current tracking steady-state error. The robustness of the current controller is verified through several experimental tests carried out on a 3 kW platform varying the system parameters. The Bode diagrams of the system varying inductor, capacitor, and grid impedance values confirmed that the controller parameters enhance robustness against the system parameters variation. Moreover, the system remains stable even in case of grid voltage fluctuation. Both the simulation and the experimental results assess the validity of the proposed design method.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Carrasco, J.M.; Franquelo, L.G.; Bialasiewicz, J.T.; Galvan, E.; Guisado, R.C.P.; Prats, A.M.; Leon, J.I.; Moreno-Alfonso, N. Power-electronic systems for the grid integration of renewable energy sources: A survey. IEEE Trans. Ind. Electron. 2006, 53, 1002–1016. [Google Scholar]
- Wessels, C.; Dannehl, J.; Fuchs, F.W. Active Damping of LCL-Filter Resonance based on Virtual Resistor for PWM Rectifiers—Stability Analysis with Different Filter Parameters. Proceedings of the 2008 IEEE Power Electronics Specialists Conference, Rhodes, Greece, 15–19 June 2008; pp. 3532–3538.
- Castilla, M.; Miret, J.; Matas, J.; de Vicuna, L.G.; Guerrero, J.M. Control design guidelines for single-phase grid-connected photovoltaic inverters with damped resonant harmonic compensators. IEEE Trans. Ind. Electron. 2009, 56, 4492–4501. [Google Scholar]
- Yi, L.; Zhengming, Z.; Fanbo, H.; Sizhao, L.; Lu, Y. An Improved Virtual Resistance Damping Method for Grid-Connected Inverters with LCL Filters. Proceedings of the 2011 IEEE Energy Conversion Congress and Exposition (ECCE 2011), Phoenix, AZ, USA, 17–22 September 2011; pp. 3816–3822.
- Parker, S.G.; McGrath, B.P.; Holmes, D.G. Regions of Active Damping Control for LCL Filters. Proceedings of the Energy Conversion Congress and Exposition (ECCE), Raleigh, NC, USA, 15–20 September 2012; pp. 53–60.
- Bao, C.L.; Ruan, X.B.; Wang, X.H.; Li, W.W.; Pan, D.H.; Weng, K.L. Design of Injected Grid Current Regulator and Capacitor-Current-Feedback Active-Damping for LCL-Type Grid-Connected Inverter. Proceedings of the Energy Conversion Congress and Exposition (ECCE), Raleigh, NC, USA, 15–20 September 2012; pp. 579–586.
- Fukuda, S.; Yoda, T. A novel current-tracking method for active filters based on a sinusoidal internal model. IEEE Trans. Ind. Appl. 2001, 37, 888–895. [Google Scholar]
- Zmood, D.N.; Holmes, D.G. Stationary frame current regulation of PWM inverters with zero steady-state error. IEEE Trans. Power Electron. 2003, 18, 814–822. [Google Scholar]
- Esram, T.; Chapman, P.L. Comparison of photovoltaic array maximum power point tracking techniques. IEEE Trans. Energy Convers. 2007, 22, 439–449. [Google Scholar]
- Noguchi, T.; Togashi, S.; Nakamoto, R. Short-current pulse-based maximum-power-point tracking method for multiple photovoltaic-and-converter module system. IEEE Trans. Ind. Electron. 2002, 49, 217–223. [Google Scholar]
- Mutoh, N.; Ohno, M.; Inoue, T. A method for MPPT control while searching for parameters corresponding to weather conditions for PV generation systems. IEEE Trans. Ind. Electron. 2006, 53, 1055–1065. [Google Scholar]
- Petrone, G.; Spagnuolo, G.; Vitelli, M. A multivariable perturb-and-observe maximum power point tracking technique applied to a single-stage photovoltaic inverter. IEEE Trans. Ind. Electron. 2011, 58, 76–84. [Google Scholar]
- Ciobotaru, M.; Teodorescu, R.; Blaabjerg, F. A New Single-Phase PLL Structure Based on Second Order Generalized Integrator. Proceedings of the 2006 IEEE Power Electronics Specialists Conference (IEEE Cat. No. 06CH37819C), Jeju, Korea, 18–22 June 2006; pp. 1–6.
- Silva, S.M.; Lopes, B.M.; Cardoso, B.J.; Campana, R.P.; Boaventura, W.C. Performance Evaluation of PLL Algorithms for Single-Phase Grid-Connected Systems. Conference Record of the 2004 IEEE Industry Applications Conference, Seattle, WA, USA, 3–7 October 2004; Volumes 1–4, Covering Theory to Practice. pp. 2259–2263.
- Zmood, D.N.; Holmes, D.G.; Bode, G.H. Frequency-domain analysis of three-phase linear current regulators. IEEE Trans. Ind. Appl. 2001, 37, 601–610. [Google Scholar]
- Dannehl, J.; Wessels, C.; Fuchs, F.W. Limitations of voltage-oriented PI current control of grid-connected pwm rectifiers with LCL filters. IEEE Trans. Ind. Electron. 2009, 56, 380–388. [Google Scholar]
- Yepes, A.G.; Freijedo, F.D.; Doval-Gandoy, J.; Lopez, O.; Malvar, J.; Fernandez-Comesana, P. Effects of discretization methods on the performance of resonant controllers. IEEE Trans. Power Electron. 2012, 27, 4976. [Google Scholar]








| Name | Value |
|---|---|
| Fundamental frequency f1 | 50 Hz |
| Switching frequency fs | 12 kHz |
| Grid phase voltage (RMS) | 220 V |
| Grid current factor feedback Kgi | 0.04 |
| LCL filter inductor L1 | 1.88 mH |
| LCL filter inductor L2 | 0.34 mH |
| LCL filter capacitor C | 6.6 μF |
| Stable margins | Nominal parameters | L1 | C | L2 | |||
|---|---|---|---|---|---|---|---|
| Increased by 20% | Decreased by 20% | Increased by 20% | Decreased by 20% | Increased by 150% | Decreased by 20% | ||
| Magnitude margin | 3.31 dB | 3.1 dB | 3.63 dB | 3.3 dB | 3.33 dB | 4.5 dB | 3.06 dB |
| Phase margin | 79.6 degree | 80.3 degree | 77.6 degree | 78.4 degree | 80.8 degree | 75.9 degree | 80.6 degree |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Zhang, N.; Tang, H.; Yao, C. A Systematic Method for Designing a PR Controller and Active Damping of the LCL Filter for Single-Phase Grid-Connected PV Inverters. Energies 2014, 7, 3934-3954. https://doi.org/10.3390/en7063934
Zhang N, Tang H, Yao C. A Systematic Method for Designing a PR Controller and Active Damping of the LCL Filter for Single-Phase Grid-Connected PV Inverters. Energies. 2014; 7(6):3934-3954. https://doi.org/10.3390/en7063934
Chicago/Turabian StyleZhang, Ningyun, Houjun Tang, and Chen Yao. 2014. "A Systematic Method for Designing a PR Controller and Active Damping of the LCL Filter for Single-Phase Grid-Connected PV Inverters" Energies 7, no. 6: 3934-3954. https://doi.org/10.3390/en7063934




