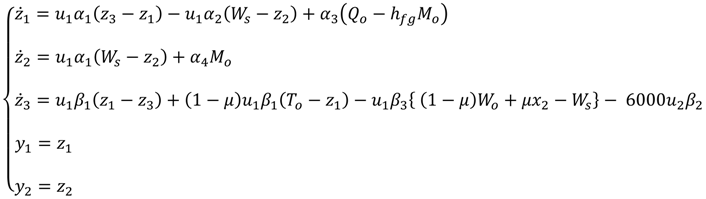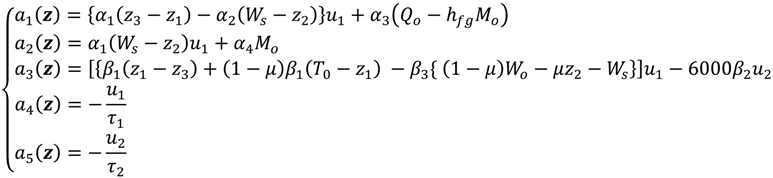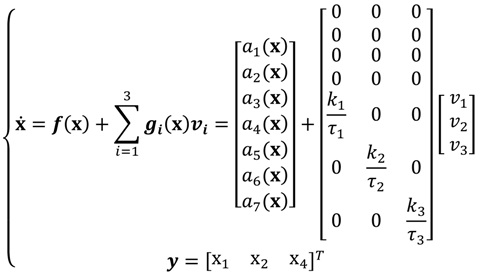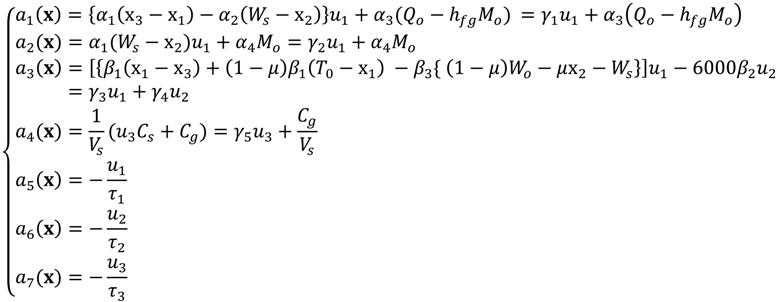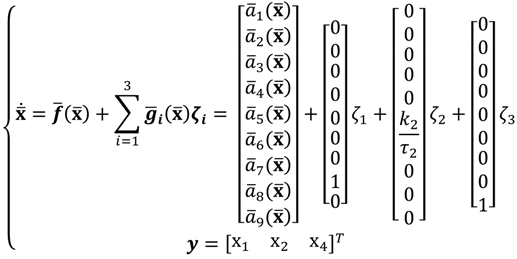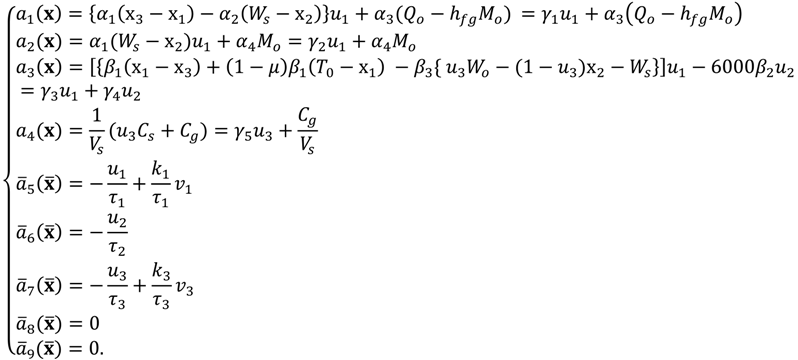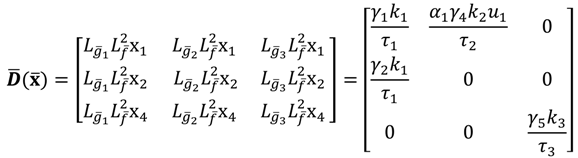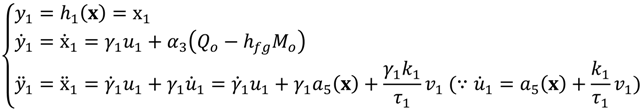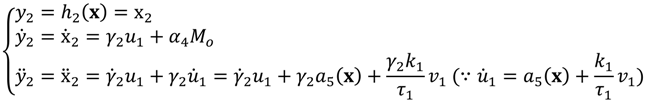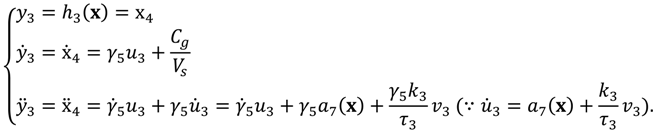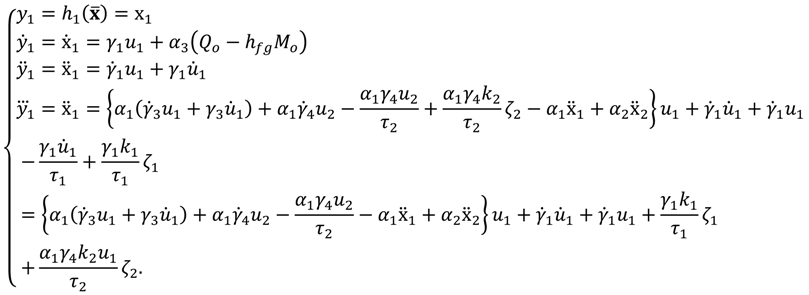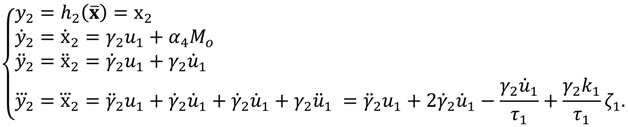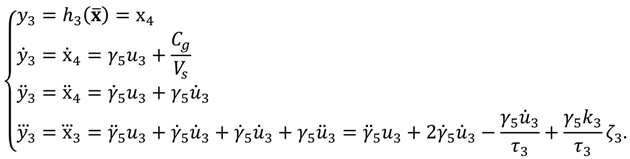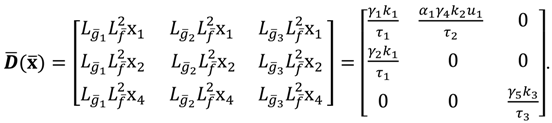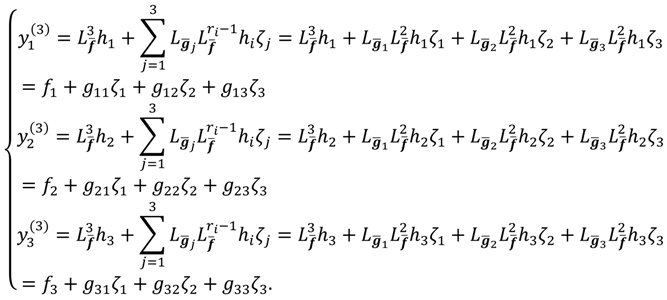1. Introduction
HVAC systems are automatic systems that control temperature and humidity in buildings, providing people with a comfortable environment. The use of HVAC systems represents more than 50% of the world energy consumption [
1,
2,
3,
4]. Thus, balancing occupant comfort and energy efficiency is a main goal of HVAC control strategies.
In most previous studies, HVAC systems have been modeled considering only the temperature and the humidity ratio [
5,
6,
7,
8]. A nonlinear HVAC model that includes dynamics of temperature and humidity ratio is proposed in [
5], which includes the design of an observer to estimate the thermal and moisture loads. In [
6], an adaptive fuzzy output feedback controller is proposed, based on an observer for the HVAC system. In [
7,
8], a back-stepping controller and a decentralized nonlinear adaptive controller are respectively applied to the same model.
Recently, the CO
2 concentration has been recognized as having an important contribution to room comfort [
9,
10]. Some researchers have proposed hybrid HVAC systems that represent the temperature and humidity ratio as continuous states and CO
2 concentration as a discrete state [
11,
12]. However, because these states are strongly interrelated, it is more appropriate to integrate these continuous and discrete dynamics into a single model that includes temperature, humidity ratio, and CO
2 concentration as states.
This paper presents a modeling and control strategy for a novel HVAC system that considers temperature, humidity ratio, and CO
2 concentration. In the process of modeling, the dynamic extension algorithm of [
13] is employed to deal with non-interacting control problem and no relative degree problem. After the dynamic extension process, a feedback linearization method can be applied to the proposed HVAC system to convert a bilinear system into a linear system. Linear controllers, pole placement and LQR can be designed for the linearized novel HVAC system to stabilize it and improve its control performance.
This paper is organized as follows: in
Section 2, we present the bilinear model for the conventional HVAC system, including valve dynamics.
Section 3 presents a novel HVAC system including CO
2 concentration and its applicability in the feedback linearization method. Also, dynamic extension algorithm is applied for solving the no relative degree and interacting control problems in the MIMO system. In
Section 4, we describe the design of linear controllers for the linearized HVAC system, such as pole placement and LQR controllers, to improve the system’s control performance and to verify the effectiveness of the proposed model.
2. Conventional HVAC System with Temperature and Humidity Ratio
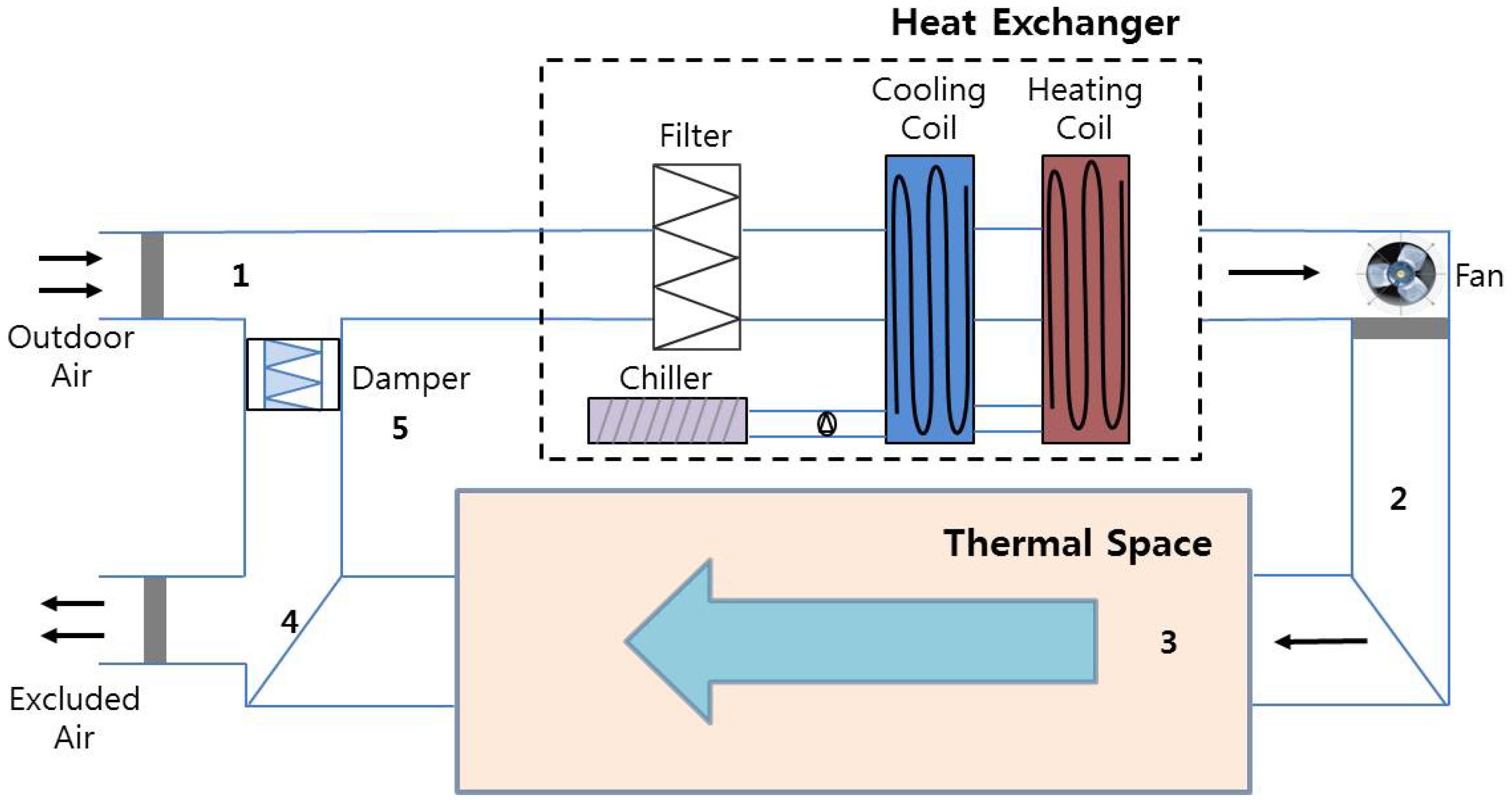
As mentioned, conventional HVAC systems control only temperature and humidity. In this paper, we consider the single-zone system shown in
Figure 1 as a representative conventional HVAC system. It consists of the following components: a heat exchanger; a chiller, which provides chilled water to the heat exchanger; a circulating air fan; the thermal space; connecting ductwork; dampers; and mixing air components [
5]. The conventional HVAC system controls the temperature and humidity ratio as follows [
5]:
Fresh air is introduced into the system and is mixed in a 25:75 ratio with recirculated air (position 5) at the flow mixer.
Second, air mixed at the flow mixer (position 1) enters the heat exchanger, where it is conditioned.
Third, the conditioned air is moved out of the heat exchanger; this air is ready to enter the thermal space, and is called supply air (position 2).
Fourth, the supply air enters the thermal space (position 3), where it offsets the sensible (actual heat) and latent (humidity) heat loads acting upon the system.
Finally, the air in the thermal space is drawn through a fan (position 4); 75% of this air is recirculated and the rest is exhausted from the system.
Figure 1.
Model of the representative conventional HVAC system.
Figure 1.
Model of the representative conventional HVAC system.
The control inputs for a conventional HVAC system are the flow rate of air, which is varied using a variable-speed fan (position 2), and the flow rate of water from the chiller to the heat exchanger. However, in our proposed HVAC system, the air recirculation rate (position 4) is added as a new control input, and some modifications are made to the basic operation rules listed above. That is to say, the 75% recirculation rate listed above in the first and last steps becomes a variable quantity, and is used as the third control input.
2.1. Mathematical Modeling of Conventional HVAC System
The conventional HVAC system is a model considering the temperature and the humidity ratio as states. The differential equations describing the dynamic behavior of the HVAC system in
Figure 1 can be derived from energy conservation principles and are given by [
5]:
The dynamic system given by Equation (1) can be converted into a state variable form for the purposes of control. Let
,
,
,
,
and define the following parameters:
,
,
,
,
,
, and
. Then, the dynamic equations given in Equation (1) can be written in the following state variable form.
The conventional HVAC system of Equation (2) is a 2-input, 2-output MIMO system: its inputs are the volumetric air flow rate and the chilled water flow rate, and its outputs are the temperature and the humidity ratio of the thermal space.
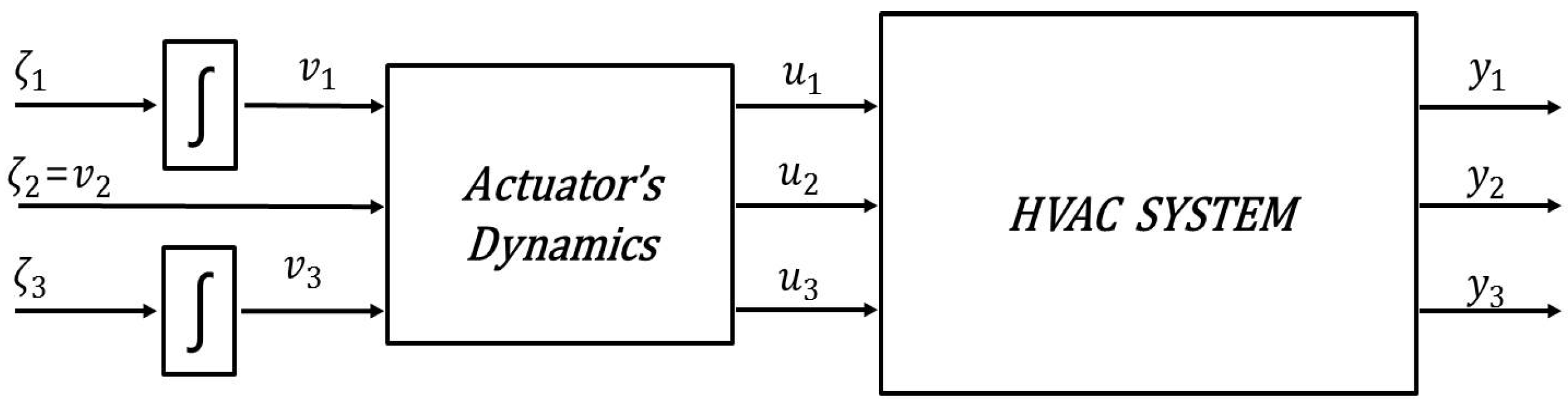
2.2. Adding Valve Dynamics to the Conventional HVAC Model
The Control input signals
in the system described in Equation (2) are implemented using liquid valves. The valve dynamics can be modeled as follows in which
is the valve inherent characteristic and
is the flow rate of the liquid which enters the valve [
14,
15]:
By considering the characteristic of a linear valve as
, the valve transfer function can be written as:
where
and
are the constant gains and the time constants, respectively;
is the control signal applied to the actuator; and
is the signal that is input to the HVAC system.
An augmented state space model with the new state vector,
can be derived as:
where:
Thus, the system in Equation (5) represents a conventional HVAC system to which valve dynamics have been applied to implement the control signals. This conventional system can regulate only the temperature and the humidity ratio; other factors such as CO2 concentration, which affects the health of occupants or workers indoors, cannot be considered.
3. Novel Modeling of HVAC System including CO2 Concentration
If the recirculated air contains too much CO2, it can affect the health and work efficiency of the building’s occupants. Therefore, CO2 concentration should be one of the quantitative indices of room comfort, along with temperature and humidity ratio. In this paper, we propose an HVAC system that continuously controls all three of these indices.
From the mass balance equation, the average CO
2 concentration
in the room can be represented as [
14]:
where
,
is the amount of CO
2 generated in the room;
is the CO
2 concentration in the inlet air;
is the CO
2 concentration of air leaving the room, and
, is the air exchange rate.
3.1. Proposed HVAC System Model
The proposed HVAC system model includes CO2 concentration as a state. The differential Equation (6) can be integrated into the dynamic equations in (1). The valve dynamics of
are added to the control input vector
, and the control signal applied to the actuator of
also can be added to the actuator input vector
.
Let
,
,
,
,
, and let an augmented state vector
. Then, the whole dynamics can be written in the state variable form as:
where:
The novel HVAC system of (7) is a 3-input, 3-output MIMO system: its inputs are the volumetric air flow rate, the chilled water flow rate, and the outdoor air flow rate, and its outputs are the temperature, humidity ratio, and CO
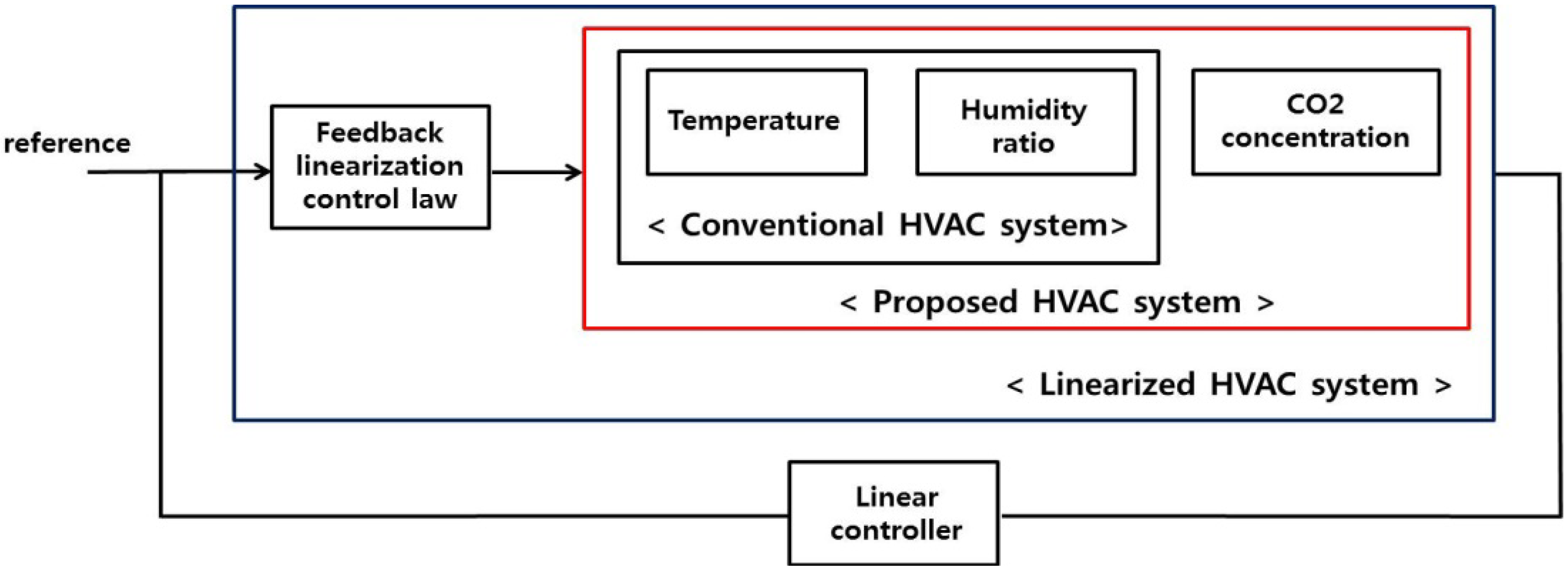
2 concentration of the thermal space. This proposed HVAC system can be linearized using a feedback linearization control method, as shown in
Figure 2. Thus, we can finally obtain a linearized HVAC system that can be controlled using linear controllers.
Figure 2.
Overall block diagram for controlling the proposed HVAC system.
Figure 2.
Overall block diagram for controlling the proposed HVAC system.
3.3. Equivalent Linearization HVAC System
To be able to apply the feedback linearization method conveniently, we can change system (8) into the equivalent system (9) by using Equation (A3):
where:
and
.
This equivalent system can apply the feedback linearization law to linearize the HVAC system. By putting proper control gain, the linearized HVAC system can be regulated to maintain the set points of temperature, humidity ratio, and CO2 concentration.
4. Control Strategies Using Feedback Linearization Control
The proposed HVAC system is linearized by a feedback linearization method. The linearized HVAC system shown can be controlled by linear controllers such as pole placement and LQR controllers.
Table 1 shows the numerical values of system parameters used in the simulations. The initial state and reference values are given in
Table 2.
Table 1.
Numerical values for system parameters.
Table 1.
Numerical values for system parameters.
| Parameter | Value | Unit |
|---|
| ρ | 0.074 | 1b/ft3 |
| Vhe | 60.75 | ft3 |
| Vs | 58464 | ft3 |
| Cp | 0.24 | Btu/lb °F |
| Ws | 0.0070 | lb/lb |
| Mo | 166.06 | lb/hour |
| Qo | 289,897.52 | Btu/hour |
| To | 85 | °F |
| Wo | 0.018 | 1b/1b |
| Co | 400 | ppm |
| τ1,τ2,τ3 | 0.008 | hour |
| k1,k2,k3 | 5 | - |
Table 2.
Initial state and reference values.
Table 2.
Initial state and reference values.
| Tinitial | 76 °F | Tinitial | 0.021 lb/lb | Tinitial | 1300ppm |
| Tinitial | 71 °F | Tinitial | 0.0092 lb/lb | Tinitial | 1200ppm |
4.1. Design of Pole Placement Control for Linearized HVAC System
Let the reference signal ,
, and matrix
. Define the tracking errors as
,
and
, and let the error matrix
.
The feedback linearization control law for the proposed HVAC system (9) is designed as:
choosing
so that the polynomial
has all its roots strictly in the left-half complex plane, thereby meeting the desired performance specifications such as those for the transient response of the steady-state error. By substituting Equation (10) into Equation (9), the linearized HVAC system can finally be obtained as follows:
where
.
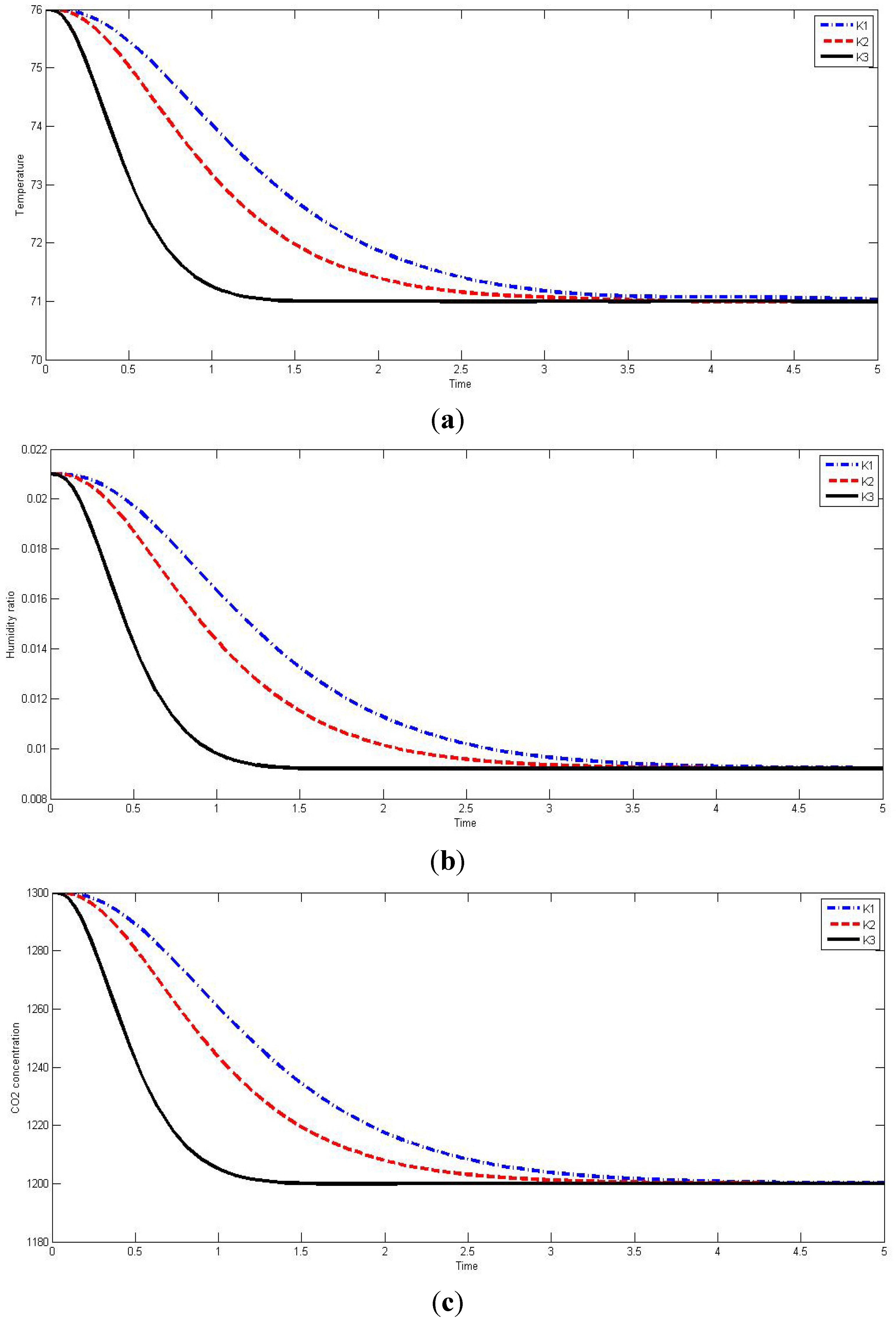
The gain K
1 corresponds to the case in which the pole is located at −2, −2, and −4, whereas the gain K
2 corresponds to the case in which the pole is located at −2, −3, and −5, and the gain K
3 corresponds to the case in which the pole is located at −5, −6, and −7. According to the pole placement, the control performance is varied.
Figure 4 show the system responses in terms of temperature, humidity ratio, and CO
2 concentration, respectively.
Table 3 shows the control performance metrics of settling time, rising time, settling max value, and settling min value for each value of gain.
Table 3.
Control performance metrics of the pole placement controller.
Table 3.
Control performance metrics of the pole placement controller.
| | Temperature | Humidity ratio | CO2 concentration |
|---|
| K1 | K2 | K3 | K1 | K2 | K3 | K1 | K2 | K3 |
|---|
| Ts | 3.2695 | 2.8431 | 1.1618 | 3.3889 | 2.7312 | 1.1595 | 3.3857 | 2.7270 | 1.1581 |
| Tr | 1.8919 | 1.5184 | 0.6804 | 1.8971 | 1.5124 | 0.6795 | 1.8970 | 1.5119 | 0.6794 |
| Settling min | 70.9962 | 71.0172 | 70.9927 | 0.0092 | 0.0092 | 0.0092 | 1200.1 | 1200 | 1199.9 |
| Settling max | 71.4929 | 71.4741 | 71.4297 | 0.0104 | 0.0104 | 0.0102 | 1209.9 | 1210 | 1208.5 |
Figure 4.
(a) Temperature response for each pole placement; (b) Humidity ratio response for each pole placement; (c) CO2 concentration response for each pole placement.
Figure 4.
(a) Temperature response for each pole placement; (b) Humidity ratio response for each pole placement; (c) CO2 concentration response for each pole placement.
4.2. Design of Linear Quadratic Regulator for Linearized HVAC System
The linearized HVAC system of (11) can be controlled by a linear controller. A linear-quadratic regulator (LQR) aims at designing stable controller which can minimize the cost function
represents the performance characteristic requirement as well as the controller input limitation [
17]. The cost function is:
where
is a positive semi-definite weight matrix and
is a positive definite weight matrix. The weighting matrices
and
are chosen by the Bryson’s rule (refer to
Appendix A5) [
18].
The feedback control law that minimizes the values of cost is:
where
;
is given by
; and
is found by solving the continuous time algebraic Riccati equation:
Table 4 shows the gain values resulting from the LQR process solving algebraic Riccati equation.
Table 4.
LQR gain values.
Table 4.
LQR gain values.
| 9 × 9 Gain matrix |
|---|
| diag([100 44.7850 9.9785],[100 44.7850 9.9785],[100 44.7850 9.9785]) |
| diag([(100 54.7214 14.4721)],[(100 54.7214 14.4721)],[(100 54.7214 14.4721)]) |
| diag([(100 88.6706 34.3124)],[(100 88.6706 34.3124)],[(100 88.6706 34.3124)]) |
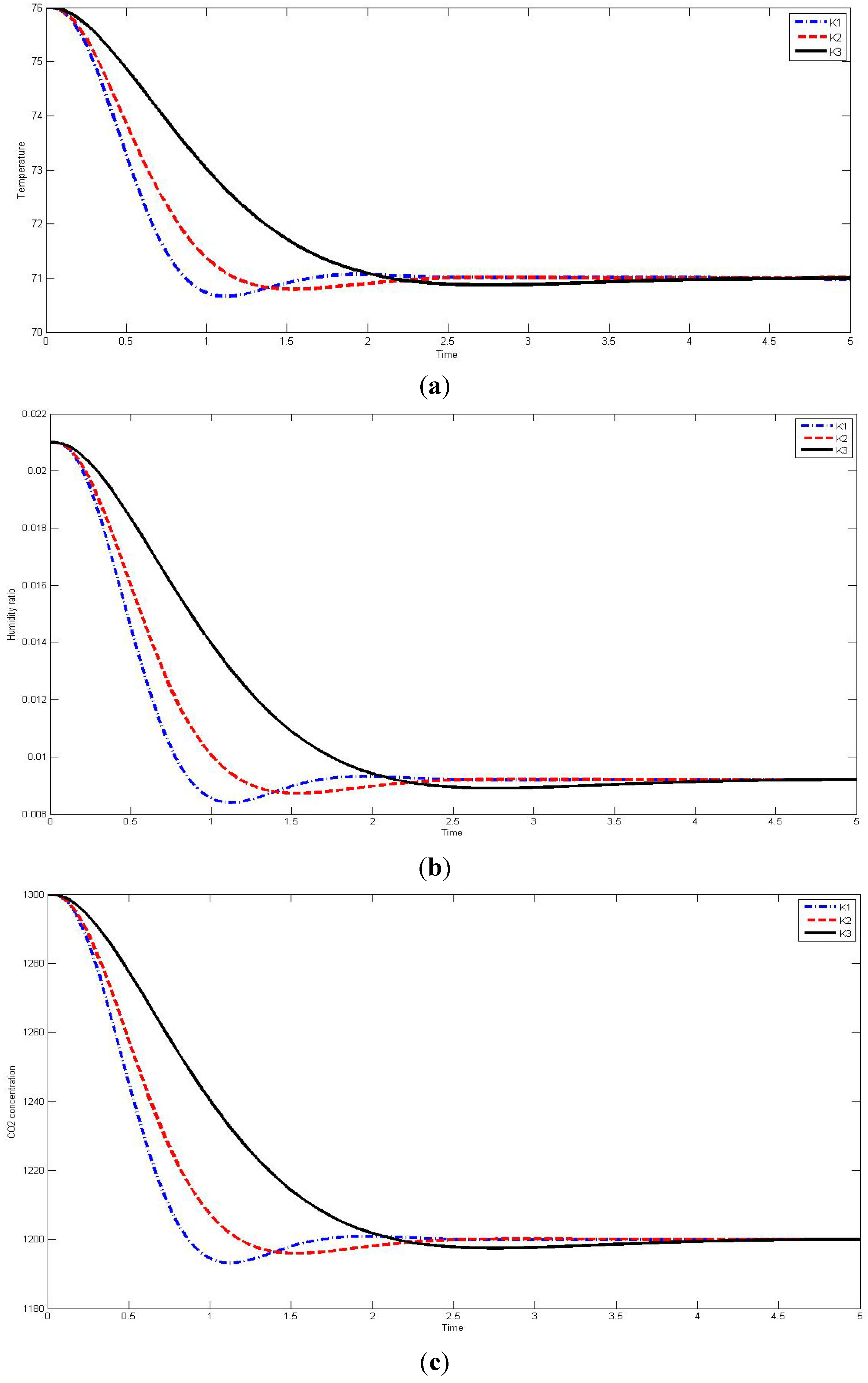
The LQR controller was applied to the proposed HVAC system model (11) and the simulation results are shown in
Figure 5. The temperature response of the proposed HVAC system is shown in
Figure 5(a), and its humidity ratio response and CO
2 concentration response are shown respectively in
Figure 5(b,c).
From these simulation results, we can see that the proposed HVAC system is effective, and that linear controllers are suitable for application to the proposed HVAC system model.
Table 5 shows the control performance metrics of settling time, rising time, settling max value, and settling min value for each value of gain.
Table 5.
Control performance metrics of the LQR controller.
Table 5.
Control performance metrics of the LQR controller.
| | Temperature | Humidity ratio | CO2 concentration |
|---|
| K1 | K2 | K3 | K1 | K2 | K3 | K1 | K2 | K3 |
|---|
| Ts | 1.4886 | 2.0107 | 3.2315 | 1.4982 | 1.9880 | 3.2028 | 1.5049 | 1.9873 | 3.1964 |
| Tr | 0.5279 | 0.7187 | 1.3093 | 0.5277 | 0.7189 | 1.3098 | 0.5277 | 0.7189 | 1.3098 |
| Settling min | 70.6601 | 70.7922 | 70.8702 | 0.0084 | 0.0087 | 0.0089 | 1193.2 | 1196 | 1197.5 |
| Settling max | 71.4249 | 71.3586 | 71.4777 | 0.0102 | 0.0100 | 0.0103 | 1208.5 | 1207.2 | 1209.6 |
Figure 5.
(a) Temperature response by LQR; (b) Humidity ratio response by LQR; (c) CO2 concentration response by LQR.
Figure 5.
(a) Temperature response by LQR; (b) Humidity ratio response by LQR; (c) CO2 concentration response by LQR.
5. Conclusions
Herein we have presented a novel HVAC system model that considers not only temperature and humidity ratio, but also CO2 concentration as the quantitative indices of comfort in a room. In applying an input-output feedback linearization method to linearize the HVAC system, problems of singularity, no relative degree, and interacting controls were encountered and a dynamic extension algorithm was used to solve these problems. The key contribution of this report is the addition of a continuous CO2 concentration state and corresponding valve dynamics to a conventional HVAC system to allow continuous control of CO2 concentration. Two types of linear controllers, pole placement and LQR controllers, were able to regulate the linearized HVAC system at the desired set point. Simulation results validated the proposed HVAC model, demonstrating its effectiveness in maintaining comfortable conditions. In future work, we will conduct further study on developing disturbance observer based controllers or intelligent controllers using fuzzy logic or artificial neural networks for a HVAC system considering parameter uncertainty and disturbance effect.