Statistical Diagnosis of the Best Weibull Methods for Wind Power Assessment for Agricultural Applications
Abstract
: The best Weibull distribution methods for the assessment of wind energy potential at different altitudes in desired locations are statistically diagnosed in this study. Seven different methods, namely graphical method (GM), method of moments (MOM), standard deviation method (STDM), maximum likelihood method (MLM), power density method (PDM), modified maximum likelihood method (MMLM) and equivalent energy method (EEM) were used to estimate the Weibull parameters and six statistical tools, namely relative percentage of error, root mean square error (RMSE), mean percentage of error, mean absolute percentage of error, chi-square error and analysis of variance were used to precisely rank the methods. The statistical fittings of the measured and calculated wind speed data are assessed for justifying the performance of the methods. The capacity factor and total energy generated by a small model wind turbine is calculated by numerical integration using Trapezoidal sums and Simpson's rules. The results show that MOM and MLM are the most efficient methods for determining the value of k and c to fit Weibull distribution curves.1. Introduction
Energy and environment are the twin major crises in the world [1]. Because of this, both developed and developing countries are becoming increasingly more interested in using pollution free, cost effective and renewable sources of energy [2]. As a renewable and alternative energy, wind is the most common and fastest-growing source of energy in the world [3–5]. The characteristics of wind energy are important in different aspects regarding wind energy exploitation [6,7]. Wind is highly variable, both in space and in time [8]. The importance of this variability becomes critical since it is amplified by the cubic relationship of the available power to the wind speed (p = 0.5ρAV3). The wind power production faces the fluctuation of the wind velocity [9–12]. Therefore, accurate knowledge about the wind characteristics is needed for planning, design and operation of wind turbines [13–16]. For the proper assessment, the variability of the wind over time can be divided into three distinct time scales. Firstly, the large time scale variability describes the variations of the amount of wind from one year to another, or even over periods of decades or more. Secondly, the medium time scale covers periods up to a year. These seasonal variations of the wind are much more predictable. Finally, the short term time scale variability covers time scales of minutes to seconds, also well known by the term “turbulence” and which is of critical interest in the wind turbine design process [17–23]. For more than half a century the Weibull distribution has attracted the attention of statisticians working on theory and methods as well as various fields of statistics [22,24–27]. Hundreds of papers have been written on this distribution; however the research is still ongoing. Together with the normal, exponential distributions, the Weibull distribution is the most popular model in statistics [28,29]. It is of utmost interest to theory orientated statisticians because of its great number of special features, and to practitioners because of its ability to fit to data from various fields, ranging from life data to weather data or observations made in economics and business administration, in health, in physical and social science, in hydrology, in biology or in the engineering sciences [30–36].
Research is ongoing worldwide on the Weibull distribution to find the most reliable methods for wind energy estimation. The main question is how precisely the values of the Weibull shape factor “k” and scale factor “c” can be determined [37–39]. For this reason different scientists and engineers have developed different methods to find the Weibull parameters for wind energy assessment. That is why several methods are found in literature to estimate the Weibull factors [38,40–43]. Recently, Mohammadi and Mostafaeipour [44] used two methods (STDM and PDM) for wind data assessment in Zarrineh, Iran. In 2012, Costa Rocha et al. [45] dealt with the analysis and comparison of seven numerical methods for the assessment of effectiveness in determining the parameters for the Weibull distribution, using wind data collected for Camocim and Paracuru cities in the northeast region of Brazil. Before that, Chang [41] made a statistical study to compare the performance of six numerical methods in estimating Weibull parameters for wind energy application. Seguro and Lambert [43] concluded that the maximum likelihood method (MLM) performs better than the popularly used graphical method (GM). Akdağ and Dinler [40], Azad and Saha [46], and Azad and Alam [47] reviewed three conventional methods and Akdag and Dinler [40] also proposed a new method, namely the energy pattern factor method, for estimating the Weibull parameters. Chu and Ke [48] and Bhattacharya and Bhattacharjee [49] examined the estimation comparison between the MLM and the least squares method [50]. They found that the least squares method significantly outperforms the MLM when sample size is the same. Jowder [51] used empirical and graphical methods to analyze the wind power density at 10, 30, and 60 m height in the Kingdom of Bahrain; two Weibull parameters were estimated and compared. From the analysis, it was found that the empirical methods provide more accurate prediction of average wind speed and power density than the GM. Odo et al. [52] used the Weibull distribution based model for prediction of wind energy potential in Enugu, Nigeria over a period of 13 years. Oyedepo et al. [53] also analyzed south-east Nigeria wind data that spans from 24 years to 37 years and was measured at 10 m height. Abbas et al. [54] statistically analyzed the wind speed data in Pakistan to determine the best fitting distribution of wind speed. For this purpose, two parameters Gamma, Weibull, Lognormal and Rayleigh distributions, and three parameters Burr and Frechet distributions were fitted to data and parameters for each distribution were estimated using the MLM [42,50,55–61].
Seguro and Lambart [43] calculated the value of the Weibull parameters by three methods. They recommended that the MLM is useful for time series wind speed data and the modified maximum likelihood method (MMLM) is recommended for use with wind data in frequency distribution format. Philippopoulos and Deligiorgi [62] statistically simulated the wind speed data in Athens, Greece based on the Weibull and autoregressive-moving average (ARMA) method. They found that ARMA methods are superior in simulating the frequency distribution of wind speed. Karpa and Naess [63] also analyzed the extreme value statistics of wind speed by the average conditional exceedance rate (ACER) method. Morgan et al. [64] examined the probability distributions for offshore wind speed. They concluded that the two-parameter lognormal distribution performs best for estimating extreme wind speeds, but still gives estimates with significant error. Stathopoulos et al. [65] used both numerical and statistical models for wind power prediction. Zhou et al. [66] comprehensively evaluated wind speed distribution models for a case study of North Dakota country sites. Wind energy estimation and analysis of wind regions through the Weibull distribution methods is widely used nowadays [35,37,67–80].
This study summarizes the results of the 10-min time series wind speed data measured at 20 m and 30 m height in three windy sites, namely Kuakata, Kutubdia and Sitakunda, located in Bangladesh. Table 1 shows the site information in which DL9210 anemometer used to measure wind speed at a 10-min interval. The anemometers have two sensors each of 32 KB memory and have one/two sockets. Statistical work was involved to find the best method of Weibull distribution with high efficiency. The assessment of wind energy potential has been done by using the best method of Weibull distribution. Section 2 offers a detailed outline of the methodology and associated theories for the statistical analysis. The results and discussions are presented in Section 3. Concluding remarks are presented in Section 4.
2. Outline of the Methodology and Associated Theories
To investigate the feasibility of the wind energy resource at any site, there are basically two ways at present to evaluate wind power. The first and the most accurate method to calculate wind power potential is based on measured values that are recorded at meteorological stations. The second method to assess wind power potential is by using probability distribution functions, namely the Rayleigh distribution, Chi-squared distribution, Normal distribution, Binomial distribution, Poisson distribution and Weibull distribution. In this study, the authors used only the Weibull distribution for wind power assessment as presented and discussed below.
2.1. Weibull Probability Density Function
The Weibull probability density function is a two-parameter function characterized by a dimensionless shape parameter (k) and scale parameter (c in m/s). These two parameters determine the wind speed for optimum performance of a wind conversion system as well as the speed range over which the device is likely to operate [52,84–87] as given in Equation (1):
2.2. Cumulative Distribution Function or the Weibull Function
Cumulative distribution function is the integration of the Weibull density function. It is the cumulative of relative frequency of each velocity interval [31]. The equation of the Weibull Function is given by:
All these distributions are used to determine the probability of occurrence. The nature of the occurrence affects the shape of the probability curve, and in the case of the wind regime, the cumulative curve probability nature mostly fits to the Weibull Function. Several methods to estimate Weibull factors are found in the literature. Some of these methods are:
- (1)
Graphical method (GM);
- (2)
Method of moments (MOM);
- (3)
Standard deviation method (STDM);
- (4)
Maximum likelihood method (MLM);
- (5)
Power density method (PDM);
- (6)
Modified maximum likelihood method (MMLM);
- (7)
Equivalent energy method (EEM).
2.2.1. GM
The graph is constructed in such a way that the cumulative Weibull distribution becomes a straight line, with the shape factor k as its slope. Taking the logarithm of both sides, the expression of Equation (3) can be rewritten as:
The above equation represents a relationship between ln(v) and −ln{1 − F(v)}. Therefore, the horizontal axis of this plot on the Weibull paper is v while the vertical axis is ln(1 − F(v))−1. The result is a straight line with slope k. For v = c, one finds F(v) = 1 − e−1 = 0.632 and t an estimation for the value of c, by drawing a horizontal line at F(v) = 0.632. The intersection point with the Weibull line gives the value of c.
2.2.2. MOM
The MOM is another technique commonly used in the field of parameter estimation. If the numbers v1, v2, …, vn represent a set of data, then an unbiased estimator for the n-th origin moment is given by:
After a few manipulations:
This formula can easily be handled by pocket calculators in energy output calculations. The accuracy of the approximation is within 0.5% for 1.6 < k < 3.5.Then from Equation (8) we can find the first and the second moments as follows:
When we divide m2 by the square of m1, we get an expression which is a function of the shape factor k only:
On taking the square roots of the equation, we have the coefficient of variation (COV):
In this case, this method can be used as an alternative to the MLM. The value of k and c can be easily determined by the following equations:
After some calculation we can find:
The Weibull scale factor can be calculated by:
2.2.3. STDM
In the STDM, the Weibull factors can be obtained as follows:
By determining the mean wind speed v̄, the standard deviation σ of wind speed becomes:
One can find next an expression for σ in terms of k and c with v̄ = c × Γ(1 + 1/k) and also Γ(x) is the gamma function and is defined as:
2.2.4. MLM
Maximum likelihood estimation has been the most widely used method for estimating the parameters of the Weibull distribution. The commonly used procedure of MLM proposed by Cohe [50], Harter and Moore [55] and Gove [89] due to its very desirable properties. Let v1, v2, … vn be a random sample of size n drawn from a probability density function f(vi, θ), where θ is an unknown parameter. The likelihood function of this random sample is the joint density of the n random variables and is a function of the unknown parameter [89] given as:
Thus, Equation (24) is the likelihood function. The maximum likelihood estimator (MLE) of θ, say θ̂, is the value of θ that maximizes L or, equivalently, the logarithm of L. Often, but not always, the MLE of θ is a solution of (dlogL)/dθ = 0, where solutions that are not functions of the sample values v1, v2, …, vn are not admissible, nor are solutions which are not in the parameter space. Now, we are going to apply the MLE to estimate the Weibull parameters, namely the shape and the scale parameters [90]. Consider the Weibull probability density function given in Equation (3), and then the likelihood function will be represented as:
On taking the logarithms of both sides of Equation (25), we obtain the estimating log-likelihood function:
Differentiating Equation (26) with respect to k and c in turn and equating to zero, we have:
From Equation (27):
When k̂ is obtained, then ĉ is can be determined. To solve k̂ by using the Newton-Raphson method as given below, let f(k) be the same as Equation (28) and taking the first differential of f(k), we have:
Substituting Equation (29) into Equation (28) gives:
Substituting Equation (29) into Equation (30), we get:
Therefore, k̂ is obtained from the equation below by carefully choosing an initial value for ki and iterating the process until it converges:
2.2.5. PDM
To obtain the shape factor and scale factor through this method, firstly the energy pattern factor is computed. The energy pattern factor usage is for turbine aerodynamic design. The energy pattern factor is related to the averaged data of wind speed and is defined as a ratio between mean of cubic wind speed to cube of mean wind speed. The energy pattern factor Epf is expressed as [40,45]:
Once the energy pattern factor is calculated by using the above equation, the Weibull shape factor and scale factor can be estimated from the following formulas:
2.2.6. MMLM
The MMLM can only be considered if the available data of wind speed are already in the shape of the Weibull distribution. The solution of the equations in the MLM requires some numerical iteration by the Newton-Raphson method [41]. The Weibull parameters are determined by the following equations:
2.2.7. EEM
Consider a random sample of v1, v2, …, vn by relative frequency of occurrence in a given interval of wind speed. Then a random variable observation discrete Wv associated with wind speed can be obtained from:
This observation random is also related with the Weibull parameters k and c from the equation of the probability of occurrence W. W(v) is the observed frequency of the wind speed for the interval of (v − 1) ≤ V < v. The mathematical representation of W(v) is:
The first hypothesis says that “The energy density is a parameter that helps in the determination of parameters of the Weibull distribution for applications in wind energy”. The related factor part deterministic must meet the following conditions: (a) be variable with random value expected value equal to 0: E(ε) = 0; (b) be variable random variance with constant: v(ε) = σ2; and (c) the occurrences of ε are non-correlated: COV(εi, εj). To ensure the condition of equivalence initially proposed in the hypothesis, it is the equality between Equation (4) and . The equation resulting from this transaction expresses the parameter c as a function of speed cubed average of observations and the parameter k as:
Substituting Equation (43) into Equation (42) gives:
The estimate of the parameter k may be obtained from an estimator of least squares given by the expression [45]:
2.3. COV
The COV is defined as the ratio between mean standard deviation to mean wind speed expressed as a percentage. It demonstrates the mutability of wind speed and can be expressed as [29]:
2.4. Wind Speed Varies with Altitude
Wind energy is indirect solar energy because it is generated by the temperature difference between the equator and the poles which drives the thermal system by solar radiation. It is known that wind speed varies with altitude, however, wind blows relatively slowly at low altitude and wind speed then increases with altitude. Different relationships are found in the literature to calculate wind speed at any height [91–93]. The Weibull factors used for these calculations must be obtained from the best possible method of Weibull distribution. For this purpose, the Weibull factors are initially calculated at desired heights, then wind speed and wind power are obtained [94,95]. The calculation procedures use the following relationships:
The mean energy density over a period of time, T, is the product of mean power density and the time period. k10 and c10 are the shape factor and scale factor at a height of 10 m and η is the power law coefficient. kh, ch, vh, zh and Ph are shape factor, scale factor, wind speed and wind power at the desired height, respectively. The zref is the reference height. ρ is the air density and for standard conditions (i.e., at sea level with temperature of 15 °C and pressure of 1 atmosphere) and is equal to 1.225 kg/m3 and v is the wind speed (m/s).In this paper the authors used the Weibull factors to find wind speed and wind power at a height of 50 m.
2.5. Statistical Error Analysis/Goodness of Fit
To find the best method for the analysis, some statistical parameters were used to analyze the efficiency of the above mentioned methods. The following tests were used to achieve this goal:
- (a)
zRelative percentage of error (RPE)
- (b)
Root mean square error (RMSE)
- (c)
Mean percentage error (MPE)
- (d)
- (e)
Chi-square error
- (f)
Analysis of variance or efficiency of the method
where N is the number of observations; yi,m is the frequency of observation or i-th calculated value from measured data; xi,w is the frequency of Weibull or i-th calculated value from the Weibull distribution; zi,v̄ is the mean of i-th calculated value from measured data. RPE shows the percentage deviation between the calculated values from the Weibull distribution and the calculated values from measured data. MPE shows the average of percentage deviation between the calculated values from the Weibull distribution and the calculated values from measured data, and MAPE shows the absolute average of percentage deviation between the calculated values from the Weibull distribution and the calculated values from measured data. Best results are obtained when these values are close to zero. R2 determines the linear relationship between the calculated values from the Weibull distribution and the calculated values from measured data. The ideal value of R2 is equal to 1 [30,44,45,96,97].
3. Results and Discussion
In this statistical analysis, data from three wind monitoring stations were used to diagnose the best method of the Weibull distribution. The most important results of this analysis, based on hourly, monthly, seasonal and annual figures, are presented. Table 2 shows a lot of information about the sites based on monthly mean as well as annual mean wind speed, number of observations in hours, maximum and minimum wind speed, standard deviation, and COV/turbulence intensity at 20 m and 30 m height.
A sample data frequency distribution and cumulative frequency distribution has been presented in Table 3.
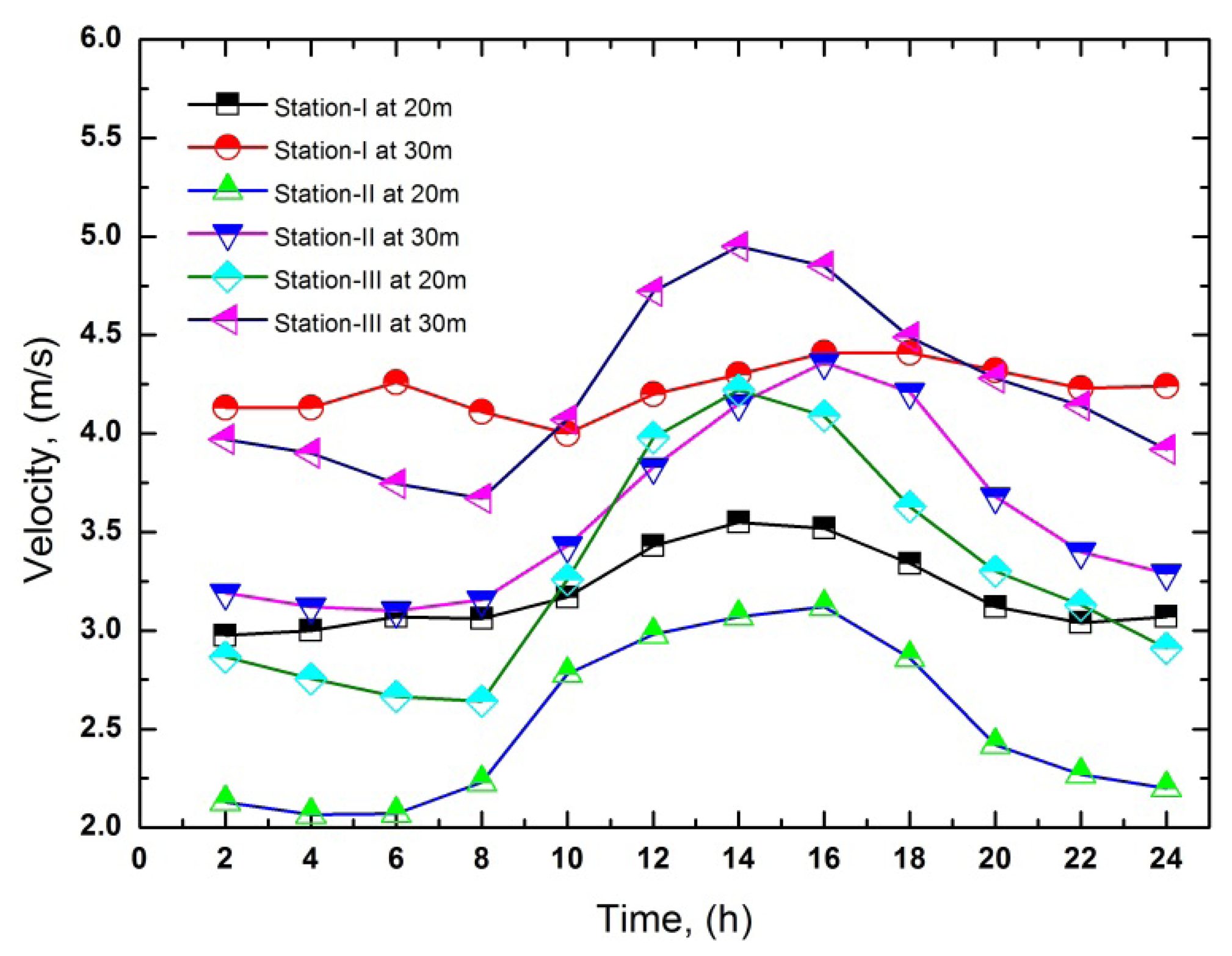
The hourly variation of wind speed at the selected altitude has been presented in Figure 1. Wind speed is higher during the daytime than the nighttime at every site. The COV/turbulence with the time series is at its minimum during the higher windy periods.
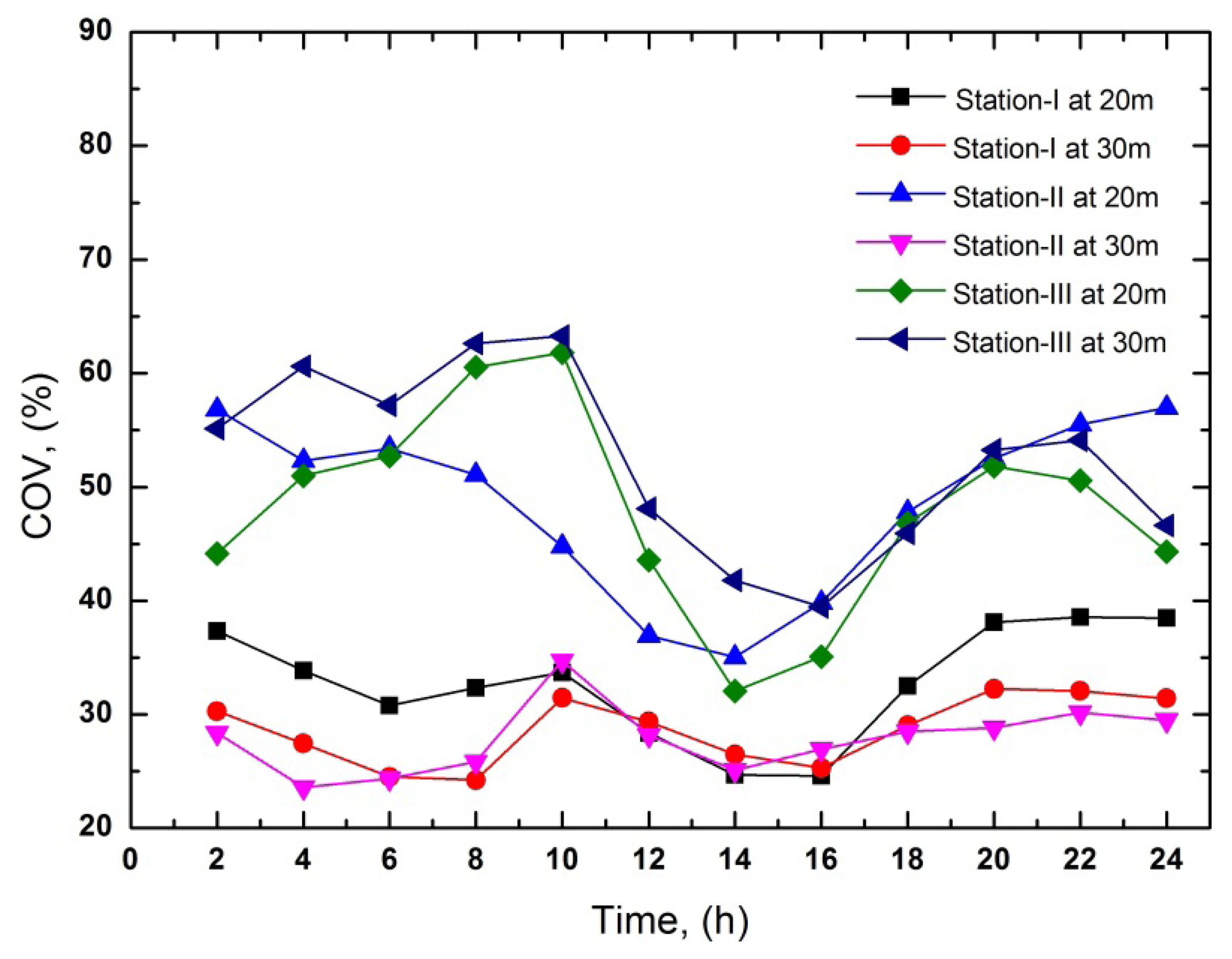
The hourly mean COV is presented in Figure 2. An important issue which has been clearly shown in Figure 2 is that turbulence is comparatively low at 30 m height than at 20 m height. Therefore, at the higher level the wind velocity stream is more uniform, i.e., the COV is lower.
From the sample frequency distribution (Table 3), it can be clearly seen that more than 50% of the frequency is between 5 m/s and 13 m/s of wind speed at every station. Table 3 can be used to clearly identify the total number of hours at certain wind speed available in a month. Anyone can find monthly wind speed scenario at a glance from the Table. The results are similar for other months at each station. Figures 1 and 2, shows the hourly mean variations of wind speed and coefficient of variation for the period of 24 h as a mean of a year. It has been shown that the wind speed is low until 8:00 AM to 10:00 AM, and after that it increases during the day until the maximum value is gained from 2:00 PM to 4:00 PM, and afterwards it decrease again until the end of the day. The same wind characteristics have been found at 20 m and 30 m height at every station. The maximum and minimum values of hourly mean wind speeds at 30 m height are 4.95 m/s at Station-III and 3.10 m/s at Station-II. The variation of wind speed at Station-I is lower than the others. The COV is lower when the wind speeds become a maximum. Its values are very high at nighttime. From Table 3 and Figures 1 and 2, it is clear that 30 m height wind speed data at Station-I shows better results than the other sites. To find the best Weibull method, the statistical analysis of the Weibull distribution at 20 m and 30 m height is presented in Tables 4, 5, 6, 7, 8 and 9.
In the statistical analysis, seven methods were used to determine the shape parameter k and scale parameter c of the Weibull distribution. For comparison of these seven methods to each other and to find out the efficiency of the methods, six statistical tools were used, i.e., relative percentage error (RPE), RMSE, MPE, MAPE, chi-square error (χ2), and analysis of variance or efficiency of the method (R2). It is important to note that only one column is required to rank the methods, since the above six criteria all gave the same relative results. For a more precisely diagnosis, the authors used these six statistical tools to rank the methods. The statistical analysis results for the seven numerical methods and the six statistical test results are shown in Tables 4, 5, 6, 7, 8 and 9 for the three stations at 20 m and 30 m height, respectively. The results show that the method of moments (MOM) and MLM give better results than other methods, where the value of k and c becomes almost the same by these two methods. For MLM, RPE and RMSE becomes zero and the value of MPE becomes negative, because, by this method, the calculated value becomes greater than the measured one. But the most important statistical test gives a chi-square error of χ2 = 0.0010 and the efficiency of the method is R2 = 0.9997, where the best results are obtained when these values are close to zero and unity, respectively. For Station-II, in Table 7, MLM and PDM methods show better performance than others. The common factor is that the MLM gives the better performance at every site. Therefore, it can be said that the MLM is the fisrt and MOM is the second most efficient method for wind data assessment at 30 m height.
From Table 4, it can be clearly seen that MOM (χ2 = 0.0001, R2 = 0.9999), MLM (χ2 = 0.0005, R2 = 0.9998) and MMLM (χ2 = 0.0002, R2 = 0.9999) give very close results and show better performance than other methods. In Table 6, MOM and PDM methods show better results than others. In the case of Station-III, MLM and PDM methods show better results than others in Table 8. Summarizing these results, it can be easily said that MOM and MLM methods were applicable for every height at any location wind data assessment. The PDM method is better for wind data assessment at the lower height, but not perfect for the higher height.
Table 10 summaries the test results of the seven methods and ranking of the methods according to their performance and efficiency in wind data assessment. The rankings were done by considering minimum error and maximum efficiency according to first to seventh positions respectively. Regarding this test, six statistical tools have been used and considered four decimal places of each value by numerical iteration methods. One test is enough to rank the methods, but for more precise analysis, the authors used more tools which helped to verify the discussion about the best method. In this statistical research work, it has been found that the MOM achieved the first position and the MLM took the second position in rank. Although the PDM got the third position, this method has better performance for low height wind data assessment. At increased height, PDM was a less efficient method than others. But MOM and MLM methods were applicable at any altitude with minimum error and maximum efficiency. Our first goal has been satisfied by the above statistical analysis where we identified the best methods to determine the Weibull distribution. Another goal is to select the best wind site by using these best methods, which has been analyzed below.
The procedure mentioned in this study is not only applicable in case study sits, it can be applied in any climatic conditions at any site in any countries in the world. For example, Mohammadi and Mostafaeipour [44] used STDM and PDM for wind turbine utilization in Zarriuneh at Kurdistan mountainous province in Iran. Chang [41] used moment method, empirical method, GM, MLM, MMLM and energy pattern factor method at three wind farms (Dayuan, Hengchun and Penghu) experiencing different weather conditions in Taiwan. Costa Rocha et al. [45] used EEM, moment method, MLM, etc. for wind energy generation in coastal area of the State of Ceara, located in the northeast region of Brazil. Dorvlo [98] used moment method, Chi-square method, empirical method and regression method for estimation of wind energy in four weather stations (Marmul, Masirah, Sur and Thumrait) in Oman. Many authors have already used the methods at different geographical locations for wind energy estimation [30,43,99]. The paper presented more generalized form of the Weibull distribution methods which is validated by widely acceptable error correction methods for practical application. This procedure is applicable at any geographical location; at any weather condition (i.e., summer, winter, spring etc.) at any altitude in any country in the world. The main outcome of the study is the development of the processes for identifying best methods for wind power generation which is applicable to any location.
Table 11 presents the variation of wind speed during different months of the year and the annual mean values. From the average values, the variation of the maximum and minimum wind speed occurred in April to September and October to March respectively at every station. At Station-I, the maximum and minimum wind speed occurred in June and October with values of 5.07 m/s and 2.57 m/s, respectively. The COV and standard deviation at this site varies between 21.01%–35.68% and 0.54–2.13, respectively. On the other hand, Station-III has wind speeds similar to Station-I, but the COV and standard deviation varies between 15.93%–129.53% and 0.71–13.07, respectively. In August and September, the COV is 50.1% and 129.53%, which means that these months have some irregular wind behavior, i.e., gusty wind exists during these months. Station-II has wind behavior (wind speed) performance lower than other stations. Therefore, Station-I has shown better wind characteristics than the other Stations, hence it is the selected wind site. The mean available power and energy in the wind at 30 m height at Station-I is analyzed below.
The monthly mean available power is analyzed using both MOM and MLM methods in Table 12. From this table, it can be seen that the available power from April to September was above 100 W/m2 and the maximum and minimum power occurred in August, 179.36 W/m2, and October, 11.8 W/m2, respectively. Only two statistical tools (RMSE and Chi-square error) have been used for comparing the MOM and MLM methods. Here, the MLM method gives better performance with minimum error. Using the MLM method, the Weibull shape factor and scale factor vary between 2.52–5.65 and 2.79–6.69 m/s. respectively.
Therefore, the six months from April to September show more potential wind generated power than other months in the year. In this research work, the Weibull parameters at heights of 30 m and 20 m were determined.
Table 13 presents the seasonal analysis of wind speed, Weibull parameters and available power at 20 m and 30 m height. It also presents the extrapolated values at 50 m. The months in each season can be classified as winter (November, December and January), spring (February, March and April), summer (May, June and July), and autumn (August, September and October).
The mean velocity, shape factor, scale factor, etc. at 50 m were extrapolated using Equations (44)–(48) and these extrapolated results are presented in Table 14.
Table 15 also includes yearly or annual mean values. According to this table, the maximum and minimum values of wind speed and wind power have been observed in summer and spring with the values of 5.26 m/s and 4.03 m/s and the power is 108.24 W/m2 and 48.16 W/m2 respectively at 30 m height. In the literatures, Elliot et al. [100], Yu et al. [101], Ilinca et al. [102] and Zhou et al. [103] classified the wind power in seven categories which are shown in Table 14. Considering these wind power classes, it has been found that Station-I has poor wind power at every height (i.e., 20 m, 30 m and 50 m). For a more realistic analysis, the available energy in the wind of this site was determined by using numerical iteration methods and is presented in Table 15.
The energy estimation of wind regimes by the Weibull based approach has been presented in Table 15. It also shows the most frequent wind speed, velocity contributing the maximum energy, energy density and total energy intensity. From the above table, it can be clearly seen that the energy density and total energy intensity are higher in summer than during autumn seasons and also are a minimum in spring. Therefore, summers have more wind potential than any other seasons. To find out the energy generated by a wind turbine, a small model wind turbine (NACA 4418 turbine power curve) with rated power of 20 kW or 0.02 MW, rated speed of 8 m/s and hub height of 30 m has been used for this calculation. Values of capacity factor and total energy output were obtained using numerical integration methods of Trapezoidal Sums and Simpson's 1/3 Rule and the values were verified to four decimal places. From Table 16, it can be seen that, in summer, 13.2938 MW·h of energy can be extracted by the suggested model wind turbine. This means that only 147.67 kW/day of power can be generated by the wind turbine in summer and the value becomes 50% less in the rainy season. Therefore, it can be finally concluded that the analytical results show that Station-I does not have the necessary available wind power potential for large turbines but has sufficient wind power for small wind turbine both for electricity generation and pumping water for irrigation.
4. Conclusions
In this work, statistical diagnosis of the best Weibull distribution methods for wind data analysis is presented. By using the available wind data, the values of shape factor k and scale factor c were determined using seven methods and were then investigated as to how efficiently the methods can estimate the Weibull factors with minimum error. To satisfy the main objectives of this work, six statistical tools were used to find the best method of Weibull distribution. It is important to note that any one of these statistical tools, namely RPE, RMSE, MPE, MAPE, chi-square error (χ2), and analysis of variance or efficiency of the method (R2) is good enough to rank the methods, however, analysis using all of them was done to rank more precisely. The results show that the MOM and MLM are the most efficient methods for determining the value of k and c to fit the Weibull distribution curves. The PDM is more efficient for low altitude wind data but is not efficient for higher altitude wind data. MOM and MLM methods are more efficient with less error and are applicable for any altitude. Other methods such as MMLM, EEM, GM and STDM are the least efficient methods to fit the Weibull distribution curves for the assessment of wind speed data. Another objective of this work was to find the best wind site using the best Weibull distribution methods and calculate available wind power. Monthly mean wind speed was found to be relatively higher in Station-I than that of the other sites. As a result this is our selected site. The MLM method has shown better results than MOM in calculating monthly mean wind power at Station-I. The value of shape factor, scale factor, wind speed and power was determined at 50 m height using extrapolation of numerical equations to satisfy the wind power classes as discussed in this paper. The poor class wind power has been found in this site in each altitude. Furthermore, energy density and total energy intensity per unit area has been analyzed by numerical iteration methods. Finally, the energy extracted by a small model wind turbine has been analyzed by using numerical integration methods of Trapezoidal Sums and Simpson's 1/3 Rule. This study offers a new pathway on how to evaluate feasible locations for wind energy assessment which is applicable at any windy sites in any country in the world.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Baños, R.; Manzano-Agugliaro, F.; Montoya, F.G.; Gil, C.; Alcayde, A.; Gómez, J. Optimization methods applied to renewable and sustainable energy: A review. Renew. Sustain. Energy Rev. 2011, 15, 1753–1766. [Google Scholar]
- Cruz-Peragon, F.; Palomar, J.M.; Casanova, P.J.; Dorado, M.P.; Manzano-Agugliaro, F. Characterization of solar flat plate collectors. Renew. Sustain. Energy Rev. 2012, 16, 1709–1720. [Google Scholar]
- Acker, T.L.; Williams, S.K.; Duque, E.P.; Brummels, G.; Buechler, J. Wind resource assessment in the state of Arizona: Inventory, capacity factor, and cost. Renew. Energy 2007, 32, 1453–1466. [Google Scholar]
- Munteanu, I.; Bratcu, A.I.; Cutululis, N.A.; Ceanga, E. Optimal Control of Wind Energy Systems: Towards A Global Approach; Springer: London, UK, 2008. [Google Scholar]
- Montoya, F.G.; Aguilera, M.J.; Manzano-Agugliaro, F. Renewable energy production in Spain: A review. Renew. Sustain. Energy Rev. 2014, 33, 509–531. [Google Scholar]
- Hernández-Escobedo, Q.; Manzano-Agugliaro, F.; Zapata-Sierra, A. The wind power of Mexico. Renew. Sustain. Energy Rev. 2010, 14, 2830–2840. [Google Scholar]
- Hernández-Escobedo, Q.; Saldaña-Flores, R.; Rodríguez-García, E.R.; Manzano-Agugliaro, F. Wind energy resource in Northern Mexico. Renew. Sustain. Energy Rev. 2014, 32, 890–914. [Google Scholar]
- Hernandez-Escobedo, Q.; Manzano-Agugliaro, F.; Gazquez-Parra, J.A.; Zapata-Sierra, A. Is the wind a periodical phenomenon? The case of Mexico. Renew. Sustain. Energy Rev. 2011, 15, 721–728. [Google Scholar]
- Vincent, C.L.; Giebel, G.; Pinson, P.; Madsen, H. Resolving nonstationary spectral information in wind speed time series using the Hilbert-Huang transform. J. Appl. Meteorol. Climatol. 2010, 49, 253–267. [Google Scholar]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar]
- Chen, Z.; Gomez, S.A.; Mccormick, M. A Fuzzy Logic Controlled Power Electronic System for Variable Speed Wind Energy Conversion Systems. Proceedings of the 8th International Conference on Power Electronics and Variable Speed Drives, London, UK, 18–19 September 2000; pp. 114–119.
- Ahmed Shata, A.; Hanitsch, R. Electricity generation and wind potential assessment at Hurghada, Egypt. Renew. Energy 2008, 33, 141–148. [Google Scholar]
- Akhmatov, V. Influence of wind direction on intense power fluctuations in large offshore windfarms in the North Sea. Wind Eng. 2007, 31, 59–64. [Google Scholar]
- Sorensen, P.; Cutululis, N.A.; Vigueras-Rodríguez, A.; Jensen, L.E.; Hjerrild, J.; Donovan, M.H.; Madsen, H. Power fluctuations from large wind farms. IEEE Trans. Power Syst. 2007, 22, 958–965. [Google Scholar]
- Chen, Z.; Blaabjerg, F. Wind farm—A power source in future power systems. Renew. Sustain. Energy Rev. 2009, 13, 1288–1300. [Google Scholar]
- Hsieh, C.-H.; Dai, C.-F. The analysis of offshore islands wind characteristics in Taiwan by Hilbert–Huang transform. J. Wind Eng. Ind. Aerodyn. 2012, 107, 160–168. [Google Scholar]
- Belu, R.; Koracin, D. Wind characteristics and wind energy potential in western Nevada. Renew. Energy 2009, 34, 2246–2251. [Google Scholar]
- Chang, T.P. Wind energy assessment incorporating particle swarm optimization method. Energy. Convers. Manag. 2011, 52, 1630–1637. [Google Scholar]
- Adaramola, M.; Paul, S.; Oyedepo, S. Assessment of electricity generation and energy cost of wind energy conversion systems in north-central Nigeria. Energy. Convers. Manag. 2011, 52, 3363–3368. [Google Scholar]
- Ohunakin, O.S.; Akinnawonu, O.O. Assessment of wind energy potential and the economics of wind power generation in Jos, Plateau State, Nigeria. Energy. Sustain. Dev. 2012, 16, 78–83. [Google Scholar]
- Ohunakin, O.S. Assessment of wind energy resources for electricity generation using WECS in North-Central region, Nigeria. Renew. Sustain. Energy Rev. 2011, 15, 1968–1976. [Google Scholar]
- Akpinar, E.; Akpinar, S. Statistical analysis of wind energy potential on the basis of the Weibull and Rayleigh distributions for Agin-Elazig, Turkey. Proc. Inst. Mech. Eng. Part A J. Power Energy 2004, 218, 557–565. [Google Scholar]
- Ahmed, A.S. Wind energy as a potential generation source at Ras Benas, Egypt. Renew. Sustain. Energy Rev. 2010, 14, 2167–2173. [Google Scholar]
- Fadare, D. A statistical analysis of wind energy potential in Ibadan, Nigeria, based on Weibull distribution function. Pac. J. Sci. Technol. 2008, 9, 110–119. [Google Scholar]
- Akpinar, E.K. A statistical investigation of wind energy potential. Energy Sources Part A 2006, 28, 807–820. [Google Scholar]
- Ahmed Shata, A.; Hanitsch, R. Evaluation of wind energy potential and electricity generation on the coast of Mediterranean Sea in Egypt. Renew. Energy 2006, 31, 1183–1202. [Google Scholar]
- Akdağ, S.A.; Güler, Ö. Evaluation of wind energy investment interest and electricity generation cost analysis for Turkey. Appl. Energy 2010, 87, 2574–2580. [Google Scholar]
- Azad, A. Statistical Weibull distribution analysis for wind power of the two dimensional ridge areas. Int. J. Adv. Renew. Energy Res. 2013, 1, 8–14. [Google Scholar]
- Ahmed, S.; Mahammed, H. A statistical analysis of wind power density based on the Weibull and Ralyeigh models of “Penjwen Region” Sulaimani/Iraq. Jordan J. Mech. Ind. Eng. 2012, 6, 135–140. [Google Scholar]
- Celik, A.N. A statistical analysis of wind power density based on the Weibull and Rayleigh models at the southern region of Turkey. Renew. Energy 2004, 29, 593–604. [Google Scholar]
- Kavak Akpinar, E.; Akpinar, S. A statistical analysis of wind speed data used in installation of wind energy conversion systems. Energy Convers. Manag. 2005, 46, 515–532. [Google Scholar]
- Safari, B.; Gasore, J. A statistical investigation of wind characteristics and wind energy potential based on the Weibull and Rayleigh models in Rwanda. Renew. Energy 2010, 35, 2874–2880. [Google Scholar]
- Kose, R.; Ozgur, M.A.; Erbas, O.; Tugcu, A. The analysis of wind data and wind energy potential in Kutahya, Turkey. Renew. Sustain. Energy Rev. 2004, 8, 277–288. [Google Scholar]
- Zaharim, A.; Najid, S.K.; Razali, A.M.; Sopian, K. Analyzing Malaysian Wind Speed Data Using Statistical Distribution. Proceedings of the 4th IASME/WSEAS International Conference on Energy and Environment, Cambridge, UK, 24–26 February 2009; pp. 360–370.
- Islam, M.; Saidur, R.; Rahim, N. Assessment of wind energy potentiality at Kudat and Labuan, Malaysia using Weibull distribution function. Energy 2011, 36, 985–992. [Google Scholar]
- Daoo, V.; Panchal, N.; Sunny, F.; Sitaraman, V.; Krishnamoorthy, T. Assessment of wind energy potential of Trombay, Mumbai (19.1 N; 72.8 E), India. Energy Convers. Manag. 1998, 39, 1351–1356. [Google Scholar]
- Celik, A. Weibull representative compressed wind speed data for energy and performance calculations of wind energy systems. Energy Convers. Manag. 2003, 44, 3057–3072. [Google Scholar]
- Ulgen, K.; Hepbasli, A. Determination of Weibull parameters for wind energy analysis of Izmir, Turkey. Int. J. Energy Res. 2002, 26, 495–506. [Google Scholar]
- Langlois, R. Estimation of Weibull parameters. J. Mater. Sci. Lett. 1991, 10, 1049–1051. [Google Scholar]
- Akdağ, S.A.; Dinler, A. A new method to estimate Weibull parameters for wind energy applications. Energy Convers. Manag. 2009, 50, 1761–1766. [Google Scholar]
- Chang, T.P. Performance comparison of six numerical methods in estimating Weibull parameters for wind energy application. Appl. Energy 2011, 88, 272–282. [Google Scholar]
- Minami, F.; Brückner-Foit, A.; Munz, D.; Trolldenier, B. Estimation procedure for the Weibull parameters used in the local approach. Int. J. Fract. 1992, 54, 197–210. [Google Scholar]
- Seguro, J.V.; Lambert, T.W. Modern estimation of the parameters of the Weibull wind speed distribution for wind energy analysis. J. Wind Eng. Ind. Aerodyn. 2000, 85, 75–84. [Google Scholar]
- Mohammadi, K.; Mostafaeipour, A. Using different methods for comprehensive study of wind turbine utilization in Zarrineh, Iran. Energy Convers. Manag. 2013, 65, 463–470. [Google Scholar]
- Costa Rocha, P.A.; de Sousa, R.C.; de Andrade, C.F.; da Silva, M.E.V. Comparison of seven numerical methods for determining Weibull parameters for wind energy generation in the northeast region of Brazil. Appl. Energy 2012, 89, 395–400. [Google Scholar]
- Azad, A.; Saha, M. Weibull's analysis of wind power potential at coastal sites in Kuakata, Bangladesh. Int. J. Energy Mach. 2011, 4, 36–45. [Google Scholar]
- Azad, A.; Alam, M. A Statistical tools for clear energy: Weibull's distribution for potentiality analysis of wind energy. Int. J. Adv. Renew. Energy Res. 2012, 1, 240–247. [Google Scholar]
- Chu, Y.-K.; Ke, J.-C. Computation approaches for parameter estimation of Weibull distribution. Math. Comput. Appl. 2012, 17, 39–47. [Google Scholar]
- Bhattacharya, P.; Bhattacharjee, R. A study on Weibull distribution for estimating the parameters. Wind Eng. 2009, 33, 469–476. [Google Scholar]
- Cohen, A.C. Maximum likelihood estimation in the Weibull distribution based on complete and on censored samples. Technometrics 1965, 7, 579–588. [Google Scholar]
- Jowder, F.A. Wind power analysis and site matching of wind turbine generators in Kingdom of Bahrain. Appl. Energy 2009, 86, 538–545. [Google Scholar]
- Odo, F.; Offiah, S.; Ugwuoke, P. Weibull distribution-based model for prediction of wind potential in Enugu, Nigeria. Pelagia Res. Libr. Adv. Appl. Sci. Res. 2012, 3, 1202–1208. [Google Scholar]
- Oyedepo, S.O.; Adaramola, M.S.; Paul, S.S. Analysis of wind speed data and wind energy potential in three selected locations in south-east Nigeria. Int. J Energy Environ. Eng. 2012, 3. [Google Scholar] [CrossRef]
- Abbas, K.; Alamgir.; Khan, S.A.; Ali, A.; Khan, D.M.; Khalil, U. Statistical analysis of wind speed data in Pakistan. World Appl. Sci. J. 2012, 18, 1533–1539. [Google Scholar]
- Harter, H.L.; Moore, A.H. Maximum-likelihood estimation of the parameters of gamma and Weibull populations from complete and from censored samples. Technometrics 1965, 7, 639–643. [Google Scholar]
- Odell, P.M.; Anderson, K.M.; D'agostino, R.B. Maximum likelihood estimation for interval-censored data using a Weibull-based accelerated failure time model. Biometrics 1992, 48, 951–959. [Google Scholar]
- Choi, S.; Wette, R. Maximum likelihood estimation of the parameters of the gamma distribution and their bias. Technometrics 1969, 11, 683–690. [Google Scholar]
- Cacciari, M.; Mazzanti, G.; Montanari, G. Comparison of maximum likelihood unbiasing methods for the estimation of the Weibull parameters. IEEE Trans. Dielectr. Electr. Insul. 1996, 3, 18–27. [Google Scholar]
- Zanakis, S.H.; Kyparisis, J. A review of maximum likelihood estimation methods for the three-parameter Weibull distribution. J. Stat. Comput. Simul. 1986, 25, 53–73. [Google Scholar]
- Lemon, G.H. Maximum likelihood estimation for the three parameter Weibull distribution based on censored samples. Technometrics 1975, 17, 247–254. [Google Scholar]
- Jiang, S.; Kececioglu, D. Maximum likelihood estimates, from censored data, for mixed-Weibull distributions. IEEE Trans. Reliab. 1992, 41, 248–255. [Google Scholar]
- Philippopoulos, K.; Deligiorgi, D. Statistical simulation of wind speed in Athens, Greece based on Weibull and ARMA models. Int. J. Energy Environ. 2009, 3, 151–158. [Google Scholar]
- Karpa, O.; Naess, A. Extreme value statistics of wind speed data by the ACER method. J. Wind Eng. Ind. Aerodyn. 2013, 112, 1–10. [Google Scholar]
- Morgan, E.C.; Lackner, M.; Vogel, R.M.; Baise, L.G. Probability distributions for offshore wind speeds. Energy Convers. Manag. 2011, 52, 15–26. [Google Scholar]
- Stathopoulos, C.; Kaperoni, A.; Galanis, G.; Kallos, G. Wind power prediction based on numerical and statistical models. J. Wind Eng. Ind. Aerodyn. 2013, 112, 25–38. [Google Scholar]
- Zhou, J.; Erdem, E.; Li, G.; Shi, J. Comprehensive evaluation of wind speed distribution models: A case study for North Dakota sites. Energy Convers. Manag. 2010, 51, 1449–1458. [Google Scholar]
- Sardar Maran, P.; Ponnusamy, R. Wind power density estimation using meteorological tower data. Int. J. Renew. Sustain Energy. 2013, 2, 110–114. [Google Scholar]
- Bivona, S.; Bonanno, G.; Burlon, R.; Gurrera, D.; Leone, C. Stochastic models for wind speed forecasting. Energy Convers. Manag. 2011, 52, 1157–1165. [Google Scholar]
- Daniel, A.; Chen, A. Stochastic simulation and forecasting of hourly average wind speed sequences in Jamaica. Sol. Energy. 1991, 46, 1–11. [Google Scholar]
- Kamal, L.; Jafri, Y.Z. Time series models to simulate and forecast hourly averaged wind speed in Quetta, Pakistan. Sol. Energy 1997, 61, 23–32. [Google Scholar]
- Cadenas, E.; Rivera, W. Wind speed forecasting in the south coast of Oaxaca, Mexico. Renew. Energy 2007, 32, 2116–2128. [Google Scholar]
- Alexiadis, M.; Dokopoulos, P.; Sahsamanoglou, H. Wind speed and power forecasting based on spatial correlation models. IEEE Trans. Energy Convers. 1999, 14, 836–842. [Google Scholar]
- Keyhani, A.; Ghasemi-Varnamkhasti, M.; Khanali, M.; Abbaszadeh, R. An assessment of wind energy potential as a power generation source in the capital of Iran, Tehran. Energy 2010, 35, 188–201. [Google Scholar]
- Mirhosseini, M.; Sharifi, F.; Sedaghat, A. Assessing the wind energy potential locations in province of Semnan in Iran. Renew. Sustain. Energy Rev. 2011, 15, 449–459. [Google Scholar]
- Alamdari, P.; Nematollahi, O.; Mirhosseini, M. Assessment of wind energy in Iran: A review. Renew. Sustain. Energy Rev. 2012, 16, 836–860. [Google Scholar]
- Jaramillo, O.; Saldaña, R.; Miranda, U. Wind power potential of Baja California Sur, México. Renew. Energy 2004, 29, 2087–2100. [Google Scholar]
- Mathew, S.; Pandey, K.; Kumar, V.A. Analysis of wind regimes for energy estimation. Renew. Energy 2002, 25, 381–399. [Google Scholar]
- Weisser, D. A wind energy analysis of Grenada: An estimation using the “Weibull” density function. Renew. Energy 2003, 28, 1803–1812. [Google Scholar]
- Chang, T.-J.; Wu, Y.-T.; Hsu, H.-Y.; Chu, C.-R.; Liao, C.vM. Assessment of wind characteristics and wind turbine characteristics in Taiwan. Renew. Energy 2003, 28, 851–871. [Google Scholar]
- Akpinar, S.; Akpinar, E.K. Estimation of wind energy potential using finite mixture distribution models. Energy Convers. Manag. 2009, 50, 877–884. [Google Scholar]
- Exif. Kutubdia in Bangladesh, 2008. Available online: https://www.flickr.com/photos/rahmanmm/2370901630/meta/ (accessed on 15 April 2014).
- Khadem, S.K.; Hussain, M. A pre-feasibility study of wind resources in Kutubdia Island, Bangladesh. Renew. Energy 2006, 31, 2329–2341. [Google Scholar]
- Rahaman, S. A Field Report Ongeoenvironmental and Biological Aspects of Sitakunda; Jahangirnagar University: Dhaka, Bangladesh, 2010. [Google Scholar]
- Ramírez, P.; Carta, J.A. The use of wind probability distributions derived from the maximum entropy principle in the analysis of wind energy. A case study. Energy Convers. Manag. 2006, 47, 2564–2577. [Google Scholar]
- Kantar, Y.M.; Usta, I. Analysis of wind speed distributions: Wind distribution function derived from minimum cross entropy principles as better alternative to Weibull function. Energy Convers. Manag. 2008, 49, 962–973. [Google Scholar]
- Weibull, W. A statistical distribution function of wide applicability. J. Appl. Mech. 1951, 18, 293–297. [Google Scholar]
- Xiao, Y.; Li, Q.; Li, Z.; Chow, Y.; Li, G. Probability distributions of extreme wind speed and its occurrence interval. Eng. Struct. 2006, 28, 1173–1181. [Google Scholar]
- Manwell, J.F.; Mcgowan, J.G.; Rogers, A.L. Wind Energy Explained: Theory, Design and Application; John Wiley & Sons Ltd.: London, UK, 2002; p. 577. [Google Scholar]
- Gove, J.H. Moment and maximum likelihood estimators for Weibull distributions under length-and area-biased sampling. Environ. Ecol. Stat. 2003, 10, 455–467. [Google Scholar]
- Guure, C.B.; Ibrahim, N.A. Bayesian analysis of the survival function and failure rate of Weibull distribution with censored data. Math. Probl. Eng. 2012, 2012. [Google Scholar] [CrossRef]
- Sedefian, L. On the vertical extrapolation of mean wind power density. J. Appl. Meteorol. 1980, 19, 488–493. [Google Scholar]
- Justel, A.; Peña, D.; Zamar, R. A multivariate Kolmogorov-Smirnov test of goodness of fit. Stat. Probab. Lett. 1997, 35, 251–259. [Google Scholar]
- Watson, G.S. Goodness-of-fit tests on a circle. Biometrika 1961, 48, 109–114. [Google Scholar]
- Genest, C.; Rémillard, B.; Beaudoin, D. Goodness-of-fit tests for copulas: A review and a power study. Insur. Math. Econ. 2009, 44, 199–213. [Google Scholar]
- Balderrama, J.A.; Masters, F.J.; Gurley, K.R. Peak factor estimation in hurricane surface winds. J. Wind Eng. Ind. Aerodyn. 2012, 102, 1–13. [Google Scholar]
- Justus, C.; Mikhail, A. Height variation of wind speed and wind distributions statistics. Geophys. Res. Lett. 1976, 3, 261–264. [Google Scholar]
- Justus, C.; Hargraves, W.; Mikhail, A.; Graber, D. Methods for estimating wind speed frequency distributions. J. Appl. Meteorol. 1978, 17, 350–353. [Google Scholar]
- Dorvlo, A.S.S. Estimating wind speed distribution. Energy Convers. Manag. 2002, 43, 2311–2318. [Google Scholar]
- Lun, I.Y.F.; Lam, J.C. A study of Weibull parameters using long-term wind observations. Renew. Energy 2000, 20, 145–153. [Google Scholar]
- Elliott, D.L.; Schwartz, M.N. Wind Energy Potential in the United States. Proceedings of the Project Energy '93: Real Energy Technologies—Environmentally Responsible—Ready for Today, Independence, MO, USA, 21–23 June 1993.
- Yu, X.; Qu, H. Wind power in China—Opportunity goes with challenge. Renew. Sustain. Energy Rev. 2010, 14, 2232–2237. [Google Scholar]
- Ilinca, A.; Mccarthy, E.; Chaumel, J.-L.; Rétiveau, J.-L. Wind potential assessment of Quebec Province. Renew. Energy 2003, 28, 1881–1897. [Google Scholar]
- Zhou, W.; Yang, H.; Fang, Z. Wind power potential and characteristic analysis of the Pearl River Delta region, China. Renew. Energy 2006, 31, 739–753. [Google Scholar]
Nomenclature
| P | Total power, W/m2 |
| A | Area, m2 |
| Pe | Practically extractable power, W/m2 |
| k | Dimensionless shape parameter |
| c | Scale parameter (m/s) |
| f(v) | Weibull probability density function |
| F(v) | Cumulative distribution function |
| C | Constant |
| L | Likelihood function |
| COV | Coefficient of variation |
| vi | Random sample of wind speed central to bin i |
| n | Number of sample or bin |
| f(vi) | Weibull frequency for wind speed ranging within bin i |
| f(v≥0) | Probability for wind speed ≥ 0 |
| Wvi | Observed frequency of the wind speed |
Mean of the cubic wind speed, m/s | |
| εvi | Error of the approximation |
| zref | Reference height, m |
| kh | Weibull shape factor at desired height |
| ch | Weibull scale factor at desired height, m/s |
| vh | Wind speed at desired height, m/s |
| Ph | Power at desired height, W/m2 |
| N | Total number of observations |
| yi,m | i-th calculated value from measured data |
| xi,w | i-th calculated value from the Weibull distribution |
| ziv̄ | Mean of i-th calculated value from measured data |
| R2 | Analysis of variance |
| Γ | Gamma function |
| σ | Standard deviation of wind speed, m/s |
| ρ | Air density, kg/m3 |
| θ | Unknown parameter for maximum likelihood function |
| η | Power law coefficient |
| χ2 | Chi-square error |
| Wind station name | Site name | Latitude (°) N | Longitude (°) E | Height above the sea level | Reference |
|---|---|---|---|---|---|
| Station-I | Kuakata | 21°54.76′ | 90°08.24′ | 3 m | [81] |
| Station-II | Kutubdia | 21°54.71′ | 91°52.43′ | 0–4 m | [82] |
| Station-III | Sitakunda | 22°35.68′ | 91°42.52′ | 9 m | [83] |
| Wind | Month of the year | Yearly mean | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| January | February | March | April | May | June | July | August | September | October | November | December | ||||
| Station-I | H = 30 m | N (h) | 744 | 672 | 744 | 720 | 744 | 720 | 744 | 744 | 720 | 744 | 720 | 744 | 8760 |
| vmean (m/s) | 3.11 | 3.57 | 3.54 | 4.98 | 4.97 | 5.07 | 5.74 | 5.97 | 4.95 | 2.57 | 2.98 | 3.22 | 4.22 | ||
| vmax (m/s) | 5.08 | 5.79 | 5.52 | 8.26 | 8.28 | 7.55 | 9.46 | 9.29 | 9.52 | 3.5 | 5.77 | 7.45 | 7.12 | ||
| vmin (m/s) | 1.66 | 2.25 | 2.44 | 2.52 | 2.32 | 2.48 | 3.23 | 2.34 | 1.97 | 1.5 | 1.31 | 1.26 | 2.11 | ||
| σ (m/s) | 0.78 | 0.86 | 0.82 | 1.54 | 1.68 | 1.56 | 1.61 | 2.13 | 2.14 | 0.54 | 0.76 | 1.39 | 1.32 | ||
| COV (%) | 25.08 | 24.09 | 23.16 | 30.92 | 33.8 | 30.77 | 28.05 | 35.68 | 43.23 | 21.01 | 25.5 | 43.17 | 30.37 | ||
| H = 20 m | N (h) | 744 | 672 | 744 | 720 | 744 | 720 | 744 | 744 | 720 | 744 | 720 | 744 | 8760 | |
| vmean (m/s) | 2.15 | 2.62 | 2.65 | 3.76 | 3.81 | 3.82 | 4.44 | 4.75 | 3.81 | 1.76 | 2.12 | 2.55 | 3.19 | ||
| vmax (m/s) | 3.65 | 4.14 | 4.29 | 6.03 | 6.25 | 5.58 | 8.15 | 8.21 | 7.33 | 2.77 | 4.9 | 7.2 | 5.71 | ||
| vmin (m/s) | 1.22 | 1.68 | 1.78 | 1.88 | 1.69 | 1.77 | 2.71 | 1.72 | 1.53 | 0.99 | 0.9 | 0.97 | 1.57 | ||
| σ (m/s) | 0.52 | 0.69 | 0.66 | 1.1 | 1.24 | 1.17 | 1.37 | 1.83 | 1.73 | 0.45 | 0.65 | 1.4 | 1.07 | ||
| COV (%) | 24.19 | 26.34 | 24.91 | 29.26 | 32.55 | 30.63 | 30.86 | 38.53 | 45.41 | 25.57 | 30.66 | 54.9 | 32.82 | ||
| Station-II | H = 30 m | N (h) | 744 | 672 | 744 | 720 | 744 | 720 | 744 | 744 | 720 | 744 | 720 | 744 | 8760 |
| vmean (m/s) | 3.11 | 2.8 | 3.15 | 3.73 | 4.24 | 4.53 | 5.42 | 4.74 | 3.39 | 2.25 | 2.96 | 2.65 | 3.58 | ||
| vmax (m/s) | 5.26 | 5.69 | 4.81 | 6.36 | 6.95 | 7.35 | 7.58 | 7.58 | 7.48 | 3.31 | 4.15 | 4.37 | 5.91 | ||
| vmin (m/s) | 1.64 | 1.29 | 1.67 | 2.22 | 2.35 | 2.06 | 2.82 | 1.99 | 1.29 | 1.25 | 1.7 | 1.73 | 1.83 | ||
| σ (m/s) | 0.95 | 1.33 | 0.69 | 1.16 | 1.39 | 1.52 | 1.17 | 1.56 | 1.74 | 0.59 | 0.5 | 0.64 | 1.1 | ||
| COV (%) | 30.55 | 47.5 | 21.9 | 31.1 | 32.78 | 33.55 | 21.59 | 32.91 | 51.33 | 26.22 | 16.89 | 24.15 | 30.87 | ||
| H = 20 m | N (h) | 744 | 672 | 744 | 720 | 744 | 720 | 744 | 744 | 720 | 744 | 720 | 744 | 8760 | |
| vmean (m/s) | 1.69 | 1.79 | 1.9 | 2.73 | 3.3 | 3.81 | 4.63 | 3.95 | 2.58 | 1.26 | 1.45 | 1.11 | 2.52 | ||
| vmax (m/s) | 3.51 | 4.47 | 3.7 | 5.1 | 6.31 | 6.31 | 7.26 | 6.79 | 7.13 | 2.41 | 2.68 | 2.42 | 4.84 | ||
| vmin (m/s) | 0.7 | 0.64 | 0.76 | 1.49 | 1.39 | 1.38 | 2.24 | 1.61 | 0.87 | 0.56 | 0.59 | 0.5 | 1.06 | ||
| σ (m/s) | 0.71 | 1.25 | 0.61 | 1.08 | 1.42 | 1.41 | 1.18 | 1.45 | 1.84 | 0.46 | 0.43 | 0.44 | 1.02 | ||
| COV (%) | 42.01 | 69.83 | 32.11 | 39.56 | 43.03 | 37.01 | 25.49 | 36.71 | 71.32 | 36.51 | 29.66 | 39.64 | 41.91 | ||
| Station-III | H = 30 m | N (h) | 744 | 672 | 744 | 720 | 744 | 720 | 744 | 744 | 720 | 744 | 720 | 744 | 8760 |
| vmean (m/s) | 2.72 | 3.17 | 3.36 | 4.35 | 4.46 | 4.81 | 5.36 | 5.15 | 10.09 | 2.25 | 2.7 | 2.32 | 4.23 | ||
| vmax (m/s) | 4.16 | 6.21 | 5.14 | 7.36 | 7.55 | 8.16 | 7.59 | 13.76 | 39.2 | 3.48 | 3.69 | 3.67 | 9.16 | ||
| vmin (m/s) | 1.16 | 1.24 | 1.96 | 2.09 | 2.63 | 2.14 | 2.91 | 2.31 | 1.49 | 1.23 | 1.86 | 1.11 | 1.84 | ||
| σ (m/s) | 0.84 | 1.43 | 0.82 | 1.42 | 1.4 | 1.79 | 1.14 | 2.58 | 13.07 | 0.48 | 0.43 | 0.71 | 2.18 | ||
| COV (%) | 30.88 | 45.11 | 24.4 | 32.64 | 31.39 | 37.21 | 21.27 | 50.1 | 129.53 | 21.33 | 15.93 | 30.6 | 39.2 | ||
| H = 20 m | N (h) | 744 | 672 | 744 | 720 | 744 | 720 | 744 | 744 | 720 | 744 | 720 | 744 | 8760 | |
| vmean (m/s) | 1.96 | 2.47 | 2.64 | 3.72 | 3.84 | 4.26 | 4.79 | 4.87 | 5.97 | 1.43 | 1.82 | 1.66 | 3.29 | ||
| vmax (m/s) | 3.36 | 5.61 | 4.35 | 6.62 | 6.86 | 7.34 | 6.89 | 14.35 | 18.58 | 2.6 | 2.67 | 2.7 | 6.83 | ||
| vmin (m/s) | 0.66 | 0.79 | 1.33 | 1.65 | 2.01 | 1.56 | 2.31 | 1.73 | 1.28 | 0.76 | 0.93 | 0.86 | 1.32 | ||
| σ (m/s) | 0.73 | 1.45 | 0.82 | 1.42 | 1.42 | 1.79 | 1.09 | 2.88 | 5.33 | 0.42 | 0.36 | 0.52 | 1.52 | ||
| COV (%) | 37.24 | 58.7 | 31.06 | 38.17 | 36.98 | 42.02 | 22.76 | 59.14 | 89.28 | 29.37 | 19.78 | 31.33 | 41.32 | ||
| Wind speed (m/s) | Station-I | Station-II | Station-III | |||
|---|---|---|---|---|---|---|
| Frequency (%) | Cumulative frequency (%) | Frequency (%) | Cumulative frequency (%) | Frequency (%) | Cumulative frequency (%) | |
| 0–1 | 0.403 | 0.403 | 0.269 | 0.269 | 0.134 | 0.134 |
| 1–2 | 2.151 | 2.554 | 1.882 | 2.151 | 0.806 | 0.94 |
| 2–3 | 5.242 | 7.796 | 3.629 | 5.78 | 5.645 | 6.585 |
| 3–4 | 9.005 | 16.801 | 14.247 | 20.027 | 17.339 | 23.924 |
| 4–5 | 17.742 | 34.543 | 19.086 | 39.113 | 24.059 | 47.983 |
| 5–6 | 20.43 | 54.973 | 24.328 | 63.441 | 18.414 | 66.397 |
| 6–7 | 18.011 | 72.984 | 18.28 | 81.721 | 17.742 | 84.139 |
| 7–8 | 12.634 | 85.618 | 11.559 | 93.28 | 8.199 | 92.338 |
| 8–9 | 8.602 | 94.22 | 5.242 | 98.522 | 3.898 | 96.236 |
| 9–10 | 4.032 | 98.252 | 1.344 | 99.866 | 2.016 | 98.252 |
| 10–11 | 1.613 | 99.865 | 0 | 99.866 | 1.344 | 99.596 |
| 11–12 | 0.134 | 100 | 0.134 | 100 | 0.269 | 99.865 |
| 12–13 | - | - | - | - | 0.134 | 100 |
| Statistical methods | The Weibull parameters | Statistical test efficiency | ||||||
|---|---|---|---|---|---|---|---|---|
| k (-) | c (m/s) | RPE (%) | RMSE | MPE (%) | MAPE (%) | χ2 | R2 | |
| GM | 3.63 | 3.55 | 0.0785 | 0.0500 | 0.8283 | 4.2571 | 0.1432 | 0.9577 |
| MOM | 3.58 | 3.54 | −0.0523 | 0.0408 | −0.0394 | 0.0394 | 0.0001 | 0.9999 |
| STDM | 3.99 | 4.46 | 26.6736 | 0.9219 | 27.9826 | 27.982 | 2.2593 | 0.1542 |
| MLM | 3.5 | 3.55 | 0.0000 | 0.0000 | −0.0438 | 0.3700 | 0.0005 | 0.9998 |
| PDM | 3.11 | 3.53 | −0.7845 | 0.1581 | −0.6649 | 0.6648 | 0.0285 | 0.9917 |
| MMLM | 3.54 | 3.55 | 0.0784 | 0.0500 | 0.0723 | 0.1885 | 0.0002 | 0.9999 |
| EEM | 3.37 | 3.54 | −0.2876 | 0.0957 | 0.1507 | 2.4687 | 0.0451 | 0.9866 |
Note: Dimensionless shape factor (k) and scale factor (c) in m/s, relative percentage error (RPE), root mean square error (RMSE), mean percentage error (MPE), mean absolute percentage error (MAPE), chi-square error (χ2), analysis of variance or efficiency of the method (R2).
| Statistical methods | The Weibull parameters | Statistical test efficiency | ||||||
|---|---|---|---|---|---|---|---|---|
| k (-) | c (m/s) | RPE (%) | RMSE | MPE (%) | MAPE (%) | χ2 | R2 | |
| GM | 2.71 | 4.79 | 0.8880 | 0.1930 | 0.6250 | 1.7040 | 0.0350 | 0.9900 |
| MOM | 3.87 | 4.68 | −0.5530 | 0.1530 | −0.5420 | 0.5890 | 0.0023 | 0.9990 |
| STDM | 2.64 | 4.78 | 1.7370 | 0.2710 | 2.3310 | 3.7180 | 0.2380 | 0.9320 |
| MLM | 3.78 | 4.68 | 0.0000 | 0.0000 | −0.0560 | 0.3440 | 0.0010 | 0.9997 |
| PDM | 2.58 | 4.66 | −1.2040 | 0.2250 | −1.1870 | 1.2390 | 0.0150 | 0.9960 |
| MMLM | 3.18 | 4.67 | −0.8090 | 0.1850 | −0.9210 | 0.9540 | 0.0064 | 0.9980 |
| EEM | 3.26 | 4.73 | 0.4930 | 0.1440 | 0.6290 | 1.6220 | 0.0290 | 0.9920 |
| Statistical methods | The Weibull parameters | Statistical test efficiency | ||||||
|---|---|---|---|---|---|---|---|---|
| k (-) | c (m/s) | RPE (%) | RMSE | MPE (%) | MAPE (%) | χ2 | R2 | |
| GM | 3.11 | 2.70 | −3.8742 | 0.3120 | −4.1546 | 4.5644 | 0.1336 | 0.9787 |
| MOM | 2.82 | 2.81 | 0.0662 | 0.0408 | 0.0422 | 0.0422 | 0.0002 | 0.9999 |
| STDM | 3.4 | 3.74 | 34.2053 | 0.9278 | 40.0035 | 40.003 | 2.8453 | 0.3654 |
| MLM | 2.84 | 2.9 | 3.0463 | 0.2768 | 6.7823 | 7.0891 | 0.3063 | 0.9475 |
| PDM | 2.65 | 2.82 | 0.1324 | 0.0577 | 0.1170 | 0.2672 | 0.0003 | 0.9999 |
| MMLM | 2.84 | 2.85 | 1.5894 | 0.2000 | 3.4823 | 3.6671 | 0.0795 | 0.9865 |
| EEM | 2.88 | 2.76 | −1.8212 | 0.2140 | −1.9377 | 2.1966 | 0.0337 | 0.9945 |
| Statistical methods | The Weibull parameters | Statistical test efficiency | ||||||
|---|---|---|---|---|---|---|---|---|
| k (-) | c (m/s) | RPE (%) | RMSE | MPE (%) | MAPE (%) | χ2 | R2 | |
| GM | 4.17 | 3.88 | −1.8150 | 0.2550 | −1.5198 | 2.7444 | 0.0610 | 0.9790 |
| MOM | 3.99 | 3.94 | −0.5820 | 0.1440 | −0.5930 | 0.6490 | 0.0074 | 0.9974 |
| STDM | 4.47 | 4.83 | 22.6440 | 0.9004 | 23.8630 | 23.863 | 1.9020 | 0.1780 |
| MLM | 3.92 | 3.96 | −0.0930 | 0.0580 | −0.0920 | 0.5220 | 0.0020 | 0.9990 |
| PDM | 3.25 | 3.99 | −0.2560 | 0.0960 | −0.2560 | 0.2560 | 0.0004 | 0.9998 |
| MMLM | 3.59 | 3.98 | −6.5160 | 0.4830 | −8.3160 | 8.5270 | 2.3420 | 0.2280 |
| EEM | 4.23 | 4.39 | 11.1940 | 0.6330 | 11.7710 | 11.771 | 0.5180 | 0.7970 |
| Statistical methods | The Weibull parameters | Statistical test efficiency | ||||||
|---|---|---|---|---|---|---|---|---|
| k (-) | c (m/s) | RPE (%) | RMSE | MPE (%) | MAPE (%) | χ2 | R2 | |
| GM | 3.04 | 3.66 | 0.0254 | 0.0289 | −0.8825 | 4.4901 | 0.1568 | 0.979 |
| MOM | 3.14 | 3.62 | −0.2536 | 0.0913 | −0.1711 | 0.1711 | 0.0031 | 0.9996 |
| STDM | 3.43 | 4.95 | 35.1255 | 1.0743 | 34.5353 | 34.535 | 5.7001 | 0.0331 |
| MLM | 3.13 | 3.65 | 0.1775 | 0.0764 | 0.0826 | 0.4453 | 0.0011 | 0.9998 |
| PDM | 2.77 | 3.65 | −0.0507 | 0.0408 | −0.0311 | 0.0311 | 0.0001 | 0.9999 |
| MMLM | 3.14 | 3.64 | −1.1666 | 0.1958 | −0.8205 | 1.4034 | 0.0924 | 0.9877 |
| EEM | 2.91 | 3.66 | 0.0000 | 0.0000 | −0.449 | 2.2702 | 0.041 | 0.9945 |
| Statistical methods | The Weibull parameters | Statistical test efficiency | ||||||
|---|---|---|---|---|---|---|---|---|
| k (-) | c (m/s) | RPE (%) | RMSE | MPE (%) | MAPE (%) | χ2 | R2 | |
| GM | 2.1 | 4.71 | −0.5910 | 0.1580 | −0.5250 | 2.8630 | 0.0640 | 0.9950 |
| MOM | 3.76 | 4.45 | 0.0790 | 0.0580 | 0.1320 | 0.1650 | 0.0010 | 0.9999 |
| STDM | 2.3 | 3.73 | −21.540 | 0.9540 | −11.410 | 13.920 | 20.680 | 0.3470 |
| MLM | 3.66 | 4.5 | −0.4730 | 0.1414 | −0.3095 | 0.5340 | 0.0140 | 0.9990 |
| PDM | 2.32 | 4.74 | 1.4980 | 0.2520 | −0.0730 | 3.4630 | 0.3080 | 0.9740 |
| MMLM | 2.99 | 4.62 | 0.1580 | 0.0820 | −0.4510 | 1.9760 | 0.0580 | 0.9950 |
| EEM | 3.03 | 4.09 | −11.845 | 0.7080 | −6.0510 | 7.4310 | 5.9690 | 0.5632 |
| Statistical methods | Station-I | Station-II | Station-III | Discussion | |||
|---|---|---|---|---|---|---|---|
| 20 m | 30 m | 20 m | 30 m | 20 m | 30 m | ||
| GM | Sixth | Sixth | Fifth | Fourth | Sixth | Fourth | - |
| MOM | First | Second | First | Third | Third | First | The First choice |
| STDM | Seventh | Seventh | Seventh | Seventh | Seventh | Seventh | - |
| MLM | Third | First | Sixth | Second | Second | Second | The second choice |
| PDM | Fourth | Fourth | Second | First | First | Fifth | The third choice |
| MMLM | Second | Third | Fourth | Sixth | Fifth | Third | - |
| EEM | Fifth | Fifth | Third | Fifth | Fourth | Sixth | - |
| Month | Power law coefficient η | Measured value | Extrapolated value | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| At 20 m height | At 30 m height | At 50 m height | ||||||||
| v20 | k20 | c20 | v30 | k30 | c30 | v50 | k50 | c50 | ||
| January | 0.262 | 2.15 | 4.33 | 2.35 | 3.11 | 4.42 | 3.40 | 3.55 | 4.63 | 3.89 |
| February | 0.25 | 2.62 | 4.18 | 2.89 | 3.57 | 4.41 | 3.91 | 4.05 | 4.62 | 4.44 |
| March | 0.251 | 2.65 | 4.12 | 2.91 | 3.54 | 4.41 | 3.87 | 4.02 | 4.62 | 4.4 |
| April | 0.219 | 3.76 | 3.86 | 4.16 | 4.98 | 3.58 | 5.53 | 5.57 | 3.75 | 6.18 |
| May | 0.219 | 3.81 | 3.45 | 4.25 | 4.97 | 3.30 | 5.55 | 5.58 | 3.46 | 6.21 |
| June | 0.218 | 3.82 | 3.95 | 4.23 | 5.07 | 3.84 | 5.63 | 5.69 | 4.02 | 6.29 |
| July | 0.207 | 4.44 | 3.41 | 4.93 | 5.74 | 3.82 | 6.34 | 6.39 | 4.00 | 7.05 |
| August | 0.203 | 4.75 | 2.91 | 5.34 | 5.97 | 3.17 | 6.69 | 6.66 | 3.32 | 7.42 |
| September | 0.218 | 3.81 | 2.4 | 4.31 | 4.95 | 2.52 | 5.60 | 5.56 | 2.64 | 6.26 |
| October | 0.28 | 1.76 | 4.36 | 1.94 | 2.57 | 5.65 | 2.79 | 2.98 | 5.92 | 3.22 |
| November | 0.266 | 2.12 | 3.06 | 2.34 | 2.98 | 3.70 | 3.26 | 3.37 | 3.87 | 3.73 |
| December | 0.256 | 2.55 | 1.99 | 2.89 | 3.22 | 2.49 | 3.63 | 3.68 | 2.61 | 4.14 |
| Month | Power (W/m2) | MOM | MLM | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| k (-) | c (m/s) | P (W/m2) | RMSE | χ2 | k (-) | c (m/s) | P (W/m2) | RMSE | χ2 | ||
| January | 18.75 | 4.50 | 3.41 | 21.84 | 1.7578 | 0.9904 | 4.42 | 3.4 | 21.67 | 1.7088 | 0.9724 |
| February | 27.87 | 4.71 | 3.90 | 32.63 | 2.1817 | 4.41 | 3.91 | 33.24 | 2.3173 | ||
| March | 26.71 | 4.92 | 3.86 | 31.40 | 2.1656 | 4.41 | 3.87 | 31.96 | 2.2913 | ||
| April | 73.11 | 3.58 | 5.53 | 97.57 | 4.9457 | 3.58 | 5.53 | 97.57 | 4.9457 | ||
| May | 71.47 | 3.25 | 5.55 | 101.46 | 5.4763 | 3.3 | 5.55 | 101.04 | 5.4378 | ||
| June | 75.87 | 3.6 | 5.63 | 102.85 | 5.1942 | 3.84 | 5.63 | 101.21 | 5.0339 | ||
| July | 110.11 | 3.98 | 6.34 | 143.45 | 5.7741 | 3.82 | 6.34 | 144.7 | 5.8813 | ||
| August | 123.88 | 3.06 | 6.68 | 181.11 | 7.5651 | 3.17 | 6.69 | 179.36 | 7.4485 | ||
| September | 70.61 | 2.48 | 5.58 | 118.12 | 6.8927 | 2.52 | 5.6 | 117.25 | 6.8293 | ||
| October | 10.05 | 5.47 | 2.78 | 11.70 | 1.2845 | 5.65 | 2.79 | 11.8 | 1.3229 | ||
| November | 16.21 | 4.42 | 3.27 | 19.38 | 1.7804 | 3.7 | 3.26 | 19.82 | 1.9000 | ||
| December | 20.81 | 2.48 | 3.63 | 32.46 | 3.4132 | 2.49 | 3.63 | 32.37 | 3.4000 | ||
| Seasons | η | Measured data | Extrapolated data | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| At 20 m height | At 30 m height | At 50 m height | |||||||||||
| v20 | k20 | c20 | P20 | v30 | k30 | c30 | P30 | v50 | k50 | c50 | P50 | ||
| Winter | 0.24 | 3.19 | 3.5 | 3.55 | 26.21 | 4.22 | 3.78 | 4.7 | 59.1 | 4.76 | 3.96 | 5.27 | 83.6 |
| Spring | 0.24 | 3.01 | 4.05 | 3.32 | 20.2 | 4.03 | 4.13 | 4.4 | 48.2 | 4.55 | 4.33 | 5.01 | 68.7 |
| Summer | 0.21 | 4.02 | 3.6 | 4.47 | 48.64 | 5.26 | 3.65 | 5.8 | 108.24 | 5.89 | 3.83 | 6.52 | 157.2 |
| Autumn | 0.23 | 3.44 | 3.22 | 3.86 | 34.1 | 4.5 | 3.78 | 5.1 | 72.3 | 5.07 | 3.96 | 5.63 | 100.67 |
| Power class | Potential | Power density and wind speed at 10 m (33 ft) | Power density and wind speed at 30 m (98 ft) | Power density and wind speed at 50 m (164 ft) | |||
|---|---|---|---|---|---|---|---|
| Power (W/m2) | Speed (m/s) | Power (W/m2) | Speed (m/s) | Power (W/m2) | Speed (m/s) | ||
| Class-I | Poor | P10 ≤ 100 | ≤4.4 | P30 ≤ 160 | ≤5.1 | P50 ≤ 200 | ≤5.6 |
| Class-II | Marginal | P10 ≤ 150 | ≤5.1 | P30 ≤ 240 | ≤6.0 | P50 ≤ 300 | ≤6.0 |
| Class-III | Moderate | P10 ≤ 200 | ≤5.6 | P30 ≤ 320 | ≤6.5 | P50 ≤ 400 | ≤7.0 |
| Class-IV | Good | P10 ≤ 250 | ≤6.0 | P30 ≤ 400 | ≤7.0 | P50 ≤ 500 | ≤7.5 |
| Class-V | Very good | P10 ≤ 300 | ≤6.4 | P30 ≤ 480 | ≤7.5 | P50 ≤ 600 | ≤8.0 |
| Class-VI | Excellent | P10 ≤ 400 | ≤7.0 | P30 ≤ 640 | ≤8.2 | P50 ≤ 800 | ≤8.8 |
| Class-VII | Excellent | P10 ≤ 1000 | ≤9.4 | P30 ≤ 1600 | ≤11.0 | P50 ≤ 2000 | ≤11.9 |
| Seasons | VFmax (m/s) | VEmax (m/s) | Energy density, ED (kW/m2) | Total energy intensity, EDT (kW/m2) |
|---|---|---|---|---|
| Winter | 4.31 | 5.24 | 0.0586 | 129.408 |
| Spring | 4.15 | 4.88 | 0.0492 | 105.082 |
| Summer | 5.35 | 6.58 | 0.1148 | 253.531 |
| Autumn | 4.64 | 5.63 | 0.0728 | 160.667 |
| Yearly mean | 4.31 | 5.24 | 0.0586 | 513.412 |
| Seasons | Numerical integration | |||
|---|---|---|---|---|
| Trapezoidal sums | Simpson's rule | |||
| Capacity factor, CF | Total energy output, ET (MW·h) | Capacity factor, CF | Total energy output, ET, (MW·h) | |
| Winter | 0.1238 | 5.4689 | 0.1238 | 5.4689 |
| Spring | 0.0920 | 3.9283 | 0.0920 | 3.9283 |
| Summer | 0.3010 | 13.2937 | 0.3010 | 13.2938 |
| Autumn | 0.1698 | 7.5005 | 0.1698 | 7.5005 |
| Yearly mean | 0.1238 | 21.6973 | 0.1238 | 21.6974 |
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Azad, A.K.; Rasul, M.G.; Yusaf, T. Statistical Diagnosis of the Best Weibull Methods for Wind Power Assessment for Agricultural Applications. Energies 2014, 7, 3056-3085. https://doi.org/10.3390/en7053056
Azad AK, Rasul MG, Yusaf T. Statistical Diagnosis of the Best Weibull Methods for Wind Power Assessment for Agricultural Applications. Energies. 2014; 7(5):3056-3085. https://doi.org/10.3390/en7053056
Chicago/Turabian StyleAzad, Abul Kalam, Mohammad Golam Rasul, and Talal Yusaf. 2014. "Statistical Diagnosis of the Best Weibull Methods for Wind Power Assessment for Agricultural Applications" Energies 7, no. 5: 3056-3085. https://doi.org/10.3390/en7053056





