Development of an Indoor Airflow Energy Harvesting System for Building Environment Monitoring
Abstract
: Wireless sensor networks (WSNs) have been widely used for intelligent building management applications. Typically, indoor environment parameters such as illumination, temperature, humidity and air quality are monitored and adjusted by an intelligent building management system. However, owing to the short life-span of the batteries used at the sensor nodes, the maintenance of such systems has been labor-intensive and time-consuming. This paper discusses a battery-less self-powering system that converts the mechanical energy from the airflow in ventilation ducts into electrical energy. The system uses a flutter energy conversion device (FECD) capable of working at low airflow speeds while installed on the ventilation ducts inside of buildings. A power management strategy implemented with a circuit system ensures sufficient power for driving commercial electronic devices. For instance, the power management circuit is capable of charging a 1 F super capacitor to 2 V under ventilation duct airflow speeds of less than 3 m/s.1. Introduction
Energy-efficient environment management has attracted much research interest in recent years. In the United States, residential and office buildings account for nearly 70% of the electric energy consumption and nearly 40% of CO2 emissions [1]. Much of this energy consumption can however be eliminated by monitoring and adjusting indoor illumination, temperature, humidity and CO2 levels. For instance, the utilization of intelligent wireless sensor nodes is estimated to reduce energy usage by about 20% [2]. However, in practice, the performance of wireless sensor networks (WSN) is severely limited by the fact that the sensor nodes need to be recharged every several months because the associated batteries are discharged rapidly as a consequence of the relatively high power consumption of the microprocessors, transceivers, etc. used in the system. Furthermore, recharging of batteries is not a trivial exercise as the sensor nodes are typically embedded into building structures. These problems could however be avoided by incorporating energy harvesting technologies capable of autonomously scavenging energy from various ambient energy resources.
Photovoltaic (PV) cells have been widely used for outdoor solar energy harvesting in recent years. In general, there are three types of commercial PV cells: monocrystalline silicon PV, polycrystalline PV, and amorphous silicon PV. Monocrystalline silicon PV cells have efficiencies in the range 13%∼17%, polycrystalline silicon PV cells have a little less efficiency (11%∼15%), and amorphous silicon PV cells have even lower efficiencies (6%∼8%). However, under typical indoor lighting conditions (1∼5 W/m2 light intensity conditions), monocrystaline PV cells have an efficiency of less than 1%∼3%, while amorphous PV cells are more sensitive to different wavelengths, so the latter exhibit higher efficiencies (3%∼7%). This means that the photovoltaic cells can provide a power density ranging from 0.1 to 0.3 mW/cm2 under indoor artificial illumination conditions [3]. In view of the typically constant illumination conditions of indoor applications, the maximum power point can be easily determined and the maximum power point tracking circuit in the power management system can be simplified substantially.
Another attractive indoor harvesting technique is to use a thermal energy generator (TEG). A TEG device can produce a voltage across temperature gradient based on the Seebeck effect. The available indoor temperature differences include those between a human body and the surrounding cold air or between a warm indoor environment and the cold outdoors. However, a significant disadvantage of a thermal generator is that the useful part of heat is limited by Carnot factor (η = ΔT/Th), where ΔT = Th − Tl is the temperature difference across the thermoelectric, Th is the higher temperature of the inlet, and Tl is the lower temperature of the outlet. Several researchers have recently suggested methods of improving the output efficiencies of thermalelectric devices [4–7].
Mechanical vibrations also can be utilized as an indoor energy source. Theoretically, any kind of vibration source can be transformed into electric power [8]. There are three basic techniques for this kind of conversion: piezoelectric transducers—energy is induced by the deformation of piezoelectric materials, like PZT ceramics, PVDF films and piezoelectric composite fibers [9]; spring-mass electromagnetic transducers—energy is generated between a moving magnet and a coil based on Faraday's law [10–12]; and electrostatic transducers—energy is generated by charged vibrating capacitor electrodes [13,14].
Other available ambient energy sources include acoustic noise, electromagnetic waves and magnetic field. Compared with outdoor energy harvesting methods, indoor ambient energy sources are much weaker and are largely dependent on the building environment. Table 1 summarizes the capabilities of some commonly used indoor energy sources for powering wireless sensor networks [15].
This paper describes an energy harvesting technology that is different from all the technologies described above. Specifically, it utilizes the flutter energy of airflow in household ventilation ducts. “Flutter” is an aerodynamic phenomenon where self-exited oscillations are amplified by positive feedback between an elastic structure and aerodynamic forces. Structural flutter takes place when the instability limit is exceeded, so the airflow energy is extracted by the oscillating structure. The mechanism of using aeroelastic flutter to extract mechanical energy from airflow in outdoor conditions has been discussed in our prior publication in 2012 [16]. Details of the mechanical design of our flutter energy conversion system are provided in [16]. This paper presents our results in converting flutter energy induced by indoor duct flows into useful electrical energy. We note that other researchers have also reported using elastic devices to harvest energy from airflows in the past decade [17,18]. In most buildings, air velocities need to be within certain limits to avoid pressure loss and to reduce noise. The air velocity in flow ducts is usually in the range 1.8–4 m/s in hospitals and 2.0–4.5 m/s in offices. More details on commonly accepted duct velocities are given in Table 2 [19].
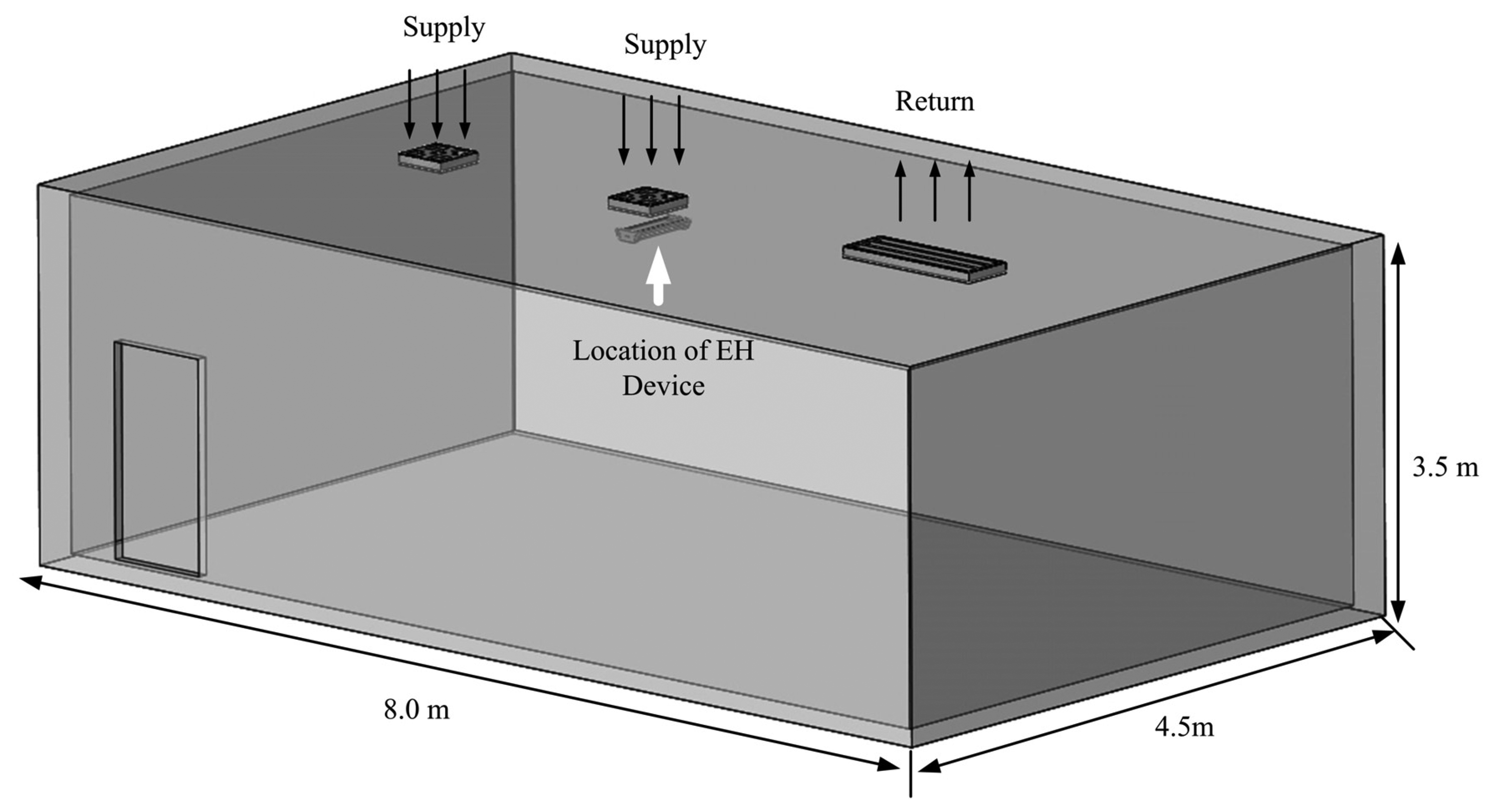
In this study, the airflow from a 0.5 m × 0.5 m duct (with airflow speed of ∼3 m/s) was used to generate electrical power in a laboratory setting (see Figure 1). The air supplies and returns are connected to the central air conditioning system in the building. An air strainer operates in the air return to prevent the absorption of excessive pollution from blocking the ventilation duct, while a filter reduces airflow speed around the air return duct, thus reducing the outflow speed. As a result, the optimum location for the flutter device is close to the air supply ducts.
In our prototype, the tensile belt is driven by low speed airflow (i.e., ∼3 m/s) in the air duct, which then shakes the electromagnetic resonator at the same frequency (see Figure 2). The oscillation frequency of the belt is not only influenced by the airflow speed, but can also be controlled by the tension force on the belt.
Experiments have shown that low speed airflow requires a smaller tension force. The maximum harvested power is achieved when the oscillation frequency matches the natural frequency of the electromagnetic resonator. A power condition/management circuit is used to rectify the induced voltage and charge the super capacitors so the latter can supply the power needed by distributed sensor nodes. A systematic modeling and analysis coupling the aerodynamic input motion to electrical energy output will be presented in following sections.
2. Demonstration of Self-Excited Aerodynamic Flutter Harvester
2.1. Study of Aerodynamic Flutter Instability
Research on the instability of long flexible structures had started as early as in the late 19th and early 20th centuries, when a number of long-span suspension bridges were built in the US. As it turned out, many of them met with instability problems precipitated by aerodynamic forces and wind turbulence. In particular, the wind-induced collapse of Tacoma Narrows Bridge prompted a flurry of research on wind-flutter instability and self-excited aerodynamic forces. For instance, Bleich conducted a series of wind tunnel experiments on Tacoma Narrows [20]. Pugsley proposed a framework for the measurement of aerodynamic forces associated with the bridge flutter problem [21]. Later during the 1960s, Ukeguchi et al. analyzed both lift and moment to vertical pitch and torsion coupled flutter [22]. Scanlan established the classic aerodynamic flutter theory with two-dimensional smooth airflow and the force is considered proportional to the displacement [23]. In Scanlan's theory, the method to implement such analysis is defined as the interaction between airflow and the body perpendicular to the direction of airflow, so the body motion could be simplified as:
The unsteady aerodynamic force acting on a bluff body can be represented with the aerodynamic coefficients expressed as a function of reduced frequency. The aerodynamic force simultaneously causes both a vertical and a torsional motion of the structure.
Figure 3 illustrates the aerodynamic forces contributing to flutter: a vertical lift force, L, as well as a pitching moment, M, are induced by the interaction between airflow, U, and oscillations in the structure. The fluid-structure interaction which results in the flutter motion can be represented as:
Substituting with the terms for the critical damping ratios, ξh and ξα, and the natural resonant frequencies, ωh and ωα, Equation (1) can be rewritten as:
However, the estimation of the critical damping ratio and the natural resonant frequencies is difficult in practice. Such difficulties can be avoided by using Scanlan's linearized equations between the forces and the motion using the flutter derivatives [24]:
In Equation (4), the terms related to ḧ, α̈ and h are usually ignored because of their negligible influences on L and M. The coefficients, Hi and Ai, are called the “flutter derivatives” and can be estimated experimentally from cross sectional studies conducted in a wind tunnel. The flutter derivatives are decided mainly by the wind speed and structure contours. Considering the similarity between the belt and ideal thin plate, these self-excited forces can be rewritten as:
To analyze the vibration amplitude and frequency of the fluttering belt, a high speed camera (PCO 1200S, PCO AG, Kelheim, Germany) image-capturing system was used to measure its vertical displacement h and angle displacement α (see Figure 4a). The high speed camera captured a series of pictures at 5 ms intervals when the belt oscillates. The displacement and pitch angle of the fluttering belt could thus be measured by comparing the states of these pictures (see Figure 4b,c). Note that the maximum angle of attack and displacement will be different when an EMG resonator is loaded.
2.2. Analysis of Flutter with Fluid–Structure Interaction
For most flutter-related applications (wind bridge engineering, airfoil designs, etc.), the thin plate theory is too simplistic to be able to solve airflow-induced oscillation problems associated with complicated structural contours. However, progress in computational fluid dynamics and computer technologies has allowed effective flutter derivative identification. Figure 5 illustrates the numerical problem domains associated with 2D flutter: (i) the fluid domain occupied by incompressible flows; (ii) the structural domain associated with the elastic belt/plate; and (iii) the interface region, including inlet and outlet.
The dependent variables for this solution domain include pressure p and the fluid particle velocity vector u = {u,v,w}T, where x, y and z are the Cartesian directions. To simplify the problem, the fluid flow is assumed to be laminar and Newtonian, and the constant air density ρ is 1.225 kg/m3. We have conduted 2D simulations by using COMSOL Multiphysics to determine the aerodynamic parameters around the belt during the flutter process. The belt width was set at 25 mm, corresponding to the experiments. The belt's attack angle was varied to visualize the 2D idealized flow and pressure distribution. When the airflow speed was 2.8 m/s and the attack angle was 0°, the laminar flow was lightly disturbed while passing through the belt (see Figure 6a which shows the velocity field around the flexible belt). When the attack angle was increased to 15°, turbulent flow appears, and the flow velocity around the top layer becomes less than that at the bottom layer (see Figure 6b). The pressure difference also increased between the top and bottom layers, which resulted in torsion and lift forces, as observed during experiments. Figure 7 shows further details concerning the pressure difference arising when the attack angle was varied from 0° to 15°.
2.3. Model of Electromagnetic Transducer with Fixed Coils
An electromagnetic generator (EMG) model using static coils is illustrated in Figure 8. In contrast to the electromagnetic resonator with moving coils [25], the permanent magnet attached to a spring is excited by the external force F. The motion of the mass induces a voltage, V, in the coils and provides electric power to the load, RL. The total force on the magnetic mass includes:
| Mass weight: | W; |
| Excitation force: | F; |
| Spring force: | Fspring = −kx; |
| Damping friction force: | |
| Electromagnetic force: | FEM = −NBli; |
The kinematic equation for an EMG with fixed coils then becomes:
Rearranging, the electromagnetic force, FEM, can be expressed as:
The average flux density, B, can be measured using a Gauss meter (Model GM1A, AML, Baltimore, MD, USA); Ks is the spring constant; Kf is the friction constant. Thus, the electric power can be directly calculated by the work performed by the electromagnetic force:
2.4. Dynamic Simulations with Aerodynamic Flutter Model and EMG Model
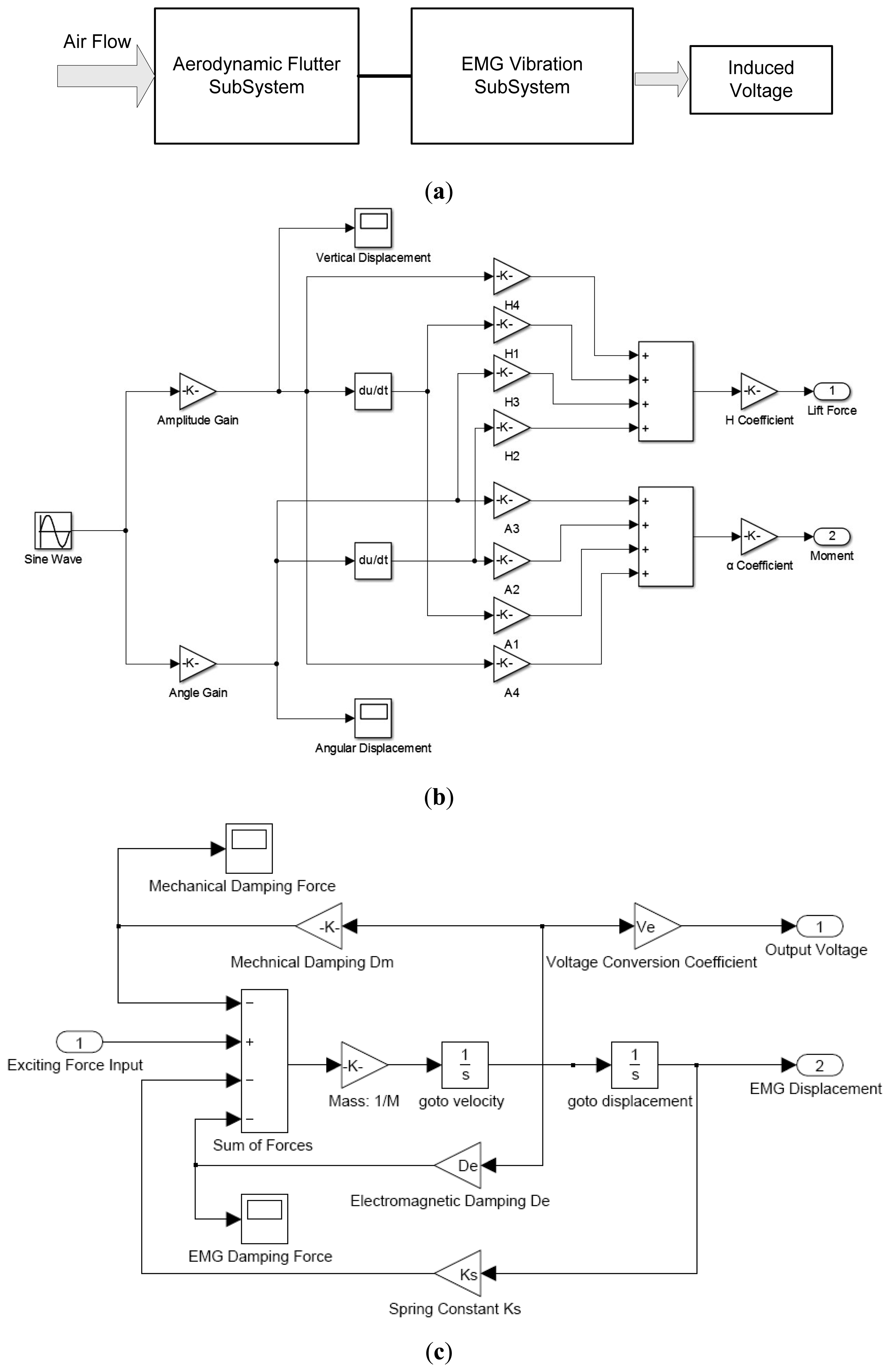
Following the availability of the flutter belt model and the linear EMG model, the entire energy harvesting system could be simulated using MATLAB® Simulink (Math Works Inc., Natick, MA, USA), as illustrated in Figure 9. From the aerodynamic flutter equations, it was evident that the performance of the entire energy harvesting system is dominated by the magnitude of the airflow velocity.
Since the stable flutter has been proven to be a sinusoidal motion as shown in Equation (1), we used a unit sinusoidal signal as the input of flutter for the Simulink model (the frequency of sinusoidal signal is decided by the output-induced voltage with oscilloscope, and the amplitude and angle were determined by high speed camera images). The most important parameters A1, A2, A3, A4, H1, H2, H3, and H4, i.e., “flutter derivatives”, could be calculated by introducing the thin plate assumption into classic flutter theory (which has been discussed in our prior work [16]). With the measured wind speed, observed flutter amplitude and angle, and calculated flutter coefficients, we could approximate the aerodynamic force and moment generated by the fluttering belt. As shown in Figure 9b, the “flutter derivatives” are required in the Simulink model in order to determine the output lift force and moment due to the sinusoidal input. The flutter model in Figure 9b was derived from Equation (5), and the flutter derivatives related terms defined as follows:
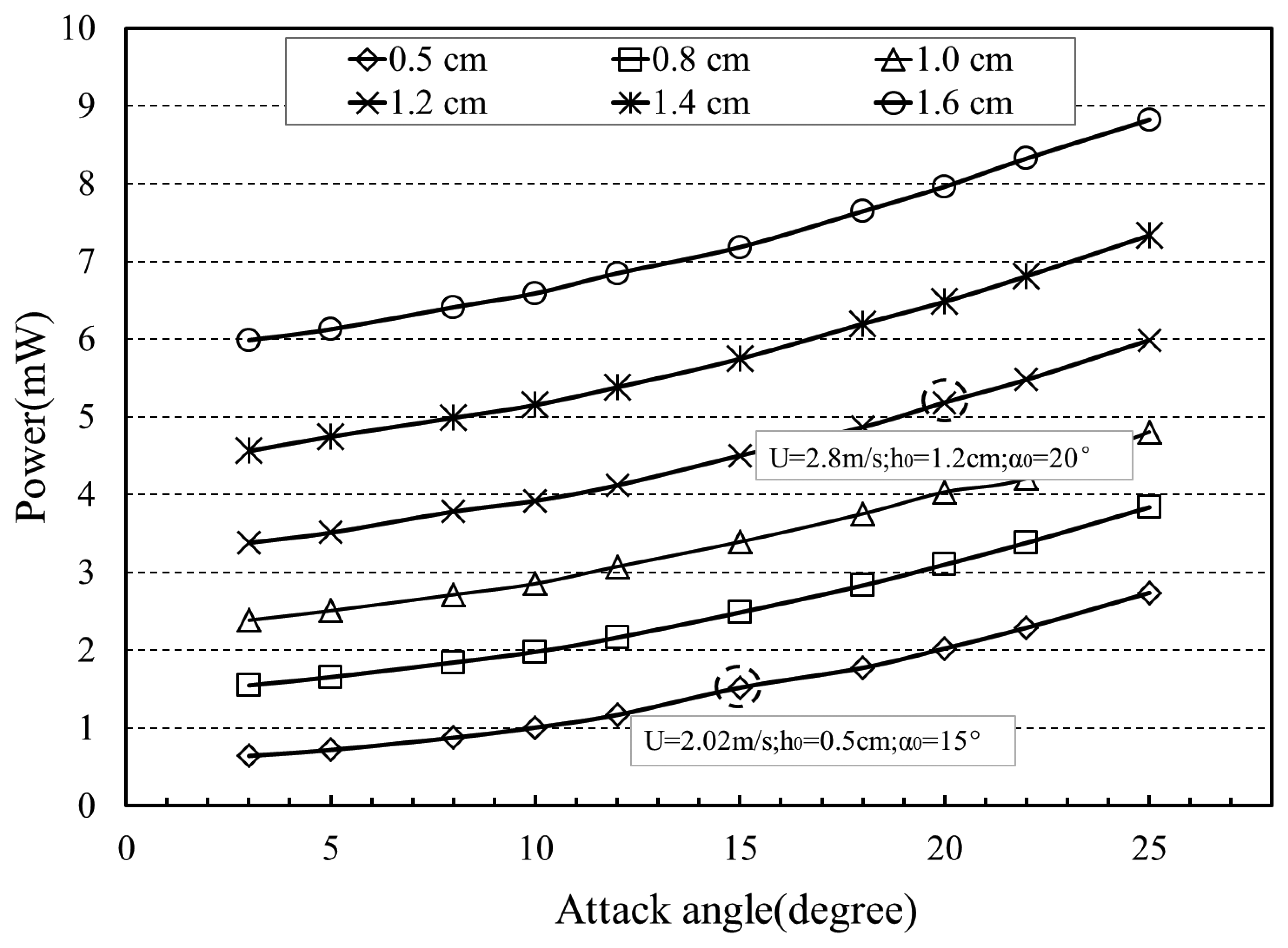
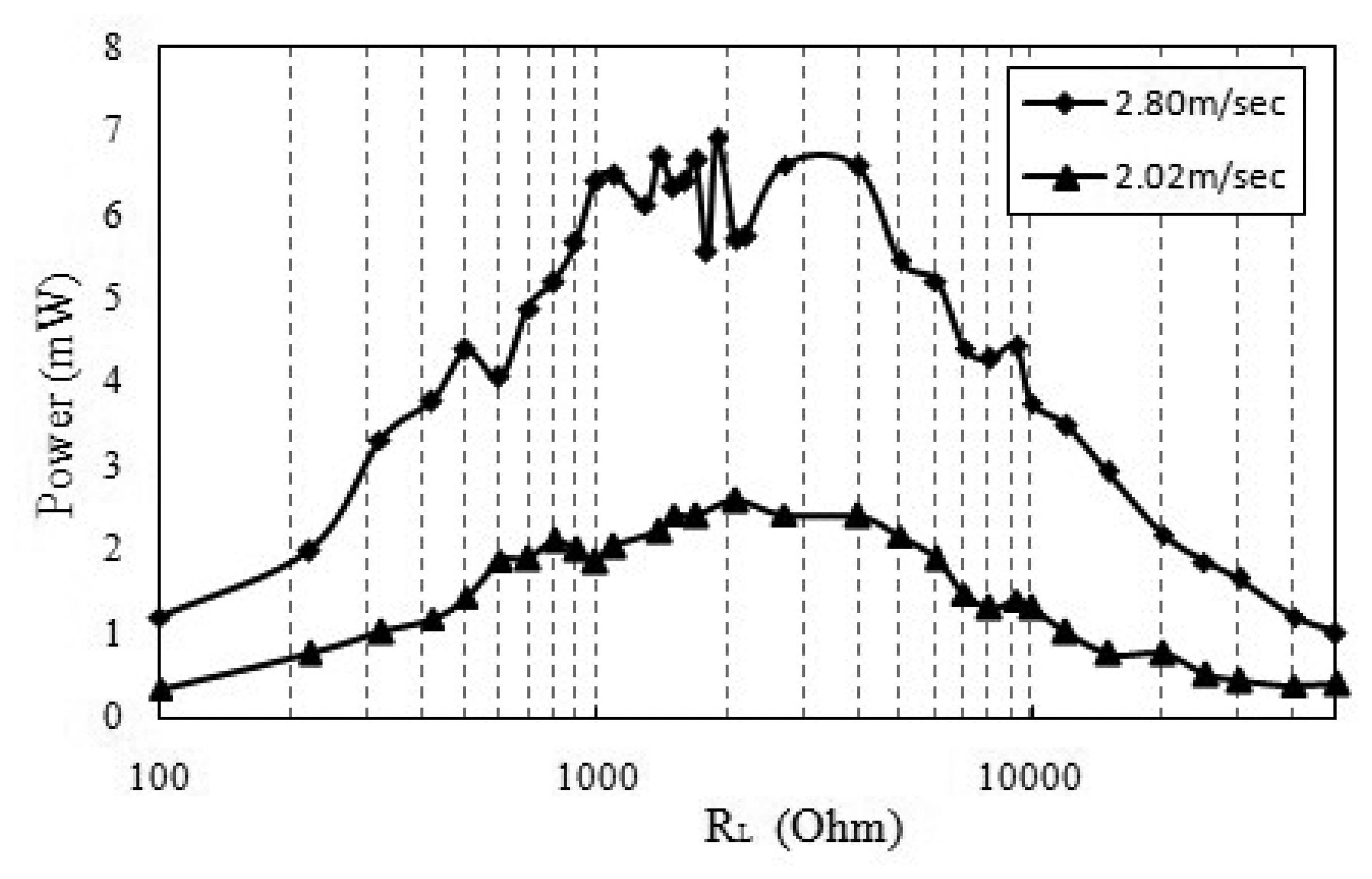
Once the airflow settled down, the vertical displacement and the angular displacement were imported into the Simulink model, so the output voltage across the 1 kΩ load resistance could be calculated (see Figure 10). Based on this load resistance and the corresponding voltage difference, the available output electrical power could be estimated as 1.62 mW (at 2.02 m/s, h0 = 0.5 cm, α0 = 15°) and 5.12 mW (at 2.80 m/s, h0 = 1.2 cm, α0 = 20°). These simulation results were validated against our experimental data (see Figure 11) as shown in Table 3. From the comparison between experimental and simulation data, we find that the experimental data is about 20% higher than the simulation results. This difference can be attributed to the simplification of our simulation model, i.e., we only introduced the upward and downward lift force into the electromagnetic model without considering the torsional moments, which could contribute additional mechanical energy input into the energy conversion system. However, the simulation results do reflect the trend and order-of-magnitude of the input-output relationship of the system, and could be used as a reference for next-generation designs with different amplitudes and attack angles.
3. Power Management and Performance of Indoor Duct Generator
Our system described in this paper is composed of two parts: (1) a flutter belt to transform the airflow into vibration energy, and (2) the electromagnetic resonator to convert the vibrations into electrical energy. The design rules of electromagnetic generator have been discussed by others already (e.g., see Roundy [26] and Beeby, et al. [8]). The potential power harvesting capabilities for typical ambient energy sources is provided as follows. Ambient light could provide a power density of ∼100mW/cm2 for a device directed towards bright sunlight, and ∼100 μW/cm2 for a device illuminated by office light. The power density of thermoelectric device is about 60 μW/cm2; the power density of vibration source is from 4 μW/cm3 (human motions) to 800 μW/cm3 (machines) [27]. The volume of the core of our electromagnetic resonator (as shown in Figure 8) is about 15 cm3, which could provide nearly 7 mW of electrical power according to Figure 11. Hence, the output power density of our system described in this paper is about 445 μW/cm3.
3.1. Design Considerations Associated with Ambient Energy Harvesting Management Circuits
Power management is an important issue associated with most ambient energy harvesting technologies. If the system is a battery powered system, the current and voltage are stable and can be anticipated, so the power management circuit seeks mainly to extend the lifetime of the battery. In the case of an energy harvesting technology, most ambient sources are unable in providing high enough current or voltage for synchronous power consumption, so the strategy is based on “duty-cycle” work principle, which means accumulating energy in a temporary energy buffer to enable utilization as bursts over short periods. Thus the main functions of an ambient energy harvesting power management circuit include amplifying the voltage generated, storing and releasing buffered energy, and regulating the voltage to satisfy the requirements of electronic devices served. Figure 12 schematically illustrates the power management circuits used in our indoor airflow energy harvesting devices. The important parts of this circuit system are described below.
Voltage Multiplier: The voltage multiplier increases the lower-voltage of alternating current for high-voltage input needs. It is widely used in energy harvesting circuits since it cannot only increase the input voltage, but also work as a rectifier. Depending on the layers of the voltage multiplier, it can be a voltage doubler, a voltage tripler, a voltage quadrupler, and so forth. Our prototype uses a doubler as the original output voltage of electromagnetic resonator is about 1∼5 volts.
Super Capacitor: Although a rechargeable battery continues to be the first choice for embedded energy storage solutions, an alternative choice is the super capacitor. Unlike regular capacitors, a super capacitor provides much higher capacitance within a small package. Compared with batteries, super capacitors have the disadvantage of having a smaller energy density, but have a higher power density which could shorten the charging and discharging times at higher currents. Also, super capacitors have longer life time, i.e., charge-discharge cycles, than batteries (many thousands of times vs. only 1,000 times). Another advantage is that the charging circuit for a super capacitor is much simpler than that needed by a battery; the charging procedure for batteries always requires constant current and an over-charging protective circuit.
DC–DC Converter: A DC–DC converter converts one direct input current into another stepped-up or stepped-down output. However, most IC-packaged DC–DC converters require a minimum input voltage and have constraint on maximum output current, so these parameters should be the most important design factors for ambient harvester capability and electronics consumption estimation.
3.2. Charging Ability of Indoor Duct Harvester
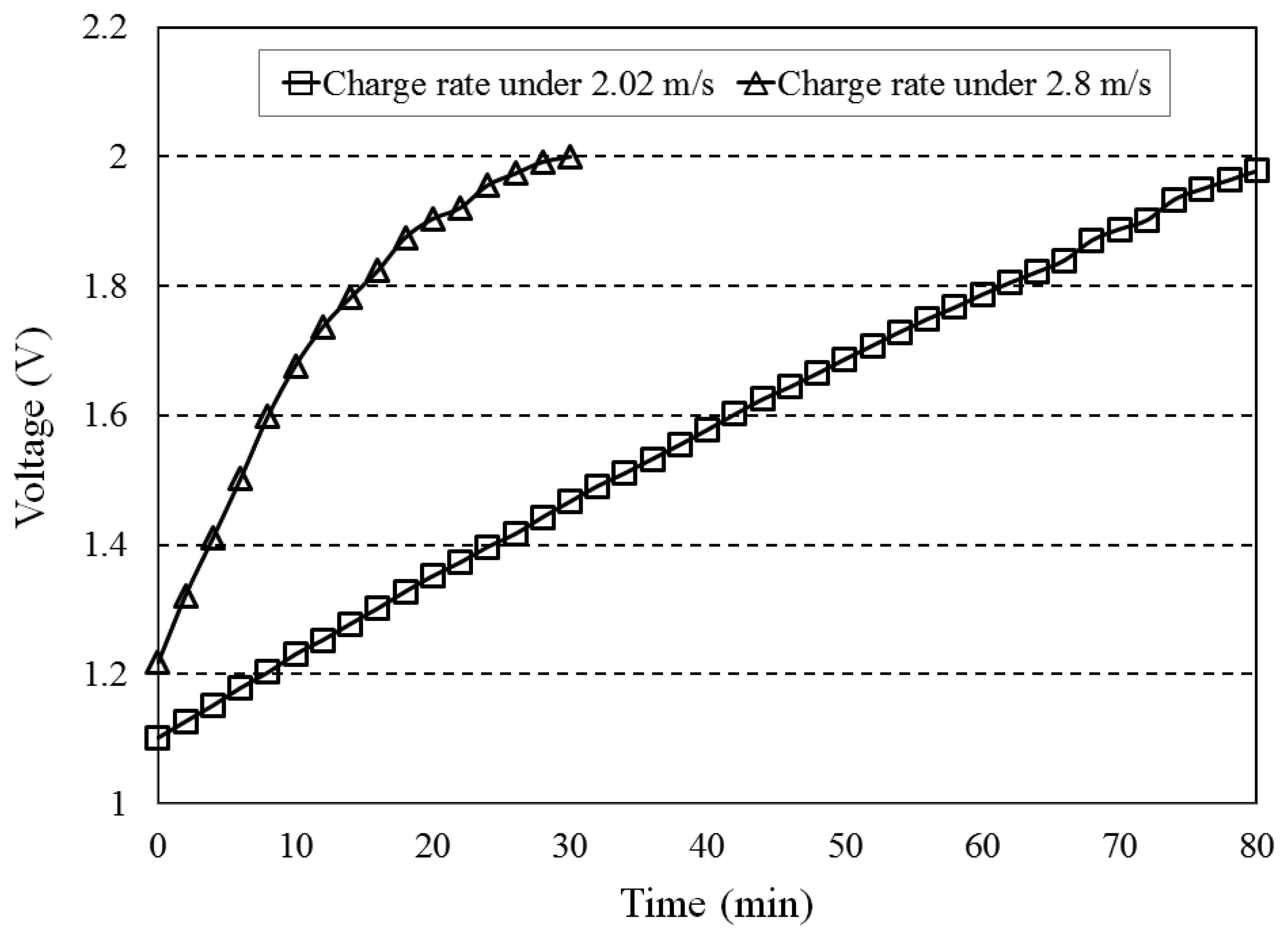
In many office buildings, the airflow speed in the ducts is limited to less than 5 m/s. For instance, the size of the air return duct in our office is 0.5 m × 0.5 m and only gives a maxium airflow speed of ∼3 m/s, which limits the power output for the indoor airflow energy harvesting system. As shown in Figure 13, when the output power of the system is used to charge a 1 F super capacitor directly, it takes nearly 30 min to charge a super capacitor to2.0 V under the airflow speed of 2.8 m/s. When the airflow speed drops to 2.02 m/s, it will take more than 80 min to charge up the super capacitor.
Figure 14 shows the operating process flow of the power management circuit. When the voltage of the super capacitor Vcap reaches 2.0 V, the output of the charge pump (Model S-852Z, Seiko Instruments Inc., Chiba, Japan) connects to the super capacitor and begins discharging, as shown in Figure 14a. The output voltage of the charge pump, Vpout, always stays at zero during the charging step. No current leakage means that there is no energy loss during the charging process. In addition, when the input of the DC–DC converter (Model MAX757, Maxim Integrated, San Jose, CA, USA) detects a high voltage at the output port of the charge pump, the converter starts working and it changes the output voltage Vdout from 0 V to 3.3 V (see Figure 14b). The voltage across the super capacitor Vcap decreases slowly as the load consumes electrical energy. When Vcap drops to 1.5 V, the discharge process ends, the output voltage of the charge pump falls back to 1.2 V and the DC–DC converter stops working. Then another charging cycle is initiated, as shown in Figure 14c,d.
4. Conclusions
This paper has introduced an aerodynamic flutter-based energy conversion device driven by the airflow in an indoor ventilation duct. A coupled model using an aerodynamic flutter model and a linear EMG model are presented and simulated using the Matlab® Simulink software. The electrical power generated is estimated using a coupling model with airflow speed and the flutter displacement as input variables. A power management circuit with a super capacitor, a charge pump and a DC–DC converter is integrated to store the harvested energy and to support applications requiring power at the mW-level. The charging rate of the super capacitor and the energy harvesting efficiency are found to depend essentially on the ventilation duct airflow speed.
Acknowledgments
This research is supported by a grant from the Natural Science Foundation of Guangdong Province, China (S2012040007657) and a Shenzhen Science and Technology Research Grant (JCYJ20120618140504947). We also want to thank the Department of Mechanical and Automation Engineering of The Chinese University of Hong Kong for partially supporting the work reported in this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- U.S. GreenBuilding Council. Available online: http://www.usgbc.org (accessed on 4 December 2013).
- O'Donnell, J. Specification of an information delivery tool to support optimal holistic environmental and energy management in buildings. Proceedings of the 3rd National Conference of IBPSA-USA, Berkeley, CA, USA, 30 July–1 August 2008.
- Nasiri, A.; Zabalawi, S.A.; Mandic, G. Indoor power harvesting using photovoltaic cells for low-power applications. IEEE Trans. Ind. Electron. 2009, 56, 4502–4509. [Google Scholar]
- Lhermet, H.; Condemine, C.; Plissonnier, M.; Salot, R.; Audebert, P.; Rosset, M. Efficient power management circuit: From thermal energy harvesting to above-IC microbattery energy storage. IEEE J. Solid-St. Circuits 2008, 43, 246–255. [Google Scholar]
- Carlson, E.J.; Strunz, K.; Otis, B.P. A 20 mV input boost converter with efficient digital control for thermoelectric energy harvesting. IEEE J. Solid-St. Circuits 2010, 45, 741–750. [Google Scholar]
- Xie, J.; Lee, C.; Feng, H. Design, fabrication, and characterization of CMOS MEMS-based thermoelectric power generators. J. Microelectromechan. Syst. 2010, 19, 317–324. [Google Scholar]
- Tan, Y.K.; Panda, S.K. Energy harvesting from hybrid indoor ambient light and thermal energy sources for enhanced performance of wireless sensor nodes. IEEE Trans. Ind. Electron. 2011, 58, 4424–4435. [Google Scholar]
- Beeby, S.P.; Tudor, M.J.; White, N. Energy harvesting vibration sources for microsystems applications. Meas. Sci. Technol. 2006, 17, R175. [Google Scholar]
- Swallow, L.; Luo, J.; Siores, E.; Patel, I.; Dodds, D. A piezoelectric fibre composite based energy harvesting device for potential wearable applications. Smart Mater. Struct. 2008, 17, 025017. [Google Scholar]
- Beeby, S.P.; Torah, R.; Tudor, M.; Glynne-Jones, P.; O'Donnell, T.; Saha, C.; Roy, S. A micro electromagnetic generator for vibration energy harvesting. J. Micromechan. Microeng. 2007, 17, 1257–1265. [Google Scholar] [CrossRef]
- Saha, C.; O'Donnell, T.; Wang, N.; McCloskey, P. Electromagnetic generator for harvesting energy from human motion. Sens. Actuators A: Phys. 2008, 147, 248–253. [Google Scholar]
- Yang, B.; Lee, C.; Xiang, W.; Xie, J.; He, J.H.; Kotlanka, R.K.; Low, S.P.; Feng, H. Electromagnetic energy harvesting from vibrations of multiple frequencies. J. Micromechan. Microeng. 2009, 19, 035001. [Google Scholar]
- Torres, E.O.; Rincón-Mora, G.A. Electrostatic energy-harvesting and battery-charging CMOS system prototype. IEEE Trans. Circuits Syst. I 2009, 56, 1938–1948. [Google Scholar]
- Suzuki, Y.; Miki, D.; Edamoto, M.; Honzumi, M. A MEMS electret generator with electrostatic levitation for vibration-driven energy-harvesting applications. J. Micromechan. Microeng. 2010, 20, 104002. [Google Scholar]
- Colomer-Farrarons, J.; Miribel-Catala, P.; Saiz-Vela, A.; Samitier, J. A multiharvested self-powered system in a low-voltage low-power technology. IEEE Trans. Ind. Electron. 2011, 58, 4250–4263. [Google Scholar]
- Fei, F.; Mai, J.D.; Li, W.J. A wind-flutter energy converter for powering wireless sensors. Sens. Actuators A: Phys. 2012, 173, 163–171. [Google Scholar]
- Tang, L.; Païdoussis, M.P.; Jiang, J. Cantilevered flexible plates in axial flow: Energy transfer and the concept of flutter-mill. J. Sound Vib. 2009, 326, 263–276. [Google Scholar]
- Li, S.; Lipson, H. Vertical-stalk flapping-leaf generator for wind energy harvesting. Proceedings of the Conference on Smart Materials, Adaptive Structures and Intelligent Systems, Oxnard, CA, USA, 21–23 September 2009.
- Engineering Toolbox. Available online: http://www.engineeringtoolbox.com (accessed on 4 December 2013).
- Bleich, F. Dynamic instability of truss-stiffened suspension bridges under wind action. Trans. Am. Soc. Civ. Eng. 1949, 114, 1177–1222. [Google Scholar]
- Pugsley, A. Some experimental work on model suspension bridges. Struct. Eng. 1949, 27, 327–347. [Google Scholar]
- Ukeguchi, N.; Sakata, H.; Nishitani, H. An investigation of aeroelastic instability of suspension bridges. Proceedings of the Suspension Bridges Symposium, Lisbon, Portugal, 7–11 November 1966.
- Scanlan, R. The action of flexible bridges under wind, I: Flutter theory. J. Sound Vib. 1978, 60, 187–199. [Google Scholar]
- Scanlan, R.H.; Tomo, J. Air foil and bridge deck flutter derivatives. J. Soil Mechan. Found. Div. 1971, 97, 1717–1737. [Google Scholar]
- Beeby, S.; Tudor, M.; Torah, R.; Roberts, S.; O'Donnell, T.; Roy, S. Experimental comparison of macro and micro scale electromagnetic vibration powered generators. Microsyst. Technol. 2007, 13, 1647–1653. [Google Scholar]
- Roundy, S. On the effectiveness of vibration-based energy harvesting. J. Intell. Mater. Syst. Struct. 2005, 16, 809–823. [Google Scholar]
- Paradiso, J.A.; Starner, T. Energy scavenging for mobile and wireless electronics. IEEE Pervasive Comput. 2005, 4, 18–27. [Google Scholar]









| Energy Sources | Power Density | Harvesting Methods |
|---|---|---|
| Ambient Light | 100 μW/cm2 (illumination office) | Indoor solar cells |
| 100 mW/cm2 (toward bright sunlight) | Solar cells | |
| Vibrationa | 4 μW/cm3 (Human motion Hz range) | Piezoelectric |
| Electrostatic | ||
| 800 μW/cm3 (Machine-kHz) | ||
| Electromagnetic | ||
| Temperature | Human 25–60 μW/cm2 | Thermal electric |
| Industry 10 mW/cm2 | ||
| Radio Frequency (RF) | GSM 4 μW/cm2 | Coupling coils |
| WiFi 0.001 mW/cm2 |
| Service | Velocity—(m/s) | |
|---|---|---|
| Public Buildings | Industrial Plant | |
| Air intake from outside | 2.5–4.5 | 5.0–6.0 |
| Heater connection to fan | 3.5–4.5 | 5.0–7.0 |
| Main supply ducts | 5.0–8.0 | 6.0–12.0 |
| Branch supply ducts | 2.5–3.0 | 4.5–9.0 |
| Supply registers and grilles | 1.2–2.3 | 1.5–2.5 |
| Main extract ducts | 4.5–8.0 | 6.0–12.0 |
| Branch extract ducts | 2.5–3.0 | 4.5–9.0 |
| Airflow Velocity | Amplitude/Attack Angle | Load Resistance | Output Power (Experiments) | Output Power (Simulation) |
|---|---|---|---|---|
| 2.02 m/s | h0 = 0.5 cm; α0 = 15° | 1,000 Ohm | 1.74 mW | 1.62 mW |
| 2.80 m/s | h0 = 1.2 cm; α0 = 20° | 1,000 Ohm | 6.32 mW | 5.12 mW |
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Fei, F.; Zhou, S.; Mai, J.D.; Li, W.J. Development of an Indoor Airflow Energy Harvesting System for Building Environment Monitoring. Energies 2014, 7, 2985-3003. https://doi.org/10.3390/en7052985
Fei F, Zhou S, Mai JD, Li WJ. Development of an Indoor Airflow Energy Harvesting System for Building Environment Monitoring. Energies. 2014; 7(5):2985-3003. https://doi.org/10.3390/en7052985
Chicago/Turabian StyleFei, Fei, Shengli Zhou, John D. Mai, and Wen Jung Li. 2014. "Development of an Indoor Airflow Energy Harvesting System for Building Environment Monitoring" Energies 7, no. 5: 2985-3003. https://doi.org/10.3390/en7052985





