A Method for Balancing a Single-Phase Loaded Three-Phase Induction Generator

Abstract

When a three-phase induction generator (IG) supplies unbalanced loads, its terminal voltages and line currents are also unbalanced, which may cause the IG to overheat and need to be derated. A single-phase loaded self-excited induction generator (SEIG) works under most unfavorable load unbalance conditions. This paper proposes a three-capacitor circuit scheme and a method to find the values of the self-excitation capacitors that allow the SEIG to be balanced. The SEIG is modeled by a two-port network equivalent circuit that resolves the SEIG into its positive- and negative-sequence circuits associated with the self-excitation capacitors and the load. The network can then be analyzed by common AC circuit analysis techniques. Successful results for balancing the SEIG supplying a single-phase load have been achieved by properly choosing the values of the excitation capacitors. The proposed method has also been validated by experiments on a 0.37 kW SEIG.

1. Introduction

Induction generators (IGs) are receiving more attention than in the past because of their low prices, simple construction, little maintenance, ruggedness and the fact they do not need dc sources and brushes, which make them particularly suitable as an energy conversion device for renewable energy sources such as wind, biogas and micro-hydro. In many developing countries where a significant percentage of the population and areas still suffer from electricity shortages, employing IGs for generating electricity from renewable energy has become an important means of rural electrification and reduction of greenhouse gases emissions [1].

IGs can be operated in stand-alone or grid-interactive mode. In grid-interactive mode, an IG is directly connected to the grid that imposes its voltage and frequency and supplies the required reactive power. The analysis of a grid-connected IG does not differ much from that of an induction motor (IM). On the other hand, in stand-alone mode, self-excitation capacitors are needed to supply reactive power to the generator and load, and the generated voltage and frequency depend on the rotational speed, the load impedance and the values of excitation capacitors. Hence, the analysis of a self-excited induction generator (SEIG) is more complicated.

People living off the grid in remote islands, rural or mountain areas usually have single-phase type loads. Hence, a single-phase SEIG is an ideal option for electric power supply. While high capacity single-phase IMs up to 10 hp are available in the market, three-phase IMs above 5 hp (3.7 kW) are cheaper than single-phase IMs of the same ratings [2]. The use of a three-phase IM operated as an SEIG to generate single-phase electricity has been employed in many places for economic reasons. However, a three-phase SEIG operated as a single-phase generator is working under a very unbalanced condition, necessitating it to be derated to avoid overheating.

In the literature, studies on the three-phase SEIG feeding single-phase loads can roughly be categorized into two groups. The first group endeavors to minimize the voltage regulation and at the same time maximize the single-phase power output of the generator by properly choosing the values of the self-excitation capacitors, considering possible changes in the rotational speed of the prime mover. To mention some examples, Wang and Cheng [3] determined the minimum and maximum values of a single excitation capacitor required by a three-phase SEIG supplying a single-phase resistive load using the eigenvalue sensitivity method. Fukami et al. [4] proposed and analyzed a self-regulated three-phase SEIG working as a single-phase generator that consisted of two equal capacitors connected in series and another capacitor in parallel with the load resistor, and provided improved performance of voltage regulation. This generator scheme was further optimized by Mahato et al. [5] using the sequential unconstrained minimization technique to obtain a maximum power output for both capacitive and inductive single-phase loads.

The second group stresses the need for mitigating the voltage and current unbalance of a three-phase SEIG working as a single-phase generator. Al-Bahrani and Malik [6] analyzed the performance of a three-phase SEIG composed of a single capacitor in parallel with a single-phase load, i.e., the single-phasing mode. Chan [7] developed a method based on symmetrical components for analyzing a three-phase SEIG supplying a single-phase load. Chan’s method was applicable to the single-phasing mode as well as the Steinmetz connection. Chan and Lai [8,9] also developed a method to determine the minimum capacitance for voltage building-up of a three-phase SEIG with Steinmetz connection. It is noted that [6,7,8,9] only give methods for analyzing a three-phase SEIG feeding a single-phase load and do not report any method for balancing it. Chan and Lai [10] proposed a circuit scheme to balance the SEIG. In addition to the load resistance and excitation capacitance in the Steinmetz connection, they added an auxiliary load resistance and an auxiliary excitation capacitance. They used a phasor diagram to explain how to find the appropriate values of the auxiliary resistance and capacitance that allow a perfectly balanced three-phase voltage and current to be obtained. Alolah and Alkanhal [11] proposed another scheme that consisted of two excitation capacitors, the values of which were determined using a sequential genetic and gradient optimization method. The voltage unbalance factor of the SEIG using the capacitance values found by that proposed algorithm was reported to range from 2% to 7%, showing a system that is not perfectly balanced.

In fact, achieving balanced loading on a three-phase generator provides benefits to the generator’s performance which include: (1) making full use of the generator rating; (2) eliminating the pulsating torque caused by the negative-sequence current and hence reducing shaft mechanical vibration; and (3) eliminating voltage unbalance at the generator terminals caused by unbalanced load currents, which also improves voltage regulation of the generator.

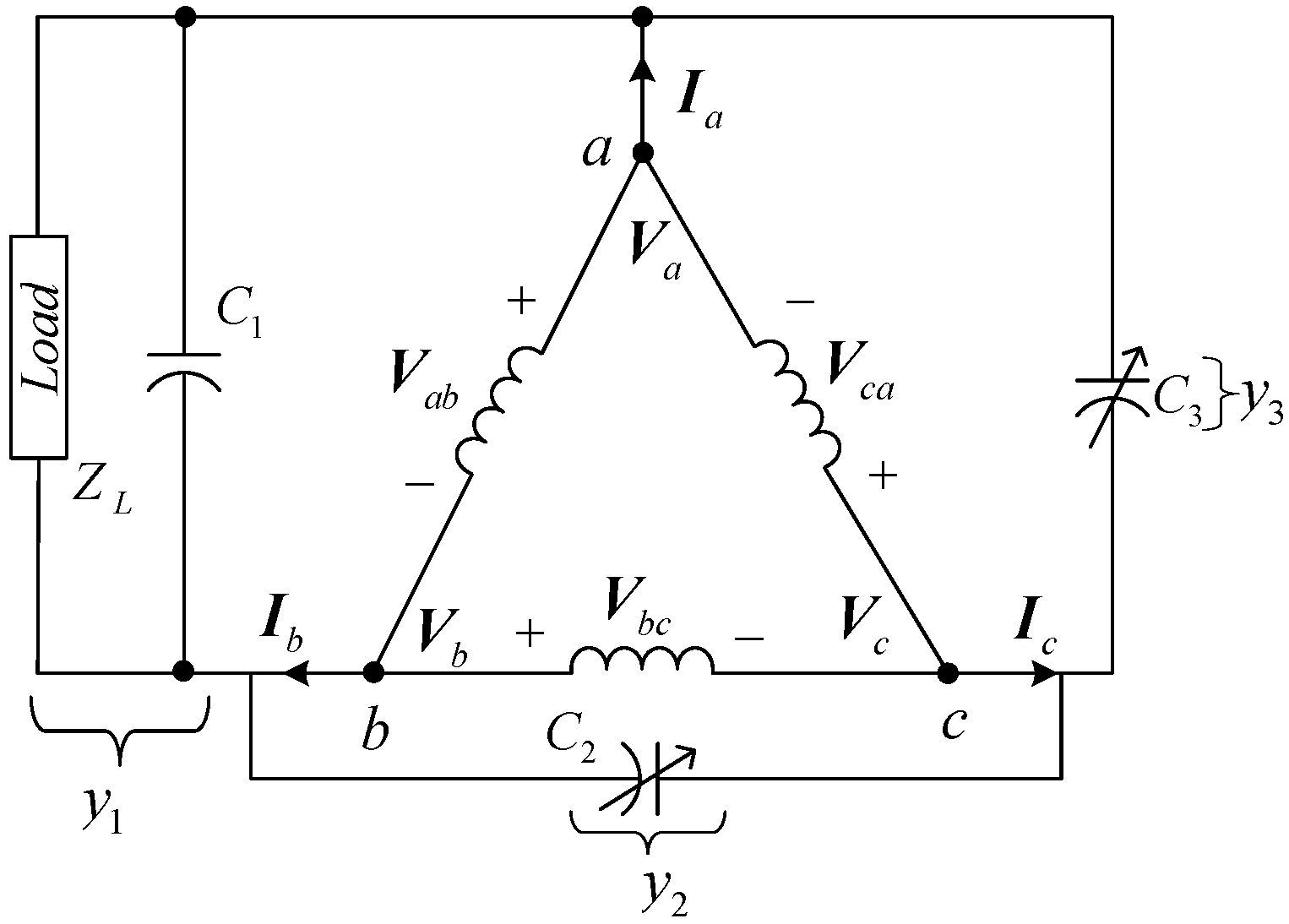
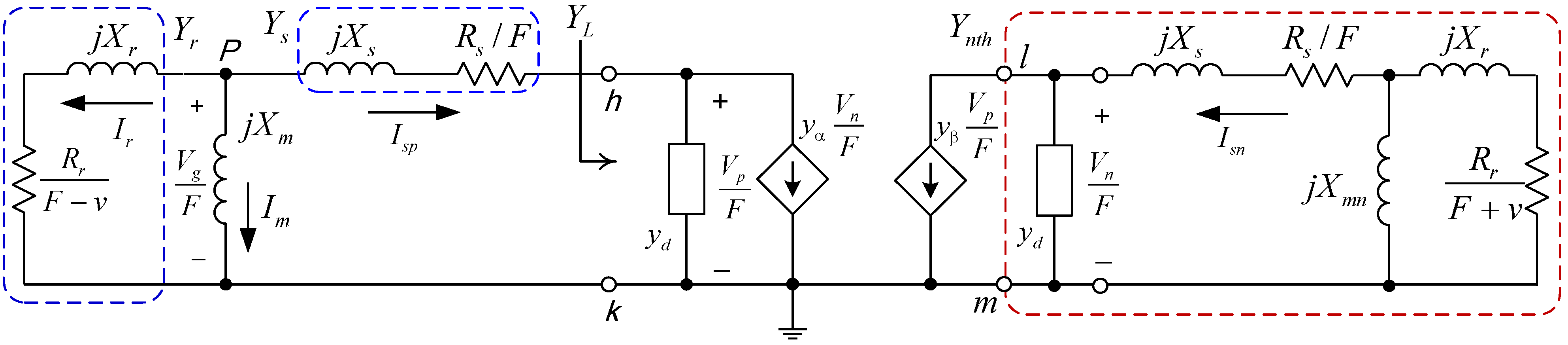
In this paper, the authors propose a three-capacitor scheme that is able to perfectly balance a three-phase SEIG supplying a single-phase load. The three capacitors include a fixed capacitor that supplies the required reactive power to the system, and two variable capacitors that play the role of balancer. The two variable capacitors can be realized by two static var compensators (SVCs), a parallel combination of a fixed capacitor and a thyristor-controlled reactor (TCR). The three-capacitor scheme is represented by a two-port network IG model developed by Wang and Huang [12] for analysis. A solution method based on this two-port network model is also proposed for determining the values of the three capacitors. The circuit scheme and the method for finding capacitances to balance the SEIG are validated by comparing results obtained by the two-port network SEIG model and by experiments on a 0.375 kW induction generator.

2. Generator and Load Modeling

The two-port network model for a three-phase SEIG supplying unbalanced load developed in [12] is briefly described here and is used to analyze the proposed generator scheme. In addition, the voltage unbalance factor expressed as a function of the two-port network model’s parameters is also derived.

2.1. Generator Scheme

Figure 1 shows the proposed three-capacitor scheme, which is composed of a ∆-connected three-phase induction machine and three capacitors C₁, C₂ and C₃ across each terminal pair. The single-phase load impedance Z_L is connected across terminals a and b. Capacitors C₂ and C₃ are variable according to the generator rotational speed and the load impedance, while C₁ is fixed and serves to supply additional reactive power to the machine and load. We note that the scheme shown in Figure 1 is indeed an IG supplying a ∆-connected unbalanced load composed of three admittances y₁, y₂ and y₃.

Figure 1. Three-capacitor scheme of SEIG feeding a single-phase load.

Figure 1. Three-capacitor scheme of SEIG feeding a single-phase load.

2.2. Modelling of an Unbalanced Three-Phase Load

Unbalanced loads can be combined and modeled as a ∆-connected three-phase load as shown in Figure 2a, where y₁, y₂ and y₃ are load admittances. Mixture of Y-connected and single-phase loads can also be converted to this model by appropriate transformation formulae. In Figure 2a, V_a, V_b and V_c refer to the phase voltages at the load terminals, and I_a, I_b and I_c to the line currents flowing into the load.

The relation between the three-phase voltages and currents can be written as:

$$\mathit{I}=\left[\begin{array}{c}{I}_a\\ I_b\\ I_c\end{array}\right]=\left[\begin{array}{ccc}{y}_3+y_1& -y_1& -y_3\\ -y_1& y_1+y_2& -y_2\\ -y_3& -y_2& y_2+y_3\end{array}\right]\left[\begin{array}{c}{V}_a\\ V_b\\ V_c\end{array}\right]=\mathit{Y}\mathit{V}$$

(1)

where I and V are current and voltage vectors, respectively; and Y the nodal admittance matrix. Let the corresponding symmetrical voltage and current component vectors be V_s and I_s, respectively. V_s and I_s can be expressed as:

V_s = [V₀ V_p V_n]^T, I_s = [I₀ I_p I_n]^T

(2)

The subscripts 0, p and n refer to zero-, positive- and negative-sequence components, respectively. From Equation (1) and the symmetrical component equation for currents, we can write:

I_s = A⁻¹I = A⁻¹YV = A⁻¹YAV_s = Y_sV_s

(3)

where:

$${\mathit{Y}}_s={\mathit{A}}^{-1}\mathit{Y}\mathit{A},\mathit{A}=\left[\begin{array}{ccc}1& 1& 1\\ 1& a^2& a\\ 1& a& a^2\end{array}\right],a=1\angle 120°$$

(4)

In Equation (4), Y_s is the similarity transformation of admittance matrix Y. Equation (4) in a more detailed form can be given by:

$${\mathit{Y}}_s=\left[\begin{array}{ccc}0& 0& 0\\ 0& y_d& y_{\alpha }\\ 0& y_{\beta }& y_d\end{array}\right]$$

(5)

where:

y_α = − (ay₁ + y₂ + a²y₃), y_β = − (a²y₁ + y₂ + ay₃), y_d = y₁ + y₂ + y₃

(6)

Hence, Equation (3) can be rewritten as:

$$\left[\begin{array}{c}{I}_0\\ I_p\\ I_n\end{array}\right]=\left[\begin{array}{ccc}0& 0& 0\\ 0& y_d& y_{\mathsf{\alpha }}\\ 0& y_{\mathsf{\beta }}& y_d\end{array}\right]\left[\begin{array}{c}{V}_0\\ V_p\\ V_n\end{array}\right]$$

(7)

Since the zero-sequence current I₀ = 0, Equation (7) can be written in a more compact form as:

$$\left[\begin{array}{c}{I}_p\\ I_n\end{array}\right]=\left[\begin{array}{cc}{y}_d& y_{\mathsf{\alpha }}\\ y_{\mathsf{\beta }}& y_d\end{array}\right]\left[\begin{array}{c}{V}_p\\ V_n\end{array}\right]$$

(8)

Equation (8) implies a two-port network as shown in Figure 2b.

Figure 2. A delta-connected three-phase unbalanced load. (a) Circuit showing the nodal voltages and line currents; (b) The corresponding two-port network equivalent circuit.

Figure 2. A delta-connected three-phase unbalanced load. (a) Circuit showing the nodal voltages and line currents; (b) The corresponding two-port network equivalent circuit.

2.3. Combination of Load and Generator Models

The load model shown in Figure 2b and the generator positive- and negative-sequence equivalent circuits can be combined to represent the SEIG with unbalanced loads. It is noted that voltages V_p and V_n and admittances y_α, y_β and y_d shown in Figure 2b need to be corrected by the per-unit frequency F. The complete sequence network of the SEIG with unbalanced loads is depicted in Figure 3, in which the left part is the positive-sequence network while the right part is the negative-sequence network. The two parts interact with each other through two dependent current sources. The effects of load unbalance are clearly expressed by parameters y_α, y_β and y_d. It is noted again that y_α, y_β and y_d are functions of F. When three-phase loads are balanced, i.e., y₁ = y₂ = y₃, both y_α and y_β are equal to zero, implying no interaction between the positive- and the negative-sequence networks. The two-port equivalent circuit in Figure 3 fully represents the SEIG supplying unbalanced loads. A single-phase load is a particular case, and also the worst case, of unbalanced loads. In Figure 3, Y_r refers to the rotor admittance, Y_s to the stator admittance, and Y_L to the admittance looking to the right of terminals h and k. Y_nth is the admittance to the right of terminals l and m. Calculation of Y_nth is made easier if jX_mn is removed. This is a good approximation since the parallel branch $\left|(R_r/F+v)+j{X}_r\right|$ is much smaller than $\left|j{X}_{mn}\right|$, which gives:

$$Y_{nth}=y_d+{\left[\frac{R_s}{F}+\frac{R_r}{F+v}+j(X_s+X_r)\right]}^{-1}$$

(9)

The circuit shown in Figure 3 allows the positive-sequence stator current I_sp to be written as:

$$I_{sp}=Y_L\cdot \left(\frac{V_p}{F}\right)=y_d\cdot \frac{V_p}{F}+y_{\alpha }\cdot \frac{V_n}{F}$$

(10)

in which V_n /F can be given by:

$$\frac{V_n}{F}=-\frac{1}{Y_{nth}}·y_{\beta }·\frac{V_p}{F}$$

(11)

Combining Equations (10,11) allows I_sp to be written as:

$$I_{sp}=\left(y_d-\frac{y_{\alpha }{y}_{\beta }}{Y_{nth}}\right)\cdot \frac{V_p}{F}=Y_L\cdot \frac{V_p}{F}$$

(12)

which implies:

$$Y_L=y_d-\frac{y_{\alpha }{y}_{\beta }}{Y_{nth}}$$

(13)

Figure 3. Two-port network model of a three-phase SEIG with unbalanced load.

Figure 3. Two-port network model of a three-phase SEIG with unbalanced load.

2.4. Analysis of the Sequence Networks

Analysis of the circuit of Figure 3 aims at finding the voltages and currents of the SEIG so that its performance under a specified operation condition can be predicted. In this paper, a two-step method is used to find the per-unit frequency F and the magnetizing reactance X_m in sequence. In Figure 3, we specify the air-gap voltage V_g to be the reference phasor. That is, $V_g=V_g\angle 0°$. The magnetizing current I_m must be a pure imaginary quantity since the magnetizing reactance jX_m, which is a saturable reactance, is a pure imaginary quantity. The sum of the currents leaving node P equals zero, which means that (I_r + I_sp) = −I_m is also an imaginary number. The sum (I_r + I_sp) can be given by:

$$I_r+I_{sp}=\frac{V_g}{F}{Y}_r+\frac{(V_g/F)}{Y_L^{-1}+Y_s^{-1}}=\frac{V_g}{F}\cdot \left(Y_r+\frac{Y_L{Y}_s}{Y_L+Y_s}\right)$$

(14)

Since Vg is a real quantity and (I_r + I_sp) an imaginary quantity, the real part of the admittance $Y_r+\frac{Y_L{Y}_s}{Y_L+Y_s}$ must be zero. If we define:

Y_T(F) = Y_r = Y_LY_s/(Y_L + Y_L)

(15)

then the following relation holds:

Re[Y_T + (F)] = Re[Y_r + Y_LY_s/(Y_L + Y_s)] = 0

(16)

Since Y_T is a function of Y_r, Y_s and Y_L, it is also a function of the per-unit frequency F. Equation (16) has only one unknown F, and can be solved for F using a numerical method such as the secant method or the false position method [13]. Determination of F does not need to know the value of X_m, largely simplifying the analysis. Once F is obtained by solving Equation (16), Y_T can then be found. Note that Y_T is indeed the total admittance in parallel with jX_m. The following relation holds:

I_m(jX_m +1/Y_T) = 0

(17)

Hence, we have:

jX_m = −1/Y_T

(18)

After the per-unit frequency F is obtained, the air-gap voltage V_g is to be determined. Figure 4 shows that the working point is at the intersection of the magnetizing curve and a load line defined by the equation:

$$V_g/F=j{X}_m\cdot I_m=-I_m/Y_T$$

(19)

Figure 4. Determination of the air-gap voltage V_g and the maximum magnetizing reactance X_cr.

Figure 4. Determination of the air-gap voltage V_g and the maximum magnetizing reactance X_cr.

The expression of Y_T has been given in Equation (15). An iterative procedure can be taken to find the working point. The iterative procedure starts at an initial value of V_g or I_m, and finally converges at the intersection point. It is noted that the magnetizing curve must be obtained from the experiment. As shown in Equation (19), the slope of the load line is equal to X_m, which is a function of the rotational speed, the load impedance Z_L and the excitation capacitances C₁, C₂ and C₃. When the load line is just tangent to the magnetizing curve as shown by the (red) tangent line in Figure 4, X_m attains a critical value X_cr over which the generator is unable to build voltage. Hence, comparing the obtained X_m with X_cr is a useful criterion to judge if the generator can build voltage.

When F, V_g and I_m are known, all the voltages and currents in Figure 3 are easily obtainable. The voltages and currents shown in Figure 3 are positive- and negative-sequence components that need to be converted into the phase domain to find the corresponding three-phase quantities. An important quantity is the voltage unbalance factor τ, defined as the magnitude of the ratio of the negative- to positive-sequence voltage. From (11), the voltage unbalance factor τ can be expressed as a function of y_β and Y_nth:

$$\tau =VUF=\left|\frac{V_n}{V_p}\right|=\left|\frac{y_{\beta }}{Y_{nth}}\right|$$

(20)

3. The Solution Method

The analysis in Section 2 reveals that the voltage unbalance factor τ of the SEIG is determined by the ratio of y_β to Y_nth. When the SEIG is working at a balanced condition, the voltage unbalance factor τ must be equal to zero, which means that the numerator of Equation (20) is zero. Namely, the real and imaginary parts of admittance y_β must both be zero. These two conditions combined with the relation for the per unit frequency F described by Equation (16) allow the following three simultaneous nonlinear equations to be written:

$$Re\left[y_{\beta }(F)\right]=Re\left[-(a^2\cdot y_1+y_2+a\cdot y_3)\right]=0$$

(21)

$$Im\left[y_{\beta }(F)\right]=Im\left[-(a^2\cdot y_1+y_2+a\cdot y_3)\right]=0$$

(22)

Given that C₁ and Z_L are known, the values of F, C₂ and C₃ can be found by solving Equations (16,21,22) using the Newton-Raphson method if appropriate initial guess values are provided. The obtained values of C₂ and C₃ allow the SEIG to work at a balanced condition. In comparison with the Hooke and Jeeves search technique used in Chan’s work [7], the proposed method of directly solving three simultaneous nonlinear equations is much easier. In this paper, the nonlinear simultaneous equations have been solved using Mathcad [13], which is a widely used general-purpose mathematic software tool.

4. Numerical Applications

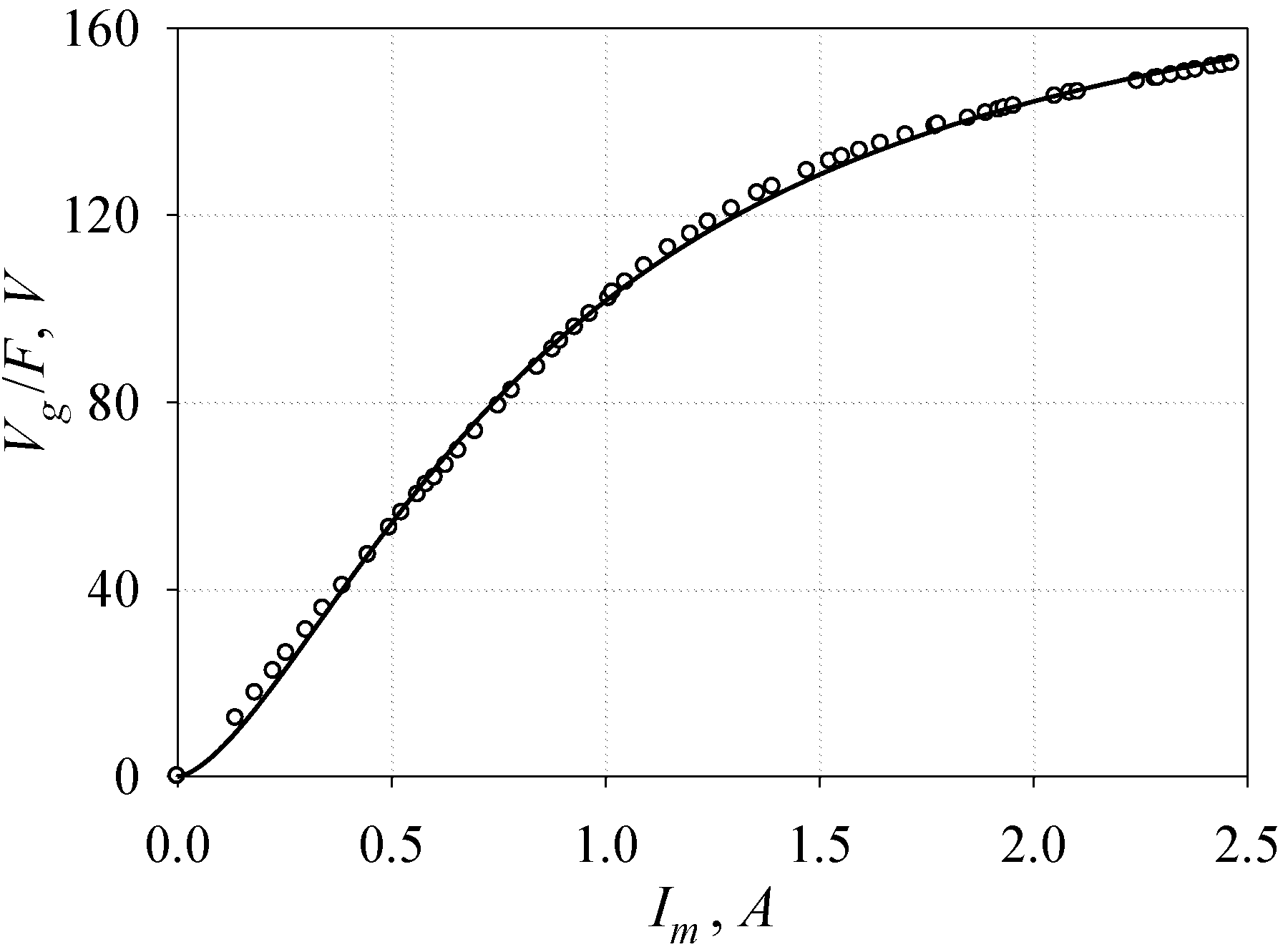
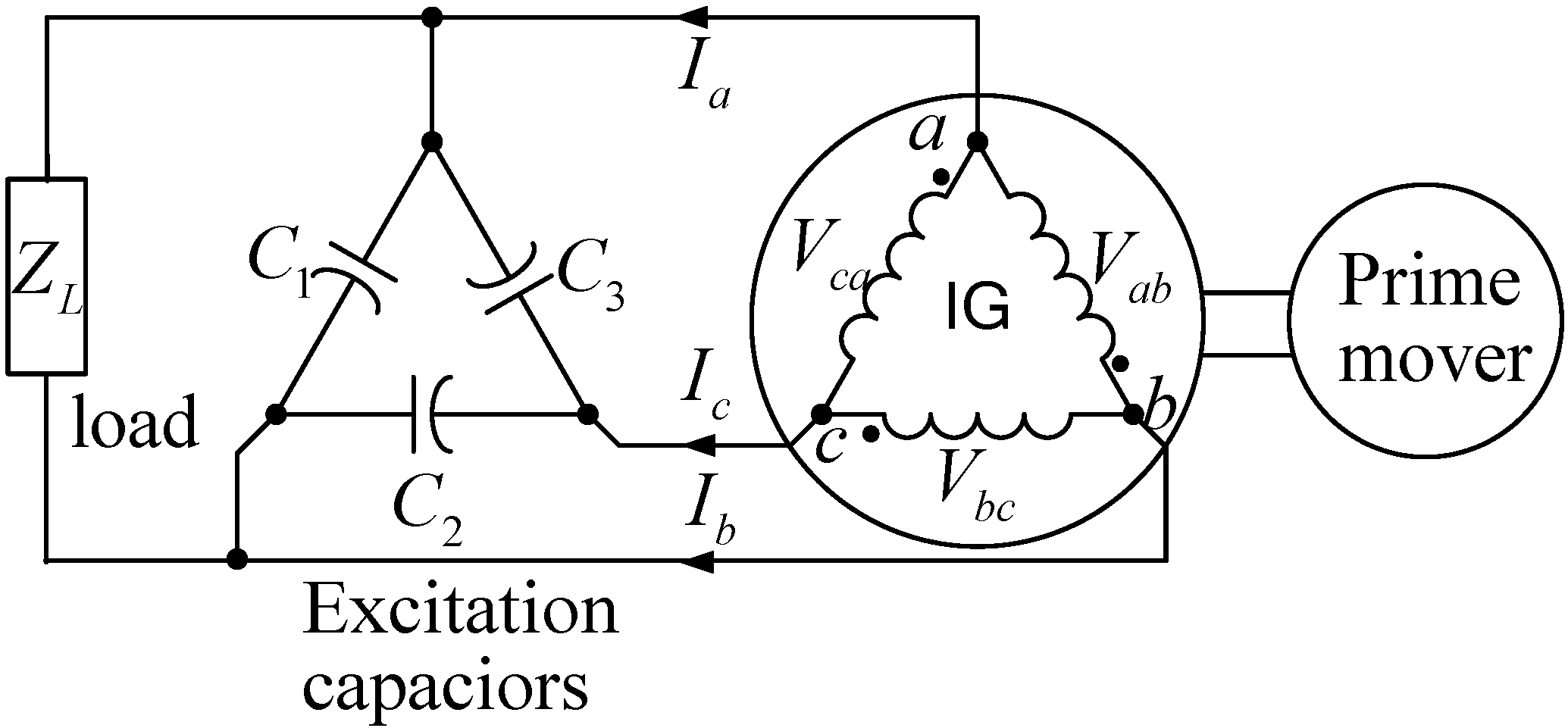
An induction motor working as an SEIG supplying a single-phase load has been used to illustrate the proposed methods for solving C₂ and C₃ to balance the generator. It has been set up as shown in Figure 5. The generator is a 3-phase, 220-V, ∆-connected, 60-Hz, 4-pole, 1/2 hp squirrel-cage induction machine. The motor characteristics and test methods for obtaining the parameters of the generator equivalent circuit are given in the appendix. Also included in the appendix are the test method for the magnetizing saturation curve, and how the fixed capacitor C₁ is determined in this study.

Figure 5. Experimental set-up of an SEIG feeding a single-phase load.

Figure 5. Experimental set-up of an SEIG feeding a single-phase load.

In the following sections, we firstly show a few examples of applying the proposed solution method for finding the values of C₂ and C₃ that balance the generator when Z_L, C₁ and the rotational speed are known. The example that follows is the use of the capacitance values found by the solution method for the experiment on the 1/2 hp squirrel-cage induction machine to see whether the generator is working under balanced conditions.

4.1. Verification of the Obtained Capacitance Values

The solution method described in Section 3 has been employed to find the values of C₂ and C₃ when the generator runs at 1764 rpm and C₁ is fixed to 10 μF. The solved results for resistive loads Z_L = 400 Ω and Z_L = 1000 Ω, and inductive loads Z_L = 500 + j1130.97 Ω and Z_L = 467.13 + j123.91 Ω (at 60 Hz) are shown in Table 1.

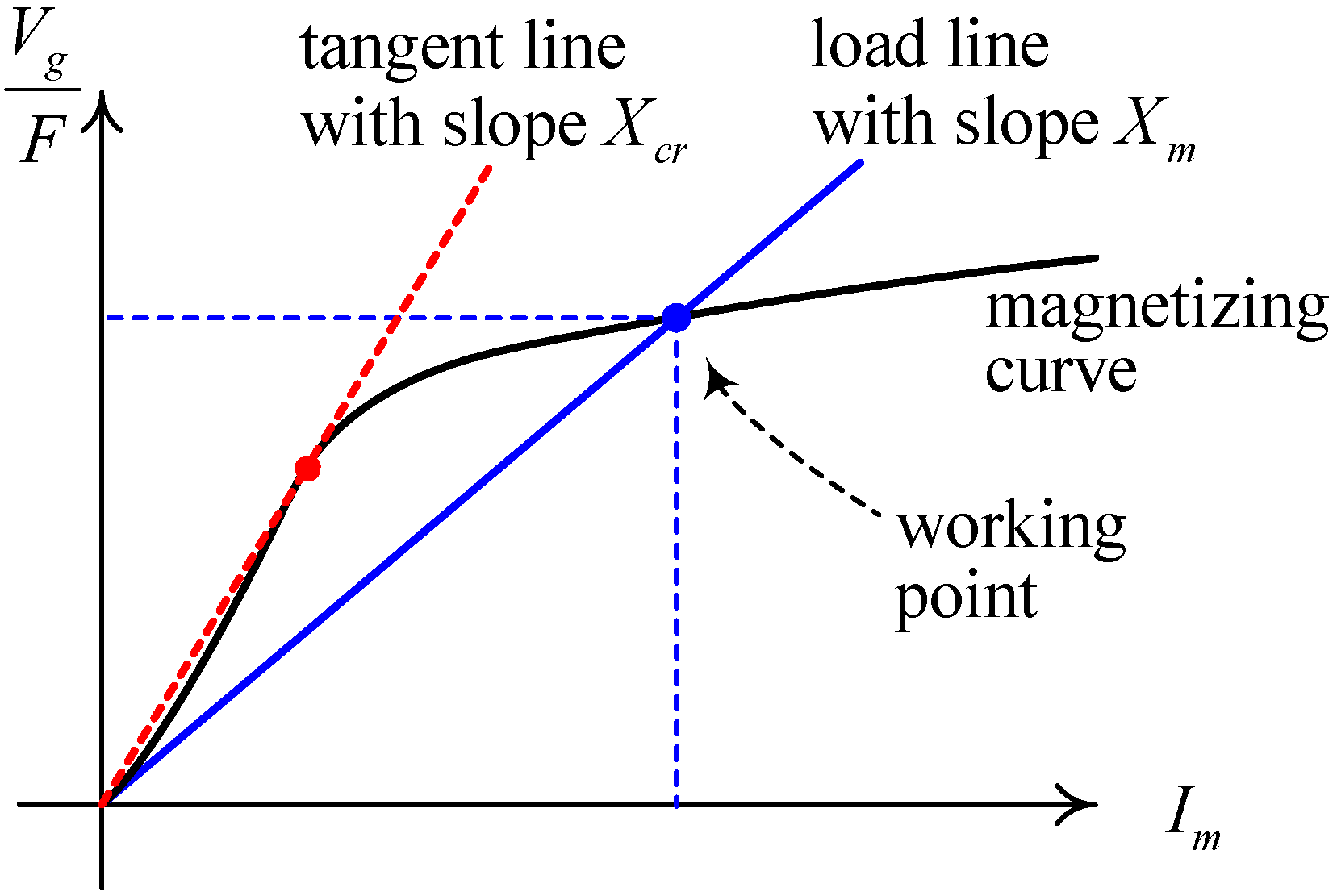
In the table, the values of τ corresponding to the solution values of C₂ and C₃ are also listed, being all very close to zero and showing that the obtained capacitance values can balance the generator. The values of the magnetizing reactance X_m listed in Table 1 are all smaller than X_cr/F, meaning that the capacitance values obtained allow the generator to build voltage.

Table 1. Capacitance values C₂ and C₃ and the resulting voltage unbalance factor for different load impedances at a rotating speed of n = 1764 rpm.

n (rpm)	1764
ZL (Ω)	400 Ω	1000 Ω	R-L (series) R = 500 Ω, L = 3000 mH	R//L (parallel) R = 500 Ω, L = 5000 mH
C2 (μF)	13.98	11.58	8.490	11.66
C3 (μF)	6.019	8.421	7.420	5.321
τ (%)	1.86 × 10−6	2.97 × 10−7	1.62 × 10−7	3.7 × 10−7
Pout (W)	125.76	57.27	9.17	59.20
F (p.u.)	0.96182	0.97004	0.97543	0.96590
Im (A)	1.36	1.49	0.83	0.90
Xm (Ω)	93.44	89.10	110.98	108.98

Table 1. Capacitance values C₂ and C₃ and the resulting voltage unbalance factor for different load impedances at a rotating speed of n = 1764 rpm.

n (rpm)	1764
ZL (Ω)	400 Ω	1000 Ω	R-L (series) R = 500 Ω, L = 3000 mH	R//L (parallel) R = 500 Ω, L = 5000 mH
C2 (μF)	13.98	11.58	8.490	11.66
C3 (μF)	6.019	8.421	7.420	5.321
τ (%)	1.86 × 10−6	2.97 × 10−7	1.62 × 10−7	3.7 × 10−7
Pout (W)	125.76	57.27	9.17	59.20
F (p.u.)	0.96182	0.97004	0.97543	0.96590
Im (A)	1.36	1.49	0.83	0.90
Xm (Ω)	93.44	89.10	110.98	108.98

The values of C₂ and C₃ solved by the proposed method for operating conditions of n = 1800 rpm with load Z_L equal to 500, 2000, 600 + j1357.16 and 373.7 + j99.12 Ω (at 60 Hz), respectively, are listed in Table 2, in which the resulting voltage unbalance factors τ are small too, verifying that the obtained capacitance values can balance the generator. Checks on the magnetizing reactance X_m also assure building-up of the generator voltage.

Table 2. Values of C₂ and C₃ for different load impedances at a speed of n = 1800 rpm.

n (rpm)	1800
ZL (Ω)	500 Ω	2000 Ω	R-L (series) R = 600 Ω, L = 3600 mH	R//L (parallel) R = 400 Ω, L = 4000 mH
C2 (μF)	13.11	10.77	8.769	12.07
C3 (μF)	6.887	9.229	7.930	4.285
τ (%)	3.18 × 10−7	1.94 × 10−7	0.0041	0.00019
Pout (W)	118.98	33.22	12.35	69.35
F (p.u.)	0.98395	0.99249	0.99528	0.98297
Im (A)	1.53	1.66	1.14	0.85
Xm (Ω)	88.09	84.13	100.93	110.46

Table 2. Values of C₂ and C₃ for different load impedances at a speed of n = 1800 rpm.

n (rpm)	1800
ZL (Ω)	500 Ω	2000 Ω	R-L (series) R = 600 Ω, L = 3600 mH	R//L (parallel) R = 400 Ω, L = 4000 mH
C2 (μF)	13.11	10.77	8.769	12.07
C3 (μF)	6.887	9.229	7.930	4.285
τ (%)	3.18 × 10−7	1.94 × 10−7	0.0041	0.00019
Pout (W)	118.98	33.22	12.35	69.35
F (p.u.)	0.98395	0.99249	0.99528	0.98297
Im (A)	1.53	1.66	1.14	0.85
Xm (Ω)	88.09	84.13	100.93	110.46

The values of C₂ and C₃ found for operating conditions of n = 1836 rpm with load Z_L equal to 600, 3000, 700 + j1507.96 and 560.55 + j148.69 Ω (at 60 Hz), respectively, are summarized in Table 3. The resulting voltage unbalance factors are again very close to zero. Voltage building-up is also checked for each loading condition.

Table 3. Values of C₂ and C₃ for different load impedances at a speed of n = 1836 rpm.

n (rpm)	1836
ZL (Ω)	600 Ω	3000 Ω	R-L (series) R = 700 Ω, L = 4000 mH	R//L (parallel) R = 600 Ω, L = 6000 mH
C2 (μF)	12.54	10.50	8.961	11.38
C3 (μF)	7.461	9.496	8.215	6.306
τ (%)	1.12 × 10−6	5.88 × 10−9	2.25 × 10−7	3.97 × 10−8
Pout (W)	113.21	24.73	14.03	89.10
F (p.u.)	1.00527	1.01311	1.01499	1.00648
Im (A)	1.67	1.79	1.35	1.31
Xm (Ω)	83.59	80.28	93.93	95.05

Table 3. Values of C₂ and C₃ for different load impedances at a speed of n = 1836 rpm.

n (rpm)	1836
ZL (Ω)	600 Ω	3000 Ω	R-L (series) R = 700 Ω, L = 4000 mH	R//L (parallel) R = 600 Ω, L = 6000 mH
C2 (μF)	12.54	10.50	8.961	11.38
C3 (μF)	7.461	9.496	8.215	6.306
τ (%)	1.12 × 10−6	5.88 × 10−9	2.25 × 10−7	3.97 × 10−8
Pout (W)	113.21	24.73	14.03	89.10
F (p.u.)	1.00527	1.01311	1.01499	1.00648
Im (A)	1.67	1.79	1.35	1.31
Xm (Ω)	83.59	80.28	93.93	95.05

4.2. Experimental Results

The 1/2 hp squirrel-cage induction machine operating as an SEIG is set up as shown in Figure 5 for experiments. The SEIG’s rotational speed and excitation capacitor C₁ are fixed at 1800 rpm and 10 μF, respectively. Both pure resistive loads and inductive loads are tested.

For the case of pure resistive loads, when the load Z_L varies from 500 to 2000 Ω, the proposed solution method is used to find the corresponding values of C₂ and C₃ that balance that generator. These capacitance values are then used in the two-port network model and in the experiments. The capacitance values obtained by the solution method are directly used as the inputs to the two-port network method. However, for the experiments, the (parallel and series combinations of) capacitors with values closest to the calculated values are used. Table 4 lists the load resistance values, the capacitance values calculated by solving Equations (16,21,22), the capacitance values actually used in the experiments, the measured values of voltage unbalance factor (VUF) and the current unbalance factor (CUF). The measured VUF values listed in Table 4 are all lower than 1%, validating the proposed method. Figure 6 compares the measured values (scattered dots) of frequency, three-phase voltages, currents and output power, with the results obtained by the proposed analytical method (solid lines), for the resistive load continuously varying from 500 to 2000 Ω. Good agreement has been achieved. The comparison of line voltages and currents depicted in Figure 6(b,c) only shows the values in one phase for the calculated results (solid lines) since the calculated voltages and currents are nearly perfectly balanced. Nevertheless, the measured three-phase voltages and currents are given in detail to allow the unbalance to be observed.

The experimental results for inductive loads are summarized in Table 5. Since the impedance value does not vary continuously, it is not appropriate to present these results graphically, so only a table is given. In this table, both calculated and actually used capacitance values are listed. The load resistance is easily adjusted using a rheostat, but the load inductance is more unstable because of magnetic saturation. The experiment has been carried out by firstly choosing an approximate value of inductance, and then finding its accurate inductance value by calculation from the measured voltage and current of the inductor. After the load resistance and inductance are obtained, the same procedure as in the case of pure resistive loads has been followed to find the capacitances C₂ and C₃. Also listed in Table 5 are measured VUF and CUF values. Except for the first row, the VUF values are all lower than 1%. The VUF value in the first row is higher because the value of C₃ used in the experiment deviates slightly more significantly from its theoretical value than those in other rows.

Figure 6. Comparison of the results obtained by experiments (scattered dots) and by the analytical method (solid line) for resistive load Z_L varying from 500 Ω to 2000 Ω. (a) Frequency; (b) Line voltages; (c) Line currents; (d) Output power.

Figure 6. Comparison of the results obtained by experiments (scattered dots) and by the analytical method (solid line) for resistive load Z_L varying from 500 Ω to 2000 Ω. (a) Frequency; (b) Line voltages; (c) Line currents; (d) Output power.

Table 4. Theoretical and experimental capacitance values and measured VUF and CUF for pure resistive loads.

ZL (Ω) (resistive)	Theoretical		Experimental
	C2 (μF)	C3 (μF)	C2 (μF)	C3 (μF)	VUF (%)	CUF (%)
500	13.11	6.888	13.2	6.8	0.74	1.96
750	12.07	7.933	12.1	8.0	0.60	1.70
1,000	11.55	8.452	11.5	8.5	0.40	0.82
1,250	11.24	8.763	11.2	8.7	0.31	0.62
1,500	11.03	8.970	11.0	9.0	0.35	0.71
1,750	10.88	9.118	10.8	9.1	0.44	0.86
2,000	10.77	9.228	10.6	9.2	0.40	0.83

Table 4. Theoretical and experimental capacitance values and measured VUF and CUF for pure resistive loads.

ZL (Ω) (resistive)	Theoretical		Experimental
	C2 (μF)	C3 (μF)	C2 (μF)	C3 (μF)	VUF (%)	CUF (%)
500	13.11	6.888	13.2	6.8	0.74	1.96
750	12.07	7.933	12.1	8.0	0.60	1.70
1,000	11.55	8.452	11.5	8.5	0.40	0.82
1,250	11.24	8.763	11.2	8.7	0.31	0.62
1,500	11.03	8.970	11.0	9.0	0.35	0.71
1,750	10.88	9.118	10.8	9.1	0.44	0.86
2,000	10.77	9.228	10.6	9.2	0.40	0.83

Table 5. Theoretical and experimental capacitance values and measured VUF and CUF for inductive loads.

ZL = R + jωL		Theoretical		Experimental
R (Ω)	L (mH)	C2 (μF)	C3 (μF)	C2 (μF)	C3 (μF)	VUF (%)	CUF (%)
50	1663.56	14.47	10.40	14.45	10.24	1.02	5.54
150	1701.34	14.49	11.07	14.60	11.07	0.28	0.84
400	1787.83	13.95	12.02	14.10	11.95	0.51	0.59
600	1888.30	13.27	12.14	13.35	12.10	0.21	0.46

Table 5. Theoretical and experimental capacitance values and measured VUF and CUF for inductive loads.

ZL = R + jωL		Theoretical		Experimental
R (Ω)	L (mH)	C2 (μF)	C3 (μF)	C2 (μF)	C3 (μF)	VUF (%)	CUF (%)
50	1663.56	14.47	10.40	14.45	10.24	1.02	5.54
150	1701.34	14.49	11.07	14.60	11.07	0.28	0.84
400	1787.83	13.95	12.02	14.10	11.95	0.51	0.59
600	1888.30	13.27	12.14	13.35	12.10	0.21	0.46

5. Conclusions

This paper has proposed a three-capacitor circuit scheme that is able to balance an SEIG supplying a single-phase load. The three-capacitor scheme consists of a fixed capacitor and two variable capacitors. The fixed capacitor is chosen to compensate the reactive power required by the generator and the load, while the two variable capacitors serve to balance the generator according to the load impedance and the rotational speed of the generator.

In order to find the values of the two variable capacitors, a two-port network model of the SEIG has been employed to analyze the generator with arbitrary unbalanced loads. With the aid of this circuit model, a method that involves solving a set of three nonlinear simultaneous equations has been proposed to find the values of the two capacitors that minimize the voltage unbalance of the generator. The proposed method has further been validated by experiments on a 1/2 hp three-phase squirrel-cage induction motor working as an induction generator feeding a single-phase load. Both resistive and inductive single-phase loads have been tested and satisfactory results have been obtained.