Influences of the Load of Suspension Point in the z Direction and Rigid Body Oscillation on Steel Catenary Riser Displacement and Frequency Under Wave Action
Abstract
:1. Introduction
- (1)
- The structure is affected by the oscillating effect of rigid body swing. At present, commercial finite element programs cannot calculate it directly. The effect can be taken into account by a certain coefficient in engineering, but the coefficient still needs to be calculated and analyzed.
- (2)
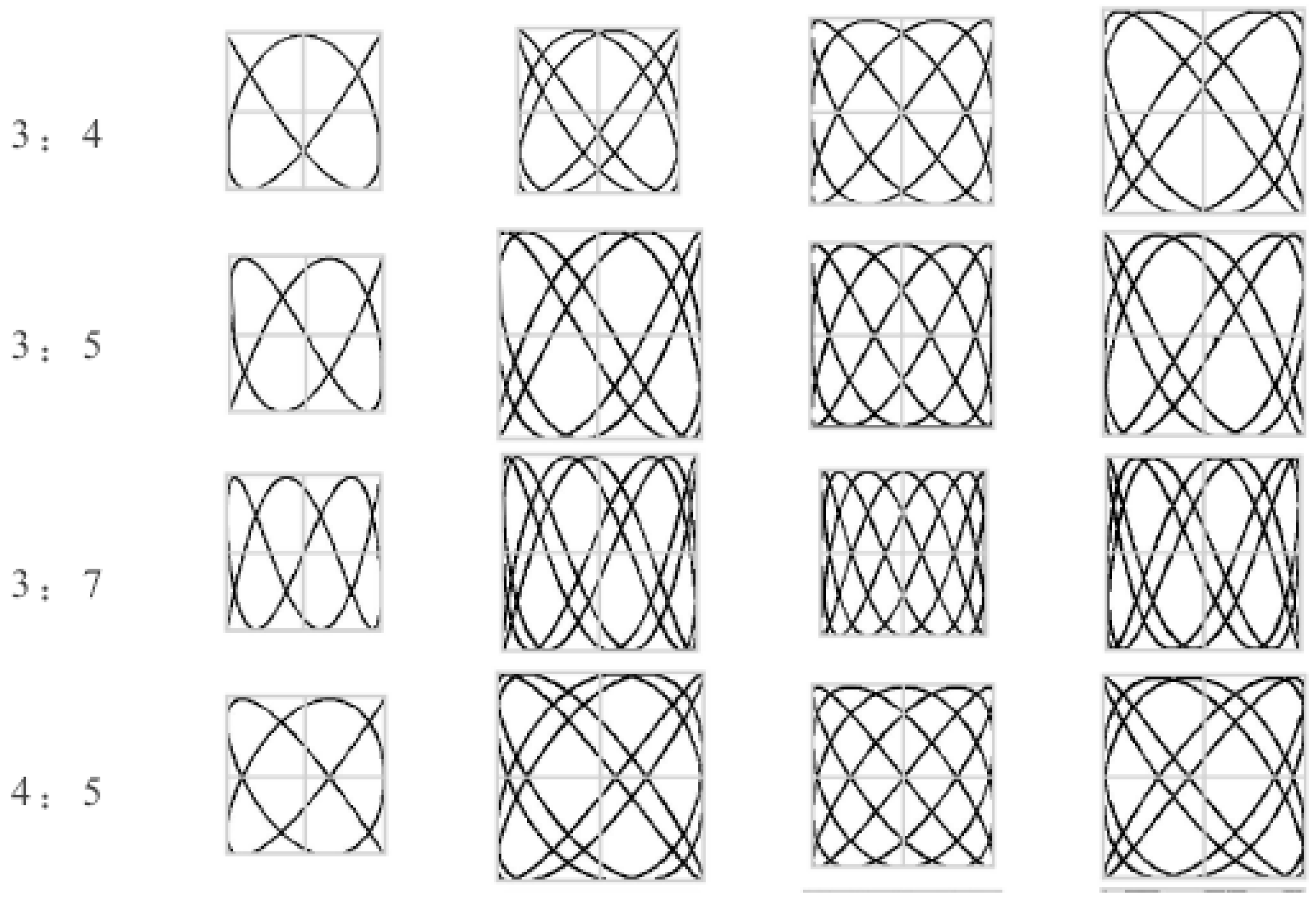
- The actual SCR structure is subject to relatively more loads perpendicular to each other. VIV, represented by vertical lift and drag, is studied in depth. However, there are few studies for waves and the top platform, which are perpendicular to each other. Whether the Lissajous’ Figure can be used as the mathematical validation is worthy of attention.
- (3)
- In the plane, the Lissajous’ Figures with wave and load of suspension point in the z direction are presented. In space, the plane load has two characteristics: in-plane wave load and out-of-plane rigid body swing.
- (4)
- The structural response is affected by waves, top loads in the z direction, rigid body swing and natural vibration frequencies, but there is no simple formula for calculating the load frequency, especially the frequency of rigid body swing.
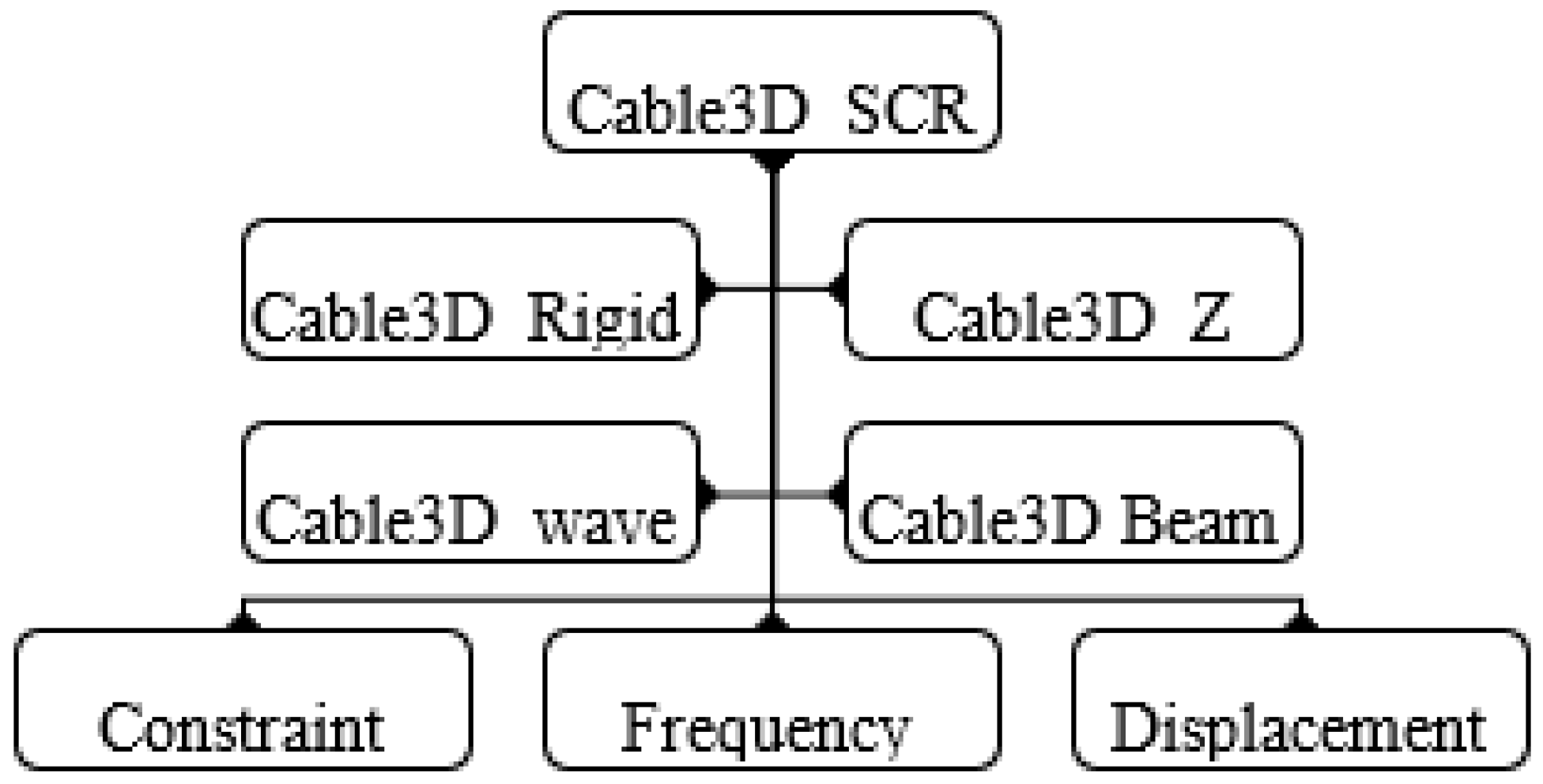
2. SCR Numerical Simulation Model
2.1. General Description of the Numerical Model
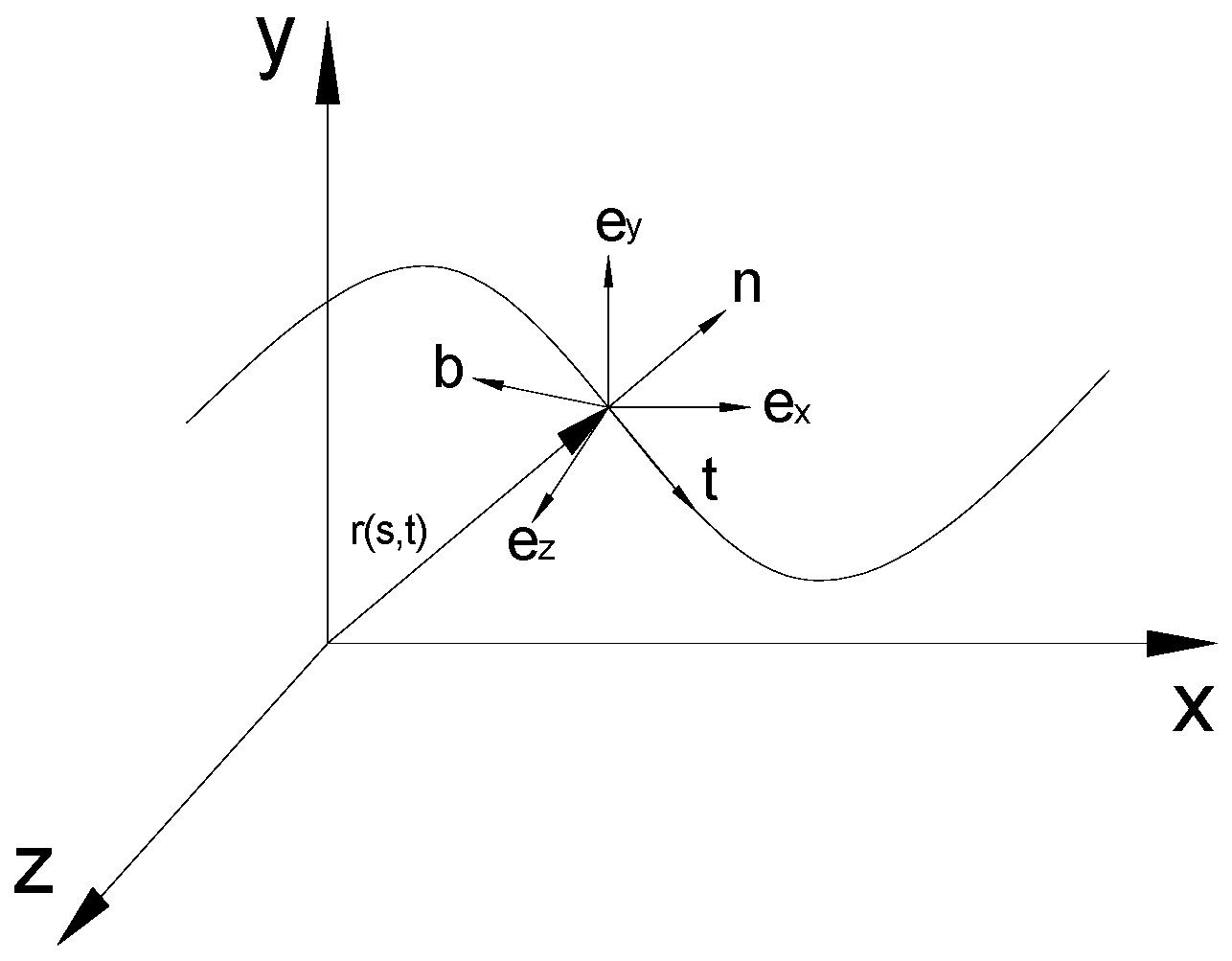
2.2. Basic Control Equation of SCR Motion
2.3. SCR Rigid Body Rotation Submodel
2.4. SCR Wave Load Submodel
2.5. SCR Load Submodel of Suspension Point in the z Direction
2.6. Boundary Constraints and Iteration Conditions
2.7. Summary of the Numerical Model
3. The parameters and Verification for SCR Structure Simulation
3.1. The Parameters of the SCR Structure
3.2. SCR Structural Lissajous Phenomenon and Verification
3.3. Structural Load Frequency Analysis and Verification
3.4. The Summary of Verification
4. Response Analysis of the SCR Structure
4.1. General Description of Response
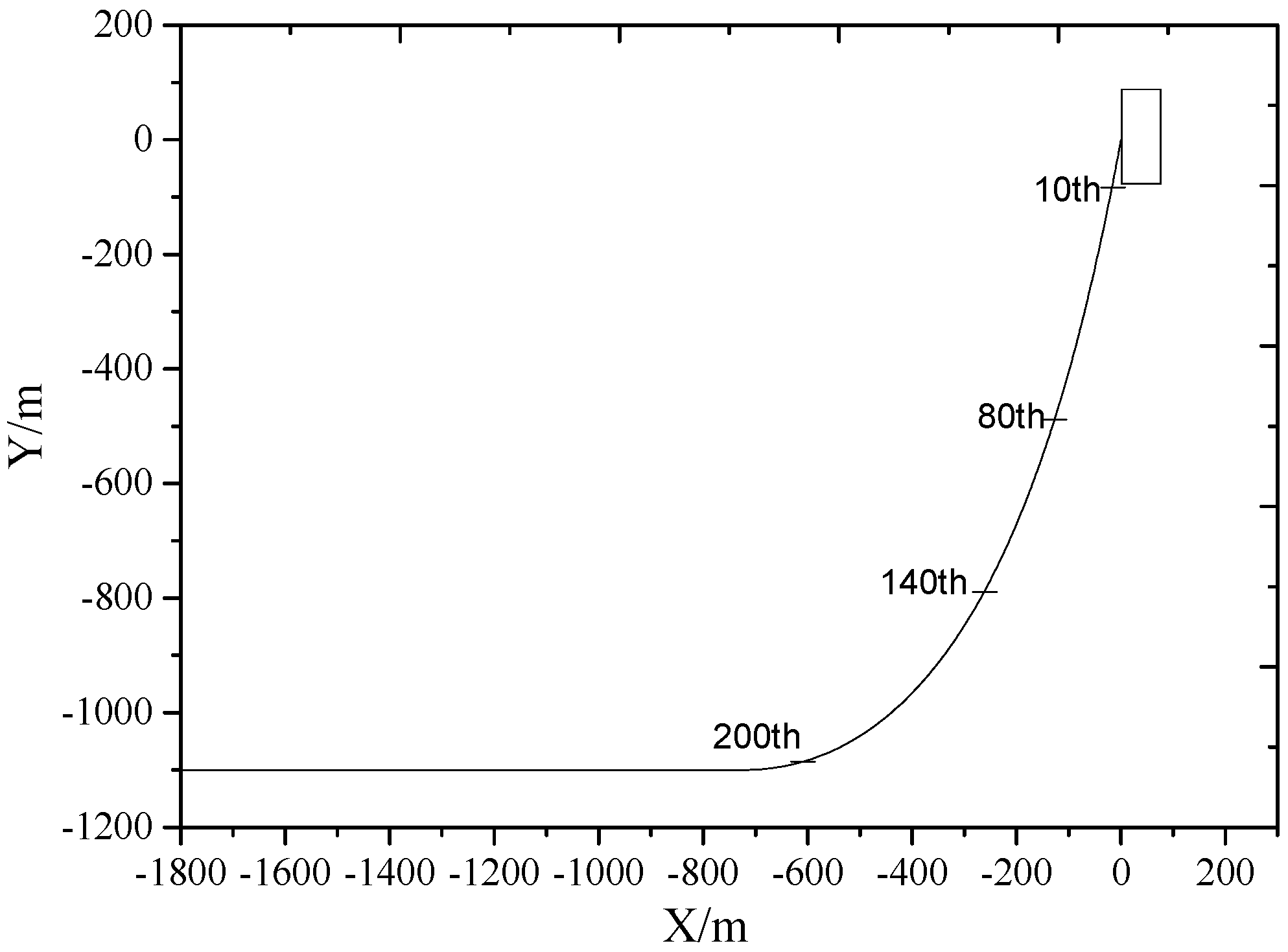
4.2. SCR Three-Dimensional and Two-Dimensional Response Analysis
4.3. Analysis of the z-Direction Response of the SCR Structure
4.3.1. SCR Response Analysis
4.3.2. Response Analysis of the Top Suspension Point of the SCR Structure
4.4. Spectral Analysis
4.4.1. Basic Theory of FFT Calculation
4.4.2. Analysis of Structural Main Frequency and the Influence Frequency
4.4.3. Analysis of the Structural Main Frequency
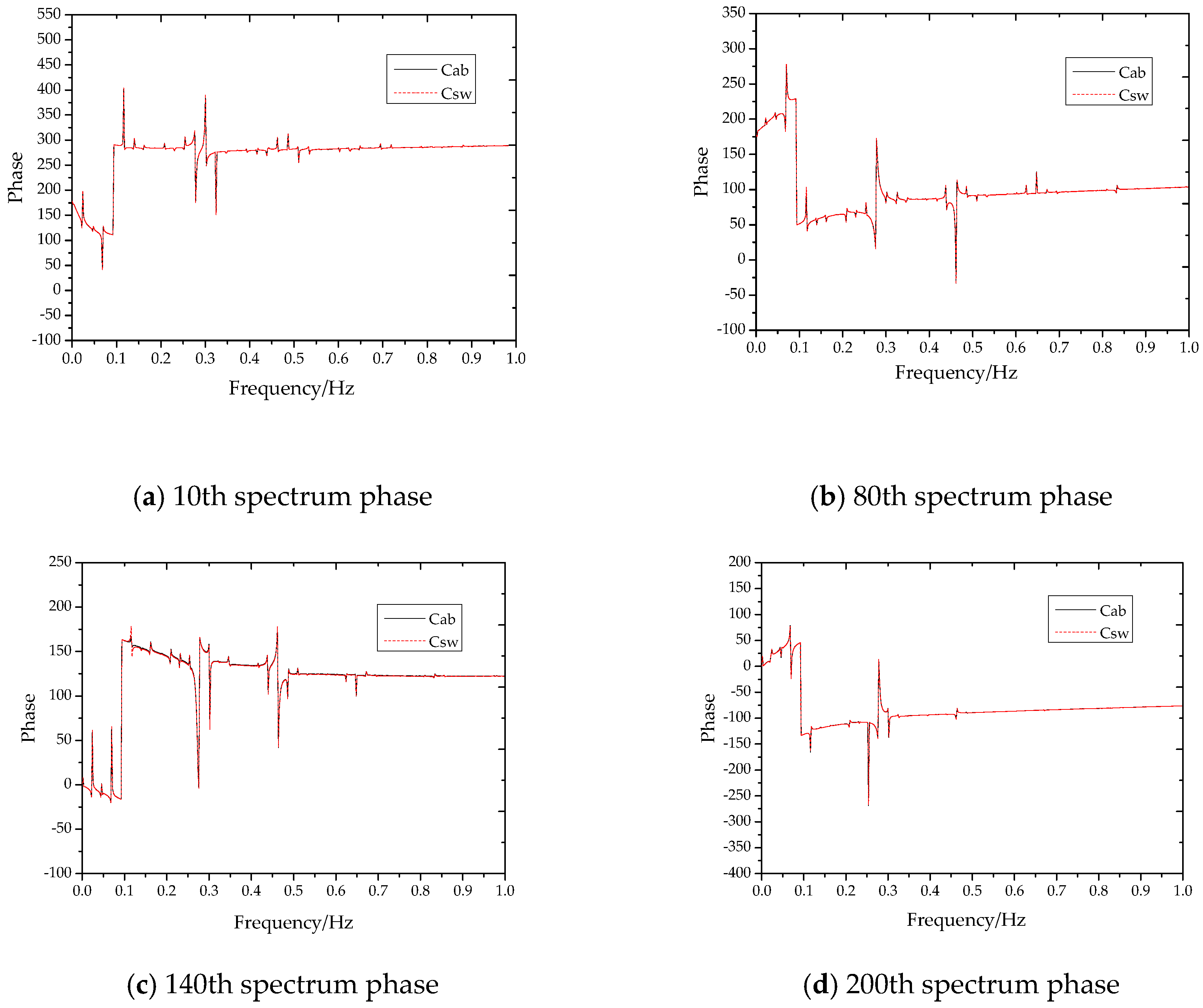
4.4.4. Analysis of the Structural Phase Response
4.5. The Summary of Response Analysis
5. Conclusions
- (1)
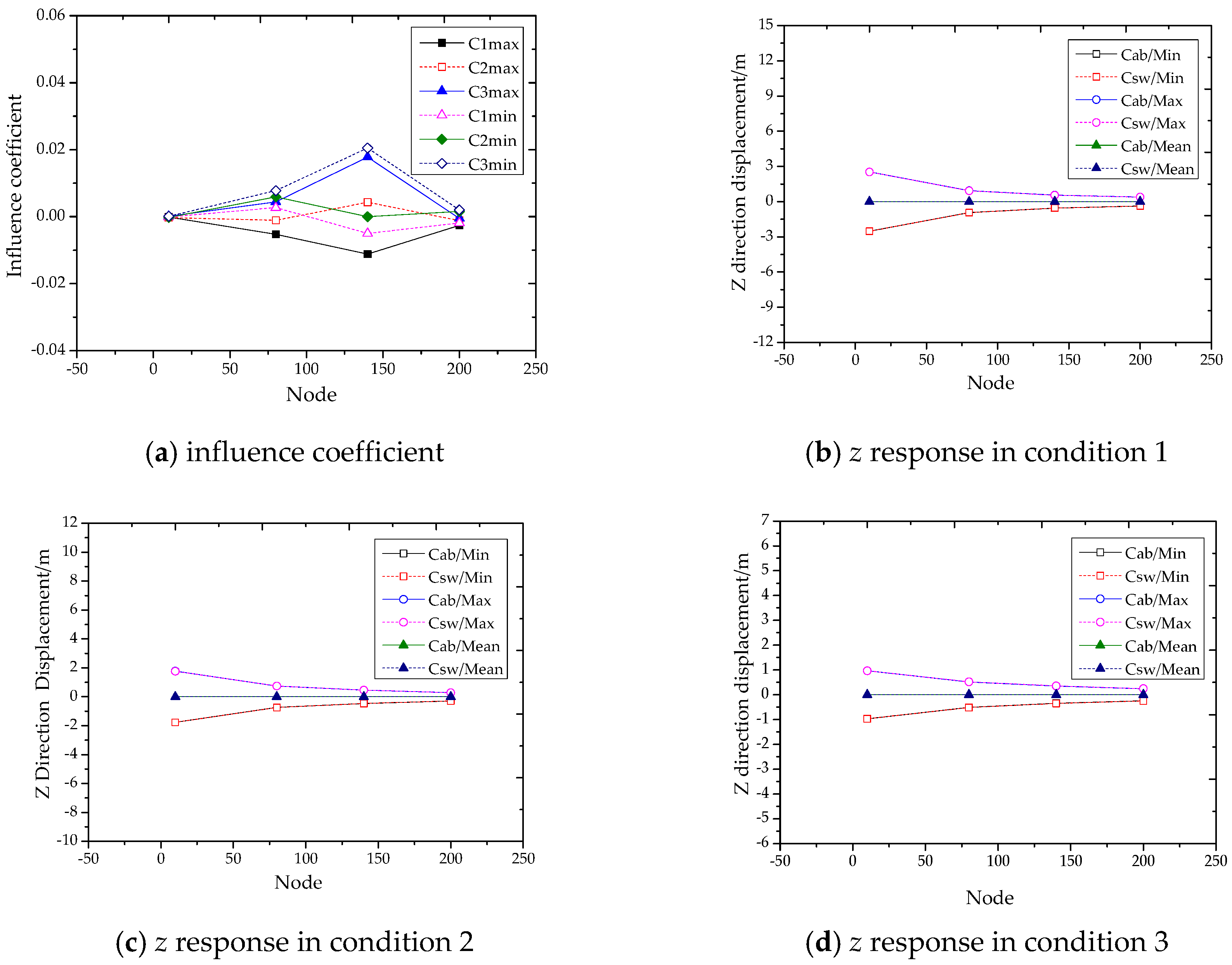
- Program for rigid body swingares few and their iteration is relatively complex. For structural design it is relatively appropriate to consider the influence of rigid body swing by multiplying the response of the main load by a coefficient. According to the statistics of multiple conditions described in this paper, the influence coefficient range of displacement is −0.02–0.02 and the influence coefficient range of the main frequency amplitude is −0.007–0.002.
- (2)
- Waves are perpendicular to the rigid body swing and load of the suspension point in the z direction in this paper. The analysis of the Lissajous curve for qualitative verification and spectral phase for quantitative verification together can provide a relatively good verification for the rigid body swing.
- (3)
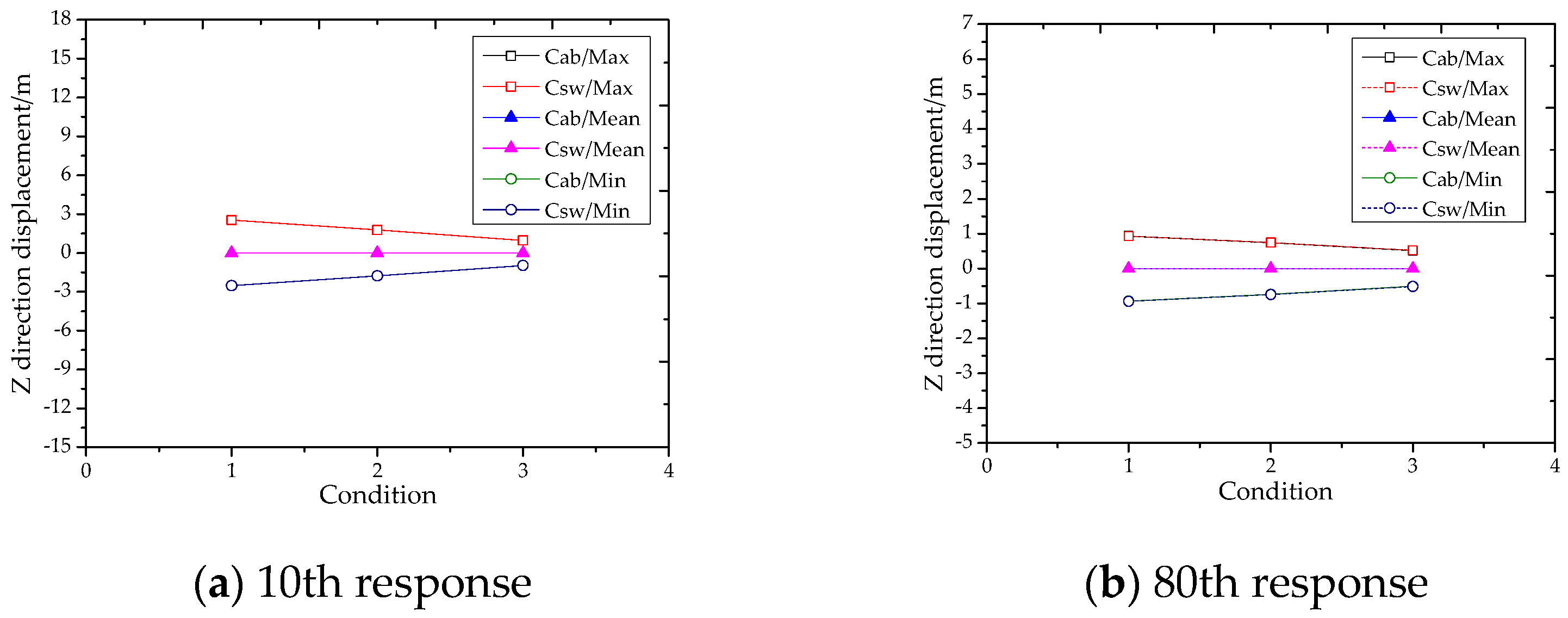
- In terms of overall spatial movement, the response is gradually complicated along the depth. The motion response varies from the yz plane at the 10th node to the zx plane at the 200th.There is a rotation around the z axis in this process. There are phase differences between rigid body swing, wave and the load of the suspension point in the z direction. The structural response is related to the conditions and its trend is relatively uncertain. As an influencing term, the effect of rigid body swing with depth displays a positive linear correlation with the diameter vector S.The response and main frequency have different attenuations at different nodes with depth. The response of the topside 10th–80th region has a sharp decrease, while the response of the 80th-bottom region has a smaller decrease. The response of nodes shows a strong positive correlation with the load of suspension point in the z direction. And it is a forced motion. For the response in top region, it poses a threat to the SCR as a whole for its large amplitude, fast attenuation and strong intensity plane vibration.
- (4)
- In terms of frequency analysis, the result of the rigid body swing frequency solved by the Rayleigh method and the natural frequency of the bending vibration solved by the simply supported beam method are close to that of the FFT transformation. This can relatively meet the requirements of verification for further research. After a spectrum analysis, the results reveal that the load frequency of the suspension point in the z direction is the main frequency. In addition, the main load frequencies of the structure do not resonate with the frequency of the bending vibration. For phase analysis, the trajectory curve under load changes, and the phase curve will show a cliff or rapid change. On the contrary, this kind of variation can distinguish structural load frequencies well. In terms of deficiencies and prospects of this work, there is no real platform load and nonlinear calculation such as random wave. It is still necessary to continue to research the influence in a more realistic environment.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Huang, W.P.; Li, H.J. A New type of deepwater riser in offshore oil & gas production:the steel catenary, SCR. Period. Ocean Univ. China 2006, 36, 775–780. [Google Scholar]
- Zhu, H.J.; Gao, Y. Vortex induced vibration response and energy harvesting of a marine riser attached by a free-to-rotate impeller. Energy 2017, 134, 532–544. [Google Scholar] [CrossRef]
- Qiu, W.; Lee, D.Y.; Lie, H.; Rousset, J.M.; Mikami, T.; Sphaier, S.; Tao, L.B.; Wang, X.F.; Magarovskii, V. Numerical benchmark studies on drag and lift coefficients of a marine riser at high Reynolds numbers. Appl. Ocean Res. 2017, 69, 245–251. [Google Scholar] [CrossRef]
- Li, H.J.; Wang, C.; Liu, F.S.; Hu, S.J. Stress wave propagation analysis on vortex-induced vibration of marine risers. China Ocean Eng. 2017, 31, 30–36. [Google Scholar] [CrossRef]
- Teixeira, D.C.; Morooka, C.K. A time domain procedure to predict vortex-induced vibration response of marine risers. Ocean Eng. 2017, 142, 419–432. [Google Scholar] [CrossRef]
- Xu, J.; Wang, D.S.; Huang, H.; Duan, M.L.; Gu, J.J.; An, C. A vortex-induced vibration model for the fatigue analysis of a marine drilling riser. Ships Offshore Struct. 2017, 12, S280–S287. [Google Scholar] [CrossRef]
- Cabrera-Miranda, J.M.; Paik, J.K. On the probabilistic distribution of loads on a marine riser. Ocean Eng. 2017, 134, 105–118. [Google Scholar] [CrossRef] [Green Version]
- Do, K.D.; Lucey, A.D. Boundary stabilization of extensible and unshearable marine risers with large in-plane deflection. Automatica 2017, 77, 279–292. [Google Scholar] [CrossRef]
- Zhang, X.D.; Gou, R.Y.; Yang, W.W.; Chang, X.P. Vortex-induced vibration dynamics of a flexible fluid-conveying marine riser subjected to axial harmonic tension. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 8. [Google Scholar] [CrossRef]
- Liu, J. Study of Out-Of-Plane Motion of SCRs with Rigid Swing. Ph.D. Thesis, China Ocean University, Qingdao, China, 2013. [Google Scholar]
- Yao, X.L. On the Dynamic Response and Fatigue of Steel Catenary Riser with Rigid Swinging. Ph.D. Thesis, China Ocean University, Qingdao, China, 2018. [Google Scholar]
- Komachiy, M.S.; Tabeshpour, M.R. Wake and structure model for simulation of cross-flow/in-line vortex induced vibration of marine risers. J. Vibroeng. 2018, 20, 152–164. [Google Scholar]
- Domala, V.; Sharma, R. An experimental study on vortex-induced vibration response of marine riser with and without semi subm-ersible. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2018, 232, 176–198. [Google Scholar]
- Hong, K.S.; Shah, U.H. Vortex-induced vibrations and control of marine risers: A review. Ocean Eng. 2018, 152, 300–315. [Google Scholar] [CrossRef]
- Alfosail, F.K.; Nayfeh, A.H.; Younis, M.I. A state space approach for the eigenvalue problem of marine risers. Meccanica 2018, 53, 747–757. [Google Scholar] [CrossRef]
- Yang, W.W.; Ai, Z.J.; Zhang, X.D.; Gou, R.Y.; Chang, X.P. Nonlinear three-dimensional dynamics of a marine viscoelastic riser subjected to uniform flow. Ocean Eng. 2018, 149, 38–52. [Google Scholar] [CrossRef]
- O’Halloran, S.M.; Harte, A.M.; Shipway, P.H.; Leen, S.B. An experimental study on the key fretting variables for flexible marine risers. Tribol Int. 2018, 117, 141–151. [Google Scholar] [CrossRef]
- Wang, X.H.; Guan, Z.C.; Xu, Y.Q.; Tian, Y. Signal analysis of acoustic gas influx detection method at the bottom of marine riser in deepwater drilling. J. Process Control. 2018, 66, 23–38. [Google Scholar] [CrossRef]
- Hu, Y.L.; Cao, J.J.; Yao, B.h.; Zeng, Z.; Lian, L. Dynamic behaviors of a marine riser with variable length during the installation of a subsea production tree. J. Marine Sci. Technol. 2018, 23, 378–388. [Google Scholar] [CrossRef]
- Yang, J.X. Study on the properties of Lissajous’ Figures. J. Xihua Univ. Nat. Sci. 2008, 27, 98–100, 125. [Google Scholar]
- Yang, J.X. Study on the synthesized Path of Two Simple Harmonic Vibrations with one Vertical to another. J. Xihua Univ. Nat. Sci. 2008, 2, 5, 76–78, 82. [Google Scholar]
- Li, J.W.; Tang, Y.G.; Li, Y. Influence of areodynamic imbalance on an offshore wind turbine during pitch controller fault. Ocean Eng. 2017, 35, 37–43. [Google Scholar]








| Structure | Function | Material | Density (kg/m3) |
|---|---|---|---|
| Bearing layer | Load bearing, etc. | API X-65 | 7850 |
| Anticorrosive coating | Prevent osmotic corrosion | Epoxy resin | 1440 |
| Bonding layer | Interlayer bonding | Polypropylene | 980 |
| Thermal insulation layer | Cold oil not be transported | Foam Polypropylene | 800 |
| Protective layer | Prevent seabed damage, etc. | Polyethylene | 900 |
| Parameters | Value | Unit | Parameters | Value | Unit |
|---|---|---|---|---|---|
| The outer diameter | 0.355 | m | The moment of inertia | 0.36123 × 10−3 | m4 |
| The inner diameter | 0.305 | m | The outer diameter area | 0.99315 × 10−1 | m2 |
| Modulus elasticity | 207.0 | Gpa | The inner diameter area | 0.72966 × 10−1 | m2 |
| Minimum yield strength | 408.0 | MPa | Unit length mass | 0.2960 | kg/m3 |
| Poisson’s ratio | 0.3 | / | Unit length buoyancy | 0.2137 4 × 104 | N/m |
| Cdt | Load | Direction | Amplitude/m | Frequency/Hz | Wave | ZDL | RBS |
|---|---|---|---|---|---|---|---|
| 1 | Cab1 | Transverse flow | 3.0 | 0.093 | √ | √ | |
| 2 | Cab 2 | Transverse flow | 2.0 | 0.101 | √ | √ | |
| 3 | Cab 3 | Transverse flow | 1.0 | 0.111 | √ | √ | |
| 4 | Csw1 | Transverse flow | 3.0 | 0.093 | √ | √ | √ |
| 5 | Csw 2 | Transverse flow | 2.0 | 0.101 | √ | √ | √ |
| 6 | Csw 3 | Transverse flow | 1.0 | 0.111 | √ | √ | √ |
| Frequency | Theory | FFT | Literature [11] 0.27 m/s | Literature [11] 0.30 m/s | |
|---|---|---|---|---|---|
| WAVE (Hz) | 0.11622 | 0.11600 | / | / | |
| ZDL (Hz) | 0.09300 | 0.09299 | / | / | |
| RBS(Hz) | 0.02900 | 0.02400 | 0.02800 | 0.02860 | |
| BV (Hz) | 1st | 0.01600 | / | 0.01550 | 0.01560 |
| 2nd | 0.06400 | 0.06800 | / | / | |
| X/m | Y/m | |
|---|---|---|
| 10 | −15.8273 | −54.1376 |
| 80 | −163.2674 | −467.0530 |
| 140 | −343.3629 | −796.3470 |
| 200 | −616.8364 | −1049.0293 |
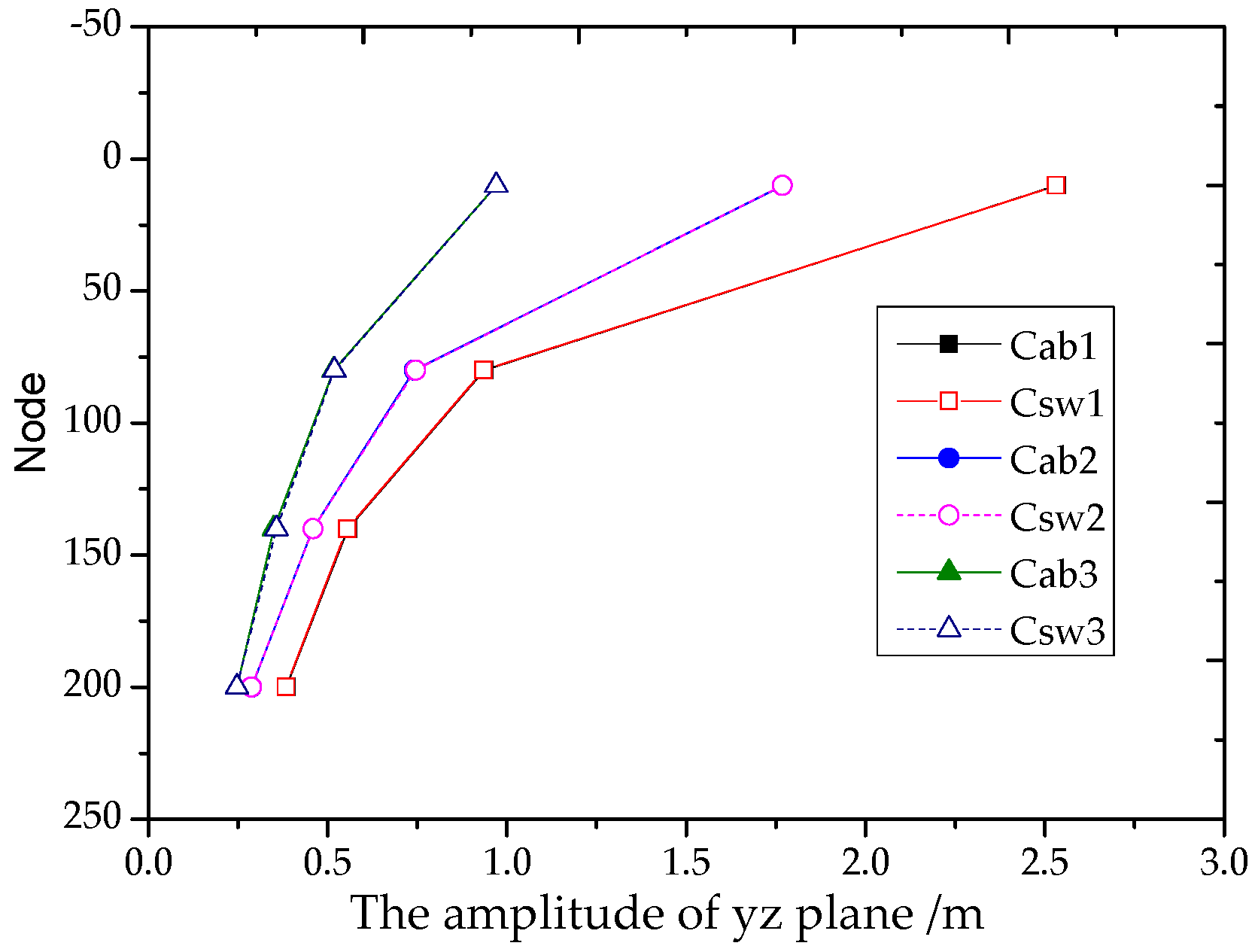
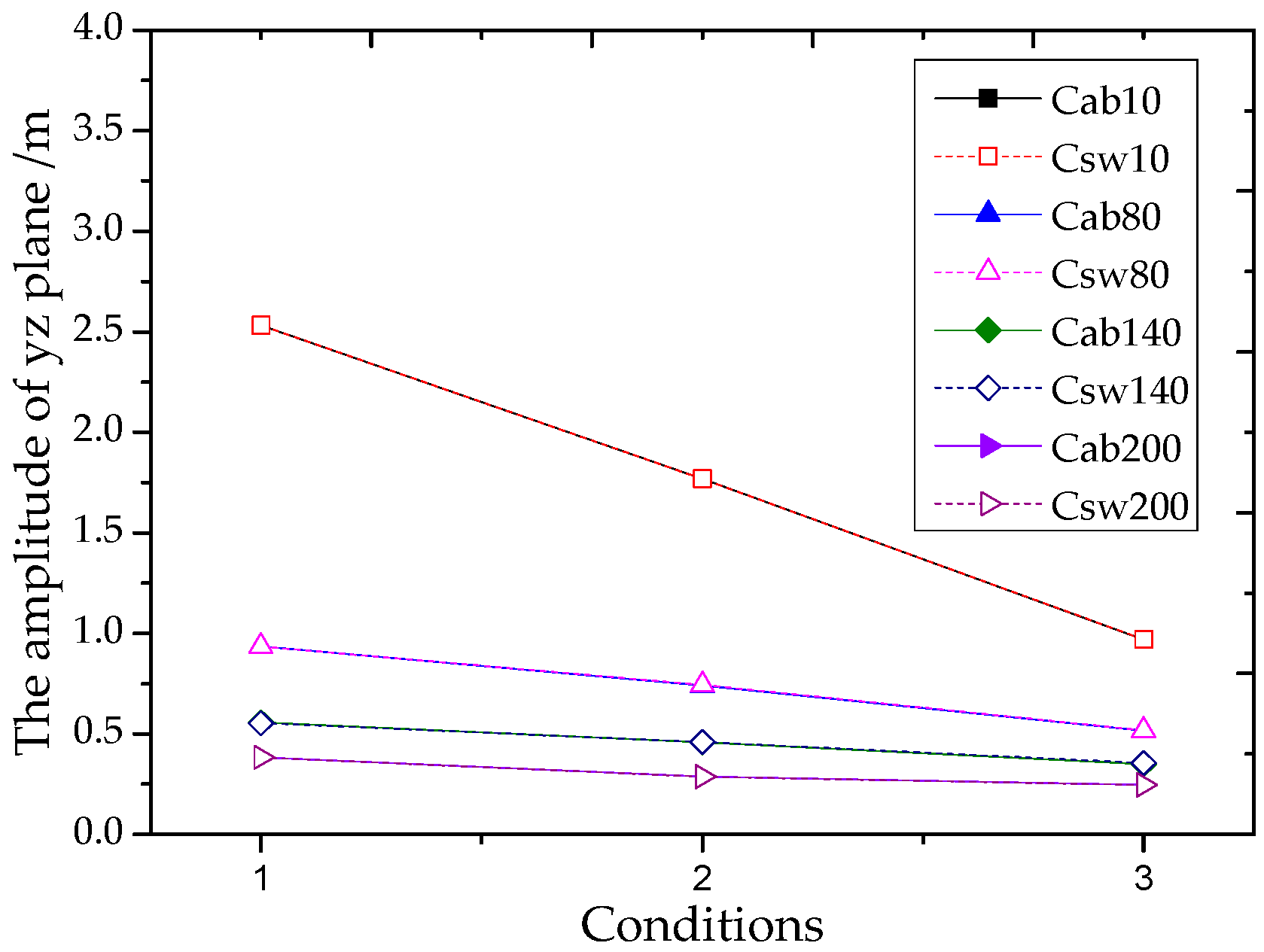
| Cdt | Node | Cab (m) | Csw (m) | Diff |
|---|---|---|---|---|
| 1 | 10th | 2.53294 | 2.53254 | −0.016% |
| 1 | 80th | 0.93671 | 0.93484 | −0.200% |
| 1 | 140th | 0.55687 | 0.55431 | −0.460% |
| 1 | 200th | 0.38464 | 0.38395 | −0.179% |
| 2 | 10th | 1.76859 | 1.76816 | −0.024% |
| 2 | 80th | 0.74119 | 0.74525 | 0.548% |
| 2 | 140th | 0.45918 | 0.45993 | 0.163% |
| 2 | 200th | 0.28813 | 0.28781 | −0.111% |
| 3 | 10th | 0.97038 | 0.97032 | −0.006% |
| 3 | 80th | 0.51709 | 0.51871 | 0.313% |
| 3 | 140th | 0.35021 | 0.35704 | 1.950% |
| 3 | 200th | 0.24737 | 0.24684 | −0.214% |
| Cdt | Node | Cabmax (m) | Cswmax (m) | Incmax | Cabmin (m) | Cswmin (m) | Incmin |
|---|---|---|---|---|---|---|---|
| 1 | 10th | 2.53031 | 2.52998 | −0.01% | −2.52323 | −2.52298 | −0.01% |
| 1 | 80th | 0.93399 | 0.92900 | −0.53% | −0.93500 | −0.93754 | 0.27% |
| 1 | 140th | 0.55306 | 0.54688 | −1.12% | −0.55430 | −0.55152 | −0.50% |
| 1 | 200th | 0.38398 | 0.38300 | −0.26% | −0.38312 | −0.38239 | −0.19% |
| 2 | 10th | 1.76981 | 1.76936 | −0.03% | −1.76465 | −1.76436 | −0.02% |
| 2 | 80th | 0.74551 | 0.74471 | −0.11% | −0.73664 | −0.74101 | 0.59% |
| 2 | 140th | 0.45820 | 0.46017 | 0.43% | −0.45952 | −0.45950 | 0.00% |
| 2 | 200th | 0.28697 | 0.28663 | −0.12% | −0.28717 | −0.28764 | 0.16% |
| 3 | 10th | 0.96836 | 0.96843 | 0.01% | −0.96587 | −0.96594 | 0.01% |
| 3 | 80th | 0.51933 | 0.52159 | 0.44% | −0.50926 | −0.51324 | 0.78% |
| 3 | 140th | 0.35072 | 0.35698 | 1.78% | −0.34172 | −0.34872 | 2.05% |
| 3 | 200th | 0.24683 | 0.24670 | −0.05% | −0.24590 | −0.24638 | 0.20% |
| Cdt | Node | Cabmean (m) | Cswmean (m) | Cabstd (m) | Cswstd (m) |
|---|---|---|---|---|---|
| 1 | 10th | 0.00315 | 0.00315 | 1.71816 | 1.71816 |
| 1 | 80th | −0.00238 | −0.00238 | 0.62457 | 0.62443 |
| 1 | 140th | 0.00111 | 0.00112 | 0.37026 | 0.37051 |
| 1 | 200th | 0.00144 | 0.00149 | 0.25996 | 0.25951 |
| 2 | 10th | 1.00 × 10−4 | 9.87 × 10−5 | 1.1907 | 1.19067 |
| 2 | 80th | 6.71 × 10−4 | 6.68 × 10−4 | 0.49967 | 0.4997 |
| 2 | 140th | 5.90 × 10−4 | 5.86 × 10−4 | 0.31063 | 0.31095 |
| 2 | 200th | 4.23 × 10−4 | 4.29 × 10−4 | 0.19729 | 0.19767 |
| 3 | 10th | 4.77 × 10−4 | 4.72 × 10−4 | 0.63321 | 0.63322 |
| 3 | 80th | 4.28 × 10−4 | 3.98 × 10−4 | 0.34035 | 0.34057 |
| 3 | 140th | 4.75 × 10−4 | 4.23 × 10−4 | 0.23391 | 0.23431 |
| 3 | 200th | 4.34 × 10−4 | 3.81 × 10−4 | 0.17002 | 0.16968 |
| Cdt | Node | Cabmax (m) | Cswmax (m) | Rdtcab | Rdtcsw | Diff | Nmlcab | Nmlcsw |
|---|---|---|---|---|---|---|---|---|
| 1 | 10th | 2.52716 | 2.52683 | 62.95% | 63.14% | 0.19% | 1.00 | 1.00 |
| 1 | 80th | 0.93637 | 0.93138 | 15.21% | 15.26% | 0.05% | 1.00 | 1.00 |
| 1 | 140th | 0.55195 | 0.54576 | 6.70% | 6.50% | −0.20% | 1.00 | 1.00 |
| 1 | 200th | 0.38254 | 0.38151 | 15.14% | 15.10% | −0.04% | 1.00 | 1.00 |
| 2 | 10th | 1.76971 | 1.76926 | 57.91% | 57.95% | 0.04% | 0.70 | 0.70 |
| 2 | 80th | 0.74484 | 0.74404 | 16.23% | 16.08% | −0.15% | 0.79 | 0.79 |
| 2 | 140th | 0.45761 | 0.45958 | 9.67% | 9.80% | 0.13% | 0.83 | 0.83 |
| 2 | 200th | 0.28655 | 0.28620 | 16.19% | 16.18% | −0.01% | 0.75 | 0.75 |
| 3 | 10th | 0.96788 | 0.96796 | 46.39% | 46.16% | −0.23% | 0.38 | 0.38 |
| 3 | 80th | 0.51890 | 0.52119 | 17.42% | 17.01% | −0.41% | 0.55 | 0.55 |
| 3 | 140th | 0.35025 | 0.35656 | 10.73% | 11.39% | 0.66% | 0.62 | 0.63 |
| 3 | 200th | 0.24640 | 0.24632 | 25.46% | 25.45% | −0.01% | 0.64 | 0.64 |
| Cdt | Node | Cabmin (m) | Cswmin (m) | Rdtcab | Rdtcsw | Diff | Nmlcab | Nmlcsw |
|---|---|---|---|---|---|---|---|---|
| 1 | 10th | −2.52323 | −2.52298 | 62.94% | 62.84% | −0.10% | 1.00 | 1.00 |
| 1 | 80th | −0.9350 | −0.93754 | 15.09% | 15.30% | 0.21% | 1.00 | 1.00 |
| 1 | 140th | −0.5543 | −0.55152 | 6.78% | 6.70% | −0.08% | 1.00 | 1.00 |
| 1 | 200th | −0.38312 | −0.38239 | 15.18% | 15.16% | −0.03% | 1.00 | 1.00 |
| 2 | 10th | −1.76465 | −1.76436 | 58.26% | 58.00% | −0.25% | 0.70 | 0.70 |
| 2 | 80th | −0.73664 | −0.74101 | 15.70% | 15.96% | 0.25% | 0.79 | 0.79 |
| 2 | 140th | −0.45952 | −0.45950 | 9.77% | 9.74% | −0.03% | 0.83 | 0.83 |
| 2 | 200th | −0.28717 | −0.28764 | 16.27% | 16.30% | 0.03% | 0.75 | 0.75 |
| 3 | 10th | −0.96587 | −0.96594 | 47.27% | 46.87% | −0.41% | 0.38 | 0.38 |
| 3 | 80th | −0.50926 | −0.51324 | 17.35% | 17.03% | −0.31% | 0.54 | 0.55 |
| 3 | 140th | −0.34172 | −0.34872 | 9.92% | 10.59% | 0.67% | 0.62 | 0.63 |
| 3 | 200th | −0.24590 | −0.24638 | 25.46% | 25.51% | 0.05% | 0.64 | 0.64 |
| C | Node | X (Hz) | Cab/Y (m2·s) | Csw/Y (m2·s) |
|---|---|---|---|---|
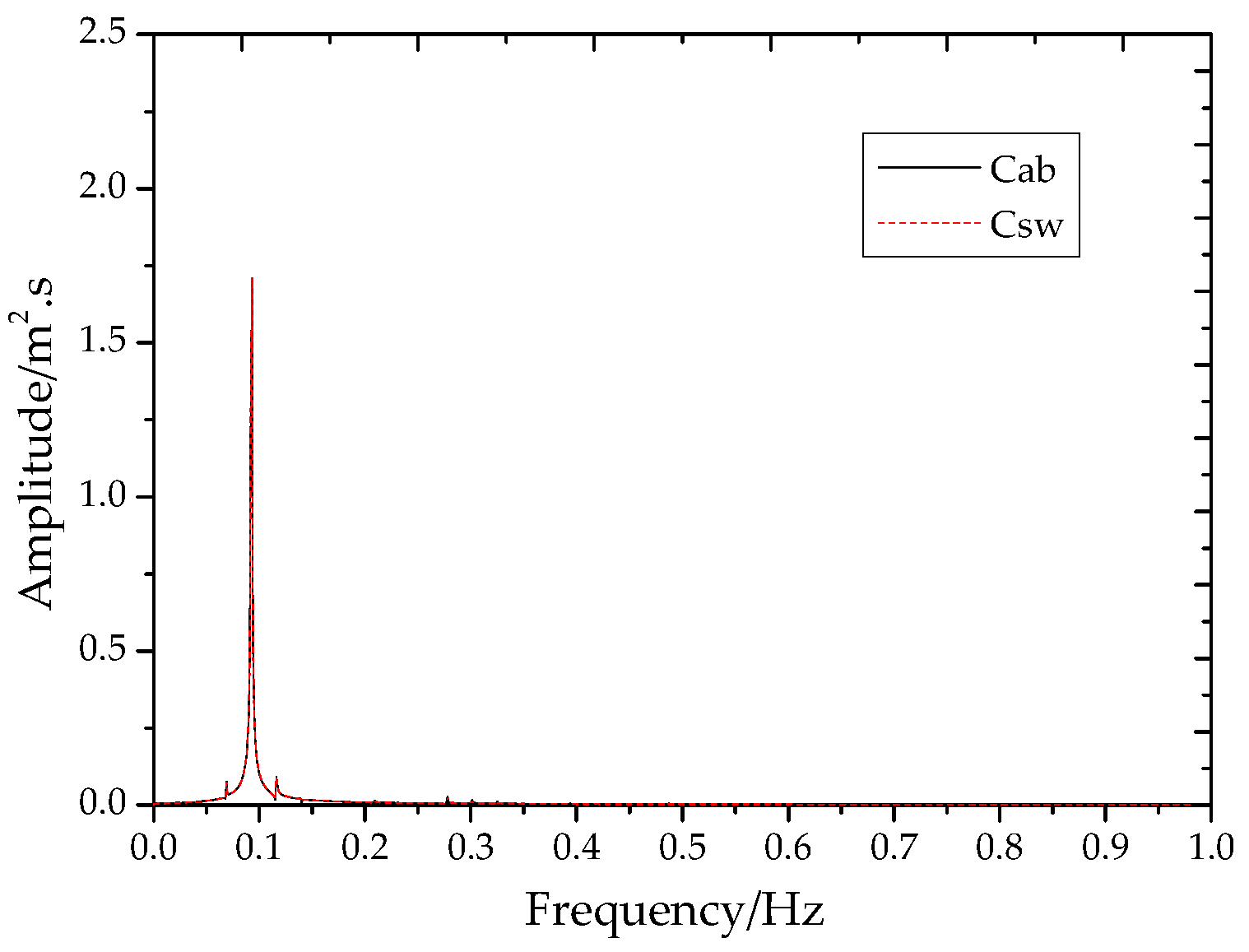
| 1 | 10th | 0.092991 | 1.710155 | 1.710178 |
| 2 | 10th | 0.100990 | 1.676353 | 1.676343 |
| 3 | 10th | 0.110989 | 0.885023 | 0.885041 |
| Node | Cdt | RBS | RBS | BV | BV | ZDL | ZDL | WAVE | WAVE |
|---|---|---|---|---|---|---|---|---|---|
| X (Hz) | Y (m2·s) | X (Hz) | Y (m2·s) | X (Hz) | Y (m2·s) | X (Hz) | Y (m2·s) | ||
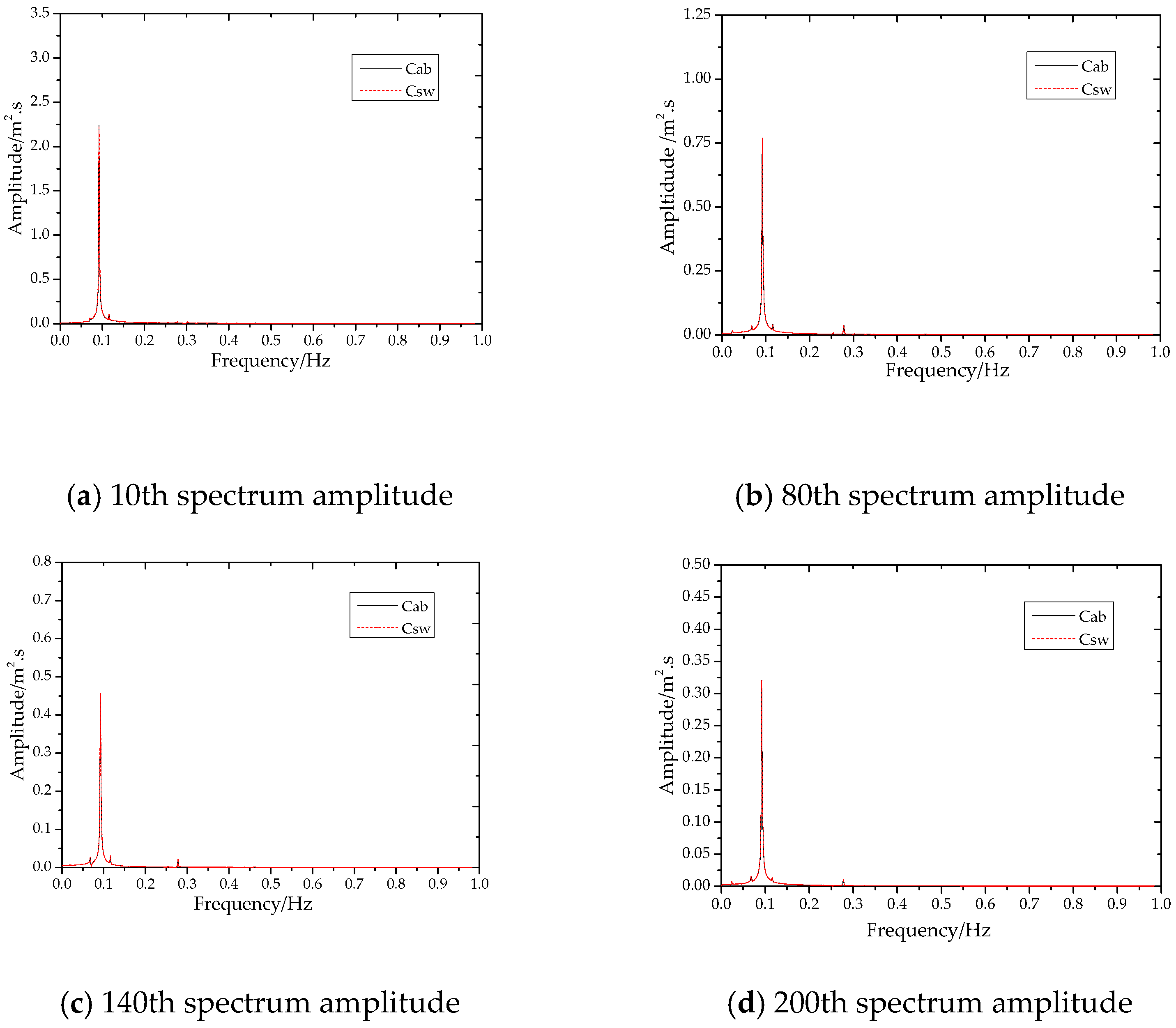
| 10th | Cab | 0.024 | 0.011804 | 0.0681 | 0.021044 | 0.0921 | 2.238628 | 0.1161 | 0.107761 |
| Csw | 0.024 | 0.012534 | 0.0681 | 0.020742 | 0.0921 | 2.223184 | 0.1161 | 0.105901 | |
| 80th | Cab | 0.024 | 0.016019 | 0.0680 | 0.035739 | 0.0920 | 0.770012 | 0.1160 | 0.041897 |
| Csw | 0.024 | 0.016045 | 0.0681 | 0.035919 | 0.0921 | 0.769957 | 0.1161 | 0.038988 | |
| 140th | Cab | 0.024 | 0.005458 | 0.0681 | 0.027404 | 0.0920 | 0.457074 | 0.1161 | 0.025370 |
| Csw | 0.024 | 0.005445 | 0.0681 | 0.027346 | 0.0920 | 0.457155 | 0.1161 | 0.029915 | |
| 200th | Cab | 0.024 | 0.007584 | 0.0680 | 0.015419 | 0.0920 | 0.320702 | 0.1160 | 0.013523 |
| Csw | 0.024 | 0.007606 | 0.0680 | 0.015786 | 0.0920 | 0.320106 | 0.1160 | 0.014074 | |
| Theory | 0.0290 | / | 0.0640 | / | 0.0930 | / | 0.1162 |
| Node | Cdt | RBS | BV | ZDL | WAVE |
|---|---|---|---|---|---|
| 10th | Cab | 0.496% | 0.884% | 94.090% | 4.529% |
| Csw | 0.531% | 0.878% | 94.109% | 4.483% | |
| 80th | Cab | 1.855% | 4.138% | 89.156% | 4.851% |
| Csw | 1.864% | 4.172% | 89.435% | 4.529% | |
| 140th | Cab | 1.059% | 5.318% | 88.700% | 4.923% |
| Csw | 1.047% | 5.260% | 87.938% | 5.754% | |
| 200th | Cab | 2.123% | 4.316% | 89.775% | 3.786% |
| Csw | 2.127% | 4.415% | 89.522% | 3.936% |
| Cdt | Node | Cabx (Hz) | Caby (m2·s) | Cswx (Hz) | Cswy (m2·s) | Cabrdt | Cswrdt | Diffrdt |
|---|---|---|---|---|---|---|---|---|
| 1 | 10th | 0.092991 | 2.238628 | 0.092991 | 2.223184 | 65.60% | 65.37% | −0.24% |
| 1 | 80th | 0.092991 | 0.770012 | 0.092991 | 0.769957 | 13.98% | 14.07% | 0.09% |
| 1 | 140th | 0.092991 | 0.457074 | 0.092991 | 0.457155 | 6.09% | 6.16% | 0.07% |
| 1 | 200th | 0.092991 | 0.320702 | 0.092991 | 0.320106 | 14.33% | 14.40% | 0.07% |
| 2 | 10th | 0.100990 | 1.209967 | 0.100990 | 1.209961 | 62.08% | 62.09% | 0.01% |
| 2 | 80th | 0.100990 | 0.458852 | 0.100990 | 0.458673 | 11.75% | 11.73% | −0.02% |
| 2 | 140th | 0.100990 | 0.316691 | 0.100990 | 0.316708 | 9.46% | 9.43% | −0.03% |
| 2 | 200th | 0.100990 | 0.202235 | 0.100990 | 0.202626 | 16.71% | 16.75% | 0.03% |
| 3 | 10th | 0.110989 | 0.597511 | 0.110989 | 0.597504 | 46.20% | 46.24% | 0.04% |
| 3 | 80th | 0.110989 | 0.321454 | 0.110989 | 0.321218 | 16.88% | 16.87% | −0.01% |
| 3 | 140th | 0.110989 | 0.220580 | 0.110989 | 0.220394 | 10.02% | 10.04% | 0.03% |
| 3 | 200th | 0.110989 | 0.160731 | 0.110989 | 0.160395 | 26.90% | 26.84% | −0.06% |
| Cdt | Node | X (Hz) | Caby (m2·s) | Cswy (m2·s) | Diff | Cabnml | Cswnml |
|---|---|---|---|---|---|---|---|
| 1 | 10th | 0.092991 | 2.238628 | 2.223184 | −0.69% | 1.00 | 1.00 |
| 2 | 10th | 0.100990 | 1.209967 | 1.209961 | 0.00% | 0.54 | 0.54 |
| 3 | 10th | 0.110989 | 0.597511 | 0.597504 | 0.00% | 0.27 | 0.27 |
| 1 | 80th | 0.092991 | 0.770012 | 0.769957 | −0.01% | 1.00 | 1.00 |
| 2 | 80th | 0.100990 | 0.458852 | 0.458673 | −0.04% | 0.60 | 0.60 |
| 3 | 80th | 0.110989 | 0.321454 | 0.321218 | −0.07% | 0.42 | 0.42 |
| 1 | 140th | 0.092991 | 0.457074 | 0.457155 | 0.02% | 1.00 | 1.00 |
| 2 | 140th | 0.100990 | 0.316691 | 0.316708 | 0.01% | 0.69 | 0.69 |
| 3 | 140th | 0.110989 | 0.22058 | 0.220394 | −0.08% | 0.48 | 0.48 |
| 1 | 200th | 0.092991 | 0.320702 | 0.320106 | −0.19% | 1.00 | 1.00 |
| 2 | 200th | 0.100990 | 0.202235 | 0.202626 | 0.19% | 0.63 | 0.63 |
| 3 | 200th | 0.110989 | 0.160731 | 0.160395 | −0.21% | 0.50 | 0.50 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, B.; Huang, W.; Yao, X.; Liu, J.; Fu, X. Influences of the Load of Suspension Point in the z Direction and Rigid Body Oscillation on Steel Catenary Riser Displacement and Frequency Under Wave Action. Energies 2019, 12, 273. https://doi.org/10.3390/en12020273
Zhu B, Huang W, Yao X, Liu J, Fu X. Influences of the Load of Suspension Point in the z Direction and Rigid Body Oscillation on Steel Catenary Riser Displacement and Frequency Under Wave Action. Energies. 2019; 12(2):273. https://doi.org/10.3390/en12020273
Chicago/Turabian StyleZhu, Bo, Weiping Huang, Xinglong Yao, Juan Liu, and Xiaoyan Fu. 2019. "Influences of the Load of Suspension Point in the z Direction and Rigid Body Oscillation on Steel Catenary Riser Displacement and Frequency Under Wave Action" Energies 12, no. 2: 273. https://doi.org/10.3390/en12020273





