A Theoretical Study on Performance and Design Optimization of Linear Dielectric Compound Parabolic Concentrating Photovoltaic Systems
Abstract
:1. Introduction
2. Three-Dimensional Radiation Transfer Model
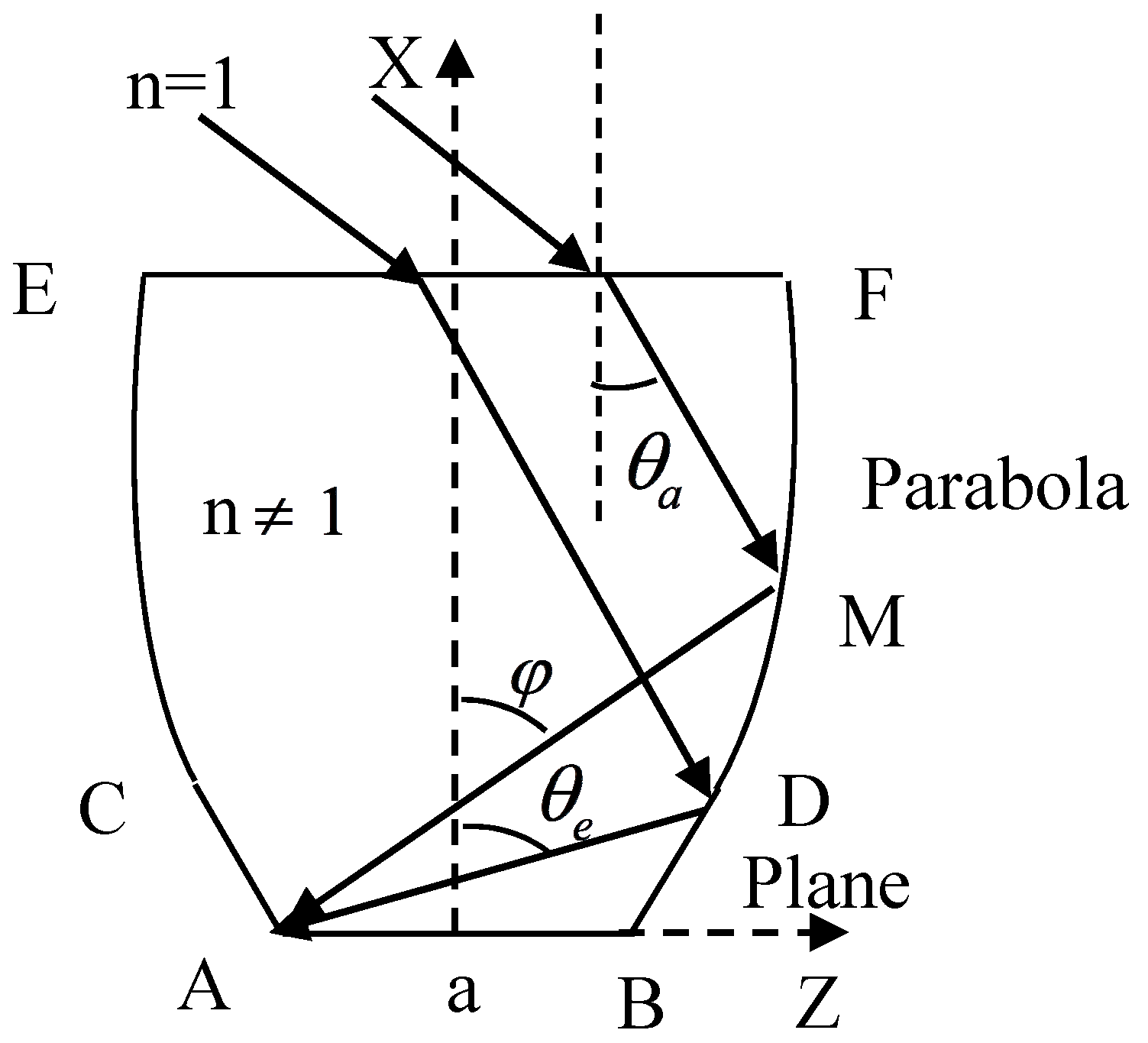
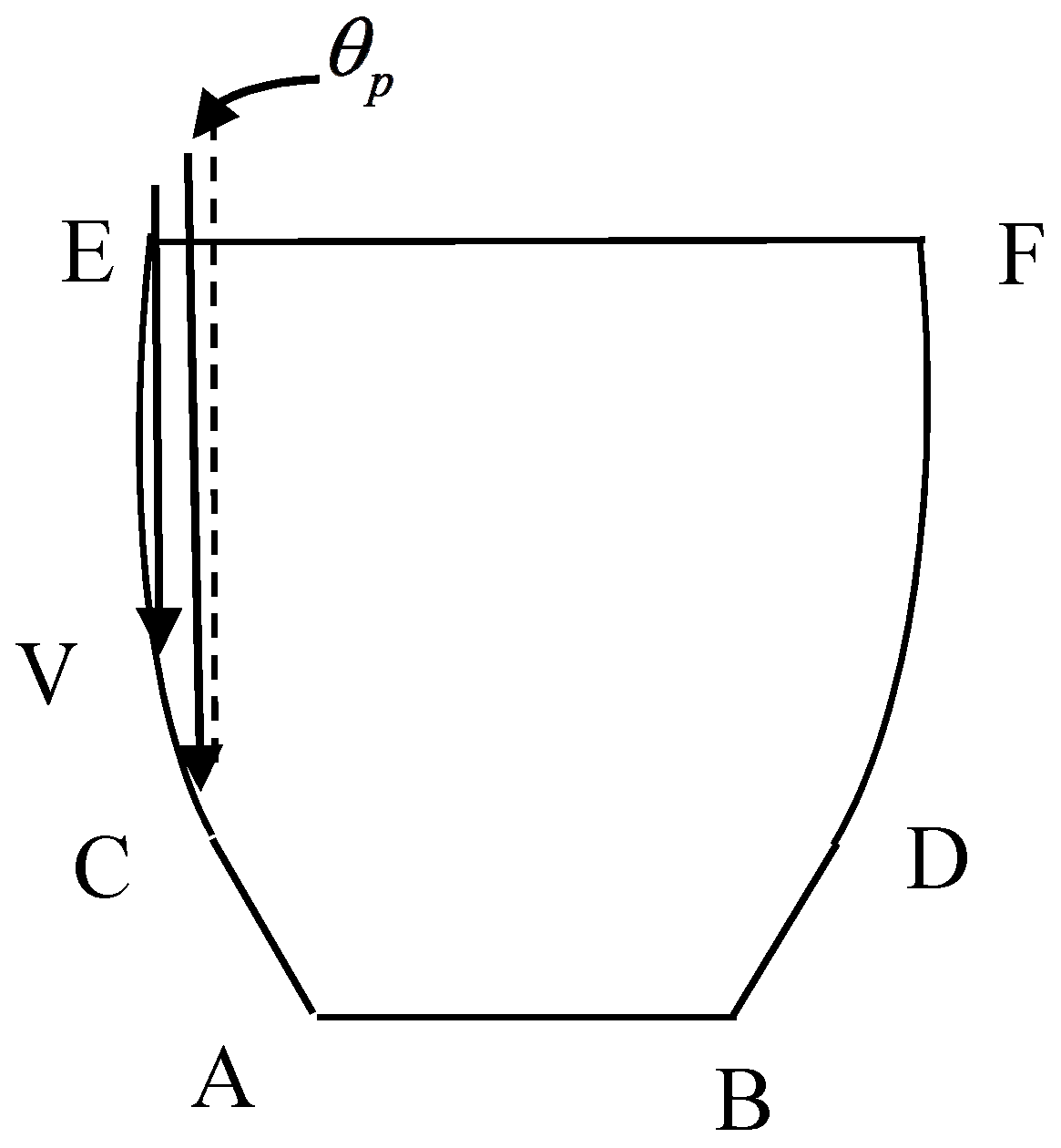
2.1. Equation of Linear DCPC’s Walls
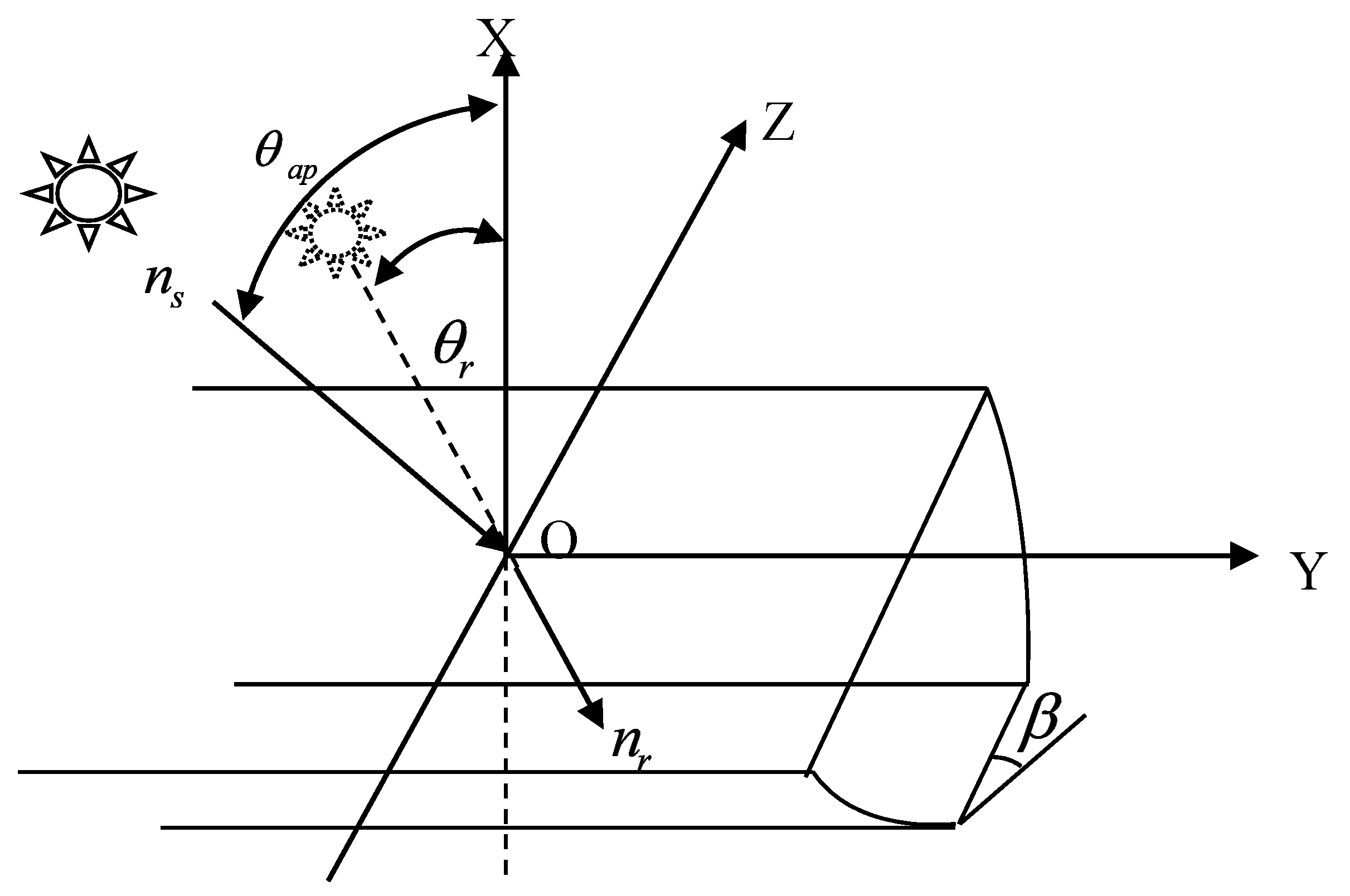
2.2. Vectors of Incident and Refractive Rays
2.3. Transmittance of Solar Rays at Air-Dielectric Aperture
2.4. Optical and Photovoltaic Performance of Linear DCPVs
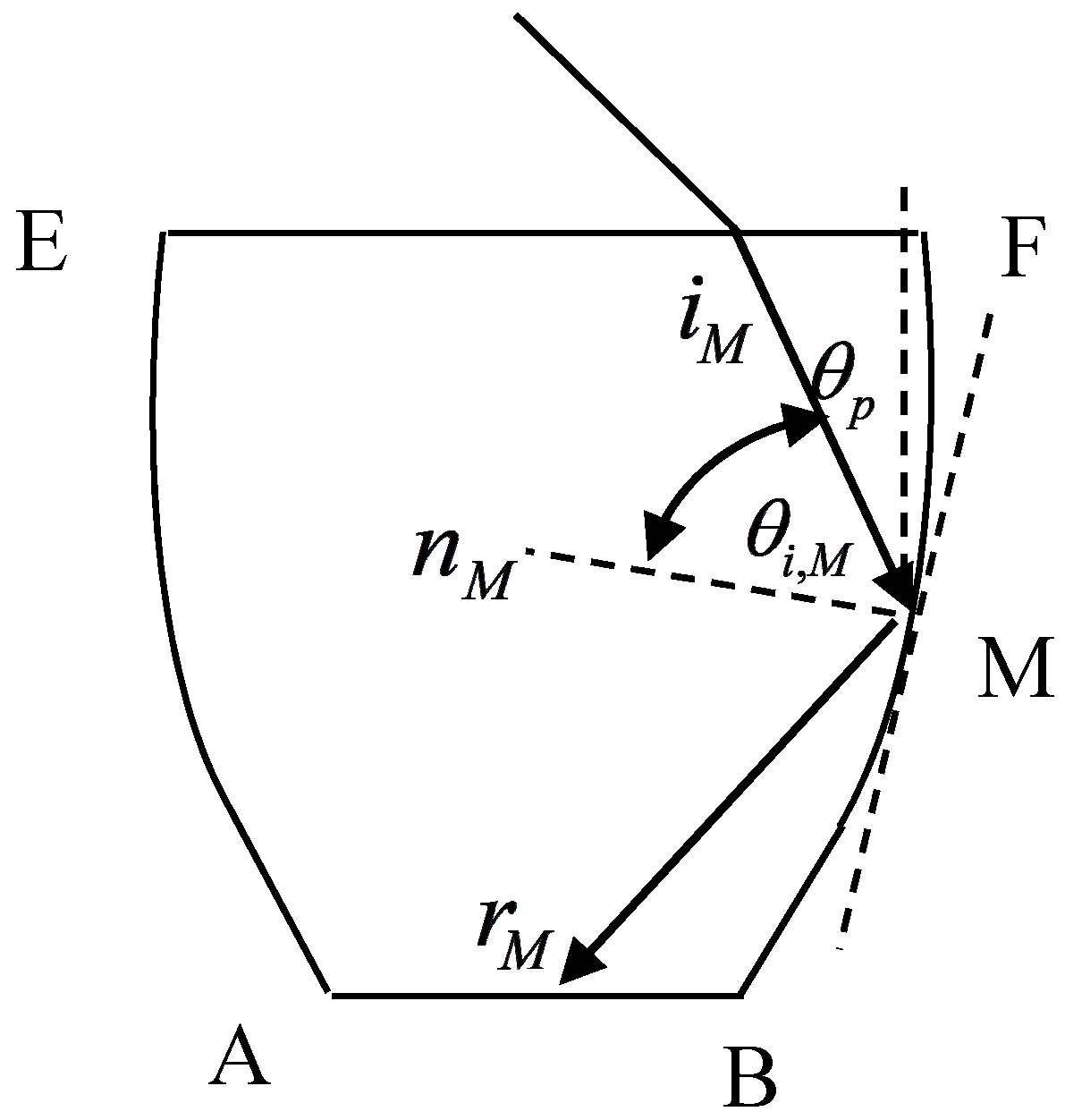
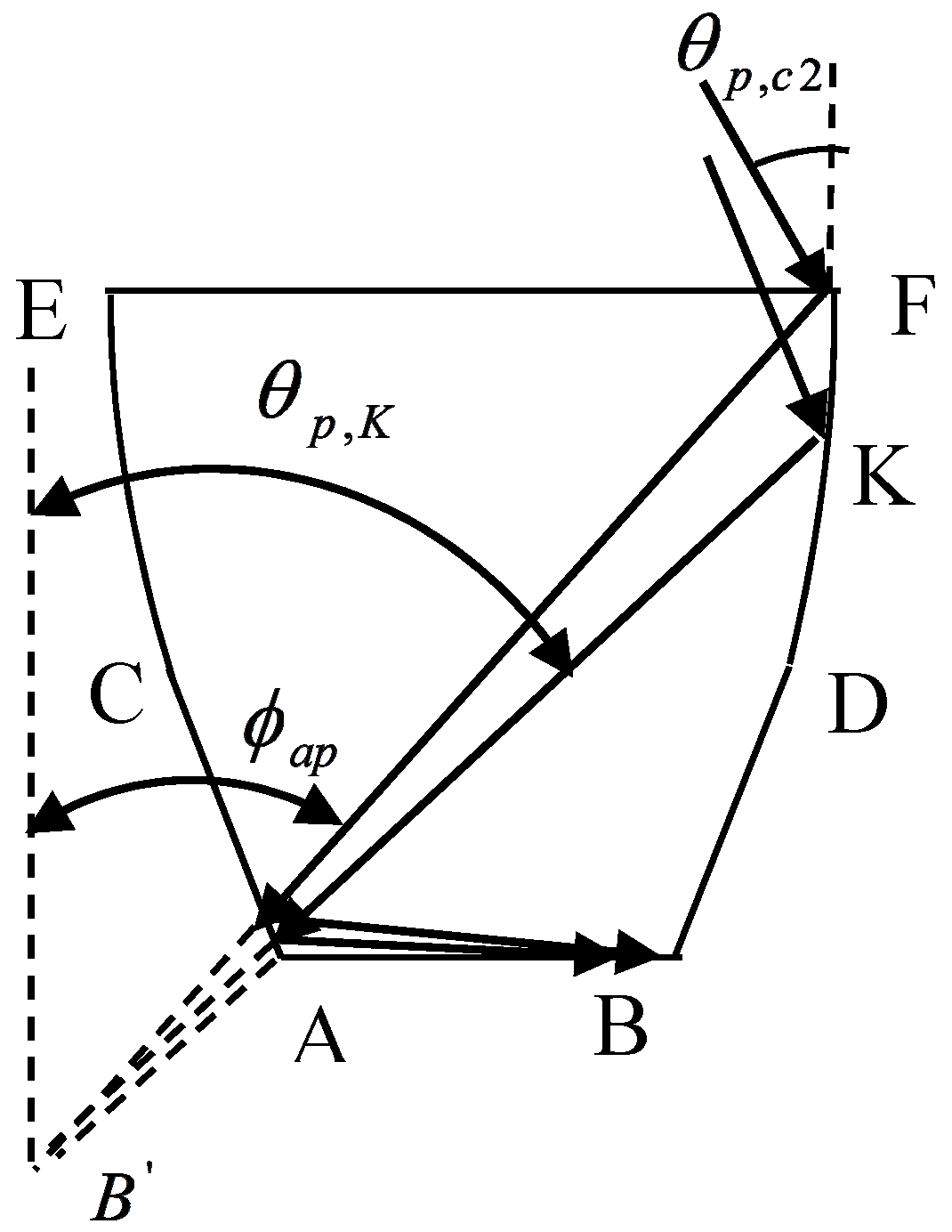
2.4.1. Calculation of and
2.4.2. Calculation of and
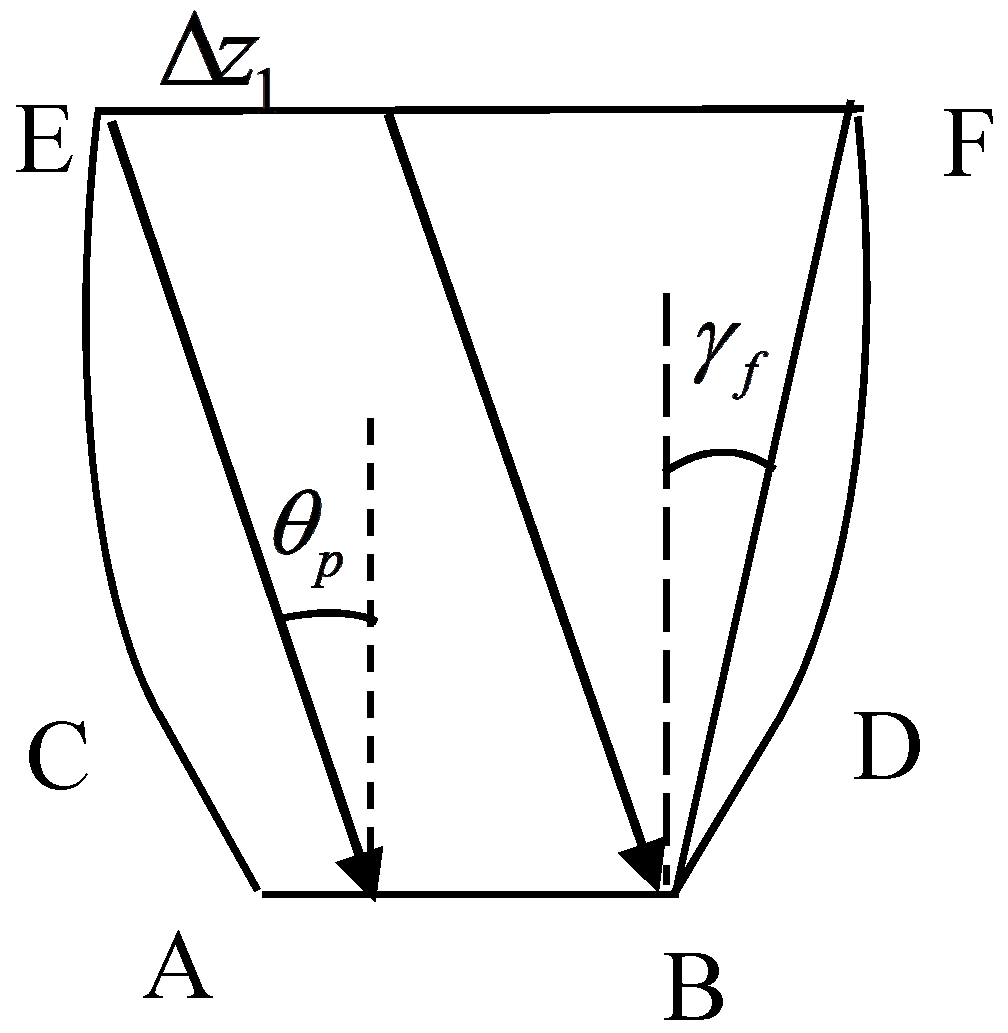
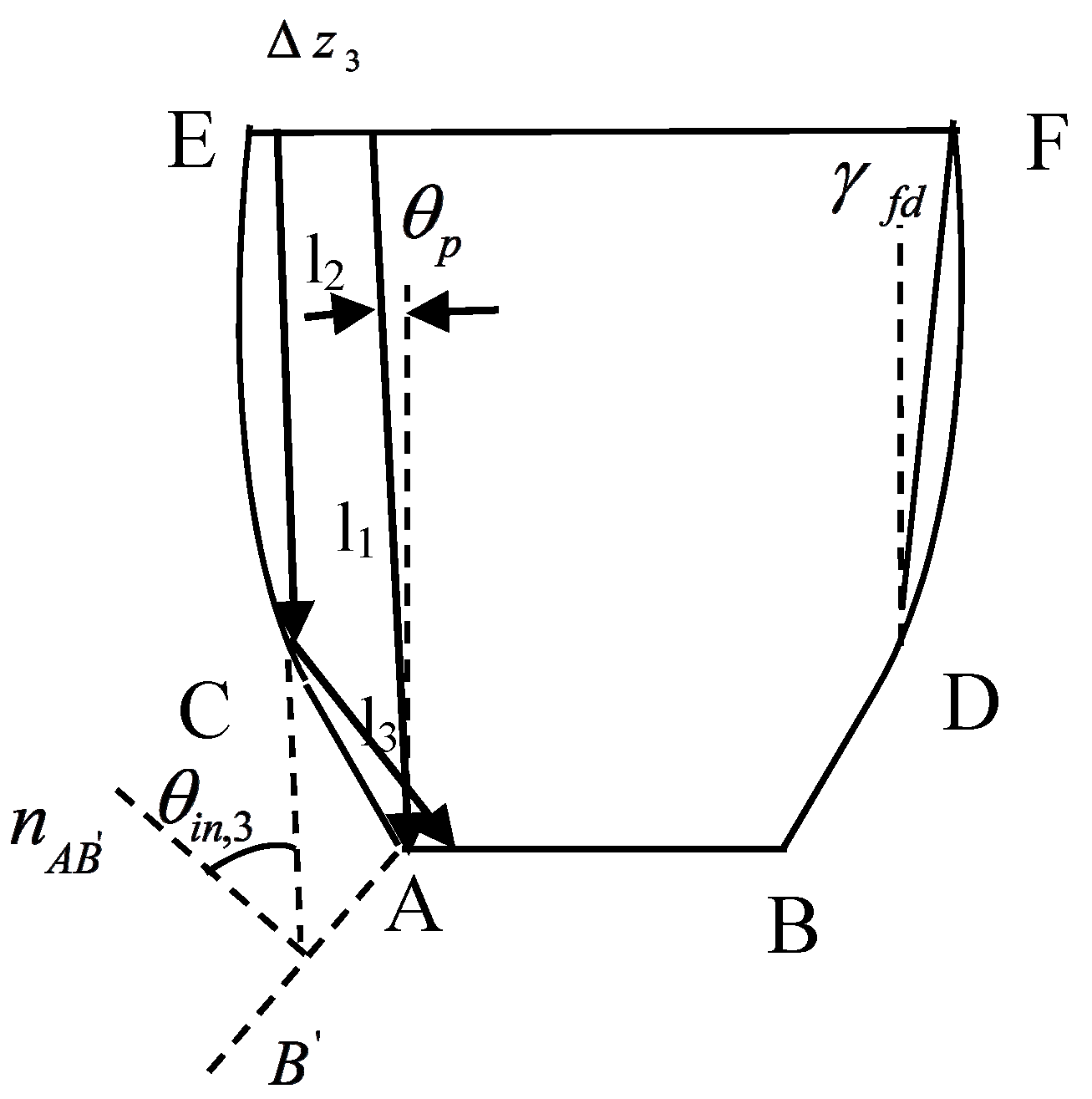
2.4.3. Calculation of and
2.4.4. Method for calculating and
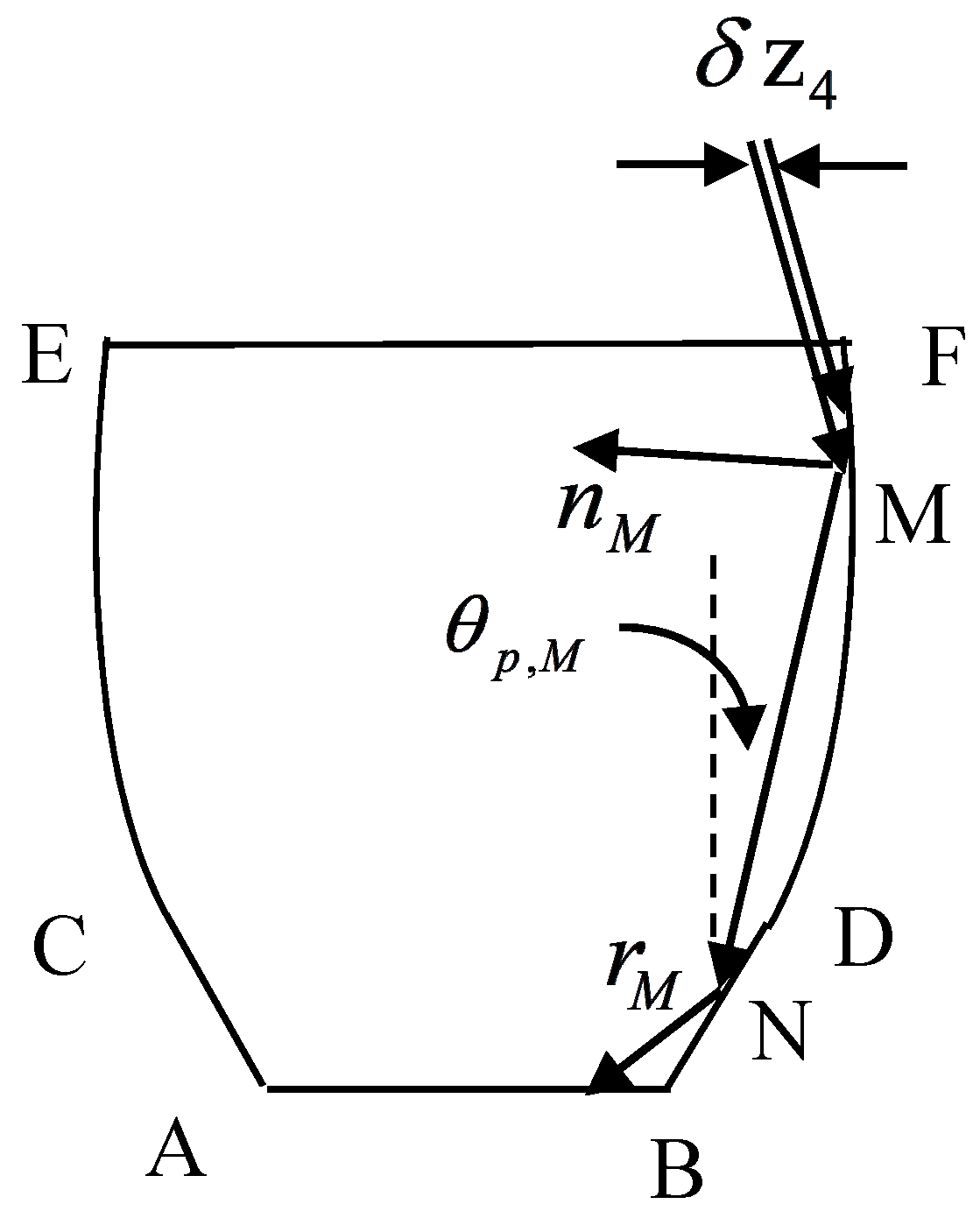
2.4.5. Calculation of and
2.4.6. Calculation of and
3. Annual Optical and Photovoltaic Performance of DCPVs
4. Results and Discussions
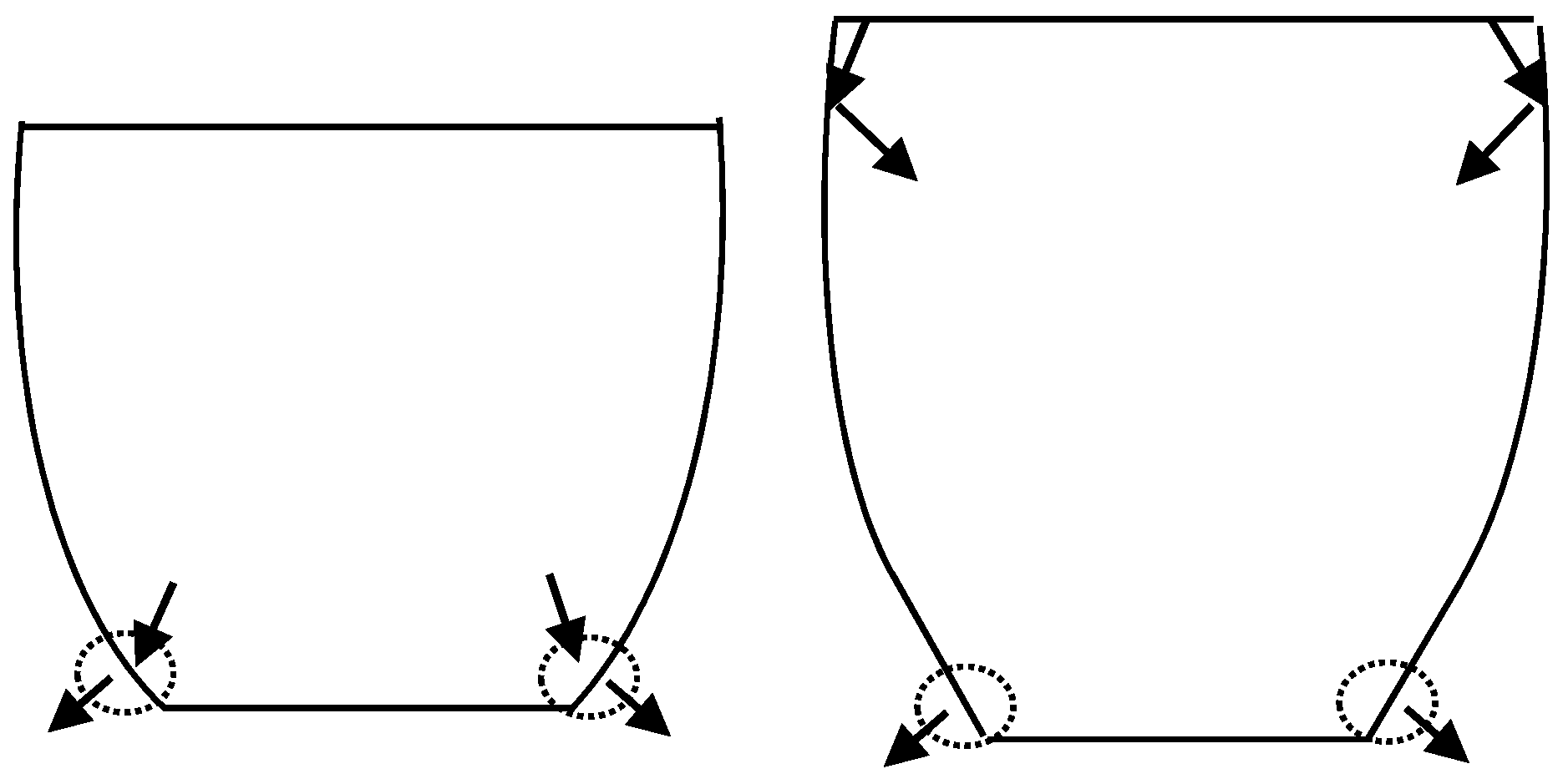
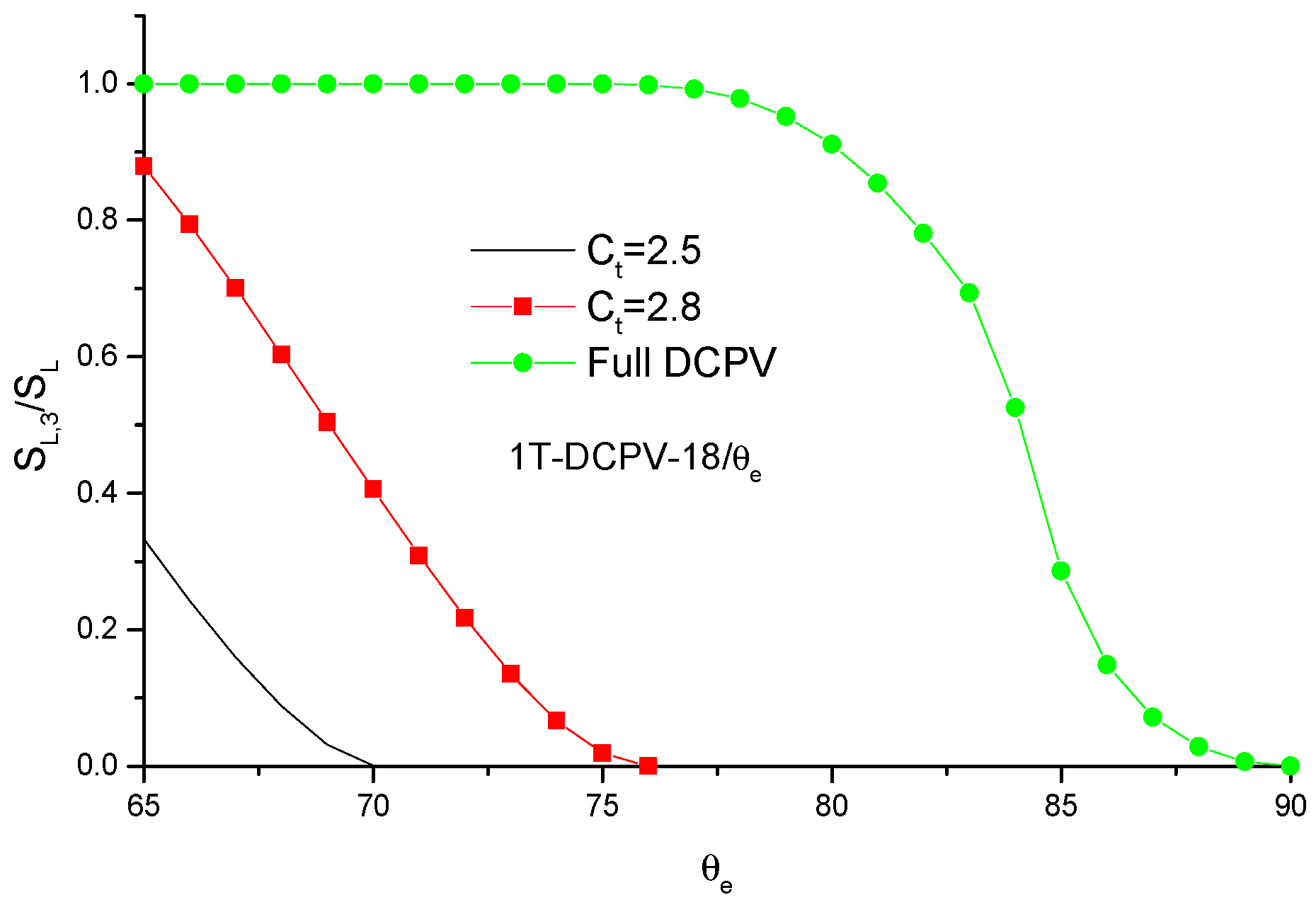
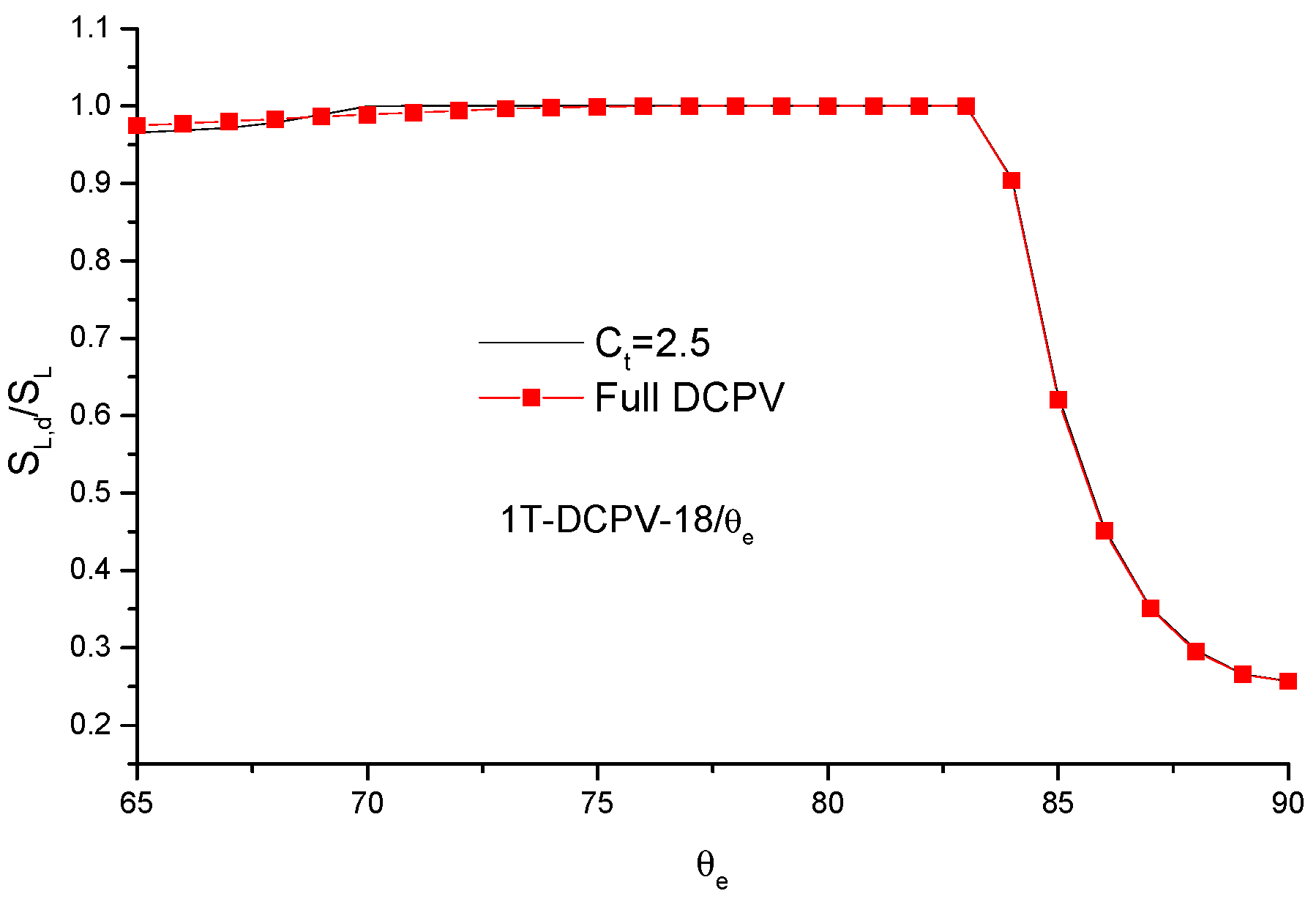
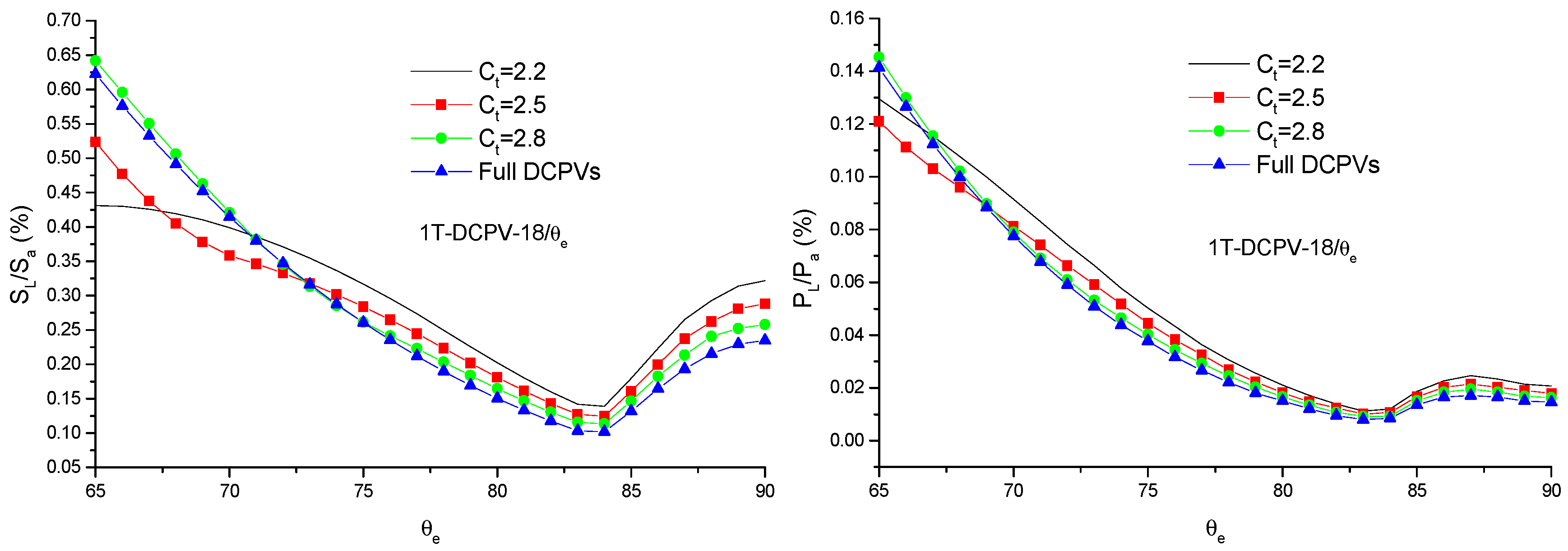
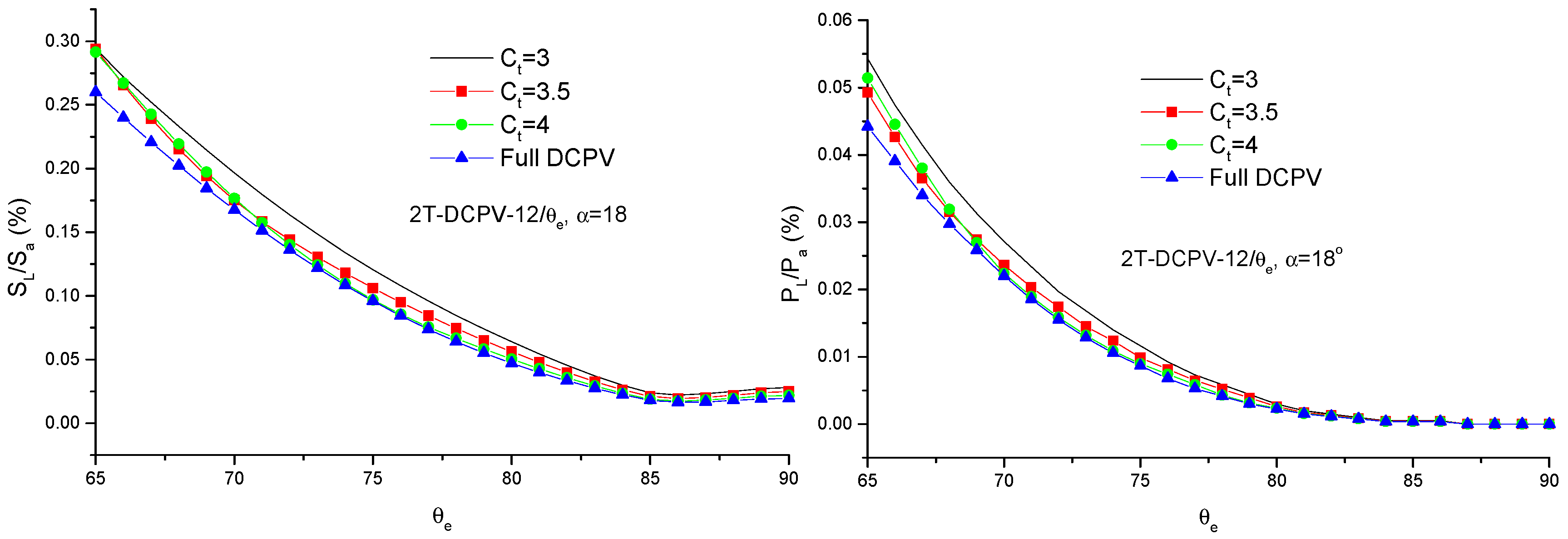
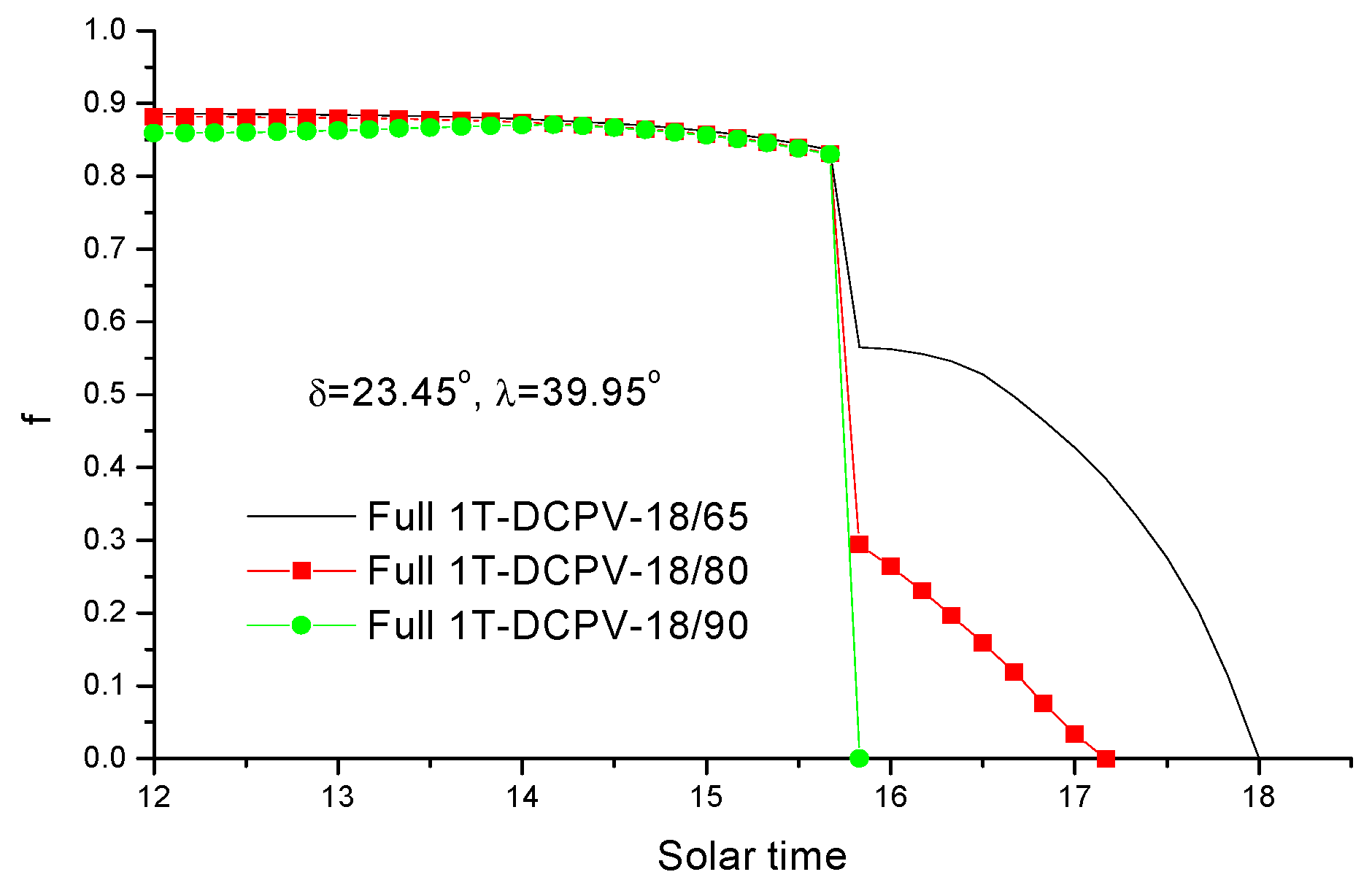
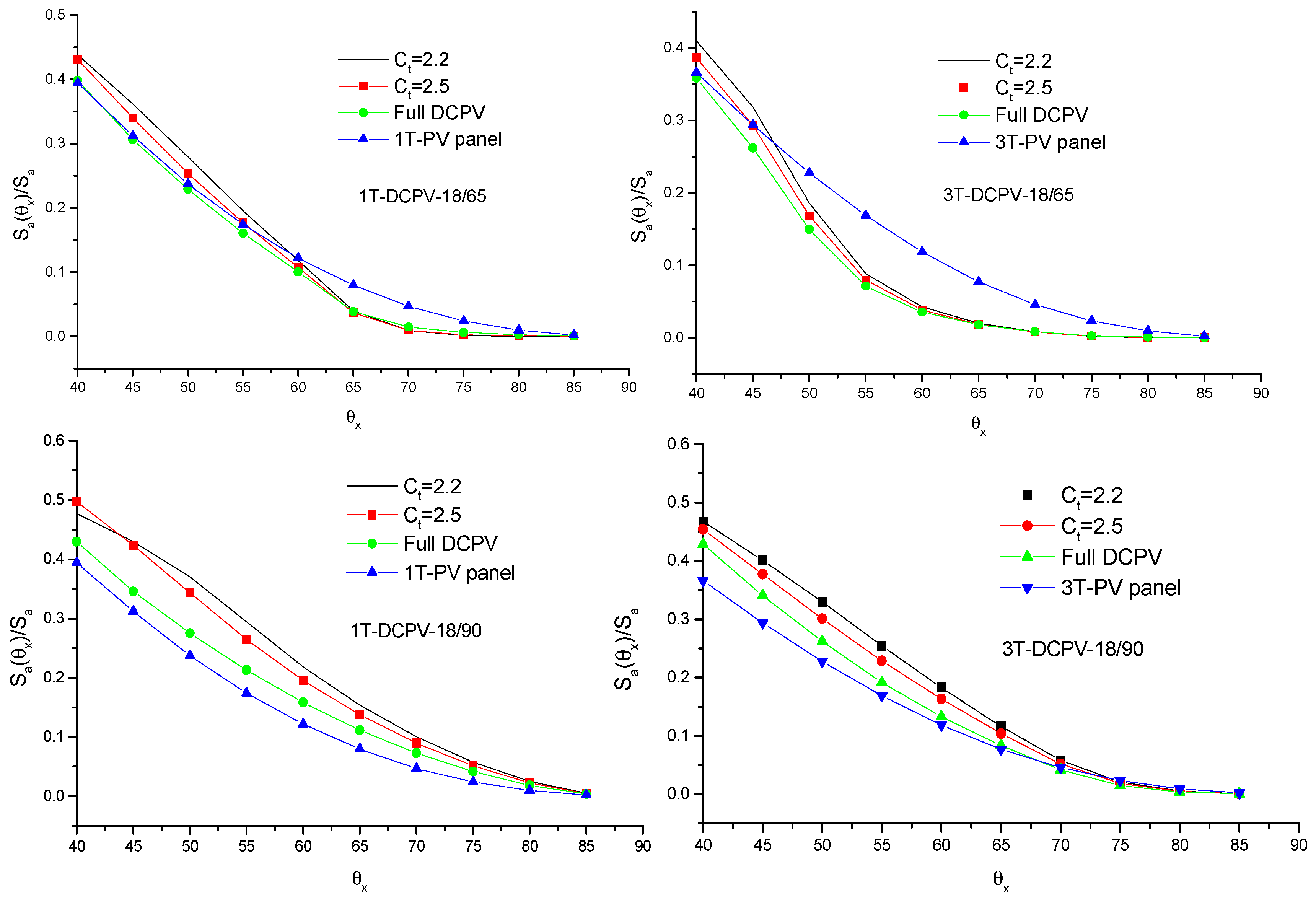
4.1. Radiation Leakage from Walls
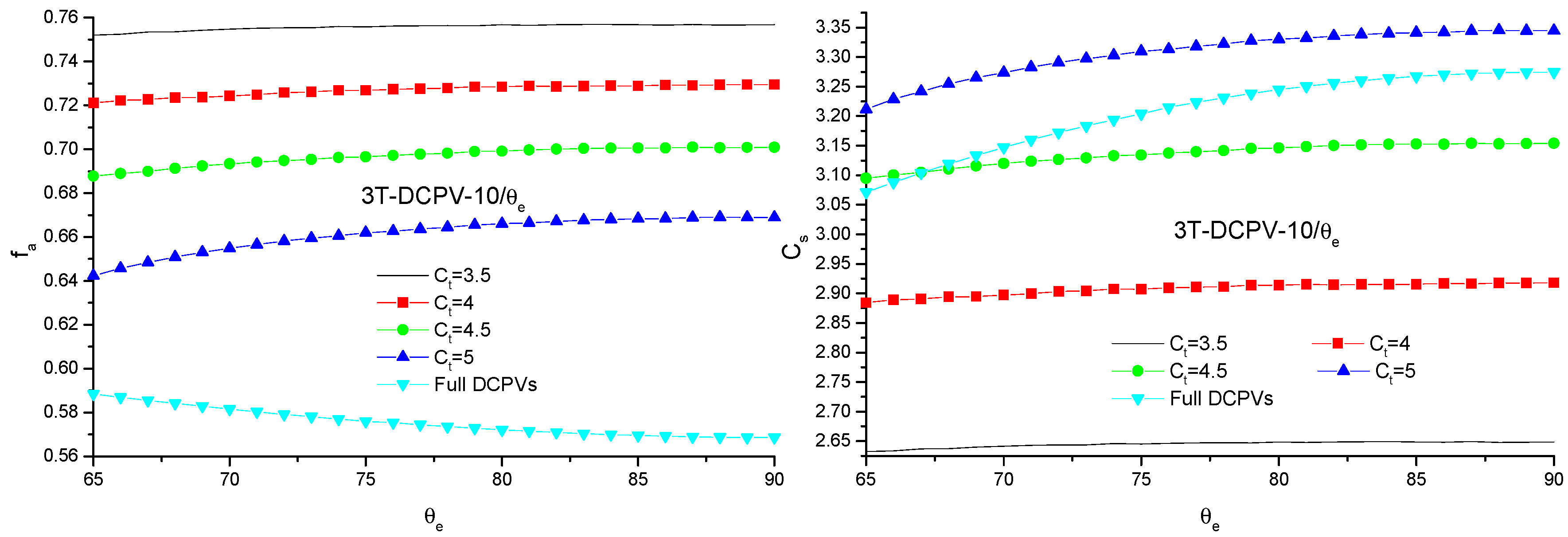
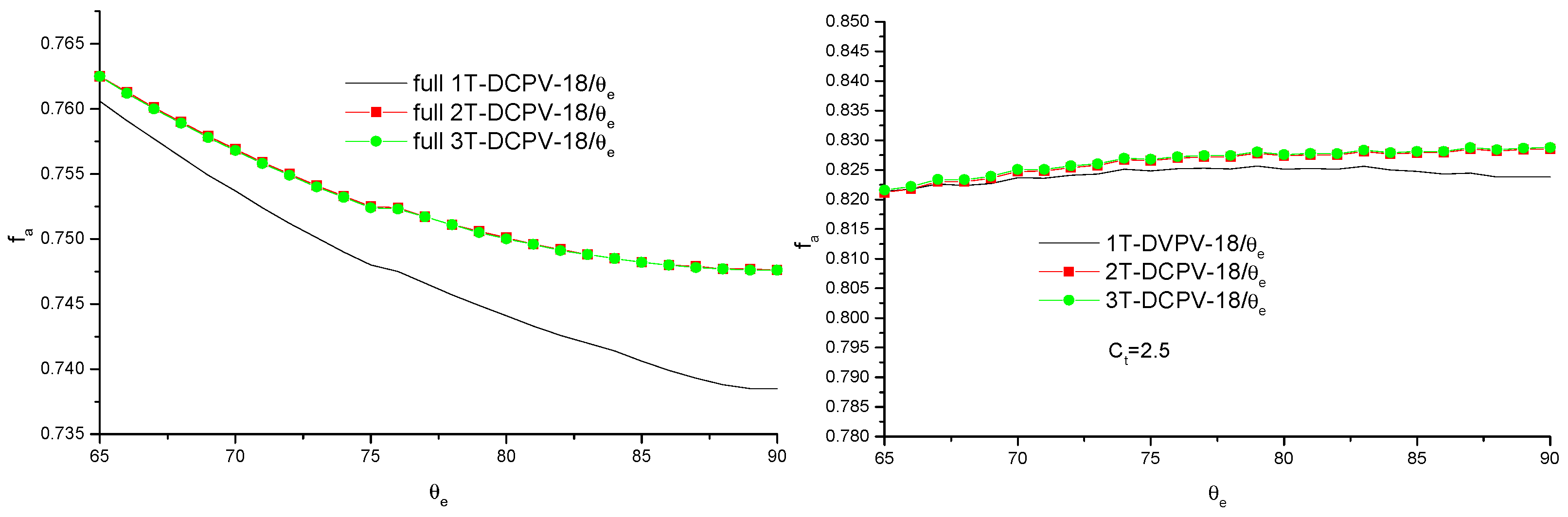
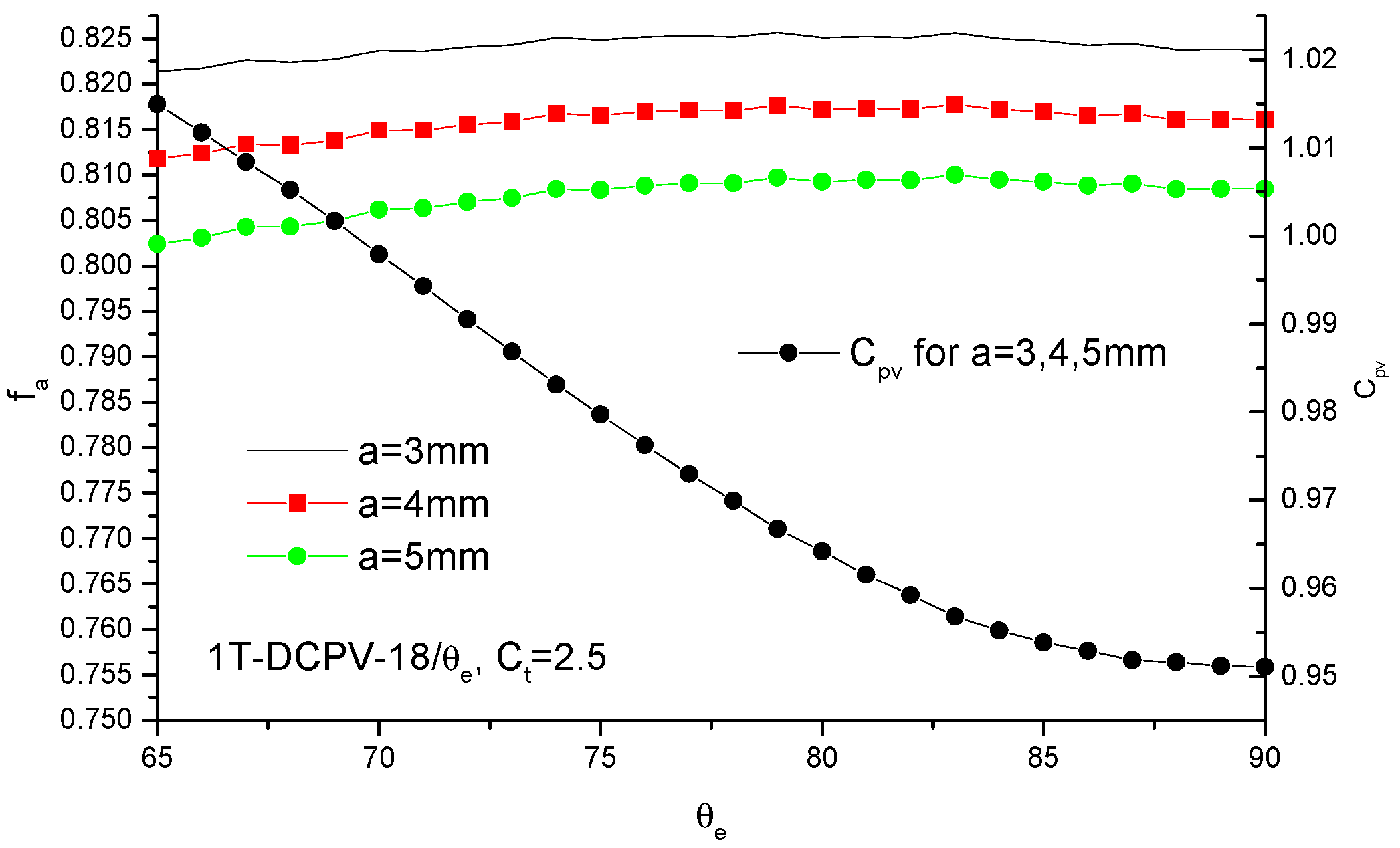
4.2. Optical Performance of DCPVs
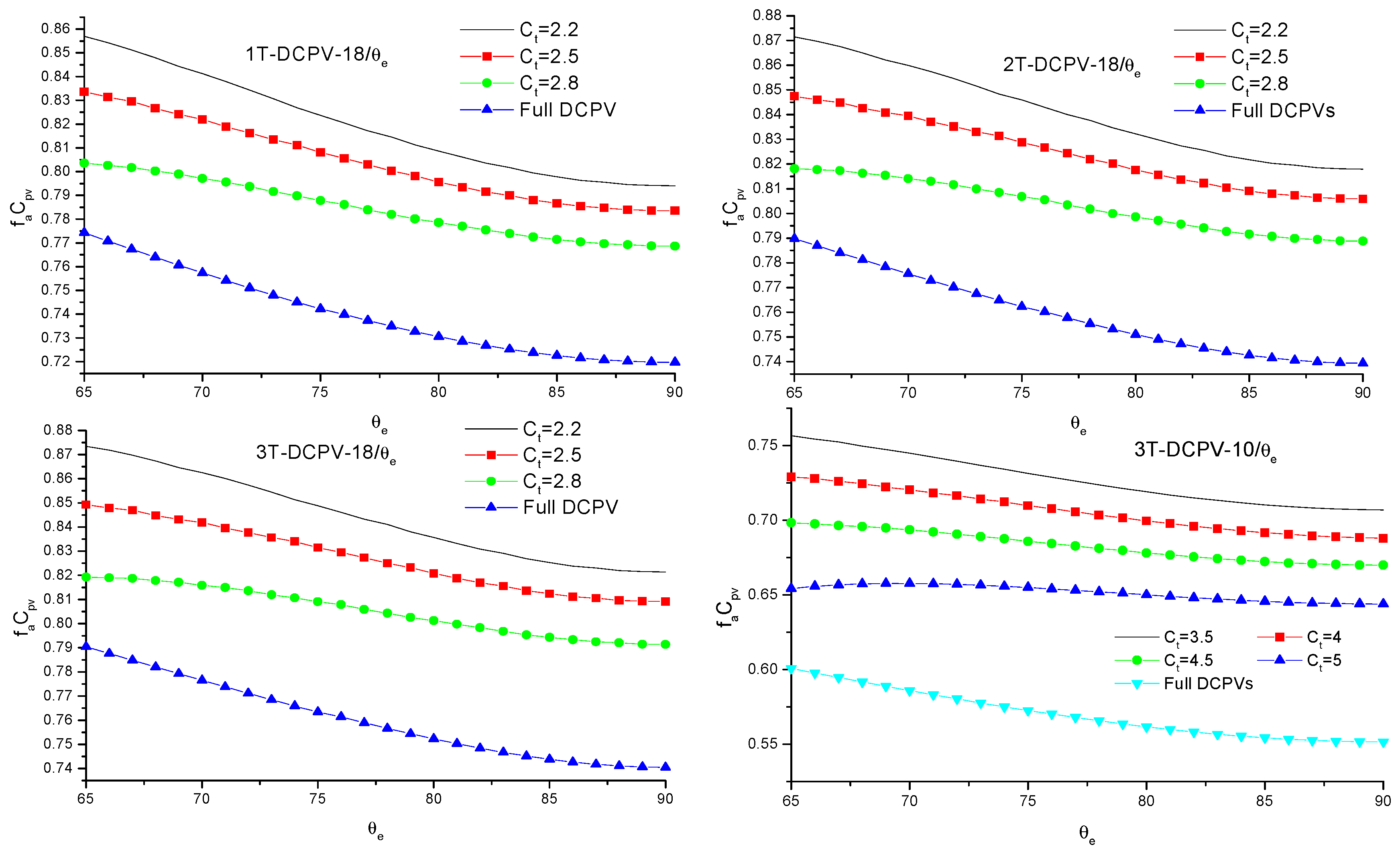
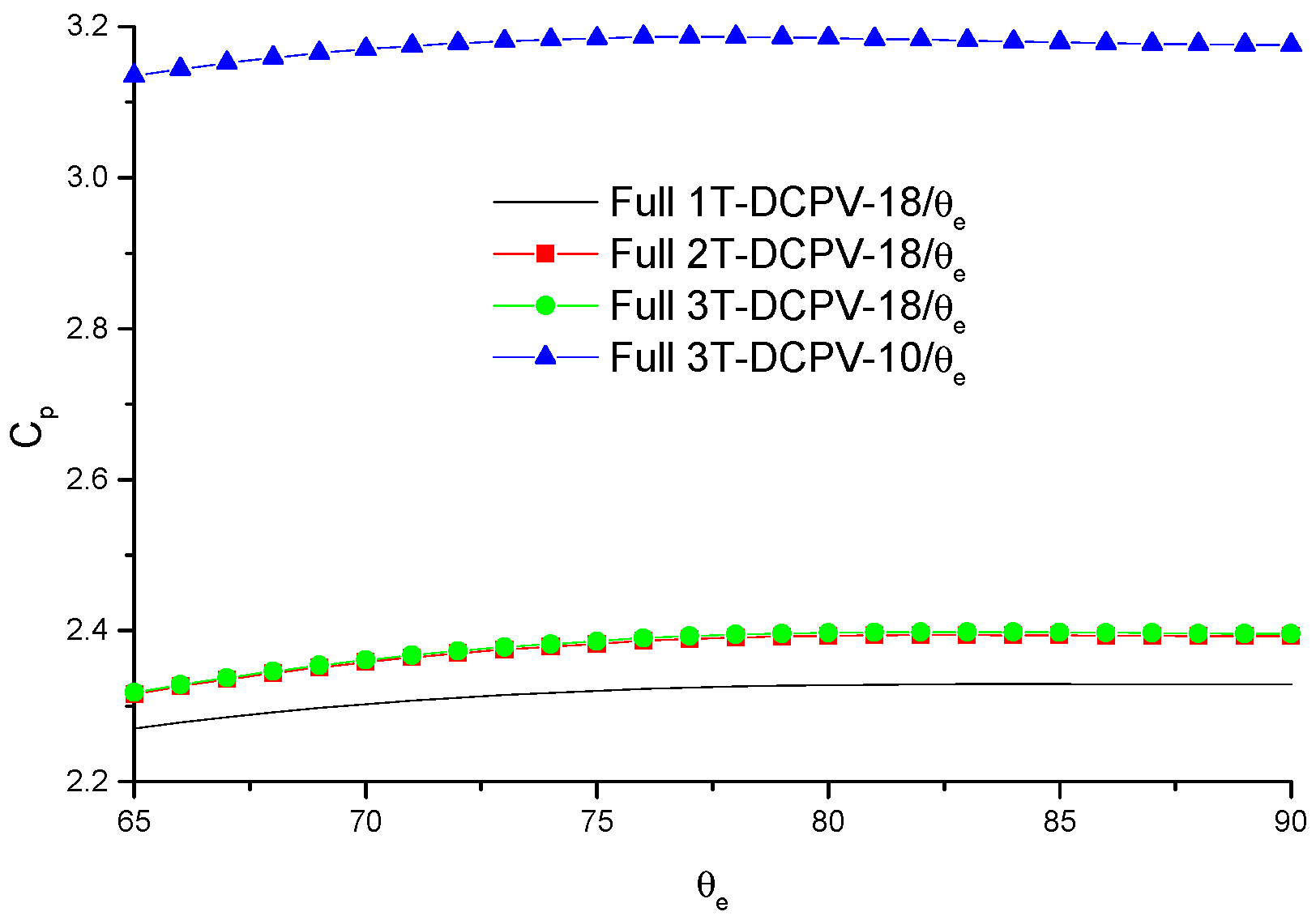
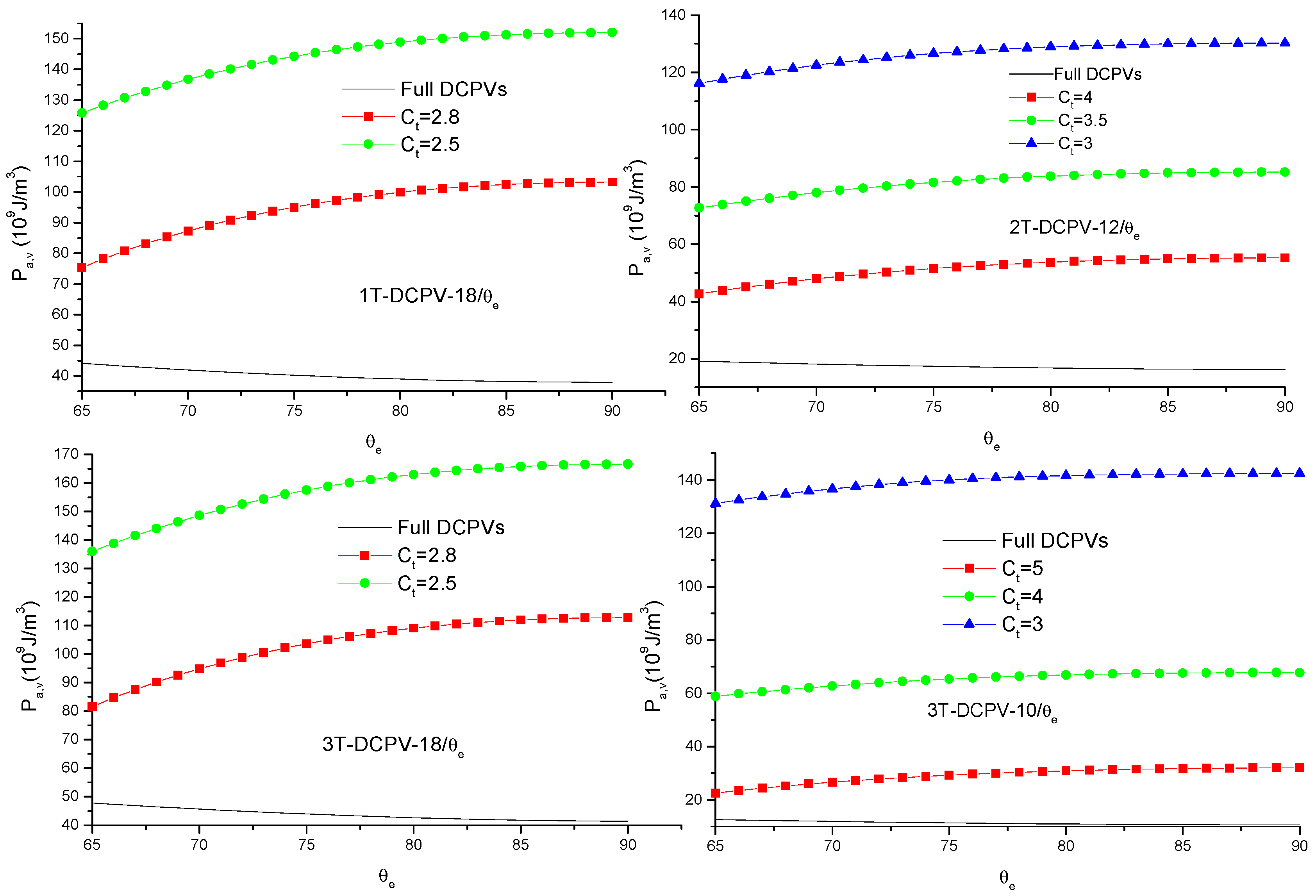
4.3. Photovoltaic Performance of DCPVs
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Glossary
| a | width of solar cells in DCPVs (m) |
| Ac | area of cross-section of DCVs (m2) |
| Ct | geometric concentration of DCPVs (dimensionless) |
| Cpv | ratio of annual average photovoltaic efficiency of solar cells for concentrated radiation to that of similar non-concentrating solar cells (dimensionless) |
| Cp | annual power output increase factor of DCPVs as compared to similar PV panel (dimensionless) |
| Cs | annual solar gain increase factor of DCPVs as compared to similar PV panel (dimensionless) |
| optical efficiency of DCPVs (dimensionless) | |
| annual average optical efficiency of DCPVs (dimensionless) | |
| H | daily radiation (J/m2) |
| h | height of DCPVs (m) |
| I | collectible radiation or radiation intensity (W/m2) |
| k | extinction coefficient of dielectric material (1/m) |
| L | path length of solar rays from the aperture to solar cells of DCPVs (m) |
| N | Day number counting from equinoxes |
| n | refractive index of dielectric (dimensionless) |
| unit vector of the normal to parabolic wall at point M | |
| unit vector of incident solar rays | |
| unit vector of refractive solar rays | |
| unit vector of solar ray reflecting from M on parabolic wall | |
| Pa | annual power output from DCPVs (MJ/m2) |
| Pa,v | annual power output per unit volume of dielectric from DCPVs (J/m3) |
| P0 | annual power output from similar PV panel (MJ/m2) |
| Sa | annual collectible radiation on solar cells of DCPVs (MJ/m2) |
| Sa() | annual collectible radiation on solar cells with (MJ/m2) |
| S0 | annual collectible radiation on aperture of DCPVs or similar PV panel (MJ/m2) |
| SL | annual radiation leakage of DCPVs (MJ/m2) |
| T | solar time (s) |
| x, z | x- and z-coordinates of any point on walls of DCPC (m) |
| : | tilt-angle adjustment of DCPVs’ aperture from site latitude (the unit of all angles is radians in mathematical expressions and degrees in the text) |
| tilt-angle of DCPVs’ aperture relative to horizon | |
| declination of the Sun | |
| declination of the Sun in the days when tilt-angle adjustment is made for 3T-DCPVs | |
| polar angle of any point on parabolic wall | |
| photovoltaic conversion efficiency of DCPVs | |
| photovoltaic efficiency of solar cells (dimensionless) | |
| tilt-angle of any line relative to x-axis | |
| site latitude | |
| acceptance half-angle of DCPCs | |
| critical incident angle for total internal reflection at dielectric-air interface | |
| maximum exit angle of DCPC-/for refractive radiation within | |
| incident angle of solar rays on the aperture of DCPCs | |
| incident angle of solar rays on solar cells | |
| incident angle of solar ray at point M of parabolic wall of DCPCs | |
| Refractive angle of incident solar rays on the aperture | |
| : | Refractive angle of incident solar rays at solar-noon |
| exit angle of solar ray reflecting from M | |
| projected angle of refractive solar rays on the cross-section of DCPV | |
| edge-ray angle of truncated DCPCs | |
| reflectivity of solar ray on walls of DCPCs (dimensionless) | |
| opening angle of V concentrator formed by two plane walls of DCPCs | |
| transmittance of sola ray on the aperture (dimensionless) | |
| transmittance of solar ray from aperture to solar cells due to solar absorption (dimensionless) | |
| hour angle |
| abs | absorber of DCPC |
| ap | aperture |
| b | beam radiation |
| c | critical value |
| d | sky diffuse radiation |
| i | incident solar ray |
| L | radiation loss due to leakage |
| r | refractive ray; |
| pl | plane wall |
References
- Koussa, M.; Cheknane, A.; Hadji, S.; Haddadi, M.; Noureddine, S. Measured and modelled improvement in solar energy yield from flat plate photovoltaic systems utilizing different tracking systems and under a range of environmental conditions. Appl. Energy 2011, 88, 1756–1771. [Google Scholar] [CrossRef]
- Li, Z.; Liu, X.; Tang, R. Optical performance of inclined south-north single-axis tracked solar panels. Energy 2010, 35, 2511–2516. [Google Scholar] [CrossRef]
- Jaaz, A.H.; Hassan, H.A.; Sopian, K.; Ruslan, M.H.B.H.; Zaidi, H. Design and development of compound concentrating for photovoltaic solar collector: Review. Renew. Sustain. Energy Rev. 2017, 76, 1108–1121. [Google Scholar] [CrossRef]
- Chong, K.K.; Lao, S.L.; Yew, T.K.; Tan, P.C.L. Design and development in optics of concentrator photovoltaic system. Renew. Sustain. Energy Rev. 2013, 19, 598–612. [Google Scholar] [CrossRef]
- Mallick, T.K.; Eames, P.C.; Hyde, T.J.; Norton, B. The design and experimental characterization of an asymmetric compound parabolic photovoltaic concentrator for building façade integration in the UK. Sol. Energy 2004, 77, 319–327. [Google Scholar] [CrossRef]
- Mallick, T.K.; Eames, P.C.; Norton, B. Non-concentrating and asymmetric compound parabolic concentrating building façade integrated photovoltaic: An experimental comparison. Sol. Energy 2006, 80, 834–849. [Google Scholar] [CrossRef]
- Mallick, T.K.; Eames, P.C. Design and fabrication of low concentrating second generation PRIDE concentrator. Sol. Energy Mater. Sol. Cells 2007, 91, 597–608. [Google Scholar] [CrossRef]
- Brogren, M.; Wennerberg, J.; Kapper, R.; Karlsson, B. Design of concentrating elements with CIS thin-film solar cells for façade integration. Sol. Energy Mater. Sol. Cells 2003, 75, 567–575. [Google Scholar] [CrossRef]
- Yousef, M.S.; Rahman, A.K.A.; Ookawara, S. Performance investigation of low–Concentration photovoltaic systems under hot and arid conditions: Experimental and numerical results. Energy Convers. Manag. 2016, 128, 82–94. [Google Scholar] [CrossRef]
- Tang, R.; Wang, J. A note on multiple reflections of radiation within CPCs and its effect on calculations of energy collection. Renew. Energy 2013, 57, 490–496. [Google Scholar] [CrossRef]
- Royne, A.; Dey, C.R.; Mills, D.R. Cooling of photovoltaic cells under concentrated illumination: A critical review. Sol. Energy Mater. Sol. Cells 2005, 86, 451–483. [Google Scholar] [CrossRef]
- Yu, Y.; Tang, R.; Xia, C. Irradiation distribution on solar cells inside CPCs with a restricted exit angle. Adv. Mater. Res. 2012, 588, 603–607. [Google Scholar] [CrossRef]
- Tang, J.; Yu, Y.; Tang, R. A three-dimensional radiation transfer model to evaluate performance of compound parabolic concentrator-based photovoltaic systems. Energies 2018, 11, 896. [Google Scholar] [CrossRef]
- Baig, H.; Heasman, K.C.; Mallick, T.K. Non-uniform illumination in concentrating solar cells. Renew. Sustain. Energy Rev. 2012, 16, 5890–5909. [Google Scholar] [CrossRef]
- Hatwaambo, S.; Hakansson, H.; Nilsson, J.; Karlsson, B. Angular characterization of low concentrating PV-CPC using low-cost reflectors. Sol. Energy Mater. Sol. Cells 2008, 92, 1347–1351. [Google Scholar] [CrossRef]
- Hatwaambo, S.; Hakansson, H.; Roos, A.; Karlsson, B. Mitigating the non-uniform illumination in low concentrating CPCs using structured reflectors. Sol. Energy Mater. Sol. Cells 2009, 93, 2020–2024. [Google Scholar] [CrossRef]
- Yu, Y.; Tang, R. Diffuse reflections within CPCs and its effect on energy collection. Sol. Energy 2015, 120, 44–54. [Google Scholar] [CrossRef]
- Tang, F.; Li, G.; Tang, R. Design and optical performance of CPC based compound plane concentrators. Renew. Energy 2016, 95, 140–151. [Google Scholar] [CrossRef]
- Baig, H.; Sarmah, N.; Chemisana, D.; Rosell, J.; Mallick, T.K. Enhancing performance of a linear dielectric based concentrating photovoltaic system using a reflective film along the edgy. Energy 2014, 73, 177–191. [Google Scholar] [CrossRef]
- Yu, Y.; Liu, N.; Li, G.; Tang, R. Performance comparison of CPCs with and without exit angle restriction for concentrating radiation on solar cells. Appl. Energy 2015, 155, 284–293. [Google Scholar] [CrossRef]
- Bahaidarah, H.M.; Gandhidasan, P.; Baloch, A.A.B.; Tanweer, B.; Mahmood, M. A comparative study on the effect of glazing and cooling for compound parabolic concentrator PV systems: Experimental and analytical investigations. Energy Convers. Manag. 2016, 129, 227–239. [Google Scholar] [CrossRef]
- Bahaidarah, H.M.; Tanweer, B.; Gandhidasan, P.; Ibrahim, N.; Rehman, S. Experimental and numerical study on non-concentrating and symmetric unglazed compound parabolic photovoltaic concentration systems. Appl. Energy 2014, 136, 527–536. [Google Scholar] [CrossRef]
- Brogren, M.; Nostell, P.E.R.; Karlsson, B. Optical efficiency of a PV–thermal hybrid CPC module for high latitudes. Sol. Energy 2001, 69, 173–185. [Google Scholar] [CrossRef]
- Elsafi, A.M.; Gandhidasan, P. Comparative study of double-pass flat and compound parabolic concentrated photovoltaic–thermal systems with and without fins. Energy Convers. Manag. 2015, 98, 59–68. [Google Scholar] [CrossRef]
- Baig, H.; Siviter, J.; Li, W.; Paul, M.C.; Montecucco, A.; Rollley, M.H.; Sweet, T.K.N.; Gao, M.; Mullen, P.A.; Fernandez, E.F.; et al. Conceptual design and performance evaluate of a hybrid concentrating photovoltaic system in preparation for energy. Energy 2018, 147, 547–560. [Google Scholar] [CrossRef]
- Su, Y.H.; Pei, G.; Riffat, B.; Huang, H.L. A novel lens-walled compound parabolic concentrator for photovoltaic applications. J. Sol. Energy Eng. 2012, 134, 021010. [Google Scholar] [CrossRef]
- Li, G.Q.; Pei, G.; Su, Y.H.; Ji, J.; Riffat, R. Experiment and simulation study on the flux distribution of lens-walled compound parabolic concentrator compared with mirror compound parabolic concentrator. Energy 2013, 58, 98–403. [Google Scholar]
- Rabl, A.; Winston, R. Ideal concentration for finite sources and restricted exit angle. Appl. Opt. 1976, 15, 2880–2883. [Google Scholar] [CrossRef] [PubMed]
- Yu, M.; Yu, Y.; Tang, R. Angular distribution of annual collectible radiation on solar cells of CPC based photovoltaic systems. Sol. Energy 2016, 135, 827–839. [Google Scholar] [CrossRef]
- Winston, R. Dielectric compound parabolic concentrators. Appl. Opt. 1976, 15, 291–292. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Tang, J.; Tang, R. A note on design of linear dielectric compound parabolic concentrators. Sol. Energy 2018, 171, 500–507. [Google Scholar] [CrossRef]
- Muhammad-Sukki, F.; Abu-Bakar, S.H.; Ramirez-Iniguez, R.; McMeekin, S.G.; Stewart, B.G.; Munir, A.B.; Yasin, S.H.M.; Rahim, R.A. Performance analysis of a mirror symmetrical dielectric totally internally reflecting concentrator for building integrated photovoltaic systems. Appl. Energy 2013, 111, 288–299. [Google Scholar] [CrossRef] [Green Version]
- Sellami, N.; Mallick, T.K. Optical efficiency study of PV crossed compound parabolic concentrator. Appl. Energy 2013, 102, 868–876. [Google Scholar] [CrossRef]
- Baig, H.; Sellami, N.; Mallick, T.K. Performance modeling and testing of a building integrated concentrating photovoltaic (BICPV) system. Sol. Energy Mater. Sol. Cells 2015, 134, 29–44. [Google Scholar] [CrossRef]
- Zacharopoulos, A.; Eames, P.C.; Mclarnon, D.; Norton, B. Linear dielectric non-imaging concentrating covers for PV integrated building facades. Sol. Energy 2000, 68, 439–452. [Google Scholar] [CrossRef]
- Brunotte, M.; Geotzberger, A.; Blieske, U. Two-stage concentrator permitting concentration up to 300× with one-axis tracking. Sol. Energy 1996, 56, 285–300. [Google Scholar] [CrossRef]
- Hein, M.; Dimroth, F.; Siefer, G.; Bett, A.W. Characterisation of a 300× photovoltaic concentrator system with one-axis tracking. Sol. Energy Mater. Sol. Cells 2003, 75, 277–283. [Google Scholar] [CrossRef]
- Pei, G.; Li, G.Q.; Su, Y.H.; Ji, J.; Riffat, R.; Zheng, H.F. Preliminary ray tracing and experimental study on the effect of mirror coating on the optical efficiency of a solid dielectric compound parabolic concentrator. Energies 2012, 5, 3627–3639. [Google Scholar] [CrossRef]
- Baig, H.; Sarmah, N.; Heasman, K.C.; Mallick, T.K. Numerical modelling and experimental validation of a low concentrating photovoltaic system. Sol. Energy Mater. Sol. Cells 2013, 113, 201–219. [Google Scholar] [CrossRef]
- Rabl, A. Active Solar Collectors and Their Applications; Oxford University Press: Oxford, UK, 1985. [Google Scholar]
- Rabl, A. Comparison of solar concentrators. Sol. Energy 1976, 18, 93–111. [Google Scholar] [CrossRef]
- Khonkar, H.E.I.; Sayigh, A.A.M. Raytrace for compound parabolic concentrator. Sol. Energy 1994, 5, 376–383. [Google Scholar] [CrossRef]
- Tang, R.; Wu, M.; Yu, Y.; Li, M. Optical performance of fixed east-west aligned CPCs used in China. Renew. Energy 2010, 35, 1837–1841. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, J.; Tang, R. Design and optical performance of CPCs with evacuated tube as receivers. Energies 2016, 9, 759. [Google Scholar] [CrossRef]
- Yu, X.; Su, Y.H. A discussion of inner south projection angle for performance analysis of dielectric compound parabolic concentrator. Sol. Energy 2015, 113, 101–113. [Google Scholar] [CrossRef] [Green Version]
- Yu, Y.; Liu, N.; Tang, R. Optical performance of CPCs for concentrating solar radiation on flat receivers with a restricted incidence angle. Renew. Energy 2014, 62, 679–688. [Google Scholar] [CrossRef]
- Li, W.; Pau, M.C.; Sellami, N.; Sweet, T.; Montecucco, A.; Siviter, J.; Baig, H. Six-parameter electrical model for photovoltaic cell/module with compound concentrator. Sol. Energy 2016, 137, 551–563. [Google Scholar] [CrossRef]
- Tang, R.; Liu, X. Optical performance and design optimization of V-trough concentrators for photovoltaic applications. Sol. Energy 2011, 85, 2154–2166. [Google Scholar] [CrossRef]
- Chen, Z.Y. The Climatic Summarization of Yunnan; Weather Publishing House: Beijing, China, 2001. [Google Scholar]
- Collares-Pereira, M.; Rabl, A. The average distribution of solar radiation: correlations between diffuse and hemispherical and between hourly and daily insolation values. Sol. Energy 1979, 22, 155–164. [Google Scholar] [CrossRef]
- Carvalho, M.J.; Collares-Pereira, M.; Gordon, J.M.; Rabl, A. Truncation of CPC solar collectors and its effect on energy collection. Sol. Energy 1985, 35, 393–399. [Google Scholar] [CrossRef]
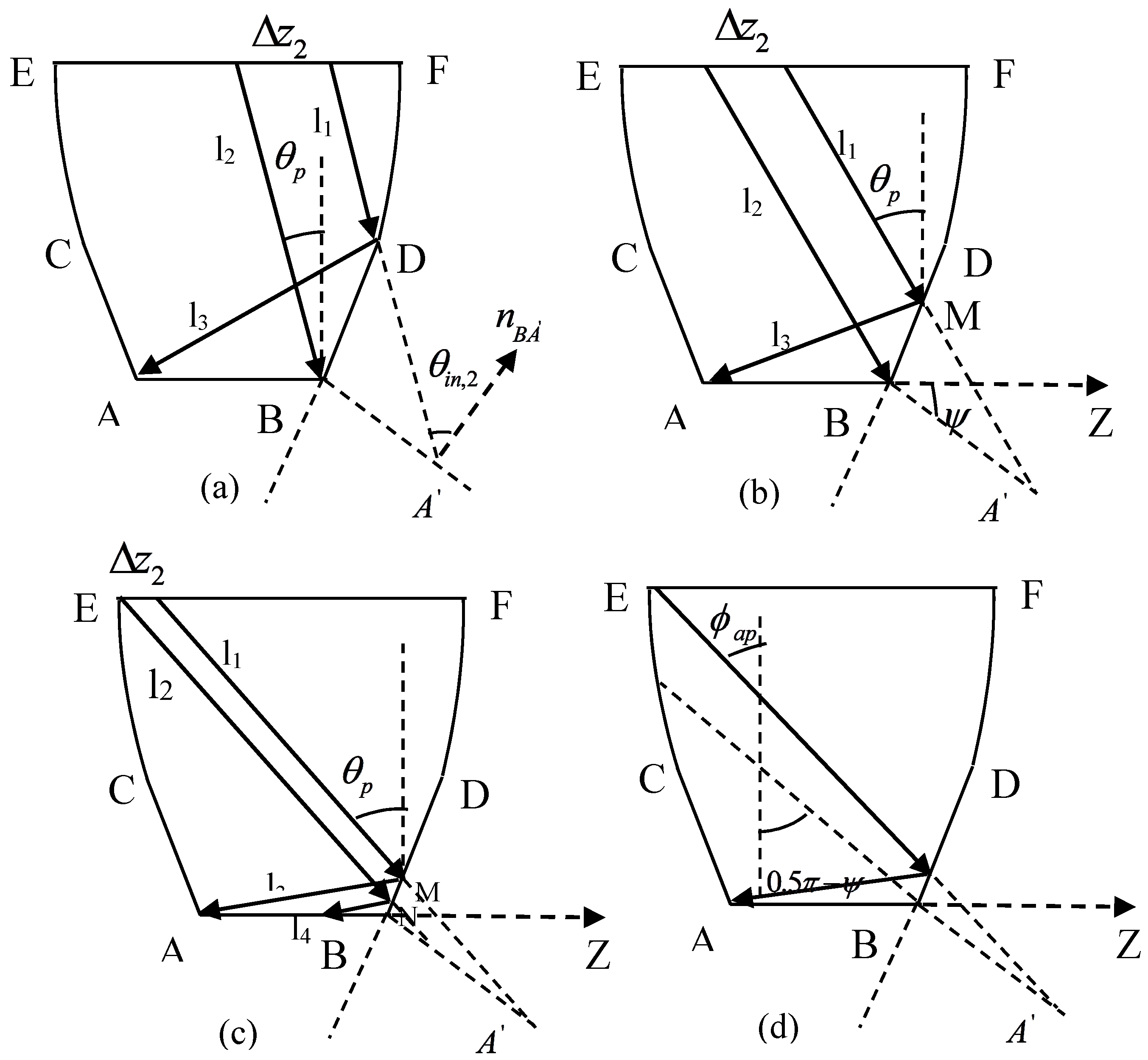






© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, G.; Tang, J.; Tang, R. A Theoretical Study on Performance and Design Optimization of Linear Dielectric Compound Parabolic Concentrating Photovoltaic Systems. Energies 2018, 11, 2454. https://doi.org/10.3390/en11092454
Li G, Tang J, Tang R. A Theoretical Study on Performance and Design Optimization of Linear Dielectric Compound Parabolic Concentrating Photovoltaic Systems. Energies. 2018; 11(9):2454. https://doi.org/10.3390/en11092454
Chicago/Turabian StyleLi, Guihua, Jingjing Tang, and Runsheng Tang. 2018. "A Theoretical Study on Performance and Design Optimization of Linear Dielectric Compound Parabolic Concentrating Photovoltaic Systems" Energies 11, no. 9: 2454. https://doi.org/10.3390/en11092454




