Simulation of Fluid-Thermal Field in Oil-Immersed Transformer Winding Based on Dimensionless Least-Squares and Upwind Finite Element Method
Abstract
:1. Introduction
2. Mathematical Foundation of LSFEM
2.1. Governing Equations
2.2. Conventional Scheme of LSFEM
2.3. Dimensionless Scheme of LSFEM
2.4. Preconditioning and Iterative Solution Method
3. Verification by Fluid-Thermal Coupling Problem
3.1. Transformer Winding Model
3.2. Velocity Distribution Analysis
3.3. Temperature Distribution Analysis
- (1)
- Since the indirect coupling method proposed in this paper is a combination of the dimensionless LSFEM and UFEM, while Fluent software is based on FVM, the different principle of FEM and FVM could result in some deviations.
- (2)
- Different methods are adopted to deal with boundary conditions by FEM and FVM, which could bring some influence on the calculation results.
- (3)
- There are eight nodes per element for solving the fluid field by the LSFEM, while nine nodes per element to solve the thermal field by the UFEM, which adopts the second-order element. In contrast, Fluent software adopts the linear element. So their interpolation methods are different.
3.4. Convergence Analysis
- (1)
- Among these three calculation methods, the convergence rate of the dimensionless LSFEM scheme is the fastest, followed by the Fluent software based on the FVM, and finally the conventional LSFEM. In fact, the convergence rates of the latter two methods are very close.
- (2)
- During the convergence process, the residuals of dimensionless and conventional LSFEM schemes are much smaller than those of the Fluent software. The smallest residuals can be obtained by the dimensionless LSFEM scheme while the residuals of the Fluent software are the largest.
4. Conclusions
- (1)
- Taking the results obtained by Fluent as a reference, the relative error of outlet velocity of the local winding computed by LSFEM is about 0.4%. The temperature difference between the upwind FEM and Fluent is less than 0.7 K. The LSFEM is stable and the numerical oscillations can be avoided without adding additional upwind schemes.
- (2)
- The combination of JPCGM and TSEM can effectively reduce the condition number of the equations and handle the ill-conditioned problems of the stiffness matrix. The larger the penalty functions, the larger the condition number of equations. It should be pointed out that the condition number can be reduced to the same value by preconditioning.
- (3)
- Compared with the FVM, the algorithm obtained by the dimensionless LSFEM scheme has better robustness, faster convergence, and lower residuals.
Author Contributions
Funding
Conflicts of Interest
References
- Heathcote, M.J. The J & P Transformer Book; Johnson & Phillips Ltd.: Karachi, Pakistan, 2007; pp. 121–187. [Google Scholar]
- Higaki, M.; Kako, Y.; Moriyama, M.; Hirano, M.; Hiraishi, K.; Kurita, K. Static electrification and partial discharges caused by oil flow in forced oil cooled core type transformers. IEEE Trans. Power Appar. Syst. 1979, 98, 1259–1267. [Google Scholar] [CrossRef]
- Wang, X.C.; Tao, J.P. Temperature field research of large forced-directed oil cooling transformer. Transformer 2008, 7, 6–10. [Google Scholar]
- Sen, P.K.; Pansuwan, S. Overloading and loss-of-life assessment guidelines of oil-cooled transformers. In Proceedings of the 2001 Rural Electric Power Conference, Little Rock, AR, USA, 29 April–1 May 2001; pp. B4/1–B4/8. [Google Scholar]
- Sefidgaran, M.; Mirzaie, M.; Ebrahimzadeh, A. Reliability model of the power transformer with ONAF cooling. Int. J. Electr. Power Energy Syst. 2011, 35, 97–104. [Google Scholar] [CrossRef]
- Krause, C. Power Transformer insulation-history, technology and design. IEEE Trans. Dielectr. Electr. Insul. 2012, 19, 1941–1947. [Google Scholar] [CrossRef]
- Raeisian, L.; Niazmand, H.; Ebrahimnia-Bajestan, E.; Werle, P. Thermal management of a distribution transformer: an optimization study of the cooling system using CFD and response surface methodology. Int. J. Electr. Power Energy Syst. 2018, 104, 443–455. [Google Scholar] [CrossRef]
- IEEE. IEEE Guide for Loading Mineral-Oil-Immersed Transformers; IEEE: New York, NY, USA, 1996. [Google Scholar]
- Perez, J. Fundamental principles of transformer thermal loading and protection. In Proceedings of the 11th IET International Conference on Developments in Power Systems Protection, Birmingham, UK, 29 March–1 April 2012; pp. 1–6. [Google Scholar]
- Torriano, F.; Chaaban, M.; Picher, P. Numerical study of parameters affecting the temperature distribution in a disc-type transformer winding. Appl. Therm. Eng. 2010, 30, 2034–2044. [Google Scholar] [CrossRef]
- Gong, R.H.; Ruan, J.J.; Chen, J.Z.; Quan, Y.; Wang, J. Analysis and experiment of hot-spot temperature rise of 110 kV three-phase three-limb transformer. Energies 2017, 10, 1079. [Google Scholar] [CrossRef]
- Kranenborg, E.J.; Olsson, C.O.; Samuelsson, B.R.; Lundin, L.Å.; Missing, R.M. Numerical study on mixed convection and thermal streaking in power transformer windings. In Proceedings of the 5th European Thermal-Sciences Conference, Eindhoven, The Netherlands, 18–22 May 2008. [Google Scholar]
- Skillen, A.; Revell, A.; Iacovides, H.; Wu, W. Numerical prediction of local hot-spot phenomena in transformer windings. Appl. Therm. Eng. 2012, 36, 96–105. [Google Scholar] [CrossRef]
- Bengang, W.; Hua, H.; Junshang, L.; Nannan, W.; Mingqiu, D.; Tianyi, J. Three dimensional simulation technology research of split type cooling transformer based on finite volume method. Energy Procedia 2017, 141, 405–410. [Google Scholar] [CrossRef]
- Chen, W.; Su, X.; Sun, C.; Pan, C.; Tang, J. Temperature distribution calculation based on FVM for oil-immersed power transformer windings. Electr. Power Autom. Equip. 2011, 31, 23–27. [Google Scholar]
- Guo, R.; Lou, J.; Wang, Z.; Huang, H.; Wei, B.; Zhang, Y. Simulation and analysis of temperature field of the discrete cooling system transformer based on FLUENT. In Proceedings of the 2017 1st International Conference on Electrical Materials and Power Equipment, Xi’an, China, 14–17 May 2017; pp. 287–291. [Google Scholar]
- Tsili, M.A.; Amoiralis, E.I.; Kladas, A.G.; Souflaris, A.T. Power transformer thermal analysis by using an advanced coupled 3D heat transfer and fluid flow FEM model. Int. J. Therm. Sci. 2012, 53, 188–201. [Google Scholar] [CrossRef]
- Li, L.; Niu, S.; Ho, S.L.; Fu, W.N.; Li, Y. A novel approach to investigate the hot-spot temperature rise in power transformers. IEEE Trans. Magn. 2015, 51, 1–4. [Google Scholar]
- Amoiralis, E.I.; Tsili, M.A.; Kladas, A.G.; Souflaris, A.T. Geometry optimization of power transformer cooling system based on coupled 3D FEM thermal-CFD analysis. In Proceedings of the 2010 14th Biennial IEEE Conference on Electromagnetic Field Computation, Chicago, IL, USA, 9–12 May 2010. [Google Scholar]
- Torriano, F.; Campelo, H.; Quintela, M.; Labbé, P.; Picher, P. Numerical and experimental thermofluid investigation of different disc-type power transformer winding arrangements. Int. J. Heat Fluid Flow. 2018, 69, 62–72. [Google Scholar] [CrossRef]
- Córdoba, P.A.; Silin, N.; Osorio, D.; Dari, E. An experimental study of natural convection in a distribution transformer slice model. Int. J. Therm. Sci. 2018, 129, 94–105. [Google Scholar] [CrossRef]
- Arabul, A.Y.; Arabul, F.K.; Senol, I. Experimental thermal investigation of an ONAN distribution transformer by fiber optic sensors. Electr. Power Syst. Res. 2018, 155, 320–330. [Google Scholar] [CrossRef]
- Zhang, X.; Daghrah, M.; Wang, Z.; Liu, Q.; Jarman, P.; Negro, M. Experimental verification of dimensional analysis results on flow distribution and pressure drop for disc-type windings in od cooling modes. IEEE Trans. Power Deliv. 2018, 33, 1647–1656. [Google Scholar] [CrossRef]
- Godina, R.; Rodrigues, E.M.G.; Matias, J.C.O.; Catalão, J.P.S. Effect of loads and other key factors on oil-transformer ageing: Sustainability benefits and challenges. Energies 2015, 8, 12147–12186. [Google Scholar] [CrossRef]
- Ramos, J.C.; Beiza, M.; Gastelurrutia, J.; Rivas, A.; Antón, R.; Larraona, G.S. Numerical modelling of the natural ventilation of underground transformer substations. Appl. Therm. Eng. 2013, 51, 852–863. [Google Scholar] [CrossRef]
- Wang, L.; Zhou, L.; Tang, H.; Wang, D.; Cui, Y. Numerical and experimental validation of variation of power transformers’ thermal time constants with load factor. Appl. Therm. Eng. 2017, 126, 939–948. [Google Scholar] [CrossRef]
- Zhang, Y.; Ho, S.L.; Fu, W. Applying response surface method to oil-immersed transformer cooling system for design optimization. IEEE Trans. Magn. 2018, 1–5. [Google Scholar] [CrossRef]
- Liao, C.; Ruan, J.; Liu, C.; Wen, W.; Du, Z. 3-D coupled electromagnetic-fluid-thermal analysis of oil-immersed triangular wound core transformer. IEEE Trans. Magn. 2014, 50, 1–4. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, H.; Peng, Z.; Liu, P.; Zhang, T.; Hu, W. 3-D coupled electromagnetic-fluid-thermal analysis of epoxy impregnated paper converter transformer bushings. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 630–638. [Google Scholar] [CrossRef]
- Liu, Y.; Li, G.; Guan, L.; Li, Z. The single-active-part structure of the UHVDC converter transformer with the UHVAC power grid. CSEE J. Power Energy Syst. 2017, 3, 243–252. [Google Scholar] [CrossRef]
- Zhang, B.Z.; Yin, J.A.; Zhang, H.J. Numerical method of fluid mechanics. Mech. Eng. Press. 2003, 68–180. [Google Scholar]
- Hendriana, D.; Bathe, K. On upwind methods for parabolic finite elements in incompressible flows. Int. J. Numer. Methods Eng. 2015, 47, 317–340. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Taylor, R.L.; Nithiarasu, P. The Finite Element Method for Fluid Dynamics, 6th ed.; Elsevier Butterworth-Heinemann: Oxford, UK, 2005; pp. 525–537. [Google Scholar]
- Brooks, A.N.; Hughes, T.J.R. Streamline upwind/petrov-galerkin formulations for convection dominated flows with particular emphasis on the incompressible navier-stokes equations. Comput. Methods Appl. Mech. Eng. 2015, 32, 199–259. [Google Scholar] [CrossRef]
- Heinrich, J.C.; Huyakorn, P.S.; Zienkiewicz, O.C.; Mitchell, A.R. An ‘upwind’ finite element scheme for two-dimensional convective transport equation. Int. J. Numer. Methods Eng. 2010, 11, 131–143. [Google Scholar] [CrossRef]
- Liu, G.; Jin, Y.J.; Ma, Y.Q.; Wang, L.P.; Chi, C.; Li, L. Two-dimensional temperature field analysis of oil-immersed transformer based on non-uniformly heat source. High Volt. Eng. 2017, 43, 3361–3370. [Google Scholar]
- Wang, Y.Q.; Ma, L.; Lü, F.C.; Bi, J.G.; Wang, L.; Wan, T. Calculation of 3D temperature field of oil immersed transformer by the combination of the finite element and finite volume method. High Volt. Eng. 2014, 40, 3179–3185. [Google Scholar]
- Jiang, B.N. The least-squares finite element method. Int. J. Numer. Methods Eng. 1998, 54, 3591–3610. [Google Scholar]
- Bochev, P.B.; Gunzburger, M.D. Least-Squares Finite Element Methods; Springer: Berlin, Germany, 2009; pp. S23–S24. [Google Scholar]
- Pontaza, J.P. A least-squares finite element formulation for unsteady incompressible flows with improved velocity–pressure coupling. J. Comput. Phys. 2006, 217, 563–588. [Google Scholar] [CrossRef]
- Tao, S.; Yang, Z.; Jiang, B.; Gu, W.J. Application comparison of least square finite element method and finite volume method in CFD. Comput. Aided Eng. 2012, 21, 1–6. [Google Scholar]
- Xie, Y.Q.; Li, L.; Song, Y.W.; Wang, S.B. Multi-physical field coupled method for temperature rise of winding in oil-immersed power transformer. Proc. CSEE 2016, 36, 5957–5965. [Google Scholar]
- Xie, Y.Q. Study on flow field and temperature field coupling finite element methods in oil-immersed power transformer. Ph.D. Thesis, North China Electric Power University (Beijing), Beijing, China, July 2017. [Google Scholar]
- Fialko, S.Y.; Zeglen, F. Preconditioned conjugate gradient method for solution of large finite element problems on CPU and GPU. J. Telecommun. Inform. Technol. 2016, 2, 26–33. [Google Scholar]
- Wallot, J. XLIX. Dimensional analysis. Lond. Edinb. Dublin Philos. Mag. J. Sci. 2009, 3, 496. [Google Scholar] [CrossRef]
- Liu, C.S. A two-side equilibration method to reduce the condition number of an ill-posed linear system. Comput. Model. Eng. Sci. 2013, 91, 17–42. [Google Scholar]
- Liao, C.B.; Ruan, J.J.; Liu, C.; Wen, W.; Wang, S.S.; Liang, S.Y. Comprehensive analysis of 3-D electromagnetic-fluid-thermal fields of oil-immersed transformer. Electr. Power Autom. Equip. 2015, 35, 150–155. [Google Scholar]

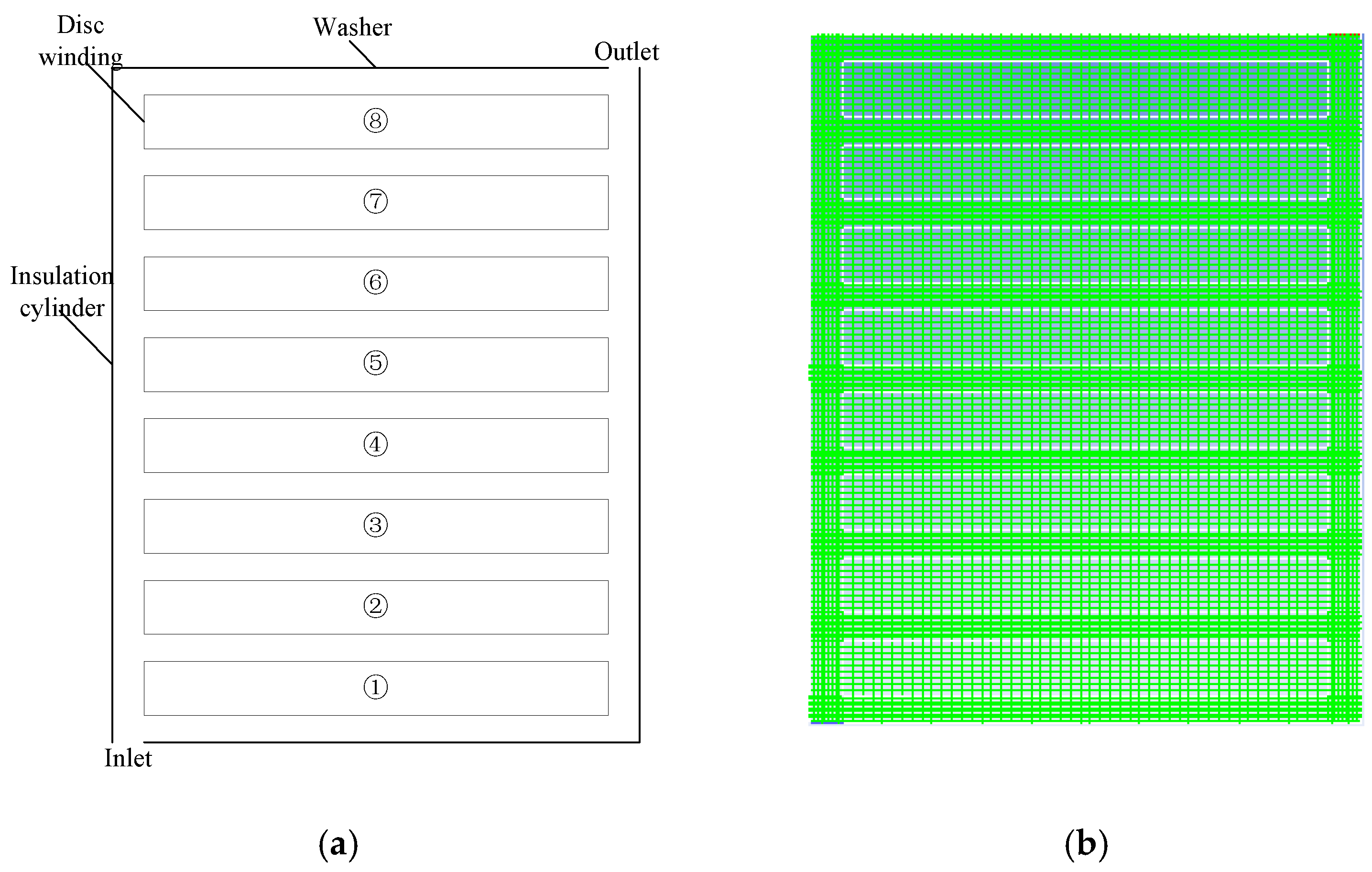
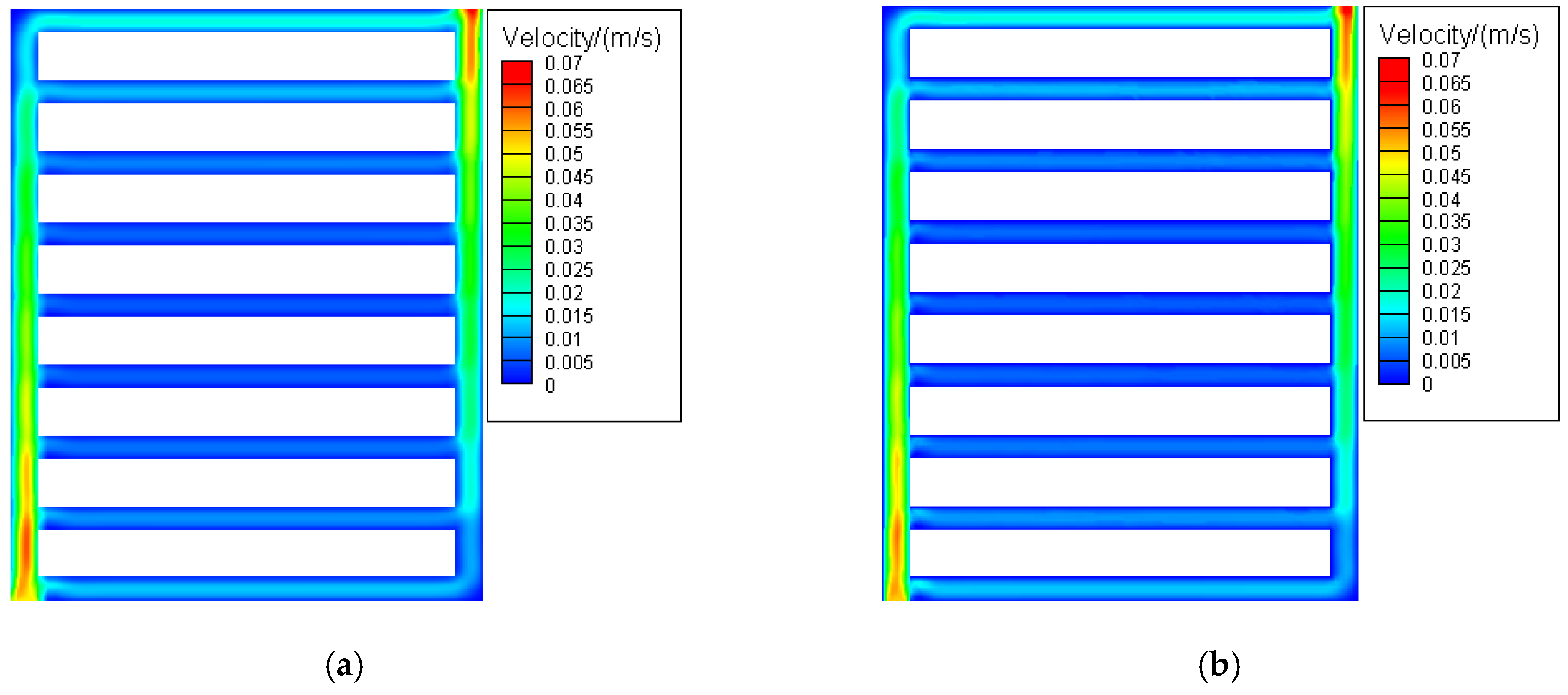

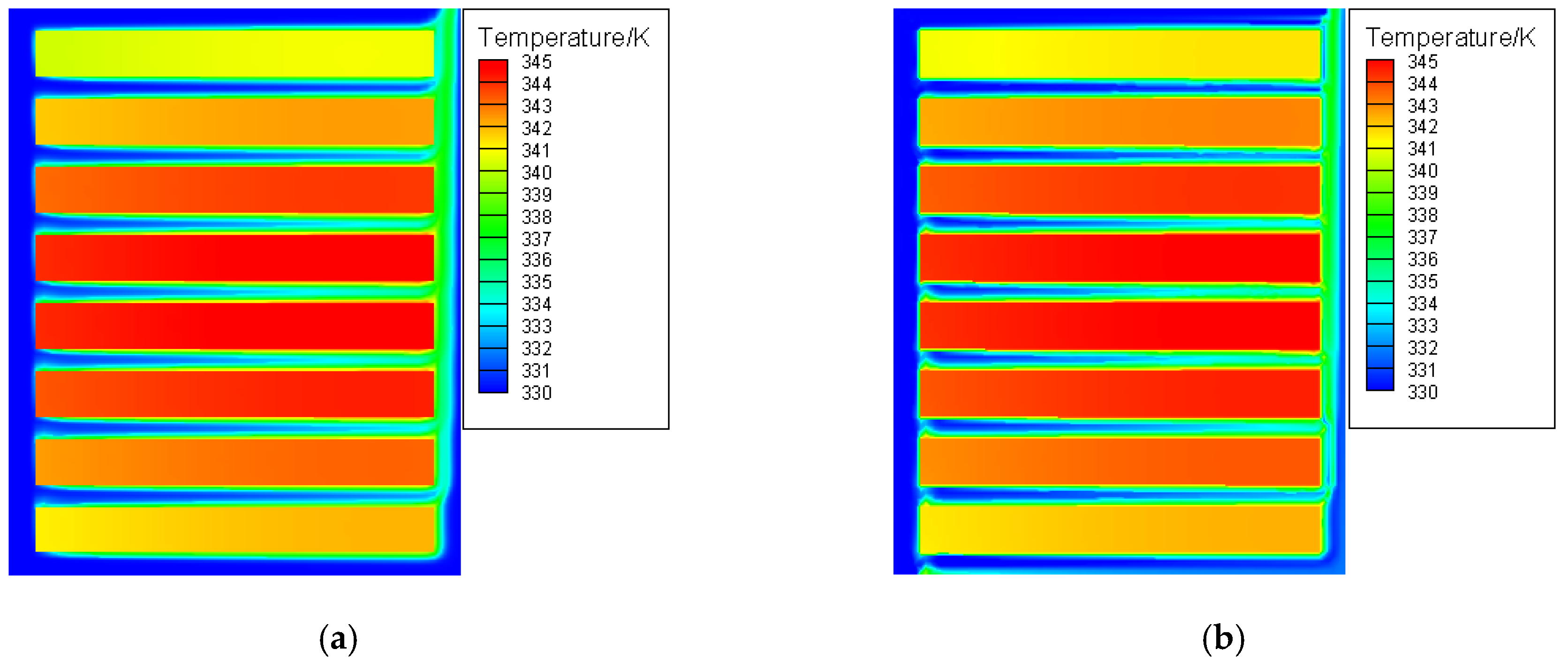

| Component | Size |
|---|---|
| Total Size of Model | 0.1 m × 0.125 m |
| Size of Disc | 0.088 m × 0.01 m |
| Length of Insulation Cylinder | 0.125 m |
| Length of Washer | 0.094 m |
| Width of Inlet | 0.06 m |
| Width of Outlet | 0.06 m |
| Materials | Physical Parameters | Function Fitting |
|---|---|---|
| Transformer oil | Density/kg·m−3 | 1098.72 − 0.712 T |
| Specific heat capacity/J·(kg·K)−1 | 807.163 + 3.58 T | |
| Heat conductivity/W·(m·K)−1 | 0.1509 − 7.101 × 10−5 T | |
| Viscosity/Pa·s | 0.0846 − 4 × 10−4T + 5 × 10−7 T2 | |
| Winding | Density/kg·m−3 | 8900 |
| Specific heat capacity/J·(kg·K)−1 | 381 | |
| Heat conductivity/W·(m·K)−1 | 387.6 |
| Sequence Number of Disc | Left 1/4 | Right 1/4 | ||||
|---|---|---|---|---|---|---|
| UFEM | Fluent | Error | UFEM | Fluent | Error | |
| 1 | 341.5 | 340.9 | +0.6 | 342.0 | 341.5 | +0.5 |
| 2 | 342.8 | 342.1 | +0.7 | 343.3 | 342.6 | +0.7 |
| 3 | 343.7 | 343.1 | +0.6 | 344.2 | 343.6 | +0.6 |
| 4 | 344.2 | 343.7 | +0.5 | 344.7 | 344.2 | +0.5 |
| 5 | 344.3 | 343.7 | +0.6 | 344.7 | 344.2 | +0.5 |
| 6 | 343.5 | 343.0 | +0.5 | 343.9 | 343.4 | +0.5 |
| 7 | 342.3 | 341.7 | +0.6 | 342.7 | 342.1 | +0.6 |
| 8 | 340.9 | 340.3 | +0.6 | 341.2 | 340.6 | +0.6 |
| Preconditioned Methods | JPCGM | JPCGM & TSEM | |||||
|---|---|---|---|---|---|---|---|
| Penalty Function Size | 104 | 106 | 108 | 108 | 108 | 108 | |
| Conventional Scheme | Condition Number 1 | 1.40 × 1018 | 1.40 × 1020 | 1.40 × 1022 | 1.88 × 1018 | 1.88 × 1020 | 1.88 × 1022 |
| Condition Number 2 | 9.89 × 109 | 1.13 × 108 | |||||
| Iteration Numbers | Misconvergence | 127 | 127 | 127 | |||
| Computation Time (s) | 618 | 614 | 621 | ||||
| Dimensionless Scheme | Condition Number 1 | 8.27 × 1012 | 8.23 × 1014 | 8.23 × 1016 | 8.27 × 1012 | 8.23 × 1014 | 8.23 × 1016 |
| Condition Number 2 | 2.55 × 107 | 2.55 × 107 | |||||
| Iteration Numbers | Convergence, wrong results | 24 | 24 | 24 | |||
| Computation Time (s) | 125 | 126 | 126 | ||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, G.; Zheng, Z.; Yuan, D.; Li, L.; Wu, W. Simulation of Fluid-Thermal Field in Oil-Immersed Transformer Winding Based on Dimensionless Least-Squares and Upwind Finite Element Method. Energies 2018, 11, 2357. https://doi.org/10.3390/en11092357
Liu G, Zheng Z, Yuan D, Li L, Wu W. Simulation of Fluid-Thermal Field in Oil-Immersed Transformer Winding Based on Dimensionless Least-Squares and Upwind Finite Element Method. Energies. 2018; 11(9):2357. https://doi.org/10.3390/en11092357
Chicago/Turabian StyleLiu, Gang, Zhi Zheng, Dongwei Yuan, Lin Li, and Weige Wu. 2018. "Simulation of Fluid-Thermal Field in Oil-Immersed Transformer Winding Based on Dimensionless Least-Squares and Upwind Finite Element Method" Energies 11, no. 9: 2357. https://doi.org/10.3390/en11092357





